Electromagnetic Control and Dynamics of Generalized Burgers’ Nanoliquid Flow Containing Motile Microorganisms with Cattaneo–Christov Relations: Galerkin Finite Element Mechanism
Abstract
1. Introduction
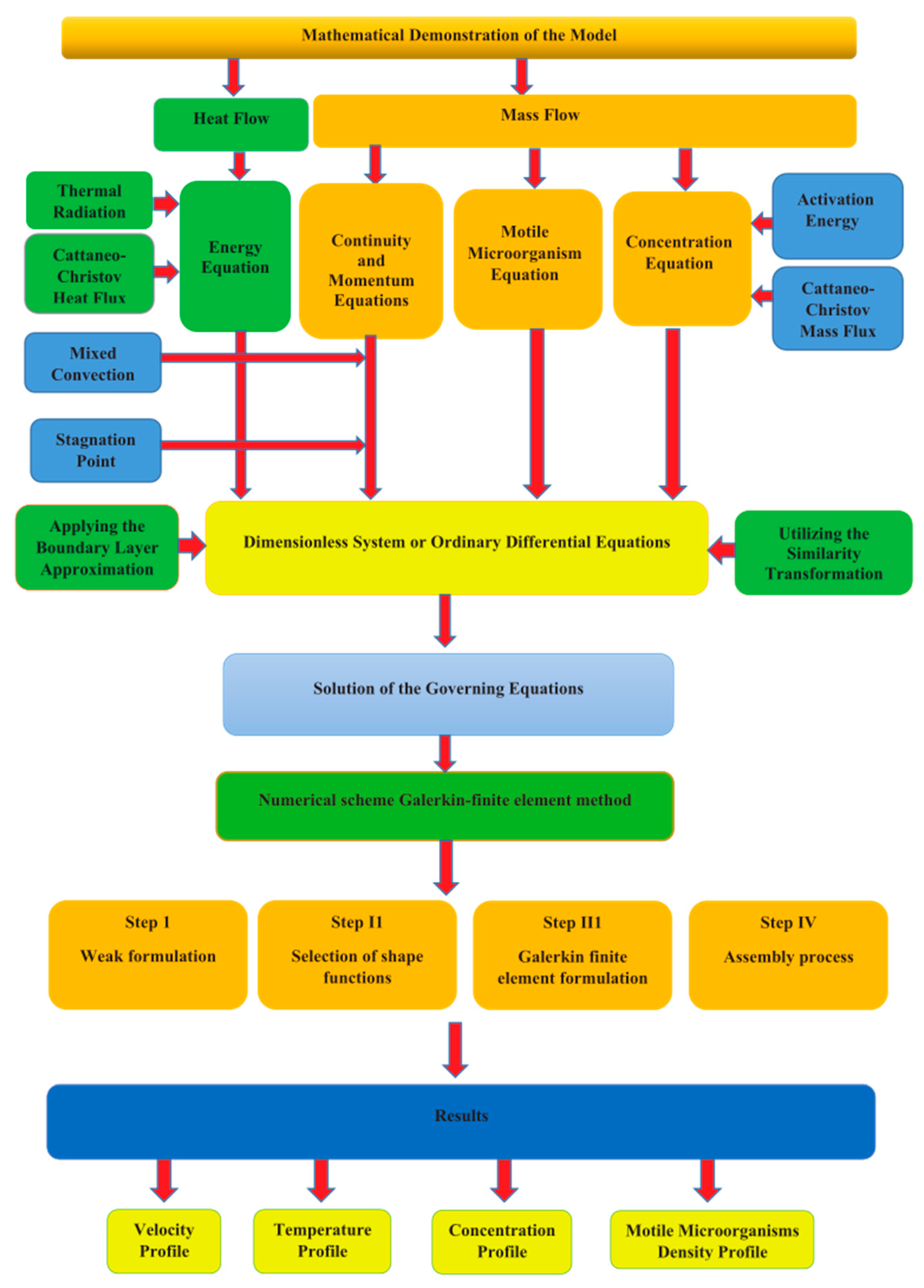
2. Governing Equations and Material
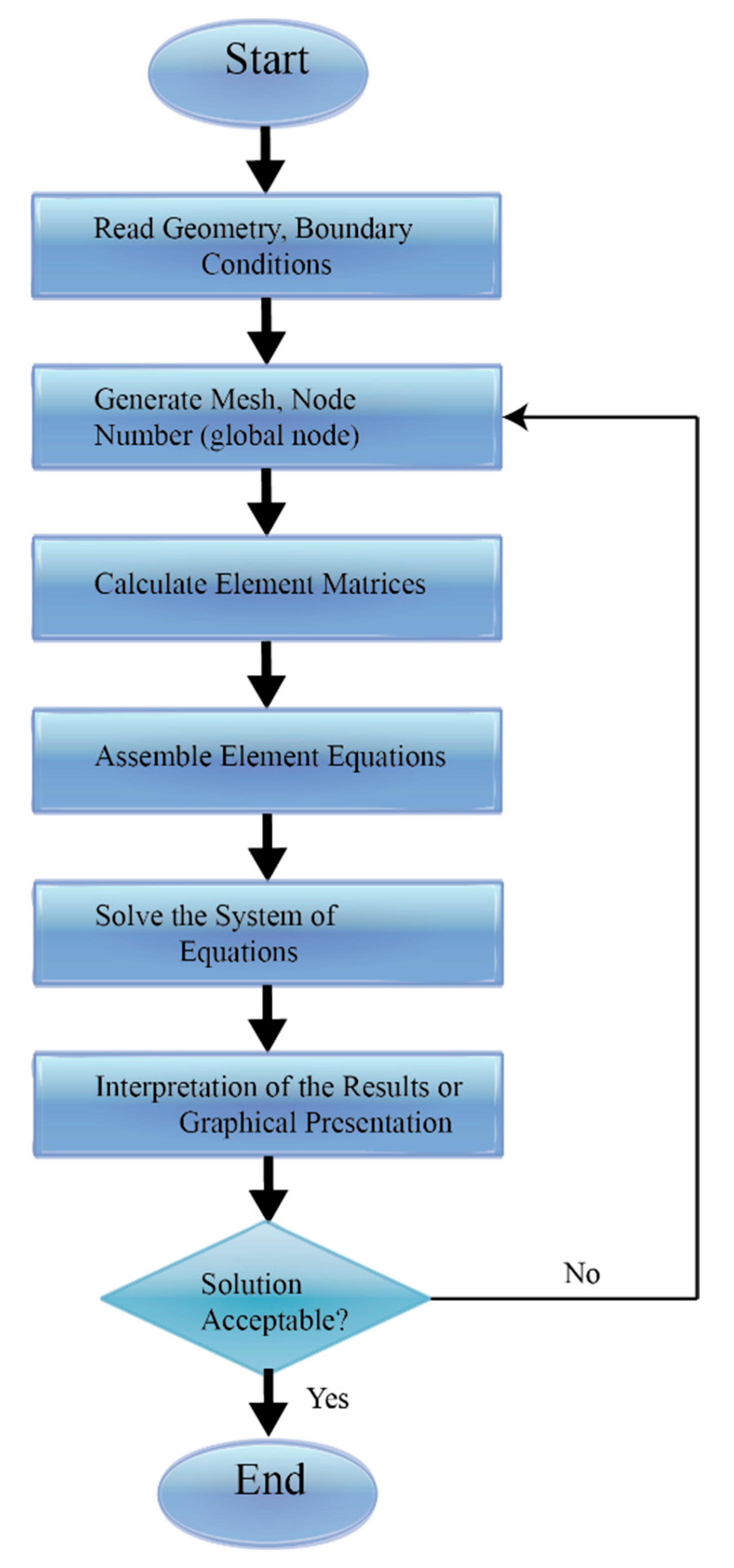
3. Galerkin Finite Element TechniqueGalerkin Finite Element Technique
4. Validity of Code
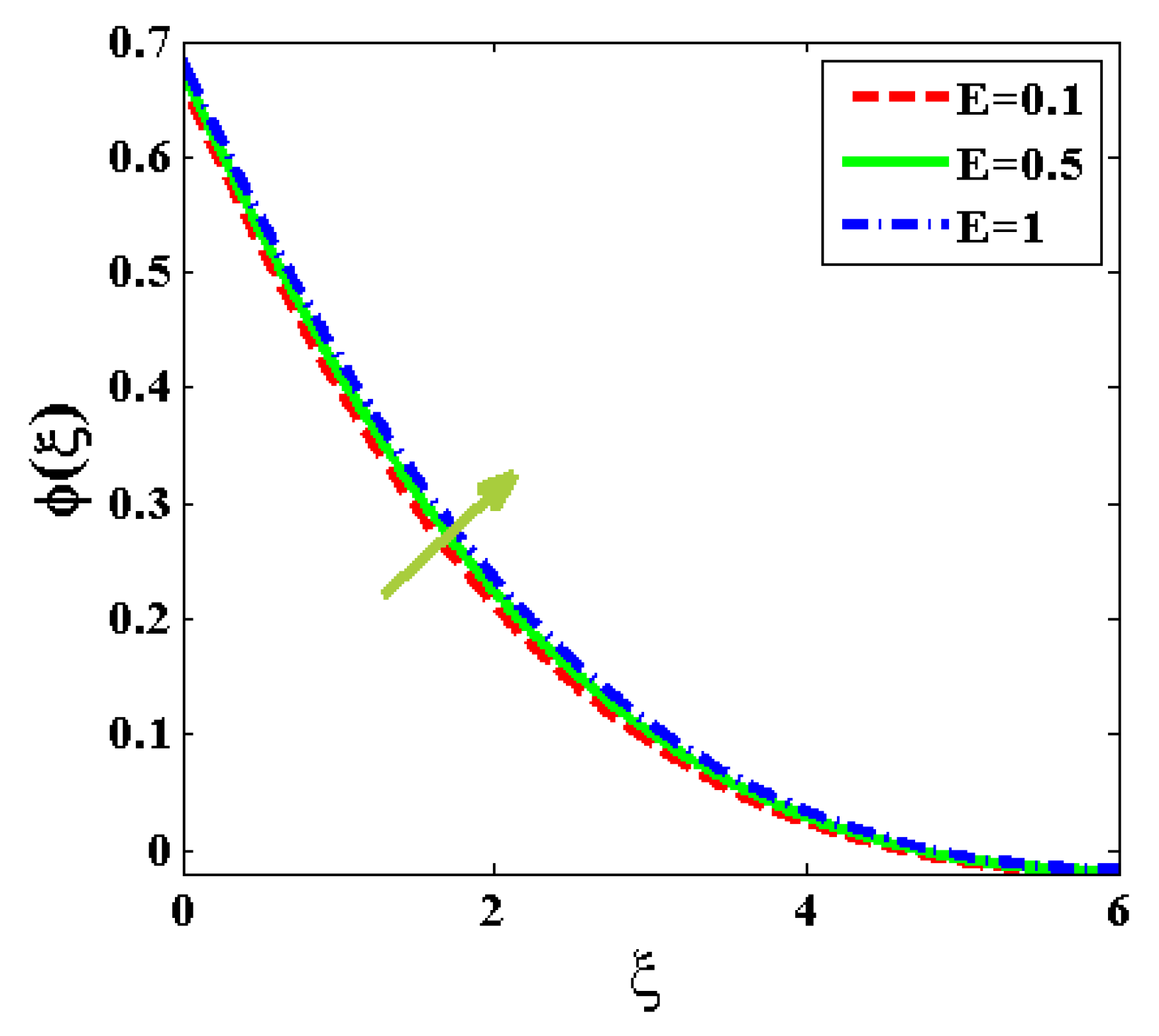
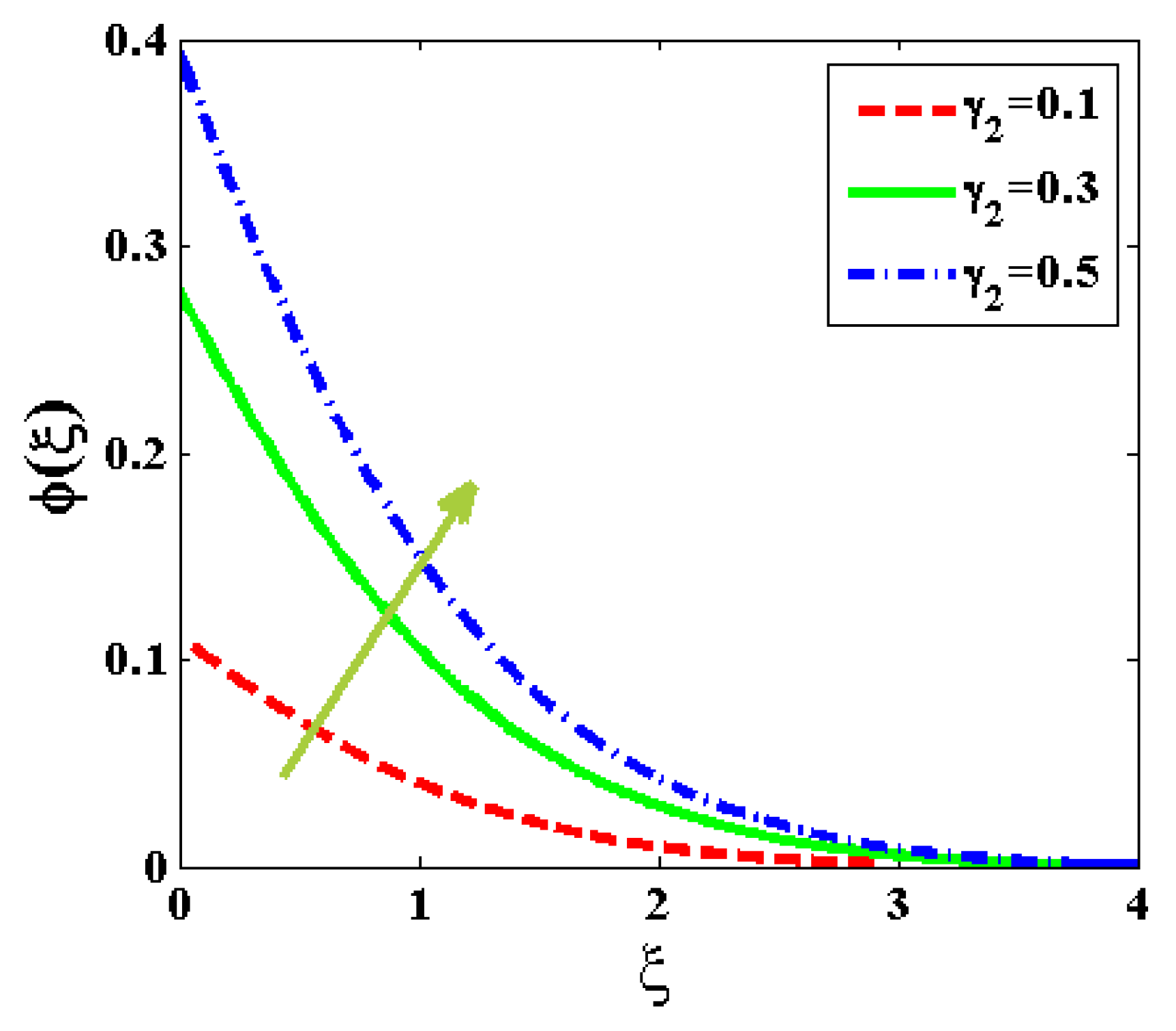
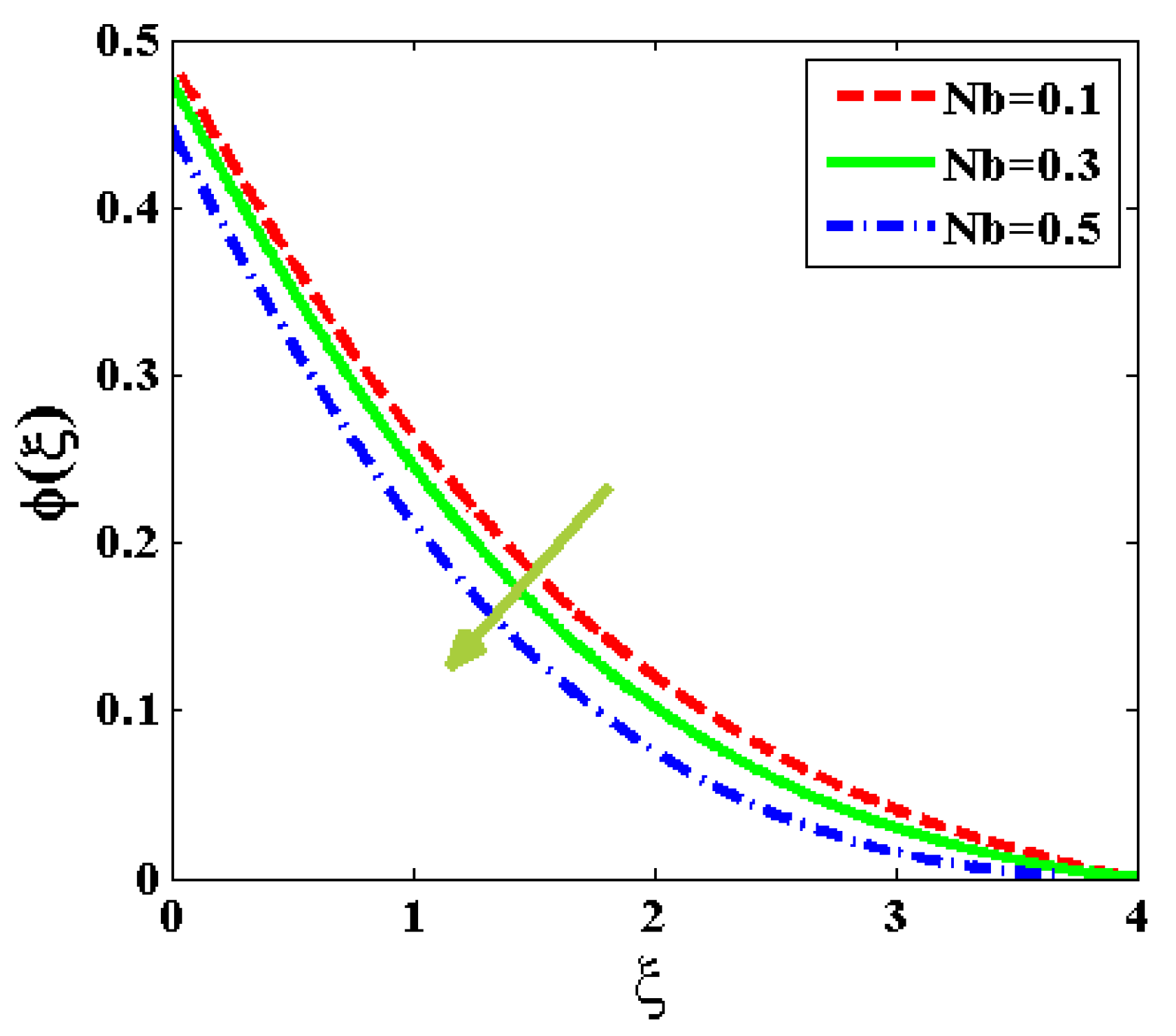
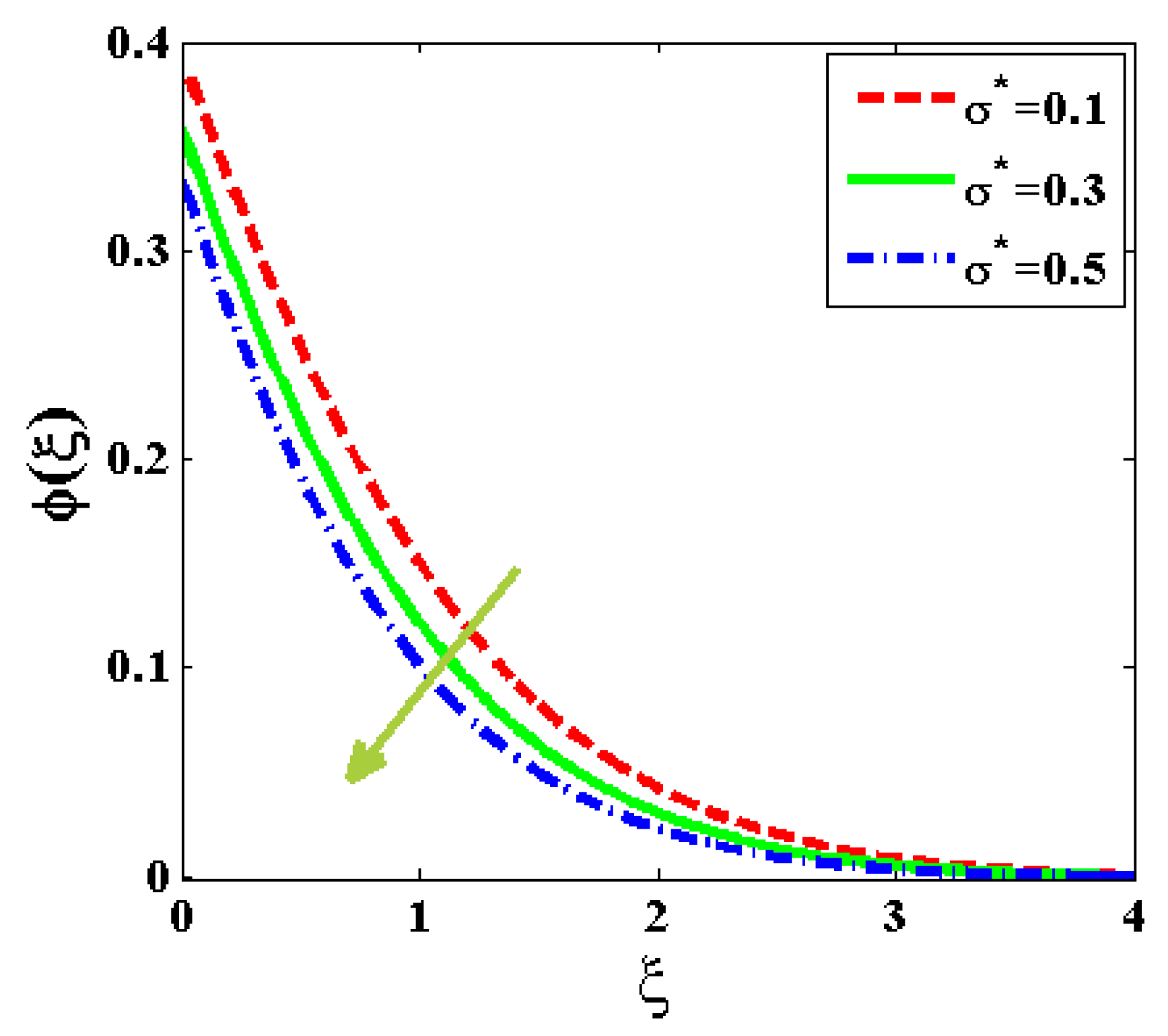
5. Results and Discussion
6. Table Discussion
7. Conclusions
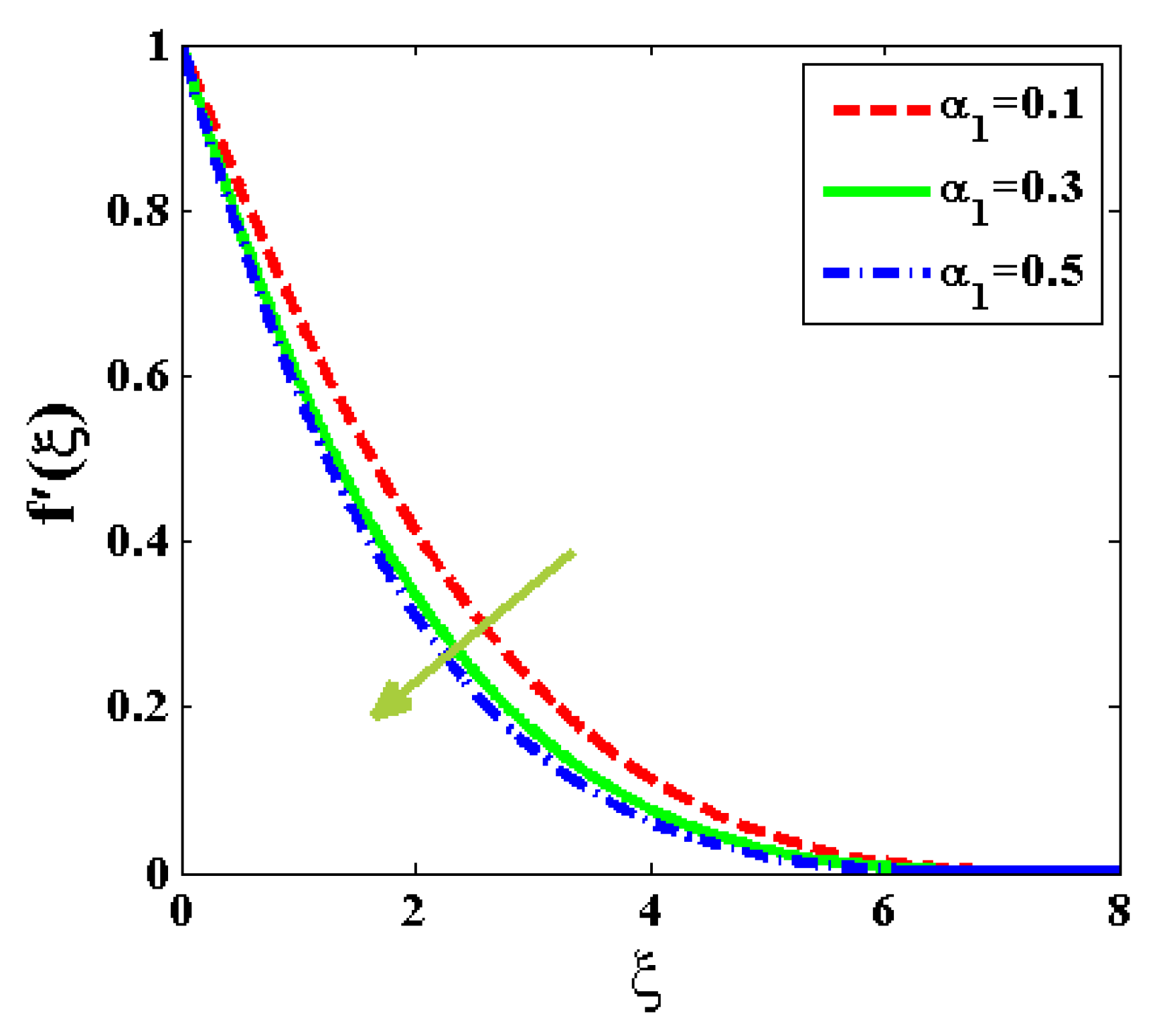
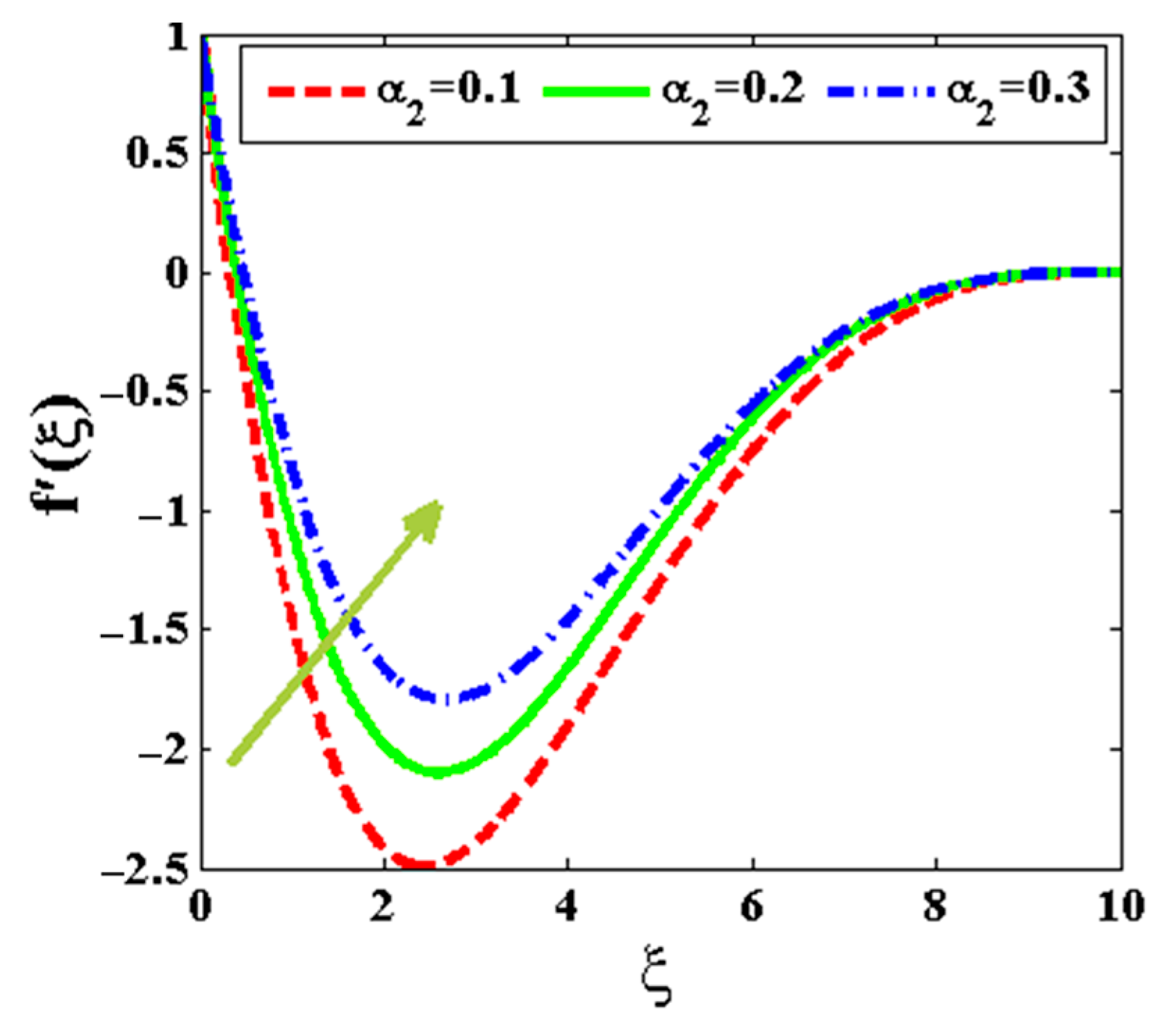
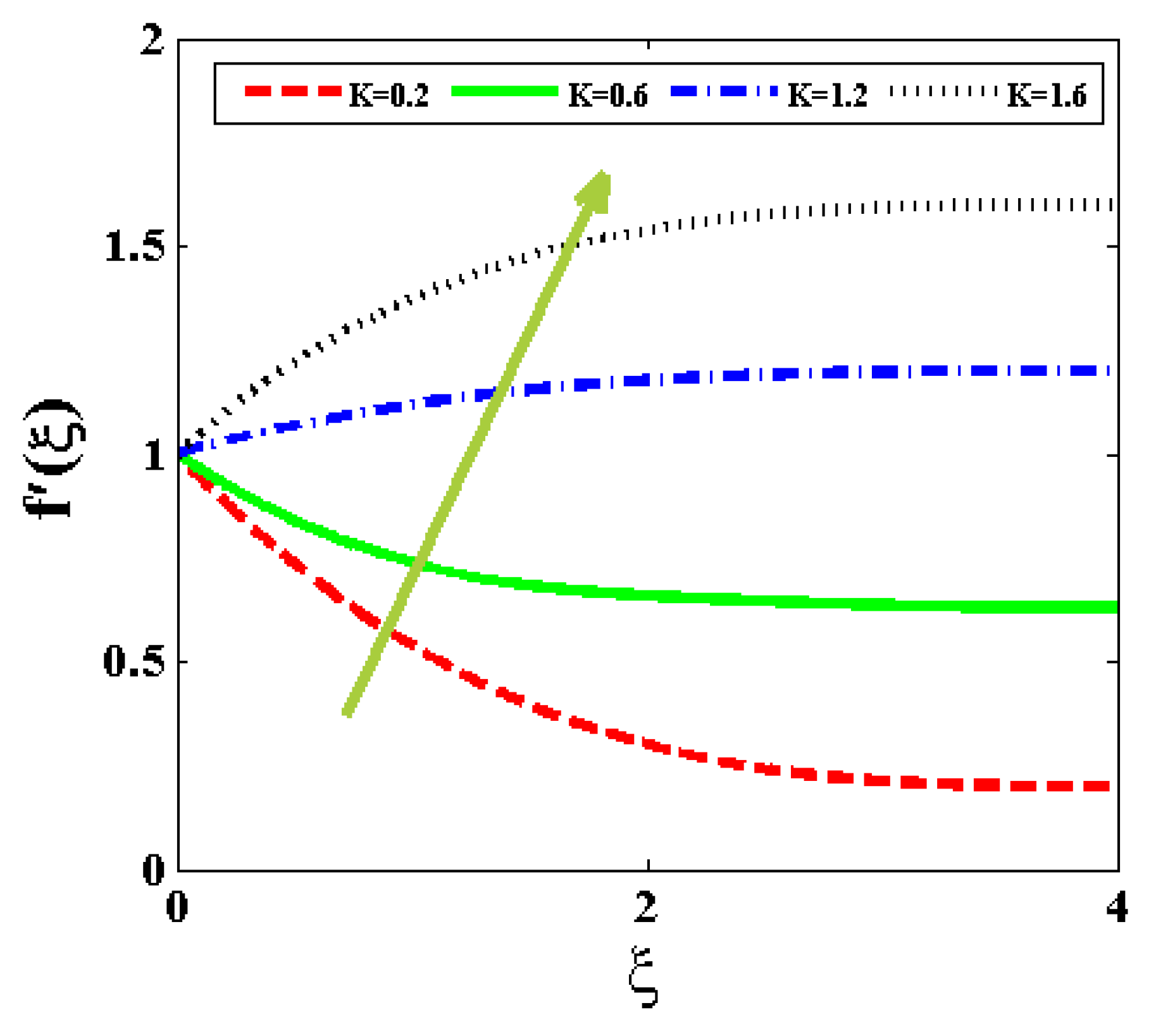
- A significant monotonic increase in the flow velocity is seen for variations in the Rayleigh number and Deborah pseudoplastic number, and .
- A growing magnetic field term generates significant electromagnetic force, which increases shear stress and dampens the velocity profile.
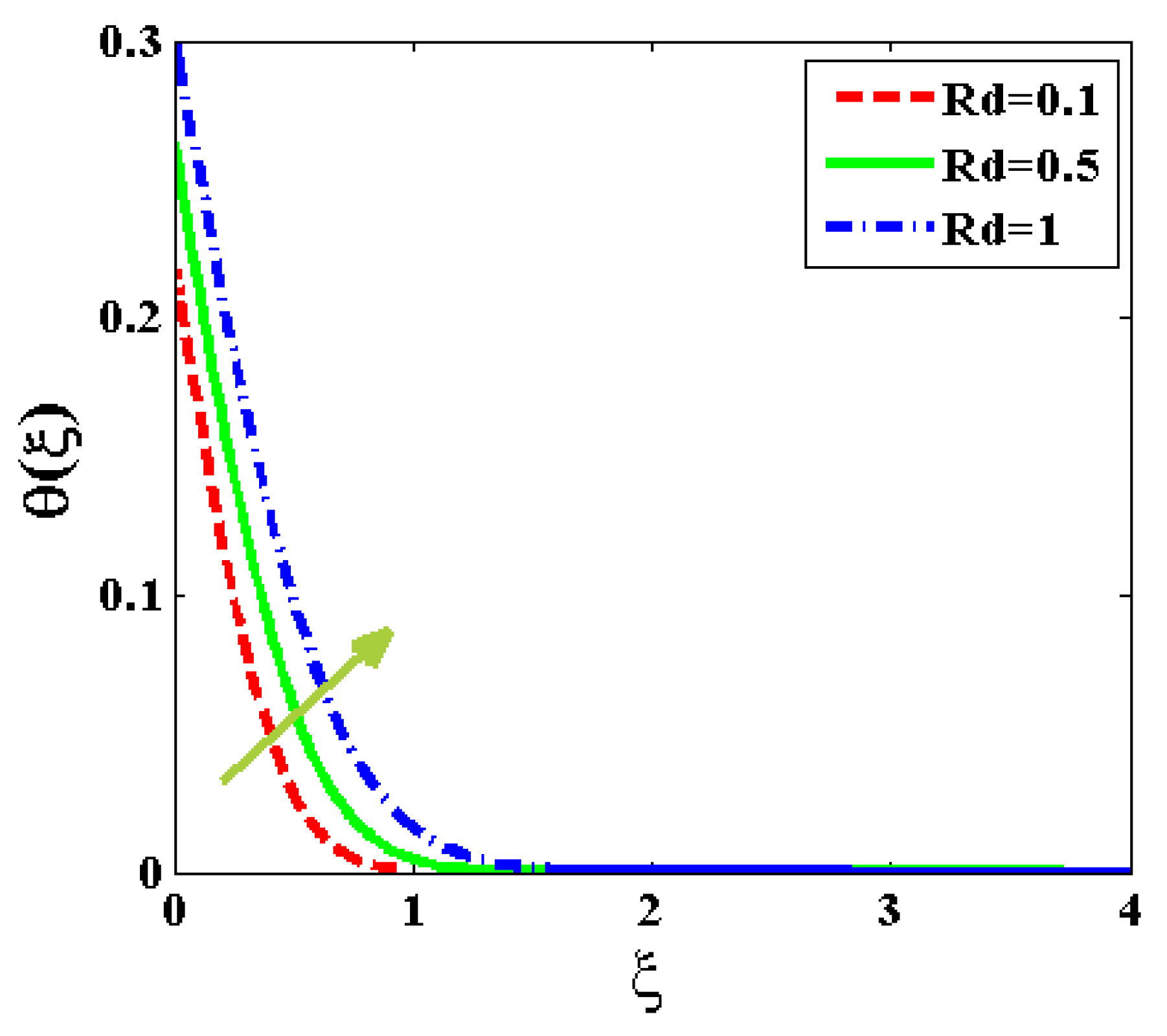
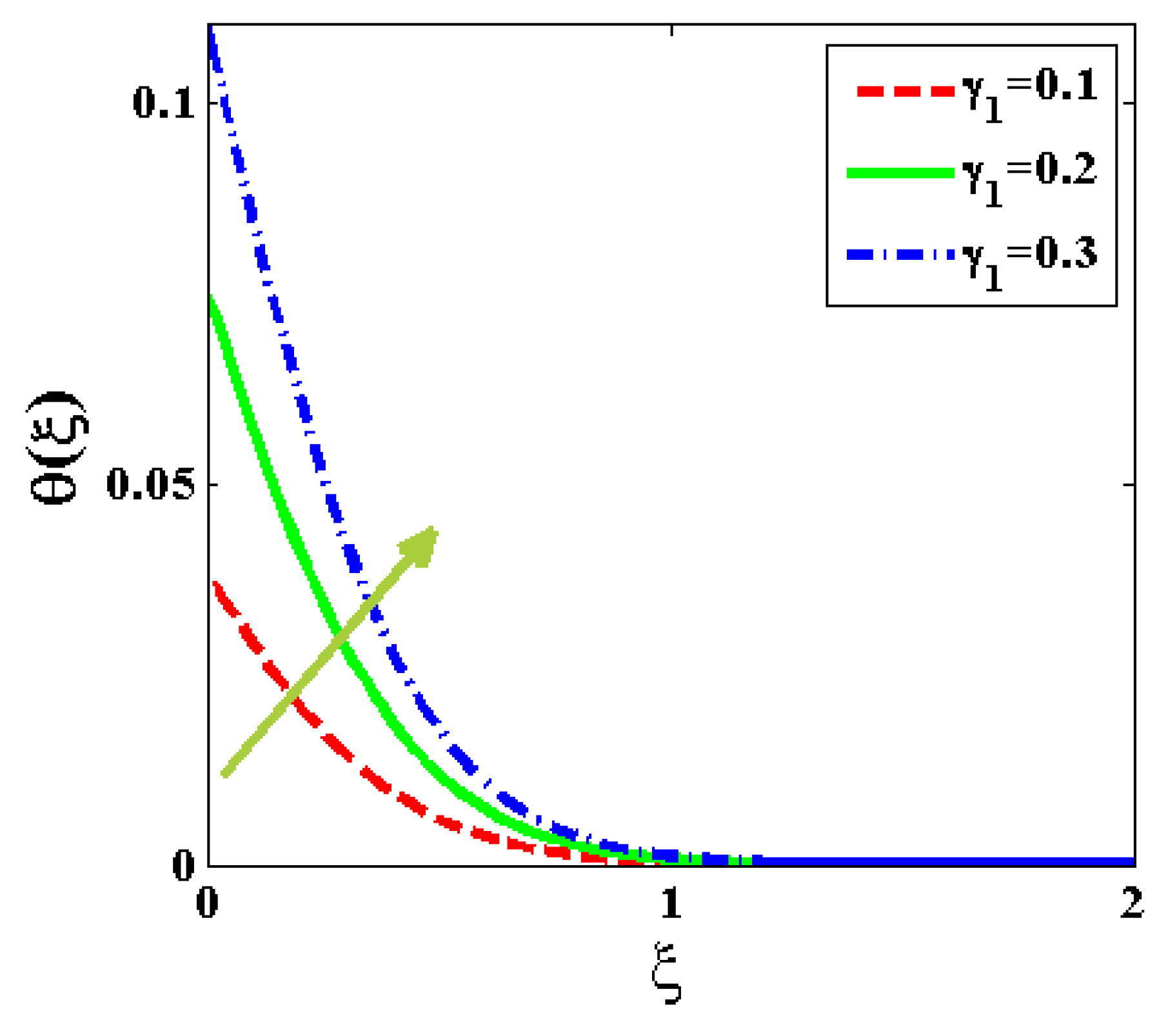
- The suspended nanoparticles’ heat conduction and distribution of motile microbes are enhanced with rising radiation, bioconvective, and heat Biot number terms.
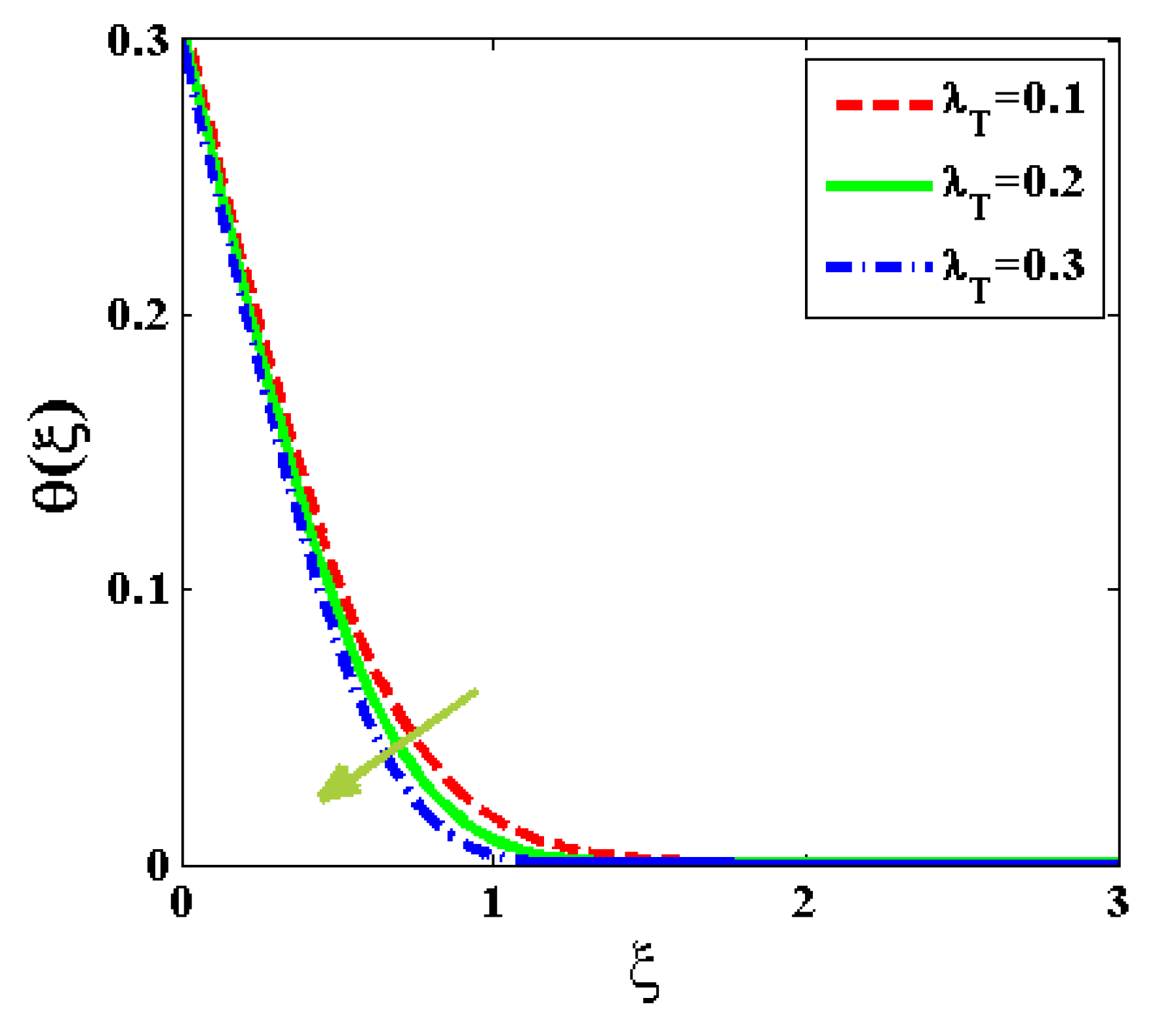
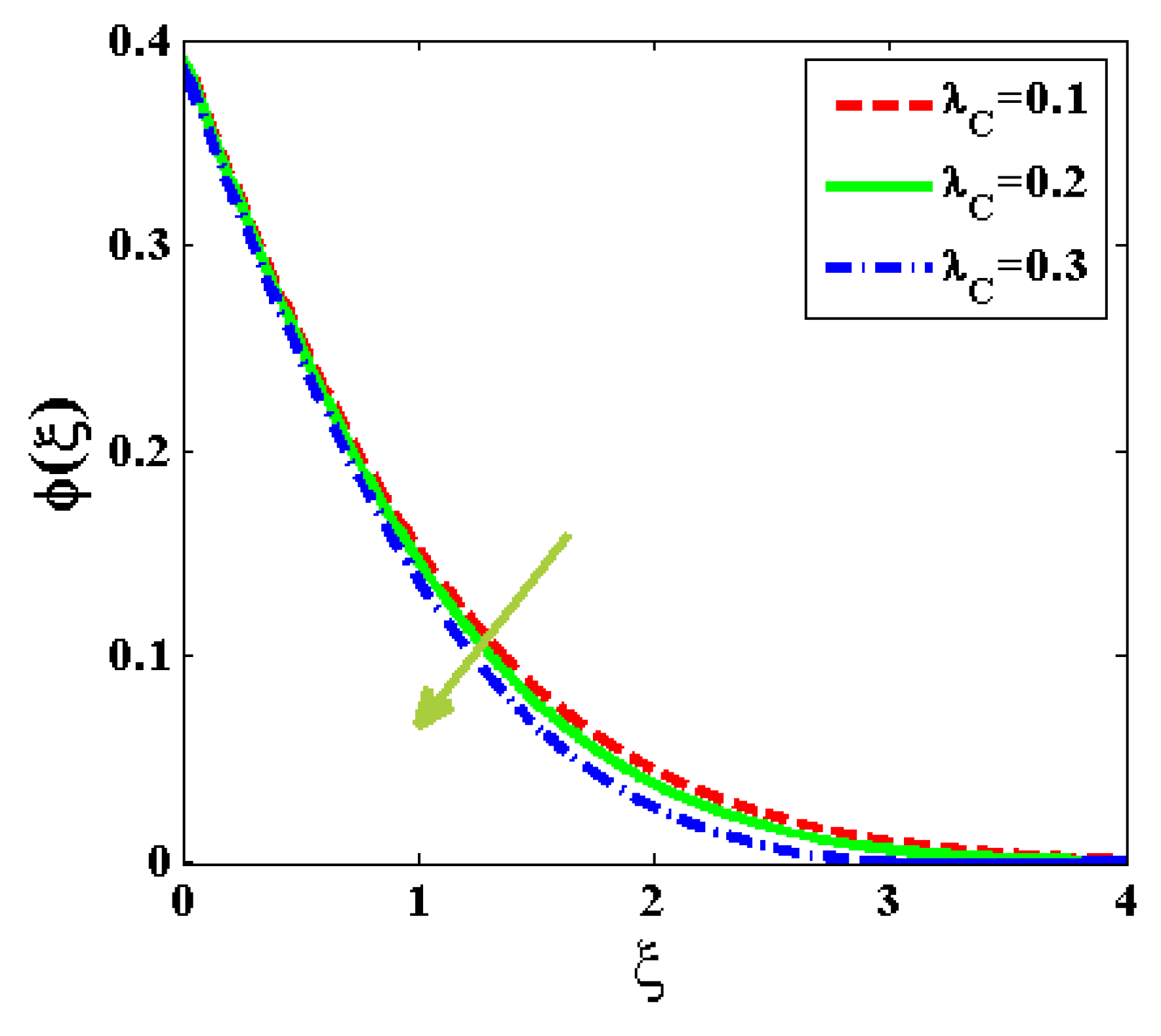
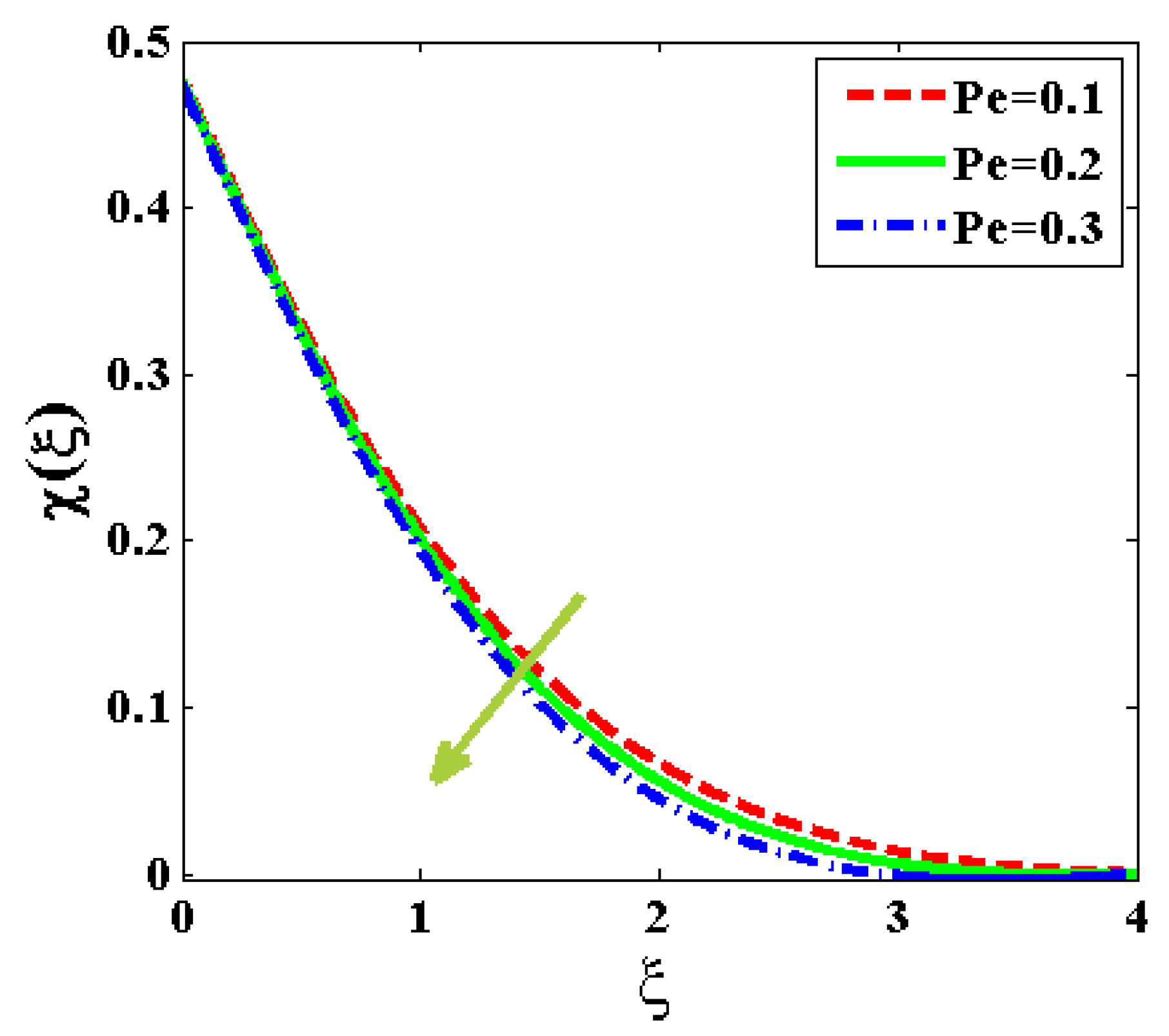
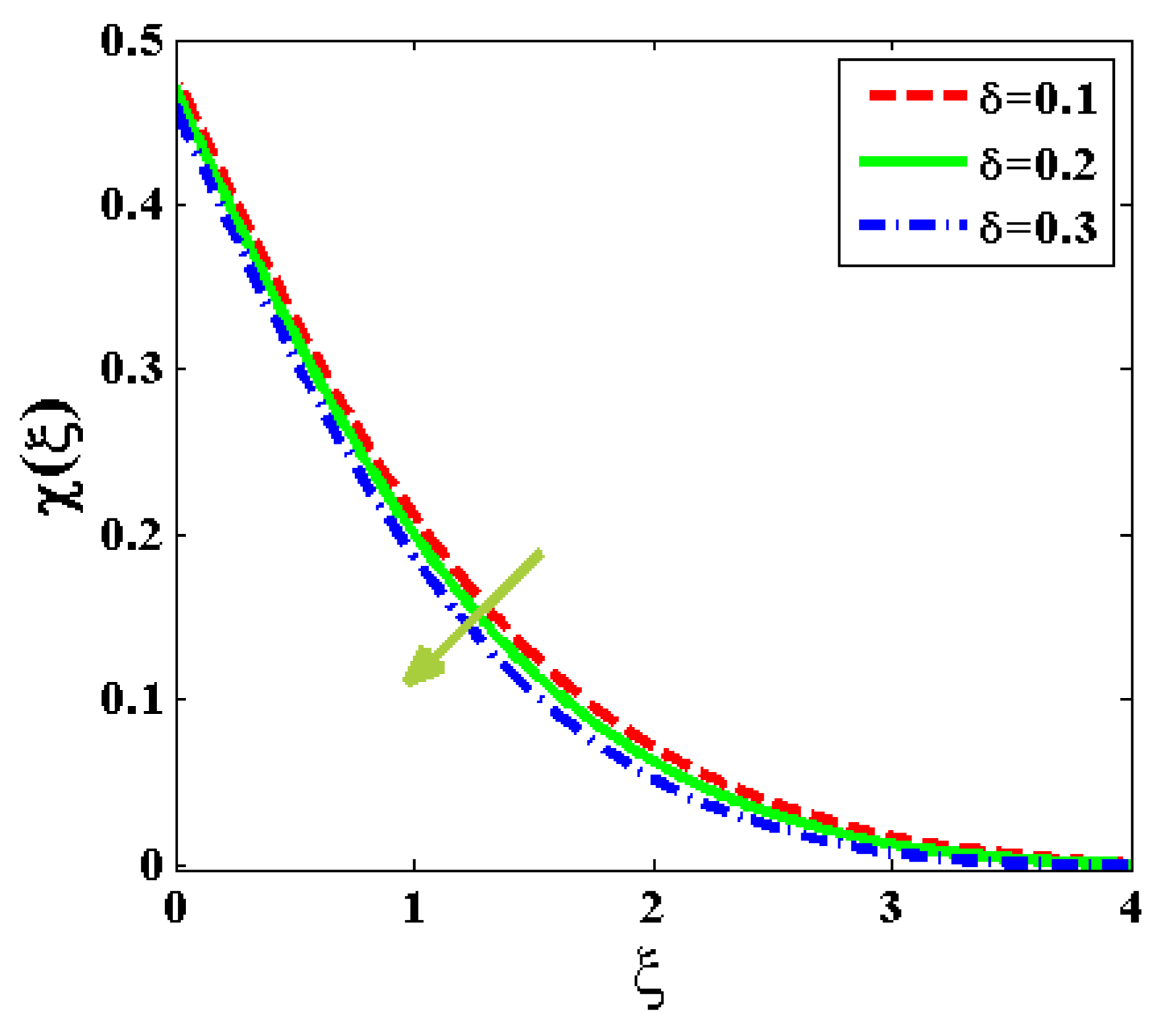
- The mass transfer and concentricity distribution are decreased for an increasing value of Brownian motion, Lewis number, and relaxation time.
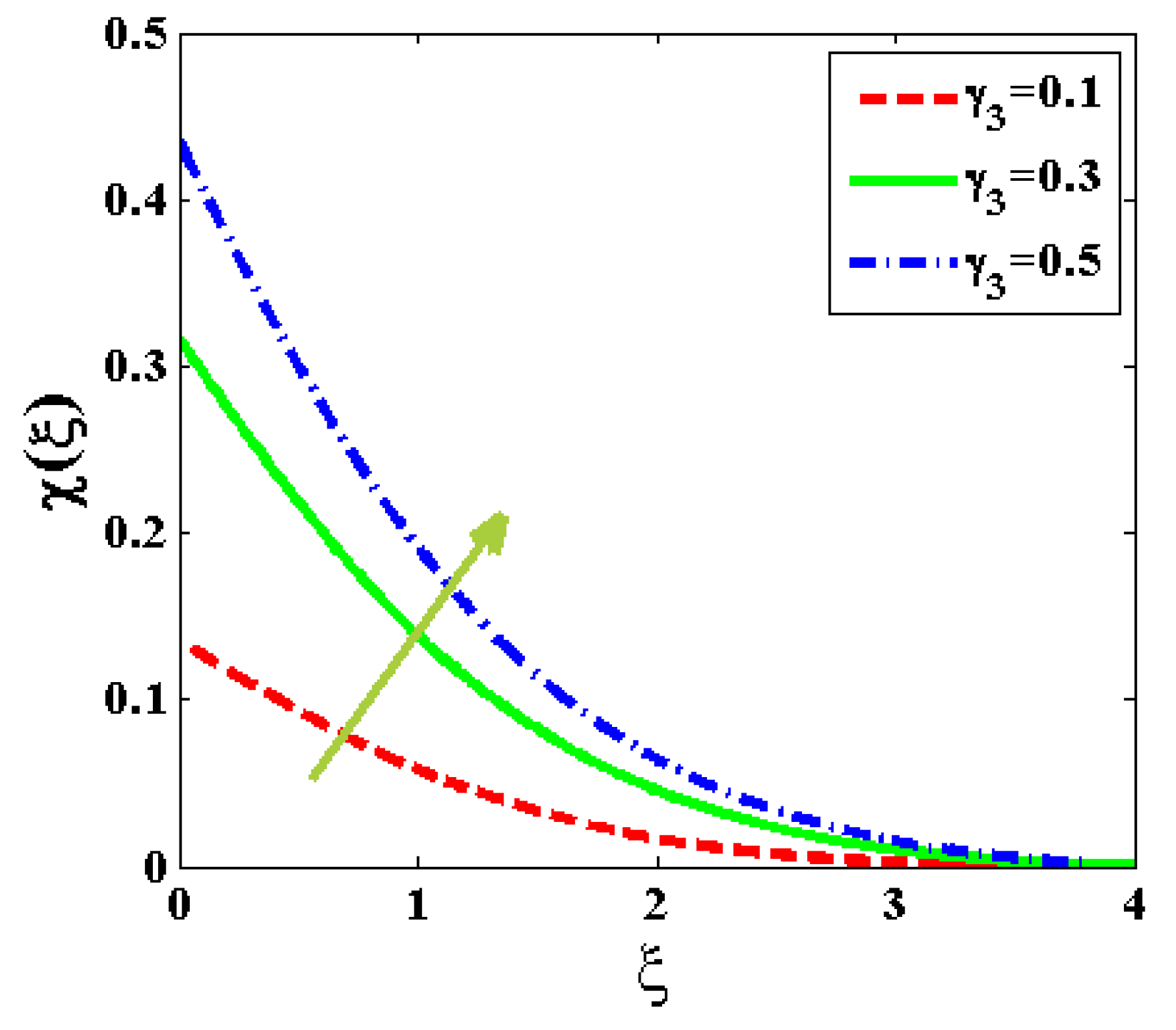
- It is plausible to conclude that increasing the chemical reaction parameter and concentricity relaxation variable or reducing the Prandtl number, concentricity Biot quantity, and active energy factor can considerably enhance the concentration dispersion of nanoparticles.
- A rising value of bioconvective and microorganism Biot number spurred motile microorganism distribution.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| relaxation time parameters of Burgers’ fluid | |
| retardation time parameters of Burgers’ fluid | |
| activation energy | |
| relaxation time of heat | |
| relaxation time of mass | |
| liquid temperature | |
| liquid concentration | |
| ambient temperature | |
| ambient concentration | |
| coefficient of diffusion | |
| heat flux | |
| mass flux | |
| density | |
| pressure | |
| specific heat capacity | |
| thermal conductivity of the liquid |
References
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; DeWitt, D.P. Introduction to Heat Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Serrano, J.; Olmeda, P.; Arnau, F.; Reyes-Belmonte, M.; Lefebvre, A. Importance of heat transfer phenomena in small turbochargers for passenger car applications. SAE Int. J. Engines 2013, 6, 716–728. [Google Scholar] [CrossRef]
- Zhang, H.; Zhuang, J. Research, development and industrial application of heat pipe technology in China. Appl. Therm. Eng. 2003, 23, 1067–1083. [Google Scholar] [CrossRef]
- Ramesh, K.N.; Sharma, T.K.; Rao, G.A.P. Latest advancements in heat transfer enhancement in the micro-channel heat sinks: A review. Arch. Comput. Methods Eng. 2021, 28, 3135–3165. [Google Scholar] [CrossRef]
- Pozhar, L.A. Structure and dynamics of nanofluids: Theory and simulations to calculate viscosity. Phys. Rev. E 2000, 61, 1432–1446. [Google Scholar] [CrossRef] [PubMed]
- Rafati, M.; Hamidi, A.A.; Niaser, M.S. Application of nanofluids in computer cooling systems (heat transfer performance of nanofluids). Appl. Therm. Eng. 2012, 45, 9–14. [Google Scholar] [CrossRef]
- Polidori, G.; Fohanno, S.; Nguyen, C.T. A note on heat transfer modelling of Newtonian nanofluids in laminar free convection. Int. J. Therm. Sci. 2007, 46, 739–744. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Application of nanofluids in heat exchangers: A review. Renew. Sustain. Energy Rev. 2012, 16, 5625–5638. [Google Scholar] [CrossRef]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Ramadhan, A.I.; Azmi, W.H. The effect of nanoparticles composition ratio on dynamic viscosity of Al2O3-TiO2-SiO2 nanofluids. Mater. Today Proc. 2022, 48, 1920–1923. [Google Scholar] [CrossRef]
- Ramadhan, A.I.; Azmi, W.H.; Mamat, R.; Diniardi, E.; Hendrawati, T.Y. Experimental Investigation of Cooling Performance in Automotive Radiator using Al2O3-TiO2-SiO2 Nanofluids. Automot. Exp. 2022, 5, 28–39. [Google Scholar] [CrossRef]
- Seyyedi, S.M.; Hashemi-Tilehnoee, M.; Sharifpur, M. Impact of fusion temperature on hydrothermal features of flow within an annulus loaded with nanoencapsulated phase change materials (NEPCMs) during natural convection process. Math. Probl. Eng. 2021, 2021, 4276894. [Google Scholar] [CrossRef]
- Hashemi-Tilehnoee, M.; del Barrio, E.P.; Seyyedi, S.M. Magneto-turbulent natural convection and entropy generation analyses in liquid sodium-filled cavity partially heated and cooled from sidewalls with circular blocks. Int. Commun. Heat Mass Transf. 2022, 134, 106053. [Google Scholar] [CrossRef]
- Fikri, M.; Faizal, W.; Adli, H.; Bo, Z.; Jiang, X.; Ramadhan, A. Experimental Determination of Water, Water/Ethylene Glycol and TiO2-SiO2 Nanofluids mixture with Water/Ethylene Glycol to Three Square Multilayer Absorber Collector on Solar Water Heating System: A Comparative Investigation. Conf. Ser. Mater. Sci. Eng. 2021, 1062, 012019. [Google Scholar] [CrossRef]
- Malvandi, A.; Moshizi, S.A.; Soltani, E.G.; Ganji, D.D. Modified Buongiorno’s model for fully developed mixed convection flow of nanofluids in a vertical annular pipe. Comput. Fluids 2014, 89, 124–132. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Nield, D.A. Natural convective boundary-layer flow of a Nano fluid past a vertical plate. Int. J. Therm. Sci. 2010, 49, 243–247. [Google Scholar] [CrossRef]
- Tzou, D.Y. Thermal instability of nanofluids in natural convection. Int. J. Heat Mass Transf. 2008, 51, 2967–2979. [Google Scholar] [CrossRef]
- Hwang, K.S.; Jang, S.P.; Choi, S.U.S. Flow and convective heat transfer characteristics of water-based Al2O3 nanofluids in fully developed laminar flow regime. Int. J. Heat Mass Transf. 2009, 52, 193–199. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. The Cheng–Minkowycz problem for natural convective boundary-layer flow in a porous medium saturated by a nanofluid. Int. J. Heat Mass Transf. 2009, 52, 5792–5795. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. The Cheng–Minkowycz problem for the double-diffusive natural convective boundary layer flow in a porous medium saturated by a nanofluid. Int. J. Heat Mass Transf. 2011, 54, 374–378. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Malvandi, A.; Ganji, D.D.; Hedayati, F.; Rad, E.Y. An analytical study on entropy generation of nanofluids over a flat plate. Alex. Eng. J. 2013, 52, 595–604. [Google Scholar] [CrossRef]
- Malvandi, A.; Hedayati, F.; Domairry, G. Stagnation point flow of a nanofluid toward an exponentially stretching sheet with nonuniform heat generation/absorption. J. Thermodyn. 2013, 2013, 764827. [Google Scholar] [CrossRef]
- Malvandi, A.; Hedayati, F.; Ganji, D.D.; Rostamiyan, Y. Unsteady boundary layer flow of nanofluid past a permeable stretching/shrinking sheet with convective heat transfer. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2014, 228, 1175–1184. [Google Scholar] [CrossRef]
- Aziz, A.; Khan, W.A. Natural convective boundary layer flow of a nanofluid past a convectively heated vertical plate. Int. J. Therm. Sci. 2012, 52, 83–90. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Gorji-Bandpay, M.; Ganji, D.D. Magnetic field effects on natural convection around a horizontal circular cylinder inside a square enclosure filled with nanofluid. Int. Commun. Heat Mass Transf. 2012, 39, 978–986. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Gorji-Bandpy, M.; Ganji, D.D.; Soleimani, S.; Seyyedi, S.M. Natural convection of nanofluids in an enclosure between a circular and a sinusoidal cylinder in the presence of magnetic field. Int. Commun. Heat Mass Transf. 2012, 39, 1435–1444. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D. Heat transfer of Cu-water nano fluid flow between parallel plates. Powder Technol. 2013, 235, 873–879. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D.; Ashorynejad, H.R. Investigation of squeezing unsteady Nano fluid flow using ADM. Powder Technol. 2013, 239, 259–265. [Google Scholar] [CrossRef]
- Gupta, U.; Ahuja, J.; Wanchoo, R.K. Magneto convection in a nano fluid layer. Int. J. Heat Mass Transf. 2013, 64, 1163. [Google Scholar] [CrossRef]
- Haddad, Z.; Abu-Nada, E.; Oztop, H.F.; Mataoui, A. Natural convection in nanofluids: Are the thermophoresis and Brownian motion effects significant in nanofluid heat transfer enhancement. Int. J. Therm. Sci. 2012, 57, 152–162. [Google Scholar] [CrossRef]
- Sheikhzadeh, G.A.; Dastmalchi, M.; Khorasanizadeh, H. Effects of nanoparticles transport mechanisms on Al2O3–water nanofluid natural convection in a square enclosure. Int. J. Therm. Sci. 2013, 66, 51–62. [Google Scholar] [CrossRef]
- Yacob, N.A.; Ishak, A.; Nazar, R.; Pop, I. Falkner–Skan problem for a static and moving wedge with prescribed surface heat flux in a nano fluid. Int. Commun. Heat Mass Transf. 2011, 38, 149–153. [Google Scholar] [CrossRef]
- Daungthongsuk, W.; Wongwises, S. A critical review of convective heat transfer of nanofluids. Renew. Sustain. Energy Rev. 2007, 11, 797–817. [Google Scholar] [CrossRef]
- Wang, X.-Q.; Mujumdar, A.S. Heat transfer characteristics of nanofluids: A review. Int. J. Therm. Sci. 2007, 46, 1–19. [Google Scholar] [CrossRef]
- Jamil, M.; Fetecau, C. Some exact solutions for rotating flows of a generalized Burgers’ fluid in cylindrical domain. J. Non-Newton. Fluid 2010, 165, 1700–1712. [Google Scholar] [CrossRef]
- Fetecau, C.; Hayat, T.; Khan, M.; Fetecau, C. A note on longitudinal oscillations of a generalized Burger fluid in cylindrical domains. J. Non-Newton. Fluid 2010, 165, 350–361. [Google Scholar] [CrossRef]
- Xue, C.; Nie, J.; Tan, W.C. An exact solution of start-up flow for the fractional generalized Burgers’ fluid in a porous half space. Nonlinear Analysis Theo. Math. Appl. 2008, 69, 2086–2094. [Google Scholar] [CrossRef]
- Khan, M.; Anjum, A.; Fetecau, C.; Qi, H. Exact solutions for some oscillating motion of a motions of a fractional Burgers’ fluid. Math. Comp. Mod. 2010, 51, 682–692. [Google Scholar] [CrossRef]
- Liu, Y.; Zheng, L.; Zhang, X. MHD flow and heat transfer of a generalized Burgers’ fluid due to an exponential accelerating plate with the effects of radiation. Comp. Math. Appl. 2011, 62, 3123–3131. [Google Scholar] [CrossRef][Green Version]
- Javed, M.; Hayat, T.; Alsaedi, A. Peristaltic flow of Burgers’ fluid with complaint walls and heat transfer. Appl. Math. Comp. 2014, 244, 654–671. [Google Scholar] [CrossRef]
- Awais, M.; Hayat, T.; Alsaedi, A. Investigation of heat transfer in flow of Burgers’ fluid during a melting process. J. Egyp. Math. Soc. 2015, 23, 410–415. [Google Scholar] [CrossRef]
- Bees, M.A. Advances in bioconvection. Ann. Rev. Fluid Mech. 2020, 52, 449–476. [Google Scholar] [CrossRef]
- Khan, M.; Irfan, M.; Khan, W.A.; Sajid, M. Consequence of convective conditions for flow of Oldroyd-B nanofluid by a stretching cylinder. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 116. [Google Scholar] [CrossRef]
- Tlili, I.; Waqas, H.; Almaneea, A.; Khan, S.U.; Imran, M. Activation energy and second order slip in bioconvection of Oldroyd-B nanofluid over a stretching cylinder: A proposed mathematical model. Processes 2019, 7, 914. [Google Scholar] [CrossRef]
- Waqas, H.; Shehzad, S.A.; Khan, S.U.; Imran, M. Novel numerical computations on flow of nanoparticles in porous rotating disk with multiple slip effects and microorganisms. J. Nanofluids 2019, 8, 1423–1432. [Google Scholar] [CrossRef]
- Waqas, H.; Khan, S.U.; Hassan, M.; Bhatti, M.M.; Imran, M. Analysis on the bioconvection flow of modified second-grade nanofluid containing gyrotactic microorganisms and nanoparticles. J. Mol. Liq. 2019, 291, 111231. [Google Scholar] [CrossRef]
- Khan, S.U.; Waqas, H.; Bhatti, M.M.; Imran, M. Bioconvection in the rheology of magnetized couple stress nanofluid featuring activation energy and Wu’s slip. J. Non-Equilib. Thermodyn. 2020, 45, 81–95. [Google Scholar] [CrossRef]
- Wang, Y.; Waqas, H.; Tahir, M.; Imran, M.; Jung, C.Y. Effective Prandtl aspects on bio-convective thermally developed magnetized tangent hyperbolic nanoliquid with gyrotactic microorganisms and second order velocity slip. IEEE Access 2019, 7, 130008–130023. [Google Scholar] [CrossRef]
- Waqas, H.; Khan, S.U.; Imran, M.; Bhatti, M.M. Thermally developed Falkner-Skan bioconvection flow of a magnetized nanofluid in the presence of a motile gyrotactic microorganism: Buongiorno’s nanofluid model. Phys. Scr. 2019, 94, 115304. [Google Scholar] [CrossRef]
- Khan, S.U.; Rauf, A.; Shehzad, S.A.; Abbas, Z.; Javed, T. Study of bioconvection flow in Oldroyd-B nanofluid with motile organisms and effective Prandtl approach. Physica A 2019, 527, 121179. [Google Scholar] [CrossRef]
- Li, Y.; Waqas, H.; Imran, M.; Farooq, U.; Mallawi, F.; Tlili, I. A numerical exploration of modified second-grade nanofluid with motile microorganisms, thermal radiation, and Wu’s slip. Symmetry 2020, 12, 393. [Google Scholar] [CrossRef]
- Chu, Y.M.; Khan, M.I.; Waqas, H.; Farooq, U.; Khan, S.U.; Nazeer, M. Numerical simulation of squeezing flow Jeffrey nanofluid confined by two parallel disks with the help of chemical reaction: Effects of activation energy and microorganisms. Int. J. Chem. React. Eng. 2021, 19, 717–725. [Google Scholar] [CrossRef]
- Logan, D.L. A First Course in the Finite Element Method, Cengage Learning; CL Engineering: Dbayeh, Lebanon, 2011; ISBN 978-0495668251. [Google Scholar]
- Hrennikoff, A. Solution of problems of elasticity by the framework method. J. Appl. Mech. 1941, 8, 169–175. [Google Scholar] [CrossRef]
- Courant, R. Variational methods for the solution of problems of equilibrium and vibrations. Bull. Am. Math. Soc. 1943, 49, 1–23. [Google Scholar] [CrossRef]
- CПб ЭMИ PAH. Available online: https://www.rusprofile.ru/id/3724410 (accessed on 17 March 2018).
- Hinton, E.; Irons, B. Least squares smoothing of experimental data using finite elements. Strain 1968, 4, 24–27. [Google Scholar] [CrossRef]
- Seyyedi, S.M.; Hashemi-Tilehnoee, M.; Sharifpur, M. Effect of inclined magnetic field on the entropy generation in an annulus filled with NEPCM suspension. Math. Probl. Eng. 2021, 2021, 8103300. [Google Scholar] [CrossRef]
- Hashemi-Tilehnoee, M.; Sahebi, N.; Dogonchi, A.; Seyyedi, S.M.; Tashakor, S. Simulation of the dynamic behavior of a rectangular single-phase natural circulation vertical loop with asymmetric heater. Int. J. Heat Mass Transf. 2019, 139, 974–981. [Google Scholar] [CrossRef]
- ARamadhan, I.; Basri, H.; Diniardi, E.; Almanda, D. Aplikasi Hibrida Nanofluida Di Sistem Pendingin Kendaraan Ringan Roda Empat. In Prosiding Seminar Nasional Penelitian LPPM UMJ; Universitas Muhammadiyah Jakarta (UMJ): Ciputat, Indonesia, 2021. [Google Scholar]
- Ramadhan, A.I.; Azmi, W.H.; Mamat, R. Experimental investigation of thermo-physical properties of tri-hybrid nanoparticles in water-ethylene glycol mixture. Walailak J. Sci. Technol. 2021, 18, 9335. [Google Scholar] [CrossRef]
- Ramadhan, A.I.; Diniardi, E.; Dermawan, E. Numerical study of effect parameter fluid flow nanofluid Al2O3-water on heat transfer in corrugated tube. AIP Conf. Proc. 2016, 1737, 050003. [Google Scholar]
- SAP-IV Software and Manuals. NISEE e-Library, The Earthquake Engineering Online Archive. Available online: https://nisee.berkeley.edu/elibrary/getpkg?id=SAP4 (accessed on 30 May 2022).
- Paulsen, G.; Andersen, H.W.; Collett, J.P.; Stensrud, I.T.; Trust, B. The History of DNV 1864–2014; Dinamo Forlag A/S: Lysaker, Norway, 2014; ISBN 978-82-8071-256-1. pp. 121–436. [Google Scholar]
- Strang, G.; Fix, G. An Analysis of The Finite Element Method. Prentice Hall; Prentice-Hall: Englewood Cliffs, NJ, USA, 1973; ISBN 978-0-13-032946-2. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals; Butterworth-Heinemann: Oxford, UK, 2013; ISBN 978-0-08-095135-5. [Google Scholar]
- Bathe, K.J. Finite Element Procedures; Klaus-Jürgen Bathe: Cambridge, MA, USA, 2006; ISBN 978-0979004902. [Google Scholar]
- Wang, F.; Iqbal, Z.; Zhang, J.; Abdelmohimen, M.A.H.; Almaliki, A.H.; Galal, A.M. Bidirectional stretching features on the flow and heat transport of Burgers nanofluid subject to modified heat and mass fluxes. Waves Random Complex Media 2022, in press. [Google Scholar] [CrossRef]
- Ramzan, M.; Algehyne, E.A.; Saeed, A.; Dawar, A.; Kumam, P.; Watthayu, W. Homotopic simulation for heat transport phenomenon of the Burgers nanofluids flow over a stretching cylinder with thermal convective and zero mass flux conditions. Nanotechnol. Rev. 2022, 11, 1437–1449. [Google Scholar] [CrossRef]
- Qureshi, M.A. A case study of MHD driven Prandtl-Eyring hybrid nanofluid flow over a stretching sheet with thermal jump conditions. Case Stud. Therm. Eng. 2021, 28, 101581. [Google Scholar] [CrossRef]
- Jamshed, W.; Aziz, A. Entropy Analysis of TiO2-Cu/EG Casson Hybrid Nanofluid via Cattaneo-Christov Heat Flux Model. Appl. Nanosci. 2018, 8, 1–14. [Google Scholar]
- Jamshed, W. Numerical Investigation of MHD Impact on Maxwell Nanofluid. Int. Commun. Heat Mass Transf. 2021, 120, 104973. [Google Scholar] [CrossRef]
- Jamshed, W.; Nisar, K.S. Computational single phase comparative study of Williamson nanofluid in parabolic trough solar collector via Keller box method. Int. J. Energy Res. 2021, 45, 10696–10718. [Google Scholar] [CrossRef]
- Jamshed, W.; Devi, S.U.; Nisar, K.S. Single phase-based study of Ag-Cu/EO Williamson hybrid nanofluid flow over a stretching surface with shape factor. Phys. Scr. 2021, 96, 065202. [Google Scholar] [CrossRef]
- Jamshed, W.; Nisar, K.S.; Ibrahim, R.W.; Shahzad, F.; Eid, M.R. Thermal expansion optimization in solar aircraft using tangent hyperbolic hybrid nanofluid: A solar thermal application. J. Mater. Res. Technol. 2021, 14, 985–1006. [Google Scholar] [CrossRef]
- Jamshed, W.; Nisar, K.S.; Ibrahim, R.W.; Mukhtar, T.; Vijayakumar, V.; Ahmad, F. Computational frame work of Cattaneo-Christov heat flux effects on Engine Oil based Williamson hybrid nanofluids: A thermal case study. Case Stud. Therm. Eng. 2021, 26, 101179. [Google Scholar] [CrossRef]
- Jamshed, W.; Mishra, S.R.; Pattnaik, P.K.; Nisar, K.S.; Devi, S.S.U.; Prakash, M.; Shahzad, F.; Hussain, M.; Vijayakumar, V. Features of entropy optimization on viscous second grade nanofluid streamed with thermal radiation: A Tiwari and Das model. Case Stud. Therm. Eng. 2021, 27, 101291. [Google Scholar] [CrossRef]
- Jamshed, W.; Nasir, N.A.A.M.; Isa, S.S.P.M.; Safdar, R.; Shahzad, F.; Nisar, K.S.; Eid, M.R.; Abdel-Aty, A.-H.; Yahia, I.S. Thermal growth in solar water pump using Prandtl–Eyring hybrid nanofluid: A solar energy application. Sci. Rep. 2021, 11, 18704. [Google Scholar] [CrossRef]
- Jamshed, W. Finite element method in thermal characterization and streamline flow analysis of electromagnetic silver-magnesium oxide nanofluid inside grooved enclosure. Int. Commun. Heat Mass Transf. 2021, 130, 105795. [Google Scholar] [CrossRef]
- Jamshed, W.; Eid, M.R.; Hussain, S.M.; Abderrahmane, A.; Safdar, R.; Younis, O.; Pasha, A.A. Physical specifications of MHD mixed convective of Ostwald-de Waele nanofluids in a vented-cavity with inner elliptic cylinder. Int. Commun. Heat Mass Transf. 2022, 134, 106038. [Google Scholar] [CrossRef]


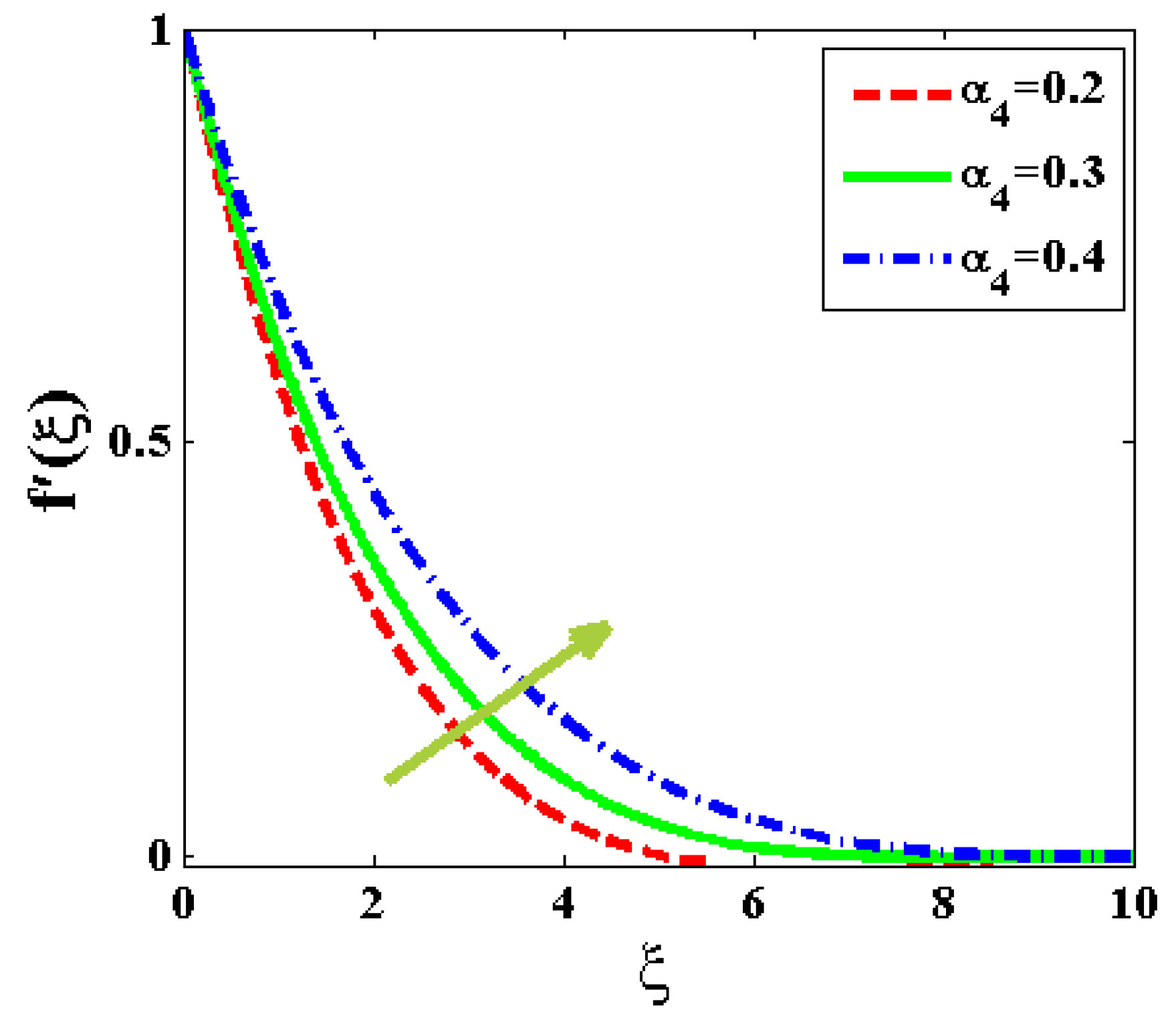
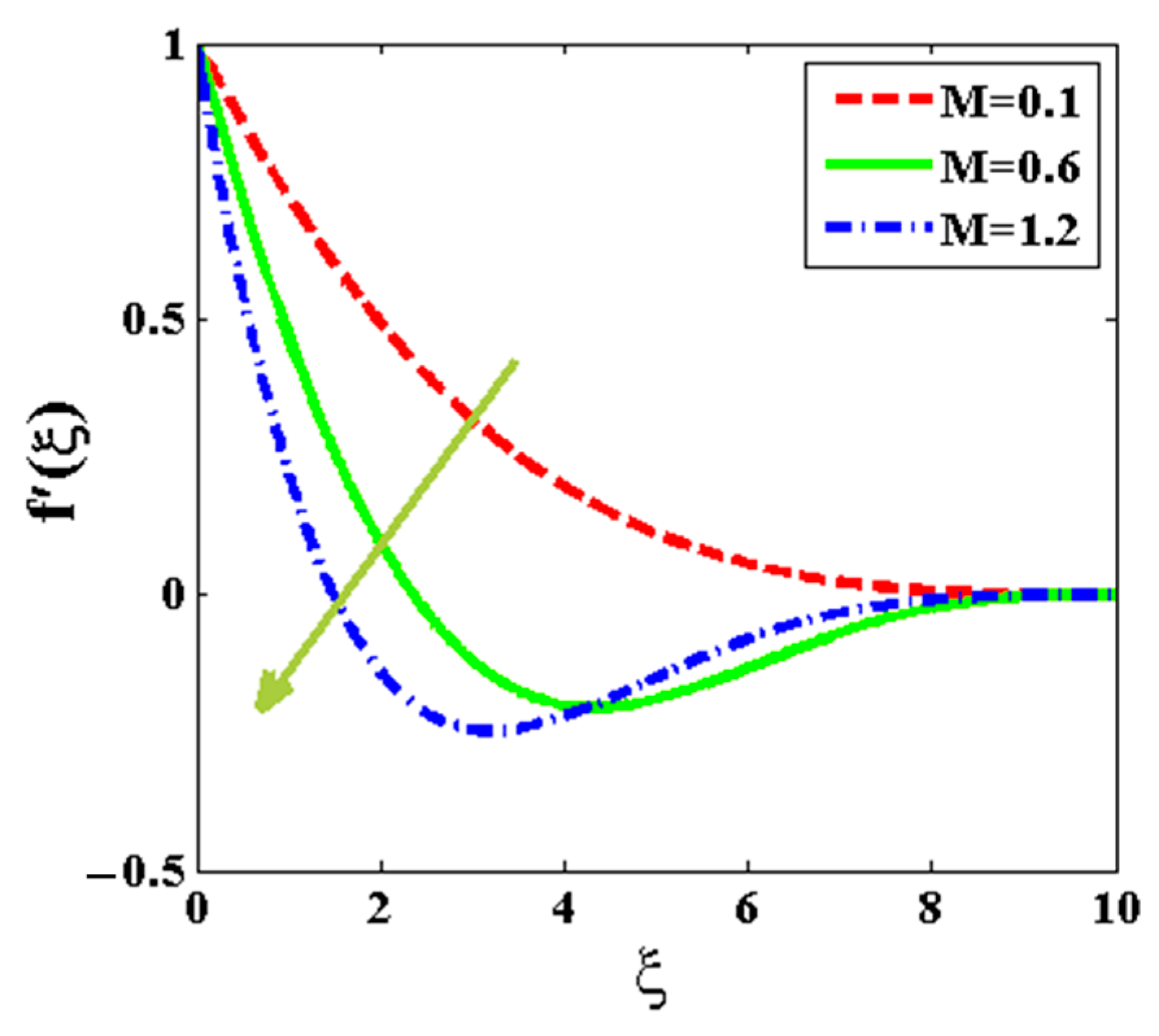
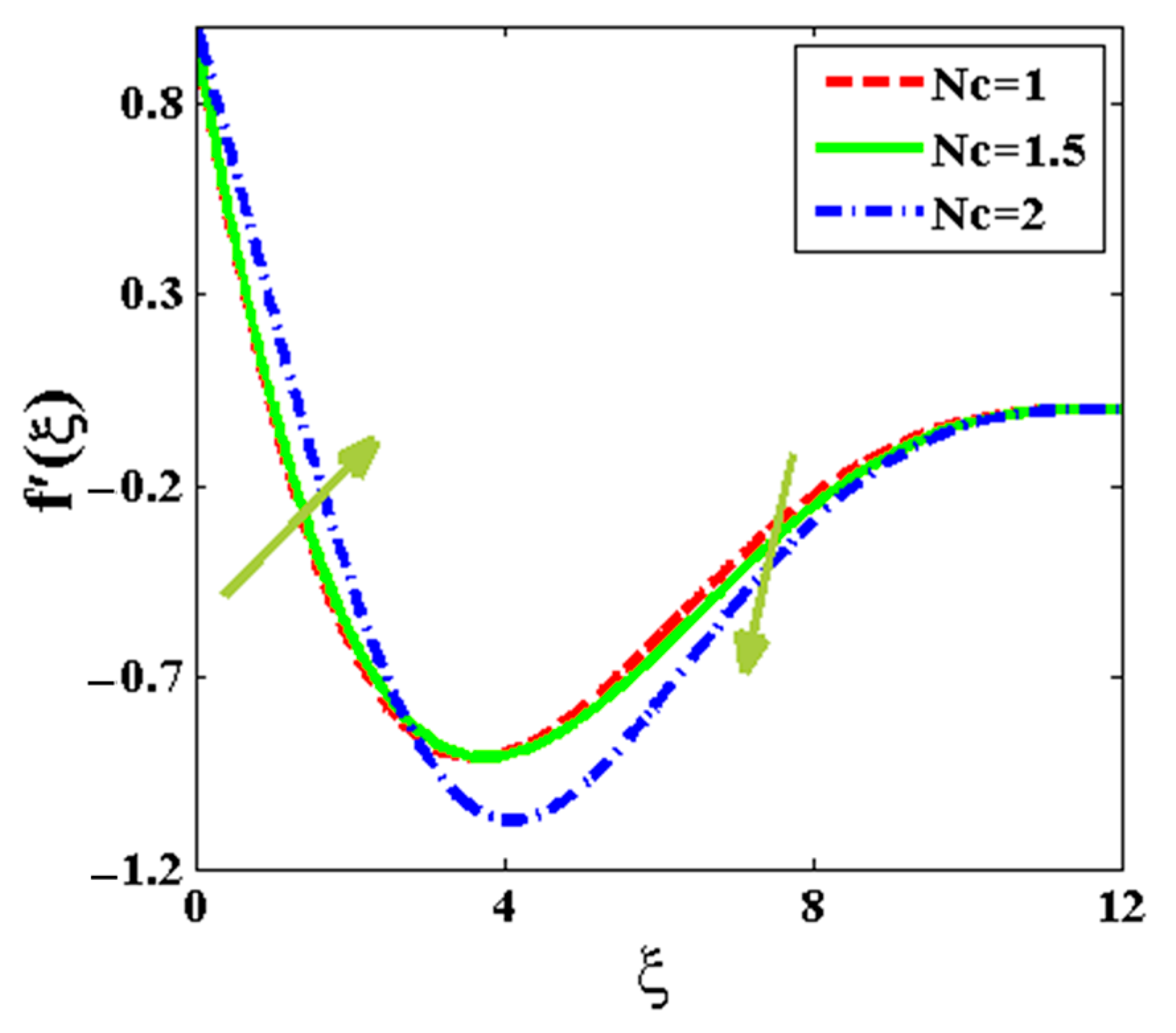

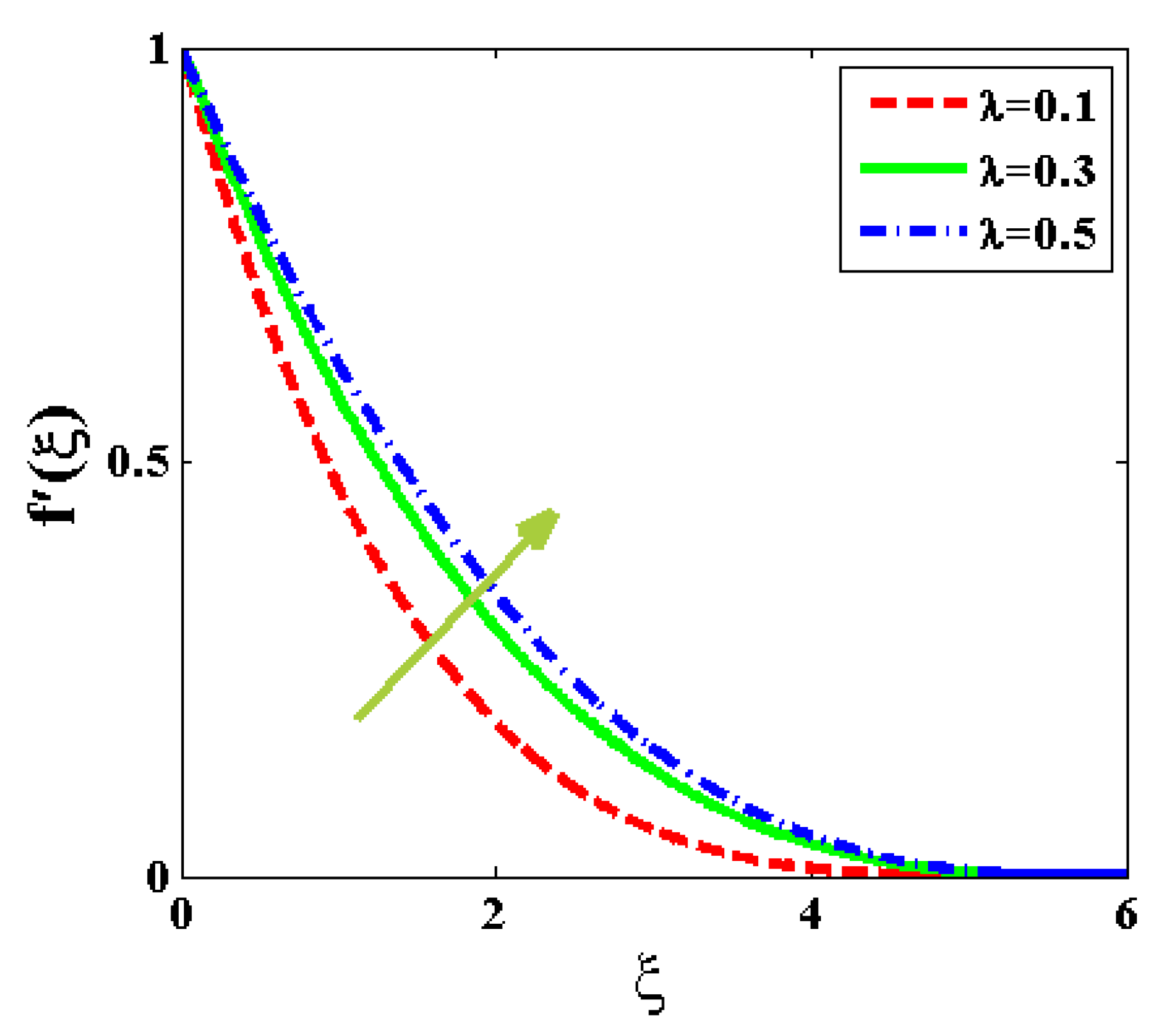





| Qureshi [72] | This Study | |
|---|---|---|
| 0.72 | 0.8087618 | 0.8087612 |
| 1.0 | 1.0000000 | 1.0000000 |
| 3.0 | 1.9235742 | 1.9235734 |
| 7.0 | 3.0731465 | 3.0731465 |
| 10 | 3.7205542 | 3.7205511 |
| 0.1 | 0.2 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.8 | 0.2 | 0.5 | 0.2 | 0.37638 | 0.33370 | 0.31245 |
| 0.3 | 0.37637 | 0.33368 | 0.31241 | ||||||||||
| 0.5 | 0.37636 | 0.33366 | 0.31237 | ||||||||||
| 0.2 | 0.37638 | 0.33370 | 0.31244 | ||||||||||
| 0.3 | 0.37638 | 0.33370 | 0.31245 | ||||||||||
| 0.4 | 0.37639 | 0.33371 | 0.31246 | ||||||||||
| 0.1 | 0.37449 | 0.30341 | 0.31175 | ||||||||||
| 0.6 | 0.37448 | 0.30338 | 0.31171 | ||||||||||
| 1.2 | 0.37443 | 0.30328 | 0.31156 | ||||||||||
| 0.1 | 0.37449 | 0.30340 | 0.31174 | ||||||||||
| 0.5 | 0.37450 | 0.30001 | 0.31166 | ||||||||||
| 1.0 | 0.37451 | 0.29711 | 0.31159 | ||||||||||
| 0.1 | 0.37449 | 0.30340 | 0.31174 | ||||||||||
| 0.2 | 0.37298 | 0.30340 | 0.31701 | ||||||||||
| 0.3 | 0.37100 | 0.32076 | 0.32332 | ||||||||||
| 0.1 | 0.41908 | 0.31143 | 0.31185 | ||||||||||
| 0.2 | 0.41314 | 0.30657 | 0.31178 | ||||||||||
| 0.3 | 0.40608 | 0.30495 | 0.31176 | ||||||||||
| 0.1 | 0.36629 | 0.30721 | 0.31179 | ||||||||||
| 0.3 | 0.33780 | 0.31810 | 0.31194 | ||||||||||
| 0.5 | 0.30110 | 0.32900 | 0.31209 | ||||||||||
| 0.4 | 0.37449 | 0.30340 | 0.24656 | ||||||||||
| 0.8 | 0.37449 | 0.30340 | 0.30087 | ||||||||||
| 1.2 | 0.37449 | 0.30340 | 0.33914 | ||||||||||
| 0.1 | 0.37607 | 0.30340 | 0.31174 | ||||||||||
| 0.2 | 0.37568 | 0.30340 | 0.31174 | ||||||||||
| 0.3 | 0.37529 | 0.30340 | 0.31174 | ||||||||||
| 0.1 | 0.37449 | 0.30340 | 0.31174 | ||||||||||
| 0.5 | 0.37417 | 0.35409 | 0.31293 | ||||||||||
| 0.9 | 0.37411 | 0.37965 | 0.31360 | ||||||||||
| 0.1 | 0.37450 | 0.30280 | 0.31175 | ||||||||||
| 0.2 | 0.37450 | 0.30294 | 0.31175 | ||||||||||
| 0.3 | 0.37450 | 0.30309 | 0.31175 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahzad, F.; Jamshed, W.; Sajid, T.; Shamshuddin, M.; Safdar, R.; Salawu, S.O.; Eid, M.R.; Hafeez, M.B.; Krawczuk, M. Electromagnetic Control and Dynamics of Generalized Burgers’ Nanoliquid Flow Containing Motile Microorganisms with Cattaneo–Christov Relations: Galerkin Finite Element Mechanism. Appl. Sci. 2022, 12, 8636. https://doi.org/10.3390/app12178636
Shahzad F, Jamshed W, Sajid T, Shamshuddin M, Safdar R, Salawu SO, Eid MR, Hafeez MB, Krawczuk M. Electromagnetic Control and Dynamics of Generalized Burgers’ Nanoliquid Flow Containing Motile Microorganisms with Cattaneo–Christov Relations: Galerkin Finite Element Mechanism. Applied Sciences. 2022; 12(17):8636. https://doi.org/10.3390/app12178636
Chicago/Turabian StyleShahzad, Faisal, Wasim Jamshed, Tanveer Sajid, MD. Shamshuddin, Rabia Safdar, S. O. Salawu, Mohamed R. Eid, Muhammad Bilal Hafeez, and Marek Krawczuk. 2022. "Electromagnetic Control and Dynamics of Generalized Burgers’ Nanoliquid Flow Containing Motile Microorganisms with Cattaneo–Christov Relations: Galerkin Finite Element Mechanism" Applied Sciences 12, no. 17: 8636. https://doi.org/10.3390/app12178636
APA StyleShahzad, F., Jamshed, W., Sajid, T., Shamshuddin, M., Safdar, R., Salawu, S. O., Eid, M. R., Hafeez, M. B., & Krawczuk, M. (2022). Electromagnetic Control and Dynamics of Generalized Burgers’ Nanoliquid Flow Containing Motile Microorganisms with Cattaneo–Christov Relations: Galerkin Finite Element Mechanism. Applied Sciences, 12(17), 8636. https://doi.org/10.3390/app12178636








