Fault Diagnosis Method for Rolling Bearings Based on Two-Channel CNN under Unbalanced Datasets
Abstract
:1. Introduction
2. Feature Extraction Method
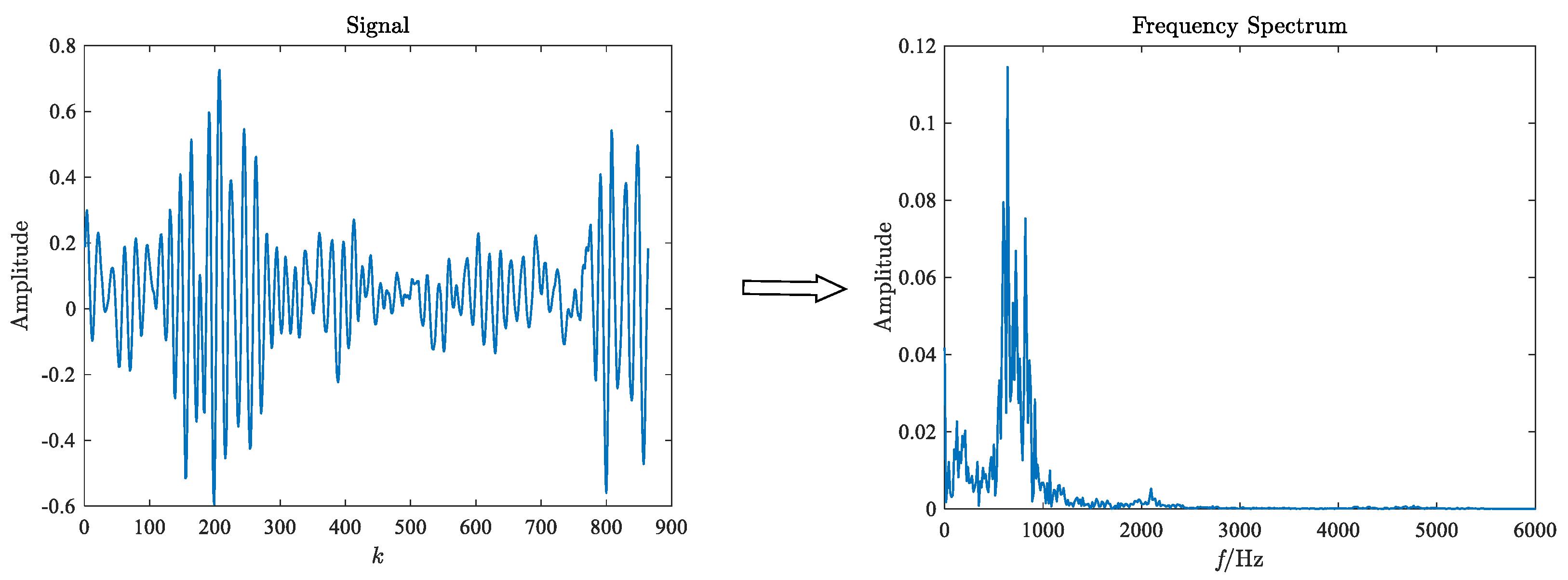
2.1. FFT
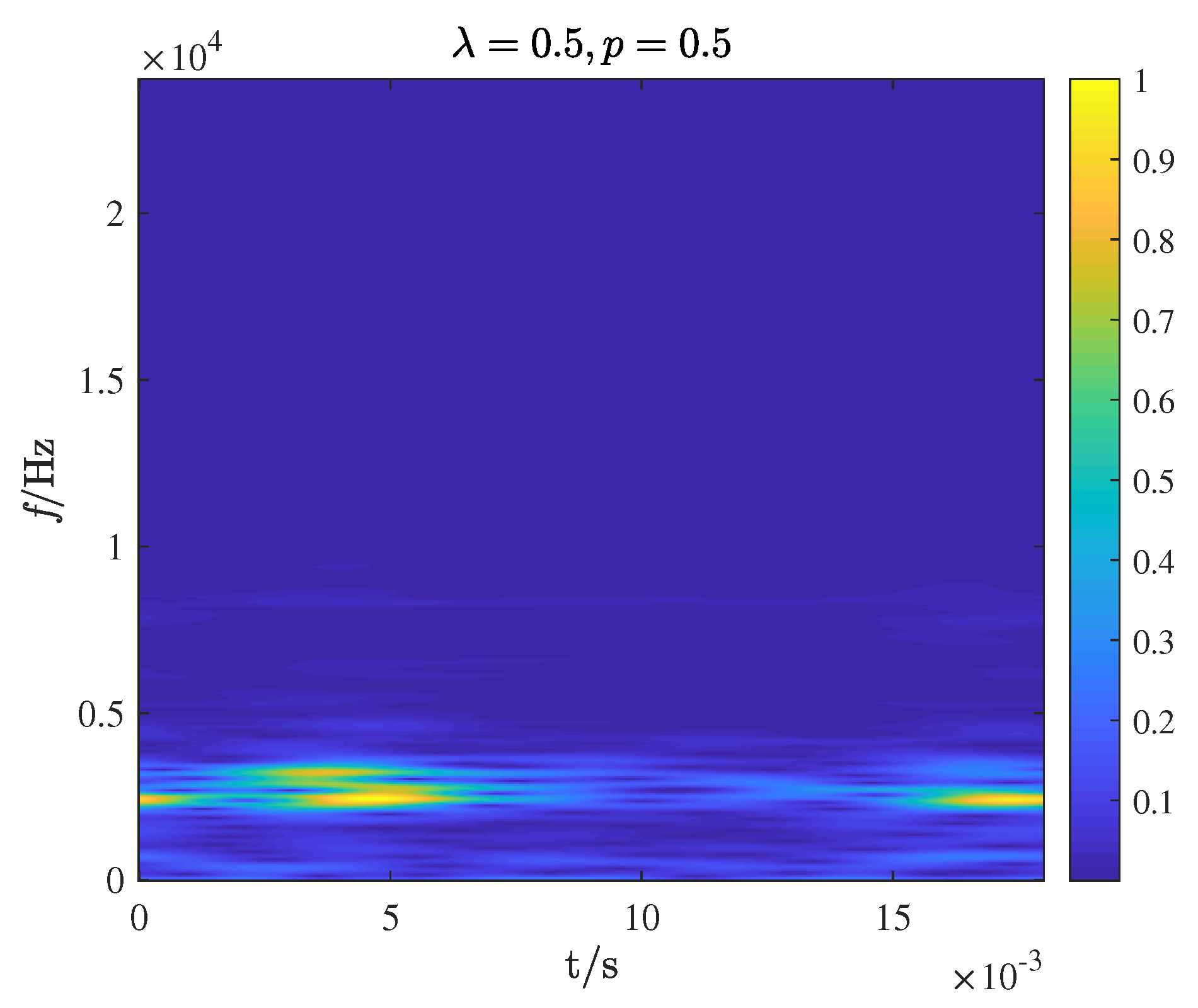
2.2. GST
3. TC-CNN Model Framework
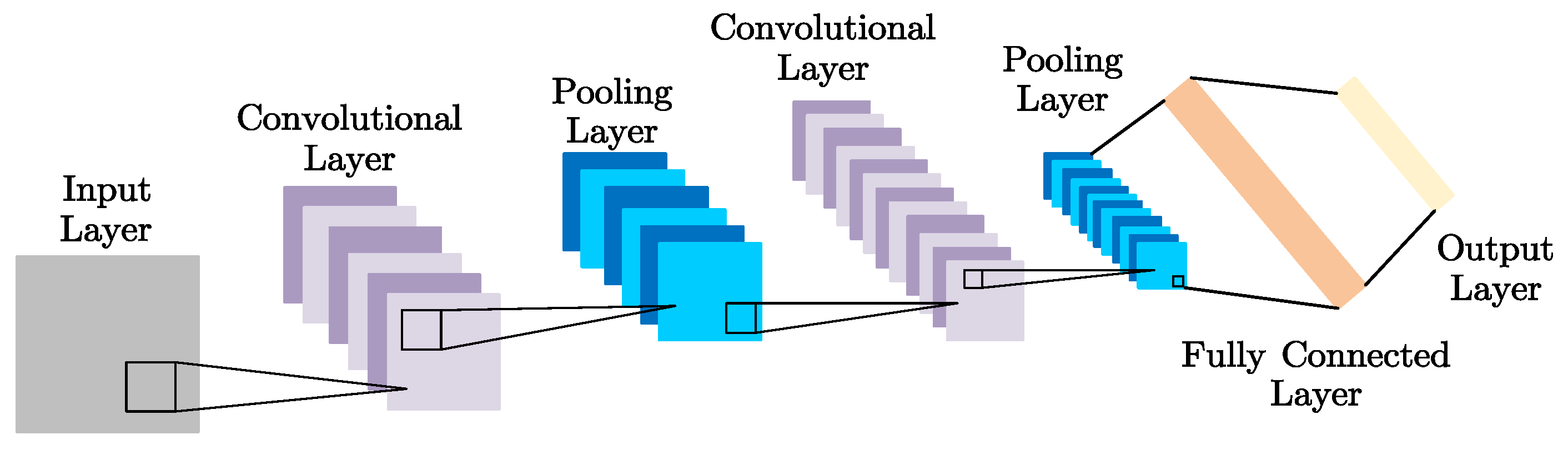
3.1. CNN
3.1.1. Convolutional Layer
3.1.2. Activation Function
3.1.3. Pooling Layer
3.1.4. Fully Connected Layer
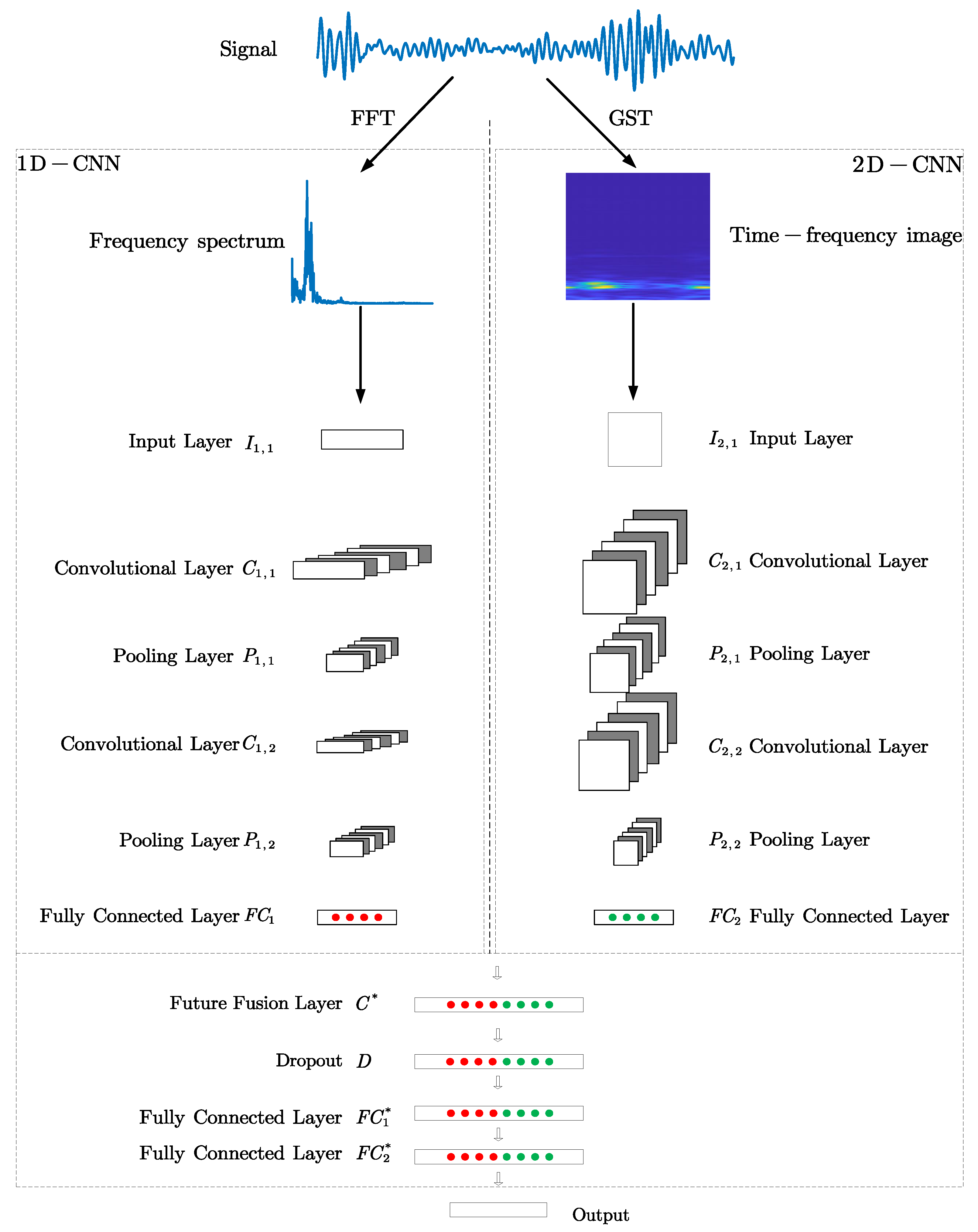
3.2. The Proposed TC-CNN Model
3.3. Evaluation Criterion
| Predicted | |||
| Actual | Positive | Negative | |
| Positive | True Positive (TP) | False Positive (FP) | |
| Negative | False Negative (FN) | True Negative (TN) | |
3.3.1. Accuracy
3.3.2. Precision
3.3.3. Recall
3.3.4. F1 Score
4. Experimental Analysis
4.1. Experimental Data
4.2. Model Parameters
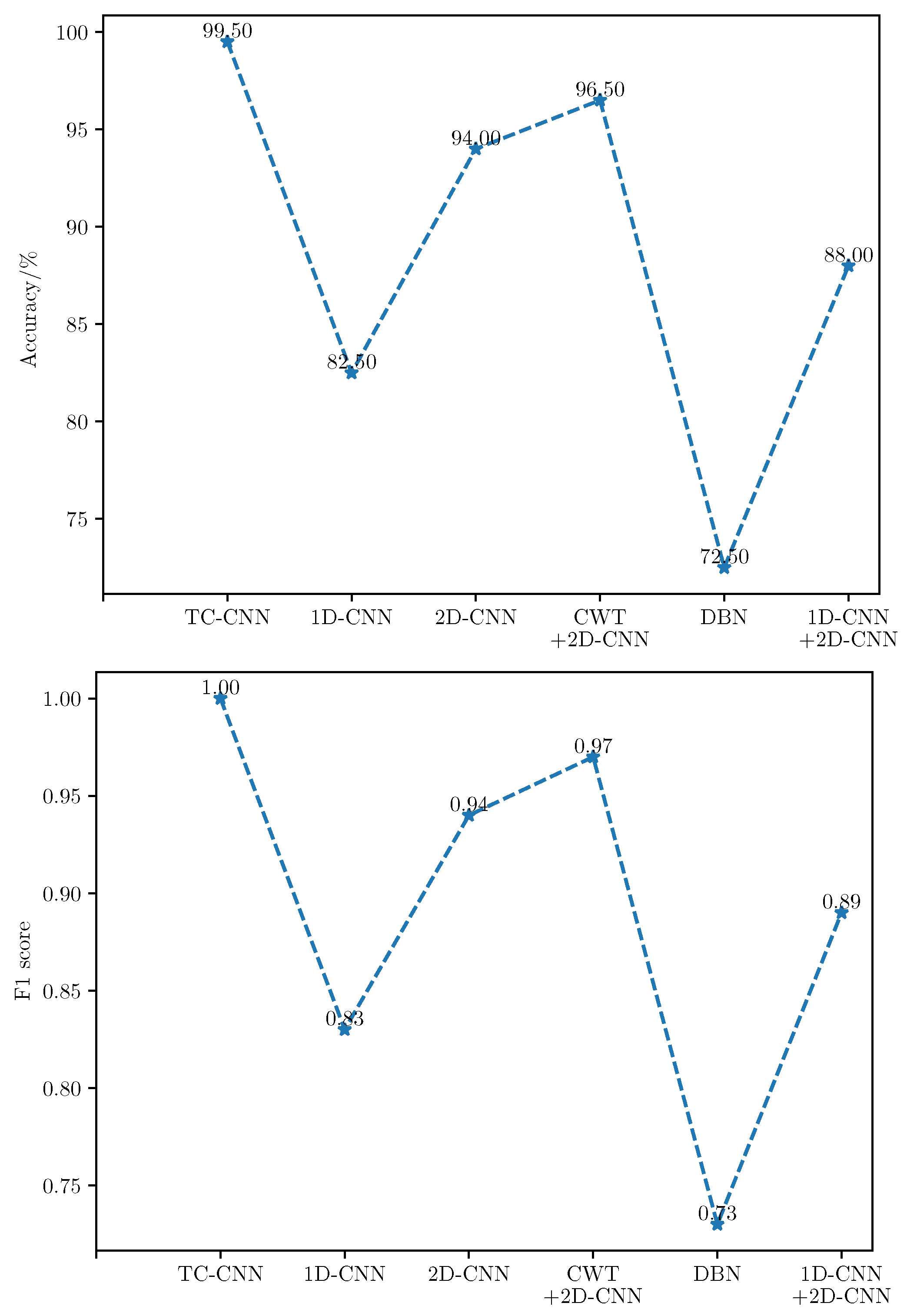
4.3. Fault Diagnosis Results under a Balanced Dataset
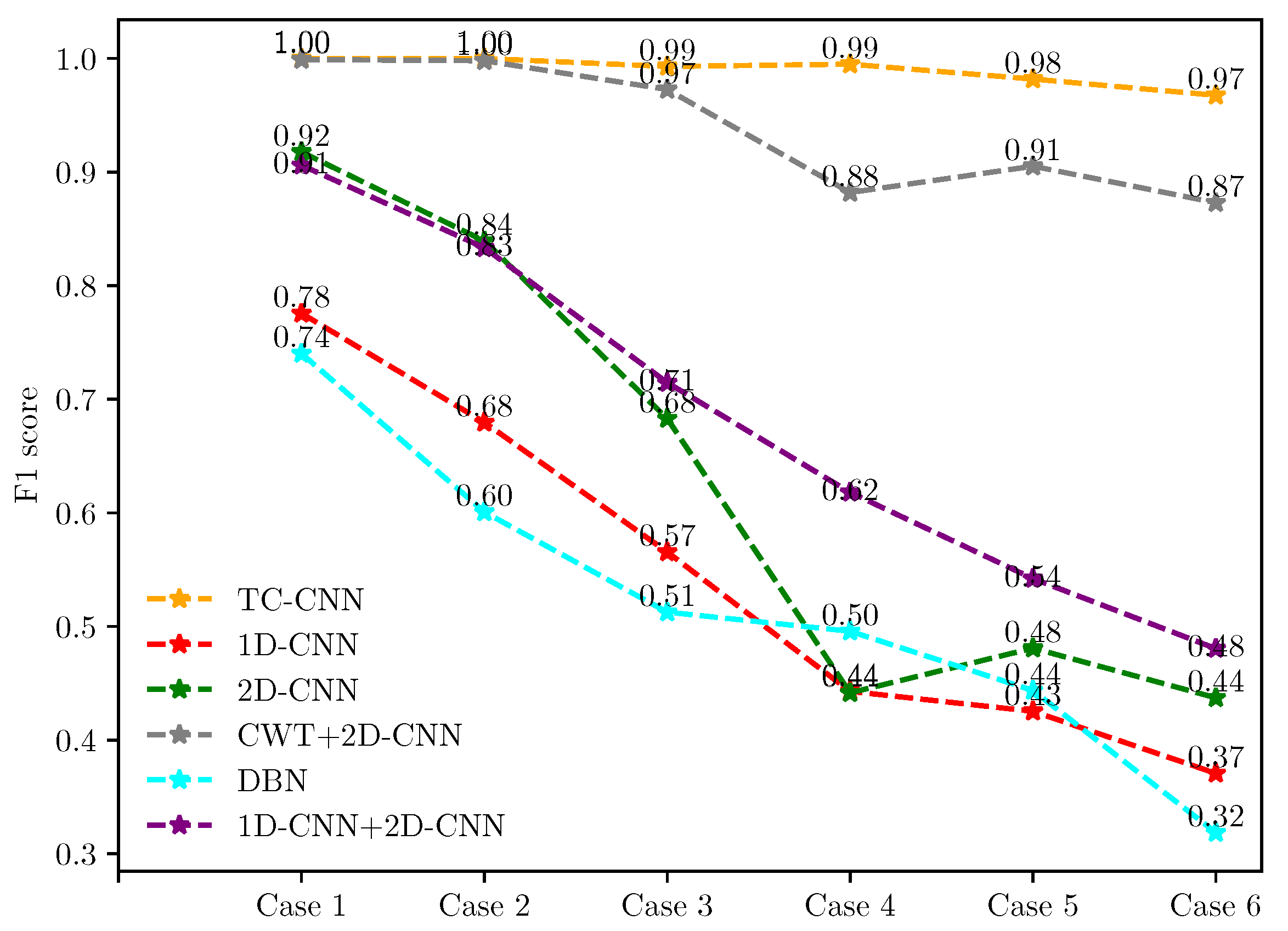
4.4. Fault Diagnosis Results under the Unbalanced Dataset
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, B.; Cai, W.; Han, Y.; Yu, G. A novel probability confidence CNN model and its application in mechanical fault diagnosis. IEEE Trans. Instrum. Meas. 2021, 70, 3517111. [Google Scholar] [CrossRef]
- Yang, X.; Yan, X. A transferrable data-driven method for IGBT open-circuit fault diagnosis in three-phase inverters. IEEE Trans. Power Electron. 2021, 70, 13474–13488. [Google Scholar] [CrossRef]
- Samanta, A.; Chowdhuri, S.; Williamson, S.S. Machine learning-based data-driven fault detection/diagnosis of Lithium-Ion battery: A critical review. Electronics 2021, 10, 1309. [Google Scholar] [CrossRef]
- Zheng, Z.; Fu, J.; Lu, C.; Zhu, Y. Research on rolling bearing fault diagnosis of small dataset based on a new optimal transfer learning network. Measurement 2021, 177, 109285. [Google Scholar] [CrossRef]
- Rabah, A.; Abdelhafid, K. Rolling bearing fault diagnosis based on improved complete ensemble empirical mode of decomposition with adaptive noise combined with minimum entropy deconvolution. J. Vibroeng. 2018, 20, 240–257. [Google Scholar] [CrossRef]
- Andreas, K.; Robbersmyr, K.G. Cross-correlation of whitened vibration signals for low-speed bearing diagnostics. Mech. Syst. Signal Process. 2019, 118, 226–244. [Google Scholar] [CrossRef]
- Chen, Z.; Cen, J.; Xiong, J. Rolling bearing fault diagnosis using time-frequency analysis and deep transfer convolutional neural network. IEEE Access 2020, 8, 150248–150261. [Google Scholar] [CrossRef]
- Udmale, S.S.; Singh, S.K. Application of spectral kurtosis and improved extreme learning machine for bearing fault classification. IEEE Trans. Instrum. Meas. 2019, 68, 4222–4233. [Google Scholar] [CrossRef]
- Kannan, V.; Li, H.; Dao, D.V. Demodulation band optimization in envelope analysis for fault diagnosis of rolling element bearings using a real-coded genetic algorithm. IEEE Access 2019, 7, 168828–168838. [Google Scholar] [CrossRef]
- Roy, S.S.; Dey, S.; Chatterjee, S. Autocorrelation aided random forest classifier-based bearing fault detection framework. IEEE Sensors J. 2020, 20, 10792–10800. [Google Scholar] [CrossRef]
- He, J.; Yang, S.; Gan, C. Unsupervised fault diagnosis of a gear transmission chain using a deep belief network. Sensors 2017, 17, 1564. [Google Scholar] [CrossRef]
- Ma, M.; Sun, C.; Chen, X. Deep coupling autoencoder for fault diagnosis with multimodal sensory data. IEEE Trans. Ind. Informatics 2018, 14, 1137–1145. [Google Scholar] [CrossRef]
- Jing, L.; Zhao, M.; Li, P.; Xu, X. A convolutional neural network based feature learning and fault diagnosis method for the condition monitoring of gearbox. Measurement 2017, 111, 1–10. [Google Scholar] [CrossRef]
- Dixit, S.; Verma, N.K.; Ghosh, A.K. Intelligent fault diagnosis of rotary machines: Conditional auxiliary classifier GAN coupled with meta learning using limited data. IEEE Trans. Instrum. Meas. 2021, 70, 3517811. [Google Scholar] [CrossRef]
- Nasiri, A.; Taheri-Garavand, A.; Omid, M.; Carlomagnoc, G.M. Intelligent fault diagnosis of cooling radiator based on deep learning analysis of infrared thermal images. Appl. Therm. Eng. 2019, 163, 114410. [Google Scholar] [CrossRef]
- Gu, Y.; Cao, J.; Song, X.; Yao, J. A denoising autoencoder-based bearing fault diagnosis system for time-domain vibration signals. Wirel. Commun. Mob. Comput. 2021, 2021, 9790053. [Google Scholar] [CrossRef]
- Saucedo-Dorantes, J.J.; Arellano-Espitia, F.; Delgado-Prieto, M.; Osornio-Rios, R.A. Diagnosis methodology based on deep feature learning for fault identification in metallic, hybrid and ceramic bearings. Sensors 2021, 21, 5832. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Zhao, H.; Wang, F. An enhancement deep feature fusion method for rotating machinery fault diagnosis. Knowl.-Based Syst. 2017, 119, 200–220. [Google Scholar] [CrossRef]
- Levent, E. Bearing fault detection by one-dimensional convolutional neural networks. Math. Probl. Eng. 2017, 2017, 8617315. [Google Scholar] [CrossRef]
- Pan, J.; Zi, Y.; Chen, J.; Zhou, Z.; Wang, B. LiftingNet: A novel deep learning network with layerwise feature learning from noisy mechanical data for fault classification. IEEE Trans. Ind. Electron. 2018, 65, 4973–4982. [Google Scholar] [CrossRef]
- Qiao, H.; Wang, T.; Wang, P.; Zhang, L.; Xu, M. An adaptive weighted multiscale convolutional neural network for rotating machinery fault diagnosis under variable operating conditions. IEEE Access 2019, 7, 118954–118964. [Google Scholar] [CrossRef]
- Peng, X.; Zhang, B.; Gao, D. Research on fault diagnosis method of rolling bearing based on 2DCNN. In Proceedings of the 2020 Chinese Control and Decision Conference, Hefei, China, 22–24 August 2020; pp. 693–697. [Google Scholar] [CrossRef]
- He, Z.; Shao, H.; Cheng, J.; Zhao, X.; Yang, Y. Support tensor machine with dynamic penalty factors and its application to the fault diagnosis of rotating machinery with unbalanced data. Mech. Syst. Signal Process. 2020, 141, 106441. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Tang, H.; Gao, S.; Wang, L.; Li, X.; Li, B.; Pang, S. A novel intelligent fault diagnosis method for rolling bearings based on wasserstein generative adversarial network and convolutional neural network under unbalanced dataset. Sensors 2021, 21, 6754. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J.; Wang, Y. An intelligent diagnosis scheme based on generative adversarial learning deep neural networks and its application to planetary gearbox fault pattern recognition. Neurocomputing 2018, 310, 213–222. [Google Scholar] [CrossRef]
- Mao, W.; Liu, Y.; Ding, L.; Li, Y. Imbalanced fault diagnosis of rolling bearing based on generative adversarial network: A comparative study. IEEE Access 2019, 7, 9515–9530. [Google Scholar] [CrossRef]
- Xuan, Q.; Chen, Z.; Liu, Y.; Huang, H.; Bao, G.; Zhang, D. Multiview generative adversarial network and its application in pearl classication. IEEE Trans. Ind. Electron. 2019, 66, 8244–8252. [Google Scholar] [CrossRef]
- Lee, Y.O.; Jo, J.; Hwang, J. Application of deep neural network and generative adversarial network to industrial maintenance: A case study of induction motor fault detection. In Proceedings of the IEEE International Conference on Big Data, Boston, MA, USA, 11–14 December 2017; pp. 3248–3253. [Google Scholar] [CrossRef]
- Han, T.; Liu, C.; Yang, W.; Jiang, D. A novel adversarial learning framework in deep convolutional neural network for intelligent diagnosis of mechanical faults. Knowledge Based Syst. 2019, 165, 474–487. [Google Scholar] [CrossRef]
- Akhenia, P.; Bhavsar, K.; Panchal, J.; Vakharia, V. Fault severity classification of ball bearing using SinGAN and deep convolutional neural network. Proc. Inst. Mech. Eng. Part J. Mech. Eng. Sci. 2022, 236, 3864–3877. [Google Scholar] [CrossRef]
- Tong, Q.; Lu, F.; Feng, Z.; Wan, Q.; An, G.; Cao, J.; Guo, T. A novel method for fault diagnosis of bearings with small and imbalanced data based on generative adversarial networks. Appl. Sci. 2022, 12, 7346. [Google Scholar] [CrossRef]
- Ruan, D.; Song, X.; Gühmann, C.; Yan, J. Collaborative optimization of CNN and GAN for bearing fault diagnosis under unbalanced datasets. Lubricants 2021, 9, 105. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Liang, X.; Huang, W. Application of bandwidth EMD and adaptive multiscale morphology analysis for incipient fault diagnosis of rolling bearings. IEEE Trans. Ind. Electron. 2017, 64, 6506–6517. [Google Scholar] [CrossRef]
- Liu, H.; Li, L.; Ma, J. Rolling bearing fault diagnosis based on STFT-deep learning and sound signals. Shock Vib. 2016, 2016, 6127479.1–6127479.12. [Google Scholar] [CrossRef]
- Cai, J.; Chen, Q. Bearing fault diagnosis method based on local mean decomposition and wigner higher moment spectrum. Exp. Tech. 2016, 40, 1437–1446. [Google Scholar] [CrossRef]
- Rauber, T.W.; de Assis Boldt, F.; Varejao, F.M. Heterogeneous feature models and feature selection applied to bearing fault diagnosis. IEEE Trans. Ind. Electron. 2015, 62, 637–646. [Google Scholar] [CrossRef]
- Gou, L.; Li, H.; Zheng, H.; Li, H.; Pei, X. Aeroengine control system sensor fault diagnosis based on CWT and CNN. Math. Probl. Eng. 2020, 2020, 5357146. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, T. Feature extraction based on DWT and CNN for rotating machinery fault diagnosis. In Proceedings of the 29th Chinese Control In addition, Decision Conference, IEEE, Chongqing, China, 28–30 May 2017; pp. 3861–3866. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, X.; Li, H.; Yang, Z. Intelligent fault diagnosis of rolling bearings based on normalized CNN considering data imbalance and variable working conditions. Knowl.-Based Syst. 2020, 199, 105971. [Google Scholar] [CrossRef]
- Saif, W.S.; Alshawi, T.; Esmail, M.A.; Ragheb, A.; Alshebeili, S. Separability of histogram based features for optical performance monitoring: An investigation using t-SNE technique. IEEE Photonics J. 2019, 11, 7203012. [Google Scholar] [CrossRef]
- Ma, L.; Yang, Y.; Wang, H. DBN based automatic modulation recognition for ultra-low SNR RFID signals. In Proceedings of the 2016 35th Chinese Control Conference, IEEE, Chengdu, China, 27–29 July 2016; pp. 7054–7057. [Google Scholar] [CrossRef]

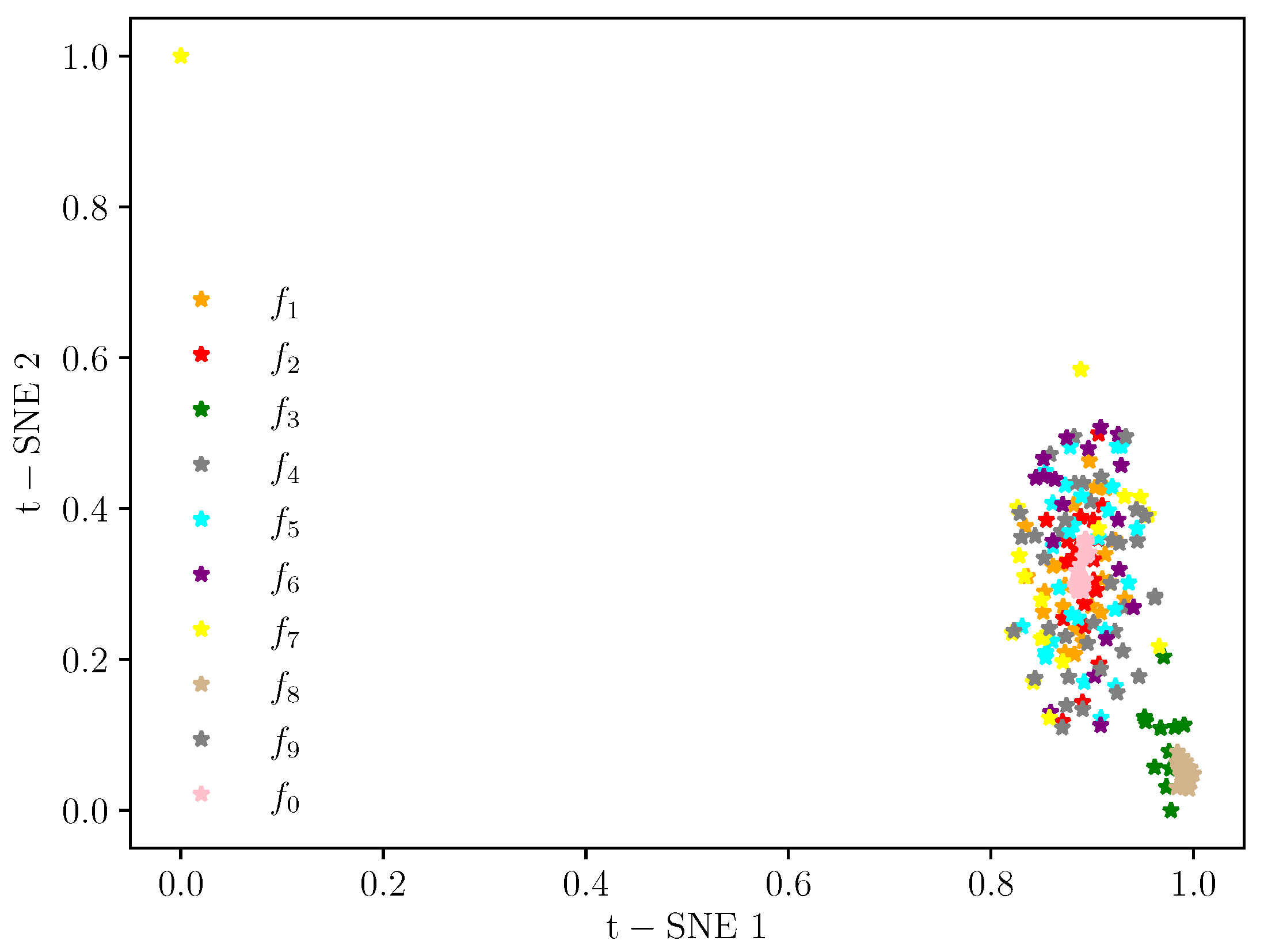
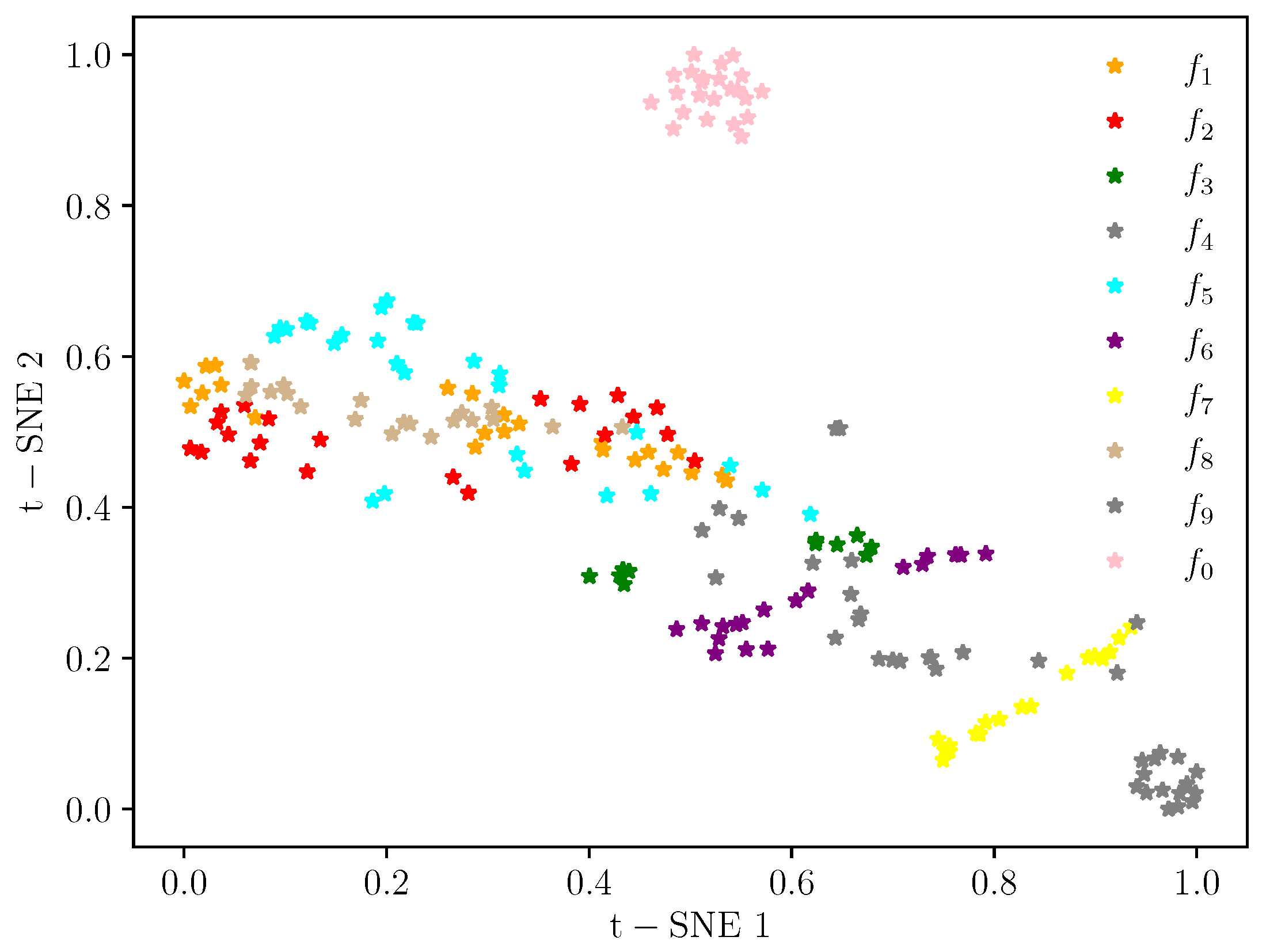
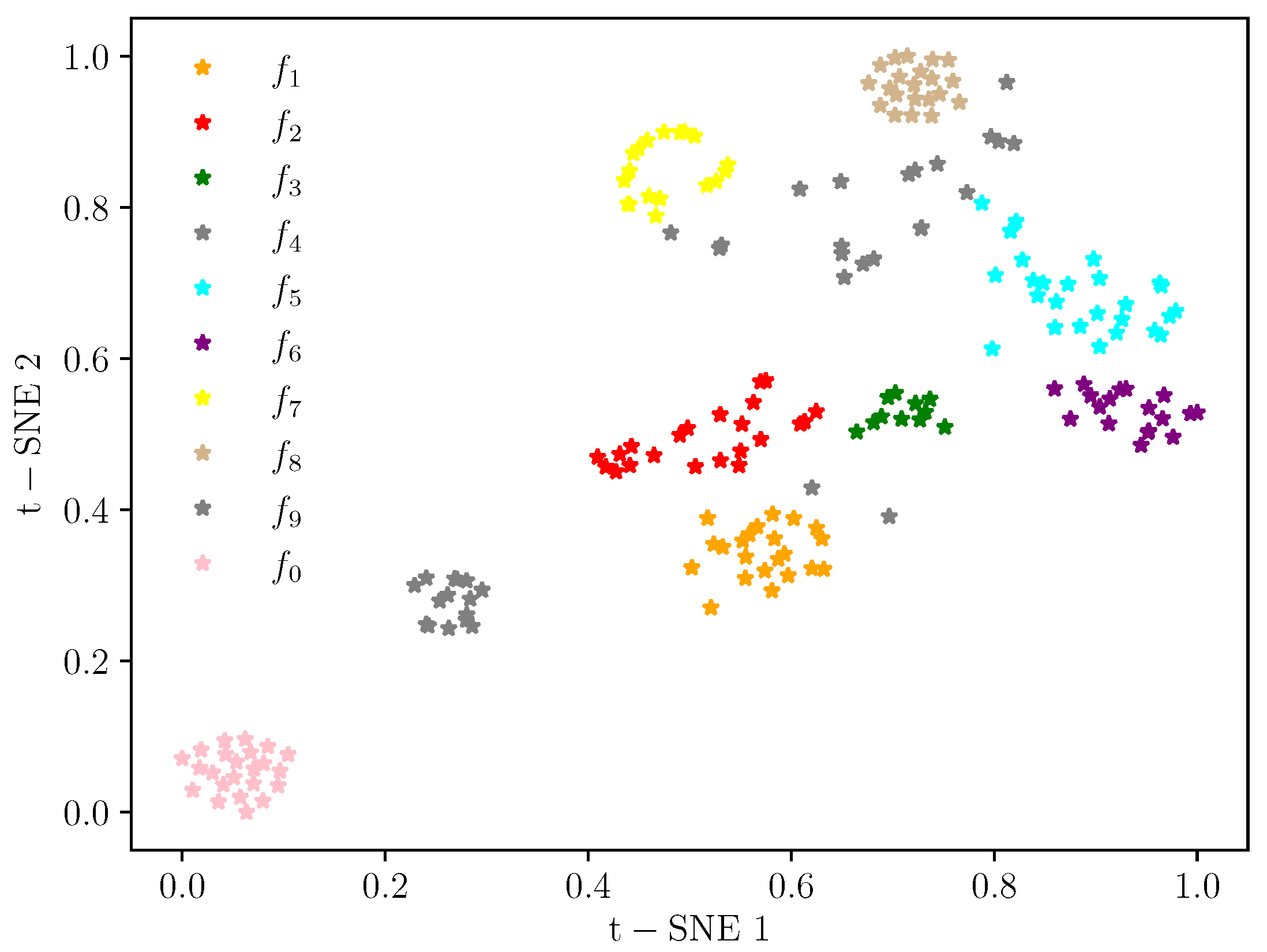
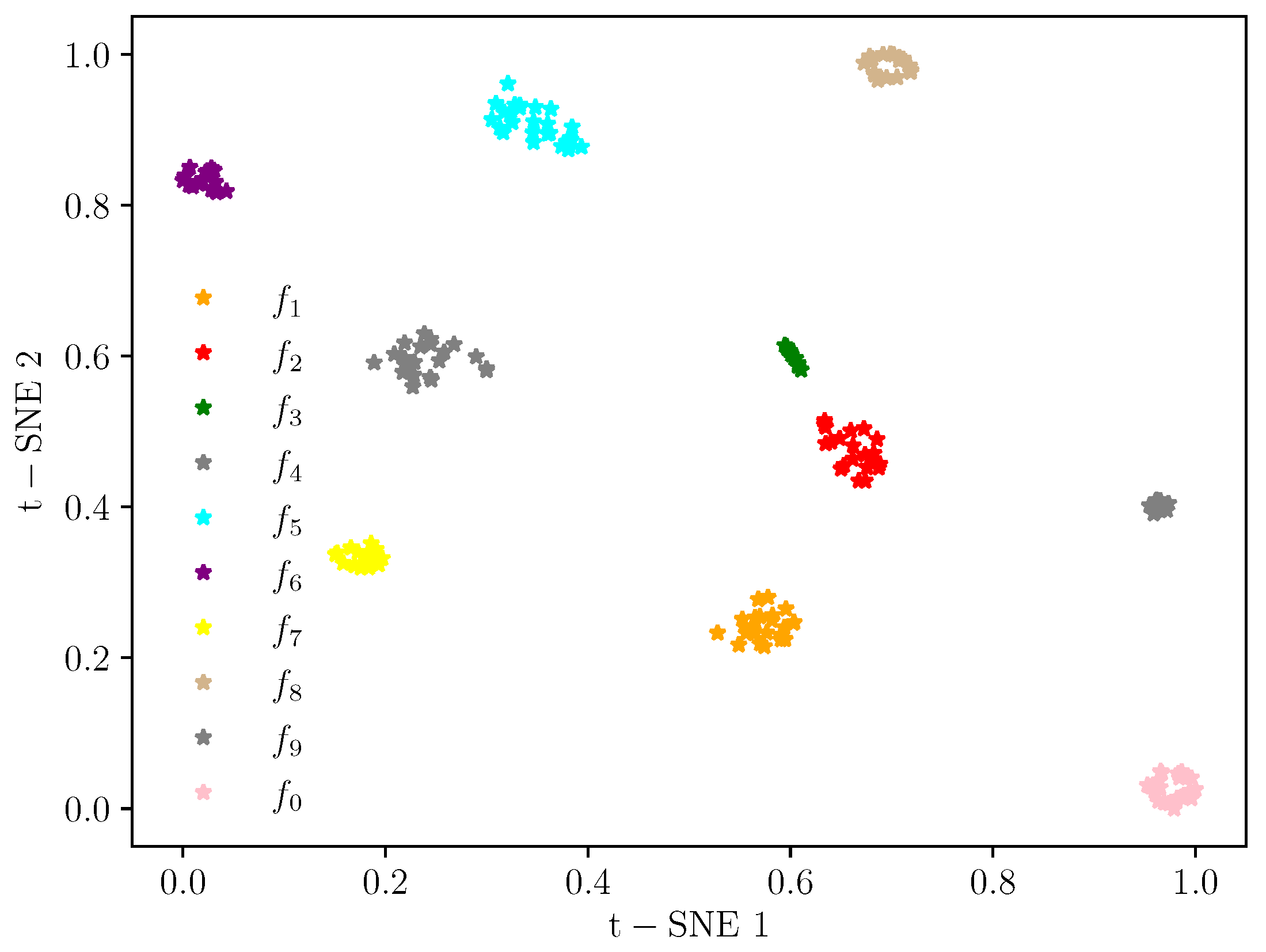

| Location | Fault Diameter (inch) | Fault Orientation | Label |
|---|---|---|---|
| Ball | 0.007 | - | |
| Ball | 0.014 | - | |
| Ball | 0.021 | - | |
| Inner race | 0.007 | - | |
| Inner race | 0.014 | - | |
| Inner race | 0.021 | - | |
| Outer race | 0.007 | Center @6:00 | |
| Outer race | 0.014 | Center @6:00 | |
| Outer race | 0.021 | Center @6:00 | |
| Normal | - | - |
| Layer Name | Parameter | Layer Size |
|---|---|---|
| - | ||
| - | ||
| Conv(), kernel size = 6 | ||
| Conv(), kernel size = 5 | ||
| kernel size = 4 | ||
| kernel size = 2 | ||
| Conv(), kernel size = 5 | ||
| Conv(), kernel size = 5 | ||
| kernel size = 3 | ||
| kernel size = 2 | ||
| - | 656 | |
| - | 2704 | |
| - | 3360 | |
| D | - | 3360 |
| 84 | ||
| SVM | 10 | |
| O | - |
| Method | Accuracy (%) | ||
|---|---|---|---|
| Training Set | Validation Set | Test Set | |
| TC-CNN | 100.00 | 99.50 | 99.50 |
| 1D-CNN | 100.00 | 81.25 | 82.50 |
| 2D-CNN | 100.00 | 95.00 | 94.00 |
| CWT+2DCNN | 97.71 | 96.25 | 96.50 |
| DBN | 100.00 | 74.00 | 72.50 |
| 1D-CNN+2D-CNN | 100.00 | 91.00 | 88.00 |
| Label | Method | |||||
|---|---|---|---|---|---|---|
| TC-CNN | 1D-CNN | 2D-CNN | CWT+2DCNN | DBN | 1D-CNN+2D-CNN | |
| 1.00 | 0.74 | 0.86 | 0.94 | 0.58 | 0.73 | |
| 1.00 | 0.70 | 0.77 | 0.96 | 0.71 | 0.75 | |
| 1.00 | 0.87 | 1.00 | 0.90 | 1.00 | 1.00 | |
| 1.00 | 0.81 | 1.00 | 1.00 | 0.58 | 0.87 | |
| 0.98 | 0.71 | 0.92 | 0.98 | 0.51 | 0.88 | |
| 1.00 | 0.81 | 1.00 | 1.00 | 0.72 | 0.89 | |
| 1.00 | 0.96 | 1.00 | 1.00 | 0.74 | 0.97 | |
| 1.00 | 1.00 | 1.00 | 0.90 | 1.00 | 1.00 | |
| 1.00 | 0.81 | 0.95 | 1.00 | 0.52 | 0.83 | |
| 1.00 | 0.98 | 0.97 | 1.00 | 0.96 | 1.00 | |
| F1 score (macro) | 1.00 | 0.83 | 0.94 | 0.97 | 0.73 | 0.89 |
| Unbalanced Cases | Size of Normal Condition | Size of Each Kind of Fault Conditions | |||
|---|---|---|---|---|---|
| Training Dataset | Testing Dataset | Training Dataset | Testing Dataset | ||
| Case 1 | 2:1 | 300 | 100 | 150 | 100 |
| Case 2 | 5:1 | 300 | 100 | 60 | 100 |
| Case 3 | 10:1 | 300 | 100 | 30 | 100 |
| Case 4 | 20:1 | 300 | 100 | 15 | 100 |
| Case 5 | 30:1 | 300 | 100 | 10 | 100 |
| Case 6 | 50:1 | 300 | 100 | 6 | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, Y.; Shi, X. Fault Diagnosis Method for Rolling Bearings Based on Two-Channel CNN under Unbalanced Datasets. Appl. Sci. 2022, 12, 8474. https://doi.org/10.3390/app12178474
Qin Y, Shi X. Fault Diagnosis Method for Rolling Bearings Based on Two-Channel CNN under Unbalanced Datasets. Applied Sciences. 2022; 12(17):8474. https://doi.org/10.3390/app12178474
Chicago/Turabian StyleQin, Yufeng, and Xianjun Shi. 2022. "Fault Diagnosis Method for Rolling Bearings Based on Two-Channel CNN under Unbalanced Datasets" Applied Sciences 12, no. 17: 8474. https://doi.org/10.3390/app12178474
APA StyleQin, Y., & Shi, X. (2022). Fault Diagnosis Method for Rolling Bearings Based on Two-Channel CNN under Unbalanced Datasets. Applied Sciences, 12(17), 8474. https://doi.org/10.3390/app12178474






