Minimum Sample Size Estimate for Classifying Invasive Lung Adenocarcinoma
Abstract
1. Introduction
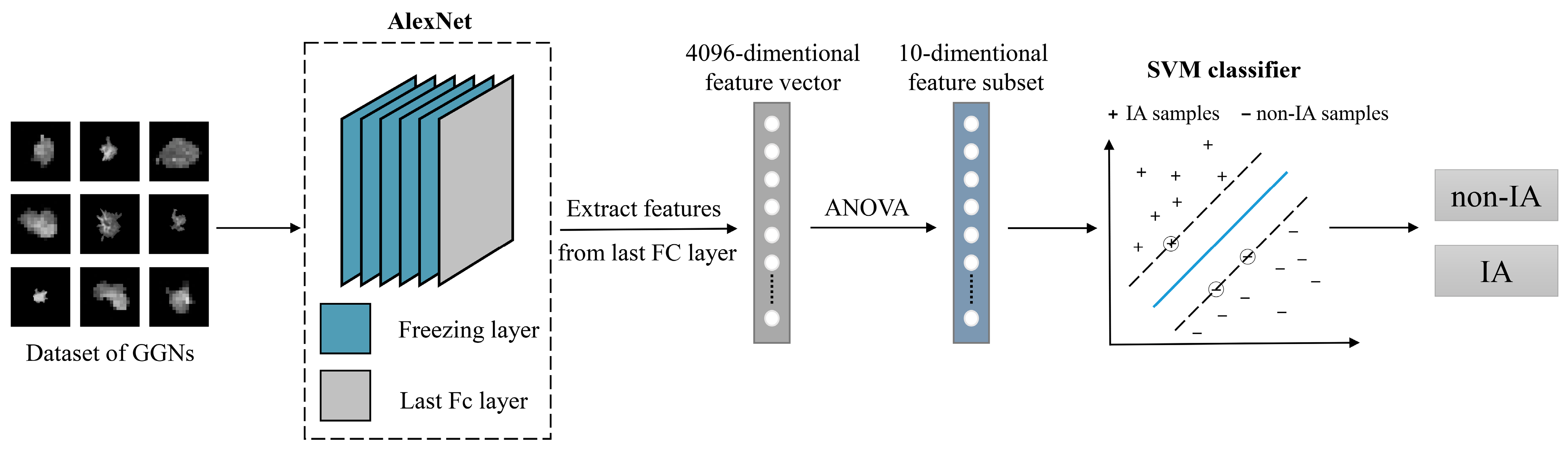
2. Materials and Methods
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, fand prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Golino, H.F.; Epskamp, S. Exploratory graph analysis: A new approach for estimating the number of dimensions in psychological research. PLoS ONE 2017, 12, e0174035. [Google Scholar] [CrossRef] [PubMed]
- Ha, M.H.; Tian, J. The theoretical foundations of statistical learning theory based on fuzzy number samples. Inf. Sci. 2008, 178, 3240–3246. [Google Scholar] [CrossRef]
- Loh, P.L. On lower bounds for statistical learning theory. Entropy 2018, 19, 667. [Google Scholar] [CrossRef]
- Jain, S. Computer-aided detection system for the classification of non-small cell lung lesions using SVM. Curr. Comput. Aided Drug Des. 2020, 16, 833–840. [Google Scholar] [CrossRef]
- Wang, J.; Liu, X.; Dong, D.; Song, J.; Xu, M.; Zang, Y.; Tian, J. Prediction of malignant and benign Lung tumors using a quantitative radiomic method. Acta Autom. Sin. 2017, 43, 2109–2114. [Google Scholar]
- Ye, Y.; Tian, M.; Liu, Q.; Tai, H.-M. Pulmonary nodule detection using v-net and high-level descriptor based SVM classifier. IEEE Access 2020, 8, 176033–176041. [Google Scholar] [CrossRef]
- Ladayya, F.; Purnami, S.W.; Irhamah. Fuzzy Support Vector Machine for Microarray Imbalanced Data Classification. In Proceedings of the 13th IMT-GT International Conference on Mathematics, Statistics and their Applications (ICMSA), Universiti Utara Malaysia, Kedah, Malaysia, 4–7 December 2017. [Google Scholar]
- Ardila, D.; Kiraly, A.P.; Bharadwaj, S.; Choi, B.; Reicher, J.J.; Peng, L.; Tse, D.; Etemadi, M.; Ye, W.; Corrado, G.; et al. End-to-end lung cancer screening with three-dimensional deep learning on low-dose chest computed tomography. Nat. Med. 2019, 25, 954–961. [Google Scholar] [CrossRef]
- Land, W.H.; Margolis, D.; Gottlieb, R.; Yang, J.Y.; Krupinski, E.A. Improving CT prediction of treatment response in patients with metastatic colorectal carcinoma using statistical learning. Int. J. Comput. Biol. Drug Des. 2010, 3, 8–15. [Google Scholar] [CrossRef]
- Muselli, M.; Ruffino, F. Consistency of Empirical Risk Minimization for Unbounded Loss Functions. In Proceedings of the 15th Italian Workshop on Neural Nets, Perugia, Italy, 14–17 September 2004. [Google Scholar]
- Zhang, X.; Ha, M.; Wu, J.; Wang, C. The Bounds on the Rate of Uniform Convergence of learning Process on Uncertainty Space. In Proceedings of the 6th International Symposium on Neural Networks, Wuhan, China, 26–29 May 2009. [Google Scholar]
- Chen, D.R.; Sun, T. Consistency of multiclass empirical risk minimization methods based on convex loss. J. Mach. Learn. Res. 2006, 7, 2435–2447. [Google Scholar]
- Naik, A.; Edla, D.R. Lung Nodule Classification on computed tomography images using deep learning. Wirel. Pers. Commun. Vol. 2021, 116, 655–690. [Google Scholar] [CrossRef]
- Alamgeer, M.; Mengash, H.A.; Marzouk, R.; Nour, M.K.; Hilal, A.M.; Motwakel, A.; Zamani, A.S.; Rizwanullah, M. Deep learning enables computer aided diagnosis model for lung cancer using biomedical CT images. Comput. Mater. Contin. 2022, 73, 1437–1448. [Google Scholar]
- Nemec, U.; Heidinger, B.; Anderson, K.R.; Westmore, M.S.; VanderLaan, P.; Bankier, A.A. Software-based risk stratification of pulmonary adenocarcinomas manifesting as pure ground glass nodules on computed tomography. Eur. Radiol. 2018, 28, 235–242. [Google Scholar] [CrossRef] [PubMed]
- Dimitri, G.M.; Spasov, S.; Duggento, A.; Passamonti, L.; Toschi, N. Unsupervised Stratification in Neuroimaging through Deep Latent Embeddings. In Proceedings of the 42nd Annual International Conference of the IEEE-Engineering-in-Medicine-and-Biology-Society, Montreal, Canada, 20–24 July 2020. [Google Scholar]
- Shin, H.-C.; Roth, H.R.; Gao, M.; Lu, L.; Xu, Z.; Nogues, I.; Yao, J.; Mollura, D.; Summers, R.M. Deep convolutional neural networks for computer-aided detection: CNN architectures, dataset characteristics and transfer learning. IEEE Trans. Med. Imaging 2016, 35, 1285–1298. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.H.; MacKinnon, T. Artificial intelligence in fracture detection: Transfer learning from deep convolutional neural networks. Clin. Radiol. 2018, 73, 439–445. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Bengio, Y.; Lecun, Y.; Hinton, G. Deep learning for AI. Commun. ACM 2021, 64, 58–65. [Google Scholar] [CrossRef]
- Affonso, C.; Rossi, A.L.D.; Vieira, F.H.A.; de Leon Ferreira, A.C.P. D eep learning for biological image classification. Expert Syst. Appl. 2017, 85, 114–122. [Google Scholar] [CrossRef]
- Rachapudi, V.; Devi, G.L. Improved convolutional neural network based histopathological image classification. Evol. Intell. 2021, 14, 1337–1343. [Google Scholar] [CrossRef]
- Da Nóbrega, R.V.M.; Rebouças Filho, P.P.; Rodrigues, M.B.; da Silva, S.P.; Dourado Júnior, C.M.; de Albuquerque, V.H.C. Lung nodule malignancy classification in chest computed tomography images using transfer learning and convolutional neural networks. Neural Comput. Appl. 2020, 32, 11065–11082. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Processing Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Pan, S.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Demir, F.; Bajaj, V.; Ince, M.C.; Taran, S.; Şengür, A. Surface EMG signals and deep transfer learning-based physical action classification. Neural Comput. Appl. 2019, 31, 8455–8462. [Google Scholar] [CrossRef]
- Polat, H.; Mehr, H.D. Classification of pulmonary CT images by using hybrid 3D-deep convolutional neural network architecture. Appl. Sci. 2019, 9, 940. [Google Scholar] [CrossRef]
- Nalik, A.; Edla, D.R. Lung nodules classification using combination of CNN, second and higher order texture features. J. Intell. Fuzzy Syst. 2021, 41, 5243–5251. [Google Scholar]
- Dutta, A.K. Detecting lung cancer using machine learning techniques. Intell. Autom. Soft Comput. 2021, 31, 1007–1023. [Google Scholar] [CrossRef]
- Shayma’a, A.H.; Sayed, M.S.; I Abdalla, M.I.; Rashwan, M.A. Breast cancer masses classification using deep convolutional neural networks and transfer learning. Multimed. Tools Appl. 2020, 79, 30735–30768. [Google Scholar]
- Cengil, E.; Nar, A. The effect of deep feature concatenation in the classification problem: An approach on COVID disease detection. Int. J. Imaging Syst. Technol. 2021, 32, 26–40. [Google Scholar] [CrossRef]
- Hou, X.X.; Xu, X.Z.; Zhu, J.; Guo, Y. Computer aided diagnosis method for breast cancer based on AlexNet and ensemble classifiers. J. Shandong Univ. Eng. Sci. 2019, 49, 74–79. [Google Scholar]
- Ma, C.C.; Yue, S.H.; Li, Q. Deep Transfer Learning Strategy for Invasive Lung Adenocarcinoma Classification Appearing as Ground Glass Nodules. In Proceedings of the 2021 IEEE International Instrumentation and Measurement Technology Conference, Glasgow, UK, 17–20 May 2021. [Google Scholar]
- Monica, L.; Gaddis, P.D. Statistical methodology: Analysis of variance, analysis of covariance, and multivariate analysis of variance. Acad. Emerg. Med. 1998, 5, 258–265. [Google Scholar]
- Song, X.S.; Jiang, X.Y.; Luo, J.H.; Wang, X. SVM parameter selection based on the bound of structure risk. Sci. Technol. Rev. 2011, 29, 72–74. [Google Scholar]
- Vaart, V.D.; Wellner, J.A. A note on bounds for VC dimensions. Inst. Math. Stat. Collect. 2009, 5, 103–107. [Google Scholar] [PubMed]
- Jayadeva. Learning a hyperplane classifier by minimizing an exact bound on the VC dimension. Neurocomputing 2015, 149, 683–689. [Google Scholar] [CrossRef][Green Version]
- Diego, M.; Rodrigo, M. Improvement of patient classification using feature selection applied to Bi-Directional Axial Transmission. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2022. [Google Scholar] [CrossRef]
- Mohammad, A.A.; Mwaffaq, O.; Hamza, J. Comprehensive and comparative global and local feature extraction framework for lung cancer detection using CT scan images. IEEE Access 2021, 9, 158140–158154. [Google Scholar]
- Dai, C. SVM Visual Classification Based on Weighted Feature of Genetic Algorithm. In Proceedings of the 2015 Sixth International Conference on Intelligent Systems Design and Engineering Applications, Guiyang, China, 18–19 August 2015. [Google Scholar]

| Number of Samples | Remp(w) | EXP (η = 0.05) | EXP (η = 0.10) | Rexp(w) in Test Set | ||
|---|---|---|---|---|---|---|
| Φ(n/h) in Equation (2) | Theoretical Value | Φ(n/h) in Equation (2) | Theoretical Value | |||
| n = 100 | 0 | 0.6877 | 0.6877 | 0.6826 | 0.6826 | 0.361 |
| n = 200 | 0.005 | 0.524 | 0.529 | 0.5207 | 0.5257 | 0.222 |
| n = 300 | 0.003 | 0.4449 | 0.4479 | 0.4423 | 0.4453 | 0.194 |
| n = 400 | 0.002 | 0.3954 | 0.3974 | 0.3932 | 0.3952 | 0.139 |
| Number of Classes | n = 3000 | n = 6000 | n = 9000 | n = 12,000 | n = 15,000 | n = 18,000 | n = 21,000 | n = 24,000 | |
|---|---|---|---|---|---|---|---|---|---|
| 95% confidence (d = 2) | c = 2 | 0.1103 | 0.0833 | 0.0710 | 0.0635 | 0.0583 | 0.0544 | 0.0514 | 0.0490 |
| c = 4 | 0.1841 | 0.1386 | 0.1176 | 0.1047 | 0.0957 | 0.0890 | 0.0838 | 0.0795 | |
| c = 6 | 0.2157 | 0.1624 | 0.1377 | 0.1225 | 0.1120 | 0.1040 | 0.0978 | 0.0928 | |
| c = 8 | 0.2416 | 0.1820 | 0.1542 | 0.1372 | 0.1253 | 0.1164 | 0.1094 | 0.1037 | |
| c = 10 | 0.2639 | 0.1989 | 0.1686 | 0.1499 | 0.1369 | 0.1272 | 0.1195 | 0.1132 | |
| 90% confidence (d = 2) | c = 2 | 0.1091 | 0.0825 | 0.0704 | 0.0630 | 0.0578 | 0.0540 | 0.0510 | 0.0486 |
| c = 4 | 0.1835 | 0.1382 | 0.1172 | 0.1044 | 0.0955 | 0.0888 | 0.0836 | 0.0793 | |
| c = 6 | 0.2151 | 0.1621 | 0.1374 | 0.1223 | 0.1117 | 0.1038 | 0.0976 | 0.0926 | |
| c = 8 | 0.2411 | 0.1817 | 0.1540 | 0.1370 | 0.1251 | 0.1163 | 0.1093 | 0.1036 | |
| c = 10 | 0.2634 | 0.1986 | 0.1683 | 0.1497 | 0.1367 | 0.1270 | 0.1193 | 0.1131 |
| Case | Number of Classes | Number of Features | EXP | Number of Samples (η = 0.05) | |
|---|---|---|---|---|---|
| Actual Value | Theoretical Value | ||||
| Diego et al. [39] | c = 2 | d = 2 | 0.32 | 301 | 235 |
| Mohammad et al. [40] | c = 2 | d = 10 | 0.31 | 1000 | 776 |
| Dai [41] | c = 2 | d = 40 | 0.47 | 1000 | 958 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, C.; Yue, S. Minimum Sample Size Estimate for Classifying Invasive Lung Adenocarcinoma. Appl. Sci. 2022, 12, 8469. https://doi.org/10.3390/app12178469
Ma C, Yue S. Minimum Sample Size Estimate for Classifying Invasive Lung Adenocarcinoma. Applied Sciences. 2022; 12(17):8469. https://doi.org/10.3390/app12178469
Chicago/Turabian StyleMa, Chenchen, and Shihong Yue. 2022. "Minimum Sample Size Estimate for Classifying Invasive Lung Adenocarcinoma" Applied Sciences 12, no. 17: 8469. https://doi.org/10.3390/app12178469
APA StyleMa, C., & Yue, S. (2022). Minimum Sample Size Estimate for Classifying Invasive Lung Adenocarcinoma. Applied Sciences, 12(17), 8469. https://doi.org/10.3390/app12178469





