Featured Application
Augmented musical creativity, computational musicology, and procedural representation of music for machine learning algorithms.
Abstract
We present GenoMus, a new model for artificial musical creativity based on a procedural approach, able to represent compositional techniques behind a musical score. This model aims to build a framework for automatic creativity, that is easily adaptable to other domains beyond music. The core of GenoMus is a functional grammar designed to cover a wide range of styles, integrating traditional and contemporary composing techniques. In its encoded form, both composing methods and music scores are represented as one-dimensional arrays of normalized values. On the other hand, the decoded form of GenoMus grammar is human-readable, allowing for manual editing and the implementation of user-defined processes. Musical procedures (genotypes) are functional trees, able to generate musical scores (phenotypes). Each subprocess uses the same generic functional structure, regardless of the time scale, polyphonic structure, or traditional or algorithmic process being employed. Some works produced with the algorithm have been already published. This highly homogeneous and modular approach simplifies metaprogramming and maximizes search space. Its abstract and compact representation of musical knowledge as pure numeric arrays is optimized for the application of different machine learning paradigms.
1. Introduction
1.1. New Challenges for Modeling Musical Creativity
Music creation and perception are extremely complex phenomena, simultaneously involving many time scales, cognitive layers, and social spheres. As an eminently creative activity, music is an excellent field of research to model mechanisms that lead to artistic production and to any human activity that requires creativity. This introduction summarizes the conceptual issues addressed by the GenoMus framework, outlined after considering many reviews of current research on automatic composition and artificial artistic creativity.
Despite the wide variety of existing systems, documented in metastudies and surveys [1,2], and the development of new techniques in artificial intelligence in many domains, the autonomous creation of music by computers is still clearly behind human skills. These limited results may be due to overly specific approaches. Pearce et al. [3] strongly criticized many investigations for narrowing their focus to processes too restricted to the idiosyncratic style of a particular composer, or to systems too oriented to the modeling of well-known historical styles. In particular, recent advances based on neural nets struggle to capture big structures, as Nierhaus [4] has noted after comparing the current paradigms in automated music generation.
Boden [5] and Rowe et al. [6] propose the necessary conditions for the emergence of artificial creativity, such as a flexible knowledge representation with a high degree of ambiguity, capable of exploring, transforming, and expanding the search space. Multiple possible representations of the same idea are also recommended. Papadopoulos and Wiggins [7], Crawford [8], and López de Mántaras [9] claim that more imaginative behavioral models will arise from hybrid multiagent systems embedding a variety of functionalities. These algorithms must devise musical patterns along with their expressive potentialities, just as humans do.
1.2. Composing Composers
Composers’ interest in rethinking and reinventing musical language have pervaded aesthetics and techniques since the 20th century. Transformation and the overcoming of well-established methods inherited from Romanticism led to post-tonal music. Linguistic structuralism applied to musical syntax stimulated a relativization and awareness of compositional procedures. Reversing the logic of this analytic knowledge, the methods of serial dodecaphonism laid the foundation stone for an inverse creative strategy: synthesize new styles from the predefinition of new rules.
The availability of computers led to the thinking of music composition from a higher level. Composers such as Stockhausen [10] and Xenakis, who designed composition tools to work “towards a metamusic” [11], began to exploit the new ideas of generative grammars in the sound domain. Computer-assisted composition enabled far more complex procedures that were too tedious or unfeasible to explore by hand. Eventually, composers began to use computers not only for analysis and the calculation of complex structures, but for the automation of the creative processes themselves. That fact opened the door to a new approach to composition: a metamusical level characterized by modeling the processes within the minds of composers.
Research in artificial musical intelligence demands formalized grammars of musical structures. Furthermore, a model of the creative mind is required to operate these abstractions. Aesthetic criteria are extremely subjective. Furthermore, the implementation of every model of automatic composition imposes, consciously or not, a limited search space. Delimiting these boundaries and setting evaluation principles can be seen as metacomposition, namely, modeling composers’ reasoning, often very obscure to themselves. As Jacob [12] analyzed, automatic composition not only creates new styles, but also new ways of perceiving and feeling the music. Beyond this, the very concept of authorship becomes paradoxical. In general, “programming creativity” is an oxymoron that inevitably leads to metaprogramming [13].
1.3. Features of a Procedural Oriented Composing-Aid System
Many modern approaches to artificial intelligence applied to the automatic composition of music are modeled using scores as their data source. The effectiveness of neural nets favors this kind of experiments. We considered the study of McCormack [14] regarding the difficulties of tuning evolutionary algorithms, as well as the comprehensive surveys that study a large number of similar projects. In the usual taxonomy of AI methods applied to music composition, GenoMus can be classified in the domain of evolutionary algorithms applied to grammars. Fernández and Vico’s exhaustive survey [1] concludes with some remarks regarding the important topic of encoding data to work with evo-devo systems. After identifying the problem of scalability, due to the enormous amount of information that a musical work can contain, they consider that many systems have addressed this bottleneck using “indirect encodings” that compress musical information by encapsulating the “list of instructions” needed to recreate a piece, but these encoding methods need to be highly improved and optimized. Otherwise, a good toy model can become intractable when scaled to handle and produce real pieces of music.
GenoMus’ design is devoted to this issue, and looks for strategies to compress and simplify as much as possible the procedural information while maintaining an interchangeable readable counterpart of this information. We conceive this indirect encoding of music as the core of the GenoMus framework: what must be learned by an AI engine is precisely this abstract representation of the composition techniques used in the creative process. With this in mind, we outlined the main characteristics of our model:
- Modularity:
- based on a very simple syntax.
- Compactness:
- the maximal compression of procedural information.
- Extensibility:
- subsets and supersets of the grammar that can be easily handled.
- Readability:
- both abstract and human-readable formats are safely interchangeable.
- Repeatibility:
- the same initial conditions always generate the same output.
- Self-referenceable:
- support for compression and iterative processes based on internal references.
- Extensibility:
- easily adaptable to other contexts and domains.
The closest proposal to GenoMus is the language and environment designed by Hofmann [15], sharing also commonalities with the projects by de la Puente et al. [16] and Ariza [17]. However, GenoMus is not only oriented to manual edition, but primarily to the encoding and compression of procedural information.
1.4. Knowledge Representation Optimized for Machine Learning by Design
After studying many different approaches, we decided to create GenoMus as a new model of the procedural representation of music optimized to be handled with different machine learning techniques. Its key feature is an identical encoded representation of both compositional procedures and musical results as one-dimensional arrays. Functional expressions and their output are both encoded as sequences of normalized floats. Some systems, such as Jive [18], have explored this conversion of pure numeric sequences into some kind of intermediate computable expression. Our system opens this formalism to be arbitrarily extensible.
The GenoMus grammar is designed to favor the broadest diversity of combinations and transformations. Genetic algorithms are suitable for the automation of incremental exploration and selection in multiple ways. Burton and Vladimirova [19] have studied several genetic methods applied to the generation of musical sequences; Dostál [20] also published a survey of techniques of evolutionary composition. GenoMus design favors genetic search processes in a very flexible manner, since data structures have no determined length and are one-dimensional. The evolution of musical ideas without constraints and based on serendipity is easily implemented and complemented.
On the other hand, approaches based on neural networks need a very controlled format of data and big training datasets. GenoMus’ format represents any piece of music as a simple one-dimensional sequence of normalized floats, which can be profitable for techniques such as recurrent neural networks, which are capable of learning patterns from sequential streams of data. Both procedural and declarative information (composition techniques and music scores) share the same data format. This correspondence inevitably resonates with other Gödelian approaches to bioinspired generative projects based on genetic algorithms [21].
The rest of the manuscript is organized as follows: Section 2 provides a formal view of the framework, Section 3 describes a practical implementation suitable for interactive experiments, Section 4 presents an example of a procedural representation and the recreation of a complete piece of music, and Section 5 discuss the possibilities opened by the characteristics of the model to enhance artificial musical creativity, as well as several possible strategies to address the evaluation and evolution of results.
2. Conceptual Framework
The artistic results of every algorithm designed for automated composition are strongly constrained by their representation of musical data. GenoMus is a framework for the exploration of artificial musical creativity based on a generative grammar focused on the abstraction of creative processes as a metalevel of compositional tasks.
We define musical genotypes as functional nested expressions, and phenotypes as the pieces created by evaluating these computable expressions. GenoMus’ grammar is designed to ease the combination of fundamental procedures behind very different styles, ranging from basic to complex contemporary techniques, particularly those that are able to produce rich outputs from very simple recursive algorithms. At the same time, maximal modularity is provided to simplify metaprogramming routines to generate, assess, transform, and categorize the selected musical excerpts. The system is conceived to maintain a long-term interrelation with different users, developing their individual musical styles. This proposed grammar can also be an analytic tool, from the point of view of composition as computation, considering that the best analysis of a piece is the shortest accurate description of the methods behind it.
2.1. Definitions and Analogies
Although its target is not only genetic algorithms but a variety of machine learning techniques, our framework uses the evolutionary analogy, similarly to many other automatic composition systems [22,23]. The Darwinian metaphor can be confusing, since each system has its particular application of the same terms, sometimes denoting even opposite concepts.
In our functional approach, the key idea is considering any piece of music as the product of a program that encloses compositional procedures. Thereupon, the bioinspired terms in the context of the GenoMus framework are defined in the following glossary:
- Genotype function:
- Minimal computable unit representing a musical procedure, designed in a modular way to enable taking other genotype functions as arguments.
- Genotype:
- Computable tree of genotype functions.
- Encoded genotype:
- Genotype coded as an array of floats .
- Decoded genotype:
- Genotype coded as a human-readable evaluable string.
- Leaf:
- Single numeric value or list of values at the end of a genotype branch.
- Phenotype:
- Music generated by a genotype.
- Encoded phenotype:
- Phenotype coded as an array of floats .
- Decoded phenotype:
- Phenotype converted to a format suitable for third-party music software.
The genotype, in its decoded format, is a computable expression. Consequently, the automatic writing and manipulation of genotypes can be seen as a metaprogramming process. This central idea of parsing languages (including musical language) to extract an essential abstract functional tree has been suggested by Bod [24]. Additionally, the construction of genotypes requires two previous elements:
- Germinal vector:
- An array of floats used as an initial decision tree to build a genotype.
- Germinal conditions:
- Minimal data required to deterministically construct a genotype, consisting of a germinal vector and several constraints to handle the generative process.
The phenotype, as the product of the evaluation of the functional expression content in a genotype, is a sequence of music events declared in a format designed to encode music according to a hierarchical structure, made by combining three formal categories:
- Event:
- Simplest musical element. An event is a wrapper for the parameters (leaves) that characterize it.
- Voice:
- Line (or layer) of music. A voice is a wrapper for a sequence of one or more events, or a wrapper for one or more voices sequentially concatenated, without overlapping.
- Score:
- Piece (or excerpt) of music. A score can be a wrapper for one or more voices, or a wrapper for one or more scores together. Scores can be concatenated sequentially (one after another) or simultaneously (sounding together).
Depending on the final desired output of the generative process, different parametric structures will be expected for each event. Hence, to allow diverse formats for decoded phenotypes, two more concepts arise:
- Species:
- A specific configuration of the internal parametric structure that constitutes an event.
- Specimen:
- A genotype/phenotype pair belonging to a species, that produces a piece of music. Data characterizing a specimen are stored in a dictionary containing the germinal conditions, along with metadata and additional analytical information.
Extending our biological analogy, a species can be alternatively defined as the group of specimens that share the same parameter structure of their musical events. The piano species used in the examples requires four attributes for each event: duration, pitch, articulation, and intensity.
A parameter required by an event can be a single value or an array of values (a multiparameter). For instance, in the piano species, an event can contain more than one pitch, to work with chords.
Events built with many parameters can be set. For instance, a species for a very specific electroacoustic setup could need events defined by dozens of features. A preliminary test of a species for complex sound synthesis and spatialization with many parameters was demonstrated with the composition of the piece Microcontrapunctus [25].
Events specification can also be extended to other domains beyond music, such as visuals, lighting, etc., along with musical events, or standalone. Ultimately, this framework can be applied to generate any output describable as sequences of actions.
2.2. Formal Definition of the GenoMus Framework
A GenoMus framework for a species is defined as the 5-tuple:
where:
- is the set of parameter types integrating a genotype functional tree,
- is the vector of parameter types that constitutes an event data structure,
- is the set of conversion functions mapping human-readable specific formats of each parameter type into numbers , and their correspondent inverse functions,
- is the set of genotype functions defined and indexed in a specific library, which take and return data structures , and
- is the set of functions covering all required transformations to compute phenotypes from germinal conditions.
For the construction of a functional tree from a germinal vector, several auxiliary parameters or restrictions are needed, collected in the 5-tuple:
where:
- is the subset of eligible functions encoded indices,
- is the output type of the genotype function tree,
- is a depth limit to the branching of the genotype function tree,
- is the maximal length for lists of parameters, and
- is a seed state used to produce deterministic results with random processes inside a genotype.
Finally, the germinal conditions needed to deterministically generate a specimen are contained in the couple , where is a germinal vector.
2.3. From Germinal Vectors to Musical Outputs
The three main abstract data structures of the GenoMus framework—germinal conditions, encoded genotypes, and encoded phenotypes—contain a vector of the same form: a simple one-dimensional array of n numbers . Due to limits for the representation of reals, but mainly to enable some crucial numeric transformations as pointers to functions (explained in Section 3.3.4), these arrays only include values with a six-digit mantissa. More formally, the only elements these vectors include are those members of the set
Data structures handled below are encoded as vectors of any length n, belonging to a finite n-dimensional vector space
The complete search space needed to contain all possible encoded representations can be defined as the vector space
a superset that contains all vectors of any length up to n, where the upper limit of n depends on the practical limitations of computation and memory.
For a given set of restrictions R, any arbitrarily long vector is a germinal vector . So, let
be the set of all possible germinal conditions.
Let be the set of all possible encoded genotypes with the same restrictions R. Every germinal condition corresponds to a valid encoded genotype capable of generating a valid functional expression representing a music score. Unlike , which accepts as germinal vector any member , includes only vectors decodable as computable functional expressions.
The surjective map transcribes any germinal conditions into an encoded genotype. Hence, the set can be defined as:
The application involves several subprocesses covered next in detail, in such a way that the germinal conditions generate a deterministic decision tree leading to the construction of a unique genotype , mapping the values to one-by-one according to restrictions R. Since the number of choices m needed to build a valid encoded genotype rarely matches the length n of a germinal vector , truncation and loops are employed:
- If has more items than needed, they are ignored, effectively acting as a truncation of the remaining unused part of .
- If needs more elements than those supplied by , reads elements repeatedly from the beginning as a circular array, until reaching a closure, to complete a valid vector . That implies that germinal vectors with even a single value are valid inputs to be transformed into functional expressions.
- To avoid infinite recursion when loops occur while applying , the restrictions R introduce some limits to the depth of functional trees and the length of parameter lists.
Let be the set of all possible decoded genotypes. Members in this set are all possible text strings representing well-formed function trees, plus a value, necessary when random processes are involved. Another surjective map, , takes an encoded genotype and produces its corresponding decoded genotype, presented as a human-readable evaluable expression. This is also a surjection, since different but equivalent encoded genotypes can generate the same executable function tree as a text output.
Similarly, the map evaluates deterministically decoded genotypes to produce encoded phenotypes; this is a surjective map too, because the same output can be obtained as the result of different music composition processes. Again, this encoded form is a sequence of values representing a musical score. Now, we can define the set of all encoded phenotypes that can be produced from decoded genotypes as:
It is noteworthy to note that the length of the vector does not correlate with the lengths of their corresponding vectors in germinal conditions and encoded genotype. Indeed, simple expressions can generate long music scores, while a single chord or melodic motif can be the result of complex manipulations.
Finally, let be the set of decoded phenotypes generated at the end of the process. Creating decoded phenotypes implies a further map to convert this data to another standard or custom musical format, either to generate symbolic information such as sheet music, or to directly synthesize sound. This is a last trivial transformation, once it is known how a score is encoded.
2.4. Retrotranscription of Decoded Genotypes as Germinal Vectors
Sometimes, we start from a manually programmed decoded genotype to build a precise musical composition procedure, and we need to find corresponding germinal conditions capable of generating it. This is a fundamental step in obtaining abstract vectorial representations of manually edited expressions so that they could be integrated into a hypothetical training dataset.
Reciprocally to , the function is a map that takes as input a couple consisting of a valid expression and an auxiliary value (for repeatability dealing with random processes), and returns a corresponding encoded genotype. This transformation of is a simple conversion from text tokens to numbers ; is an injective map since it returns only one encoded genotype from a text expression. Restrictions R for the obtained encoded genotype are derived directly from the features of the original functional expression.
The key point is that starting from a well-formed functional expression , an encoded genotype is at the same time one of its many possible germinal vectors:
The function is built in such a way that a decoded genotype generated from any germinal vector is one of its reciprocal germinal vectors itself. In other words, simultaneously represents a symbolic functional expression and the decision chain that leads to the algorithmic writing of the very same functional expression.
Hence, , and the map acts as an identity function when applied to decoded genotypes. This feature enables the repeatability and consistency of encoded genotypes regardless of changes in the function library , because the numeric pointers to eligible functions are preserved, while at the same time, the couple can be directly introduced back in the pool of germinal conditions without additional transformations.
Figure 1 illustrates this chain of surjective mappings and the retrotranscription to germinal vectors. Remarkably, a conversion from phenotype to genotype is far from trivial, as it is a reverse engineering process: the construction of a procedural generator of music can be seen as an analytical problem with many alternative solutions, since the same musical pattern can be obtained by applying a combination of very different logical relations. This last step can be provided by a variety of machine learning algorithms. Facilitating this type of abstract analysis, based on the learning of relationships between pure one-dimensional arrays, is the essence that determines the entire design of the GenoMus paradigm, and the field of research where the potential of this framework lies.
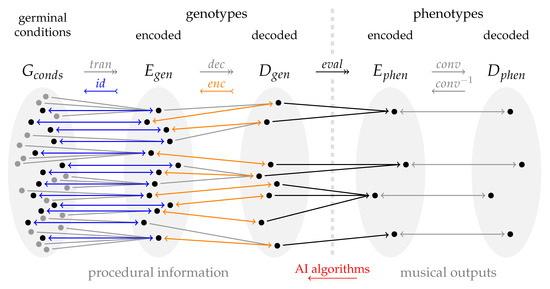
Figure 1.
Mappings from germinal conditions to musical outputs. Double-ended blue arrows illustrate the retrotranscription feature of the conversion: any encoded genotype vector belongs to the germinal vectors set as well, as it autogenerates itself. Orange arrows show how the encoding of a decoded genotype generates a unique numerical representation, although different encoded genotypes may correspond to the same decoded expression, due to the readjustment of parameters needed to fit into valid ranges.
3. Implementation
3.1. Model Overview
A prototype of the GenoMus framework (which is an open-source project freely available at https://github.com/lopezmontes/GenoMus accessed on 15 August 2022), has been implemented by using JavaScript runtime Node.js® for the core code, connected with Cycling’74 Max 8 to interact in real-time with the results of generative processes. The computer-aided composition package bach for Max, by Agostini, and Ghisi [26], allows a simple and responsive visualization of experimental results as interactive music scores, which can also send data to synthesizers or music editors using MIDI, OSC, or any custom format. The data structure of the GenoMus phenotypes is close to the hierarchical structure of music employed by bach package [27], based on scores, voices, events, and event multiparameters. Genotypes’ functional expressions are displayed in an embedded text editor, similar to the system created by Burton [28], also based on bioinspired music patterns evolution.
From the Max patch, organized as shown in Figure 2, it is possible to control the generative and evolutive processes in many ways through these actions:
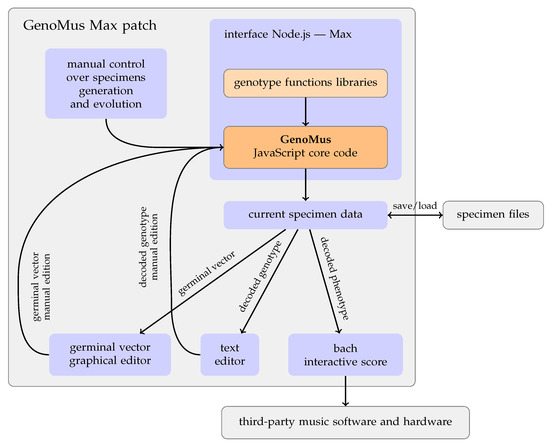
Figure 2.
Overview of the environment designed to interact with the GenoMus generative algorithm.
- Display the generated music as an editable and interactive score, whose data can be converted to sound inside Max, or sent to external software via MIDI, OSC, or custom formats.
- Mutate the current specimen changing stochastically only leaf values of the functional tree, applying new seeds for random processes, replacing complete branches, etc.
- Display decoded genotypes as editable text, so they can be manually edited from scratch.
- Set constraints to the generated specimens, limiting the length, polyphony, depth of the functional tree, forcing the inclusion of a function, etc.
- Define conditions and limitations for the search process.
- Edit germinal conditions, including the graphical edition of the germinal vector.
- Save and load specimens and germinal conditions.
- Export specimens as colored barcodes, according to the rules explained in Section 3.5.
3.2. Anatomy of a Genotype Function
The algorithmic writing of functional trees is similar to the one proposed by Laine and Kuskankaare [29], also focused on bioinspired algorithmic composition. A useful and more formal study of the algorithmic generation of trees was published by Drewes et al. [30]. A simpler but comparable project, also based on the automatic writing of executable programs, was presented by Spector and Alpern [31].
A decoded genotype is a procedural representation of a music score written as a nested functional expression under the common syntax:
where each genotype function takes other functions as arguments until it reaches the limit imposed by the germinal condition .
All genotype functions share the same modular structure, to ease the algorithmic metaprogramming of genotypes. The output of every genotype function is an object that includes the properties listed in Table 1.

Table 1.
Properties returned by a genotype function after evaluation, using as an example the expression ’lm(60,62)’, which represents a list of two MIDI pitches.
This data structure is what each genotype function expects for every argument, and what is passed to the next one. A crucial item is the property decGen, where a function returns its own code as a string. It allows reevaluations of its code in execution time, which is essential to enable generative procedures involving iteration, recursion, or stochastic processes.
3.3. Encoding and Decoding Strategies for Data Normalization and Retrotranscription
To represent different components of the functional tree as normalized values in the range , several strategies and conversions are employed, depending on the token type and the handled numeric ranges. All these mappings have been designed to cover a very wide spectrum of possible results, while also creating encodings with clear numerical contrasts that allow any analysis algorithm to easily capture the differences between vectors.
3.3.1. Leaf Type Identifiers
Identification of the next parameter type is needed to handle the right conversions, since a function is often fed with arguments of a different type. All leaf types are tagged with numbers for a reason: this number, besides being an identifier, is also used after the retrotranscription as a threshold value to decide whether a new value should be added to the list of parameters. Since the threshold imposed by germinal condition is always ≤0.5, this ensures that all values in the list are correctly encoded until a flag value 0 closes the list and ends the function.
3.3.2. Leaf Values
To maintain the readability of decoded genotypes, each parameter type uses common values (for example, pitch is represented with standard MIDI numbers). These convenient numeric ranges are converted to normalized values following these criteria:
- A wide range of values is covered (for instance, for parameters regarding rhythm and articulation, very short and long durations are available).
- For each parameter type, a central value of is assigned to a midpoint among the typical values, interval covers the usual range, and values and are reserved for extreme values rarely used in common music scores.
- To favor the predominance of ordinary values, a previous conversion similar to the lognormal function is applied to each encoded parameter value x supplied by a germinal vector:
As an example, Figure 3 illustrates the equivalence among encoded and decoded values for pitch. The curve combines a simple linear map and the lognormal-alike function shown in Equation (11).
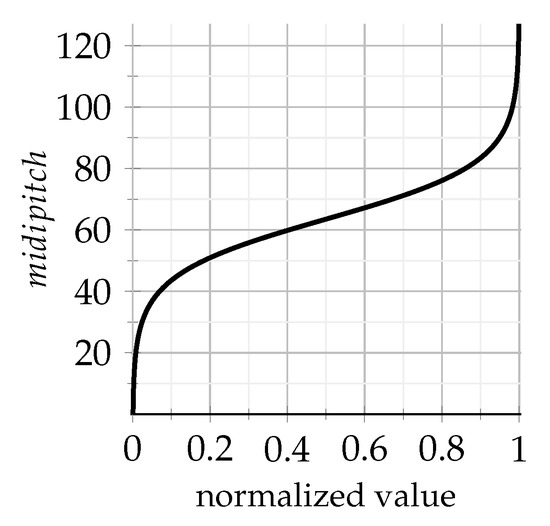
Figure 3.
Conversion of normalized values to human-readable values .
So, by randomly generating germinal vectors, uniformly distributed values are remapped to a Gaussian distribution, introducing a desired bias to produce musical scores with common characteristics, without limiting the possibilities to the generation of specimens exhibiting more extreme features.
3.3.3. Expression Structure Flags
The encoded genotypes simply use 1 and 0 to indicate the opening and closing of a genotype function. The original values from the germinal vector are simply ignored and overwritten.
3.3.4. Genotype Function Indices
Encoded genotypes must refer unequivocally to the available functions contained in any functional tree. So, as a first requirement, any genotype function must be pointed by a unique index . All functions keep their indices unchanged, to ensure that an encoded genotype will always be decoded as the same functional expression, regardless of changes in set after adding new functions to the library. At the same time, these indices must be as separated and uniformly distributed as possible in the interval to obtain distinct vectors that are easily distinguishable for machine learning algorithms. Finally, we must assign indices to new genotype functions without knowing how many new ones will be added in the future.
To deal with all these requirements, a special conversion has been implemented. We call this the golden encoded value (or simply the golden value) to a float obtained after applying a bijective map based on the well-known properties of the golden angle (an angular version of the golden section), combined with modular arithmetics.
Taking as the golden ratio and r as a function, and reducing to 6 digits the mantissa of a real number, the function
where mod is a modulus operator that works with floating-point numbers, and , the first integer producing a repeated value, returns the golden value corresponding to the integer n. The limited quantity of integers able to generate unique values until reaching a repeated golden value is >, so that there are far more different indices than are needed.
This conversion has a very convenient feature: despite ignoring how many values will be needed to be stored, the distribution across the interval is stochastically well balanced. Figure 4 shows how the distribution of indices uniformly covers the range of normalized values. This kind of mapping based on the modulation of golden-angle properties to obtain the balanced distributions of an unknown quantity of indices is not common, although some methods have been recently proposed [32] to obtain simple algorithms to deal with similar optimization problems in other domains.
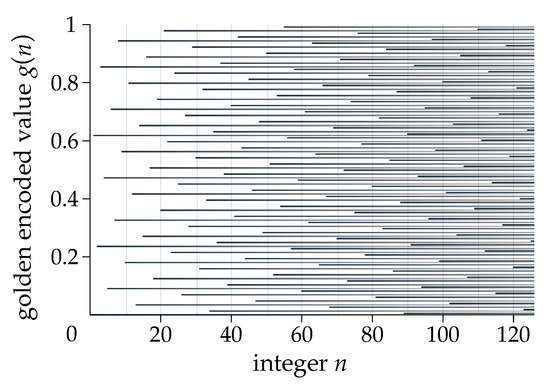
Figure 4.
First 125 golden encoded values across interval . Every value is projected horizontally to visualize the balanced accumulative distribution.
Once this bijection is defined, each new genotype function is assigned an integer index converted to its reciprocal encoded golden value. The transformation then takes each number in a germinal vector that represents a call for a genotype function and substitutes it with the closest available index of the output type required by its parent function, as illustrated in Figure 5.
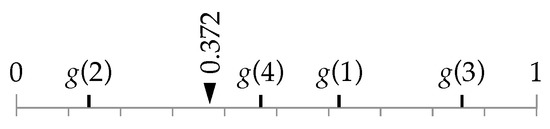
Figure 5.
For this example, we assume that only genotype functions with the decoded indices 1, 2, 3, and 4 are eligible for a given output type. Consequently, the value provided by the germinal vector is substituted by its closest number among the available golden values , , , and ; is replaced by , a permanent pointer to a function. This transformation ensures the rendering of the exact same specimen, regardless of working with an extended function library in the future.
Golden values are also useful for encoding integers in other contexts, both in genotypes and phenotypes, as shown in Figure 6 and Figure 7. Some genotype functions accept integers without a defined range as arguments, which involve this map again. For phenotype encoding, golden values are indispensable for specifying discrete features such as the number of voices per score, events per voice, and items inside a multiparameter.
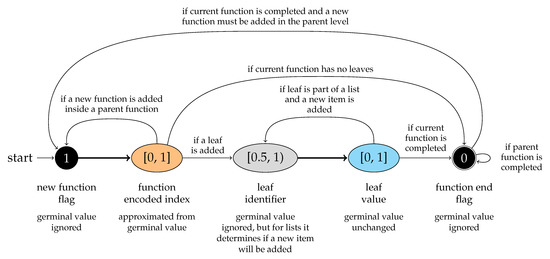
Figure 6.
Numerical transformations applied by the map to create encoded genotypes from germinal vectors. Black and gray values work as flags and identifiers that replace the original numbers of a germinal vector. Orange indicates that a golden value conversion is needed to create an exact reference to a genotype function. Values in cyan nodes are not changed, since they correspond to leaf parameters fed as numeric arguments to terminal functions.
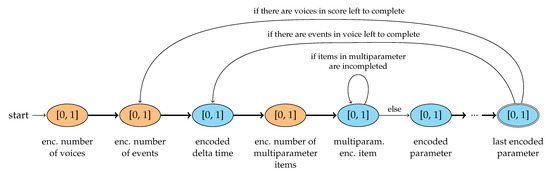
Figure 7.
Structure of encoded phenotypes vectors. As in Figure 6, orange indicates a golden value conversion. Encoded phenotypes use golden values to indicate the total number of voices, total events within a voice, and total items within an event multiparameter.
3.4. Encoding Genotypes and Phenotypes Vectors
Using this variety of conversions, the encoded representation of any functional expression is reduced to a numeric array. The encoding process can be schematized as the automaton in Figure 6.
To encode a string containing a correct and evaluable functional expression into a numerical array, the information supplied by the germinal conditions detailed in Section 2.2 is essential. On the other hand, these constraints are not used to decode back the encoded vectors of genotypes and phenotypes: such arrays constitute self-contained output information that do not need further information to be converted into evaluable expressions and music scores.
Phenotypes encoding is a simpler process, as Figure 7 shows. The decoding of GenoMus encoded phenotypes into standard formats for any musical application (which is a decoded phenotype) can be seen as an external and trivial operation, not directly concerned with this formal specification.
3.5. Minimal Examples Visualized
Below, we present several simple examples to illustrate the described framework. To help understand the encoding process, we visualize float arrays as colored barcodes. The length of each bar maps directly the value. Colors are assigned with different meanings, as detailed in Table 2. Colors in each category are not allocated linearly: small differences in values map to very different tonalities, and so bars that appear to be the same length will show contrasting hue values.

Table 2.
Color code for vector visualization.
The example in Figure 8 shows a specimen consisting of the minimal element: a leaf value. Starting from a set of germinal conditions where the output is , different transformations are applied until a minimal music token is produced.

Figure 8.
Minimal example with a parameter representing middle C. Each value in germinal vector is mapped to corresponding values in encoded genotype following the rules described in Figure 6. Note that the last two values of are ignored because they are not necessary.
In Figure 9, the specimen output is for the species , whose events have four parameters: duration, pitch, articulation, and intensity.

Figure 9.
Minimal example of a complete specimen. This score has only one voice, and the voice includes only one event. However, the type function e3Pitches generates a chord with three pitches (randomly produced with the function mRnd). Note that red-orange bars represent golden encoded values: in the genotype referring to function indices; in the phenotype indicating one voice in the score, one event in the voice, and three pitches in the event.
The germinal vector in the specimen in Figure 9 again has seven values, but it is now read multiple times as a circular array until the encoded genotype is completed. Since part of the values provided by the germinal vector are ignored in this process, we can consider that only some changes in this vector are relevant. Figure 10 explicitly shows the positions that affect the musical result (about half of the total numbers). The search space when applying machine learning algorithms is then less than apparent. Finally, Figure 11 compares several equivalent germinal vectors corresponding to the encoded genotype of the minimal specimen seen in Figure 8. The genotype can be included back in the pool of germinal vectors, because it is self-generating. As described in Section 2.4, we call this desired feature retrotranscription. It is noteworthy that this transformation also exists in genomics through the reverse transcriptase enzyme, which transcribes DNA from RNA, reversing the usual flow of genetic information. In GenoMus, this feature enables an efficient way to find a germinal vector from a functional expression created by hand.
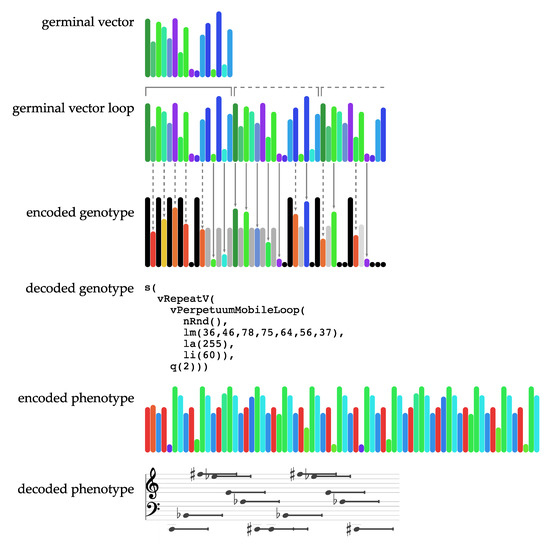
Figure 10.
Germinal vector used as a circular array to originate a longer encoded genotype vector. Solid lines relate to numbers transposed without alterations (the color does not change). These values correspond to the leaves of the functional tree expression. Dashed lines denote changes in the original value: they are function indices encoded as golden values (red-orange colors), pointing to the chosen functions to build the decoded genotype. Note that the lengths of such related values are similar since the algorithm explained in Figure 5 makes this choice by looking for the closest available function index of the required type.
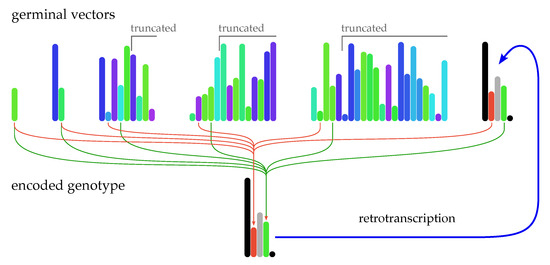
Figure 11.
Equivalent germinal vectors representing the midipitch parameter, middle C. As the red and blue arrows show, in this example, only two important values are determining the chosen function m and the parameter value 60. The retrotranscription of the encoded genotype vector is indicated by the blue arrow: the generated vector can be returned to the pool of its corresponding germinal vectors, as long as this vector generates itself. Colors help to easily identify germinal vectors created by retrotranscription.
4. Results
4.1. Clapping Music as a GenoMus Specimen
Based on the previous description, this system can be seen as a pure generative grammar. Our abstractions are focused on capturing and compressing the information contained in real music. As López de Mántaras [9] states, “in general the rules don’t make the music, it is the music that makes the rules”. In this section, we follow this advice in a pretty literal way.
To illustrate how GenoMus represents and encodes a piece of music using basic procedures in an abstract format, we model Clapping Music, a famous piece composed by Steve Reich in 1972. Like many of his works, it begins with a minimal motif that undergoes simple transformations with big consequences in the overall form. Two performers start the piece by repeating a clapped pattern. One of the performers removes the first note of the pattern after each cycle of eight repetitions, creating a phase shift among both rhythmic lines. The work is finished when both players are in phase again. Figure 12 shows the score and one of the possible analytical deconstructions in patterns.

Figure 12.
Complete score of S. Reich’s Clapping Music. Each box contains nested musical patterns derived from the initial motif A. Derived pattern L embraces the whole piece. This is only one of many possible procedural analyses of this famous work.
Our model derivates the whole composition from transformations of the first four notes (motif A), applying six generic operations using the genotype functions explained in Table 3.

Table 3.
Genotype functions used to model Clapping Music. The table shows only functions that are not mere identity functions that act as simple data containers for each parameter type.
There exist several ways to model the piece, since its patterns can be obtained using different methods. Comparing different strategies of generating this work is an interesting question beyond this paper’s scope. Each model can correspond to alternative manners of perceiving structural aspects. A different analysis but also procedural model of Clapping Music can be found in [33]. To create our model, we looked for the most concise code assembling simple and generic operations.
In Section 4.4, a new genotype function is derived from the analytical recreation of the piece, expanding the available function library. The new function enables endless variations of the original idea and its integration with other functions.
4.2. Pure Procedural Representation
The piece was modeled using a species called piano which, according to the formalism stated in Section 2.2, is defined as the set . The required elements for completing this definition are enumerated in Table 4.

Table 4.
Minimal elements in piano species required to model Clapping Music procedurally.
Beyond the simple identity functions q, ln, lm, la, and li, which simply take and return unchanged numeric values or lists that serve as leaf values of the functional tree, only a few functions are needed to model Clapping Music. The processes carried out by these functions are described in Table 3. The complete work is recreated by the decoded genotype displayed in Listing 1.

Listing 1.
Decoded genotype of Clapping Music model. The uppercase letters in the comments refer to the patterns analyzed in Figure 12.
Listing 1.
Decoded genotype of Clapping Music model. The uppercase letters in the comments refer to the patterns analyzed in Figure 12.
s2V( // score L: joins the 2 voices vertically
vSlice( // voice J: slices last cycle due to phase shift
vRepeatV( // phase G: F 13 times
vRepeatV( // cycle F: E 8 times
vConcatV( // pattern E: C + D
vConcatV( // motif C: A + B
vMotifLoop( // core motif A: 3 8th-notes and a silence
ln(1/8), // note values
lm(65), // pitch (irrelevant for this piece)
la(50), // articulation
li(60,60,90,0)), // intensities (last note louder for clarity)
vSlice( // motif B: A with 1st note sliced
vAutoref(0),
q(1))),
vSlice( // motif D: C with first two notes sliced
vAutoref(3),
q(2))),
q(8)),
q(13)),
q(-12)),
vConcatV( // voice K: F + H
vAutoref(7),
vRepeatV( // phase I: H 12 times
vSlice( // cycle H: F without 1st note, for phase shift
vAutoref(10),
q(1)),
q(12))))
|
4.3. Internal Autoreferences
As noted above, another key feature of the GenoMus grammar is the ability to set internal references to branches inside a functional tree for the purpose of reusing music materials throughout the development of a piece. The argument supplied to a vAutoref function refers to a list of subexpressions stored and updated after each genotype function is evaluated. An autoreference can refer only to the available subexpressions indexed at the time of its evaluation, which implies that during the generative metaprogramming process, a function will only reuse preexisting musical material. This reflects how human perception and memory work, establishing interrelations only with preceding elements.
To clarify the autoreferences inside a genotype, Table 5 lists all subexpressions stored at the end of the genotype evaluation. This network of internal pointers allows efficiency and data reduction, and more importantly, it reflects the deep structure of music.

Table 5.
Subexpressions of voice function type stored during the evaluation of Clapping Music genotype, available to be pointed by internal autoreferences with function vAutoref. Only voice type subexpressions are shown, although they exist for other categories too. Autoreferences can refer to foregoing autoreferences, as occurs at line 25, where vAutoref(10) points to vAutoref(7), which in turn points to a subexpression containing two more autoreferences.
Figure 13 displays the functional tree of this decoded genotype, along with its internal autoreferences. The tree is represented in inverse order, from left to right, to reflect how substructures are feeding to subsequent functions that construct larger musical patterns, as well as the subexpressions indexing order.
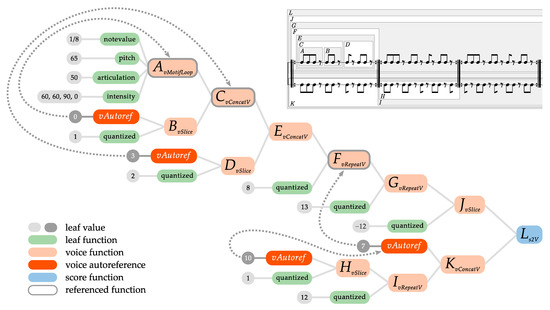
Figure 13.
Functional tree of Clapping Music decoded genotype, along with the patterns in the score. A step-by-step slideshow version of this graph with additional comments can be found in the Supplementary Materials linked at the end of the article.
The encoded genotype of our Clapping Music model consists of 117 values, which is remarkable for a piece lasting several minutes. This fact reflects how this work is a really good example of the minimalist principle of reducing the development of a composition to essential elements and to a process capable of exhibiting its own capacity for autonomous growth. Figure 14 shows the visualization of the abstract pure numerical representation of the composition.

Figure 14.
Visualization of Clapping Music encoded genotype. The decoded genotype shown in Listing 1 was encoded as a float array as described in Figure 6. The visualization of this numeric sequence, using the color code detailed in Table 2, shows that most of the code consists of genotype functions (introduced and closed by black long and short bars), while there are only a few leaf values (numeric values given as final parameters, preceded by gray bars). As discussed previously, this vector is also one of its related germinal vectors.
4.4. Creating New Functions from Musical Examples
The genotype of a whole composition like this (or only part of it) can be automatically flattened to create a new genotype function where all leaves are assembled as a single array of arguments, although the numeric values that feed arguments for the autoreferences are excluded from the arguments array of the new derivate function because of their structural character. These numbers must be immutable to preserve the internal consistency of the procedure. For instance, a new function called sClapping could be created to be handled as a new procedure, abstracted from the original piece and compacted following the structure shown in Table 6.

Table 6.
Data structure of the genotype function sClapping, a new function generated after flattening the functional tree of Clapping Music shown in Listing 1.
5. Discussion and Conclusions
The aesthetic potential of computer-generated artworks is often obscure, especially when there are aspirations to find original styles and new methods. Human composers usually conceive sequences of notes, agogics, articulation gestures, and dynamic expressiveness as a whole. There is no intrinsic value in an isolated sequence of durations and pitches if it lacks expressive attributes such as articulation and dynamics. Interrelations of different parameters, both in the short- and long term, are critical to obtain appealing results.
A good piece of music is much more than the sum of its parts. Composers often construct a piece by planning interrelations between the details of motifs and the overall structure. This holistic conception of creativity has been obviated in much previous research focused on particular compositional tasks. So, in our framework, macro- and microformal features are created and transformed as an entire entity from the beginning of the transformational operations.
Preliminary experiments with GenoMus showed that many of the randomly generated musical excerpts exhibited surprising expressive qualities: an interesting dynamic gesture can create a feeling of order and purpose when applied to sequences of notes that otherwise could be assessed as being meaningless or too random. So, to discover potential combinations, our framework fuses the generation of completely developed excerpts with the incremental transformation of the details of any element inside them.
5.1. Development and Specification of the Grammar Key Characteristics
The writing and testing process throughout the creation of our grammar proposal has been long. Since the first sketches presented in 2015 [34], each iteration of the project has been tested with the composition of real instrumental and electroacoustic pieces [25,35,36]. Those practical experiments with actual artistic applications have shown the strengths and weaknesses of each version, and have been fundamental in laying the foundations for the current prototype, which can be summarized as follows:
- Grammar based on a symbolic and generative approach to music composition and analysis. GenoMus is focused on the correspondences between compositional procedures and musical results. It employs the genotype/phenotype metaphor, as many other similar approaches, but in a very specific way. The musical analysis represented as trees has been also used by Ando et al. [37], representing classical pieces.
- Style-independent grammar, able to integrate and combine traditional and contemporary techniques. In any approach to artificial creativity, a representation system is a precondition that restricts the search space and imposes aesthetic biases a priori, either consciously or unconsciously. The design of algorithms to generate music can be ultimately seen as an act of composition itself. With this in mind, our proposal seeks to be as open and generic as possible, to represent virtually any style, and to enclose any procedure. The purpose of the project is not to imitate styles, but to create results of certain originality, worthy of being qualified as creative. A smooth integration of modern and traditional techniques is one of the purposes of our grammar. GenoMus allows for the inclusion and interaction of any compositional procedure, even those from generative techniques that imply iterative subprocesses, such as recursive formulas, automata, chaos, constraint-based and heuristic searches, L-systems, etc. This simple architecture achieves the integration of the three different paradigms described by Wooller et al. [38]: analytic, transformational, and generative. So, a genotype can be viewed as a multiagent tree.
- Optimized modularity for metaprogramming. Each musical excerpt is generated by a function tree made with a palette of procedures attending all dimensions: events, motifs, rhythmic and harmonic structures, polyphony, global form, etc. All function categories share the same input/output data structures, which eases the implementation of the metaprogramming routines encompassing all time scales and polyphonic layers of a composition, from expressive details to the overall form. This follows the advice of Jacobs [39] and Herremans et al. [40], who suggest working with larger building blocks to capture longer music structures.
- Support for internal autoreferences. In almost any composition, some essential procedures require the reuse of previously heard patterns. As many pieces consist of transformations and derivations of motifs presented at the very beginning, our framework enables pointing to preceding patterns. At execution time, each subexpression is stored and indexed, being available to be referenced by the subsequent functions of the evaluation chain. Beyond the benefits of avoiding internal redundancy when there are repeated patterns, the possibility of creating internal autorefences of nodes inside a function tree is an indispensable precondition for the inclusion of procedures that demand the recursion and reevaluation of subexpressions. This kind of reuse of genotype excerpts is also observed in genomics [41].
- Consistency of the correspondences among procedures and musical outputs. To obtain an increasing knowledge base, correspondences between expressions, encoded representations, and the resulting music must be always the same, regardless of the forthcoming evolution of the grammar and the progressive addition of new procedures by different users. To encode musical procedures, each function name is assigned a number, but to keep the encoded vectors as different as possible, function name indices are scattered across the interval and are registered in a library containing all available functions.
- Possibility of generating music using subsets of the complete library of compositional procedures. Before the automatic composition process begins, users can select which specific procedures should be included or excluded from it. It can also be used to set the mandatory functions to be used in all the results proposed by the algorithm.
- Applicability to other creative disciplines beyond music. Although this framework is presented for the automatic composition of music, the model is easily adaptable to other areas where creative solutions are sought. Whenever it is possible to decompose a result into nested procedures, a library of such compound procedures can be created, taking advantage of their encoding as numerical vectors that serve as input data for machine learning algorithms.
5.2. Perspectives for Training, Testing, and Validation of the Model
When modeling artistic creativity with algorithms, probably the most evasive issue to address is programming fitness functions. The problem of defining how to evaluate and select the products of automatic composition falls beyond the scope of this text, but some insights can be made to ground further research in this area, based on some preliminary experiments made during code testing.
By definition, the assessment of a piece of art can only make sense from a subjective point of view, since the goal of art is to provoke inner and personal reactions. These individual responses are very dependent on cultural, social, and individual contexts. Furthermore, the rating of musical ideas can be identified itself with the very act of composition, as long as composing music is ultimately making choices. However, provided with enough data, some predictions can be made regarding the expected reception for a new piece.
GenoMus is primarily conceived as a tool for discovering new music, both for users with no technical skills in music composition and for expert composers who can implement their own functions and musical data to feed the system and to create creative feedback. With this in mind, we propose some guidelines for the training of the model:
- Multiple strategies of evolution in parallel: Starting from a given genotype, a wide range of manipulations can be combined, mutating and crossing leaves and branches of the functional tree, and also introducing previously learned patterns at any time scale. The architecture of germinal vectors as universally computable inputs has been designed to enable high flexibility for any manipulation of preexisting material as simple numeric manipulations.
- Specimen autoanalysis: Some genotype functions can return an objective analysis of a set of musical characteristics, such as variability, rhythmic complexity, tonal stability, global dissonance index, level of inner autoreference, etc. These genotype metadata are very helpful for reducing the search space when looking for some specific styles, and allow any AI system to measure the relative distance and similarities to other specimens, classify results, and drive evolution processes.
- Human supervised evaluations: subjective ratings made by human users, attending to aesthetic value, originality, mood, and emotional intensity, can be stored and classified to build a database of interesting germinal conditions to be taken as starting points for new interactions with each user profile.
- Analysis of existing music: selected excerpts recreated as a decoded genotype (as shown in Section 4), both manual or automated, can enrich the corpus of the learned specimens of a general database.
Finally, we provide in the Supplementary Materials a collection of MIDI sequences generated during tests with GenoMus using the provided software, rendered without any manipulation, just to illustrate the expressiveness and stylistic variability of the outputs, even without any application of machine learning techniques. With barely the integration of very simple genotype functions in a basic library, some appealing results have already emerged.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/app12168322/s1: Figure S1: Version of Figure 13 as a step-by-step slideshow with additional comments; Application S1: Max patch described in Figure 2, along with the core JavaScript code and other required auxiliary files; Audio S1: Selection of raw music materials generated during tests with the prototype.
Author Contributions
Conceptualization, J.L.-M., M.M.-S. and W.F.; methodology, J.L.-M. and M.M.-S.; software, J.L.-M.; validation, J.L.-M. and M.M.-S.; formal analysis, J.L.-M. and M.M.-S.; investigation, J.L.-M. and M.M.-S.; resources, J.L.-M. and M.M.-S.; data curation, J.L.-M. and M.M.-S.; writing—original draft preparation, J.L.-M. and M.M.-S.; writing—review and editing, J.L.-M. and M.M.-S.; visualization, J.L.-M.; supervision, M.M.-S. and W.F.; project administration, M.M.-S. and W.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work is partly funded by FEDER/Junta de Andalucía (project A.TIC.244.UGR20) and the Spanish Government (project PID2021-125537NA-I00).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Pilar Miralles, for her intensive musical experiments with GenoMus, and Miguel Pedregosa, for his technical insight and interest in growing the project in the near future.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fernández, J.D.; Vico, F.J. AI Methods in Algorithmic Composition: A Comprehensive Survey. J. Artif. Intell. Res. 2013, 48, 513–582. [Google Scholar] [CrossRef]
- López-Rincón, O.; Starostenko, O.; Martín, G.A.S. Algoritmic music composition based on artificial intelligence: A survey. In Proceedings of the 2018 International Conference on Electronics, Communications and Computers, Cholula, Mexico, 21–23 February 2018. [Google Scholar] [CrossRef]
- Pearce, M.; Meredith, D.; Wiggins, G. Motivations and Methodologies for Automation of the Compositional Process. Music. Sci. 2002, 6, 119–147. [Google Scholar] [CrossRef]
- Nierhaus, G. Algorithmic Composition: Paradigms of Automated Music Generation, 1st ed.; Springer Publishing Company, Incorporated: New York, NY, USA, 2008. [Google Scholar]
- Boden, M.A. What Is Creativity? In Dimensions of Creativity; The MIT Press: Cambridge, MA, USA, 1996; pp. 75–118. [Google Scholar]
- Rowe, J.; Partridge, D. Creativity: A survey of AI approaches. Artif. Intell. Rev. 1993, 7, 43–70. [Google Scholar] [CrossRef]
- Papadopoulos, G.; Wiggins, G. AI Methods for Algorithmic Composition: A Survey, a Critical View and Future Prospects. AISB Symp. Music. Creat. 1999, 124, 110–117. [Google Scholar]
- Crawford, R. Algorithmic Music Composition: A Hybrid Approach; Northern Kentucky University: Highland Heights, KY, USA, 2015. [Google Scholar]
- López de Mántaras, R. Making Music with AI: Some Examples. In Proceedings of the 2006 Conference on Rob Milne: A Tribute to a Pioneering AI Scientist, Entrepreneur and Mountaineer, Amsterdam, The Netherlands, 20 May 2006; IOS Press: Amsterdam, The Netherlands, 2006; pp. 90–100. [Google Scholar]
- Schaathun, A. Formula-composition modernism in music made audible. In Inspirator–Tradisjonsbærer–Rabulist; Edition Norsk Musikforlag: Oslo, Norway, 1996; pp. 132–147. [Google Scholar]
- Xenakis, I. Formalized Music: Thought and Mathematics in Composition; Indiana University Press: Bloomington, IN, USA, 1971. [Google Scholar]
- Jacob, B.L. Algorithmic composition as a model of creativity. Organised Sound 1996, 1, 157–165. [Google Scholar] [CrossRef]
- Buchanan, B.G. Creativity at the Metalevel (AAAI-2000 Presidential Address). AI Mag. 2001, 22, 13–28. [Google Scholar]
- McCormack, J. Open Problems in Evolutionary Music and Art. In Proceedings of the Applications of Evolutionary Computing, EvoWorkshops 2005: EvoBIO, EvoCOMNET, EvoHOT, EvoIASP, EvoMUSART, and EvoSTOC, Proceedings, Lausanne, Switzerland, 30 March–1 April 2005; pp. 428–436. [Google Scholar] [CrossRef]
- Hofmann, D.M. A Genetic Programming Approach to Generating Musical Compositions. In Evolutionary and Biologically Inspired Music, Sound, Art and Design; Springer International Publishing: Cham, Switzerland, 2015; pp. 89–100. [Google Scholar] [CrossRef]
- de la Puente, A.O.; Alfonso, R.S.; Moreno, M.A. Automatic composition of music by means of grammatical evolution. In Proceedings of the 2002 Conference on APL Array Processing Languages: Lore, Problems, and Applications-APL ’02, Madrid, Spain, 22–25 July 2002; ACM Press: New York, NY, USA, 2002. [Google Scholar] [CrossRef]
- Ariza, C. An Open Design for Computer-Aided Algorithmic Music Composition: athenaCL; Dissertation.com: Boca Raton, FL, USA, 2005. [Google Scholar]
- Shao, J.; Mcdermott, J.; O’Neill, M.; Brabazon, A. Jive: A Generative, Interactive, Virtual, Evolutionary Music System. In Proceedings of the EvoApplications 2010: EvoCOMNET, EvoENVIRONMENT, EvoFIN, EvoMUSART, and EvoTRANSLOG, Istanbul, Turkey, 7–9 April 2010; Volume 6025, pp. 341–350. [Google Scholar] [CrossRef]
- Burton, A.R.; Vladimirova, T. Generation of Musical Sequences with Genetic Techniques. Comput. Music J. 1999, 23, 59–73. [Google Scholar] [CrossRef]
- Dostál, M. Evolutionary Music Composition. In Handbook of Optimization; Springer: Berlin/Heidelberg, Germany, 2013; pp. 935–964. [Google Scholar] [CrossRef]
- de Lemos Almada, C. Gödel-Vector and Gödel-Address as Tools for Genealogical Determination of Genetically-Produced Musical Variants. In Computational Music Science; Springer International Publishing: Cham, Switzerland, 2017; pp. 9–16. [Google Scholar] [CrossRef]
- Sulyok, C.; Harte, C.; Bodó, Z. On the impact of domain-specific knowledge in evolutionary music composition. In Proceedings of the Genetic and Evolutionary Computation Conference on GECCO’19, Prague, Czech Republic, 13–17 July 2019; ACM Press: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Quintana, C.S.; Arcas, F.M.; Molina, D.A.; Fernández, J.D.; Vico, F.J. Melomics: A Case-Study of AI in Spain. AI Mag. 2013, 34, 99. [Google Scholar] [CrossRef][Green Version]
- Bod, R. The Data-Oriented Parsing Approach: Theory and Application. In Computational Intelligence: A Compendium; Fulcher, J.F.J., Jain, L.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 330–342. [Google Scholar]
- López-Montes, J. Microcontrapunctus: Metaprogramación con GenoMus aplicada a la síntesis de sonido. Espacio Sonoro 2016. Available online: http://espaciosonoro.tallersonoro.com/2016/05/15/microcontrapunctus-metaprogramacion-con-genomus-aplicada-a-la-sintesis-de-sonido/ (accessed on 15 August 2022).
- Agostini, A.; Ghisi, D. A Max Library for Musical Notation and Computer-Aided Composition. Comput. Music J. 2015, 39, 11–27. [Google Scholar] [CrossRef]
- Agostini, A.; Ghisi, D. Gestures, events and symbols in the bach environment. In Proceedings of the Journées d’Informatique Musicale (JIM 2012), Mons, Belgium, 9–11 May 2012; pp. 247–255. [Google Scholar]
- Burton, A.R. A Hybrid Neuro-Genetic Pattern Evolution System Applied to Musical Composition. Ph.D. Thesis, University of Surrey, Guildford, UK, 1998. [Google Scholar]
- Laine, P.; Kuuskankare, M. Genetic algorithms in musical style oriented generation. In Proceedings of the First IEEE Conference on Evolutionary Computation, IEEE World Congress on Computational Intelligence, Orlando, FL, USA, 27–29 June 1994. [Google Scholar] [CrossRef]
- Drewes, F.; Högberg, J. An Algebra for Tree-Based Music Generation. In Proceedings of the 2nd International Conference on Algebraic Informatics, Lecture Notes in Computer Science, Thessaloniki, Greece, 21–25 May 2007; Volume 4728, pp. 172–188. [Google Scholar] [CrossRef]
- Spector, L.; Alpern, A. Induction and Recapitulation of Deep Musical Structure. In Proceedings of the IJCAI-95 Workshop on Artificial Intelligence and Music, Macao, China, 10–16 August 2019; pp. 41–48. [Google Scholar]
- Mheich, Z.; Wen, L.; Xiao, P.; Maaref, A. Design of SCMA Codebooks Based on Golden Angle Modulation. IEEE Trans. Veh. Technol. 2019, 68, 1501–1509. [Google Scholar] [CrossRef]
- Hofmann, D.M. Music Processing Suite: A Software System for Context-Based Symbolic Music Representation, Visualization, Transformation, Analysis and Generation. Ph.D. Thesis, University of Music, Karlsruhe, Germany, 2018. [Google Scholar]
- López-Montes, J. GenoMus como aproximación a la creatividad asistida por computadora. Espacio Sonoro 2015. Available online: http://espaciosonoro.tallersonoro.com/2015/01/17/genomus-como-aproximacion-a-la-creatividad-asistida-por-computadora/ (accessed on 15 August 2022).
- López-Montes, J. Ada+Babbage-Capricci, for cello and piano. Espacio Sonoro 2015. Available online: http://espaciosonoro.tallersonoro.com/2015/01/19/ada-babbage-capricci-for-cello-and-piano/’ (accessed on 15 August 2022).
- López-Montes, J.; Miralles, P. Tiento: Creatividad artificial con GenoMus para la composición colaborativa de música electrónica. In FACBA’21: Seminario La Variación Infinita; Editorial Universidad de Granada: Granada, Spain, 2021; pp. 62–69. [Google Scholar]
- Ando, D.; Dahlsted, P.; Nordahl, M.G.; Iba, H. Interactive GP with Tree Representation of Classical Music Pieces. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2007; pp. 577–584. [Google Scholar] [CrossRef]
- Wooller, R.; Brown, A.R.; Miranda, E.; Diederich, J.; Berry, R. A framework for comparison of process in algorithmic music systems. In Generative Arts Practice; David, B., Ernest, E., Eds.; Creativity and Cognition Studios: Sydney, Australia, 2005; pp. 109–124. [Google Scholar]
- Jacob, B.L. Composing with Genetic Algorithms. In Proceedings of the 1995 International Computer Music Conference, ICMC 1995, Banff, AB, Canada, 3–7 September 1995. [Google Scholar]
- Herremans, D.; Chuan, C.H.; Chew, E. A Functional Taxonomy of Music Generation Systems. ACM Comput. Surv. 2017, 50, 1–30. [Google Scholar] [CrossRef]
- Stanley, K.O.; Miikkulainen, R. A Taxonomy for Artificial Embryogeny. Artif. Life 2003, 9, 93–130. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).