Determinants of Top Speed Sprinting: Minimum Requirements for Maximum Velocity
Abstract
:1. Introduction
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
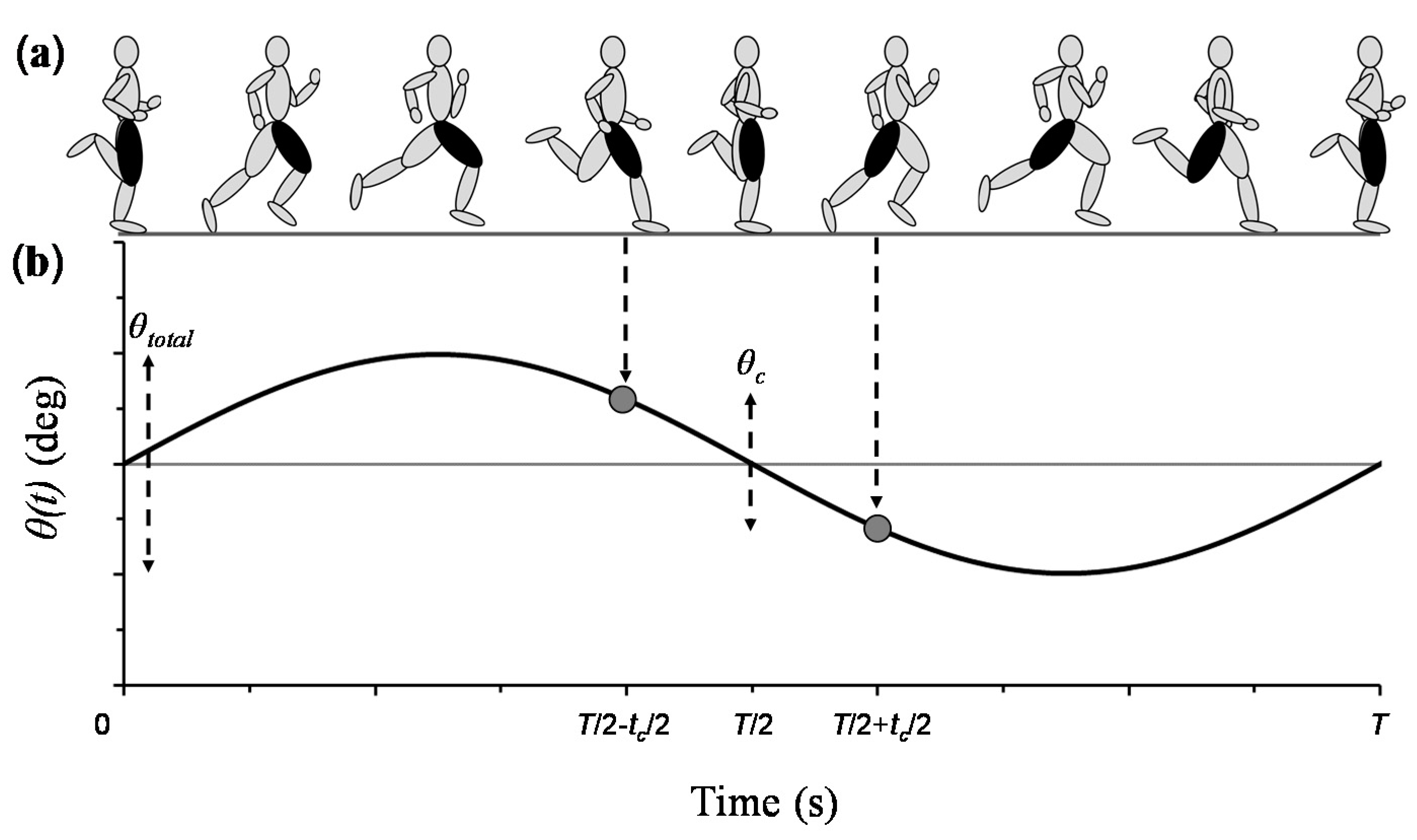
List of Symbols and Abbreviations
| θ(t) | thigh angle as a function of time (deg) |
| θc | total thigh excursion during the ground contact phase (deg) |
| θtotal | total thigh range of motion from peak extension to peak flexion (deg) |
| ωavg | thigh angular velocity averaged throughout stride cycle (deg/s) |
| αmax | modeled maximum thigh angular acceleration during swing (deg/s2) |
| FZavg/mg | ratio of stance-averaged vertical force to body weight mg |
| f | frequency of thigh angular motion (Hz) |
| g | gravitational acceleration (9.8 m/s2) |
| Lc | contact length (m) |
| L0 | leg length (m) |
| m | body mass (kg) |
| SL | step length (m) |
| SL/L0 | ratio of step length to leg length |
| Speed | runner’s forward speed |
| SR | step rate (steps/s) |
| T | time period of thigh angular motion (s) |
| t | time (s) |
| ta | aerial time (s) |
| tc | ground contact time (s) |
| tstep | step time (s) |
References
- Nummela, A.; Keränen, T.; Mikkelsson, L.O. Factors related to top running speed and economy. Int. J. Sports Med. 2007, 28, 655–661. [Google Scholar] [CrossRef] [PubMed]
- Weyand, P.G.; Sternlight, D.B.; Bellizzi, M.J.; Wright, S. Faster top running speeds are achieved with greater ground forces not more rapid leg movements. J. Appl. Physiol. 2000, 89, 1991–1999. [Google Scholar] [CrossRef] [PubMed]
- Weyand, P.G.; Sandell, R.F.; Prime, D.N.; Bundle, M.W. The biological limits to running speed are imposed from the ground up. J. Appl. Physiol. 2010, 108, 950–961. [Google Scholar] [CrossRef] [PubMed]
- Clark, K.P.; Weyand, P.G. Are running speeds maximized with simple-spring stance mechanics? J. Appl. Physiol. 2014, 117, 604–615. [Google Scholar] [CrossRef] [PubMed]
- Clark, K.P.; Meng, C.R.; Stearne, D.J. ‘Whip from the hip’: Thigh angular motion, ground contact mechanics, and running speed. Biol. Open 2020, 9, bio053546. [Google Scholar] [CrossRef] [PubMed]
- Kivi, D.M.; Maraj, B.K.; Gervais, P. A kinematic analysis of high-speed treadmill sprinting over a range of velocities. Med. Sci. Sports Exerc. 2002, 34, 662–666. [Google Scholar] [CrossRef] [PubMed]
- Mann, R.V.; Murphy, A. The Mechanics of Sprinting and Hurdling; CreateSpace Independent Publishing Platform: Las Vegas, NV, USA, 2018; pp. 155–157. [Google Scholar]
- Miyashiro, K.; Nagahara, R.; Yamamoto, K.; Nishijima, T. Kinematics of maximal speed sprinting with different running speed, leg length and step characteristics. Front. Sports Act. Liv. 2019, 1, 37. [Google Scholar] [CrossRef] [PubMed]
- Clark, K.P.; Ryan, L.J.; Meng, C.R.; Stearne, D.J. Evaluation of maximum thigh angular acceleration during the swing phase of steady-speed running. Sports Biomech. 2021; published online ahead of print. [Google Scholar]
- Beneke, R.; Taylor, M.J. What gives Bolt the edge—AV Hill knew it already! J. Biomech. 2010, 43, 2241–2243. [Google Scholar] [CrossRef] [PubMed]
- Weyand, P.G.; Davis, J.A. Running performance has a structural basis. J. Exp. Biol. 2005, 208, 2625–2631. [Google Scholar] [CrossRef] [PubMed]
- Gatesy, S.M.; Biewener, A.A. Bipedal locomotion: Effects of speed, size and limb posture in birds and humans. J. Zool. 1991, 224, 127–147. [Google Scholar] [CrossRef]
- Farley, C.T.; Glasheen, J.; McMahon, T.A. Running springs: Speed and animal size. J. Exp. Biol. 1993, 185, 71–86. [Google Scholar] [CrossRef] [PubMed]
- He, J.P.; Kram, R.; McMahon, T.A. Mechanics of running under simulated low gravity. J. Appl. Physiol. 1991, 71, 863–870. [Google Scholar] [CrossRef] [PubMed]
- Cavagna, G.A.; Thys, H.; Zamboni, A. The sources of external work in level walking and running. J. Physiol. 1976, 262, 639–657. [Google Scholar] [CrossRef]
- Clark, K.P.; Ryan, L.J.; Weyand, P.G. Foot speed, foot-strike and footwear: Linking gait mechanics and running ground reaction forces. J. Exp. Biol. 2014, 217, 2037–2040. [Google Scholar] [CrossRef]
- Clark, K.P.; Ryan, L.J.; Weyand, P.G. A general relationship links gait mechanics and running ground reaction forces. J. Exp. Biol. 2017, 220, 247–258. [Google Scholar] [CrossRef]
- McGeer, T. Passive bipedal running. Proc. Roy. Soc. Lon. B Biol. Sci. 1990, 240, 107–134. [Google Scholar] [CrossRef]
- Biewener, A.A. Scaling body support in mammals: Limb posture and muscle mechanics. Science 1989, 245, 45–48. [Google Scholar] [CrossRef]
- Gindre, C.; Lussiana, T.; Hebert-Losier, K.; Mourot, L. Aerial and terrestrial patterns: A novel approach to analyzing human running. Int. J. Sports Med. 2016, 37, 25–26. [Google Scholar] [CrossRef]
- van Oeveren, B.T.; de Ruiter, C.J.; Beek, P.J.; van Dieën, J.H. The biomechanics of running and running styles: A synthesis. Sports Biomech. 2021; published online ahead of print. [Google Scholar] [CrossRef]
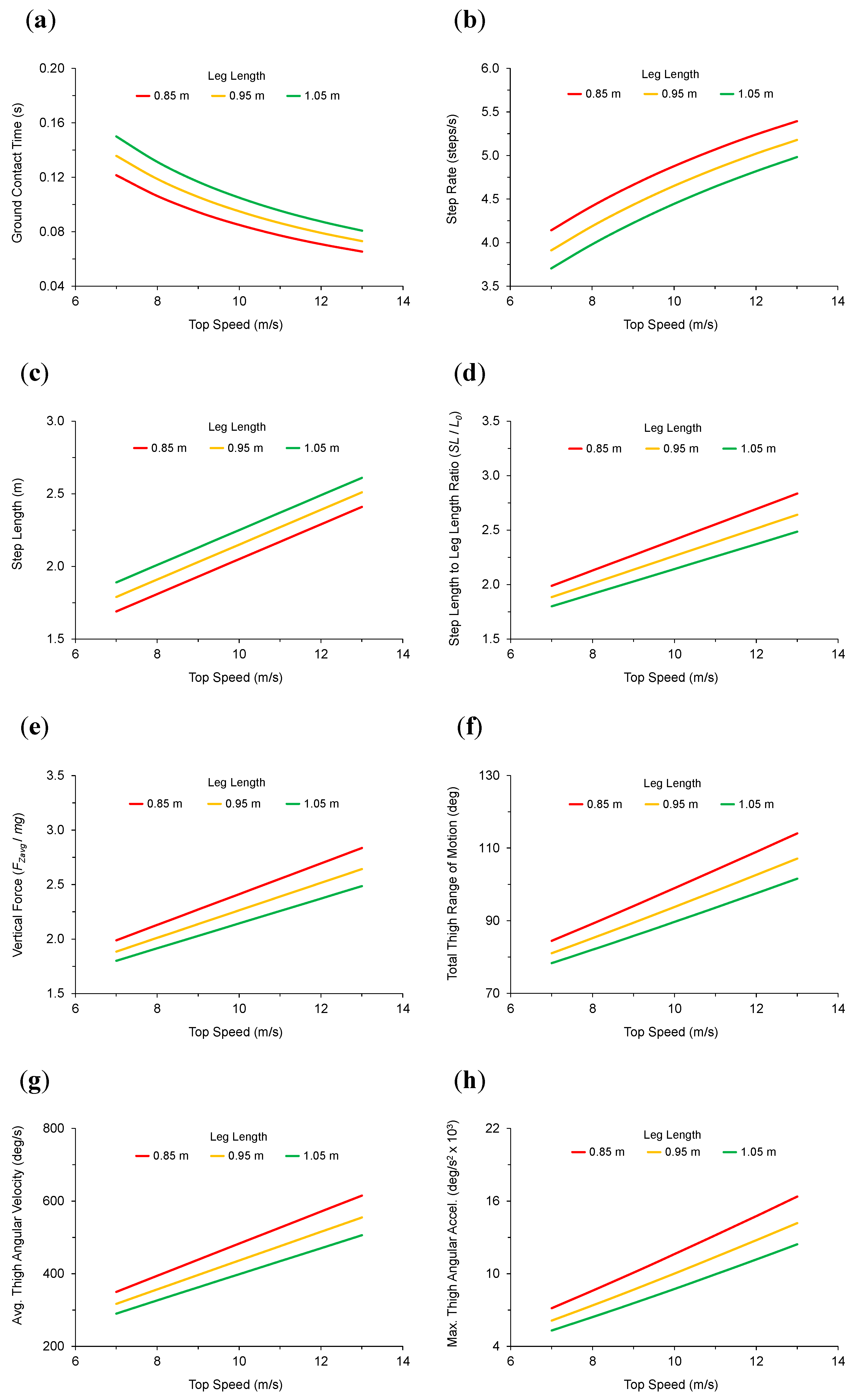
| Speed (m/s) | tc (s) | SR (steps/s) | SL (m) | SL/L0 (ratio) | FZavg/mg (ratio) | 𝜃total (deg) | ωavg (deg/s) | αmax (deg/s2 × 103) |
|---|---|---|---|---|---|---|---|---|
| 7.00 | 0.121 | 4.14 | 1.69 | 1.99 | 1.99 | 84.5 | 349.8 | 7.15 |
| 8.00 | 0.106 | 4.42 | 1.81 | 2.13 | 2.13 | 89.2 | 394.3 | 8.60 |
| 9.00 | 0.094 | 4.66 | 1.93 | 2.27 | 2.27 | 94.1 | 438.6 | 10.09 |
| 10.00 | 0.085 | 4.88 | 2.05 | 2.41 | 2.41 | 99.0 | 482.8 | 11.62 |
| 11.00 | 0.077 | 5.07 | 2.17 | 2.55 | 2.55 | 104.0 | 526.9 | 13.18 |
| 12.00 | 0.071 | 5.24 | 2.29 | 2.69 | 2.69 | 109.0 | 571.1 | 14.77 |
| 13.00 | 0.065 | 5.39 | 2.41 | 2.84 | 2.84 | 114.0 | 615.2 | 16.38 |
| Speed (m/s) | tc (s) | SR (steps/s) | SL (m) | SL/L0 (ratio) | FZavg/mg (ratio) | 𝜃total (deg) | ωavg (deg/s) | αmax (deg/s2 × 103) |
|---|---|---|---|---|---|---|---|---|
| 7.00 | 0.136 | 3.91 | 1.79 | 1.88 | 1.88 | 81.0 | 316.9 | 6.12 |
| 8.00 | 0.119 | 4.19 | 1.91 | 2.01 | 2.01 | 85.2 | 356.9 | 7.38 |
| 9.00 | 0.106 | 4.43 | 2.03 | 2.14 | 2.14 | 89.5 | 396.6 | 8.68 |
| 10.00 | 0.095 | 4.65 | 2.15 | 2.26 | 2.26 | 93.8 | 436.3 | 10.01 |
| 11.00 | 0.086 | 4.85 | 2.27 | 2.39 | 2.39 | 98.2 | 475.8 | 11.38 |
| 12.00 | 0.079 | 5.02 | 2.39 | 2.52 | 2.52 | 102.6 | 515.3 | 12.77 |
| 13.00 | 0.073 | 5.18 | 2.51 | 2.64 | 2.64 | 107.1 | 554.8 | 14.18 |
| Speed (m/s) | tc (s) | SR (steps/s) | SL (m) | SL/L0 (ratio) | FZavg/mg (ratio) | 𝜃total (deg) | ωavg (deg/s) | αmax (deg/s2 × 103) |
|---|---|---|---|---|---|---|---|---|
| 7.00 | 0.150 | 3.70 | 1.89 | 1.80 | 1.80 | 78.3 | 290.1 | 5.30 |
| 8.00 | 0.131 | 3.98 | 2.01 | 1.91 | 1.91 | 82.0 | 326.4 | 6.41 |
| 9.00 | 0.117 | 4.23 | 2.13 | 2.03 | 2.03 | 85.8 | 362.6 | 7.56 |
| 10.00 | 0.105 | 4.44 | 2.25 | 2.14 | 2.14 | 89.7 | 398.5 | 8.74 |
| 11.00 | 0.095 | 4.64 | 2.37 | 2.26 | 2.26 | 93.6 | 434.4 | 9.95 |
| 12.00 | 0.088 | 4.82 | 2.49 | 2.37 | 2.37 | 97.6 | 470.2 | 11.18 |
| 13.00 | 0.081 | 4.98 | 2.61 | 2.49 | 2.49 | 101.6 | 505.9 | 12.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clark, K.P. Determinants of Top Speed Sprinting: Minimum Requirements for Maximum Velocity. Appl. Sci. 2022, 12, 8289. https://doi.org/10.3390/app12168289
Clark KP. Determinants of Top Speed Sprinting: Minimum Requirements for Maximum Velocity. Applied Sciences. 2022; 12(16):8289. https://doi.org/10.3390/app12168289
Chicago/Turabian StyleClark, Kenneth P. 2022. "Determinants of Top Speed Sprinting: Minimum Requirements for Maximum Velocity" Applied Sciences 12, no. 16: 8289. https://doi.org/10.3390/app12168289
APA StyleClark, K. P. (2022). Determinants of Top Speed Sprinting: Minimum Requirements for Maximum Velocity. Applied Sciences, 12(16), 8289. https://doi.org/10.3390/app12168289






