Power Darna Distribution with Right Censoring: Estimation, Testing, and Applications
Abstract
:1. Introduction
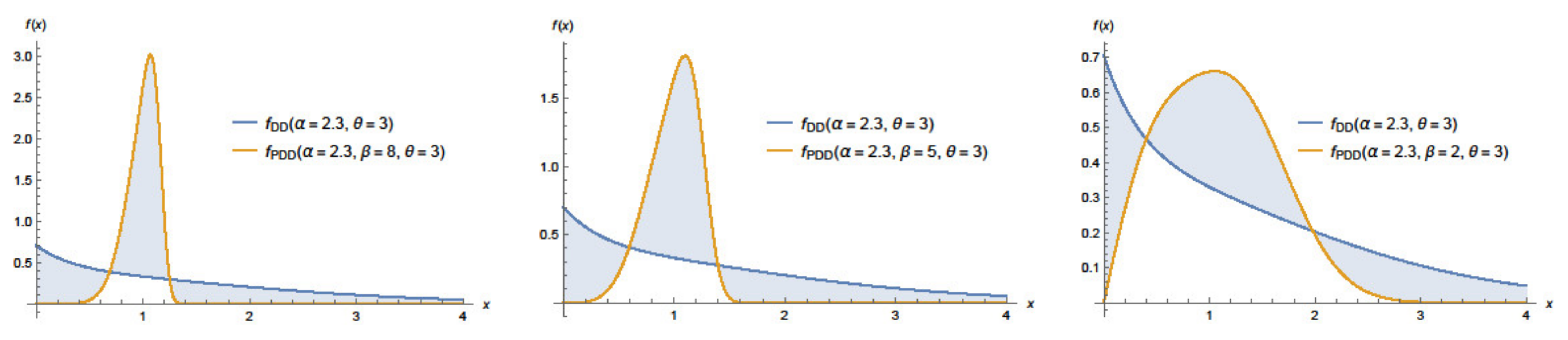
2. The Power Darna Distribution
3. Some Statistical Properties
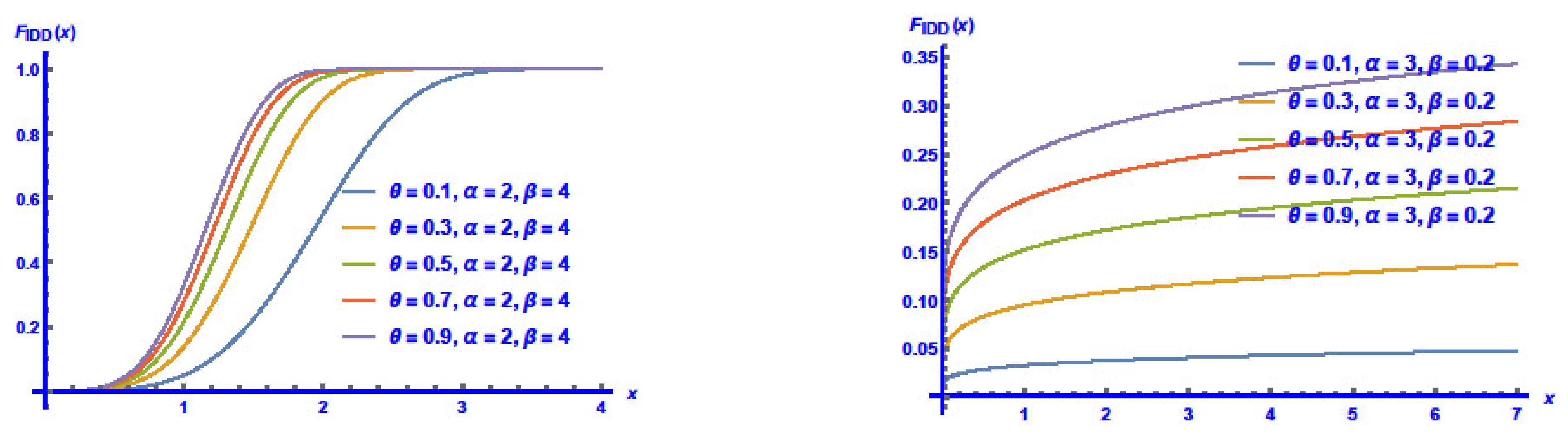
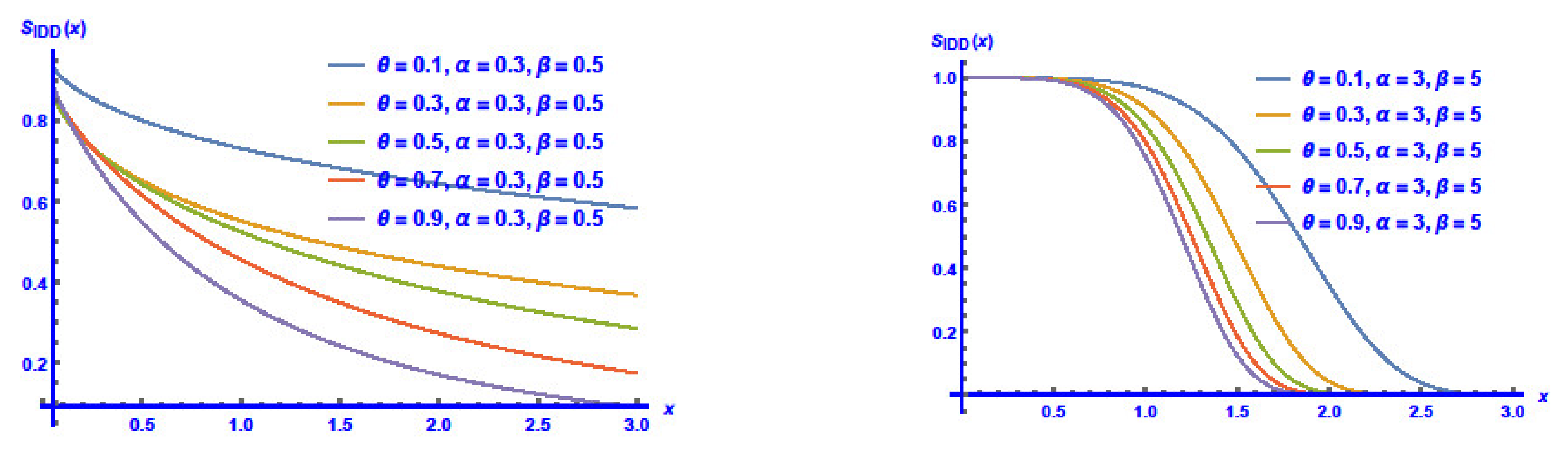
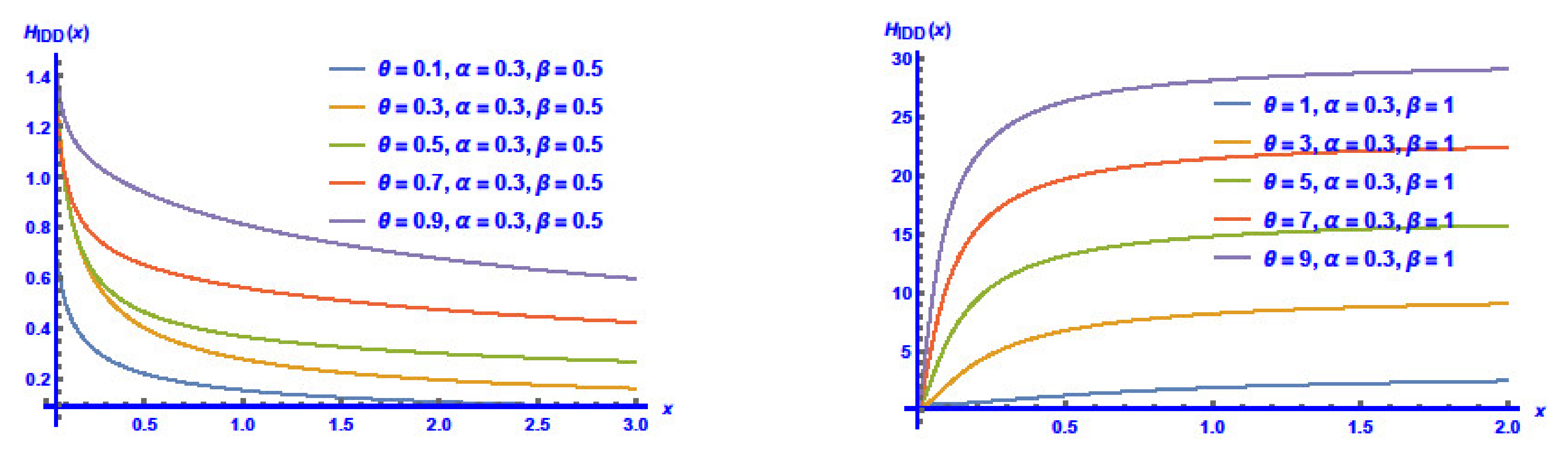
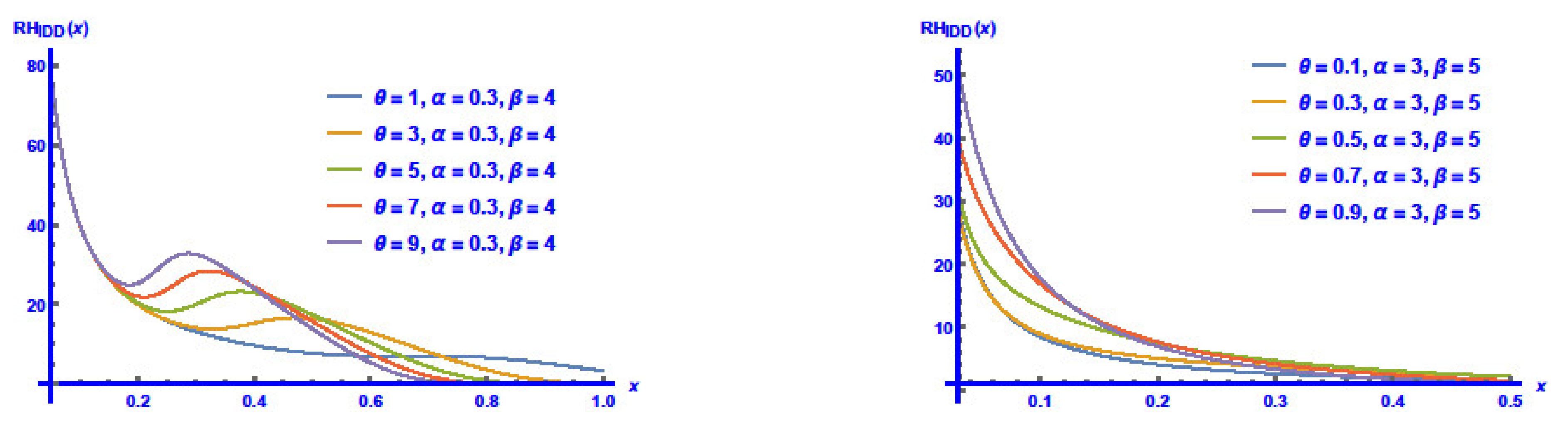
3.1. Reliability Features
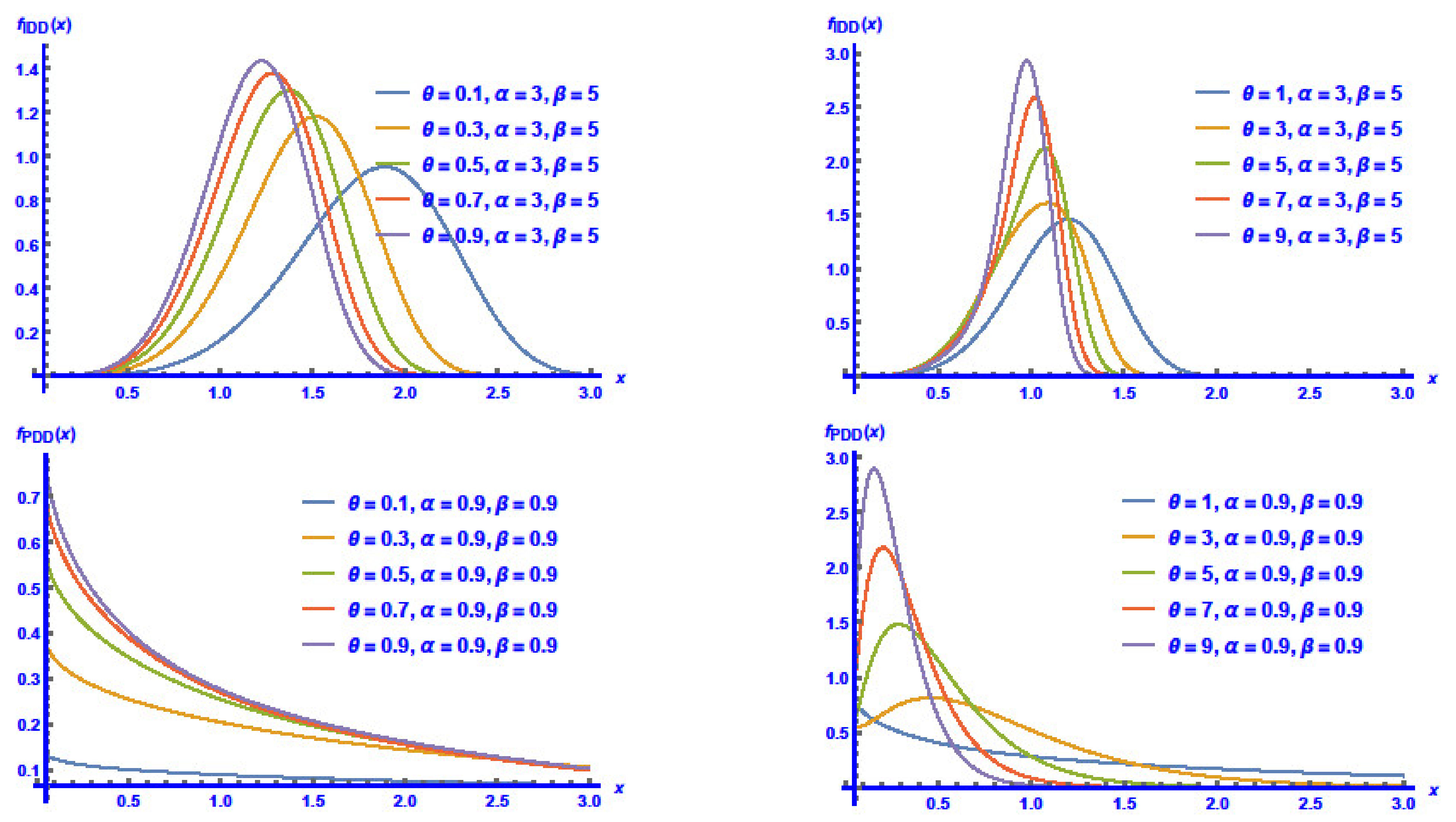
3.2. Moments and Related Measures
3.3. Quantile Function
3.4. Order Statistics
4. MLE with Right Censorship
5. Right Censored Data Test Statistic
5.1. Criteria Test for PDD
5.2. Estimated Matrix et
5.3. Estimated Matrix
6. Estimations Are Applications
6.1. Maximum Likelihood Estimation
6.2. Application to Survival Data
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mudholkar, G.S.; Srivastava, D.K. Exponentiated Weibull family for analyzing bathtub failure-rate data. IEEE Trans. Reliab. 1993, 42, 299–302. [Google Scholar] [CrossRef]
- Marshall, A.W.; Olkin, I. A new method for adding a parameter to a family of distributions with application to the exponential and Weibull families. Biometrika 1997, 84, 641–652. [Google Scholar] [CrossRef]
- Mahdavi, A.; Kundu, D. A new method for generating distributions with an application to exponential distribution. Commun. Stat. Theory Methods 2017, 46, 6543–6557. [Google Scholar] [CrossRef]
- Granzotto, D.; Louzada, F.; Balakrishnan, N. Cubic rank trans- muted distributions: Inferential issues and applications. J. Stat. Comput. Simul. 2017, 87, 2760–2778. [Google Scholar] [CrossRef]
- Abd EL-Kade, R.; AL-Dayian, G.; AL-Gendy, S. Inverted Pareto type I distribution: Properties and estimation. J. Fac. Commer. AL Azhar Univ. Girls Branch 2003, 21, 19–40. [Google Scholar]
- Al-Dayian, G. Inverted pareto type ii distribution: Properties and estimation. J. Fac. Commer. AL Azhar Univ. Girls Branch 2004, 22, 1–18. [Google Scholar]
- Sharma, V.K.; Singh, S.K.; Singh, U.; Agiwal, V. The inverse Lindley distribution: A stress-strength reliability model with application to head and neck cancer data. J. Ind. Prod. Eng. 2015, 32, 162–173. [Google Scholar] [CrossRef]
- Abd AL-Fattah, A.; El-Helbawy, A.; Al-Dayian, G. Inverted Kumaraswamy distribution: Properties and estimation. Pak. J. Stat. 2017, 33, 37–61. [Google Scholar]
- Ghitany, M.; Al-Mutairi, D.K.; Balakrishnan, N.; Al-Enezi, L. Power Lindley distribution and associated inference. Comput. Stat. Data Anal. 2013, 64, 20–33. [Google Scholar] [CrossRef]
- Rady, E.-H.A.; Hassanein, W.; Elhaddad, T. The power Lomax distribution with an application to bladder cancer data. SpringerPlus 2016, 5, 1838. [Google Scholar] [CrossRef]
- Hassan, A.S.; Assar, S.M.; Abdelghaffar, A.M. Statistical properties and estimation of power-transmuted inverse Rayleigh distribution. Stat. Transit. New Ser. 2020, 21, 93–107. [Google Scholar] [CrossRef]
- Shraa, D.H.; Al-Omari, A.I. Darna distribution: Properties and application. Electron. J. Appl. Stat. Anal. 2019, 12, 520–541. [Google Scholar]
- Habib, M.; Thomas, D. Chi-square goodness-if-fit tests for randomly censored data. Ann. Stat. 1986, 14, 759–765. [Google Scholar] [CrossRef]
- Hollander, M.; Pena, E.A. A chi-squared goodness-of-fit test for randomly censored data. J. Am. Stat. Assoc. 1992, 87, 458–463. [Google Scholar] [CrossRef]
- Galanova, N.; Lemeshko, B.Y.; Chimitova, E. Using nonparametric goodness-of-fit tests to validate accelerated failure time models. Optoelectron. Instrum. Data Processing 2012, 48, 580–592. [Google Scholar] [CrossRef]
- Bagdonavičius, V.; Nikulin, M. Chi-squared tests for general composite hypotheses from censored samples. Comptes Rendus Math. 2011, 349, 219–223. [Google Scholar] [CrossRef]
- Bagdonavicius, V.; Nikulin, M. Chi-squared goodness-of-fit test for right censored data. Int. J. Appl. Math. Stat. 2011, 24, 1–11. [Google Scholar]
- Voinov, V.; Nikulin, M.; Balakrishnan, N. Chi-Squared Goodness of Fit Tests with Applications; Academic Press: Cambridge, MA, USA; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Ravi, V.; Gilbert, P.D. BB: An R package for solving a large system of nonlinear equations and for optimizing a high-dimensional nonlinear objective function. J. Statist. Softw. 2009, 32, 1–26. [Google Scholar]
- Pike, M. A method of analysis of a certain class of experiments in carcinogenesis. Biometrics 1966, 22, 142–161. [Google Scholar] [CrossRef] [PubMed]
- Al-Omari, A.I. Maximum likelihood estimation in location-scale families using varied L ranked set sampling. RAIRO-Oper. Res. 2021, 55, S2759–S2771. [Google Scholar] [CrossRef]
- Haq, A.; Brown, J.; Moltchanova, E.; Al-Omari, A.I. Paired double ranked set sampling. Commun. Stat. Theory Methods 2016, 45, 2873–2889. [Google Scholar] [CrossRef]
| 0.1 | 2.77555 | 1.009030 | 0.363542 | 0.169015 | 2.73072 |
| 0.2 | 2.20499 | 0.802234 | 0.363827 | 0.171692 | 2.73436 |
| 0.3 | 1.92918 | 0.702782 | 0.364290 | 0.175967 | 2.73998 |
| 0.4 | 1.75650 | 0.640977 | 0.364916 | 0.181573 | 2.74697 |
| 0.5 | 1.63500 | 0.597896 | 0.365686 | 0.188170 | 2.75458 |
| 0.6 | 1.54361 | 0.565844 | 0.366573 | 0.195370 | 2.76200 |
| 0.7 | 1.47185 | 0.540977 | 0.367549 | 0.202766 | 2.76842 |
| 0.8 | 1.41381 | 0.521111 | 0.368586 | 0.209956 | 2.77313 |
| 0.9 | 1.36585 | 0.504887 | 0.369651 | 0.216565 | 2.77554 |
| 1 | 1.32556 | 0.491403 | 0.370715 | 0.222266 | 2.77525 |
| 0.1 | 3.43900 | 1.799940 | 0.523391 | 0.635962 | 3.25885 |
| 0.2 | 2.44574 | 1.284720 | 0.525287 | 0.649080 | 3.29453 |
| 0.3 | 2.01566 | 1.064510 | 0.528119 | 0.666722 | 3.33805 |
| 0.4 | 1.76773 | 0.939490 | 0.531467 | 0.684201 | 3.37319 |
| 0.5 | 1.60568 | 0.858825 | 0.534867 | 0.697297 | 3.38757 |
| 0.6 | 1.49207 | 0.802558 | 0.537882 | 0.703147 | 3.37553 |
| 0.7 | 1.40877 | 0.760964 | 0.540162 | 0.700469 | 3.33774 |
| 0.8 | 1.34573 | 0.728658 | 0.541460 | 0.689304 | 3.27907 |
| 0.9 | 1.29682 | 0.702416 | 0.541643 | 0.670571 | 3.20624 |
| 1 | 1.25808 | 0.680214 | 0.540676 | 0.64564 | 3.12596 |
| 0.1 | 1.622990 | 0.589902 | 0.363466 | 0.168286 | 2.72972 |
| 0.2 | 1.288980 | 0.468574 | 0.363523 | 0.168835 | 2.73048 |
| 0.3 | 1.127210 | 0.409874 | 0.363619 | 0.169748 | 2.73174 |
| 0.4 | 1.025630 | 0.373076 | 0.363753 | 0.171021 | 2.73350 |
| 0.5 | 0.953892 | 0.347145 | 0.363925 | 0.172648 | 2.73575 |
| 0.6 | 0.899690 | 0.327608 | 0.364134 | 0.174622 | 2.73847 |
| 0.7 | 0.856913 | 0.312242 | 0.364380 | 0.176934 | 2.74165 |
| 0.8 | 0.822119 | 0.299796 | 0.364662 | 0.179571 | 2.74526 |
| 0.9 | 0.793190 | 0.289498 | 0.364979 | 0.182519 | 2.74928 |
| 1 | 0.768740 | 0.280844 | 0.365331 | 0.185759 | 2.75365 |
| 0.1 | 3.97393 | 0.694827 | 0.174847 | 0.242579 | 3.08906 |
| 0.2 | 3.15802 | 0.553243 | 0.175187 | 0.246439 | 3.09412 |
| 0.3 | 2.76443 | 0.485789 | 0.175729 | 0.252208 | 3.10105 |
| 0.4 | 2.51873 | 0.444399 | 0.176437 | 0.259018 | 3.10799 |
| 0.5 | 2.34650 | 0.415958 | 0.177268 | 0.265869 | 3.11300 |
| 0.6 | 2.21750 | 0.395089 | 0.178169 | 0.271784 | 3.11445 |
| 0.7 | 2.11668 | 0.379070 | 0.179087 | 0.275922 | 3.11129 |
| 0.8 | 2.03551 | 0.366333 | 0.179971 | 0.277658 | 3.10317 |
| 0.9 | 1.96872 | 0.355891 | 0.180773 | 0.276613 | 3.09036 |
| 1 | 1.91282 | 0.347083 | 0.181451 | 0.272642 | 3.07364 |
| N | n = 25 | n = 50 | n = 130 | n = 350 | n = 500 |
|---|---|---|---|---|---|
| 2.9602 | 2.9677 | 2.9707 | 2.9813 | 2.9983 | |
| MSE | 0.0062 | 0.0049 | 0.0035 | 0.0021 | 0.0012 |
| 4.0422 | 4.0314 | 4.0250 | 4.0183 | 4.0034 | |
| MSE | 0.0083 | 0.0062 | 0.0055 | 0.0039 | 0.0025 |
| 0.9753 | 0.9789 | 0.9802 | 0.9898 | 0.9933 | |
| MSE | 0.0072 | 0.0057 | 0.0038 | 0.0028 | 0.0017 |
| 189 | 218 | 245 | 304 | |
| 4 | 7 | 5 | 3 | |
| 0.5012 | 0.5012 | 0.5012 | 0.5012 | |
| 1.2262 | 2.6789 | 1.9501 | 2.1657 | |
| 0.9346 | 1.9832 | 2.4702 | 4.1017 | |
| −3.4764 | −2.6677 | −1.4667 | −2.3824 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Omari, A.I.; Aidi, K.; AlSultan, R. Power Darna Distribution with Right Censoring: Estimation, Testing, and Applications. Appl. Sci. 2022, 12, 8272. https://doi.org/10.3390/app12168272
Al-Omari AI, Aidi K, AlSultan R. Power Darna Distribution with Right Censoring: Estimation, Testing, and Applications. Applied Sciences. 2022; 12(16):8272. https://doi.org/10.3390/app12168272
Chicago/Turabian StyleAl-Omari, Amer Ibrahim, Khaoula Aidi, and Rehab AlSultan. 2022. "Power Darna Distribution with Right Censoring: Estimation, Testing, and Applications" Applied Sciences 12, no. 16: 8272. https://doi.org/10.3390/app12168272
APA StyleAl-Omari, A. I., Aidi, K., & AlSultan, R. (2022). Power Darna Distribution with Right Censoring: Estimation, Testing, and Applications. Applied Sciences, 12(16), 8272. https://doi.org/10.3390/app12168272






