Improved Twin Delayed Deep Deterministic Policy Gradient Algorithm Based Real-Time Trajectory Planning for Parafoil under Complicated Constraints
Abstract
1. Introduction
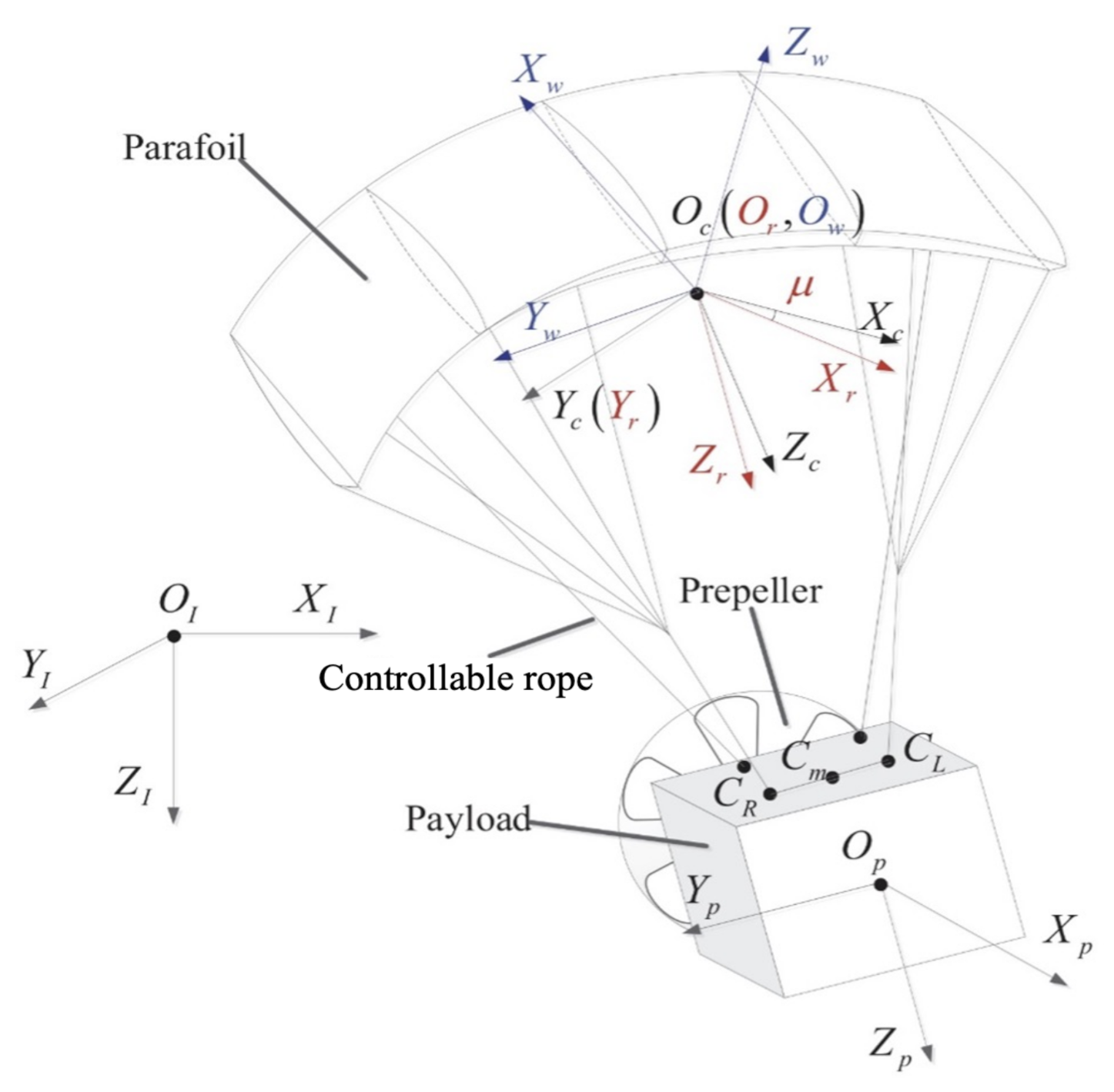
2. Model of the Parafoil Delivery System
3. Trajectory Optimization Method Based on Improved Twin Delayed Deep Deterministic Policy Gradient
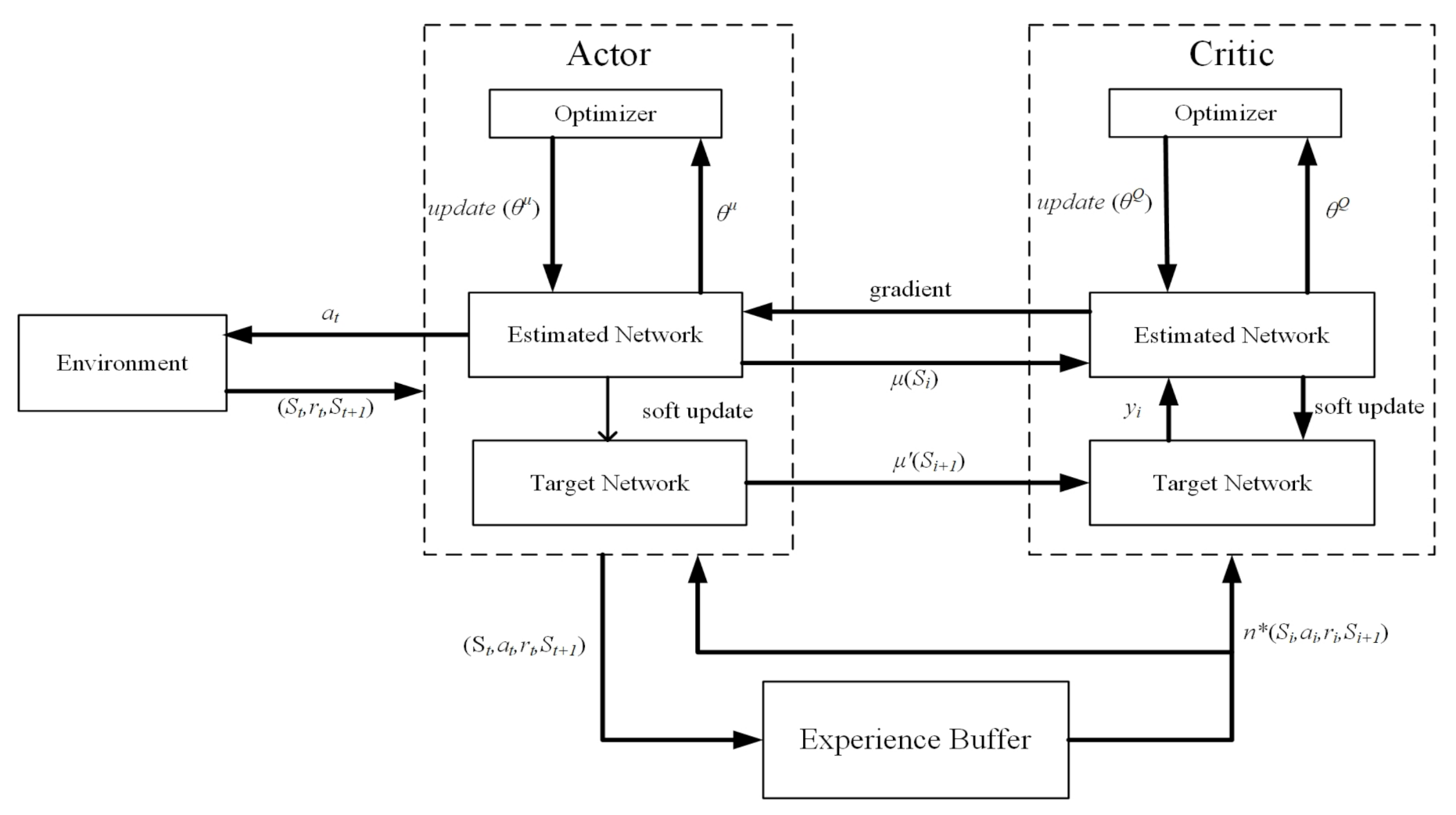
3.1. Deep Deterministic Policy Gradient Algorithm
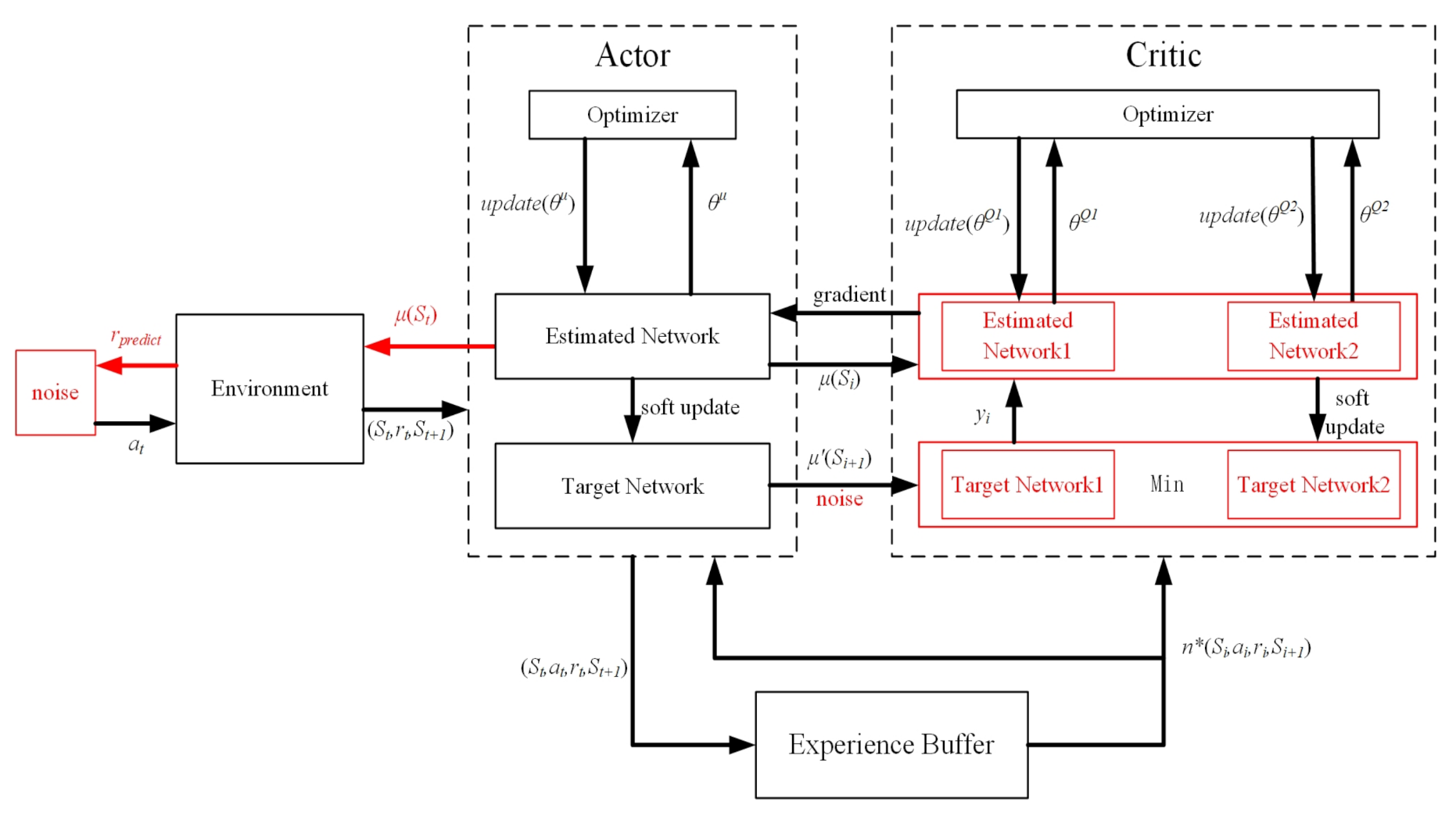
3.2. Improved Twin Delayed Deep Deterministic Policy Gradient Algorithm
| Algorithm 1 Improved TD3 |
|
4. Trajectory Constraints and Reward Design
4.1. Trajectory Constraints
4.2. Reward Design
5. Comparison
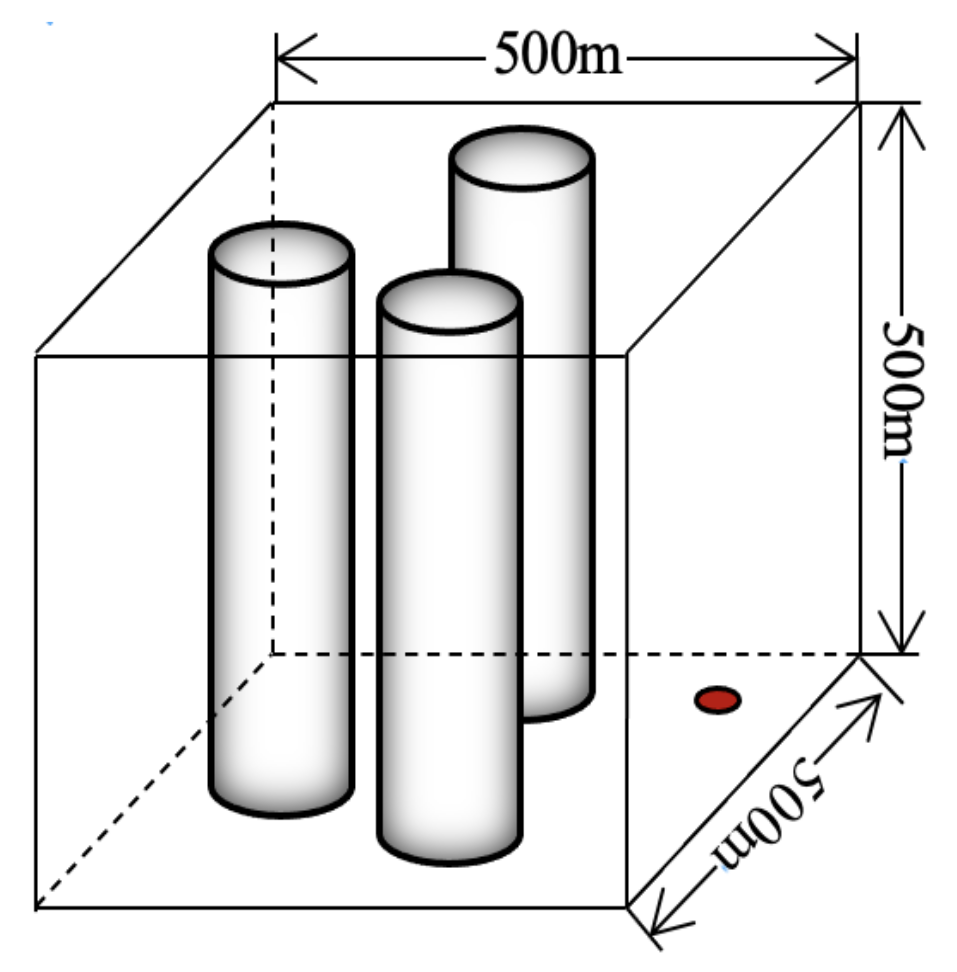
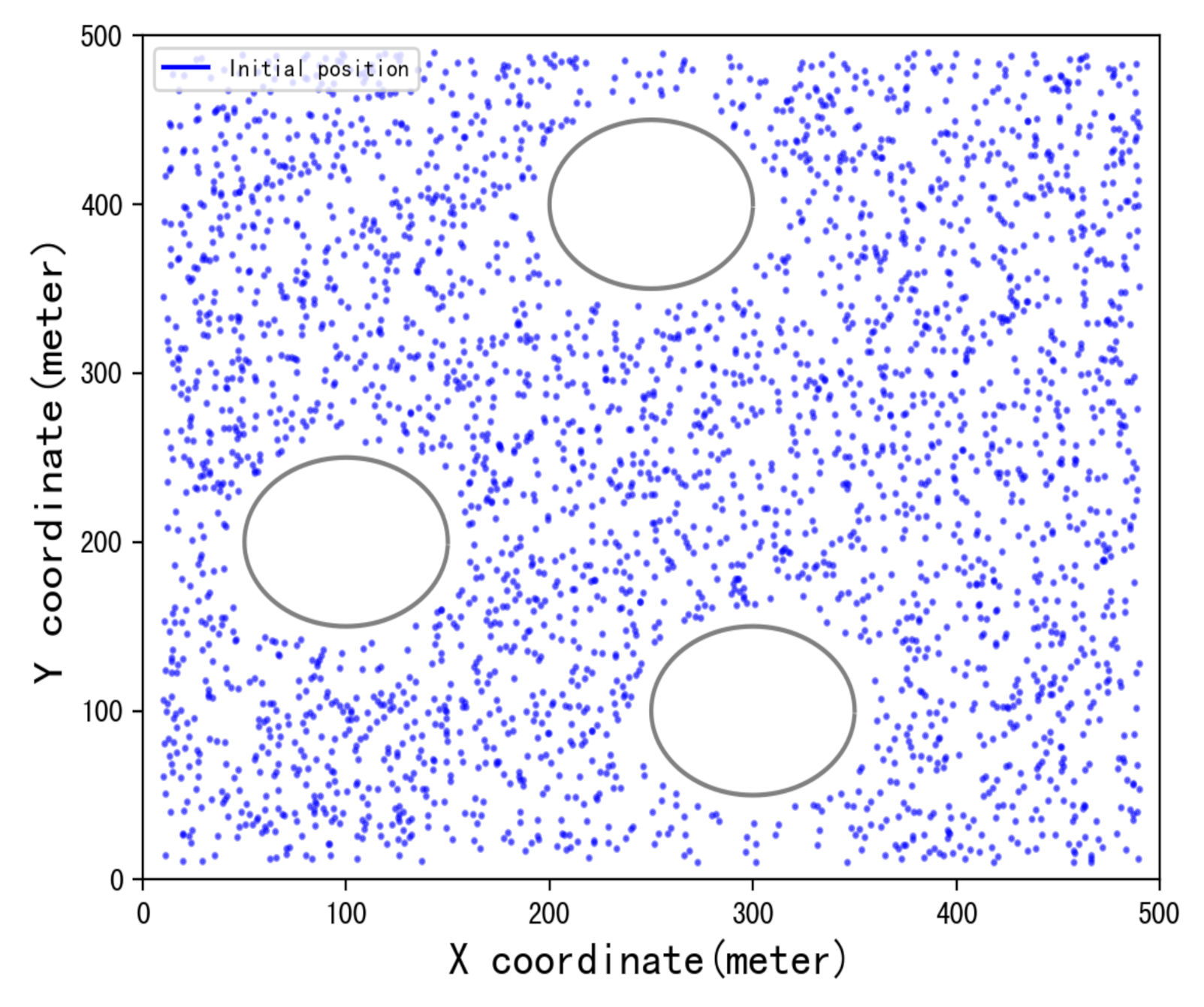
5.1. Simulation Environment
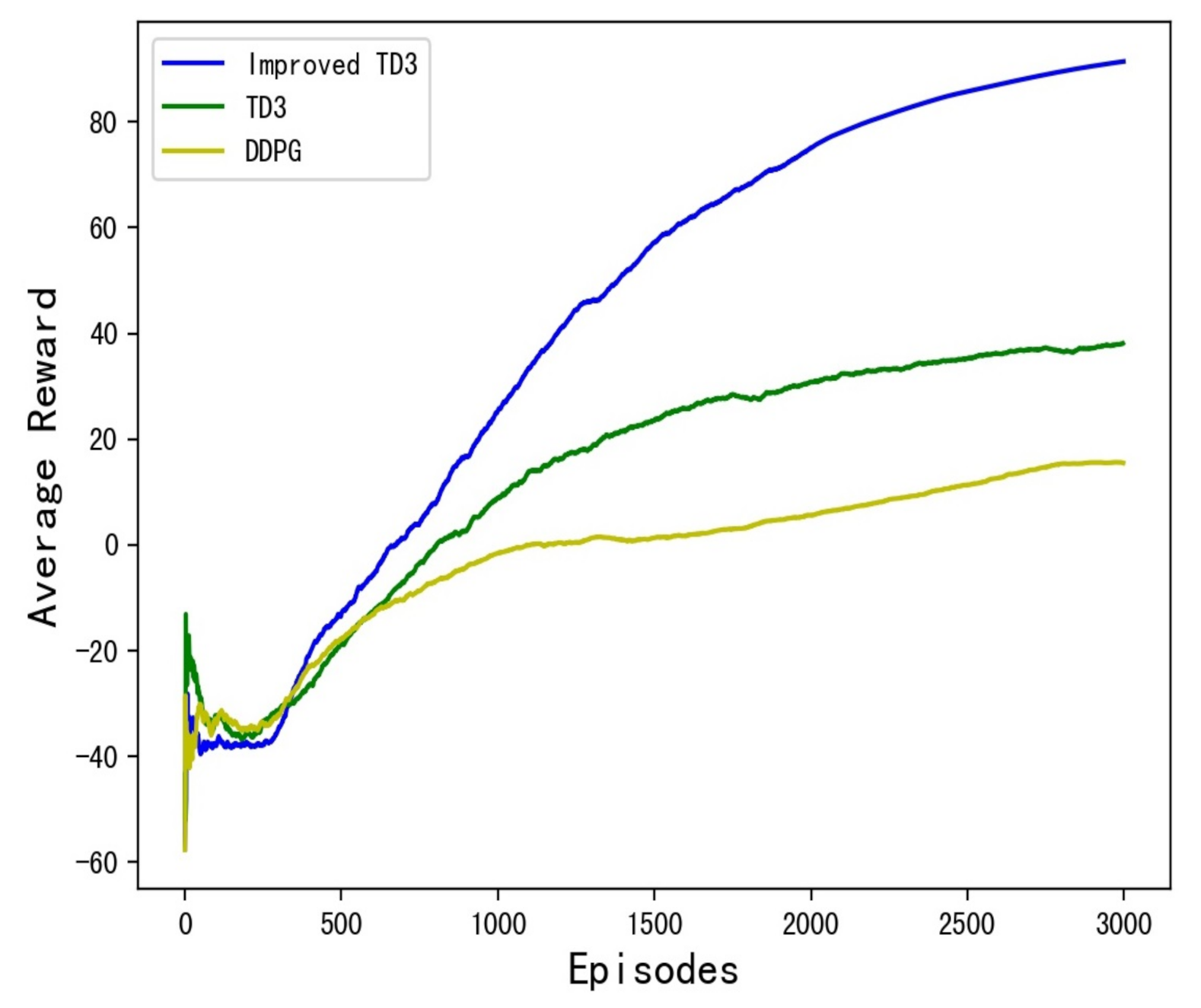
5.2. Training and Results
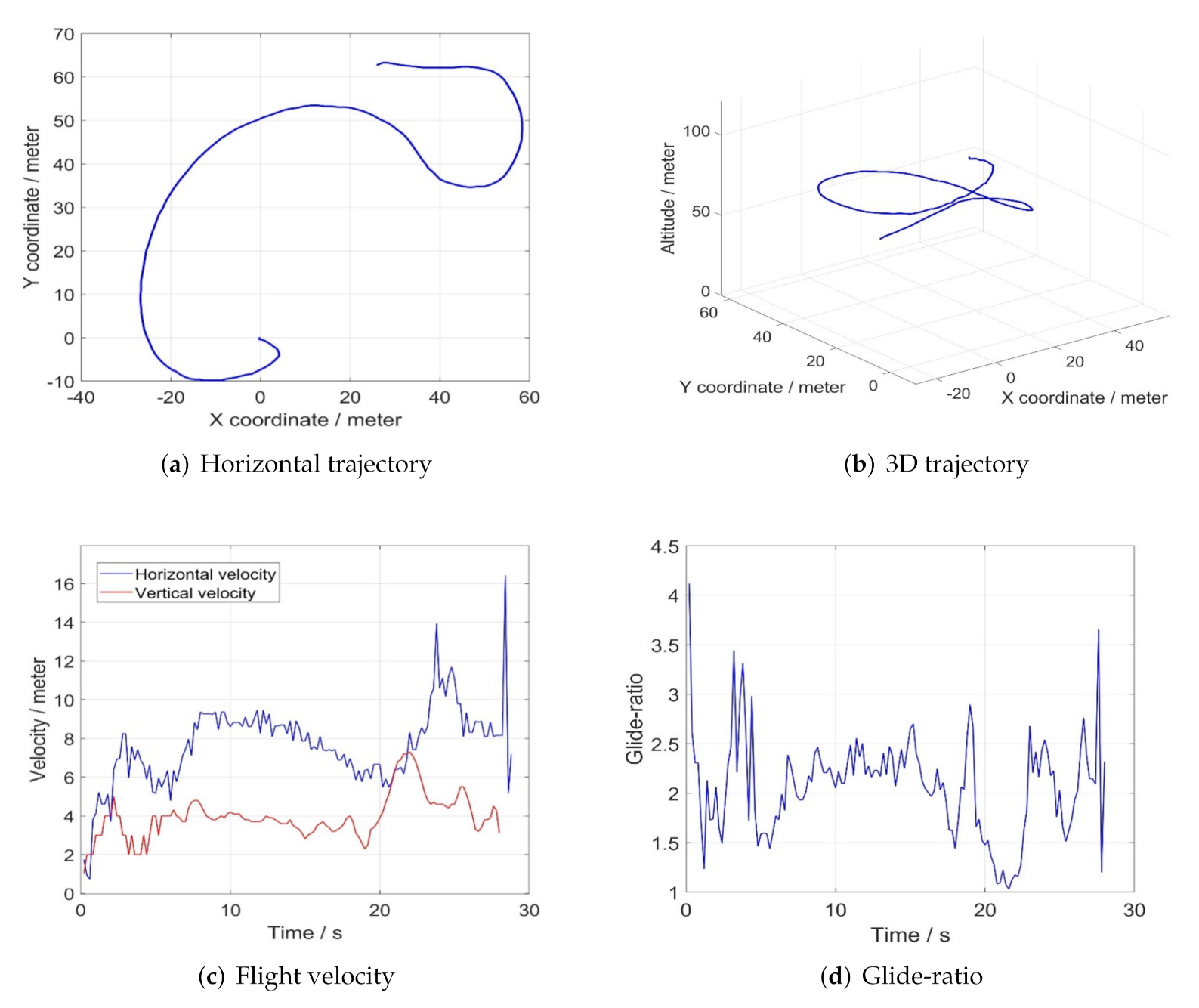
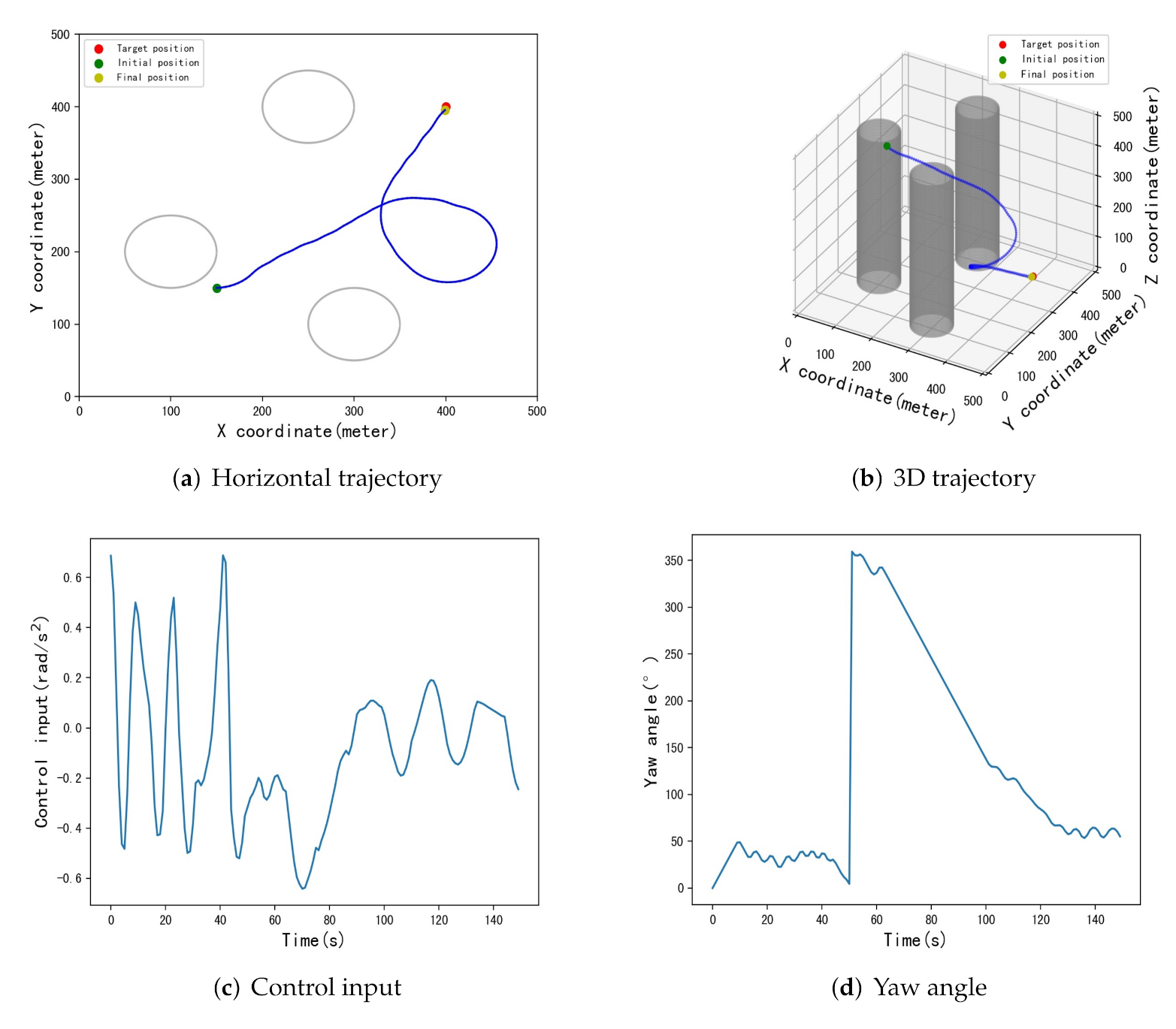
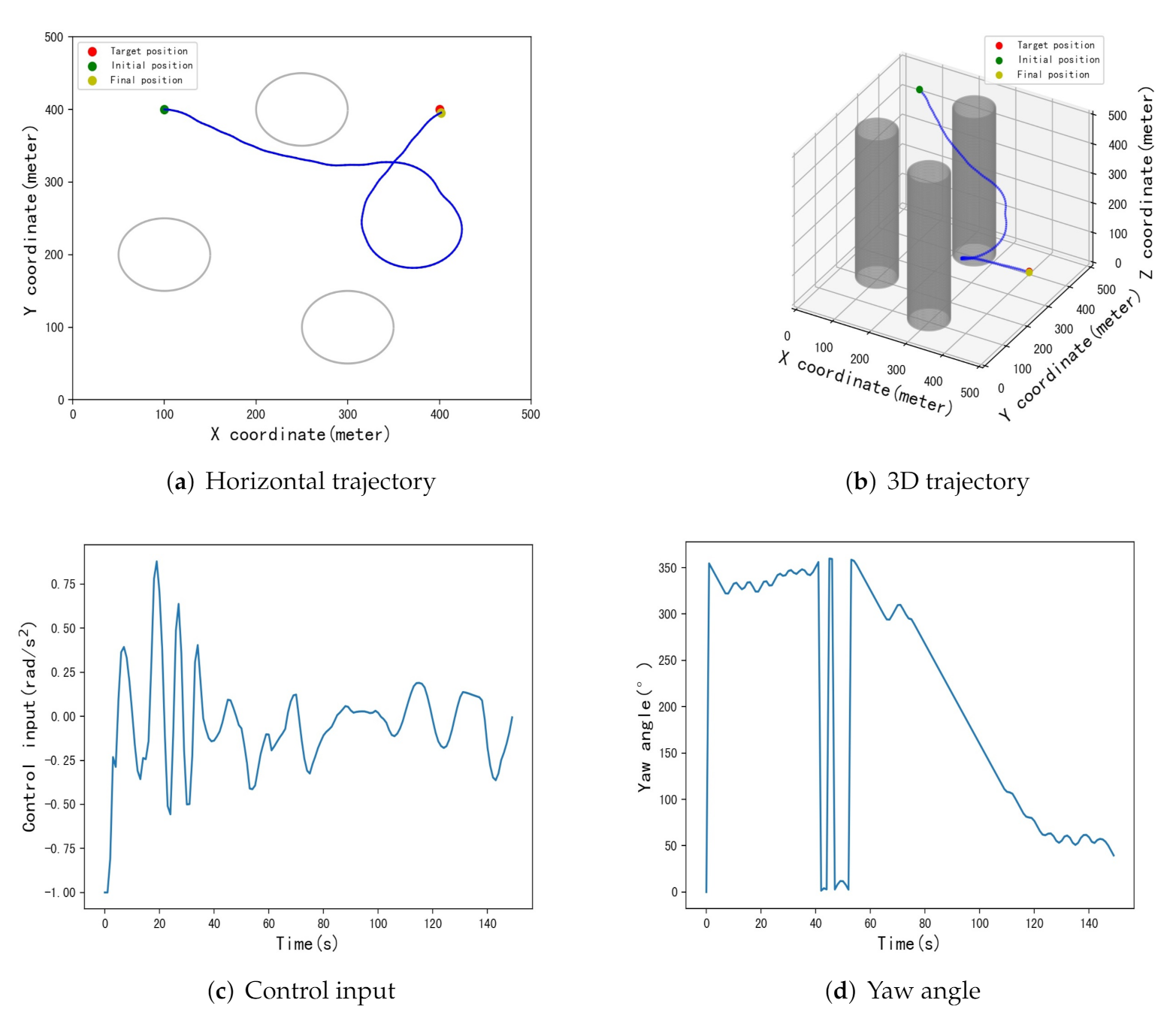
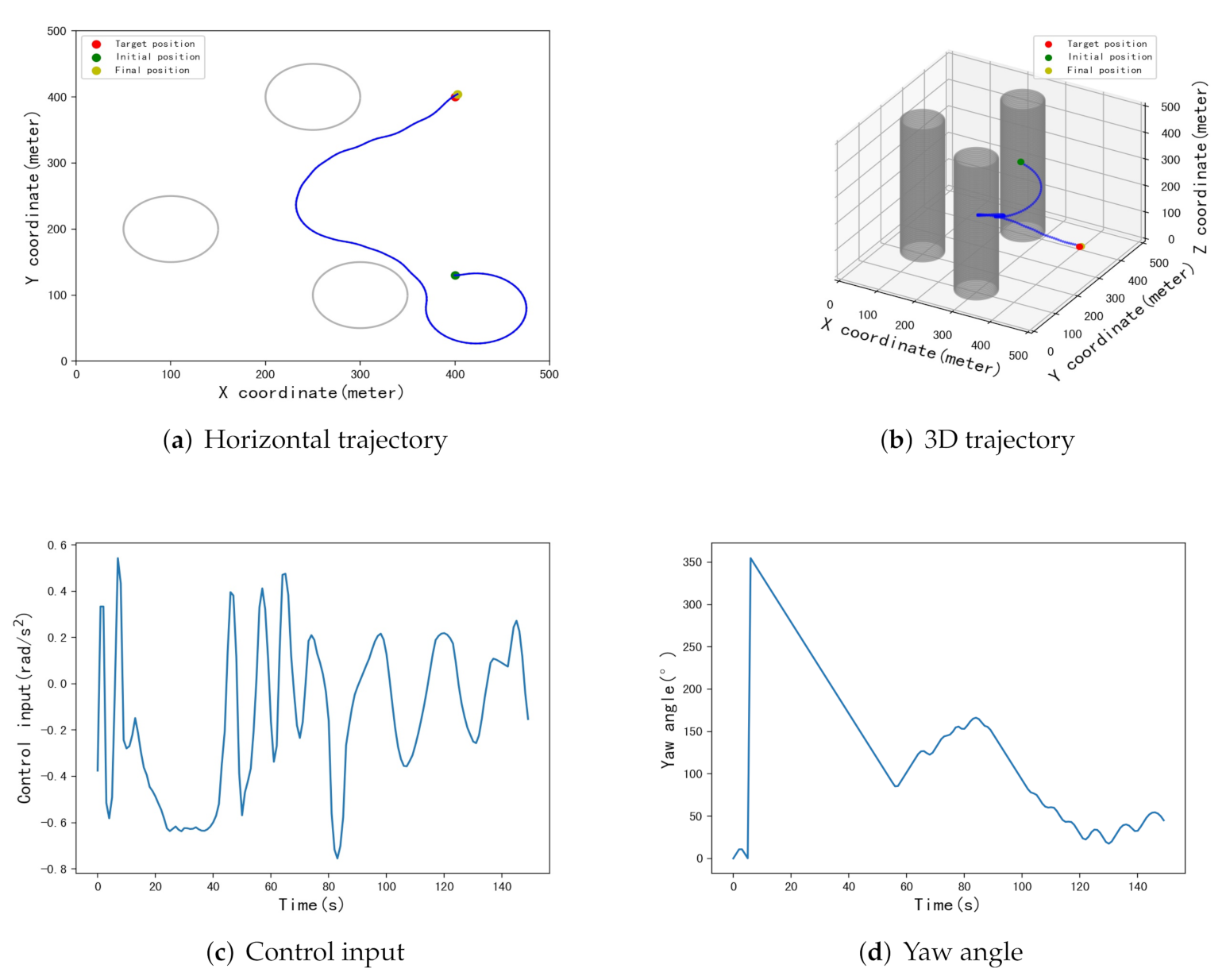
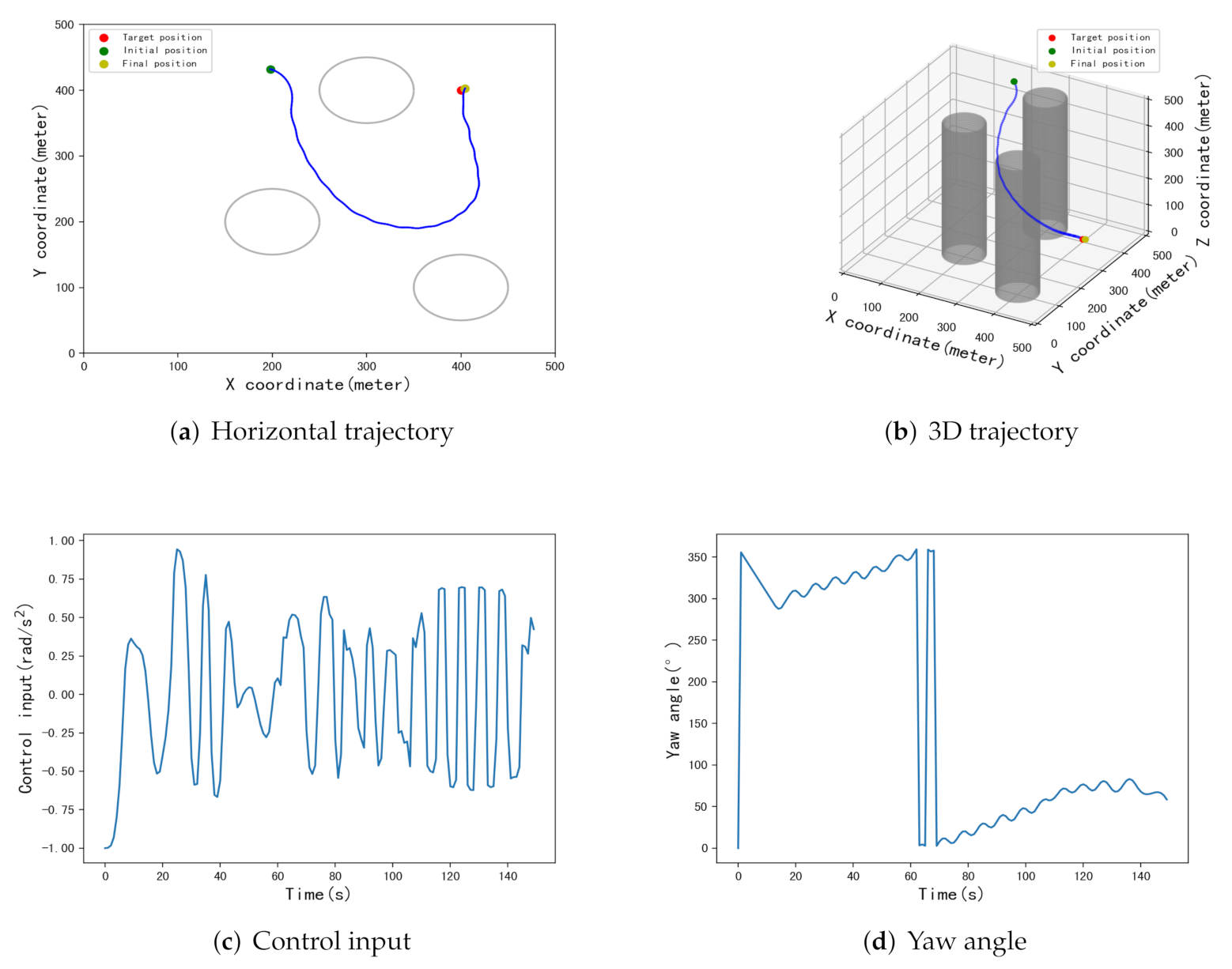
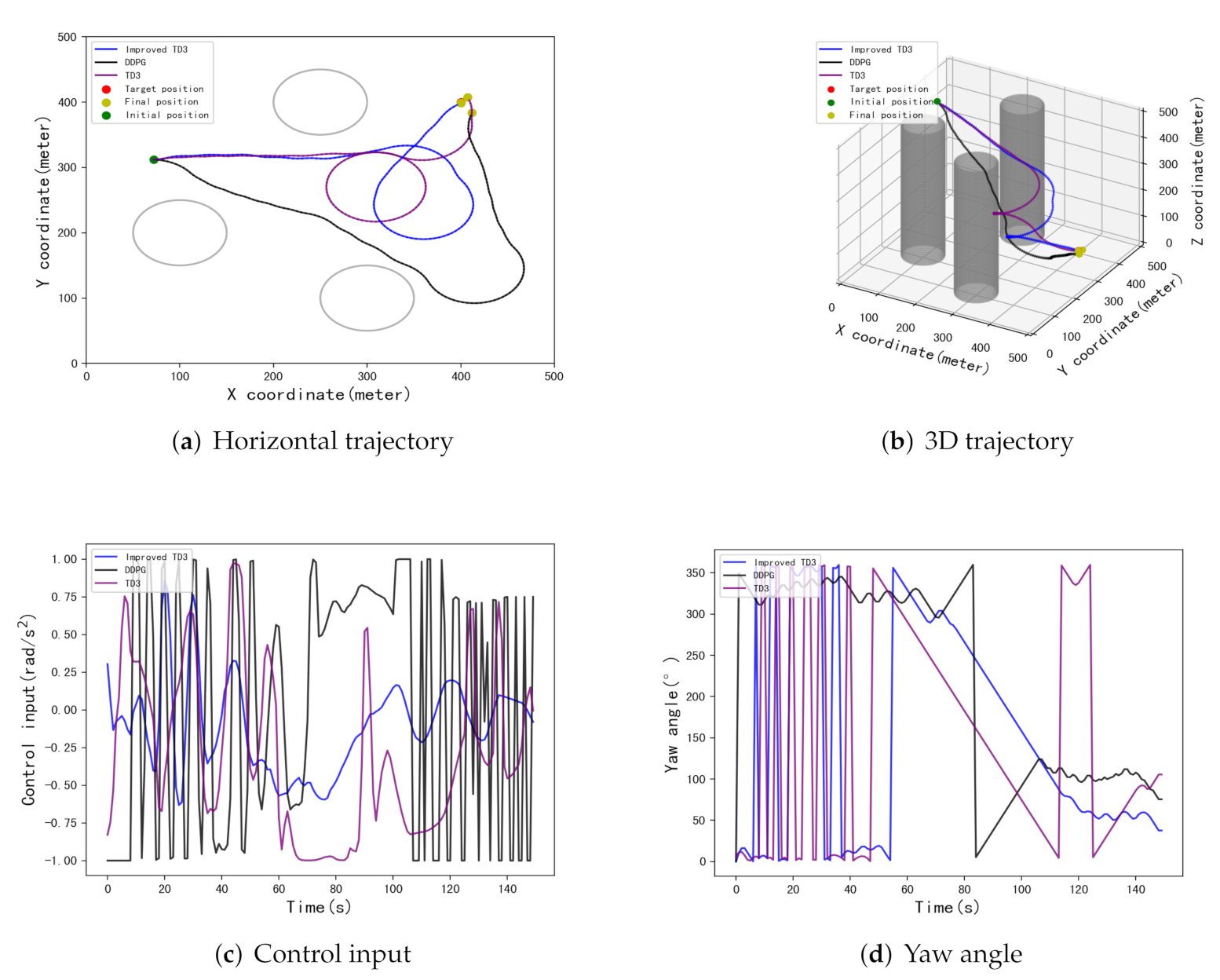
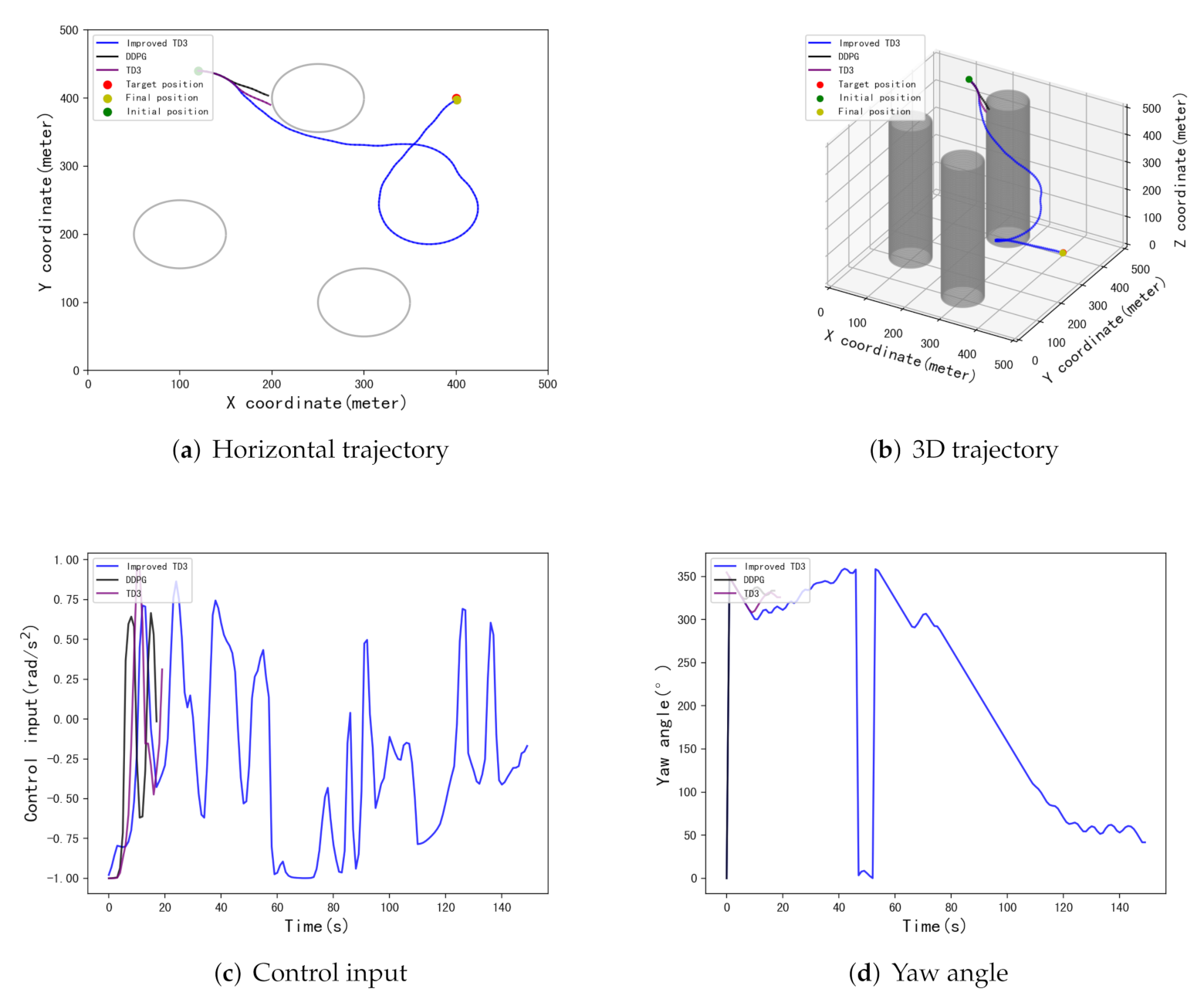
5.3. Testing and Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yakimenko, O.A. Precision Aerial Delivery Systems: Modeling, Dynamics, and Control; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 2015. [Google Scholar]
- Al-Madani, B.; Svirskis, M.; Narvydas, G.; Maskeliūnas, R.; Damaševičius, R. Design of fully automatic drone parachute system with temperature compensation mechanism for civilian and military applications. J. Adv. Transp. 2018, 2018, 2964583. [Google Scholar] [CrossRef]
- Moriyoshi, T.; Yamada, K.; Nishida, H. The Effect of Rigging Angle on Longitudinal Direction Motion of Parafoil-Type Vehicle: Basic Stability Analysis and Wind Tunnel Test. Int. J. Aerosp. Eng. 2020, 2020, 8861714. [Google Scholar] [CrossRef]
- Slegers, N.; Costello, M. Aspects of control for a parafoil and payload system. J. Guid. Control. Dyn. 2003, 26, 898–905. [Google Scholar] [CrossRef]
- Stein, J.; Madsen, C.; Strahan, A. An overview of the guided parafoil system derived from X-38 experience. In Proceedings of the 18th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Munich, Germany, 23–26 May 2005; p. 1652. [Google Scholar]
- Smith, J.; Bennett, T.; Fox, R. Development of the NASA X-38 parafoil landing system. In Proceedings of the 15th Aerodynamic Decelerator Systems Technology Conference, Toulouse, France, 8–11 June 1999; p. 1730. [Google Scholar]
- Jann, T. Advanced features for autonomous parafoil guidance, navigation and control. In Proceedings of the 18th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Munich, Germany, 23–26 May 2005; p. 1642. [Google Scholar]
- Jann, T. Aerodynamic model identification and GNC design for the parafoil-load system ALEX. In Proceedings of the 16th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Boston, MA, USA, 21–24 May 2001; p. 2015. [Google Scholar]
- Ghoreyshi, M.; Bergeron, K.; Jirásek, A.; Seidel, J.; Lofthouse, A.J.; Cummings, R.M. Computational aerodynamic modeling for flight dynamics simulation of ram-air parachutes. Aerosp. Sci. Technol. 2016, 54, 286–301. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, L.; Wu, Z.H.; Jia, H.; Liu, X. Numerical investigation of ram-air parachutes inflation with fluid-structure interaction method in wind environments. Aerosp. Sci. Technol. 2021, 109, 106400. [Google Scholar] [CrossRef]
- Wachlin, J.; Ward, M.; Costello, M. In-canopy sensors for state estimation of precision guided airdrop systems. Aerosp. Sci. Technol. 2019, 90, 357–367. [Google Scholar] [CrossRef]
- Dek, C.; Overkamp, J.L.; Toeter, A.; Hoppenbrouwer, T.; Slimmens, J.; van Zijl, J.; Rossi, P.A.; Machado, R.; Hereijgers, S.; Kilic, V.; et al. A recovery system for the key components of the first stage of a heavy launch vehicle. Aerosp. Sci. Technol. 2020, 100, 105778. [Google Scholar] [CrossRef]
- Slegers, N.; Costello, M. Model predictive control of a parafoil and payload system. J. Guid. Control Dyn. 2005, 28, 816–821. [Google Scholar] [CrossRef]
- Rogers, J.; Slegers, N. Robust parafoil terminal guidance using massively parallel processing. J. Guid. Control Dyn. 2013, 36, 1336–1345. [Google Scholar] [CrossRef]
- Slegers, N.; Brown, A.; Rogers, J. Experimental investigation of stochastic parafoil guidance using a graphics processing unit. Control Eng. Pract. 2015, 36, 27–38. [Google Scholar] [CrossRef][Green Version]
- Slegers, N.; Yakimenko, O. Terminal guidance of autonomous parafoils in high wind-to-airspeed ratios. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2011, 225, 336–346. [Google Scholar] [CrossRef]
- Luders, B.; Ellertson, A.; How, J.P.; Sugel, I. Wind uncertainty modeling and robust trajectory planning for autonomous parafoils. J. Guid. Control Dyn. 2016, 39, 1614–1630. [Google Scholar] [CrossRef]
- Chiel, B.S.; Dever, C. Autonomous parafoil guidance in high winds. J. Guid. Control Dyn. 2015, 38, 963–969. [Google Scholar] [CrossRef]
- Rademacher, B.J.; Lu, P.; Strahan, A.L.; Cerimele, C.J. In-flight trajectory planning and guidance for autonomous parafoils. J. Guid. Control Dyn. 2009, 32, 1697–1712. [Google Scholar] [CrossRef]
- Fowler, L.; Rogers, J. Bézier curve path planning for parafoil terminal guidance. J. Aerosp. Inf. Syst. 2014, 11, 300–315. [Google Scholar] [CrossRef]
- Babu, A.S.; Suja, V.C.; Reddy, C.V. Three dimensional trajectory optimization of a homing parafoil. IFAC Proc. Vol. 2014, 47, 847–854. [Google Scholar] [CrossRef]
- Murali, N.; Dineshkumar, M.; Arun, K.W.; Sheela, D. Guidance of parafoil using line of sight and optimal control. IFAC Proc. Vol. 2014, 47, 870–877. [Google Scholar] [CrossRef]
- Rosich, A.; Gurfil, P. Coupling in-flight trajectory planning and flocking for multiple autonomous parafoils. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2012, 226, 691–720. [Google Scholar] [CrossRef]
- Chen, Q.; Sun, Y.; Zhao, M.; Liu, M. Consensus-based cooperative formation guidance strategy for multiparafoil airdrop systems. IEEE Trans. Autom. Sci. Eng. 2020, 18, 2175–2184. [Google Scholar] [CrossRef]
- Chen, Q.; Sun, Y.; Zhao, M.; Liu, M. A virtual structure formation guidance strategy for multi-parafoil systems. IEEE Access 2019, 7, 123592–123603. [Google Scholar] [CrossRef]
- Zhang, L.; Gao, H.; Chen, Z.; Sun, Q.; Zhang, X. Multi-objective global optimal parafoil homing trajectory optimization via Gauss pseudospectral method. Nonlinear Dyn. 2013, 72, 1–8. [Google Scholar] [CrossRef]
- Tao, J.; Sun, Q.L.; Chen, Z.Q.; He, Y.P. NSGAII based multi-objective homing trajectory planning of parafoil system. J. Cent. South Univ. 2016, 23, 3248–3255. [Google Scholar] [CrossRef]
- Zheng, C.; Wu, Q.; Jiang, C.; Xie, Y.R. Optimization in multiphase homing trajectory of parafoil system based on IAGA. Electron. Opt. Control 2011, 18, 69–72. [Google Scholar]
- Lv, F.; He, W.; Zhao, L. An improved nonlinear multibody dynamic model for a parafoil-UAV system. IEEE Access 2019, 7, 139994–140009. [Google Scholar] [CrossRef]
- Lv, F.; He, W.; Zhao, L. A multivariate optimal control strategy for the attitude tracking of a parafoil-UAV system. IEEE Access 2020, 8, 43736–43751. [Google Scholar] [CrossRef]
- Cacan, M.R.; Costello, M.; Ward, M.; Scheuermann, E.; Shurtliff, M. Human-in-the-loop control of guided airdrop systems. Aerosp. Sci. Technol. 2019, 84, 1141–1149. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, W.; Chen, F.; Li, J. Path planning based on improved Deep Deterministic Policy Gradient algorithm. In Proceedings of the 2019 IEEE 3rd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 March 2019; pp. 295–299. [Google Scholar]
- Bouhamed, O.; Ghazzai, H.; Besbes, H.; Massoud, Y. Autonomous UAV navigation: A DDPG-based deep reinforcement learning approach. In Proceedings of the 2020 IEEE International Symposium on Circuits and Systems (ISCAS), Seville, Spain, 12–14 October 2020; pp. 1–5. [Google Scholar]
- Hu, Z.; Wan, K.; Gao, X.; Zhai, Y.; Wang, Q. Deep reinforcement learning approach with multiple experience pools for uav’s autonomous motion planning in complex unknown environments. Sensors 2020, 20, 1890. [Google Scholar] [CrossRef]
- Bouhamed, O.; Wan, X.; Ghazzai, H.; Massoud, Y. A DDPG-based Approach for Energy-aware UAV Navigation in Obstacle-constrained Environment. In Proceedings of the 2020 IEEE 6th World Forum on Internet of Things (WF-IoT), New Orleans, LA, USA, 2–16 June 2020; pp. 1–6. [Google Scholar]
- Wan, K.; Gao, X.; Hu, Z.; Wu, G. Robust motion control for UAV in dynamic uncertain environments using deep reinforcement learning. Remote Sens. 2020, 12, 640. [Google Scholar] [CrossRef]
- Chen, J.; Wu, T.; Shi, M.; Jiang, W. PORF-DDPG: Learning personalized autonomous driving behavior with progressively optimized reward function. Sensors 2020, 20, 5626. [Google Scholar] [CrossRef]
- Dong, Y.; Zou, X. Mobile Robot Path Planning Based on Improved DDPG Reinforcement Learning Algorithm. In Proceedings of the 2020 IEEE 11th International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 16–18 October 2020; pp. 52–56. [Google Scholar]
- Yang, J.; Peng, G. DDPG with Meta-Learning-Based Experience Replay Separation for Robot Trajectory Planning. In Proceedings of the 2021 7th International Conference on Control, Automation and Robotics (ICCAR), Singapore, 23–26 April 2021; pp. 46–51. [Google Scholar]
- Li, B.; Yang, Z.P.; Chen, D.Q.; Liang, S.Y.; Ma, H. Maneuvering target tracking of UAV based on MN-DDPG and transfer learning. Def. Technol. 2021, 17, 457–466. [Google Scholar] [CrossRef]
- Zhang, S.; Li, Y.; Dong, Q. Autonomous navigation of UAV in multi-obstacle environments based on a Deep Reinforcement Learning approach. Appl. Soft Comput. 2022, 115, 108194. [Google Scholar] [CrossRef]
- He, L.; Aouf, N.; Song, B. Explainable Deep Reinforcement Learning for UAV autonomous path planning. Aerosp. Sci. Technol. 2021, 118, 107052. [Google Scholar] [CrossRef]
- Hong, D.; Lee, S.; Cho, Y.H.; Baek, D.; Kim, J.; Chang, N. Energy-Efficient Online Path Planning of Multiple Drones Using Reinforcement Learning. IEEE Trans. Veh. Technol. 2021, 70, 9725–9740. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, C.; Yang, H. Neural network-based simulation and prediction of precise airdrop trajectory planning. Aerosp. Sci. Technol. 2022, 120, 107302. [Google Scholar] [CrossRef]



| Parameter | Value/Unit |
|---|---|
| Span | 2/m |
| Chord | 0.8/m |
| Area of canopy | 3/m |
| Length of suspending ropes | 1.4/m |
| Mass of payload | 12.5/kg |
| Mass of canopy | 0.9/kg |
| Parameter | Value |
|---|---|
| Max Episodes | 3000 |
| Discount Factor | 0.99 |
| Soft Update Factor | 0.01 |
| Critic Learning Rate | 0.0005 |
| Actor Leaning Rate | 0.001 |
| Reply Buffer Size | |
| Batch Size | 256 |
| Delay Steps | 3 |
| Algorithm | LR10 | LR20 | LR50 | Crash | Average Landing Errors |
|---|---|---|---|---|---|
| DDPG | 1% | 19% | 63% | 20% | 33.8 m |
| TD3 | 17% | 74% | 92% | 13% | 16.6 m |
| Improved TD3 | 89% | 92% | 93% | 5% | 5.7 m |
| Algorithm | LR10 | LR20 | LR50 | Crash | Average Landing Errors |
|---|---|---|---|---|---|
| DDPG | 5% | 41% | 60% | 33% | 37.7 m |
| TD3 | 8% | 48% | 82% | 15% | 21.8 m |
| Improved TD3 | 76% | 91% | 94% | 4% | 6.4 m |
| Initial Position | DDPG | TD3 | Improved TD3 | |||
|---|---|---|---|---|---|---|
| Final Position | Landing Error | Final Position | Landing Error | Final Position | Landing Error | |
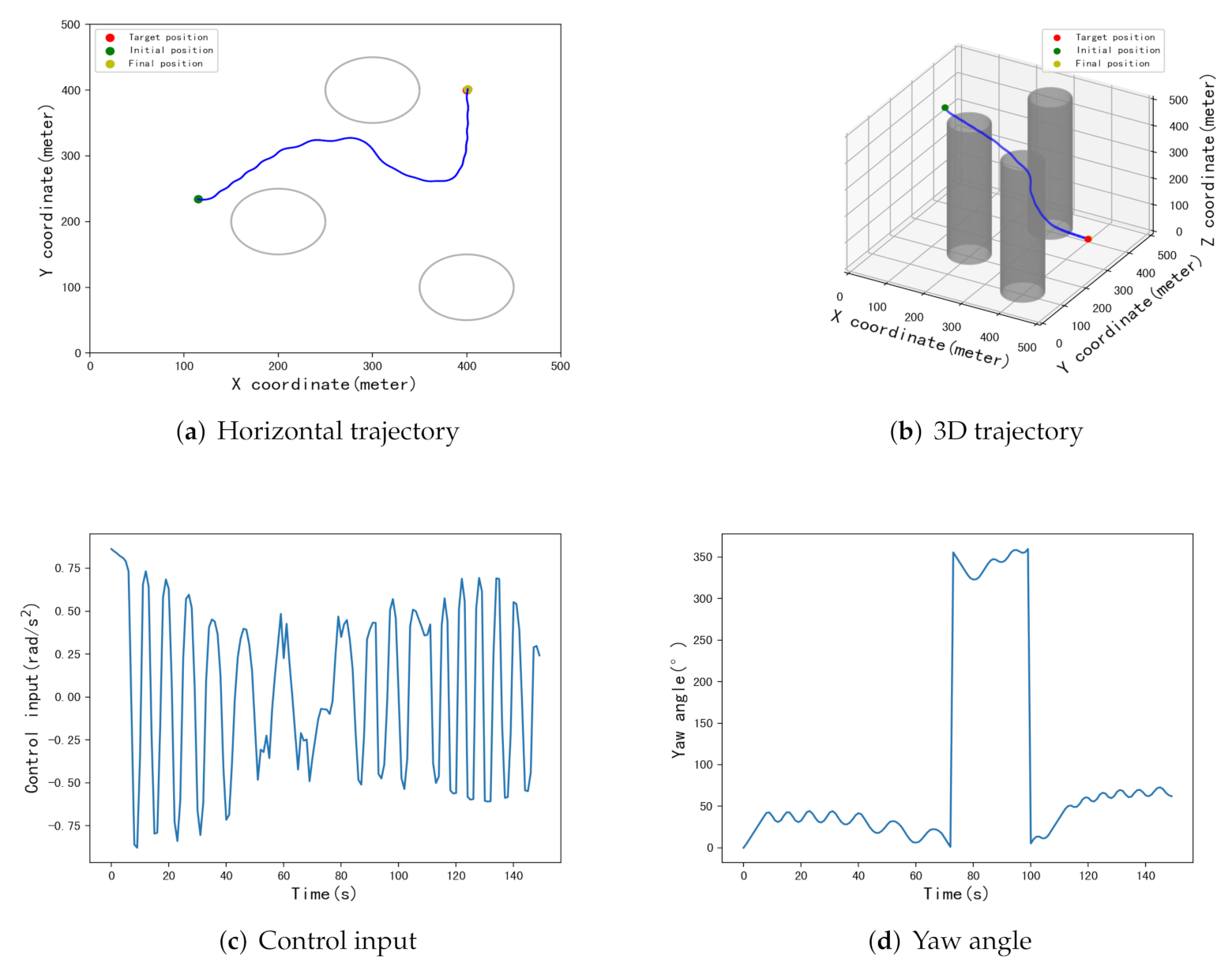
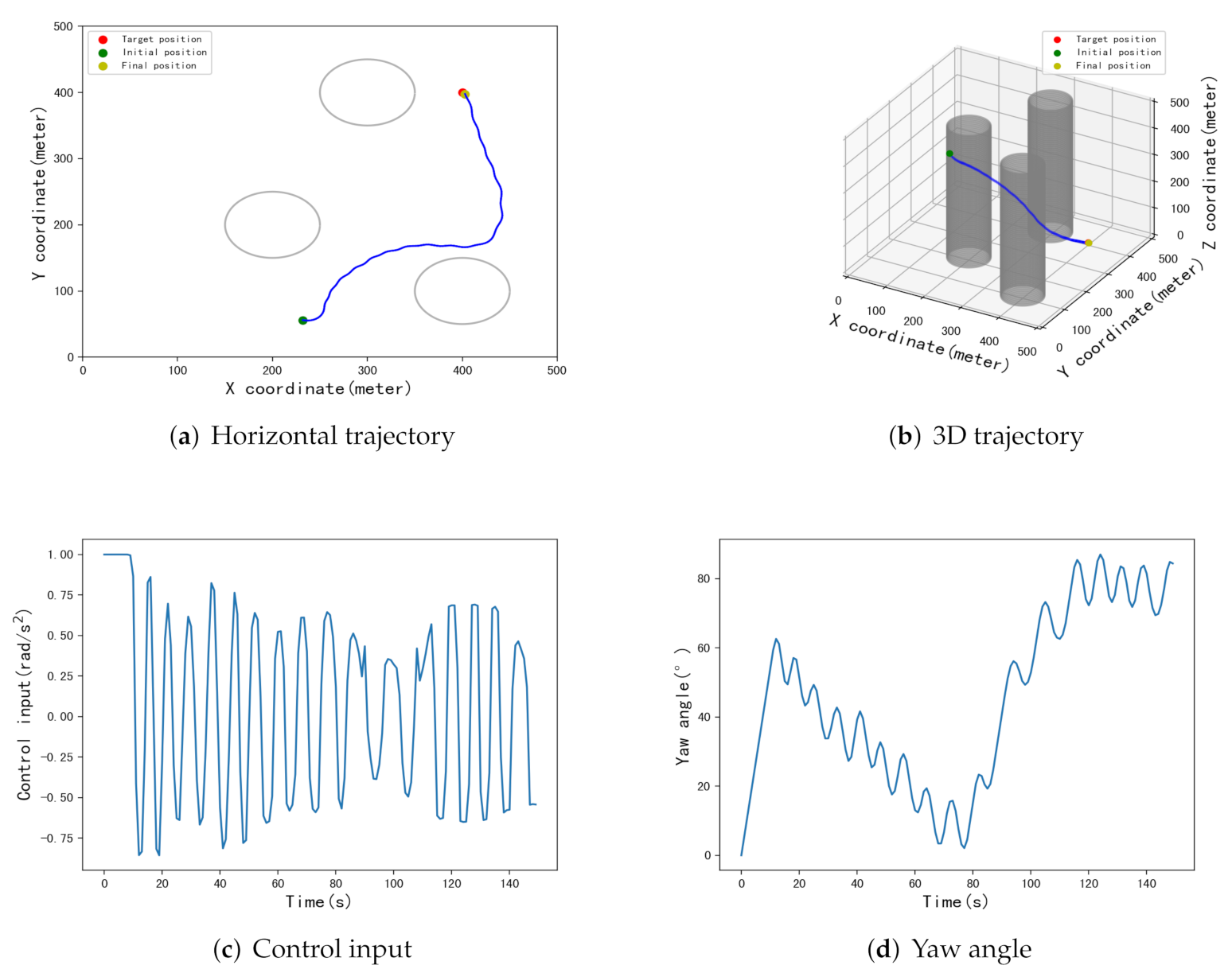
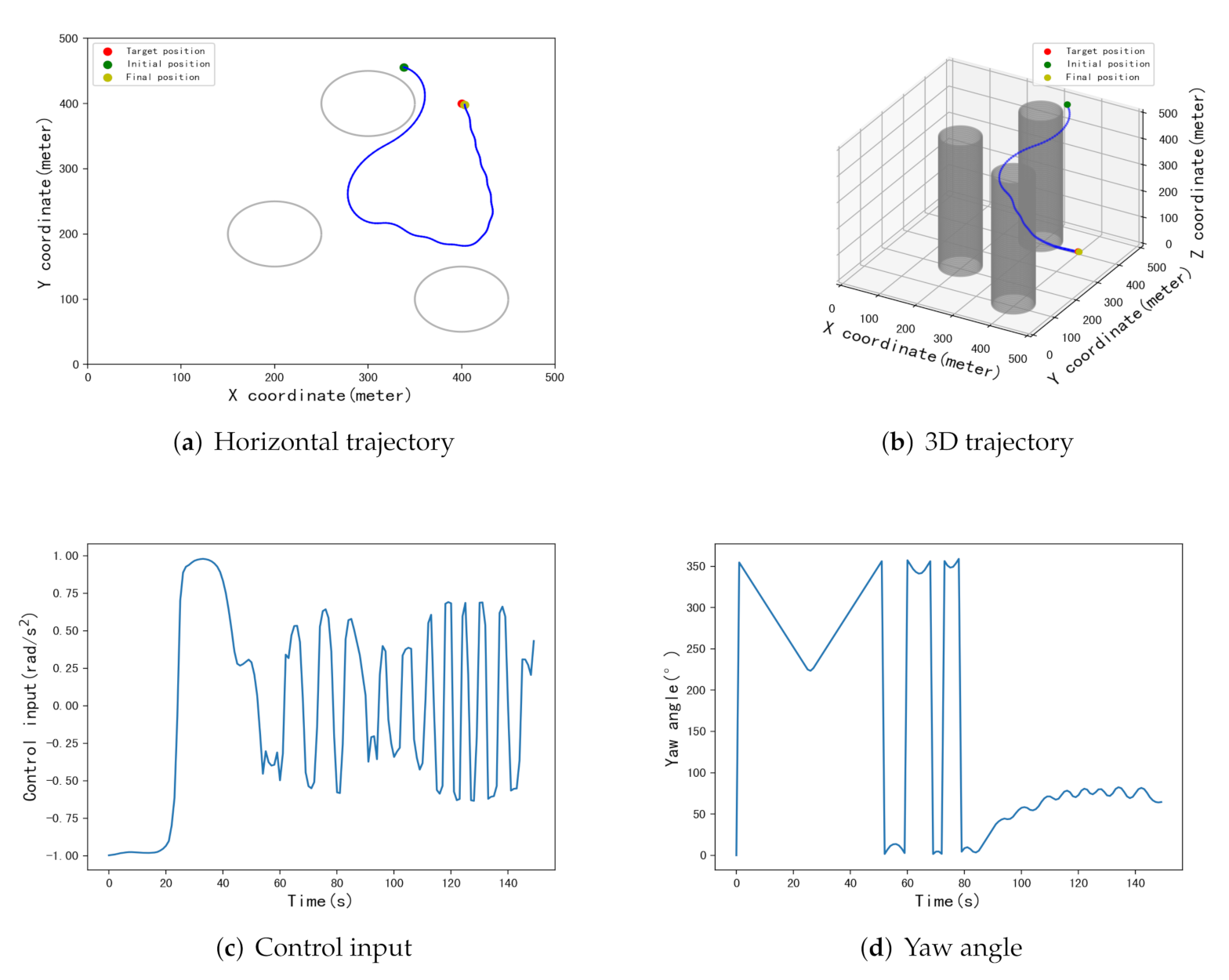
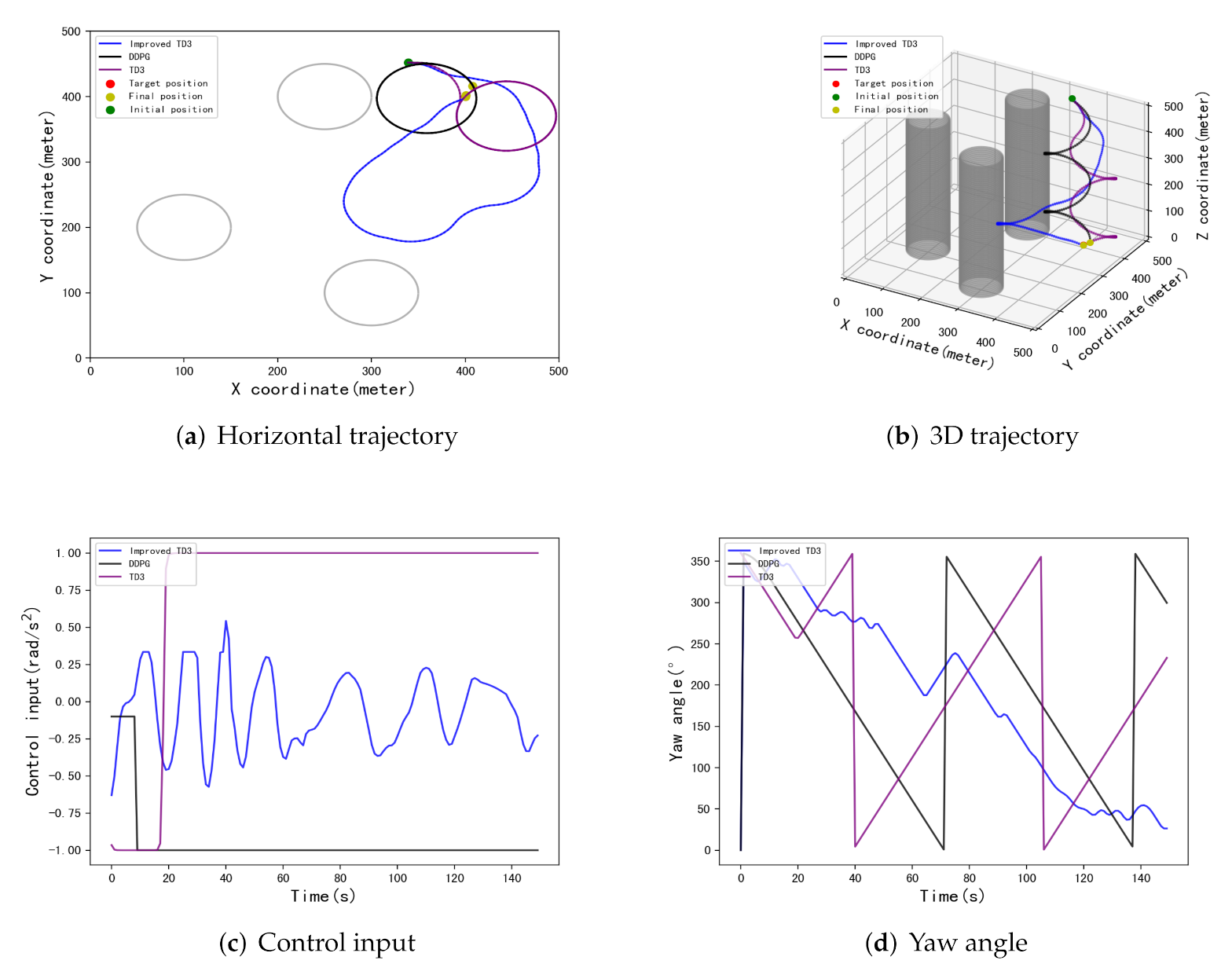
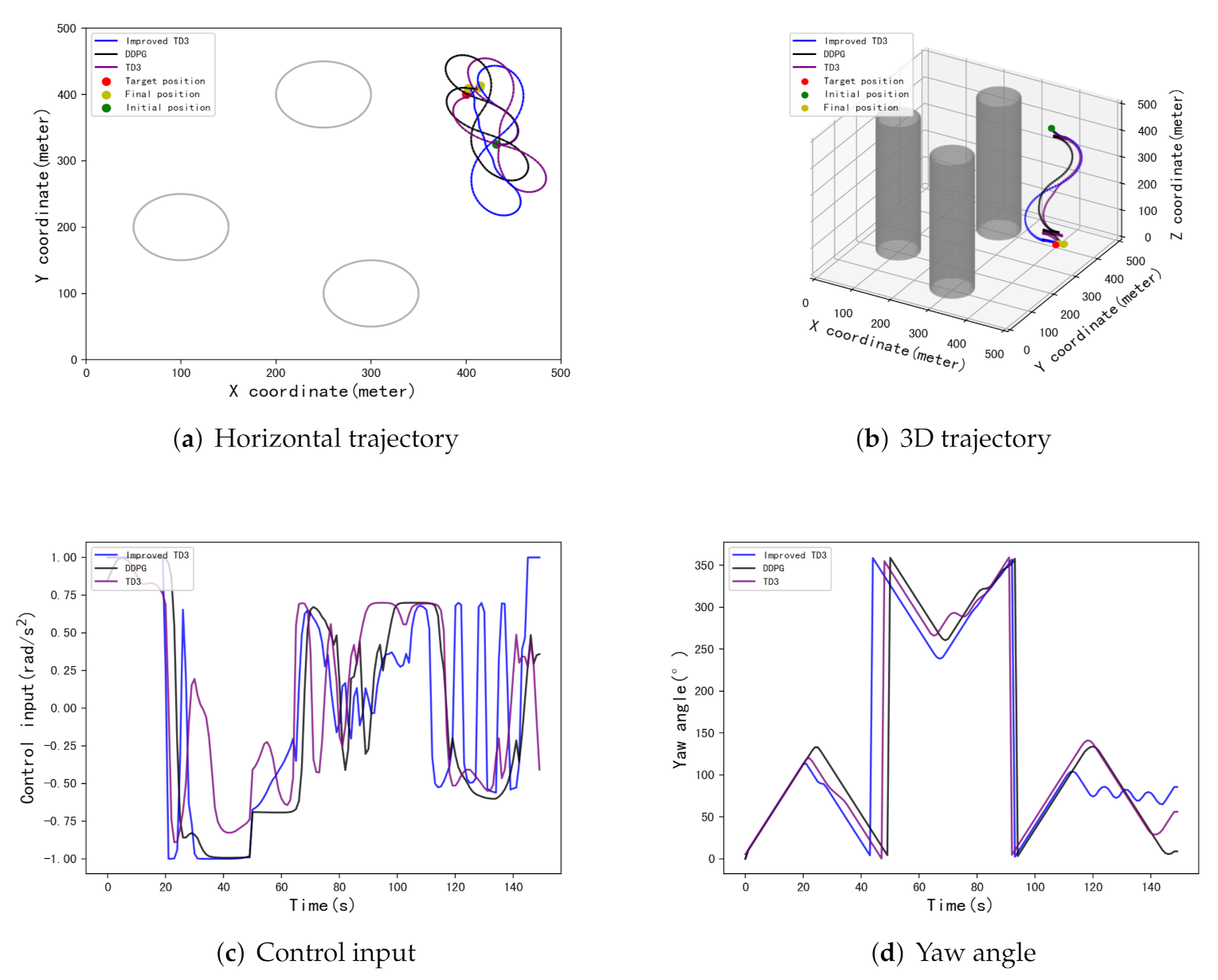
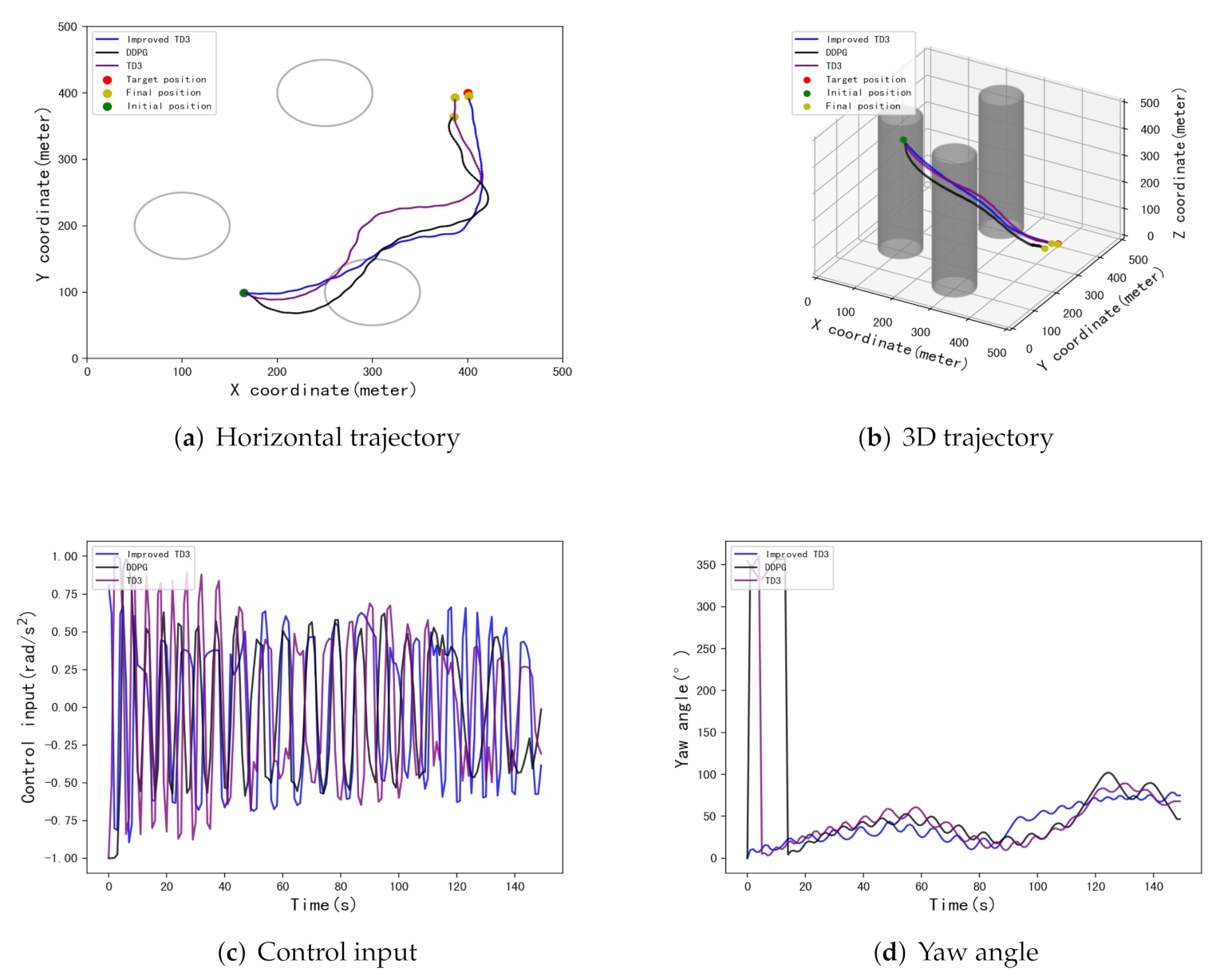
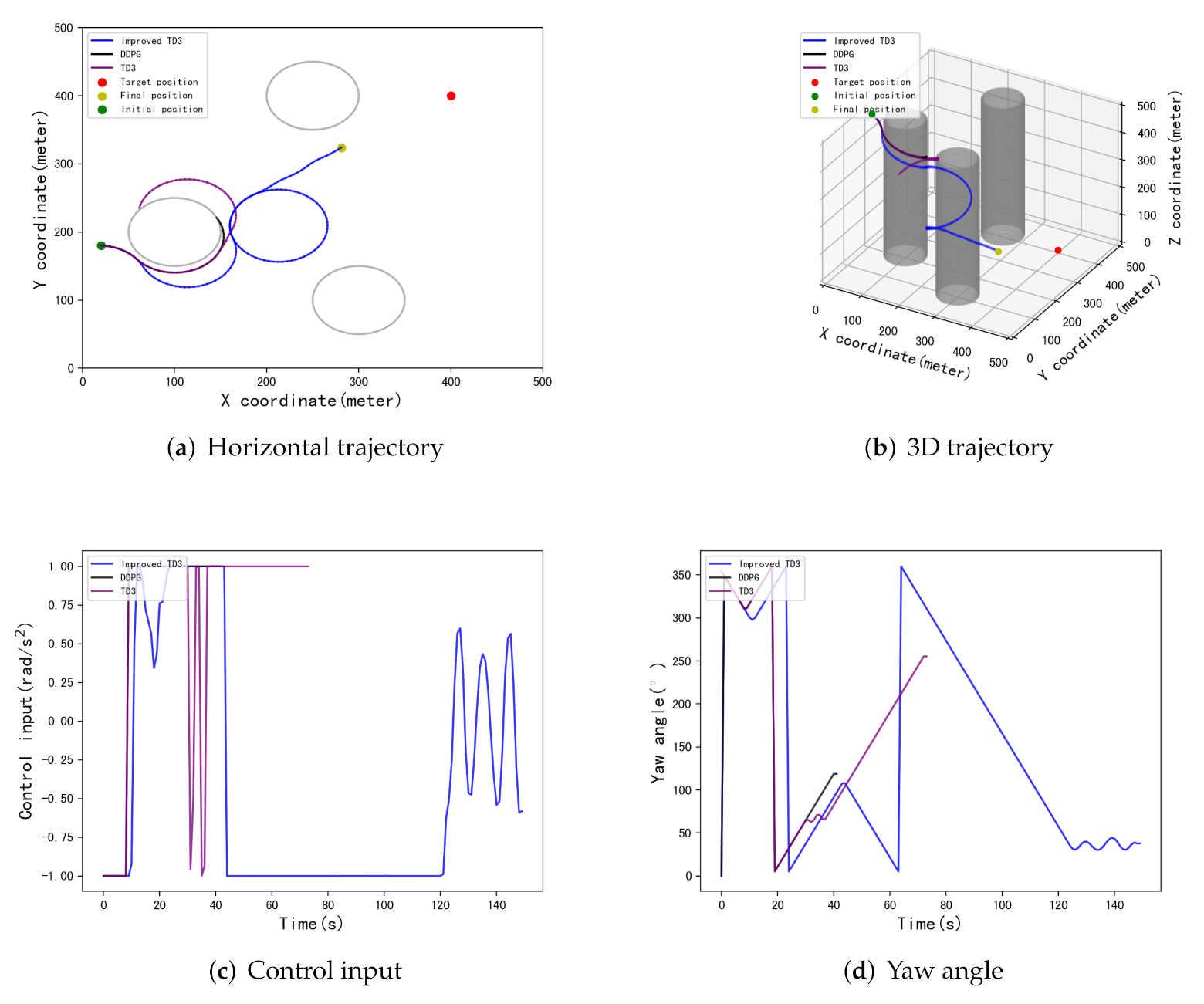
| [434,299] | [398.8,426.7] | 26.7 m | [415.4,400.5] | 15.4 m | [399.7,397.6] | 2.4 m |
| [72,312] | [412,383.9] | 20 m | [407.4,407.5] | 10.5 m | [400.3,398.4] | 1.6 m |
| [339,452] | [408,416.5] | 18.3 m | [400,400.1] | 0.1 m | [400.9,397.8] | 2.4 m |
| [432,325] | [414.2,408.5] | 16.5 m | [415.4,414.7] | 21.2 m | [402,409.6] | 9.8 m |
| [165,99] | [385.6,364.4] | 38.4 m | [386.6,393] | 15.1 m | [401.6,396.5] | 3.8 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Sun, H.; Sun, J. Improved Twin Delayed Deep Deterministic Policy Gradient Algorithm Based Real-Time Trajectory Planning for Parafoil under Complicated Constraints. Appl. Sci. 2022, 12, 8189. https://doi.org/10.3390/app12168189
Yu J, Sun H, Sun J. Improved Twin Delayed Deep Deterministic Policy Gradient Algorithm Based Real-Time Trajectory Planning for Parafoil under Complicated Constraints. Applied Sciences. 2022; 12(16):8189. https://doi.org/10.3390/app12168189
Chicago/Turabian StyleYu, Jiaming, Hao Sun, and Junqing Sun. 2022. "Improved Twin Delayed Deep Deterministic Policy Gradient Algorithm Based Real-Time Trajectory Planning for Parafoil under Complicated Constraints" Applied Sciences 12, no. 16: 8189. https://doi.org/10.3390/app12168189
APA StyleYu, J., Sun, H., & Sun, J. (2022). Improved Twin Delayed Deep Deterministic Policy Gradient Algorithm Based Real-Time Trajectory Planning for Parafoil under Complicated Constraints. Applied Sciences, 12(16), 8189. https://doi.org/10.3390/app12168189







