Optimal Time–Jerk Trajectory Planning for Delta Parallel Robot Based on Improved Butterfly Optimization Algorithm
Abstract
:1. Introduction
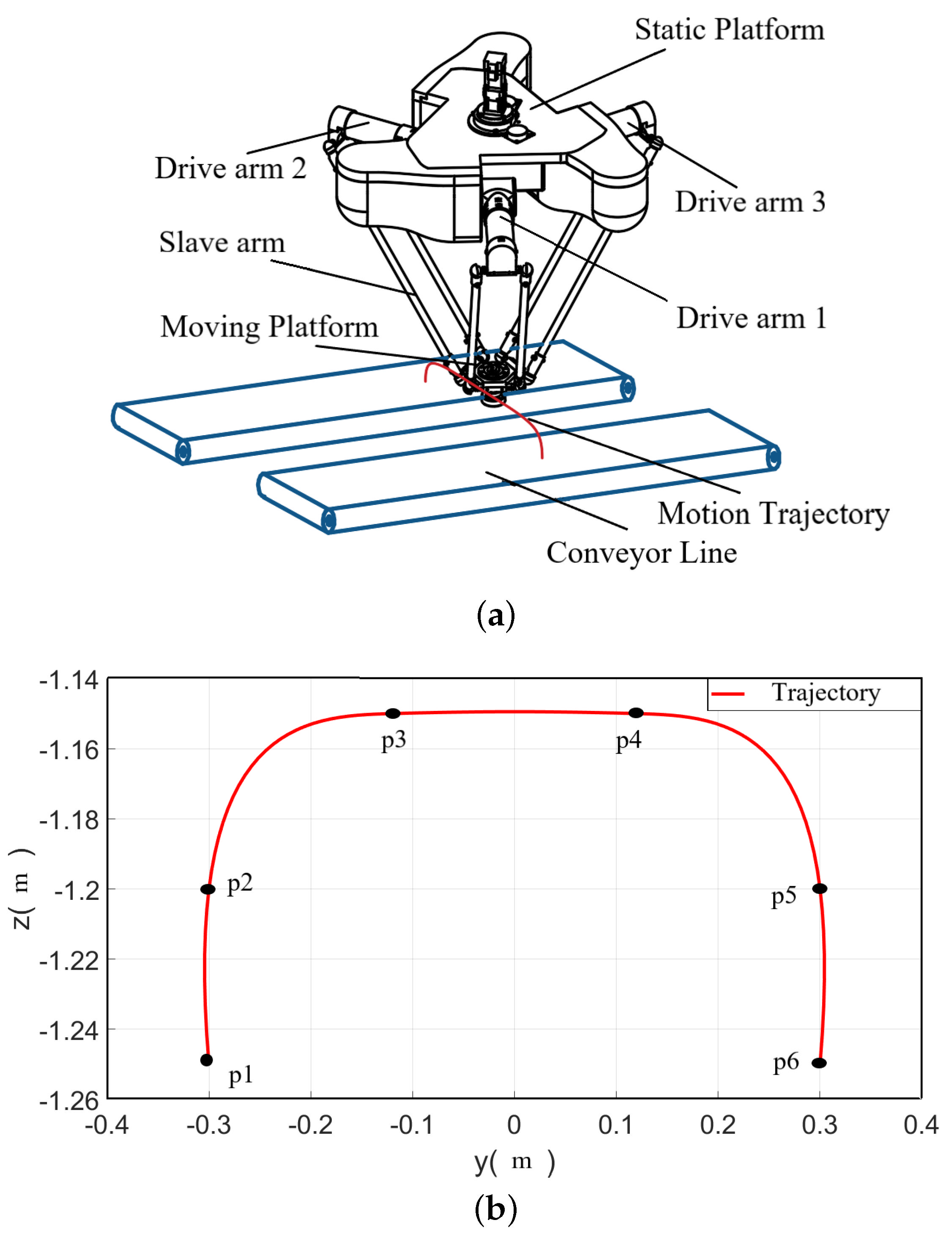
2. Delta Parallel Robot
3. Optimal Time–Jerk Problem Description
4. Trajectory Planning in Operation Space
4.1. Trajectory Description
4.2. Trajectory Construction by Means of Fifth-Order NURBS Curve
5. Improved Butterfly Optimization Algorithm
5.1. Butterfly Optimization Algorithm
5.2. IBOA
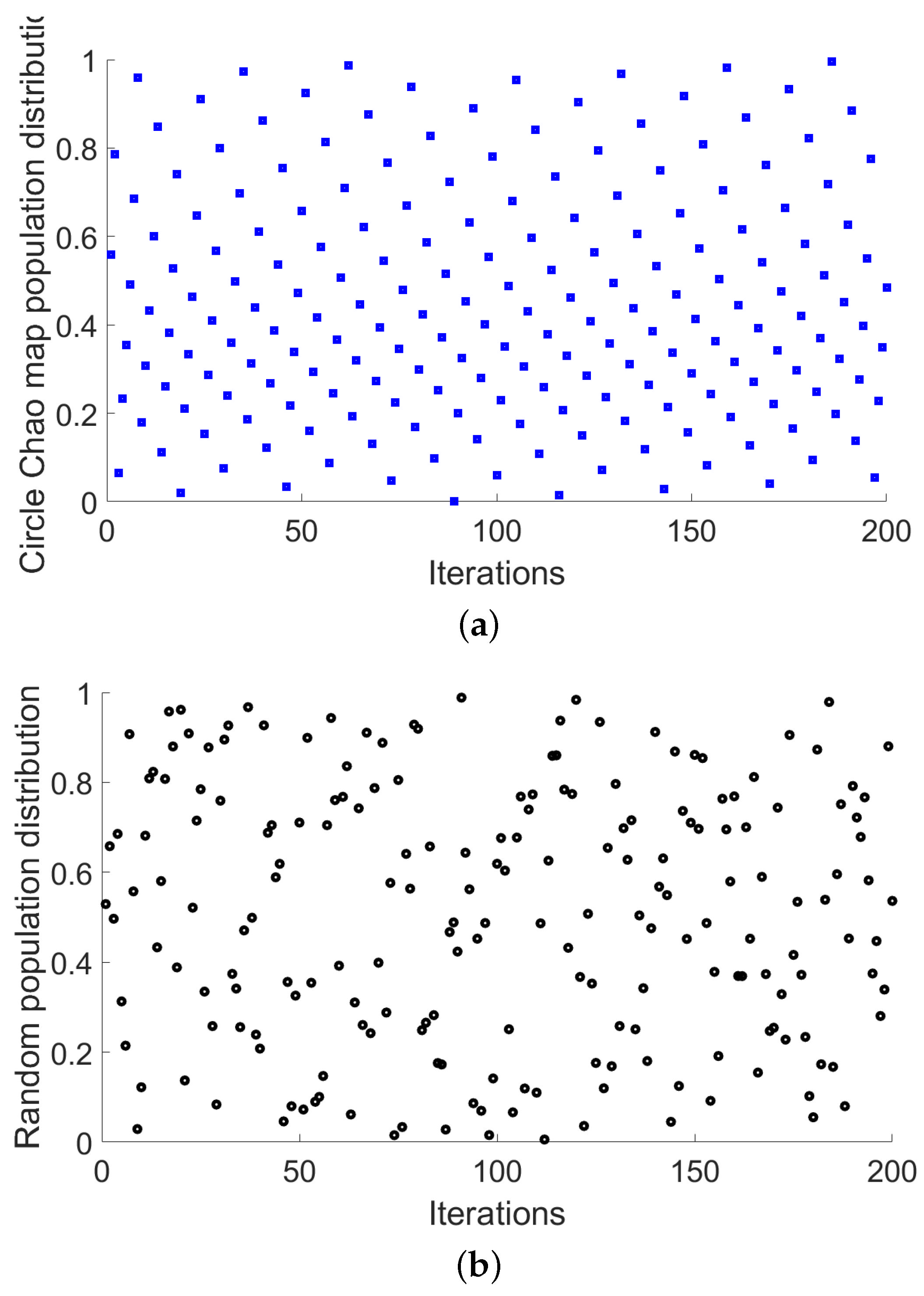
5.2.1. Chaotic Mapping
5.2.2. Fractional Derivative
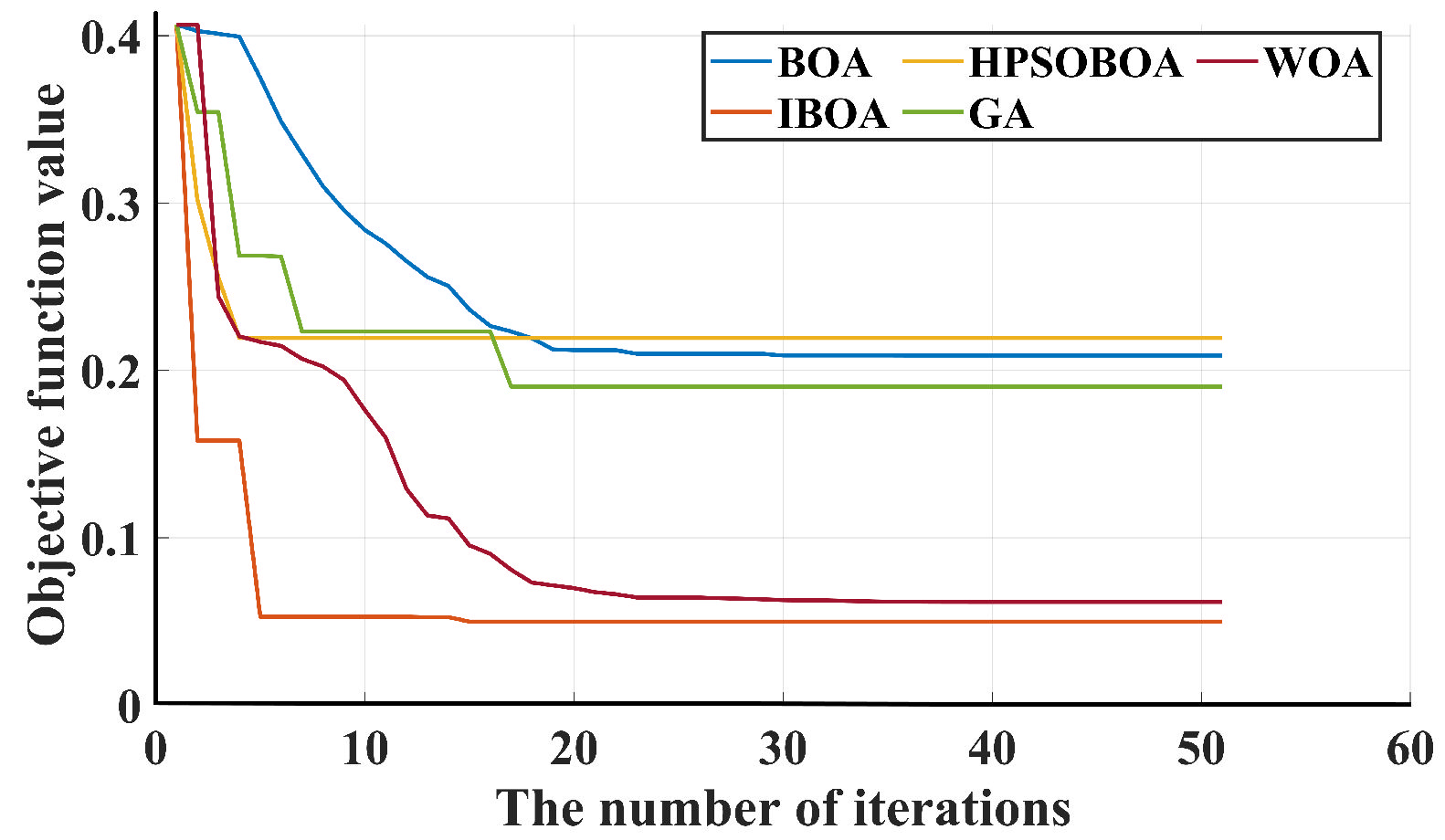
6. Simulation Test and Results Analysis
6.1. Experimental Test of IBOA
6.1.1. Test of IBOA Population
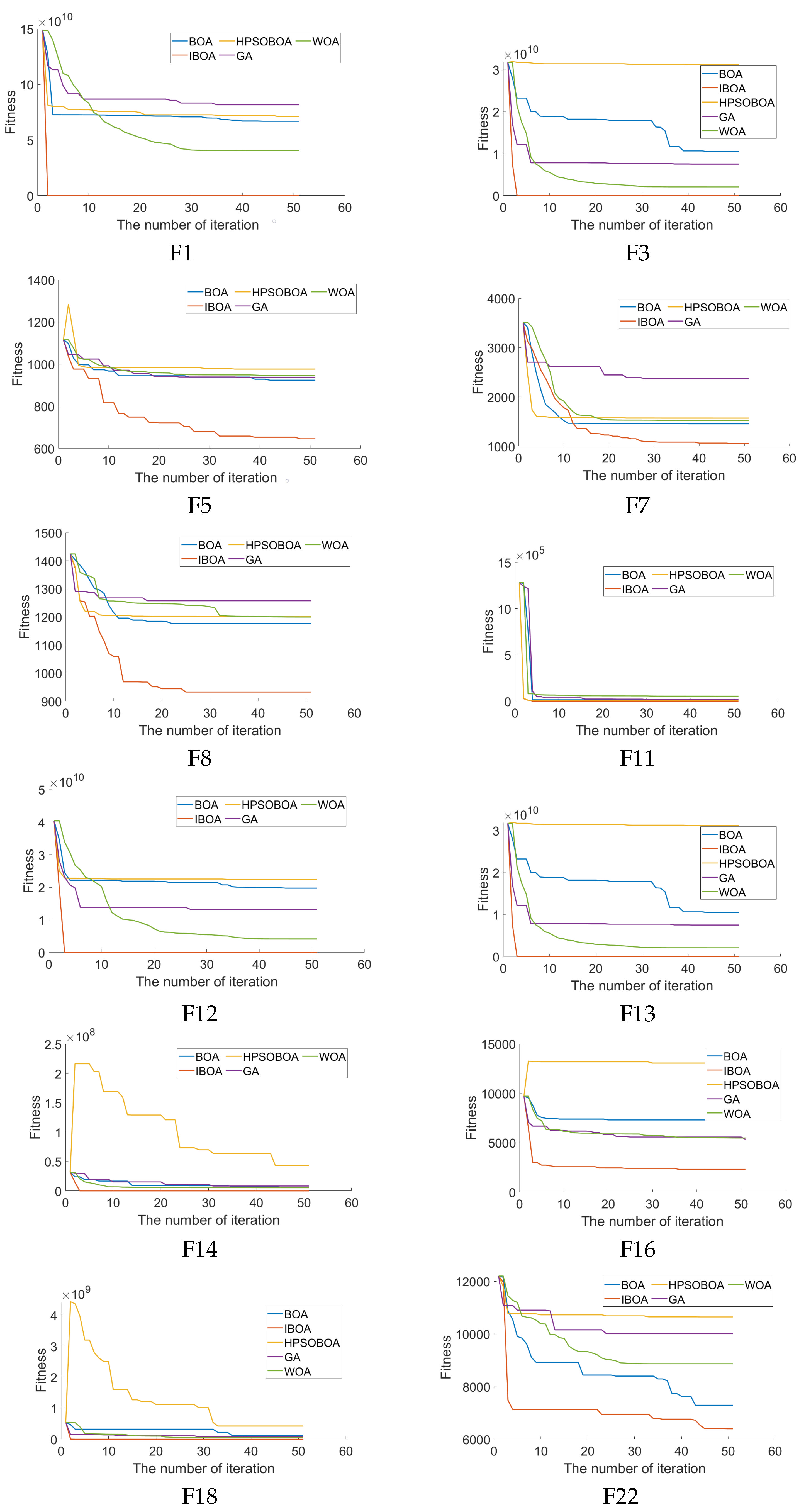
6.1.2. Results for Benchmark Test Functions
6.1.3. Non-Parametric Test
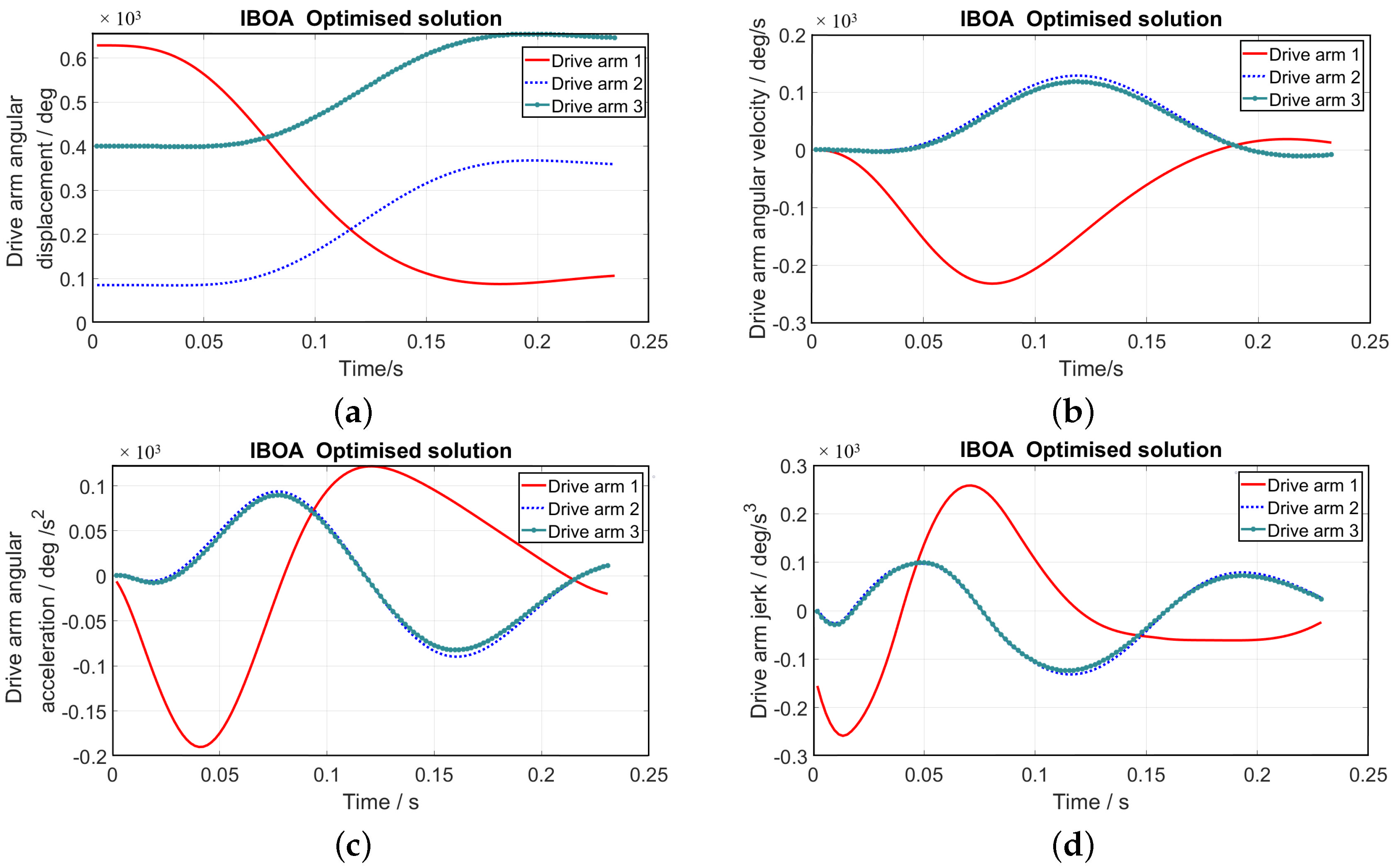
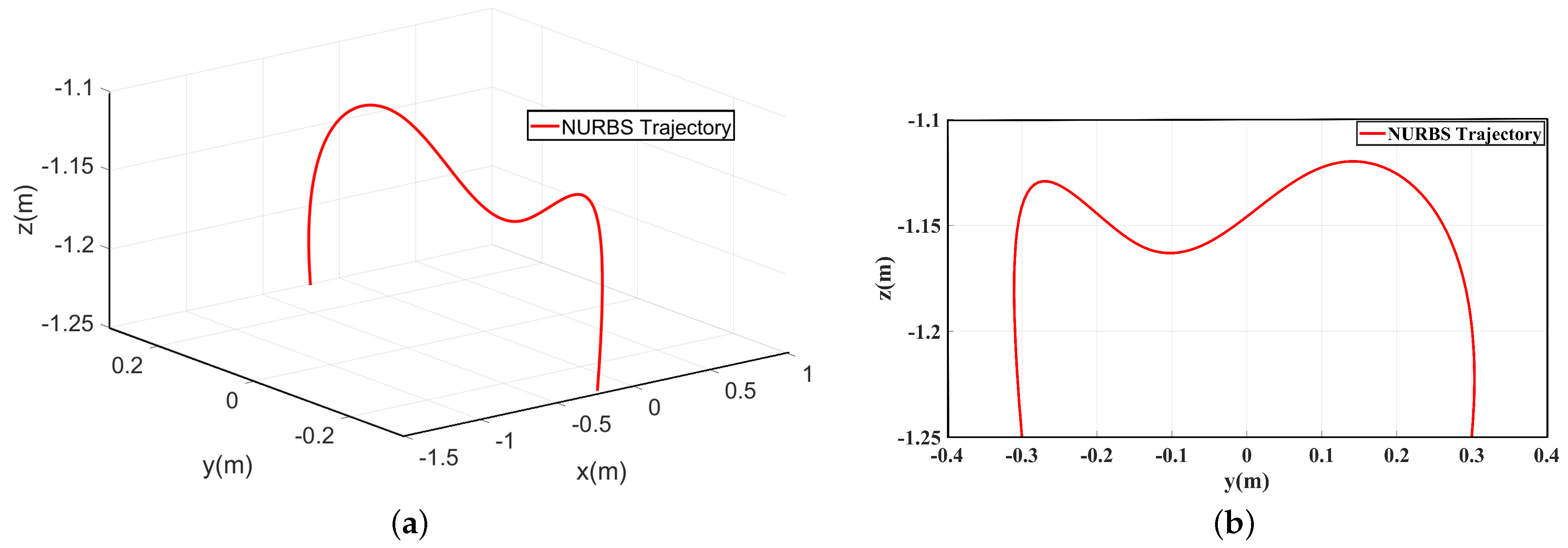
6.2. Trajectory Planning for Delta High-Speed Parallel Robots
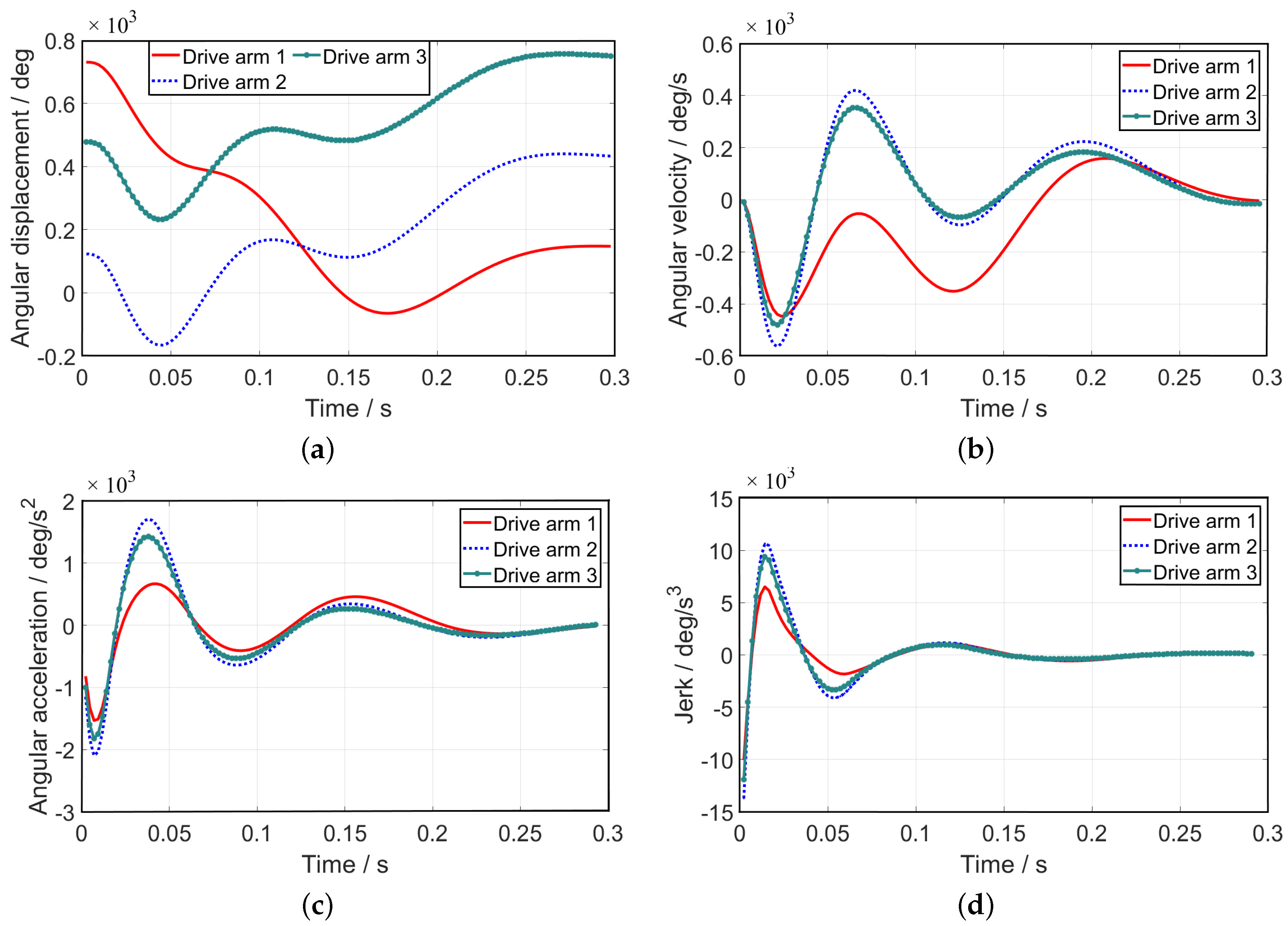
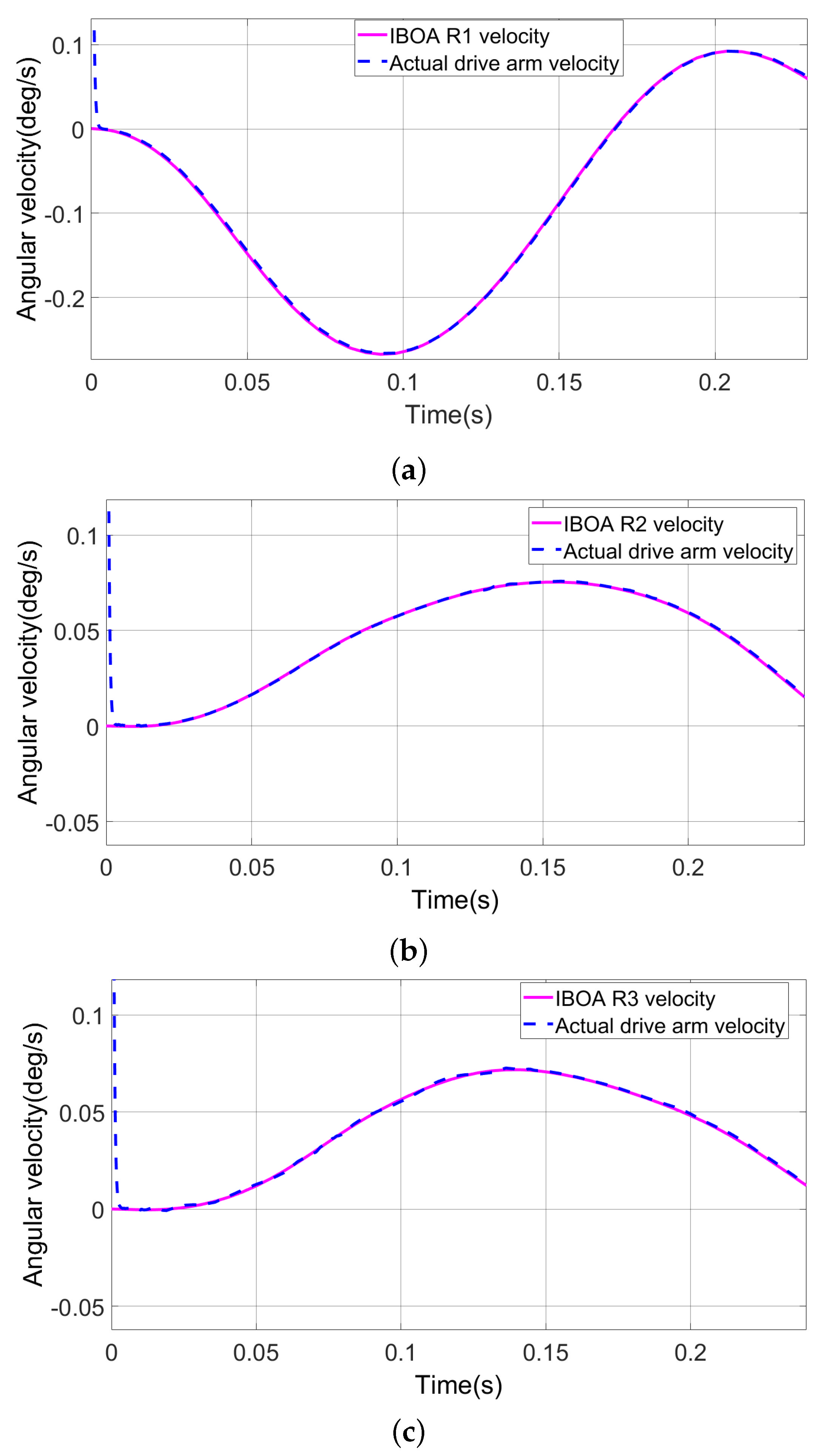
6.3. Verification of the IBOA Trajectory Optimization
6.4. Simulation Experiments for Trajectory Optimization
7. Conclusions
- The trajectory planning was carried out in Cartesian space, and the NURBS curve was used to generate the trajectory. The picking trajectory was designed according to the actual robot picking span, and the displacement, velocity, acceleration, and jerk curve of each driving arm were obtained through velocity, acceleration, and jerk constraints.
- In order to improve the dynamic performance of the robot, BOA was used for optimization. Aiming at resolving the problems of the standard BOA, such as low convergence speed and ease of falling into a local optimum in multi-objective optimizations, chaotic mapping and fractional differentiation were used to improve the butterfly optimization algorithm. This not only expanded the search scope of the algorithm but also increased the iteration memory, which helped to improve the convergence speed and accuracy. Then, numerous simulation tests were carried out. The obtained results showed that the improved algorithm had more significant competitiveness and could reduce the jerk in multi-objective optimizations by 87.6%.
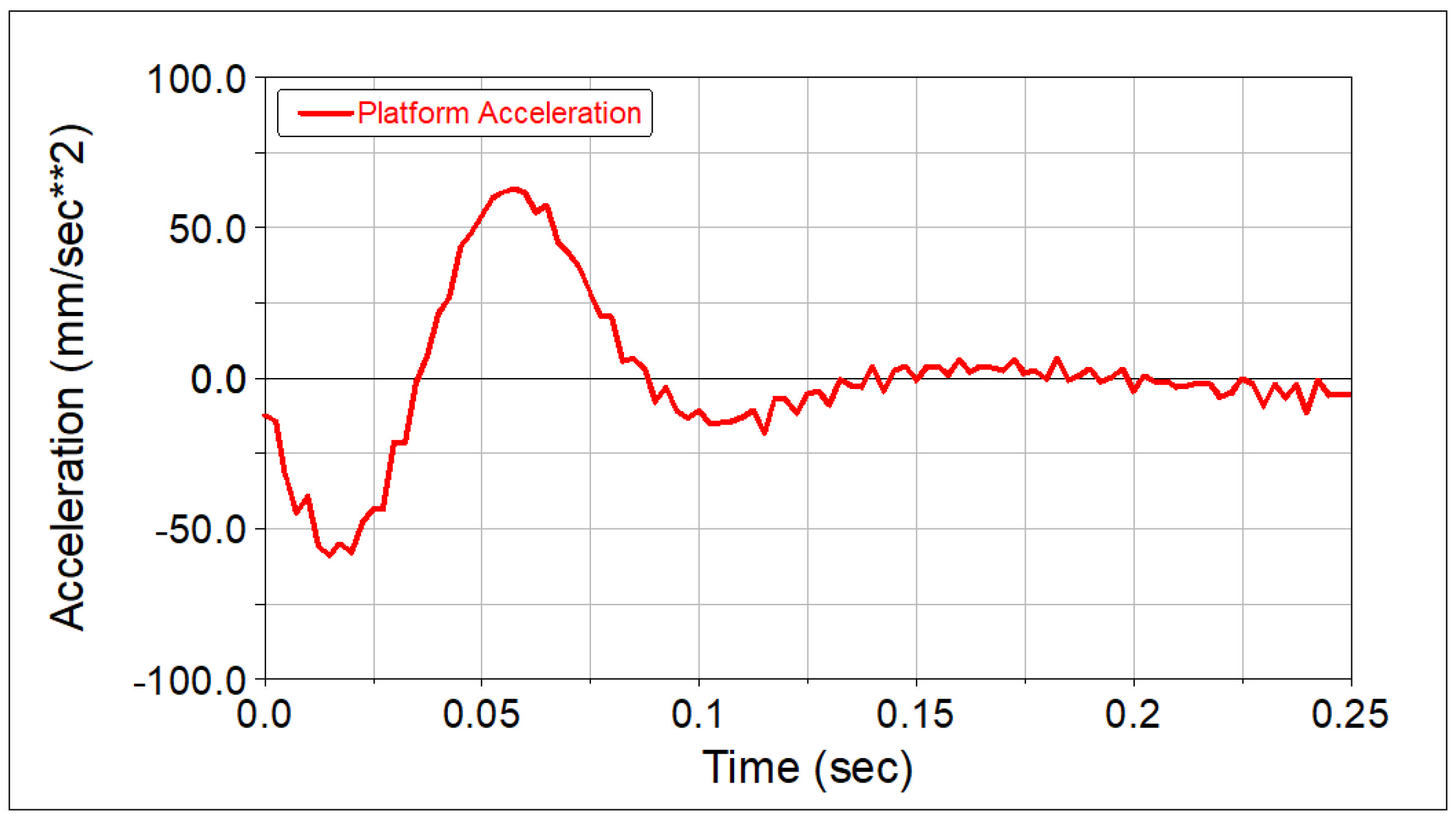
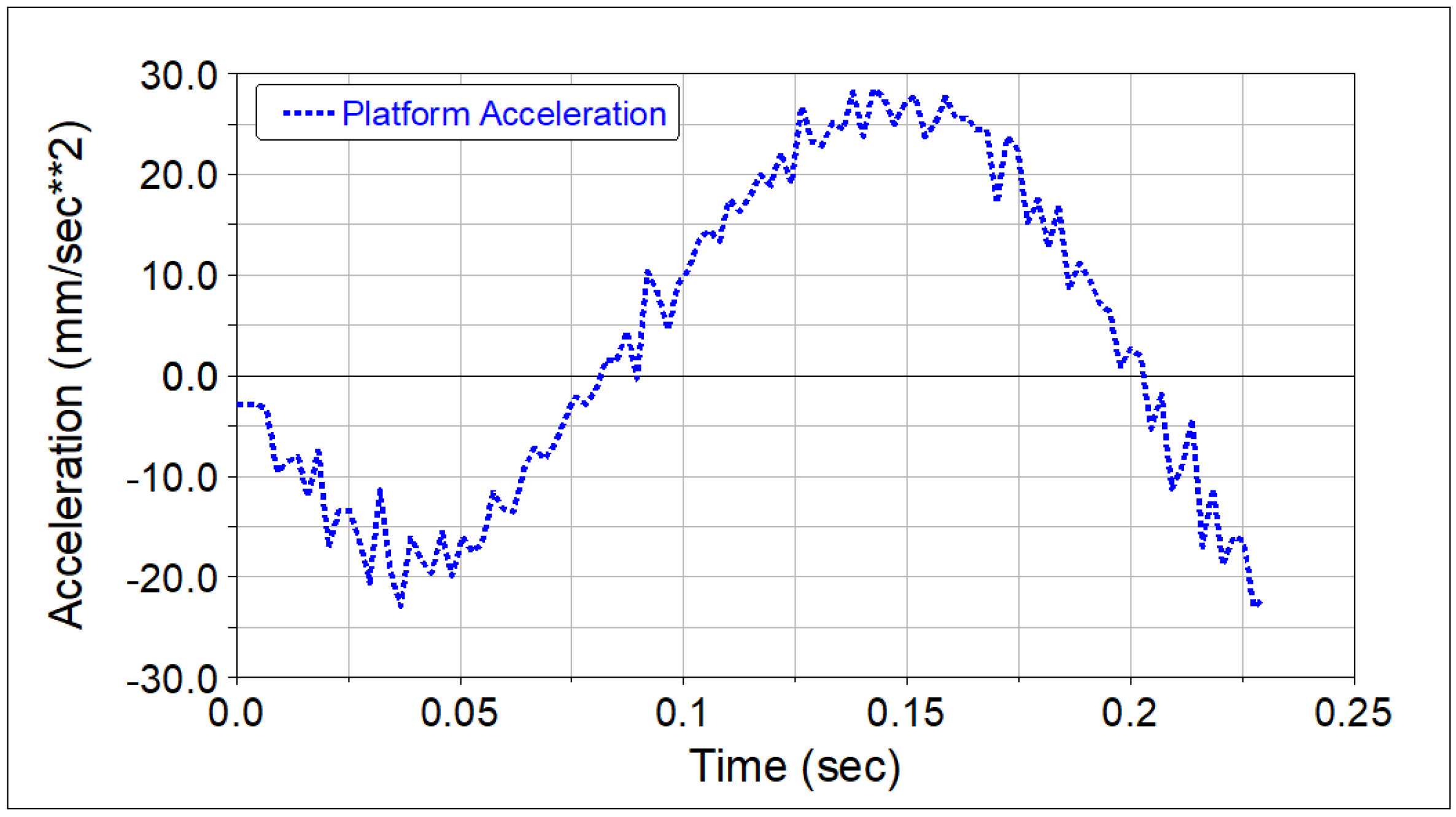
- The vibration accelerations of the robot terminal platform before and after optimization were compared numerically. The simulation results showed that the optimized trajectory effectively reduced the vibration acceleration of the terminal platform.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Patel, Y.D.; George, P.M. Parallel manipulators applications—A survey. Mod. Mech. Eng. 2012, 2, 57–64. [Google Scholar] [CrossRef]
- Song, X.G.; Zhao, Y.J.; Jin, L.; Zhang, P.; Chen, C.W. Dynamic feedforward control in decoupling space for a four-degree-of-freedom parallel robot. Int. J. Adv. Robot. Syst. 2019, 2, 1–10. [Google Scholar]
- Connolly, C. ABB high-speed picking robots establish themselves in food packaging. Ind. Robot. Int. J. 2007, 34, 281–284. [Google Scholar] [CrossRef]
- Company, O.; Marquet, F.; Pierrot, F. A new high-speed 4-DOF parallel robot synthesis and modeling issues. IEEE Trans. Robot. Autom. 2003, 19, 411–420. [Google Scholar] [CrossRef]
- Chen, Y.D.; Li, L. Predictable trajectory planning of industrial robots with constraints. Appl. Sci. 2018, 8, 2648. [Google Scholar] [CrossRef]
- Stilman, M. Global manipulation planning in robot joint space with task constraints. IEEE Trans. Robot. 2010, 26, 576–584. [Google Scholar] [CrossRef]
- Mei, J.P.; Zang, J.W.; Qiao, Z.Y.; Liu, S.T.; Song, T. Trajectory planning of 3-DOF Delta parallel manipulator. J. Mech. Eng. 2016, 52, 9–17. [Google Scholar] [CrossRef]
- Li, Y.H.; Huang, T.; Chetwynd, D.G. An approach for smooth trajectory planning of high-speed pick-and-place parallel robots using quintic B-splines. Mech. Mach. Theory 2018, 126, 479–490. [Google Scholar] [CrossRef]
- Gauthier, J.F.; Angeles; Nokleby, S. Optimization of a test trajectory for SCARA systems. In Advances in Robot Kinematics: Analysis and Design; Springer: Dordrecht, The Netherlands, 2008; pp. 225–234. [Google Scholar]
- Su, T.T.; Cheng, L.; Wang, Y.K.; Liang, X.; Zheng, J.; Zhang, H.J. Time-optimal trajectory planning for delta robot based on quintic pythagorean-hodograph curves. IEEE Access 2018, 6, 28530–28539. [Google Scholar] [CrossRef]
- Wang, S.A.; Wu, S.; Kang, C.; Li, X. Trajectory planning of a parallel manipulator based on kinematic transmission property. Intell. Serv. Robot. 2015, 8, 129–139. [Google Scholar] [CrossRef]
- Han, S.J.; Shan, X.C.; Fu, J.X.; Xu, W.J.; Mi, H.Y. Industrial robot trajectory planning based on improved pso algorithm. J. Phys. Conf. Ser. 2021, 1820, 012185. [Google Scholar] [CrossRef]
- Perez-Carabaza, S.; Besada-Portas, E.; Lopez-Orozco, J.A.; Jesus, M. Ant colony optimization for multi-UAV minimum time search in uncertain domains. Appl. Soft Comput. 2018, 62, 789–806. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Ming, Z.F. Trajectory planning and optimization for a Par4 parallel robot based on energy consumption. Appl. Sci. 2019, 9, 2770. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, S.; Guo, J.X.; Gao, X.S. Time-optimal path tracking for robots under dynamics constraints based on convex optimization. Robotica 2016, 34, 2116–2139. [Google Scholar] [CrossRef]
- Yu, X.L.; Dong, M.S.; Yin, W.M. Time-optimal trajectory planning of manipulator with simultaneously searching the optimal path. Comput. Commun. 2022, 181, 446–453. [Google Scholar] [CrossRef]
- Yu, R.; Wang, C.J.; Guo, Y.C.; Zhang, Y.P. Time-optimal trajectory planning of robot based on breed algorithm. Mech. Drive 2018, 42, 55–59. [Google Scholar]
- Chen, Y.; Yan, L.; Wei, H.; Wang, T. Optimal trajectory planning for industrial robots using harmony search algorithm. Ind. Robot. Int. J. 2013, 40, 502–512. [Google Scholar] [CrossRef]
- Wang, W.J.; Tao, Q.; Cao, Y.T.; Wang, X.H.; Zhang, X. Robot time-optimal trajectory planning based on improved cuckoo search algorithm. IEEE Access 2020, 8, 86923–86933. [Google Scholar] [CrossRef]
- Liu, C.; Cao, G.H.; Qu, Y.Y.; Cheng, Y.M. An improved PSO algorithm for time-optimal trajectory planning of Delta robot in intelligent packaging. Int. J. Adv. Manuf. Technol. 2020, 107, 1091–1099. [Google Scholar] [CrossRef]
- Zhou, J.; Cao, H.J.; Jiang, P.; Li, C.B.; Yi, H.; Liu, M.L. Energy-Saving Trajectory Planning for Robotic High-Speed Milling of Sculptured Surfaces. IEEE Trans. Autom. Sci. Eng. 2021, 19, 2278–2294. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Peng, J.Z.; Ding, S. A Bio-inspired trajectory planning method for robotic manipulators based on improved bacteria foraging optimization algorithm and tau theory. Math. Biosci. Eng. 2022, 19, 643–662. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.; Zhao, J.D.; Jiang, L.; Liu, H. Time-jerk optimal trajectory planning of a 7-DOF redundant robot. Turk. J. Electr. Eng. Comput. Sci. 2017, 25, 4211–4222. [Google Scholar] [CrossRef]
- Wang, T.; Xin, Z.J.; Miao, H.B.; Zhang, H.; Chen, Z.Y.; Du, Y.F. Optimal trajectory planning of grinding robot based on improved whale optimization algorithm. Math. Probl. Eng. 2020, 2020, 3424313. [Google Scholar] [CrossRef]
- Bureerat, S.; Pholdee, N.; Radpukdee, T.; Jaroenapibal, P. Self-adaptive MRPBIL-DE for 6D robot multiobjective trajectory planning. Expert Syst. Appl. 2009, 136, 133–144. [Google Scholar] [CrossRef]
- Huang, J.; Hu, P.; Wu, K.; Zeng, M. Optimal time-jerk trajectory planning for industrial robots. Mech. Mach. Theory 2018, 121, 530–544. [Google Scholar] [CrossRef]
- Chen, D.; Li, S.; Wang, J.F.; Feng, Y.; Liu, Y. A multi-objective trajectory planning method based on the improved immune clonal selection algorithm. Robot. Comput. Integr. Manuf. 2019, 59, 431–442. [Google Scholar] [CrossRef]
- Yin, S.; Ji, W.; Wang, L. A machine learning based energy efficient trajectory planning approach for industrial robots. Procedia CIRP 2019, 81, 429–434. [Google Scholar] [CrossRef]
- Rauf, H.T.; Bangyal, W.; Lali, M.I. An adaptive hybrid differential evolution algorithm for continuous optimization and classification problems. Neural Comput. Appl. 2021, 33, 10841–10867. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Comput. 2018, 23, 715–734. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. An improved butterfly optimization algorithm with chaos. J. Intell. Fuzzy Syst. 2017, 32, 1079–1088. [Google Scholar] [CrossRef]





| Formula of Function | Dim | Range | |
|---|---|---|---|
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 |
| Formula of Function | Dim | Range | |
|---|---|---|---|
| 30 | −2094.9 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 |
| Formula of Function | Dim | Range | |
|---|---|---|---|
| 2 | 1 | ||
| 4 | 0.0003 | ||
| 2 | −1.0316 | ||
| 2 | 0.398 | ||
| 2 | 3 | ||
| 3 | −3.86 | ||
| 6 | −3.32 | ||
| 4 | −10.1532 | ||
| 4 | −10.4028 | ||
| 4 | −10.536 |
| Fuctions | IBOA vs. BOA | IBOA vs. HPSOBOA | IBOA vs. GA | IBOA vs. WOA |
|---|---|---|---|---|
| 3.36 | 1.56 | 2.56 | 2.56 | |
| 2.56 | 2.33 | 2.56 | 2.58 | |
| 2.56 | 2.56 | 2.56 | 2.56 | |
| 4.56 | 2.56 | 2.60 | 2.96 | |
| 2.56 | 2.56 | 2.56 | 2.56 | |
| 2.03 | 1.56 | 1.86 | 2.16 | |
| 5.02 | 4.89 | 2.56 | 2.13 | |
| 1.88 | 1.01 | 2.56 | 1.91 | |
| 8.74 | 6.68 | 5.65 | 8.24 | |
| 3.78 | 2.86 | 6.30 | 6.30 | |
| 2.56 | 2.56 | 2.56 | 2.56 | |
| 2.56 | 1.96 | 3.71 | 2.96 |
| The Key Points | X (m) | Y (m) | Z (m) |
|---|---|---|---|
| −0.02 | 0.30 | −1.25 | |
| −0.02 | 0.30 | −1.20 | |
| −0.02 | 0.12 | −1.15 | |
| −0.02 | −0.12 | −1.15 | |
| −0.02 | −0.30 | −1.20 | |
| −0.02 | −0.30 | −1.25 |
| Joint | Velocity () | Acceleration () | Jerk () |
|---|---|---|---|
| 1 | 600 | 2000 | 15,000 |
| 2 | 600 | 2000 | 15,000 |
| 3 | 600 | 2000 | 15,000 |
| Method | No Optimization | Optimization of the Algorithm |
|---|---|---|
| WOA | 0.28 | 0.2404 |
| GA | 0.28 | 0.2365 |
| BOA | 0.28 | 0.2442 |
| HPSOBOA | 0.28 | 0.2442 |
| IBOA | 0.28 | 0.2327 |
| Method | No Optimization | Optimization of the Algorithm |
|---|---|---|
| WOA | 2.5 | 1.4472 |
| GA | 2.5 | 2.4435 |
| BOA | 2.5 | 1.8683 |
| HPSOBOA | 2.5 | 1.8245 |
| IBOA | 2.5 | 0.3089 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, P.; Wang, Z.; Jing, H.; Zhao, P. Optimal Time–Jerk Trajectory Planning for Delta Parallel Robot Based on Improved Butterfly Optimization Algorithm. Appl. Sci. 2022, 12, 8145. https://doi.org/10.3390/app12168145
Wu P, Wang Z, Jing H, Zhao P. Optimal Time–Jerk Trajectory Planning for Delta Parallel Robot Based on Improved Butterfly Optimization Algorithm. Applied Sciences. 2022; 12(16):8145. https://doi.org/10.3390/app12168145
Chicago/Turabian StyleWu, Pu, Zongyan Wang, Hongxiang Jing, and Pengfei Zhao. 2022. "Optimal Time–Jerk Trajectory Planning for Delta Parallel Robot Based on Improved Butterfly Optimization Algorithm" Applied Sciences 12, no. 16: 8145. https://doi.org/10.3390/app12168145
APA StyleWu, P., Wang, Z., Jing, H., & Zhao, P. (2022). Optimal Time–Jerk Trajectory Planning for Delta Parallel Robot Based on Improved Butterfly Optimization Algorithm. Applied Sciences, 12(16), 8145. https://doi.org/10.3390/app12168145





