Research on the Reliability of Bridge Structure Construction Process System Based on Copula Theory
Abstract
:1. Introduction
2. Basic Theory of the Copula Function
2.1. Definition of Copula Function
2.2. Metrics of Copula Function Correlation
2.2.1. Pearson Linear Correlation Coefficient
2.2.2. Kendall Rank Correlation Coefficient
- (1)
- Divide the range of each random variable into equal probability intervals, i.e., the domain of values of the cumulative distribution function of the variable into equal subintervals , … that do not overlap with each other.
- (2)
- For each random variable , a sample is taken in each of the N subintervals divided in all its (1), and each subinterval generates a unique random number (indicating the sample random number drawn in the i-th interval of the j-th variable). The sample value corresponding to this random number is obtained by the inverse transformation method .
- (3)
- The sample values of are numbered 1,2,3…, N from smallest to largest to form a matrix .The sample values of the m random variables from the first row to the m-th row are sorted from smallest to largest.
- (4)
- Randomly sort the row vector in the matrix and the resulting vector is denoted as , resulting in the matrix .
- (5)
- Then, each column vector in is a set of samples, and a total of N sets of samples are drawn.
2.3. Commonly Used Two-Dimensional Copula Functions
2.4. Identification of Optimal Copula Functions
3. Engineering Applications
3.1. Basic Information of the Algorithm
- (1)
- Use MIDAS/Civil software to establish the finite element analysis model of the whole bridge.
- (2)
- Use the modified -bound method to search for the main failure modes of the bridge structure.
- (3)
- Use the improved quadratic series response surface method to solve the failure function in different failure modes.
- (4)
- Use the wide boundary method, narrow boundary method, and PENT method to calculate the reliability indexes of the continuous rigid bridge system in the construction stage respectively.
3.2. Calculation of System Reliability Indicators
3.2.1. Establishment of Copula Function
3.2.2. Calculation of the Kendall Rank Correlation Coefficient
3.2.3. Selection of Copula Function and Calculation of Related Parameters
3.2.4. Identification of Optimal Copula Functions
3.2.5. Calculation of the System Failure Probability
3.2.6. Improvement of Computational Theory
3.3. System Reliability Analysis
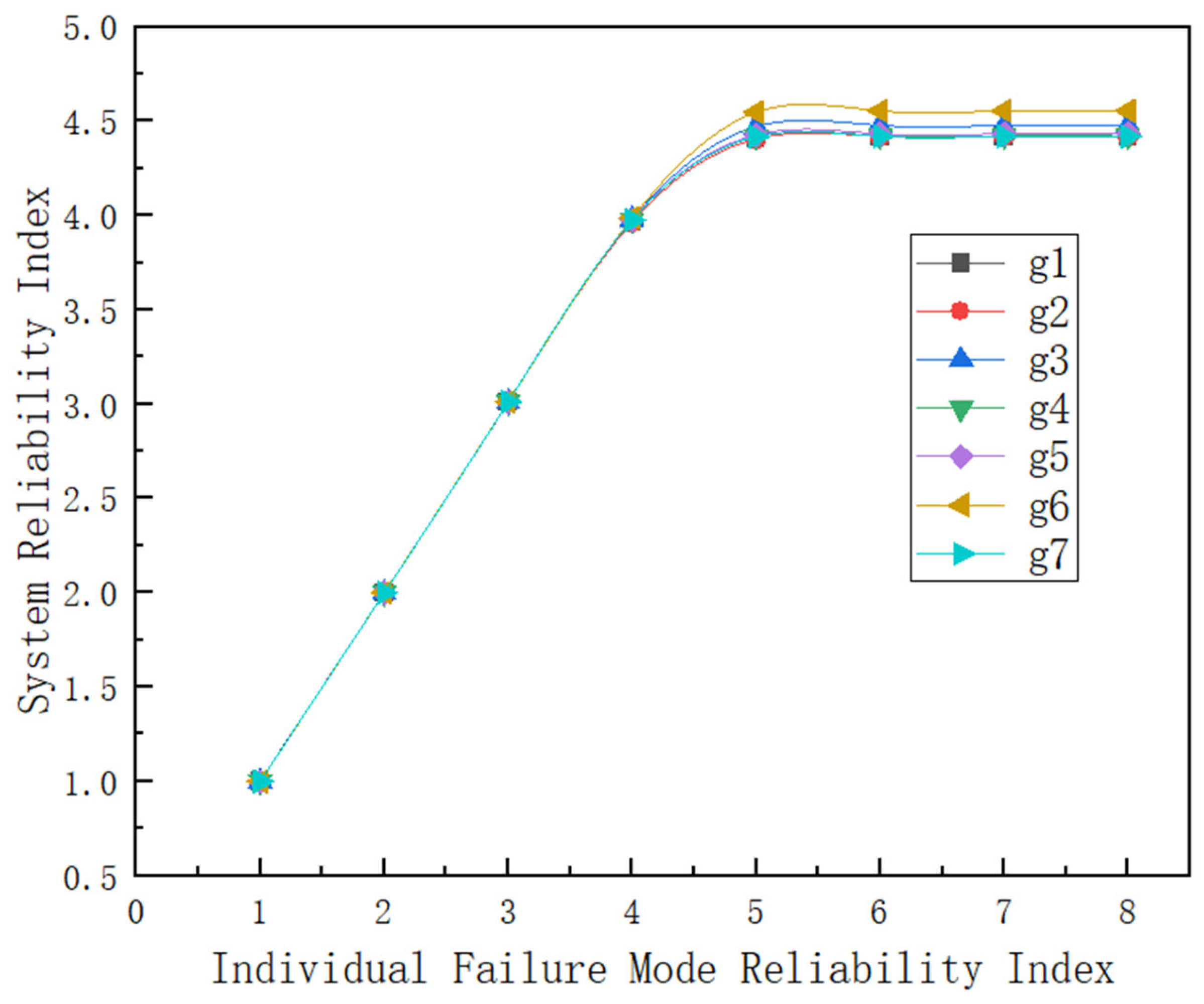
3.3.1. Relationship between System Reliability Index and Failure Mode Reliability Index
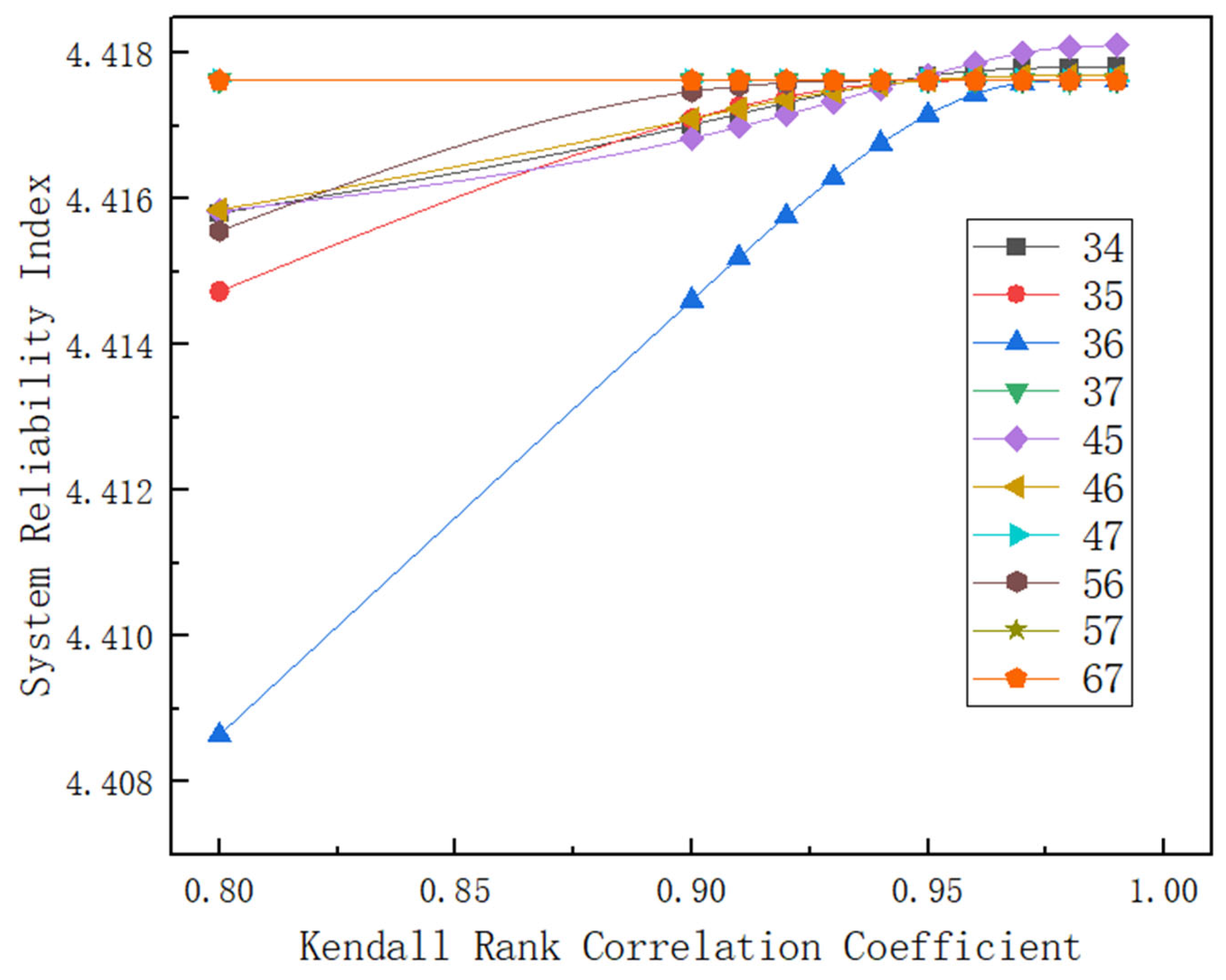
3.3.2. Variation of System Failure Probability with Failure Mode Correlation Coefficient
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Soliman, M.; Frangopol, D.M.; Kown, K. Fatigue Assessment and Service Life Prediction of Existing Steel Bridges by Integrating SHM into a Probabilistic Bilinear S-N Approach. J. Struct. Eng. 2013, 139, 1728–1740. [Google Scholar] [CrossRef]
- Sousa, H.; Bento, J.; Figueiras, J. Construction assessment and long-term prediction of prestressed concrete bridges based on monitoring data. Eng. Struct. 2013, 52, 26–37. [Google Scholar] [CrossRef]
- Li, L. Construction of GPS bridge monitoring system and its application in a bridge. Highw. Eng. 2019, 44, 222–226. [Google Scholar]
- Yu, C.; Zhang, G.; Zhao, Y.; Liu, X.; Ding, X.; Zhao, T. Bridge monitoring and early warning system based on Digital Measurement Technology. J. Shandong Univ. (Eng. Sci.) 2020, 50, 115–122. [Google Scholar]
- Wei, X.; Wu, X.; Lu, P. Research on bridge health monitoring data integration and early warning based on Component GIS. Highw. Eng. 2020, 45, 79–85. [Google Scholar]
- Ghiasi, R.; Noori, M.; Altabey, W.A.; Silik, A.; Wang, T.; Wu, Z. Uncertainty Handling in Structural Damage Detection via Non-Probabilistic Meta-Models and Interval Mathematics, a Data-Analytics Approach. Appl. Sci. 2021, 11, 770. [Google Scholar] [CrossRef]
- Beshr, A.A.A.; Zarzoura, F.H. Using artificial neural networks for GNSS observations analysis and displacement prediction of suspension highway bridge. Innov. Infrastruct. Solut. 2021, 6, 109. [Google Scholar] [CrossRef]
- Martucci, D.; Civera, M.; Surace, C. The Extreme Function Theory for Damage Detection: An Application to Civil and Aerospace Structures. Appl. Sci. 2021, 11, 1716. [Google Scholar] [CrossRef]
- Li, S.; Zhu, X.; Wang, Y.; Zhao, X. Research on the integration of bridge operation, management and maintenance based on the integration of BIM modeling and health monitoring and early warning. Traffic Transp. 2022, 38, 52–57. [Google Scholar]
- Li, Q.F.; Gao, J.L.; Le, J.Z.; Li, Z.K. Reliability Principle of Engineering Structure; The Yellow River Water Conservancy Press: Zhengzhou, China, 1999. [Google Scholar]
- Lu, N.; Liu, Y. Bridge Reliability Analysis Method and Application; Southeast University Press: Nanjing, China, 2017. [Google Scholar]
- Ditlevsen, O. Taylor Expansion of Series System Reliability. J. Eng. Mech. ASCE 1984, 110, 293–307. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, G. An approximate method for structural system reliability analysis. China Civ. Eng. J. 1993, 26, 70–76. [Google Scholar]
- Cornell, C.A. Bounds on the Reliability of Structural Systems. J. Struct. Div. 1967, 93, 171–200. [Google Scholar] [CrossRef]
- Ditlevsen, O. Narrow Reliability Bounds for Structural Systems. Mech. Based Des. Struct. Mach. 1979, 7, 453–472. [Google Scholar] [CrossRef]
- Sklar, A. Fonctions de Repartition a n Dimensions et Leurs Marges. Publ. Inst. Stat. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Li, D.Q.; Tang, X.S.; Zhou, C.B.; Fang, G.G. Reliability analysis of parallel structure system based on Copula function. Eng. Mech. 2014, 31, 32–40. [Google Scholar] [CrossRef]
- Liu, P.L.; Kiureghian, A.D. Multivariate distribution models with prescribed marginals and covariances. Probabilistic. Eng. Mech. 1986, 1, 105–112. [Google Scholar] [CrossRef]
- Goda, K. Statistical modeling of joint probability distribution using copula: Application to peak and permanent displacement seismic demands. Struct. Saf. 2010, 32, 112–123. [Google Scholar] [CrossRef]
- Kazianka, H.; Pilz, J. Bayesian spatial modeling and interpolation using copulas. Comput. Geosci. 2011, 37, 310–319. [Google Scholar] [CrossRef]
- Kazianka, H.; Pilz, J. Copula-based geostatistical modeling of continuous and discrete data including covariates. Stoch. Environ. Res. Risk Assess. 2010, 24, 661–673. [Google Scholar] [CrossRef]
- Eryilmaz, S. Multivariate copula based dynamic reliability modeling with application to weighted-k-out-of-n systems of dependent components. Struct. Saf. 2014, 51, 23–28. [Google Scholar] [CrossRef]
- Liu, Y. System Reliability Analysis of Bridge Structures Considering Correlation of Failure Modes and Proof Modes. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, May 2015. [Google Scholar]
- Zhang, L.; Tang, X.; Li, D.; Cao, Z. Reliability analysis of geotechnical structure system based on Copula function. Rock Soil Mech. 2016, 37, 193–202. [Google Scholar]
- Xiao, Q. Research on Bridge Reliability Based on Vine Copula and Bayesian Dynamic Models. Master’s Thesis, Lanzhou University, Lanzhou, China, May 2018. [Google Scholar]
- Wang, X. Time-Dependent Reliability Analysis and System Reliability Evaluation Methods for Existing Medium and Small Span Bridges. Ph.D. Thesis, Jilin University, Jilin, China, September 2020. [Google Scholar]
- Song, L. Study on the Stability Reliability Analysis Method of Three-Dimensional Slop of Concrete Faced Rockfill Dam Based on Copula Function. Ph.D. Thesis, Dalian University of Technology, Dalian, China, January 2021. [Google Scholar]
- Tang, X. Uncertainty Modeling of Correlated Geotechnical Parameters and Reliability Analysis Using Copulas. Ph.D. Thesis, Wuhan University, Wuhan, China, May 2014. [Google Scholar]
- Zhou, X. Simulation of Cross-Correlated Random Fields and Soil Slope Reliability Analysis Based on Copula Approach. Ph.D. Thesis, Wuhan University of Technology, Wuhan, China, May 2020. [Google Scholar]
- Zhang, L. Bivariate Distribution of Shear Strength Parameters of Soils and Rocks Using Copula. Ph.D. Thesis, Wuhan University, Wuhan, China, May 2017. [Google Scholar]
- Ban, X. Research on Design Theory of Precast 40 m Simply Supported Box Girder for High Speed Railway. Ph.D. Thesis, China Academy of Railway Sciences, Beijing, China, July 2021. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G.E. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Lu, N. Research Method of System Reliability for Long-Span Rigid Form Bridge. Master’s Thesis, Changsha University of Science & Technology, Changsha, China, May 2011. [Google Scholar]


| Copula Function Type | |||
|---|---|---|---|
| Gaussian | [−1, 1] | ||
| Clayton | |||
| Plackett | |||
| Frank | |||
| t | [−1, 1] | ||
| No. 16 | |||
| Gumbel |
| Failure Mode Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Location/Node | Pier 10 | 65 | 79 | 90 | 96 | 107 | 121 |
| Failure mode | Stability | Lower edge Tensile stress | Lower edge Compressive stress | Lower edge Compressive stress | Lower edge Compressive stress | Lower edge Compressive stress | Lower edge Tensile stress |
| Name | |||||||
|---|---|---|---|---|---|---|---|
| Distribution | Normal | Normal | Normal | Normal | Normal | Normal | Extreme vale type Ⅰ |
| 1.3636 | 1.3849 | 1.1420 | 1.0212 | 1.0000 | 1.0000 | 1.0000 | |
| 0.1344 | 0.1406 | 0.0967 | 0.0462 | 0.0500 | 0.1440 | 0.0862 |
| 0.00983 | 0.00386 | 0.97839 | |||
| −0.01303 | 0.01034 | 0.94616 | |||
| −0.01323 | 0.00915 | 0.94947 | |||
| −0.01242 | 0.01015 | 0.95101 | |||
| −0.01259 | 0.94389 | 0.98746 | |||
| −0.01345 | 0.97422 | 0.99070 | |||
| 0.00960 | 0.98442 | 0.98955 |
| Copula Function θ | ||||
|---|---|---|---|---|
| Gaussian | Clayton | Frank | Gumbel | |
| 0.99610 | 33.6443 | 1.3755 | 17.8221 | |
| 0.99920 | 75.5795 | 1.4054 | 38.7898 | |
| 0.99970 | 126.3697 | 1.4163 | 64.1849 | |
| 0.99940 | 90.5497 | 1.4098 | 46.2749 | |
| 0.99640 | 35.1471 | 1.3776 | 18.5736 | |
| 0.99690 | 37.5804 | 1.3808 | 19.7902 | |
| 0.99700 | 38.8247 | 1.3823 | 20.4123 | |
| 0.99980 | 157.4896 | 1.4196 | 79.7448 | |
| 0.99989 | 213.0538 | 1.4231 | 107.5269 | |
| 0.99986 | 189.3876 | 1.4218 | 95.6938 | |
| Gaussian | Clayton | Frank | Gumbel | |||||
|---|---|---|---|---|---|---|---|---|
| AIC | BIC | AIC | BIC | AIC | BIC | AIC | BIC | |
| −2394.7 | −2390.5 | −1848.5 | −1844.3 | −211.3 | −207.1 | −2431.1 | −2426.9 | |
| −3092.1 | −3087.9 | −2309.7 | −2305.5 | −216.7 | −212.4 | −3064.3 | −3060.1 | |
| −3493.5 | −3489.2 | −2693.9 | −2689.7 | −218.4 | −214.2 | −3443.5 | −3439.3 | |
| −3255.7 | −3251.5 | −2566.8 | −2562.5 | −217.4 | −213.2 | −3186.6 | −3182.3 | |
| −2444.2 | −2440.0 | −1871.0 | −1866.8 | −211.7 | −207.5 | −2502.7 | −2498.5 | |
| −2507.3 | −2503.0 | −1941.4 | −1937.2 | −212.3 | −208.1 | −2550.0 | −2545.8 | |
| −2531.2 | −2526.9 | −1962.6 | −1958.4 | −212.6 | −208.4 | −2566.7 | −2562.5 | |
| −3723.4 | −3719.2 | −2857.7 | −2853.5 | −218.9 | −214.7 | −3614.9 | −3610.7 | |
| −3901.5 | −3897.3 | −2816.5 | −2812.3 | −219.5 | −215.3 | −3759.5 | −3755.3 | |
| −3875.4 | −3871.2 | −2829.3 | −2825.1 | −219.3 | −215.1 | −3667.6 | −3663.4 | |
| Joint Failure Probability | Joint Failure Probability | ||
|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Zhang, T. Research on the Reliability of Bridge Structure Construction Process System Based on Copula Theory. Appl. Sci. 2022, 12, 8137. https://doi.org/10.3390/app12168137
Li Q, Zhang T. Research on the Reliability of Bridge Structure Construction Process System Based on Copula Theory. Applied Sciences. 2022; 12(16):8137. https://doi.org/10.3390/app12168137
Chicago/Turabian StyleLi, Qingfu, and Tianjing Zhang. 2022. "Research on the Reliability of Bridge Structure Construction Process System Based on Copula Theory" Applied Sciences 12, no. 16: 8137. https://doi.org/10.3390/app12168137
APA StyleLi, Q., & Zhang, T. (2022). Research on the Reliability of Bridge Structure Construction Process System Based on Copula Theory. Applied Sciences, 12(16), 8137. https://doi.org/10.3390/app12168137






