Missing Well Logs Prediction Based on Hybrid Kernel Extreme Learning Machine Optimized by Bayesian Optimization
Abstract
:1. Introduction
2. Principle and Modeling
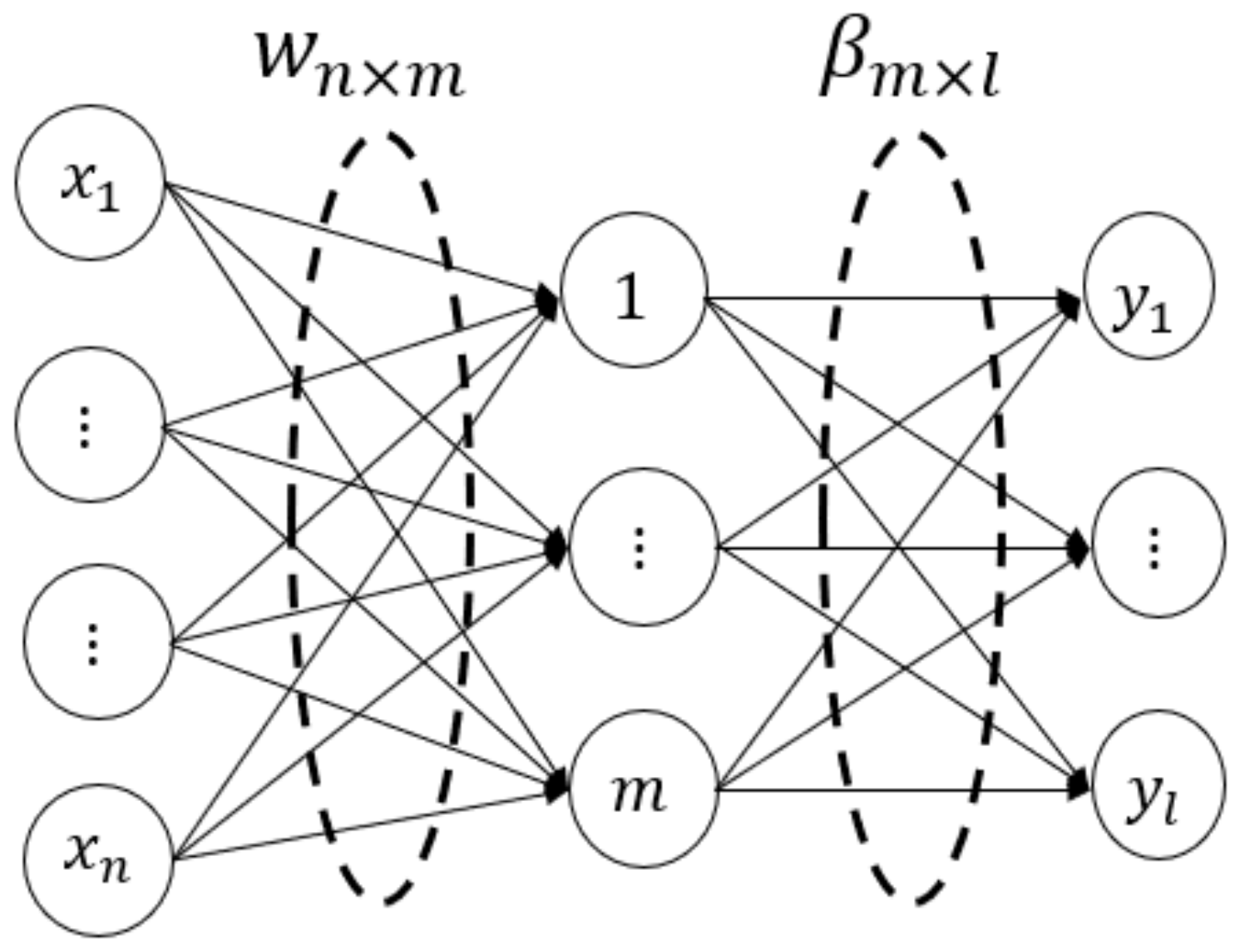
2.1. Principle of KELM
2.2. Hybrid Kernel Extreme Learning Machine
2.3. Bayesian Optimization Algorithm
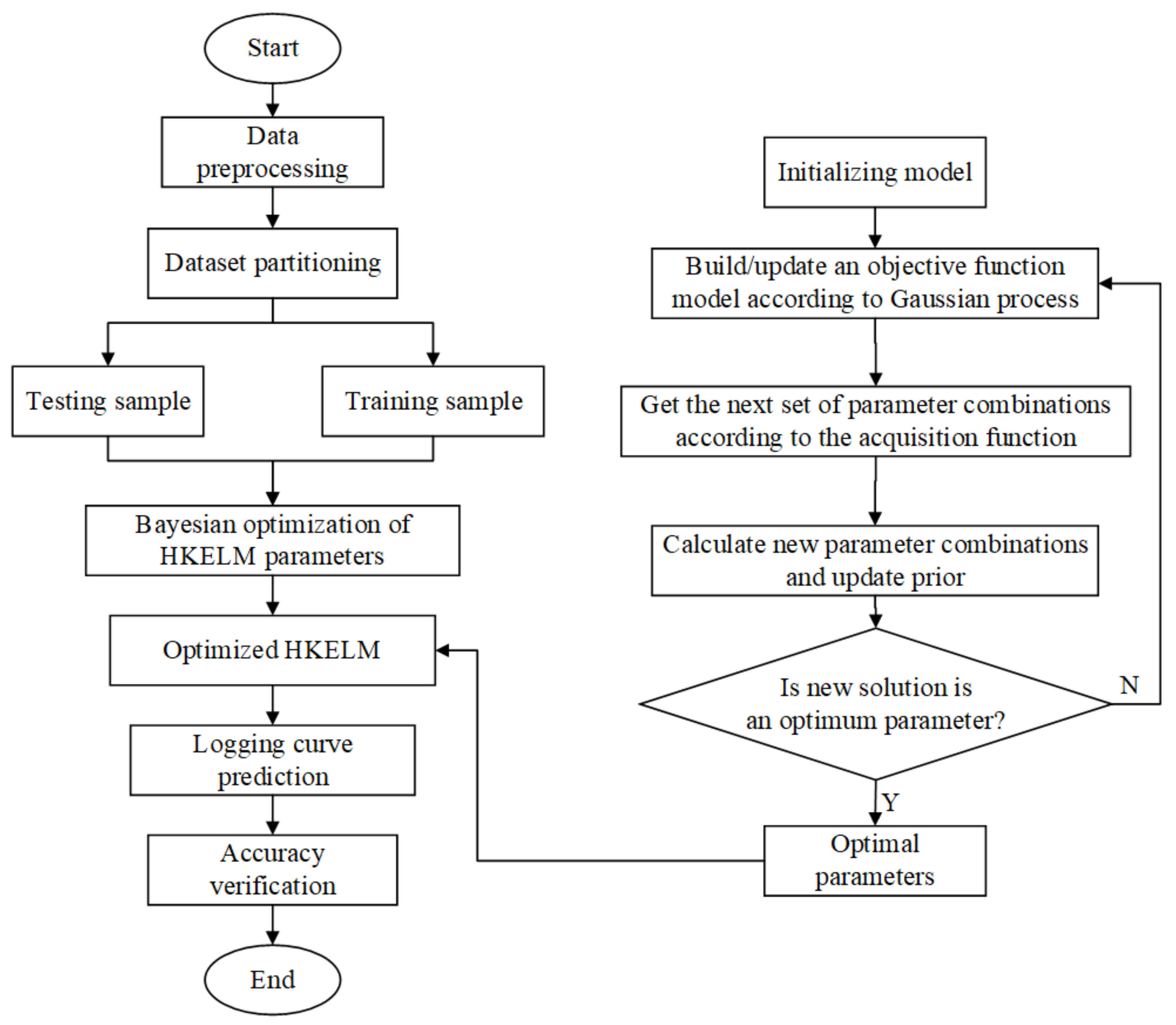
3. Process of Predicting Missing Logging Curves Based on BO-HKELM
4. Practical Application and Result Analysis
4.1. Data Preparation
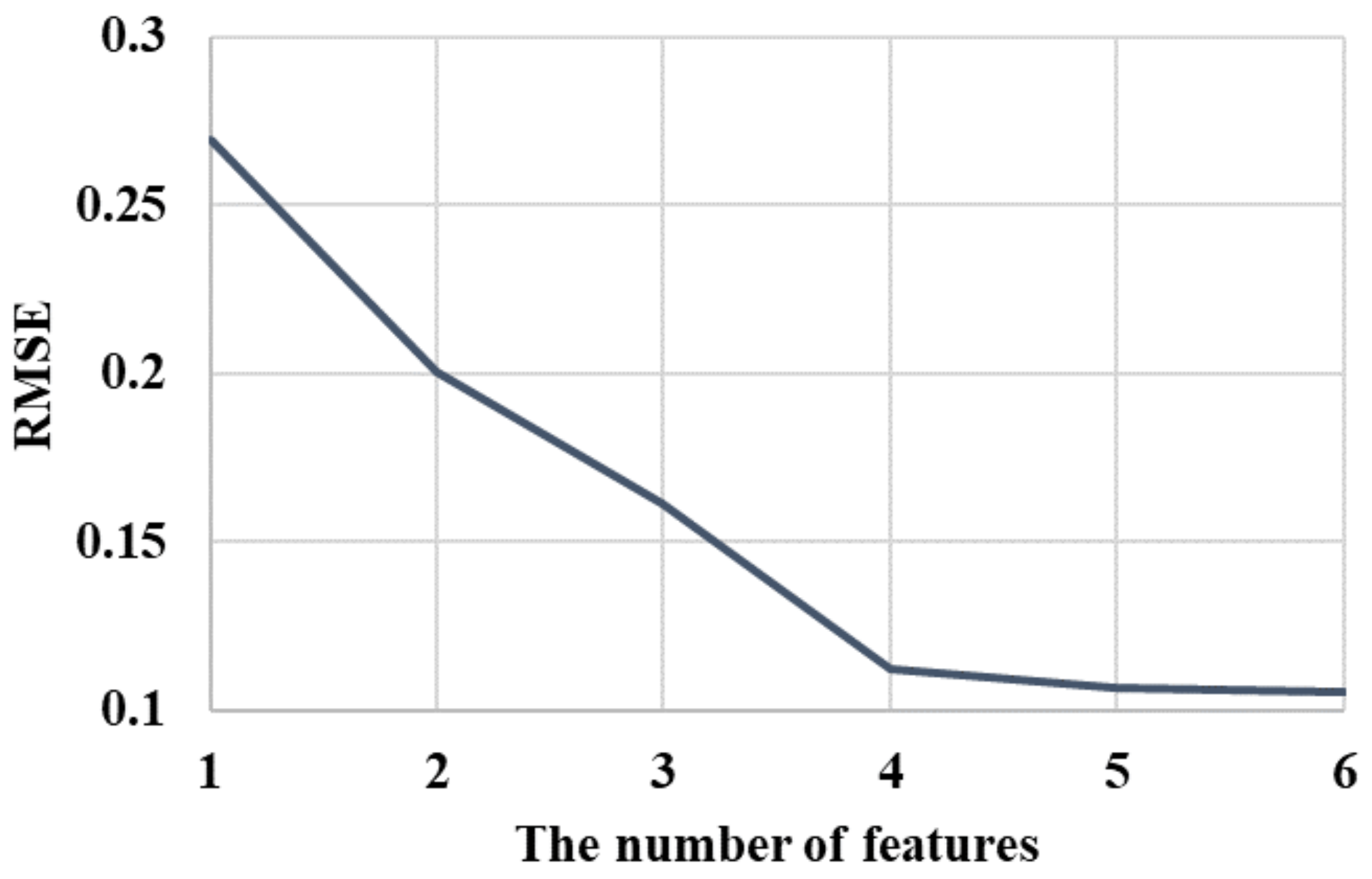
4.2. Feature Analysis
4.3. Optimization of Algorithm Parameters
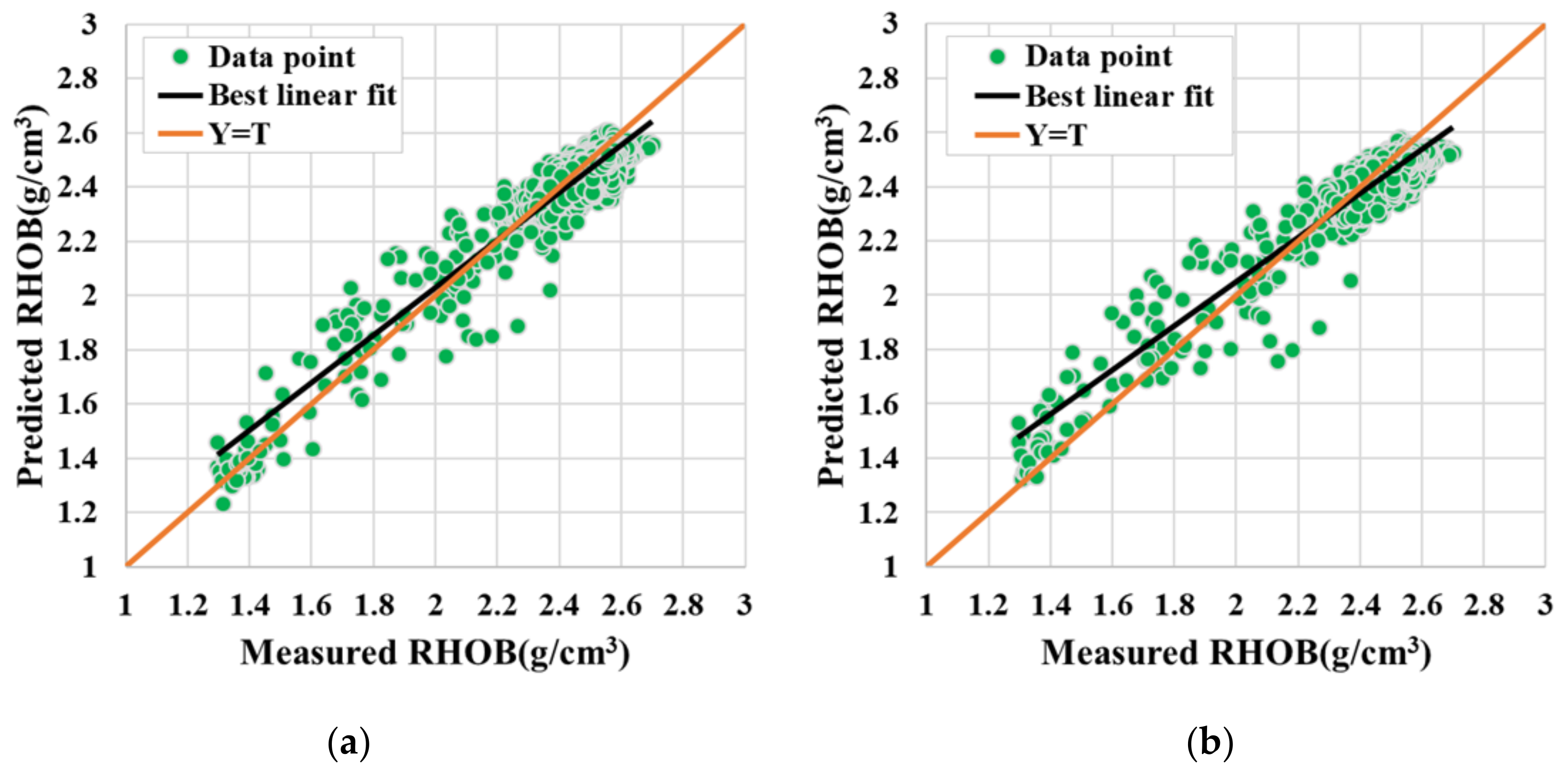
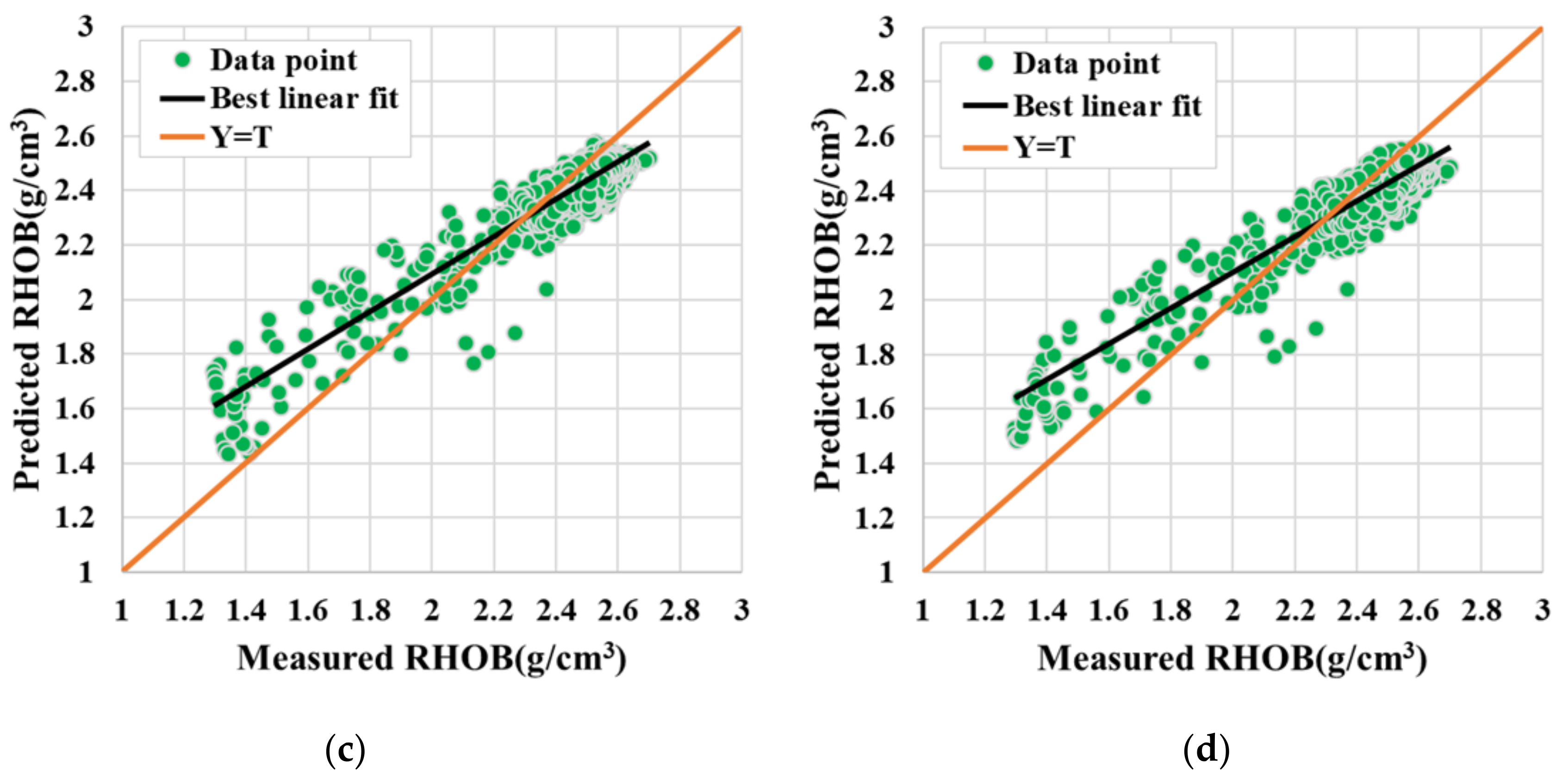
4.4. Comparative Analysis of Model Prediction Effect
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, Y.Z.; Huang, J. Application of multi-task deep learning in reservoir shear wave prediction. Prog. Geophys. 2021, 36, 799–809. [Google Scholar]
- Gardner, G.; Gardner, L.W.; Gregory, A.R. Formation velocity and density; the diagnostic basics for stratigraphic traps. Geophysics 1974, 39, 770–780. [Google Scholar] [CrossRef]
- Smith, J.H. A Method for Calculating Pseudo Sonics from E-Logs in a Clastic Geologic Setting. Gcags Transactions 2007, 57, 1–4. [Google Scholar]
- Wang, J.; Liang, L.; Qiang, D.; Tian, P.; Tan, W. Research and application of reconstructing logging curve based on multi-source regression model. Lithologic Reserv. 2016, 28, 113–120. [Google Scholar]
- Liao, H.M. Multivariate regression method for correcting the influence of expanding diameter on acoustic curve of density curve. Geophys. Geochem. Explor. 2014, 38, 174–179. [Google Scholar]
- Banchs, R.; Jiménez, J.R.; Pino, E.D. Nonlinear estimation of missing logs from existing well log data. In Proceedings of the 2001 SEG Annual Meeting, San Antonio, TX, USA, 2–6 September 2001. [Google Scholar]
- Salehi, M.M.; Rahmati, M.; Karimnezhad, M.; Omidvar, P. Estimation of the non records logs from existing logs using artificial neural networks. Egypt. J. Pet. 2016, 26, 957–968. [Google Scholar] [CrossRef]
- Ramachandram, D.; Taylor, G.W. Deep Multimodal Learning: A Survey on Recent Advances and Trends. IEEE Signal Process. Mag. 2017, 34, 96–108. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, L.T.; Chen, Z.; Li, P. A survey on deep learning for big data. Inf. Fusion 2018, 42, 146–157. [Google Scholar] [CrossRef]
- Jian, H.; Chenghui, L.; Zhimin, C.; Haiwei, M. Integration of deep neural networks and ensemble learning machines for missing well logs estimation. Flow Meas. Instrum. 2020, 73, 101748. [Google Scholar] [CrossRef]
- Lin, T.; Cai, R.; Zhang, L.; Yang, X.; Liu, G.; Liao, W. Prediction intervals forecasts of wind power based on IBA-KELM. Renew. Energy Resour. 2018, 36, 1092–1097. [Google Scholar]
- Abdullah, M.; Rashid, T.A. Fitness Dependent Optimizer: Inspired by the Bee Swarming Reproductive Process. IEEE Access 2019, 7, 43473–43486. [Google Scholar] [CrossRef]
- Cheng, R.; Jin, Y. A Competitive Swarm Optimizer for Large Scale Optimization. IEEE Trans. Cybern. 2015, 45, 191–204. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Wang, L.; Zhang, Z. Supply-Demand-Based Optimization: A Novel Economics-Inspired Algorithm for Global Optimization. IEEE Access 2019, 7, 73182–73206. [Google Scholar] [CrossRef]
- Shabani, A.; Asgarian, B.; Salido, M.A.; Gharebaghi, S.A. Search and Rescue optimization algorithm: A new optimization method for solving constrained engineering optimization problems. Expert Syst. Appl. 2020, 161, 113698. [Google Scholar] [CrossRef]
- Das, B.; Mukherjee, V.; Das, D. Student psychology based optimization algorithm: A new population based optimization algorithm for solving optimization problems—ScienceDirect. Adv. Eng. Softw. 2020, 146, 102804. [Google Scholar] [CrossRef]
- Sultana, N.; Hossain, S.; Almuhaini, S.H.; Düştegör, D. Bayesian Optimization Algorithm-Based Statistical and Machine Learning Approaches for Forecasting Short-Term Electricity Demand. Energies 2022, 15, 3425. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhou, H.; Ding, X.; Zhang, R. Extreme Learning Machine for Regression and Multiclass Classification. IEEE Trans. Syst. Man Cybern. Part B 2012, 42, 513–529. [Google Scholar] [CrossRef] [PubMed]
- Heidari, A.A.; Rahim, A.A.; Chen, H. Efficient boosted grey wolf optimizers for global search and kernel extreme learning machine training. Appl. Soft Comput. 2019, 81, 105521. [Google Scholar] [CrossRef]
- Chao, Z.; Yin, K.; Cao, Y.; Intrieri, E.; Ahmed, B.; Catani, F. Displacement prediction of step-like landslide by applying a novel kernel extreme learning machine method. Landslides 2018, 15, 2211–2225. [Google Scholar]
- Pelikan, M. Bayesian Optimization Algorithm: From Single Level to Hierarchy. Master’s Thesis, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 2002. [Google Scholar]
- Wang, X.; Zhang, G.; Lou, S.; Liang, S.; Sheng, X. Two-round feature selection combining with LightGBM classifier for disturbance event recognition in phase-sensitive OTDR system. Infrared Phys. Technol. 2022, 123, 104191. [Google Scholar] [CrossRef]





| Well Name | Index | Petrophysical Well Logs | ||||||
|---|---|---|---|---|---|---|---|---|
| DEPTH (m) | CAL (cm) | DT (μs/m) | GR (API) | NPHI (v/v) | RT (ohmm) | RHOB (g/cm3) | ||
| Well A1 | Min | 1880.00 | 21.95 | 187.38 | 14.97 | 0.03 | 6.41 | 1.21 |
| 25% | 1910.00 | 23.11 | 231.29 | 53.00 | 0.17 | 16.71 | 2.24 | |
| 50% | 1940.00 | 24.53 | 237.78 | 86.11 | 0.20 | 27.23 | 2.31 | |
| Mean | 1940.00 | 25.03 | 250.97 | 93.53 | 0.27 | 30.44 | 2.29 | |
| 75% | 1970.03 | 26.21 | 260.20 | 132.76 | 0.34 | 43.07 | 2.47 | |
| Max | 2000.00 | 41.88 | 407.97 | 212.32 | 0.92 | 70.84 | 2.70 | |
| Well A2 | Min | 1560.00 | 21.36 | 210.12 | 15.63 | 0.07 | 5.56 | 1.30 |
| 25% | 1597.46 | 22.11 | 230.24 | 65.50 | 0.12 | 16.75 | 2.34 | |
| 50% | 1635.00 | 22.40 | 238.13 | 99.62 | 0.17 | 21.78 | 2.48 | |
| Mean | 1635.00 | 23.17 | 249.17 | 91.19 | 0.19 | 22.73 | 2.39 | |
| 75% | 1672.53 | 22.87 | 251.64 | 114.39 | 0.23 | 28.39 | 2.54 | |
| Max | 1710.00 | 39.43 | 400.92 | 149.03 | 0.69 | 89.92 | 2.70 | |
| Rank | Feature | Score |
|---|---|---|
| 1 | DT | 865 |
| 2 | NPHI | 661 |
| 3 | CAL | 594 |
| 4 | GR | 466 |
| 5 | RT | 448 |
| 6 | DEPTH | 429 |
| BO-HKELM | |||||
|---|---|---|---|---|---|
| Trained by Well A1 | 21.43 | 0.24 | 2 | 69.03 | 86.03 |
| Model | RMSE | MAE | R-Square |
|---|---|---|---|
| ELM | 0.1133 | 0.0798 | 0.7916 |
| KELM | 0.1055 | 0.0638 | 0.8178 |
| HKELM | 0. 0901 | 0.0623 | 0.8874 |
| BO-HKELM | 0.0767 | 0.0613 | 0.9029 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, L.; Cui, Y.; Jia, Z.; Xiao, K.; Su, H. Missing Well Logs Prediction Based on Hybrid Kernel Extreme Learning Machine Optimized by Bayesian Optimization. Appl. Sci. 2022, 12, 7838. https://doi.org/10.3390/app12157838
Qiao L, Cui Y, Jia Z, Xiao K, Su H. Missing Well Logs Prediction Based on Hybrid Kernel Extreme Learning Machine Optimized by Bayesian Optimization. Applied Sciences. 2022; 12(15):7838. https://doi.org/10.3390/app12157838
Chicago/Turabian StyleQiao, Lei, You Cui, Zhining Jia, Kun Xiao, and Haonan Su. 2022. "Missing Well Logs Prediction Based on Hybrid Kernel Extreme Learning Machine Optimized by Bayesian Optimization" Applied Sciences 12, no. 15: 7838. https://doi.org/10.3390/app12157838
APA StyleQiao, L., Cui, Y., Jia, Z., Xiao, K., & Su, H. (2022). Missing Well Logs Prediction Based on Hybrid Kernel Extreme Learning Machine Optimized by Bayesian Optimization. Applied Sciences, 12(15), 7838. https://doi.org/10.3390/app12157838





