Simplified Expansions of Common Latitudes with Geodetic Latitude and Geocentric Latitude as Variables

Abstract

Using the symbolic calculation program Mathematica and based on the power series expansions of the common latitude with geodetic latitude as a variable, power series expansions of the common latitude with geocentric latitude as the variable are derived. The coefficients of the two groups of formulas are based on the ellipsoid eccentricity e and the ellipsoid third flattening n, which make the expansions more uniform. Taking the CGCS2000 as an example, numerical analysis is applied to verify the accuracy and reliability of the derived power series expansions. By analyzing and calculating the truncation error of the common latitude based on ellipsoidal eccentricity e and the third flattening n expansion to different orders, we obtain simplified, practical formulas for the common latitude that satisfy the requirement of geodesic accuracy. Moreover, we show that the practical formula derived has higher calculation efficiency and easier dissemination, enriches the theory of map projection, and provides a basis for better display of remote sensing images.

1. Introduction

In remote sensing surveying, it is necessary to use map projection to display remote sensing images more intuitively and scientifically on a plane [1,2]. Precise measurements are required to achieve accurate navigation and positioning, and tools such as maps and geographic coordinates are used to intuitively express the information obtained [3,4,5]. In surveying and mapping, we often calculate the six common latitudes and their transformations: geodetic latitude, geocentric latitude, reduced latitude, rectifying latitude, conformal latitude, and authalic latitude [6,7]. Given the continued application and research of map projections, more stringent requirements are required for accurate and efficient transformations between different projections. The key is to complete mutual transformation of important variables, such as common latitude, more efficiently to ensure high accuracy [8,9,10,11,12]. Much in-depth research has been conducted on this, leading to theories of latitude change. For example, Qihe et al. [3,13,14] derived and calculated the relations between common latitudes and the positive and negative solutions of common latitude functions. Some of these calculations involve an elliptic integral of the second kind, which cannot be obtained analytically, and some are expressed in the form of practical expansions [15].

Because of historical factors and manual calculation, the formulas still have errors. With the development of computer algebra, Shaofeng et al. [16] derived power series expansions of the common latitude with geodetic latitude as a variable. They obtained more uniform, symbolic expressions in form, which are suitable for the Earth’s ellipsoid. Chenchen et al. [17,18] derived the symbolic expressions of the positive and negative solutions of the common latitude with geocentric latitude as a variable and extended the power series of coefficients in the formula to more directly represent the relationship between common latitude and geocentric latitude. Houpu et al. [19,20,21] studied and derived the power series expansions of the common latitude with naturalized latitude as a variable, as well as power series expressions of auxiliary latitude functions. To solve the problems of elliptic integration of the second kind in latitude transformation and make the forms neat and unified, the coefficients in the commonly used latitude expansion formula are often expressed as the power series form of the first eccentricity. To ensure the accuracy of latitude transformation, it is often expanded to $e^{10}$ [22,23]. In this form, the coefficients of the expansion formula are complex, and the convergence speed is slow. In addition, the formula is long and cannot express the relations between latitudes succinctly, which is not good for propagation.

Although some achievements have been made in previous studies on latitude transformation, it is still incomplete and has some shortcomings: 1. Most power series expansions are long and inefficient; 2. Part of the formulas involve iterative calculation and lack theoretical support; 3. Some of the formulas are numerical forms, which are only applicable to a specific earth ellipsoid and lack universality [24]; 4. Some formulas have approximate substitution, some errors, and occasionally, coefficient errors. In general, the traditional latitude transformation formulas cannot meet the needs of the rapid development of modern map projection theory, and there is still a large space for improvement.

What is more, in recent years, the third flattening $n$ has been applied to ellipsoidal geodesy, which has solved problems related to the calculation of meridian arc length, various auxiliary latitudes, and projection transformation [25,26]. Given this, with the help of the symbolic computation program Mathematica, we can derive the common latitude expansions with geodetic latitude and geocentric latitude as variables. The coefficients in the formulas are expressed as a power series of ellipsoidal eccentricity $e$ and the third flattening n. A comparative analysis shows that the coefficients of the power series expansion based on the third flattening $n$ are simpler and produce a neater and more compact result. In addition, the CGCS2000 is used for numerical analysis to test the accuracy and reliability of the derived power series expansion [27]. By analyzing and calculating the truncation errors based on the $e$ and $n$ expanded to different orders, we obtain simplified, practical formulas for the common latitude that satisfy the geodesy accuracy requirements.

2. Generation and Definition of Third Flattening

Previous reports [28] indicate that the third flattening $n$ often appears as an auxiliary parameter in the relation between latitudes. The geodetic latitude $B$ and the reduced latitude $u$ are related by $\tan u={\left(1-e^2\right)}^{-1/2}\tan B$. By introducing the Lagrange conjugate series and using the auxiliary parameter $K={\left(1-e^2\right)}^{-1/2}$, we obtain

$$\{\begin{array}{l}B-u=\frac{1-\sqrt{1-e^2}}{1+\sqrt{1-e^2}}\sin 2B-\frac{1}{2}{\left(\frac{1-\sqrt{1-e^2}}{1+\sqrt{1-e^2}}\right)}^2\sin 4B+\frac{1}{3}{\left(\frac{1-\sqrt{1-e^2}}{1+\sqrt{1-e^2}}\right)}^3\sin 6B-\dots \\ B-u=\frac{1-\sqrt{1-e^2}}{1+\sqrt{1-e^2}}\sin 2u+\frac{1}{2}{\left(\frac{1-\sqrt{1-e^2}}{1+\sqrt{1-e^2}}\right)}^2\sin 4u+\frac{1}{3}{\left(\frac{1-\sqrt{1-e^2}}{1+\sqrt{1-e^2}}\right)}^3\sin 6u+\dots \end{array}$$

(1)

To simplify Equation (1), the coefficient in the formula is defined as the third flattening $n$, namely

$$n=\frac{K-1}{K+1}=\frac{1-\sqrt{1-e^2}}{1+\sqrt{1-e^2}}$$

(2)

The third flattening $n$ is numerically smaller than the ellipsoid eccentricity $e$, which means that the expansion formula with $n$ converges faster. This is more attractive for calculating the power series expansion of common functions.

3. Common Latitude Power Series Expansions with Geodetic Latitude as Variable

Geodetic latitude is one of the most used earth science latitudes in geodetic surveys and map projection theory. To implement various projection features, five other types of auxiliary latitudes are used: geocentric latitude, reduced latitude, rectifying latitude, conformal latitude, and authalic latitude [29]. These are all functions of geodetic latitude. Practical applications often require the transformation between the five auxiliary latitudes and geodetic latitudes, which often involves complex power series expansion and the calculation of complex higher-order derivatives. Heretofore, most of these derivatives were obtained manually, which is a long, complicated process. Partial approximations were thus used to facilitate the derivation, which also led to the deviation of higher-order terms. With the help of the symbolic calculation capabilities of Mathematica, this problem can now be efficiently solved. The power series of the common latitude with geodetic latitude as a variable based on eccentricity $e$ and the third flattening $n$ are obtained as described below.

3.1. Power Series Expansion of Rectifying Latitude with Geodetic Latitude as Variable

According to the literature [30], the meridian arc length can be expressed as an elliptic integral

$$X={\displaystyle \underset{0}{\overset{B}{\mathsf{\int }}}MdB}=a\left(1-e^2\right){\displaystyle \underset{0}{\overset{B}{\mathsf{\int }}}{\left(1-e^2{\sin }^{2}B\right)}^{-3/2}dB},$$

(3)

where M is the radius of curvature in the meridian at the calculation point. Assuming the constant term

$$k_0=1+\frac{3}{4}{e}^2+\frac{45}{64}{e}^4+\frac{175}{256}{e}^6+\frac{11025}{16384}{e}^8+\frac{43659}{65536}{e}^{10}$$

(4)

then the definition of rectifying latitude $\psi \left(B\right)$ is

$$\psi \left(B\right)=\frac{X}{R}=\frac{X}{a(1-e^2)k_0}=\frac{{\displaystyle \underset{0}{\overset{B}{\int }}{\left(1-e^2{\sin }^{2}B\right)}^{-\frac{3}{2}}dB}}{k_0}=\frac{{\displaystyle \underset{0}{\overset{B}{\int }}{\left(1-e^2{\sin }^{2}B\right)}^{-\frac{3}{2}}dB}}{1+\frac{3}{4}{e}^2+\frac{45}{64}{e}^4+\frac{175}{256}{e}^6+\frac{11025}{16384}{e}^8+\frac{43659}{65536}{e}^{10}}$$

(5)

which cannot be solved by integration. The conventional solution is to expand the integrated function using Newton’s binomial theorem, transform the power form of trigonometric function into the double angle form, and then integrate it term by term. This process is long and complicated, especially when high precision is required. In addition, higher orders are difficult to calculate and errors increase at these orders. However, using Mathematica (hereafter, other calculations also were completed with Mathematica, but we do not repeat that fact further), the power series expansion of the rectifying latitude $\psi \left(B\right)$ can be expressed as

$$\psi \left(B\right)=B+{\alpha }_2\sin 2B+{\alpha }_4\sin 4B+{\alpha }_6\sin 6B+{\alpha }_8\sin 8B+{\alpha }_{10}\sin 10B.$$

(6)

The coefficients in Equation (6) are expanded in terms of $e$ up to $e^{10}$ and in terms of $n$ up to $n^5$, which gives in

Table 1. Coefficients in Equation (6).

Expand to e10 Based on the First Eccentricity e

Expand to n5 Based on the Third Flattening n

$\{\begin{array}{l}{\alpha }_2=-\frac{3}{8}{e}^2-\frac{3}{16}{e}^4-\frac{111}{1024}{e}^6-\frac{141}{2048}{e}^8-\frac{1533}{32768}{e}^{10}\\ {\alpha }_4=\frac{15}{256}{e}^4+\frac{15}{256}{e}^6+\frac{405}{8192}{e}^8+\frac{165}{4096}{e}^{10}\\ {\alpha }_6=-\frac{35}{3072}{e}^6-\frac{35}{2048}{e}^8-\frac{4935}{262144}{e}^{10}\\ {\alpha }_8=\frac{315}{131072}{e}^8+\frac{315}{65536}{e}^{10}\\ {\alpha }_{10}=-\frac{693}{1310720}{e}^{10}\end{array}$

$\{\begin{array}{l}{\alpha }_2=-\frac{3}{2}n+\frac{9}{16}{n}^3-\frac{3}{32}{n}^5{}_{}\\ {\alpha }_4=\frac{15}{16}{n}^2-\frac{15}{32}{n}^4\begin{array}{cc}{}_{}& \begin{array}{cc}& \end{array}\end{array}\\ {\alpha }_6=-\frac{35}{48}{n}^3+\frac{105}{256}{n}^5\begin{array}{cc}& \end{array}\\ \begin{array}{l}{\alpha }_8=\frac{315}{512}{n}^4\begin{array}{ccc}\begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}& & \end{array}\\ {\alpha }_{10}=-\frac{693}{1280}{n}^5\end{array}\end{array}$

.

3.2. Power Series Expansion of Authalic Latitude with Geodetic Latitude as Variable

According to map projection theory, given the constant

$$A=\frac{1}{2\left(1-e^2\right)}+\frac{1}{4e}\ln \frac{1+e}{1-e}$$

(7)

the authalic latitude formula $\vartheta \left(B\right)$ with geodetic latitude as the variable is

$$\vartheta \left(B\right)=\arcsin \left[\frac{1}{A}\left(\frac{\sin B}{2(1-e^2{\sin }^{2}B)}+\frac{1}{4e}\ln \frac{1+e\sin B}{1-e\sin B}\right)\right]$$

(8)

The third flattening $n$ and the first eccentricity $e$ of the ellipsoid are related by

$$n=\frac{a-b}{a+b}=\frac{1-\sqrt{1-e^2}}{1+\sqrt{1-e^2}}$$

(9)

We expand this expression to $e^{10}$ and $n^5$, so the authalic latitude $\vartheta \left(B\right)$ is

$$\vartheta \left(B\right)=B+{\gamma }_2\sin 2B+{\gamma }_4\sin 4B+{\gamma }_6\sin 6B+{\gamma }_8\sin 8B+{\gamma }_{10}\sin 10B.$$

(10)

The coefficients in Equation (10) are expanded in terms of $e$ up to $e^{10}$ and in terms of $n$ up to $n^5$, which gives in

Table 2. Coefficients in Equation (10).

Expand to e10 Based on the First Eccentricity e

Expand to n5 Based on the Third Flattening n

$\{\begin{array}{l}{\gamma }_2=-\frac{1}{3}{e}^2-\frac{31}{180}{e}^4-\frac{59}{560}{e}^6-\frac{42811}{604800}{e}^8-\frac{605399}{11975040}{e}^{10}\\ {\gamma }_4=\frac{17}{360}{e}^4+\frac{61}{1260}{e}^6+\frac{76969}{1814400}{e}^8+\frac{215431}{5987520}{e}^{10}\\ {\gamma }_6=-\frac{383}{45360}{e}^6-\frac{3347}{259200}{e}^8-\frac{1751791}{119750400}{e}^{10}\\ {\gamma }_8=\frac{6007}{3628800}{e}^8+\frac{201293}{59875200}{e}^{10}\\ {\gamma }_{10}=-\frac{5839}{17107200}{e}^{10}\end{array}$

$\{\begin{array}{l}{\gamma }_2=-\frac{4}{3}n-\frac{4}{45}{n}^2+\frac{88}{315}{n}^3+\frac{538}{4725}{n}^4+\frac{20824}{467775}{n}^5\begin{array}{c}\end{array}\\ {\gamma }_4=\frac{34}{45}{n}^2+\frac{8}{105}{n}^3-\frac{2482}{14175}{n}^4-\frac{37192}{467775}{n}^5\begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}\\ {\gamma }_6=-\frac{1532}{2835}{n}^3-\frac{898}{14175}{n}^4+\frac{54968}{467775}{n}^5\begin{array}{ccc}\begin{array}{cc}& \end{array}& & \end{array}\\ \begin{array}{l}{\gamma }_8=\frac{6007}{14175}{n}^4+\frac{24496}{467775}{n}^5\begin{array}{cccc}\begin{array}{cccc}\begin{array}{cc}& \end{array}& & & \end{array}& & & \end{array}\\ {\gamma }_{10}=-\frac{23356}{66825}{n}^5\end{array}\end{array}$

.

3.3. Power Series Expansion of Conformal Latitude with Geodetic Latitude as Variable

According to the literature [31], the conformal latitude $\phi \left(B\right)$ can be defined as follows:

$$\phi \left(B\right)=2\arctan \left[\tan \left(\frac{\pi }{4}+\frac{B}{2}\right){\left(\frac{1-e\sin B}{1+e\sin B}\right)}^{e/2}\right]-\frac{\pi }{2}.$$

(11)

The power series expansion of the conformal latitude with geodetic latitude as the variable is

$$\phi \left(B\right)=B+{\beta }_2\sin 2B+{\beta }_4\sin 4B+{\beta }_6\sin 6B+{\beta }_8\sin 8B+{\beta }_{10}\sin 10B.$$

(12)

The coefficients in Equation (12) are expanded in terms of $e$ up to $e^{10}$ and in terms of $n$ up to $n^5$, which gives in

Table 3. Coefficients in Equation (12).

Expand to e10 Based on the First Eccentricity e

Expand to n5 Based on the Third Flattening n

$\{\begin{array}{l}{\beta }_2=-\frac{1}{2}{e}^2-\frac{5}{24}{e}^4-\frac{3}{32}{e}^6-\frac{281}{5760}{e}^8-\frac{7}{240}{e}^{10}\\ {\beta }_4=\frac{5}{48}{e}^4+\frac{7}{80}{e}^6+\frac{697}{11520}{e}^8+\frac{93}{2240}{e}^{10}\\ {\beta }_6=-\frac{13}{480}{e}^6-\frac{461}{13440}{e}^8-\frac{1693}{53760}{e}^{10}\\ {\beta }_8=\frac{1237}{161280}{e}^8+\frac{131}{10080}{e}^{10}\\ {\beta }_{10}=-\frac{367}{161280}{e}^{10}\end{array}$

$\{\begin{array}{l}{\beta }_2=-2n+\frac{2}{3}{n}^2+\frac{4}{3}{n}^3-\frac{82}{45}{n}^4+\frac{32}{45}{n}^5\\ {\beta }_4=\frac{5}{3}{n}^2-\frac{16}{15}{n}^3-\frac{13}{9}{n}^4+\frac{904}{315}{n}^5\\ {\beta }_6=-\frac{26}{15}{n}^3+\frac{34}{21}{n}^4+\frac{5}{8}{n}^5\\ {\beta }_8=\frac{1237}{630}{n}^4-\frac{12}{5}{n}^5\\ {\beta }_{10}=-\frac{734}{315}{n}^5\end{array}$

.

3.4. Power Series Expansion of Reduced Latitude with Geodetic Latitude as Variable

According to the geodesy theory, the reduced latitude $u\left(B\right)$ is related to the geodetic latitude $B$ by

$$\tan u=\sqrt{1-e^2}\tan B.$$

(13)

The power series expansion of the reduced latitude with geodetic latitude as the variable is

$$u\left(B\right)=B+m_2\sin 2B+m_4\sin 4B+m_6\sin 6B+m_8\sin 8B+m_{10}\sin 10B$$

(14)

The coefficients in Equation (14) are expanded in terms of $e$ up to $e^{10}$ and in terms of $n$ up to $n^5$, which gives in

Table 4. Coefficients in Equation (14).

Expand to e10 Based on the First Eccentricity e	Expand to n5 Based on the Third Flattening n
$\{\begin{array}{l}{m}_2=-\frac{1}{4}{e}^2-\frac{1}{8}{e}^4-\frac{5}{64}{e}^6-\frac{7}{128}{e}^8-\frac{21}{512}{e}^{10}\\ m_4=\frac{1}{32}{e}^4+\frac{1}{32}{e}^6+\frac{7}{256}{e}^8+\frac{3}{128}{e}^{10}\\ m_6=-\frac{1}{192}{e}^6-\frac{1}{128}{e}^8-\frac{9}{1024}{e}^{10}\\ m_8=\frac{1}{1024}{e}^8+\frac{1}{512}{e}^{10}\\ m_{10}=-\frac{1}{5120}{e}^{10}\end{array}$	$\{\begin{array}{l}{m}_2=-n\\ m_4=\frac{1}{2}{n}^2\\ m_6=-\frac{1}{3}{n}^3\\ m_8=\frac{1}{4}{n}^4\\ m_{10}=-\frac{1}{5}{n}^5\end{array}$

.

3.5. Power Series Expansion of Geocentric Latitude with Geodetic Latitude as Variable

According to the geodesy theory, the geocentric latitude $\varphi \left(B\right)$ is related to the geodetic latitude $B$ by

$$\tan \varphi =\left(1-e^2\right)\tan B.$$

(15)

The power series expansion of the reduced latitude with geodetic latitude as the variable is

$$\varphi \left(B\right)=B+n_2\sin 2B+n_4\sin 4B+n_6\sin 6B+n_8\sin 8B+n_{10}\sin 10B.$$

(16)

The coefficients in Equation (16) are expanded in terms of $e$ up to $e^{10}$ and in terms of $n$ up to $n^5$, which gives in

Table 5. Coefficients in Equation (16).

Expand to e10 Based on the First Eccentricity e	Expand to n5 Based on the Third Flattening n
$\{\begin{array}{l}{n}_2=-\frac{1}{2}{e}^2-\frac{1}{4}{e}^4-\frac{1}{8}{e}^6-\frac{1}{16}{e}^8-\frac{1}{32}{e}^{10}\\ n_4=\frac{1}{8}{e}^4+\frac{1}{8}{e}^6+\frac{3}{32}{e}^8+\frac{1}{16}{e}^{10}\\ n_6=-\frac{1}{24}{e}^6-\frac{1}{16}{e}^8-\frac{1}{16}{e}^{10}\\ n_8=\frac{1}{64}{e}^8+\frac{1}{32}{e}^{10}\\ n_{10}=-\frac{1}{160}{e}^{10}\end{array}$	$\{\begin{array}{l}{n}_2=-2n+2n^3-2n^5\\ n_4=2n^2-4n^4\\ n_6=-\frac{8}{3}{n}^3+8n^5\\ n_8=4n^4\\ n_{10}=-\frac{32}{5}{n}^5\end{array}$

.

In sum, compared with the common latitude expansions based on eccentricity $e$, when the common latitude is expanded based on the third flattening $n$, the coefficients of the power series expansions of common latitude have fewer digits and are more concise. In particular, the coefficients of the rectifying latitude, geocentric latitude, and reduced latitude are greatly simplified and the number of terms is almost halved when expanded in a power series based on the third flattening $n$, which increases the efficiency of the calculation and allows the relationship between different latitudes to be expressed more intuitively.

4. Common Latitude Power Series Expansions with Geocentric Latitude as Variable

In related theories of geodesy and map projection, the geocentric latitude $\varphi$ is used as an auxiliary variable in addition to using the geodetic latitude $B$ as the independent variable. We use geocentric latitude as the independent variable because it simplifies the theoretical problems of space geodesy, especially geometric problems. For example, in the ellipsoidal sundial projection, the projection from the ellipsoid onto the sphere is analyzed based on the geocentric latitude. Geocentric latitude also plays an important role in determining satellite orbit and measuring altitude. These problems often involve converting geocentric latitudes to other common latitudes [32]. Using Mathematica, the power series of the common latitude with geocentric latitude as a variable based on eccentricity $e$ and the third flattening $n$ are expressed as detailed below.

4.1. Power Series Expansion of Authalic Latitude with Geocentric Latitude as Variable

According to the map projection theory, on an ellipsoid, the area of an arc-type trapezoid bounded by the equator, the geocentric longitude of $\varphi$, and the two lines of longitude separated by one degree, which is the authalic latitude function, is generally expressed as

$$F(\varphi )={\displaystyle {\int }_0^{\varphi }M(\varphi )rd\varphi }=a^2(1-e^2){\displaystyle {\int }_0^{\varphi }\frac{\cos \varphi \sqrt{(1-(2-e^2)e^2{\cos }^2\varphi )}}{{(1-e^2{\cos }^2\varphi )}^2}}d\varphi .$$

(17)

Given the radius squared $R^2$, the area bounded by the equator, the geocentric longitude $\varphi$, and the two lines of longitude separated by one degree are $F\left(\varphi \right)$. Therefore, according to the spherical integral formula, we conclude that

$$\sin \vartheta =\frac{F(\varphi )}{R^2}=\frac{F(\varphi )}{a^2(1-e^2)A}.$$

(18)

In Equation (18)

$$A=1+\frac{2}{3}{e}^2+\frac{3}{5}{e}^4+\frac{4}{7}{e}^6+\frac{5}{9}{e}^8+\frac{6}{11}{e}^{10},$$

(19)

and $\vartheta$ is the authalic latitude. The manual differentiation is bypassed, and the power series expansion formula of the authalic latitude with geocentric latitude as the variable is

$$\vartheta (\varphi )=\varphi +b_2\sin 2\varphi +b_4\sin 4\varphi +b_6\sin 6\varphi +b_8\sin 8\varphi +b_{10}\sin 10\varphi .$$

(20)

The coefficients in Equation (20) are expanded in terms of $e$ up to $e^{10}$ and in terms of $n$ up to $n^5$, which gives in

Table 6. Coefficients in Equation (20).

Expand to e10 Based on the First Eccentricity e

Expand to n5 Based on the Third Flattening n

$\{\begin{array}{l}{b}_2=\frac{1}{6}{e}^2+\frac{7}{90}{e}^4+\frac{281}{5040}{e}^6+\frac{27869}{604800}{e}^8+\frac{593207}{14968800}{e}^{10}\\ b_4=\frac{1}{180}{e}^4+\frac{1}{252}{e}^6+\frac{10669}{1814400}{e}^8+\frac{507841}{59875200}{e}^{10}\\ b_6=-\frac{131}{45360}{e}^6-\frac{8669}{1814400}{e}^8-\frac{537259}{119750400}{e}^{10}\\ b_8=-\frac{5933}{3628800}{e}^8-\frac{81229}{23950080}{e}^{10}\\ b_{10}=-\frac{80011}{119750400}{e}^{10}\end{array}$

$\{\begin{array}{l}{b}_2=\frac{2}{3}n-\frac{4}{45}{n}^2+\frac{62}{105}{n}^3+\frac{778}{4725}{n}^4-\frac{193082}{467775}{n}^5\\ b_4=\frac{4}{45}{n}^2-\frac{32}{315}{n}^3+\frac{12338}{14175}{n}^4-\frac{92696}{467775}{n}^5\\ b_6=-\frac{524}{2835}{n}^3-\frac{1618}{14175}{n}^4+\frac{612536}{467775}{n}^5\\ b_8=-\frac{5933}{14175}{n}^4-\frac{8324}{66825}{n}^5\\ b_{10}=\frac{320044}{467775}{n}^5\end{array}$

.

4.2. Power Series Expansion of Rectifying Latitude with Geocentric Latitude as Variable

According to the map projection theory, the meridian arc length $X$ on an ellipsoid from the equator to geocentric latitude $\varphi$ is

$$X={\displaystyle {\int }_0^{\varphi }M(\varphi )d\varphi }=a\sqrt{1-e^2}{\displaystyle {\int }_0^{\varphi }\sqrt{\frac{1-\left(2-e^2\right)e^2{\cos }^2\varphi }{{\left(1-e^2{\cos }^2\varphi \right)}^3}}}d\varphi .$$

(21)

Similarly, given that an arc with the angle $\psi$ and the radius $R=a(1-e^2)k_0$ is numerically equivalent to the meridian arc length, the rectifying latitude can be expressed as

$$\psi =\frac{X}{R}=\frac{X}{a(1-e^2)k_0},$$

(22)

$$k_0=1+\frac{3}{4}{e}^2+\frac{45}{64}{e}^4+\frac{175}{256}{e}^6+\frac{11025}{16384}{e}^8+\frac{43659}{65536}{e}^{10},$$

(23)

where $\psi$ is the rectifying latitude. The manual differentiation process is bypassed and the power series expansion formula for rectifying the latitude with geocentric latitude as the variable is

$$\psi (\varphi )=\varphi +a_2\sin 2\varphi +a_4\sin 4\varphi +a_6\sin 6\varphi +a_8\sin 8\varphi +a_{10}\sin 10\varphi .$$

(24)

The coefficients in Equation (24) are expanded in terms of $e$ up to $e^{10}$ and in terms of $n$ up to $n^5$, which gives in

Table 7. Coefficients in Equation (24).

Expand to e10 Based on the First Eccentricity e

Expand to n5 Based on the Third Flattening n

$\{\begin{array}{l}{a}_2=\frac{1}{8}{e}^2+\frac{1}{16}{e}^4+\frac{53}{1024}{e}^6+\frac{95}{2048}{e}^8+\frac{1359}{32768}{e}^{10}\\ a_4=-\frac{1}{256}{e}^4-\frac{1}{256}{e}^6+\frac{5}{8192}{e}^8+\frac{21}{4096}{e}^{10}\\ a_6=-\frac{5}{1024}{e}^6-\frac{15}{2048}{e}^8-\frac{1811}{262144}{e}^{10}\\ a_8=-\frac{261}{131072}{e}^8-\frac{261}{65536}{e}^{10}\\ a_{10}=-\frac{921}{1310720}{e}^{10}\end{array}$

$\{\begin{array}{l}{a}_2=\frac{1}{2}n+\frac{13}{16}{n}^3-\frac{15}{32}{n}^5\\ a_4=-\frac{1}{16}{n}^2+\frac{33}{32}{n}^4\\ a_6=-\frac{5}{16}{n}^3+\frac{349}{256}{n}^5\\ a_8=-\frac{261}{512}{n}^4\\ a_{10}=-\frac{921}{1280}{n}^5\end{array}$

.

4.3. Power Series Expansion of Conformal Latitude with Geocentric Latitude as Variable

According to the map projection theory, the formula of the isometric latitude $q\left(B\right)$ with geocentric latitude $\varphi$ as the variable is

$$q={\displaystyle {\int }_0^{\varphi }\frac{M(\varphi )}{r}}d\varphi ={\displaystyle {\int }_0^{\varphi }\frac{\sqrt{1-\left(2-e^2\right)e^2{\cos }^2\varphi }}{\left(1-e^2{\cos }^2\varphi \right)\cos \varphi }}d\varphi .$$

(25)

If the earth is regarded as a sphere, then $e=0$ and $\varphi$ becomes the conformal latitude $\phi$:

$$\phi =2\arctan \left(e^q\right)-\frac{\pi }{2}.$$

(26)

Using Equations (25) and (26), the power series expansion of the conformal latitude with geocentric latitude as the variable is

$$\phi (\varphi )=\varphi +c_2\sin 2\varphi +c_4\sin 4\varphi +c_6\sin 6\varphi +c_8\sin 8\varphi +c_{10}\sin 10\varphi .$$

(27)

The coefficients in Equation (27) are expanded in terms of $e$ up to $e^{10}$ and in terms of $n$ up to $n^5$, which gives in

Table 8. Coefficients in Equation (27).

Expand to e10 Based on the First Eccentricity e	Expand to n5 Based on the Third Flattening n
$\{\begin{array}{l}{c}_2=\frac{1}{24}{e}^4+\frac{5}{96}{e}^6+\frac{59}{1152}{e}^8+\frac{539}{11520}{e}^{10}\\ c_4=-\frac{1}{48}{e}^4-\frac{1}{60}{e}^6-\frac{19}{2304}{e}^8-\frac{7}{5760}{e}^{10}\\ c_6=-\frac{1}{160}{e}^6-\frac{25}{2688}{e}^8-\frac{71}{7680}{e}^{10}\\ c_8=-\frac{55}{32256}{e}^8-\frac{41}{11520}{e}^{10}\\ c_{10}=-\frac{11}{23040}{e}^{10}\end{array}$	$\{\begin{array}{l}{c}_2=\frac{2}{3}{n}^2+\frac{2}{3}{n}^3-\frac{2}{9}{n}^4-\frac{14}{45}{n}^5\\ c_4=-\frac{1}{3}{n}^2+\frac{4}{15}{n}^3+\frac{43}{45}{n}^4-\frac{4}{45}{n}^5\\ c_6=-\frac{2}{5}{n}^3+\frac{2}{105}{n}^4+\frac{124}{105}{n}^5\\ c_8=-\frac{55}{126}{n}^4-\frac{16}{105}{n}^5\\ c_{10}=-\frac{22}{45}{n}^5\end{array}$

.

4.4. Power Series Expansion of Reduced Latitude with Geocentric Latitude as Variable

According to the map projection theory, the relation between geocentric latitude and reduced latitude is

$$u=\arctan \left(\frac{\tan \varphi }{\sqrt{1-e^2}}\right).$$

(28)

The difference between the geocentric latitude and the reduced latitude is small, so the expansions for the reduced latitude are often used in practical calculations. The power series expansion of the reduced latitude with geocentric latitude as the variable is

$$u(\varphi )=\varphi +d_2\sin 2\varphi +d_4\sin 4\varphi +d_6\sin 6\varphi +d_8\sin 8\varphi +d_{10}\sin 10\varphi .$$

(29)

The coefficients in Equation (29) are expanded in terms of $e$ up to $e^{10}$ and in terms of $n$ up to $n^5$, which gives in

Table 9. Coefficients in Equation (29).

Expand to e10 Based on the First Eccentricity e	Expand to n5 Based on the Third Flattening n
$\{\begin{array}{l}{d}_2=\frac{1}{4}{e}^2+\frac{1}{8}{e}^4+\frac{5}{64}{e}^6+\frac{7}{128}{e}^8+\frac{21}{512}{e}^{10}\\ d_4=\frac{1}{32}{e}^4+\frac{1}{32}{e}^6+\frac{7}{256}{e}^8+\frac{3}{128}{e}^{10}\\ d_6=\frac{1}{192}{e}^6+\frac{1}{128}{e}^8+\frac{9}{1024}{e}^{10}\\ d_8=\frac{1}{1024}{e}^8+\frac{1}{512}{e}^{10}\\ d_{10}=\frac{1}{5120}{e}^{10}\end{array}$	$\{\begin{array}{l}{d}_2=n\begin{array}{c}\end{array}\begin{array}{c}\end{array}\\ d_4=\frac{1}{2}{n}^2\\ d_6=\frac{1}{3}{n}^3\\ d_8=\frac{1}{4}{n}^4\\ d_{10}=\frac{1}{5}{n}^5\end{array}$

.

4.5. Power Series Expansion of Geodetic Latitude with Geocentric Latitude as Variable

According to Equation (13), the power series expansion of the geodetic latitude with geocentric latitude as the variable is

$$B\left(\varphi \right)=\varphi +f_2\sin 2\varphi +f_4\sin 4\varphi +f_6\sin 6\varphi +f_8\sin 8\varphi +f_{10}\sin 10\varphi .$$

(30)

The coefficients in Equation (30) are expanded in terms of $e$ up to $e^{10}$ and in terms of $n$ up to $n^5$, which gives in

Table 10. Coefficients in Equation (30).

Expand to e10 Based on the First Eccentricity e	Expand to n5 Based on the Third Flattening n
$\{\begin{array}{l}{f}_2=\frac{1}{2}{e}^2+\frac{1}{4}{e}^4+\frac{1}{8}{e}^6+\frac{1}{16}{e}^8+\frac{1}{32}{e}^{10}\\ f_4=\frac{1}{8}{e}^4+\frac{1}{8}{e}^6+\frac{3}{32}{e}^8+\frac{1}{16}{e}^{10}\\ f_6=\frac{1}{24}{e}^6+\frac{1}{16}{e}^8+\frac{1}{16}{e}^{10}\\ f_8=\frac{1}{64}{e}^8+\frac{1}{32}{e}^{10}\\ f_{10}=\frac{1}{160}{e}^{10}\end{array}$	$\{\begin{array}{l}{f}_2=2n-2n^3+2n^5\\ f_4=2n^2-4n^4\\ f_6=\frac{8}{3}{n}^3-8n^5\\ f_8=4n^4\\ f_{10}=\frac{32}{5}{n}^5\end{array}$

.

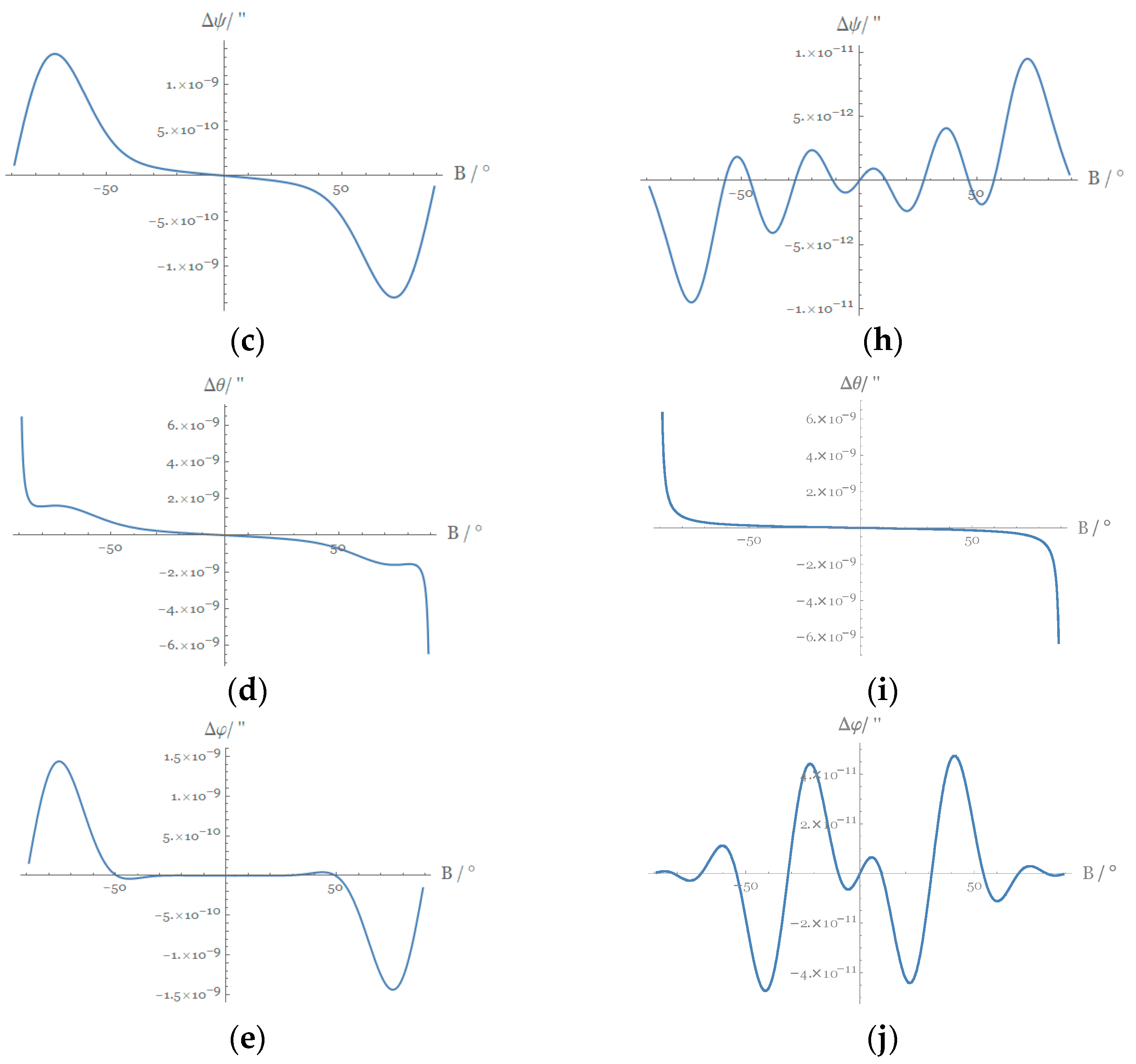
5. Truncation Error and Accuracy Analysis

The common latitude formulas with geodetic latitude and geocentric latitude as variables are expanded into a power series in terms of $e$ up to $e^{10}$ and in terms of $n$ up to $n^5$, which are symbolic expressions appropriate for ellipsoids with different parameters. To verify the accuracy and reliability of these formulas, the calculation error of each expansion formula is analyzed by using CGCS2000 (China Geodetic Coordinate System 2000) and the reference ellipsoid constants $a=6378137 m$ and $1/f=298.257222101 m$.

Taking authalic latitude as an example, we chose the determined geodetic latitude $B_0$ and inserted it into Equation (1) to obtain the theoretical value for authalic latitude ${\vartheta }_0\left(B\right)$. Inserting the determined geodetic latitude $B_0$ into Equation (5) gives the authalic latitude ${\vartheta }_1\left(B\right)$ in terms of the power series expansion of eccentricity $e$. The difference between ${\vartheta }_1\left(B\right)$ and ${\vartheta }_0\left(B\right)$ gives the error of Equation (5). Similarly, when the geodetic latitude $B$ is the variable, we obtain the calculation errors of the derived expressions of geocentric latitude, reduced latitude, rectifying latitude, conformal latitude, and authalic latitude, and the calculation error $\Delta$ varies with the geodetic latitude $B$ as shown in Figure 1. When expanded to $e^{10}$, the calculation errors of the expressions are shown as Figure 1a–e, and when expanding to $n^5$, the calculation errors of the expressions are shown as Figure 1f–j, respectively.

Similarly, when geocentric latitude $\varphi$ is the variable, we obtain the calculation errors of the derived expressions of geodetic latitude, reduced latitude, rectifying latitude, conformal latitude, and authalic latitude, and the calculation error $\Delta$ varies with geodetic geocentric latitude $\varphi$ as shown in Figure 2. When expanded to $e^{10}$, the calculation errors of the expressions are shown as Figure 2a–e, and when expanding to $n^5$, the calculation errors of the expressions are shown as Figure 2f–j, respectively.

Figure 1 and Figure 2 show that when the power series of the common latitude formulas with geodetic latitude and geocentric latitude as variables are expanded in terms of $e$ up to $e^{10}$ or in terms of $n$ up to $n^5$, the calculation errors oscillate as a function of geodetic latitude or geocentric latitude. The maximum calculation error of common latitude is less than $1.0\times {10}^{-8}{}^{}$ arc seconds, which is greater than the accuracy required by geodesy. However, the corresponding power series formulas are complicated. The calculation accuracy of the expansion formula is related to the expansion order. We analyzed the maximum error of the common latitude expansions with geodetic latitude as variables based on the ellipsoidal eccentricity and the third flattening, respectively. The results are given in

Table 11. Truncation error of common latitude expanded to different orders with geodetic latitude as the variable (units: arc seconds).

	$\mathbf{\Delta }\mathit{\varphi }\left(\mathit{B}\right)$	$\mathbf{\Delta }\mathit{u}\left(\mathit{B}\right)$	$\mathbf{\Delta }\mathit{\psi }\left(\mathit{B}\right)$	$\mathbf{\Delta }\mathit{\vartheta }\left(\mathit{B}\right)$	$\mathbf{\Delta }\mathit{\phi }\left(\mathit{B}\right)$
$e^{10}$	2.56114 × 10−9	9.31323 × 10−10	1.42609 × 10−9	1.76893 × 10−8	1.45519 × 10−9
$e^8$	4.52972 × 10−8	1.63272 × 10−7	2.44094 × 10−7	2.2928 × 10−7	2.65311 × 10−7
$e^6$	8.10159 × 10−5	3.01542 × 10−5	4.58977 × 10−5	4.24962 × 10−5	1.47941 × 10−6
$e^4$	0.0151037	0.00590163	0.00913985	0.00833335	0.0107551
$n^5$	1.60071 × 10−10	1.16415 × 10−10	1.16415 × 10−10	1.76369 × 10−8	1.45519 × 10−10
$n^4$	4.51109 × 10−8	6.1118 × 10−10	2.76486 × 10−9	1.27475 × 10−8	2.08966 × 10−8
$n^3$	1.15433 × 10−5	4.10277 × 10−7	1.58537 × 10−6	1.11121 × 10−6	8.84886 × 10−6
$n^2$	0.00455778	0.000325557	0.00126153	0.000803024	0.00312175

.

In the same way, the maximum error of the common latitude expansions with geocentric latitude as variables based on the ellipsoidal eccentricity and the third flattening, respectively is given in

Table 12. Truncation errors of common latitude expanded to different orders with geocentric latitude as the variable (units: arc seconds).

	$\mathbf{\Delta }\mathit{B}\left(\mathit{\varphi }\right)$	$\mathbf{\Delta }\mathit{u}\left(\mathit{\varphi }\right)$	$\mathbf{\Delta }\mathit{\psi }\left(\mathit{\varphi }\right)$	$\mathbf{\Delta }\mathit{\vartheta }\left(\mathit{\varphi }\right)$	$\mathbf{\Delta }\mathit{\phi }\left(\mathit{\varphi }\right)$
$e^{10}$	2.61934 × 10−9	9.31323 × 10−10	9.74978 × 10−10	9.02219 × 10−10	1.01863 × 10−9
$e^8$	4.53001 × 10−7	1.63243 × 10−7	1.42056 × 10−7	1.35537 × 10−7	1.56637 × 10−7
$e^6$	8.10159 × 10−5	3.01542 × 10−5	2.25394 × 10−5	2.19159 × 10−5	2.53659 × 10−5
$e^4$	0.0151037	0.00590163	0.0035465	0.00367417	0.00392772
$n^5$	1.89175 × 10−10	1.16415 × 10−10	1.74623 × 10−10	1.16415 × 10−10	1.74623 × 10−10
$n^4$	4.52274 × 10−8	6.40284 × 10−10	7.01402 × 10−9	6.72298 × 10−9	5.52973 × 10−9
$n^3$	1.15434 × 10−5	4.0984 × 10−7	2.18944 × 10−6	2.0791 × 10−6	2.29341 × 10−6
$n^2$	0.00455778	0.000325912	0.00109875	0.000766065	0.00107432

.

The results in Table 11 and Table 12 show that the precision of commonly used latitude power series expansions is related to the expansion order. The greater the expansion order, the greater the corresponding precision, and the longer the expression. The accuracy of the expansion based on the third flatness is greater than that of the accuracy based on the common latitude power series expansion to $n^5$ and $e^{10}$, $n^4$ and $e^8$, $n^3$ and $e^6$, or $n^2$ and $e^4$, indicating the superiority of the third flattening for the power series expansion of latitude transformation theory. An analysis and comparison allow us to conclude that when the expansion is based on the ellipsoidal eccentricity power series to $e^6$ or on the third flattening to $n^3$, the error of the expansions of the common latitude is less than 10⁻⁴″, which not only meets the requirements for geodesy but also greatly simplifies the expression. The practical expansions of the common latitude with geodetic latitude and geocentric latitude as variables are thus obtained.

When the geodetic latitude $B$ is taken as the variable, the practical, simplified expansion for rectifying latitude $\psi$, authalic latitude $\vartheta$, conformal latitude $\phi$, reduced latitude $u$, and geocentric latitude $\varphi$ are

$$\begin{array}{cc}\hfill \psi \left(B\right)& =B+\left(-\frac{3}{8}{e}^2-\frac{3}{16}{e}^4-\frac{111}{1024}{e}^6\right)\sin 2B+\left(\frac{15}{256}{e}^4+\frac{15}{256}{e}^6\right)\sin 4B-\frac{35}{3072}{e}^6\sin 6B\hfill \\ \hfill & =B+\left(-\frac{3}{2}n+\frac{9}{16}{n}^3\right)\sin 2B+\frac{15}{16}{n}^2\sin 4B-\frac{35}{48}{n}^3\sin 6B,\hfill \end{array}$$

(31)

$$\begin{array}{ll}\vartheta \left(B\right)& =B+\left(-\frac{1}{3}{e}^2-\frac{31}{180}{e}^4-\frac{59}{560}{e}^6\right)\sin 2B+\left(\frac{17}{360}{e}^4+\frac{61}{1260}{e}^6\right)\sin 4B-\frac{383}{45360}{e}^6\sin 6B\\ & =B+\left(-\frac{4}{3}n-\frac{4}{45}{n}^2+\frac{88}{315}{n}^3\right)\sin 2B+\left(\frac{34}{45}{n}^2+\frac{8}{105}{n}^3\right)\sin 4B-\frac{1532}{2835}{n}^3\sin 6B,\end{array}$$

(32)

$$\begin{array}{ll}\phi \left(B\right)& =B+\left(-\frac{1}{2}{e}^2-\frac{5}{24}{e}^4-\frac{3}{32}{e}^6\right)\sin 2B+\left(\frac{5}{48}{e}^4+\frac{7}{80}{e}^6\right)\sin 4B-\frac{13}{480}{e}^6\sin 6B\\ & =B+\left(-2n+\frac{2}{3}{n}^2+\frac{4}{3}{n}^3\right)\sin 2B+\left(\frac{5}{3}{n}^2-\frac{16}{15}{n}^3\right)\sin 4B-\frac{26}{15}{n}^3\sin 6B,\end{array}$$

(33)

$$\begin{array}{ll}u\left(B\right)& =B+\left(-\frac{1}{4}{e}^2-\frac{1}{8}{e}^4-\frac{5}{64}{e}^6\right)\sin 2B+\left(\frac{1}{32}{e}^4+\frac{1}{32}{e}^6\right)\sin 4B-\frac{1}{192}{e}^6\sin 6B\\ & =B-n\sin 2B+\frac{1}{2}{n}^2\sin 4B-\frac{1}{3}{n}^3\sin 6B,\end{array}$$

(34)

$$\begin{array}{ll}\varphi \left(B\right)& =B+\left(-\frac{1}{2}{e}^2-\frac{1}{4}{e}^4-\frac{1}{8}{e}^6\right)\sin 2B+\left(\frac{1}{8}{e}^4+\frac{1}{8}{e}^6\right)\sin 4B-\frac{1}{24}{e}^6\sin 6B\\ & =B+\left(-2n+2n^3\right)\sin 2B+2n^2\sin 4B-\frac{8}{3}{n}^3\sin 6B.\end{array}$$

(35)

When the geocentric latitude $\varphi$ is taken as the variable, the practical, simplified expansion for rectifying latitude $\psi$, authalic latitude $\vartheta$, conformal latitude $\phi$, reduced latitude $u$, and geodetic latitude $B$ are

$$\begin{array}{ll}\psi \left(\varphi \right)& =\varphi +\left(\frac{1}{8}{e}^2+\frac{1}{16}{e}^4+\frac{53}{1024}{e}^6\right)\sin 2\varphi +\left(-\frac{1}{256}{e}^4-\frac{1}{256}{e}^6\right)\sin 4\varphi -\frac{5}{1024}{e}^6\sin 6\varphi \\ & =\varphi +\left(\frac{1}{2}n+\frac{13}{16}{n}^3\right)\sin 2\varphi -\frac{1}{16}{n}^2\sin 4\varphi -\frac{5}{16}{n}^3\sin 6\varphi ,\end{array}$$

(36)

$$\begin{array}{ll}\vartheta \left(\varphi \right)& =\varphi +\left(\frac{1}{6}{e}^2+\frac{7}{90}{e}^4+\frac{281}{5040}{e}^6\right)\sin 2\varphi +\left(\frac{1}{180}{e}^4+\frac{1}{252}{e}^6\right)\sin 4\varphi -\frac{131}{45360}{e}^6\sin 6\varphi \\ & =\varphi +\left(\frac{2}{3}n-\frac{4}{45}{n}^2+\frac{62}{105}{n}^3\right)\sin 2\varphi +\left(\frac{4}{45}{n}^2-\frac{32}{315}{n}^3\right)\sin 4\varphi -\frac{524}{2835}{n}^3\sin 6\varphi ,\end{array}$$

(37)

$$\begin{array}{ll}\phi (\varphi )& =\varphi +\left(\frac{1}{24}{e}^4+\frac{5}{96}{e}^6\right)\sin 2\varphi +\left(-\frac{1}{48}{e}^4-\frac{1}{60}{e}^6\right)\sin 4\varphi -\frac{1}{160}{e}^6\sin 6\varphi \\ & =\varphi +\left(\frac{2}{3}{n}^2+\frac{2}{3}{n}^3\right)\sin 2\varphi +\left(-\frac{1}{3}{n}^2+\frac{4}{15}{n}^3\right)\sin 4\varphi -\frac{2}{5}{n}^3\sin 6\varphi ,\end{array}$$

(38)

$$\begin{array}{ll}u(\varphi )& =\varphi +\left(\frac{1}{4}{e}^2+\frac{1}{8}{e}^4+\frac{5}{64}{e}^6\right)\sin 2\varphi +\left(\frac{1}{32}{e}^4+\frac{1}{32}{e}^6\right)\sin 4\varphi +\frac{1}{192}{e}^6\sin 6\varphi \\ & =\varphi +n\sin 2\varphi +\frac{1}{2}{n}^2\sin 4\varphi +\frac{1}{3}{n}^3\sin 6\varphi ,\end{array}$$

(39)

$$\begin{array}{ll}B(\varphi )& =\varphi +\left(\frac{1}{2}{e}^2+\frac{1}{4}{e}^4+\frac{1}{8}{e}^6\right)\sin 2\varphi +\left(\frac{1}{8}{e}^4+\frac{1}{8}{e}^6\right)\sin 4\varphi +\frac{1}{24}{e}^6\sin 6\varphi \\ & =\varphi +\left(2n-2n^3\right)\sin 2\varphi +2n^2\sin 4\varphi +\frac{8}{3}{n}^3\sin 6\varphi .\end{array}$$

(40)

In conclusion, the use of Mathematica allows us to derive simplified, practical formulas for the common latitude, with geodetic latitude and geocentric latitude as variables. Equations (31) to (37) show that when the power series is expanded based on the third flattening, it is more compact, and its coefficients are simpler, which is consistent with the conclusions derived above.

6. Conclusions

In this paper, the symbolic computation program Mathematica is used to analyze the power series expansion for the common latitude with geodetic latitude and geocentric latitude as variables. The coefficients in the formulas are expressed as a power series in the third flattening n. Taking the CGCS2000 ellipsoid as an example, we analyze the accuracy of the power series expansions of the common latitude and calculate the maximum error of expansions to different orders based on ellipsoid eccentricity $e$ and the third flattening $n$. The results lead to the following conclusions:

(1)

The common latitude direct expansions with geocentric latitude as the variable are derived, and the power series expansions based on the ellipsoidal eccentricity $e$ and the third flattening $n$ are carried out, which extend map projection theory.

(2)

Compared with the power series expansions based on ellipsoid eccentricity $e$, the power series expansions based on the ellipsoid third flattening $n$ are neater and more compact, and the coefficients are simpler. In addition, they converge better and are more accurate. This shows that the third flattening $n$ is superior to the ellipsoidal eccentricity $e$ in the coefficient expansion of common latitude expressions.

(3)

As the order of the power series expansions decreases, the expressions become simpler, but the corresponding truncation error increases. By analyzing truncation errors of different orders, we conclude that when the common latitude formulas are expanded to $e^6$ based on ellipsoidal eccentricity $e$ or expanded to $n^3$ based on the third flattening $n$, they not only satisfy the precision required by geodesy but also make the expression more concise.