1. Introduction
With the development of industry and the improvement in computing power, the application of artificial intelligence in various fields of people’s lives has been becoming more popular, affecting many aspects, including medical care, logistics, face and voice recognition, etc. There is a wide application of machine learning and profound learning benefits from computing power and massive data. The traditional machine learning and deep learning model rely on data centers and require large amounts of high-quality data. With the increasing requirements of machine learning and deep learning in our lives, the requirements for data quantity and quality are also higher. In addition, in production and life, other companies and organizations need to pay to collect massive amounts of data. Aside from the cost, protecting users’ privacy is also an important factor limiting the data obtained. To address these issues, Google proposed federated learning [
1,
2,
3], which has attracted attention from scholars and organizations. Federated learning can train models using decentralized data, which significantly increases the amount and quality of data. On the other hand, the participating nodes are not required to provide their own local data in federated learning. They only need to deliver the training results to protect the user’s data privacy. However, federated learning does not make the user’s privacy completely invulnerable, and the user’s privacy may be obtained through the shared model parameters [
4,
5].
Two schemes have been proposed to improve privacy protection in federated learning, one based on homomorphic encryption [
6,
7,
8,
9] and the other based on differential privacy [
10,
11,
12,
13]. However, these methods have difficulties in practical application due to their limitations. Differential privacy relies on adding noise to the original data or training results to protect privacy, and it may reduce the model’s accuracy. Too much noise can make the model less accurate than expected. At the same time, too little noise will not achieve the protection of user privacy, making it challenging to balance privacy protection and accuracy [
8]. Homomorphic encryption techniques rely on complex encryption and decryption computations, which may cost a large amount of time. At the same time, the different computing power of devices and the different time used in complex calculations situations can make the aggregation unsynchronized [
14].
To solve the above problems of federated learning, Kalman filter-based differential privacy federated learning (KDP-FL) is proposed. The proposed scheme consists of two parts, using differential privacy to protect the gradient privacy in federated learning and using the Kalman filter to reduce the noise added to preserve privacy in order to improve the accuracy of the global model. The main contributions of this paper are as follows.
- (1)
A multiparty cooperative model training scheme that protects data privacy is proposed.
- (2)
A differential privacy federated learning algorithm is proposed to protect user data privacy by a differential privacy mechanism.
- (3)
The noise introduced by the differential privacy mechanism is reduced by Kalman filtering to improve the model’s accuracy.
2. Related Work
Federated learning has been gradually applied to protect the data privacy of all parties in scenarios where multiple parties cooperate in training and need to exchange data, such as traffic monitoring [
15], edge computing [
14], and IoT [
16], to ensure that the original data is not leaked. However, privacy analysis attacks mean that federated learning also faces the risk of privacy leakage. It is essential to solve the problems of federated learning, especially gradient privacy protection, where data privacy is a particular concern. There are currently two privacy-preserving methods in federated learning: (1) differential privacy and (2) homomorphic encryption.
Abadi et al. [
10] proposed a differential privacy deep learning method that combined machine learning or deep learning methods with differential privacy and proposed a new computational theory to obtain lower privacy consumption with smaller constraints, providing a basis for introducing differential privacy in federated learning. Hu et al. [
11] used a block coordinate descent to optimize the objective function and differential privacy, which could protect gradient privacy but performed poorly in non-convex models.
Zhao et al. [
12] used differential privacy federated learning for vehicle nets to train intelligent traffic management systems to protect vehicle location privacy but did not evaluate the accuracy under the influence of noise. Homomorphic encryption is a cryptographic method based on the computational complexity theory of mathematical puzzles, where the model parameters computed by each training node are aggregated and sent to the specified node after homomorphic encryption, and the model parameters obtained after decryption are the same as those obtained by direct aggregation without encryption, using this property to protect gradient privacy. Li et al. [
13] used the chain aggregation method to protect gradient privacy, which improved the accuracy, but the chain aggregation approach introduced a large communication overhead. Fang et al. [
8] used the Pilliar algorithm combined with federated learning to protect gradient privacy, but the Pilliar algorithm requires complex power operations, which introduced a large time overhead. Ma et al. [
9] used the multi-key homomorphic encryption (MK-HE) to solve the collusion attack leakage problem brought by a single key, which improved privacy protection for federated learning. Zhang et al. [
7] improved the encoding method during gradient transmission, reducing the computational overhead due to encryption but decreasing the accuracy.
To balance accuracy and differential privacy, this paper uses a differential privacy approach to protect gradient privacy while using Kalman filtering to reduce the impact of the noise on the accuracy.
3. Proposed Method
This section introduces the Kalman filtering-based differential privacy federated learning method, which contains a Differential Privacy mini-Batch Gradient Descent Algorithm and the Kalman reduction parameters aggregation method.
3.1. Method Overview
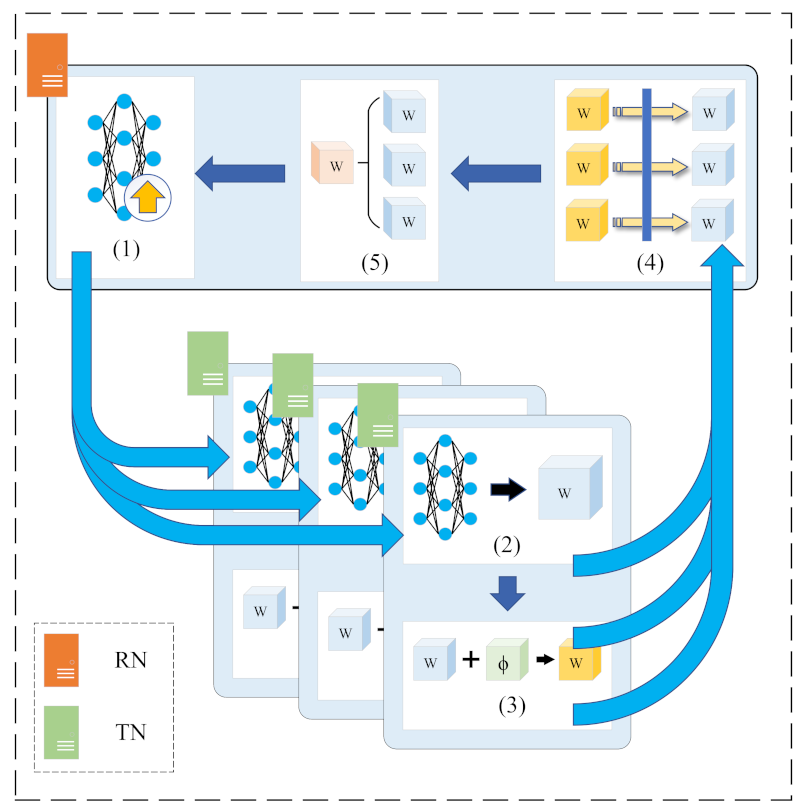
There are two types of nodes in federated learning, the Request Node (RN) and the Training Node (TN). The nodes that need others to assist in training the model are called the RN, which deliver task requests to other nodes and initialize or update the global model. The nodes that assist the RN in training the model are called the TN, which train the model using local data and provide the training results, which is also called the gradient, to the RN. There are
C TNs participating in training each round. The workflow of KDP-FL is shown in
Figure 1. Federated learning contains
T rounds of global training. Global training includes task definition, model update, and local training. The RN defines the task and initializes the global model. Then, it loops the following steps to finish the global training:
- (1)
The RN updates the global model parameters and sends them to the TN.
- (2)
The TN trains the model locally and obtains the local training result for the tth round of training after e iterations. This step is also called local training.
- (3)
The TN adds Gaussian noise to the training result and sends them to the RN.
- (4)
The RN uses Kalman filtering on all the training result to reduce the noise.
- (5)
The RN aggregates all the training results to obtain the global model parameters for the next round.
3.2. Method Details
In this section, we introduce our method in detail. Some significant symbols used in this paper are defined in
Table 1.
3.2.1. Differential Privacy-Based Stochastic Mini-BATCH Gradient Descent (DP-SGD)
TNs train the model locally instead of providing local raw data to the RNs to protect data privacy, then send the training result to the RN. Algorithm 1 describes the local training. Each TN uses
as the initial local model parameters, uses the local data as the dataset, and trains the model using the DP-SGD algorithm. In the
eth round of the DP-SGD, the TN performs several iterations to optimize the model parameters. During optimization, the training results are not sent to the RN, and noise is added to the training result at the end of the
Eth round of optimization of local training. Local training is performed using the following iteration
After
E rounds of local training, the training result should be sent to the RN. To protect the gradient privacy, the results need to be revised using a differential privacy method before sending. The differential privacy mechanism in this paper is the Gaussian mechanism, defined in Equation (
2), where
denotes a normal distribution with mean zero and variance
.
A Gaussian mechanism for a function
f with
as sensitivity satisfies
-differential privacy if
and
are satisfied [
14]. Then, the local training result noise addition of the TN is calculated as:
To address the gradient explosion that may occur during the training process, norm gradient clipping is used. In addition, gradient clipping can limit the gradient values to a certain range, which is beneficial to the Gaussian mechanism. The clipping threshold is set to M. The gradient value g does not change when the norm number of the gradient , and if , the gradient is clipped as Algorithm 1 described. The gradient clipping method can be used to control the gradient values from exceeding the set threshold and prevent the impact of gradient explosion on the model. In addition, after gradient clipping, the upper bound of the gradient value norm is . Limiting the upper bound can effectively control the variance in the noise distribution.
The use of differential privacy in SGD requires the calculation of privacy consumption, and there is a risk of privacy leakage when the privacy cost is higher than the privacy budget. Compared to the strong composition theorem [
17], using the Moment Accountant proposed by Adabi et al. [
10] can obtain a smaller
with the same privacy budget. According to the theory of Moment Account, for any
and
, the DP-BGD algorithm is
-differentially private for any
> 0 where
,
are constants, and
q is the sample probability defined in Equation (
4). The variance in the added noise is based on the number of training rounds and privacy budget.
The DP-SGD algorithm is shown in Algorithm 1.
| Algorithm 1 DP-SGD |
Input:; , M;
Output:- 1:
- 2:
fordo - 3:
Take a random batch with size B - 4:
for do - 5:
- 6:
- 7:
end for - 8:
- 9:
end for - 10:
|
3.2.2. Kalman Noise Reduction Parameter Aggregation
The TN sends the training result to the RN after adding noise using Equation (
3), and the model parameters of node TN
are noted as
; then, the RN receives the set of model parameters
.
The model parameters obtained by the RN contain noise, which will decrease the accuracy of the model. In order to reduce the impact of differential privacy on the model and improve the accuracy, it is necessary to revise the model parameters sent by the TN. In this paper, we use Kalman filtering to revise all model parameters obtained by the RN to improve the accuracy of the model under the situation where differential privacy noise has been added to the global model:
The details will be described in
Section 3.2.3. The global model parameters of the
tth round are obtained after aggregating all the model parameters revised by the Kalman filter; then, the global model is updated.
The KDP-FL algorithm is shown in Algorithm 2.
| Algorithm 2 KDP-FedAvg |
Input:; ;
Output:w- 1:
fordo - 2:
for in parallel do - 3:
TNdo: - 4:
RN do: - 5:
end for - 6:
- 7:
end for
|
3.2.3. Details of Kalman Noise Reduction
The Kalman filter is able to reduce the noise of normal distribution in the linear system [
18]. The noise added to the training result after differential privacy is Gaussian noise satisfying the condition of normal distribution, and the state update equation is linear, so the Kalman filter can be used for noise reduction in the training result to decrease the impact of differential privacy on the accuracy of the model. The noise revising has two steps, the first step is the model parameters’ update, and the second step is the parameters’ update correction.
There are
C TNs in the
tth round of federated learning; the model parameters of the TN
are
, the global model parameters are
, the parameter vector composed of the model parameters of all TNs is
, and the gradient values of TN
are
. Then, the gradient vector composed of the gradient values of all TNs is
. The linear coefficient matrix of the state prediction equation
U is a unit matrix, and
V is defined as following:
Then, the parameter update equation for model training can be transformed into the state prediction equation:
In fact, the parameter update equation Equation (
9) for model training can also be written as:
The noise added by the TN in differential privacy uses the Gaussian mechanism satisfying Gaussian distribution.
To achieve dimensional matching with
U and
V, we need the calculation described in Algorithm 3. The elements in
and
are all matrix. First, we reshape each element in
and
. Let
, and each matrix
or
shaped
will be reshaped to
. Let
be the
ith parameter in
and
be the
ith in
. Then, we can calculate Equation (
9) using Algorithm 3.
| Algorithm 3 Matrix broadcast calculation |
Input:; ; U; V;
Output:- 1:
fortoNdo - 2:
- 3:
- 4:
- 5:
end for - 6:
- 7:
fordo - 8:
- 9:
end for - 10:
|
The gradient vector contains noise added by the TN, and the distribution of the noise is known. The Gaussian noise added by the differential privacy is considered an external disturbance, i.e., uncertainty in the system.
In Kalman filtering,
is used to denote the actually obtained data, calculated using the following equation:
where
H is the data unit transformation matrix. In this paper, the data sent by the TN are the same as the data obtained by the RN; so,
H is the
dimensional unit vector.
R is the error column vector. In order to avoid the occurrence of a singular matrix in subsequent calculations, here,
is taken. The calculation of the Kalman gain matrix using the noise covariance matrix
is
Since
H is a
dimensional unit vector, the formula for the Kalman gain can be reduced to
The parameter update equation using the Kalman gain correction is
We update the covariance matrix of the norm noise:
4. Experiment and Analysis
4.1. Experiment Setting
The public datasets MNIST [
19], FMNIST [
20], and CIFAR10 [
21] were selected to train and test. The dataset was partitioned to simulate a federated learning environment, (1) independently and identically distributed (IID) for each TN [
1]: the training data were shuffled and then partitioned into 100 clients each receiving an equal amount of examples; (2) non-independently and identically distributed (Non-IID) for each TN [
22]: we distributed the data among 100 TNs, such that each TN contained samples of only two kinds; the number of samples among the TN followed a power law, as detailed in
Table 2.
Using CNN as the training model for MNIST and FMNIST, the network architecture consisted of two fully connected layers. The convolutional layers used
convolutions with stride 1, followed by a ReLU and
max pools, with 32 channels in the first layer and 64 channels in the second layer. Then the first convolution output was
after pools, and the second convolution output was
after pools. Last, we had two fully connected layers and used resnet50 [
23] to train the model for CIFAR10.
The experimental environment was an Intel(R) Xeon(R) W-2295 CPU@3.00 GHz, 64 GB RAM, NVIDIA GeForce RTX 3080 GPU, and the experimental platform was Pytorch. According to the related works [
10,
11,
12], the parameters of this paper were set as shown in
Table 3.
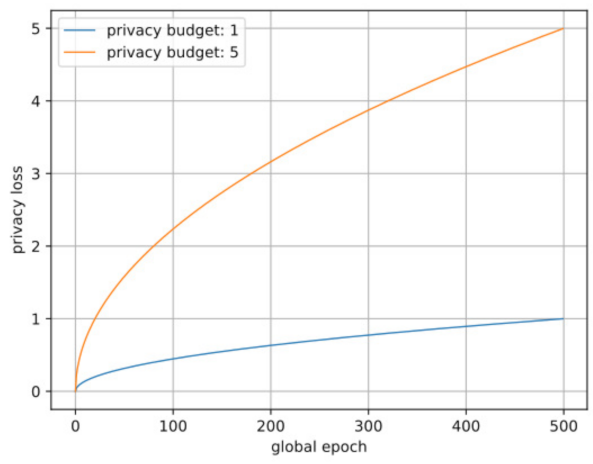
4.2. Privacy Budget Analysis
Moments Accountant can provide a tighter bound than the composition theorem on privacy loss. The privacy loss can be calculated by the noise level
. The privacy loss with the increasing global epoch is shown in
Figure 2. To test the effectiveness of the proposed method under different privacy budgets, we selected
and
. A larger privacy budget
will result in a more accurate model, and a smaller privacy budget
will achieve better privacy protection. Then, we let
and computed the noise level
using Equation (
5).
4.3. Experimental Results
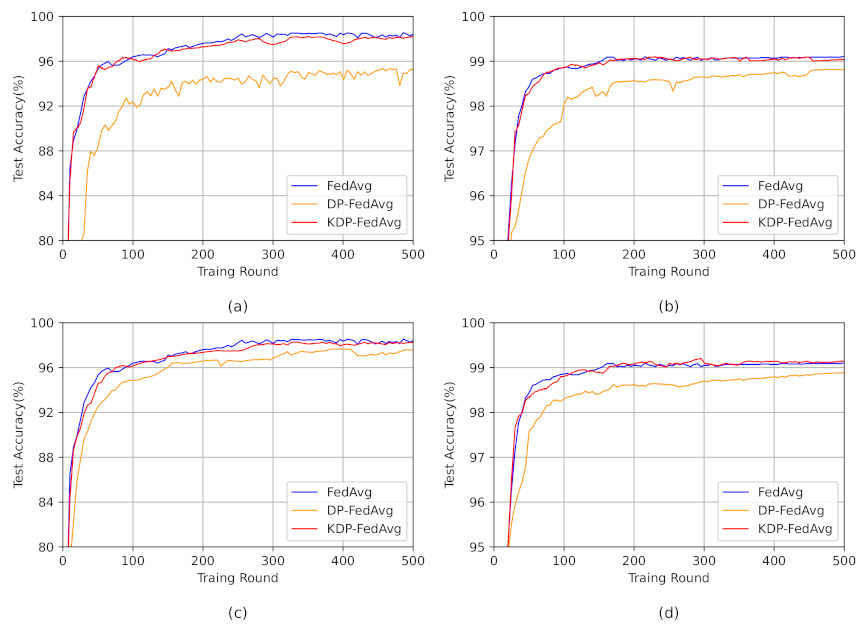
The effectiveness of the method is shown by the model accuracy, and the comparison results are shown in
Figure 3. The DP-FedAvg algorithm protected privacy by adding noise to the gradient matrix, and the impact of privacy protection depended on the size of the privacy budget. The smaller the privacy budget, the better the privacy protection. However, as the privacy budget decreased, the noise required to be added increased, which may lead to a decrease in the accuracy of the model. By comparing the accuracy under the non-IID dataset, DP-FedAvg in (a) and (c), a higher requirement for privacy protection needed a smaller
, which led to lower accuracy of the model. Furthermore, the accuracy of DP-FedAvg at
decreased about 3% compared to that at
. Furthermore, the accuracy of DP-FedAvg
was lower than
and was the same as the pattern in the IID.
In addition, using different datasets, FMNIST and CIFAR10, the experimental results in
Table 4 show that KDPFL achieved good results in the other two datasets. Hence, the model is suitable for other datasets. By testing CNN and CIFAR10, the experimental results show that KDPFL is suitable for different neural network structures and has good compatibility.
In this paper, the parameter update equation was transformed into the state update equation. Furthermore, the global model parameter update, which was completely determined by the TN’s training result, was transformed into the global model parameter update, which was jointly determined by the estimated value and the TN calculation result. The Kalman gain coefficient was calculated by the noise covariance matrix, and the weight of the estimated value and the predicted value in the global model update were calculated by the Kalman gain coefficient to realize the optimal global model update.
The Kalman filter noise reduction method, which reduced the noise at aggregation, decreased the effect of the differential privacy added noise on the model, achieved an accuracy closer to the FedAvg algorithm without added noise, and performed well with both non-IID data and IID data. With non-IID data, the accuracy was improved up to 4.5% compared to DP-FedAvg, and the accuracy was improved up to 2.5%. The above experiments show that the scheme proposed in this paper can protect the user’s privacy with little loss of accuracy.
5. Conclusions
In this paper, a Kalman filter-based differential privacy federated learning method, KDP-FL, was proposed. Federated learning was used to achieve data sharing while preserving privacy. In addition, differential privacy was added to federated learning, which can resist gradient differential attacks and further protect user privacy. Furthermore, the influence of the noise added by the differential mechanism on the accuracy of the model was reduced by the Kalman filter. The experiment results and analysis showed that the proposed method was able to train models with little loss of accuracy while protecting user privacy. KDP-FL is suitable for training privacy-preserving models under multiple nodes and can help in data cooperation among multiple nodes.
When the neural network is simple, the additional computational overhead brought by Algorithm 3 is negligible. However, when the neural network is complex with a large number of parameters, optimizing all parameters requires calculating the Kalman gain for each parameter, which will bring about a non-negligible additional computational overhead.
In addition, the proposed method used Kalman filtering, which increases the computational overhead and is not applicable to devices and nodes with weak computational power, which is a direction for future improvement.
Author Contributions
Conceptualization, X.Y. and Z.D.; data collection and analysis, Z.D.; validation, X.Y.; writing—original draft preparation, Z.D.; writing—review and editing, X.Y. and Z.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Ministry of Science and Technology of China, National Key R&D Program “Cyberspace Security” Key Project, 2017YFB0802305 and the Natural Science Foundation of Hebei Province, F2021201052.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Conflicts of Interest
The authors declare no conflict of interest.
References
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; Arcas, B.A. Communication-Efficient Learning of Deep Networks from Decentralized Data. Artif. Intell. Stat. 2017, 54, 1273–1282. [Google Scholar]
- Konečný, J.; McMahan, H.B.; Ramage, D.; Richtárik, P. Federated Optimization: Distributed Machine Learning for On-Device Intelligence. arXiv 2016, arXiv:1610.02527. [Google Scholar]
- Konečný, J.; McMahan, H.B.; Yu, F.X.; Richtárik, P.; Suresh, A.T.; Bacon, D. Federated Learning: Strategies for Improving Communication Efficiency. arXiv 2016, arXiv:1610.05492. [Google Scholar]
- Melis, L.; Song, C.; Cristofaro, E.D.; Shmatikov, V. Exploiting Unintended Feature Leakage in Collaborative Learning. In Proceedings of the IEEE Symposium on Security and Privacy, San Francisco, CA, USA, 20–22 May 2019; pp. 691–706. [Google Scholar]
- Zhao, B.; Mopuri, K.R.; Bilen, H. iDLG: Improved Deep Leakage from Gradients. arXiv 2020, arXiv:2001.02610. [Google Scholar]
- Ou, W.; Zeng, J.; Guo, Z.; Yan, W.; Liu, D.; Fuentes, S. A homomorphic-encryption-based vertical federated learning scheme for rick management. Comput. Sci. Inf. Syst. 2020, 17, 819–834. [Google Scholar] [CrossRef]
- Zhang, C.; Li, S.; Xia, J.; Wang, W.; Yan, F.; Liu, Y. BatchCrypt: Efficient Homomorphic Encryption for Cross-Silo Federated Learning. In Proceedings of the USENIX Annual Technical Conference, Boston, MA, USA, 15–17 July 2020; pp. 493–506. [Google Scholar]
- Fang, H.; Qian, Q. Privacy Preserving Machine Learning with Homomorphic Encryption and Federated Learning. Future Internet 2021, 13, 94. [Google Scholar] [CrossRef]
- Ma, J.; Naas, S.; Sigg, S.; Lyu, X. Privacy-preserving Federated Learning based on Multi-key Homomorphic Encryption. arXiv 2021, arXiv:2104.06824. [Google Scholar] [CrossRef]
- Abadi, M.; Chu, A.; Goodfellow, I.J.; McMahan, H.B.; Mironov, I.; Talwar, K.; Zhang, L. Deep Learning with Differential Privacy. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 308–318. [Google Scholar]
- Hu, R.; Guo, Y.; Li, H.; Pei, Q.; Gong, Y. Personalized Federated Learning With Differential Privacy. IEEE Internet Things J. 2020, 7, 9530–9539. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, J.; Yang, M.; Wang, T.; Wang, N.; Lyu, L.; Niyato, D.; Lam, K. Local Differential Privacy-Based Federated Learning for Internet of Things. IEEE Internet Things J. 2021, 8, 8836–8853. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, Y.; Jolfaei, A.; Yu, D.; Xu, G.; Zheng, X. Privacy-Preserving Federated Learning Framework Based on Chained Secure Multiparty Computing. IEEE Internet Things J. 2021, 8, 6178–6186. [Google Scholar] [CrossRef]
- Liu, J.; Xu, H.; Xu, Y.; Ma, Z.; Wang, Z.; Qian, C.; Huang, H. Communication-efficient asynchronous federated learning in resource-constrained edge computing. Comput. Netw. 2021, 199, 108429. [Google Scholar] [CrossRef]
- Abubaker, Z.; Javaid, N.; Almogren, A.; Akbar, M.; Zuair, M.; Ben-Othman, J. Blockchained service provisioning and malicious node detection via federated learning in scalable Internet of Sensor Things networks. Comput. Netw. 2022, 204, 108691. [Google Scholar] [CrossRef]
- Mothukuri, V.; Khare, P.; Parizi, R.M.; Pouriyeh, S.; Dehghantanha, A.; Srivastava, G. Federated-Learning-Based Anomaly Detection for IoT Security Attacks. IEEE Internet Things J. 2022, 9, 2545–2554. [Google Scholar] [CrossRef]
- Dwork, C.; Rothblum, G.N.; Vadhan, S.P. Boosting and Differential Privacy. In Proceedings of the 2010 IEEE 51st Annual Symposium on Foundations of Computer Science, Las Vegas, NV, USA, 23–26 October 2010; pp. 51–60. [Google Scholar]
- Alazard, D. Introduction to Kalman Filtering. Meas. Control-Lond. Inst. Meas. Control 1986, 19, 84–110. [Google Scholar]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-MNIST: A Novel Image Dataset for Benchmarking Machine Learning Algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- Ranzato, M.; Krizhevsky, A.; Hinton, G.E. Factored 3-Way Restricted Boltzmann Machines For Modeling Natural Images. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, AISTATS 2010, Chia Laguna Resort, Sardinia, Italy, 13–15 May 2010; Volume 9, pp. 621–628. [Google Scholar]
- Li, X.; Huang, K.; Yang, W.; Wang, S.; Zhang, Z. On the Convergence of FedAvg on Non-IID Data. arXiv 2019, arXiv:1907.02189. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).