Fibonacci Wavelet Method for the Solution of the Non-Linear Hunter–Saxton Equation

Abstract

In this article, a novel and efficient collocation method based on Fibonacci wavelets is proposed for the numerical solution of the non-linear Hunter–Saxton equation. Firstly, the operational matrices of integration associated with the Fibonacci wavelets are constructed by following the strategy of Chen and Hsiao. The operational matrices merged with the collocation method are used to convert the given problem into a system of algebraic equations that can be solved by any classical method, such as Newton’s method. Moreover, the non-linearity arising in the Hunter–Saxton equation is handled by invoking the quasi-linearization technique. To show the efficiency and accuracy of the Fibonacci-wavelet-based numerical technique, the approximate solutions of the non-linear Hunter–Saxton equation with other numerical methods including the Haar wavelet, trigonometric B-spline, and Laguerre wavelet methods are compared. The numerical outcomes demonstrate that the proposed method yields a much more stable solution and a better approximation than the existing ones.

1. Introduction

Non-linear partial differential equations play a vital role in modeling real-life phenomena, especially in the field of applied sciences such as meteorology, aerospace engineering, oceanography, geology, astronomy, and many other disciplines. For the realistic treatment of these non-linear models, several numerical techniques such as the barycentric interpolation collocation method [1], Fourier spectral method [2], and reproducing kernel method [3] have been adopted for the numerical treatment of these non-linear partial differential equations, such as the Klein–Gordon–Zakharov equations, Schrödinger equation, Duffing systems, and many more. The Hunter–Saxton equation is one among those non-linear partial differential equations that describe waves of a nematic liquid crystal in an enormous director field and arise at the short-wave limit of the Camassa–Holm equation—an integrable model of shallow-water waves propagating uni-directionally across a flat bottom [4]. This equation has both the bi-Hamiltonian and bi-variational structure of integrable partial differential equations, often referred to as the Hunter–Saxton equation, which re-expresses the geodesic flow in the diffeomorphism group of a circle. Formally, the non-linear Hunter–Saxton equation is    given by

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{\partial \eta }}\left({\displaystyle \frac{\partial u(\eta ,\zeta )}{\partial \zeta }}+u(\eta ,\zeta ){\displaystyle \frac{\partial u(\eta ,\zeta )}{\partial \eta }}\right)={\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\partial u(\eta ,\zeta )}{\partial \eta }}\right)}^2.\end{array}$$

(1)

Equation (1) can also be redrafted as

$$\begin{array}{c}\hfill {\displaystyle \frac{{\partial }^{2}u(\eta ,\zeta )}{\partial \eta \partial \zeta }}+u(\eta ,\zeta ){\displaystyle \frac{{\partial }^{2}u(\eta ,\zeta )}{\partial {\eta }^2}}+{\left({\displaystyle \frac{\partial u(\eta ,\zeta )}{\partial \eta }}\right)}^2,\end{array}$$

(2)

where $\eta$ and $\zeta$ denote the space and time coordinates, respectively, with initial and boundary conditions:

$$\begin{array}{c}\hfill u(\eta ,0)=g_0\left(\eta \right)\mathrm{and}\underset{\eta \to \infty }{lim}u(\eta ,0)=0.\end{array}$$

(3)

In practice, it is more appropriate to impose a boundary condition of the form:

$$\begin{array}{c}\hfill \underset{\eta \to \infty }{lim}u(\eta ,0)=0,\end{array}$$

(4)

or even the initial and boundary conditions:

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \begin{array}{c}\hfill \end{array}& \hfill u(\eta ,0)=f_0\left(\eta \right),{\displaystyle \frac{\partial u(\eta ,0)}{\partial \zeta }}=f_1\left(\eta \right)0\le \eta \le 1\hfill \\ \hfill & \hfill u(0,\zeta )=g_0\left(\zeta \right),{\displaystyle \frac{\partial u(0,\zeta )}{\partial \eta }}=g_1\left(\zeta \right),0<\zeta \le 1,\hfill \end{array}\right\}\end{array}$$

(5)

where $f_0\left(\eta \right),f_1\left(\eta \right),g_0\left(t\right)$, and $g_1\left(t\right)$ are sufficiently smooth functions.

Keeping in view the prolificacy of the Hunter–Saxton equation governed by the differential Equation (2), a substantial amount of research has been carried out in the quest to obtain numerical solutions via several analytical and numerical techniques. For instance, Behzadi [5] employed the homotopy analysis method (HAM) for the approximate solution of the non-linear Hunter–Saxton equation and showed that the HAM is more rapidly convergent than certain other iterative methods such as the variational iteration method, Adomian decomposition method, modified variational iteration method, and modified Adomian decomposition method, whereas Wei et al. [6] established the global solutions of the periodic Hunter–Saxton equation with weak dissipation. Aratyn et al. [7] obtained exact rational solutions of the generalized Hunter–Saxton equation by using the Padé approximation. Besides, Rouhparvar [8] proposed the reduced differential transform method for obtaining the solution of the non-linear Hunter–Saxton equation, which does not require linearization, discretization, nor perturbation of the underlying non-linear differential equation. Hashmi et al. [9] examined the efficiency of the cubic trigonometric B-spline method for obtaining the numerical solution of the non-linear Hunter–Saxton equation. Karaagac et al. [10] applied the finite element method by reducing the governing non-linear partial differential equation to a system of ordinary differential equations in terms of shape functions. Sato [11] formulated a stable and convergent finite difference method for the modified Hunter–Saxton equation on a periodic domain. Nonetheless, very recently, Ahmad et al. [12] demonstrated a highly applicable aspect of the Hunter–Saxton equation while undertaking the numerical treatment of the liquid crystal model described through the Hunter–Saxton equation by employing the Sinc collocation method via the theta weighted scheme.

Over the last couple of decades, wavelet theory has seen unprecedented progress in the form of innovative and efficient numerical algorithms. Wavelet-based numerical schemes have dethroned the usual numerical methods and have received much attention from researchers working in various disciplines of science and engineering [13,14]. In particular, the wavelet-based matrix methods have acquired a respectable status in numerical analysis due to their easy implementation, simple procedure, and rapid convergence. Moreover, they are computer-oriented and do not require calculating the inverse of the wavelet matrix, and less CPU time is needed as the major blocks of the wavelet operational matrix are computed once and reused in subsequent computations. As of now, numerous linear and non-linear differential equations have been solved by employing various wavelet families, including the Haar wavelets, Euler wavelets, Bernoulli wavelets, Chebyshev wavelets, Legendre wavelets, Hermite wavelets, Gegenbauer wavelets, and ultraspherical wavelets [15,16,17,18,19,20,21,22]. To harness the advantages of wavelet-based numerical methods in the context of the non-linear Hunter–Saxton equation, many wavelet-based methods have been employed for obtaining the numerical solution. To mention a few, Arbabi et al. [23] utilized the Haar wavelet quasi-linearization approach to obtain the approximate solution of the Hunter–Saxton equation. Recently, Srinivasa et al. [24] developed a collocation technique based on the Laguerre wavelet for the numerical solution of the Hunter–Saxton equation and exhibited the uniform convergence of the employed method.

The origin of the Fibonacci numbers dates back to the early 1200s with the seminal work of Italian mathematician Fibonacci studying the famous rabbit problem. The Fibonacci numbers $F_m=F_{m-1}+F_{m-2},m\ge 2$ with initial values $F_0=0,F_1=1$ are the terms of the sequence $\{0,1,1,2,3,5,\dots \}$. Using the Fibonacci-like recurrence relations, Catalan and Jacobsthal introduced a large class of polynomials commonly known as Fibonacci polynomials. The polynomials $F_m\left(\eta \right)$ introduced by Catalan are defined by the recurrence relation $F_m\left(\eta \right)=\eta F_{m-1}\left(\eta \right)+F_{m-2}\left(\eta \right),\eta \in \mathbb{R},m\ge 3$ with $F_1\left(\eta \right)=1,F_2\left(\eta \right)=\eta$, whereas the polynomials introduced by Jacobsthal have the general form $F_m\left(\eta \right)=F_{m-1}\left(\eta \right)+\eta F_{m-2}\left(\eta \right)$, $m\ge 3$ with $F_1\left(\eta \right)=F_2\left(\eta \right)=1$. Later on, Byrd defined another class of Fibonacci polynomials of the form $F_m\left(\eta \right)=2\eta F_{m-1}\left(\eta \right)+F_{m-2}\left(\eta \right),m\ge 2$, where $F_0\left(\eta \right)=0,F_1\left(\eta \right)=1$. Over a couple of decades, some prominent offshoots of the Fibonacci polynomials have appeared in the open literature. For instance, Falcon and Plaza [25] introduced the notion of h-Fibonacci polynomials and studied the derivatives of these polynomials in terms of the convolution of h-Fibonacci polynomials. Mathematically, the $h\left(\eta \right)$-Fibonacci polynomials ${\left\{F_{h,m}\left(\eta \right)\right\}}_{m=0}^{\infty }$ are defined by the recurrence relation $F_{h,m+1}\left(\eta \right)=h\left(\eta \right)F_{h,m}\left(\eta \right)+F_{h,m-1},m\ge 1$, where $F_{h,0}=0$, $F_{h,1}=1$, and $h\left(\eta \right)$ is a polynomial with real coefficients. It is pertinent to mention that for $h\left(\eta \right)=\eta$ and $h\left(\eta \right)=2\eta$, one can obtain the Fibonacci polynomials of the Catalan and Byrd type, respectively [26]. Lee and Asci [27] define another novel generalization of Fibonacci polynomials coined as $(p,q)$-Fibonacci polynomials and obtained several results regarding the factorization of the Pascal matrix involving these polynomials. Such polynomials are defined by the recurrence relation $F_{p,q,m+1}\left(\eta \right)=p\left(\eta \right)F_{p,q,m}\left(\eta \right)+q\left(\eta \right)F_{p,q,m-1},m\ge 1$, where $F_{p,q,0}=0,F_{p,q,1}=1$, and $p\left(\eta \right)$ and $q\left(\eta \right)$ are polynomials with real coefficients. Subsequently, Catarino [28] defined a quaternion analogue of the h-Fibonacci polynomials of the form $Q_{h,m}\left(\eta \right)={\sum }_{l=0}^3{F}_{h,m+l}\left(\eta \right)e_l,$ where $F_{h,m}\left(\eta \right)$ is the $h\left(\eta \right)$-Fibonacci polynomial. Recently, Strzałka et al. [29] introduced a new class of Fibonacci polynomials coined as distance Fibonacci polynomials, which embodies the classical Fibonacci, Jacobsthal, and Narayana polynomials simultaneously. Owing to the nice characteristics of the Fibonacci polynomials, they have been extensively employed for solving differential equations [30], integro-differential equations [31], fractional delay differential equations [32], fractional differential equations [33], and many more.

Fibonacci wavelets are a novel addition to the class of compactly supported wavelets, having the main advantage of being polynomial-based and, as such, enjoying smoothness at the expense of having compact support. In fact, these wavelets are not generated by the orthogonal polynomials; however, the Fibonacci polynomials can be represented in terms of orthogonal Chebychev orthogonal polynomials of the second kind. Unlike the shifted Legendre polynomials, the Fibonacci polynomials possess fewer terms, resulting in faster computation, thus minimizing the computational errors. The Fibonacci wavelets are dependent on two parameters k and M, which increases the rate convergence of the Fibonacci wavelet series. Indeed, the convergence of the Fibonacci wavelet method is faster than the orthogonal wavelet methods and many other numerical methods. Motivated and inspired by the nice characteristics of the Fibonacci wavelets, our goal is to introduce a new numerical technique based on Fibonacci wavelets for obtaining the solution of the non-linear Hunter–Saxton Equation (2). At the outset, the operational matrices of integration associated with Fibonacci wavelets are constructed by following the strategy of Chen and Hsiao [34], then the quasi-linearization technique is implemented to convert the underlying non-linear equation into the linearized form. Finally, the operational matrices of integration are employed to convert the problem under consideration into a system of algebraic equations, which are then solved with any conventional method, such as the Newton method.

The remainder of the article is organized as follows: Section 2 is completely devoted to an elucidation of the Fibonacci wavelet method, including the construction of operational matrices. In Section 3, the proposed method is implemented for solving the non-linear Hunter–Saxton equation. The error and convergence of the proposed method are briefly illustrated in Section 4. In Section 5, the validity and efficiency of the proposed wavelet scheme are demonstrated on certain test problems. The article ends with an epilogue in Section 6.

2. Fibonacci Wavelets and Operational Matrices

In the present section, we first construct the Fibonacci wavelets using the Fibonacci polynomials of degree M, and then, the corresponding operational matrices of integration are formulated by following the strategy of Chen and Hsiao [34]. Towards the end of the section, we shall also discuss the quasi-linearization technique, which plays a vital role in transforming the given non-linear problem into a linear differential equation.

2.1. Fibonacci Wavelets and Function Approximation

For any positive real number $\eta$, the Fibonacci polynomials are defined by the recurrence formula:

$$\begin{array}{c}\hfill F_{m+2}\left(\eta \right)=\eta F_{m+1}\left(\eta \right)+F_m\left(\eta \right),m\in \mathbb{N},\end{array}$$

(6)

with initial conditions $F_0\left(\eta \right)=0,F_1\left(\eta \right)=1$. Generally, the Fibonacci polynomials are defined by

$$\begin{array}{c}\hfill F_{m+1}\left(\eta \right)=\left\{\begin{array}{cc}\hfill 1,\hfill & \hfill m=0\hfill \\ \hfill \eta ,\hfill & \hfill m=1\hfill \\ \hfill \eta F_m\left(\eta \right)+F_{m-1}\left(\eta \right),\hfill & \hfill m\ge 2,\hfill \end{array}\right.,\end{array}$$

(7)

Wavelets constitute an orthonormal family of functions generated from dilations and translations of a fixed function called the “mother wavelet” $\psi \left(\eta \right)$. When the dilation $\alpha$ and translation parameter $\beta$ vary continuously, one can obtain the following family of continuous wavelets [13]:

$$\begin{array}{c}\hfill {\varphi }_{\alpha ,\beta }\left(\eta \right)={\left|\alpha \right|}^{-1/2}\varphi \left({\displaystyle \frac{\eta -\beta }{\alpha }}\right)\alpha ,\beta \in \mathbb{R},\alpha \ne 0\end{array}$$

(8)

If we restrict the parameters $\alpha$ and $\beta$ to discrete values, say $\alpha ={\alpha }_0^{-k},\beta =n{\beta }_0{\alpha }_0^{-k},{\alpha }_0>1,{\beta }_0>0$, for positive integers n and k, we obtain the following family of discrete wavelets:

$$\begin{array}{c}\hfill {\varphi }_{k,n}\left(\eta \right)={\left|{\alpha }_0\right|}^{k/2}\varphi \left({\alpha }_0^k\eta -n{\beta }_0\right).\end{array}$$

(9)

The discrete wavelet family ${\psi }_{k,n}\left(\eta \right)$ forms a wavelet basis for $L^2\left(\mathbb{R}\right)$. Motivated by the above construction, we define the Fibonacci wavelets on the interval $[0,1]$ as [22]:

$$\begin{array}{c}\hfill {\varphi }_{n,m}\left(\eta \right)=\left\{\begin{array}{cc}\hfill {\displaystyle \frac{2^{(k-1)/2}}{\sqrt{S_m}}}{F}_m\left(2^{k-1}\eta -n+1\right),\hfill & \hfill \left({\displaystyle \frac{n-1}{2^{k-1}}}\le \eta <{\displaystyle \frac{n}{2^{k-1}}}\right)\hfill \\ \hfill 0,\hfill & \hfill otherwise,\hfill \end{array}\right.\end{array}$$

(10)

where k and n, respectively, denote the level of resolution and translation with $k=1,2,\dots$, $n=1,2,\dots ,2^{k-1}$. The Fibonacci polynomial $F_m\left(\eta \right)$ of degree m can also be computed as [35]   

$$\begin{array}{c}\hfill F_m\left(\eta \right)=\sum _{i=0}^{\lfloor m/2\rfloor }\left(\genfrac{}{}{0pt}{}{m-i}{i}\right){\eta }^{m-2i},m\ge 0,\end{array}$$

(11)

where $\lfloor ·\rfloor$ is the usual floor function with normalization factor

$$\begin{array}{cc}\hfill S_m& \hfill ={\int }_0^1{\left(F_m\left(\eta \right)\right)}^{2}d\eta ,m=0,1,\dots ,M-1.\hfill \\ \hfill & \hfill =\sum _{i=0}^{\lfloor m/2\rfloor }\sum _{j=0}^{\lfloor m/2\rfloor }\left(\genfrac{}{}{0pt}{}{m-i}{i}\right)\left(\genfrac{}{}{0pt}{}{m-j}{j}\right){\left(2(m-i-j)+1\right)}^{-1}.\hfill \end{array}$$

(12)

If we take $k=2,M=3$, we obtain the following family of Fibonacci wavelets:

$$\begin{array}{c}\hfill \left.\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \hfill & \hfill {\varphi }_{1,0}\left(\eta \right)=\sqrt{2},\hfill \\ \hfill \hfill & \hfill {\varphi }_{1,1}\left(\eta \right)=2\sqrt{6}\eta ,\hfill \\ \hfill \hfill & \hfill {\varphi }_{1,2}\left(\eta \right)=\sqrt{\frac{15}{14}}(1+4{\eta }^2),\hfill \end{array}\right\}\eta \in \left[0,{\displaystyle \frac{1}{2}}\right)\hfill \\ \hfill \left.\begin{array}{cc}\hfill \hfill & \hfill {\varphi }_{2,0}\left(\eta \right)=\sqrt{2},\hfill \\ \hfill \hfill & \hfill {\varphi }_{2,1}\left(\eta \right)=\sqrt{6}(2\eta -1),\hfill \\ \hfill \hfill & \hfill {\varphi }_{2,2}\left(\eta \right)=\sqrt{\frac{30}{7}}\left(2{\eta }^2-2\eta +1\right)\hfill \end{array}\right\}\eta \in \left[{\displaystyle \frac{1}{2}},1\right)\hfill \end{array}\right\}.\end{array}$$

(13)

Any square integrable function $u\left(\eta \right)$ can be approximated via Fibonacci wavelets as

$$\begin{array}{c}\hfill u\left(\eta \right)\approx \sum _{n=1}^{2^{k-1}}\sum _{m=0}^{M-1}{h}_{n,m}{\varphi }_{n,m}\left(\eta \right)\end{array}$$

(14)

where $h_{n,m}$ represents the Fibonacci wavelet coefficients, given by

$$\begin{array}{c}\hfill h_{n,m}=〈u,{\varphi }_{n,m}〉={\int }_0^{1}u\left(\eta \right){\varphi }_{n,m}\left(\eta \right)d\eta .\end{array}$$

(15)

The corresponding matrix form of (14) is given by

$$\begin{array}{c}\hfill U={\mathbf{H}}^T\Phi \left(\eta \right),\end{array}$$

(16)

where $\mathbf{H}$ represents the row vector:

$$\begin{array}{cc}\hfill \mathbf{H}=& \hfill {\left[h_{1,0},\dots ,h_{1,M-1},h_{2,0},\dots ,h_{2,M-1},\dots ,h_{2^{k-1},0},\dots ,h_{2^{k-1},M-1}\right]}^T.\hfill \end{array}$$

(17)

The matrix $\Phi \left(\eta \right)$ appearing in Equation (16) represents the Fibonacci wavelet matrix of order $1\times 2^{k-1}M$ and is given by

$$\begin{array}{cc}\hfill \Phi \left(\eta \right)=& \hfill {\left[{\varphi }_{1,0},\dots ,{\varphi }_{1,M-1},{\varphi }_{2,0},\dots ,{\varphi }_{2,M-1},\dots ,{\varphi }_{2^{k-1},0},\dots ,{\varphi }_{2^{k-1},M-1}\right]}^T.\hfill \end{array}$$

(18)

The wavelet coefficient vector $\mathbf{H}$ can be attained as:

$$\begin{array}{c}\hfill {\mathbf{H}}^T=U{C}^{-1},\end{array}$$

(19)

where

$$\begin{array}{c}\hfill C=〈\Phi ,\Phi 〉={\int }_0^1\Phi \left(\eta \right){\Phi }^T\left(\eta \right)d\eta ,U=\left[u_{n,m}\right],u_{n,m}=〈u,{\varphi }_{n,m}〉\end{array}$$

The following collocation points are considered for obtaining the Fibonacci wavelet approximations:   

$$\begin{array}{c}\hfill {\eta }_{\ell }=\frac{2\ell -1}{2^{k}M},\ell =1,2,\dots ,2^{k-1}M.\end{array}$$

(20)

2.2. Operational Matrices of Integration via Fibonacci Wavelets

This subsection is committed to the construction of the operational matrices of integration associated with Fibonacci wavelets (10) by adopting the Chen and Hsiao technique [34]:

$$\begin{array}{c}\hfill {\int }_0^{\eta }{\Phi }_{n,m}\left(s\right)ds\cong \mathbf{S}{\Phi }_{n,m}\left(\eta \right),\end{array}$$

(21)

where $\mathbf{S}$ denotes the Fibonacci wavelet operational matrix of integration with order $2^{k-1}M\times 2^{k-1}M$.

For the choice $k=2,M=3$, we can integrate (13) at the collocation points given by (20) so that

$$\begin{array}{cc}\hfill & \hfill {\int }_0^{\eta }{\varphi }_{1,0}\left(s\right)ds={\left(0,\frac{\sqrt{3}}{6},0,\frac{1}{2},0,0\right)}^T{\Phi }_{6\times 6}\left(\eta \right)\hfill \\ \hfill & \hfill {\int }_0^{\eta }{\varphi }_{1,1}\left(s\right)ds={\left(-\frac{\sqrt{3}}{4},0,\frac{\sqrt{35}}{10},\frac{\sqrt{3}}{4},0,0\right)}^T{\Phi }_{6\times 6}\left(\eta \right),\hfill \\ \hfill & \hfill {\int }_0^{\eta }{\varphi }_{1,2}\left(s\right)ds={\left(-\frac{29\sqrt{105}}{1680},\frac{\sqrt{35}}{35},{\displaystyle \frac{1}{4}},\sqrt{\frac{5}{21}},0,0\right)}^T{\Phi }_{6\times 6}\left(\eta \right),\hfill \\ \hfill & \hfill {\int }_0^{\eta }{\varphi }_{2,0}\left(s\right)ds={\left(0,0,0,0,\frac{\sqrt{3}}{6},0\right)}^T{\Phi }_{6\times 6}\left(\eta \right)\hfill \\ \hfill & \hfill {\int }_0^{\eta }{\varphi }_{2,1}\left(s\right)ds={\left(0,0,0,-\frac{\sqrt{3}}{4},0,\frac{\sqrt{35}}{10}\right)}^T{\Phi }_{6\times 6}\left(\eta \right),\hfill \\ \hfill & \hfill {\int }_0^{\eta }{\varphi }_{2,2}\left(s\right)ds={\left(0,0,0,-\frac{29\sqrt{105}}{1680},\frac{\sqrt{35}}{35},{\displaystyle \frac{1}{4}}\right)}^T{\Phi }_{6\times 6}\left(\eta \right).\hfill \end{array}$$

Therefore, (21) takes the form

$$\begin{array}{c}\hfill {\int }_0^{\eta }{\Phi }_{6\times 1}\left(s\right)ds\cong {\mathbf{S}}_{6\times 6}{\Phi }_6\left(\eta \right),\end{array}$$

(22)

where

$$\begin{array}{c}\hfill {\mathbf{S}}_{6\times 6}=\left(\begin{array}{cccccc}0& \frac{\sqrt{3}}{6}& 0& \frac{1}{2}& 0& 0\\ -\frac{\sqrt{3}}{4}& 0& \frac{\sqrt{35}}{10}& \frac{\sqrt{3}}{4}& 0& 0\\ -\frac{29\sqrt{105}}{1680}& \frac{\sqrt{35}}{35}& {\displaystyle \frac{1}{4}}& \sqrt{\frac{5}{21}}& 0& 0\\ 0& 0& 0& 0& \frac{\sqrt{3}}{6}& 0\\ 0& 0& 0& -\frac{\sqrt{3}}{4}& 0& \frac{\sqrt{35}}{10}\\ 0& 0& 0& -\frac{29\sqrt{105}}{1680}& \frac{\sqrt{35}}{35}& {\displaystyle \frac{1}{4}}\end{array}\right).\end{array}$$

(23)

2.3. Quasi-Linearization Technique

First introduced by Bellman and Kalaba [36], quasi-linearization is a technique that is essentially a new variant of the well-known Newton–Raphson method, for facilitating the approximate solutions of the non-linear differential equations of degree m. For a clear understanding of this technique, we consider the following differential equation:

$$\begin{array}{cc}\hfill v″\left(\eta \right)& \hfill =f\left(v^{\prime }\left(\eta \right),v\left(\eta \right),\eta \right),\hfill \end{array}$$

(24)

subject to

$$\begin{array}{c}\hfill v\left(\alpha \right)=a,v\left(\beta \right)=b,\alpha \le \eta \le \beta .\end{array}$$

Implementing the quasi-linearization technique leads (24) to the recurrence relations:

$$\begin{array}{cc}\hfill & \hfill v_{r+1}^{″}\left(\eta \right)\hfill \\ \hfill & \hfill =f\left(v_r^{\prime }\left(\eta \right),v_r\left(\eta \right),\eta \right)+\left(v_{r+1}\left(\eta \right)-v_r\left(\eta \right)\right)f_{v_r}\left(v_r^{\prime }\left(\eta \right),v_r\left(\eta \right),\eta \right)+\left(v_{r+1}^{\prime }-v_r^{\prime }\left(\eta \right)\right)f_{v_r^{\prime }}\left(v_r^{\prime }\left(\eta \right),v_r\left(\eta \right),\eta \right),\hfill \end{array}$$

(25)

with condition $v_{r+1}\left(\alpha \right)=a,v_{r+1}\left(\beta \right)=b$.

Subsequently, the recurrence relation for the nth-order non-linear differential equations can be obtained as:

$$\begin{array}{cc}\hfill & \hfill L^n{v}_{r+1}\left(\eta \right)\hfill \\ \hfill & \hfill =f\left(v_r\left(\eta \right),v_r^{\prime }\left(\eta \right),\dots ,v_r^{n-1}\left(\eta \right),\eta \right)+\sum _{l=0}^{n-1}\left(v_{r+1}^l\left(\eta \right)-v_r^l(\left(\eta \right)\right)f_{v^l}\left(v_r\left(\eta \right),v_r^{\prime }\left(\eta \right),\dots ,v_r^{n-1}\left(\eta \right),\eta \right),\hfill \end{array}$$

(26)

with the same conditions. Equation (26) is the desired linear differential equation, which can be recursively solved for $v_{r+1}\left(\eta \right)$ from $v_r\left(\eta \right)$.

3. Method of Solution

In this section, we shall employ the operational matrices of integration based on Fibonacci wavelets as discussed in Section 2 for the numerical treatment of the non-linear Hunter–Saxton Equation (2). To begin with, we recall the non-linear Hunter–Saxton equation:

$$\begin{array}{c}\hfill {\displaystyle \frac{{\partial }^{2}u(\eta ,\zeta )}{\partial \eta \partial t}}+u(\eta ,\zeta ){\displaystyle \frac{{\partial }^{2}u(\eta ,\zeta )}{\partial {\eta }^2}}+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\partial u(\eta ,\zeta )}{\partial \eta }}\right)}^2=0,\end{array}$$

(27)

with initial condition and boundary conditions:

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \begin{array}{c}\hfill \end{array}& \hfill u(\eta ,0)=f_0\left(\eta \right),{\displaystyle \frac{\partial u(\eta ,0)}{\partial \zeta }}=f_1\left(\eta \right)0\le \eta \le 1\hfill \\ \hfill & \hfill u(0,\zeta )=g_0\left(\zeta \right),{\displaystyle \frac{\partial u(0,\zeta )}{\partial \eta }}=g_1\left(\zeta \right),0<t\le 1,\hfill \end{array}\right\}\end{array}$$

(28)

where $f_0,f_1,g_0$, and $g_1$ possess second-order continuous derivative and belong to $L^2[0,1)$. Following the quasi-linearization technique as discussed in the previous section, Relation (27) is transformed to a linear differential equation as

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^2{u}_{r+1}(\eta ,\zeta )}{\partial \eta \partial \zeta }}& \hfill +u_{r+1}(\eta ,\zeta ){\displaystyle \frac{{\partial }^2{u}_r(\eta ,\zeta )}{\partial {\eta }^2}}+{\displaystyle \frac{\partial u_r(\eta ,\zeta )}{\partial \eta }}{\displaystyle \frac{\partial u_{r+1}(\eta ,\zeta )}{\partial \eta }}+{\displaystyle \frac{\partial f_r(\eta ,\zeta )}{\partial \eta }}{\displaystyle \frac{{\partial }^2{f}_{r+1}(\eta ,\zeta )}{\partial {\eta }^2}}\hfill \\ \hfill & \hfill -{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\partial f_r(\eta ,\zeta )}{\partial \eta }}\right)}^2-{\displaystyle \frac{{\partial }^2{f}_r(\eta ,\zeta )}{\partial {\eta }^2}}{f}_r(\eta ,\zeta )=0.\hfill \end{array}$$

(29)

with initial guess $u_0(\eta ,\zeta )=f_0\left(\eta \right)+\zeta f_1\left(\eta \right)$. In order to solve (31), we approximate the highest partial derivative appearing in (29) by the Fibonacci wavelet basis as

$$\begin{array}{c}\hfill {\displaystyle \frac{{\partial }^{3}u(\eta ,\zeta )}{\partial {\eta }^2\partial \zeta }}=\sum _{\ell =0}^{2^{k-1}M}{h}_{\ell }\varphi \left(\eta \right)={\mathbf{H}}^T\Phi \left(\eta \right),\end{array}$$

(30)

where $\mathbf{H}$ is the unknown wavelet coefficient vector given by (17) to be determined. Integrating (30) with respect to $\zeta$ between limits ${\zeta }_s$ and $\zeta$ yields

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^{2}u(\eta ,\zeta )}{\partial {\eta }^2}}& \hfill =(\zeta -{\zeta }_s)\sum _{i=0}^{2^{k-1}M}{h}_{\ell }\varphi \left(\eta \right)+{\displaystyle \frac{{\partial }^{2}u(\eta ,{\zeta }_s)}{\partial {\eta }^2}}\hfill \\ \hfill & \hfill =(\zeta -{\zeta }_s){\mathbf{H}}^T{\Phi }_{\ell }+{\displaystyle \frac{{\partial }^{2}u(\eta ,{\zeta }_s)}{\partial {\eta }^2}}.\hfill \end{array}$$

(31)

Integrating (31) with respect to $\eta$ between the limits 0 and $\eta$, we obtain

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial u(\eta ,\zeta )}{\partial \eta }}=(\zeta -{\zeta }_s)\sum _{i=0}^{2^{k-1}M}{h}_{\ell }{\mathbf{S}}_{\ell ,1}\left(\eta \right)+{\displaystyle \frac{\partial u(\eta ,{\zeta }_s)}{\partial \eta }}-{\displaystyle \frac{\partial u(0,{\zeta }_s)}{\partial \eta }}+{\displaystyle \frac{\partial u(0,\zeta )}{\partial \eta }}.\end{array}$$

(32)

Again, integrating (32) with respect to $\eta$ between the limits 0 and $\eta$ yields

$$\begin{array}{c}\hfill u(\eta ,\zeta )=(\zeta -{\zeta }_s)\sum _{i=0}^{2^{k-1}M}{h}_{\ell }{\mathbf{S}}_{\ell ,2}\left(\eta \right)+u(\eta ,{\zeta }_s)-u(0,{\zeta }_s)+\eta \left({\displaystyle \frac{\partial u(0,\zeta )}{\partial \eta }}-{\displaystyle \frac{\partial u(0,{\zeta }_s)}{\partial \eta }}\right)+u(0,\zeta ).\end{array}$$

(33)

Differentiating (33) with respect to $\zeta$, we have

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial u(\eta ,\zeta )}{\partial \zeta }}=\sum _{i=0}^{2^{k-1}M}{h}_{\ell }{\mathbf{S}}_{\ell ,2}\left(\eta \right)+\eta {\displaystyle \frac{{\partial }^{2}u(0,\zeta )}{\partial \zeta \partial \eta }}+{\displaystyle \frac{\partial u(0,\zeta )}{\partial \zeta }}.\end{array}$$

(34)

Next, we differentiate (34) with respect to $\eta$ to obtain

$$\begin{array}{c}\hfill {\displaystyle \frac{{\partial }^{2}u(\eta ,\zeta )}{\partial \eta \partial \zeta }}=\sum _{i=0}^{2^{k-1}M}{h}_{\ell }{\mathbf{S}}_{\ell ,1}\left(\eta \right)+{\displaystyle \frac{{\partial }^{2}u(0,\zeta )}{\partial \eta \partial \zeta }}.\end{array}$$

(35)

By employing the initial and boundary conditions (28) and $\zeta \to {\zeta }_{s+1}$ with $\Delta \zeta ={\zeta }_{s+1}-{\zeta }_s$, Equations (31)–(34) take the form

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \begin{array}{c}\hfill {\displaystyle \frac{{\partial }^{2}u(\eta ,{\zeta }_{s+1})}{\partial {\eta }^2}}\end{array}& \hfill =\Delta \zeta {\mathbf{H}}^T{\Phi }_{\ell }+{\displaystyle \frac{{\partial }^{2}u(\eta ,{\zeta }_s)}{\partial {\eta }^2}},\hfill \\ \hfill {\displaystyle \frac{\partial u(\eta ,{\zeta }_{s+1})}{\partial \eta }}& \hfill =\Delta \zeta {\mathbf{H}}^T{\mathbf{S}}_1\left(\eta \right)+{\displaystyle \frac{\partial u(\eta ,{\zeta }_s)}{\partial \eta }}+g_1\left({\zeta }_{s+1}\right)-g_1\left({\zeta }_s\right),\hfill \\ \hfill {\displaystyle \frac{\partial u(\eta ,{\zeta }_{s+1})}{\partial \zeta }}& \hfill ={\mathbf{H}}^T{\mathbf{S}}_2\left(\eta \right)+\eta {\displaystyle \frac{\partial g_1\left({\zeta }_{s+1}\right)}{\partial \zeta }}+g_1\left({\zeta }_{s+1}\right),\hfill \\ \hfill {\displaystyle \frac{{\partial }^{2}u(\eta ,{\zeta }_{s+1})}{\partial \eta \partial \zeta }}& \hfill ={\mathbf{H}}^T{\mathbf{S}}_1\left(\eta \right)+{\displaystyle \frac{\partial g_1\left({\zeta }_{s+1}\right)}{\partial \zeta }}\hfill \end{array}\right\}\end{array}$$

(36)

$$\begin{array}{cc}\hfill u(\eta ,{\zeta }_{s+1})& \hfill =\Delta \zeta {\mathbf{H}}^T{\mathbf{S}}_2\left(\eta \right)+u(\eta ,{\zeta }_s)+\eta \left(g_1\left({\zeta }_{s+1}\right)-g_1\left({\zeta }_s\right)\right)+g_0({\zeta }_s+1)-g_0\left({\zeta }_s\right)\hfill \end{array}$$

(37)

By implementing (36), we obtain the following system of algebraic equations:

$$\begin{array}{cc}\hfill & \hfill {\mathbf{H}}^T{\mathbf{S}}_1\left(\eta \right)+\Delta \zeta {\displaystyle \frac{\partial u(\eta ,{\zeta }_s)}{\partial {\eta }^2}}{\mathbf{H}}^T{\mathbf{S}}_2\left(\eta \right)+\Delta \zeta {\displaystyle \frac{\partial u(\eta ,{\zeta }_s)}{\partial \eta }}{\mathbf{H}}^T{\mathbf{S}}_1\left(\eta \right)+\Delta \zeta u(\eta ,{\zeta }_s){\mathbf{H}}^T{\Phi }_{\ell }\hfill \\ \hfill & \hfill ={\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\partial u(\eta ,{\zeta }_s)}{\partial \eta }}\right)}^2+{\displaystyle \frac{{\partial }^{2}f(\eta ,{\zeta }_s)}{\partial {\eta }^2}}u(\eta ,{\zeta }_s)-{\displaystyle \frac{\partial g_1\left({\zeta }_{s+1}\right)}{\partial \zeta }}+u(\eta ,{\zeta }_s){\displaystyle \frac{{\partial }^{2}u(\eta ,{\zeta }_s)}{\partial {\eta }^2}}\hfill \\ \hfill & \hfill {\displaystyle \frac{{\partial }^{2}u(\eta ,{\zeta }_s)}{\partial {\eta }^2}}\left\{u(\eta ,{\zeta }_s)+\eta \left(g_1\left({\zeta }_{s+1}\right)-g_1\left({\zeta }_s\right)\right)+g_0\left({\zeta }_{s+1}\right)-g_0\left({\zeta }_s\right)\right\}\hfill \\ \hfill & \hfill +{\displaystyle \frac{\partial u(\eta ,{\zeta }_s)}{\partial \eta }}\left\{{\displaystyle \frac{\partial u(\eta ,{\zeta }_s)}{\partial \eta }}+g_1\left({\zeta }_{s+1}\right)-g_1\left({\zeta }_s\right)\right\}.\hfill \end{array}$$

(38)

Solving the system of algebraic Equation (38) at the collocation points (20) with the avail of Newton’s method in the MATLAB software, we can ascertain the Fibonacci coefficients, and thereafter, superseding the unknown coefficients in (37) yields the approximate solution of the Hunter–Saxton Equation (27) via the Fibonacci wavelet method.

4. Error Estimation and Convergence Analysis

This section is entirely devoted to study the error bounds and convergence results associated with the Fibonacci wavelet method.

Theorem 1.

Let $u^{*}\left(\eta \right)={\sum }_{n=1}^{2^{k-1}}{\sum }_{m=0}^{M-1}{h}_{n,m}{\varphi }_{n,m}\left(\eta \right)$ be the Fibonacci wavelet expansion of any sufficiently smooth real-valued function $u\left(\eta \right)$ belonging to the space $C^M[0,1)$. Then, the norm truncated error $e\left(\eta \right)$ is given by

$$\begin{array}{c}\hfill \parallel e\left(\eta \right){\parallel }_2=\parallel u-u^{*}{\parallel }_2\le {\displaystyle \frac{R}{M!\sqrt{2M+1}}}\end{array}$$

(39)

where $R={max}_{s\in [0,1)}\left|u^M\left(\eta \right)\right|.$

Proof. 

$\{1,\eta ,\dots ,{\eta }^{M-1}\}$ constitute a basis for the polynomial space of degree M. Therefore, the Taylor expansion of any $\widehat{u}\left(\eta \right)$ can be expressed as

$$\begin{array}{c}\hfill \widehat{u}\left(\eta \right)=u\left(0\right)+\eta u^{\prime }\left(0\right)+{\displaystyle \frac{{\eta }^2}{2!}}{u}^{\left(2\right)}\left(0\right)+\dots +{\displaystyle \frac{{\eta }^{M-1}}{(M-1)!}}{u}^{(M-1)}\left(0\right).\end{array}$$

From the above expansion, one can obtain

$$\begin{array}{c}\hfill |u\left(\eta \right)-\widehat{u}\left(\eta \right)|={\displaystyle \frac{u^{\left(M\right)}\left(s\right){\eta }^M}{M!}},s\in [0,1).\end{array}$$

(40)

As the interval $[0,1)$ can be divided into sub-intervals of the form $I_{n,k}=\left[\frac{(n-1)}{2^{k-1}},\frac{n}{2^{k-1}}\right)$, therefore, by virtue of (40), we obtain

$$\begin{array}{cc}\hfill \parallel u-u^{*}{\parallel }_{L^2[0,1]}^2& \hfill =\parallel u-C^T\Phi {\parallel }_{L^2[0,1]}^2\hfill \\ \hfill & \hfill =\sum _{n=1}^{2^{k-1}}\parallel u-A^T\widehat{F}{\parallel }_{I_{n,k}}^2\hfill \\ \hfill & \hfill \le \sum _{n=1}^{2^{k-1}}\parallel u-u^{*}{\parallel }_{I_{n,k}}^2\hfill \\ \hfill & \hfill \le \sum _{n=1}^{2^{k-1}}{\int }_{I_n,k}{\left[u\left(\eta \right)-u^{*}\left(\eta \right)\right]}^{2}d\eta \hfill \\ \hfill & \hfill \le \sum _{n=1}^{2^{k-1}}{\int }_{I_n,k}{\left({\displaystyle \frac{{\eta }^{M}ma{x}_{x\in I_{n,k}}\left|u^M\left(s\right)\right|}{M!}}\right)}^{2}d\eta \hfill \\ \hfill & \hfill \le {\int }_0^1{\left({\displaystyle \frac{{\eta }^{M}ma{x}_{x\in I_{n,k}}\left|u^M\left(s\right)\right|}{M!}}\right)}^{2}d\eta \hfill \\ \hfill & \hfill ={\displaystyle \frac{R^2}{M{!}^2\sqrt{2M+1}}},\hfill \end{array}$$

where $\widehat{F}\left(\eta \right)={\left[F_0\left(\eta \right),F_1\left(\eta \right),\dots ,F_{M-2}\left(\eta \right),F_{M-1}\left(\eta \right)\right]}^T$ and $R={max}_{s\in [0,1)}\left|u^M\left(\eta \right)\right|$. Hence, $\parallel e\left(\eta \right)\parallel \to 0\mathrm{as}M\to \infty$. This completes the proof of Theorem 1.    □

Theorem 2.

Let $u\left(\eta \right)$ be a bounded continuous function in $L^2[0,1)$ with bound $\tilde{M}$. Then, the Fibonacci wavelet expansion given by (14) converges uniformly to $u\left(\eta \right)$ with

$$\begin{array}{c}\hfill \left|h_{n,m}\right|<{\displaystyle \frac{\tilde{M}\delta r}{2^{k-1/2}{2}^m}},\delta =\frac{1}{\sqrt{S_m}}.\end{array}$$

(41)

Proof. 

$u\left(\eta \right)\in L^2[0,1)$ can be approximated by the Fibonacci wavelets as

$$\begin{array}{c}\hfill u\left(\eta \right)\approx \sum _{n=1}^{2^{k-1}}\sum _{m=0}^{M-1}{h}_{n,m}{\varphi }_{n,m}\left(\eta \right),\end{array}$$

where

$$\begin{array}{cc}\hfill h_{n,m}& \hfill =〈u,{\varphi }_{n,m}〉\hfill \\ \hfill & \hfill ={\int }_0^{1}u\left(\eta \right){\varphi }_{n,m}\left(\eta \right)d\eta \hfill \\ \hfill & \hfill ={\int }_{\frac{(n-1)}{2^{k-1}}}^{\frac{n}{2^{k-1}}}u\left(\eta \right){\varphi }_{n,m}\left(\eta \right)d\eta \hfill \\ \hfill & \hfill =2^{k-1}\delta {\int }_{\frac{(n-1)}{2^{k-1}}}^{\frac{n}{2^{k-1}}}u\left(\eta \right)F_m(2^{k-1}\eta -n+1)d\eta .\hfill \end{array}$$

By taking $2^{k-1}\eta -n+1=t$, we obtain

$$\begin{array}{c}\hfill h_{n,m}={\displaystyle \frac{\delta }{2^{k-1}}}{\int }_0^{1}u\left({\displaystyle \frac{t+n-1}{2^{k-1}}}\right)F_m\left(t\right)dt.\end{array}$$

Consequently, we obtain

$$\begin{array}{cc}\hfill |h_{n,m}|& \hfill ={\displaystyle \frac{\delta }{2^{k-1}}}{\int }_0^1\left|u\left({\displaystyle \frac{t+n-1}{2^{k-1}}}\right)\right|\left|F_m\left(t\right)\right|dt\hfill \\ \hfill & \hfill \le {\displaystyle \frac{\delta }{2^{k-1}}}\tilde{M}{\int }_0^1\left|F_m\left(t\right)\right|dt.\hfill \end{array}$$

(42)

Applying the property of Fibonacci polynomials, we have

$$\begin{array}{c}\hfill {\int }_0^1\left|F_m\left(t\right)\right|dt\le {\displaystyle \frac{r}{2^m}},\end{array}$$

(43)

where r is a constant. Therefore, (42) becomes

$$\begin{array}{c}\hfill \left|h_{n,m}\right|<{\displaystyle \frac{\tilde{M}\delta r}{2^{k-1/2}{2}^m}},\end{array}$$

Thus, we conclude that ${\sum }_{n=1}^{2^k-1}{\sum }_{m=0}^{M-1}{h}_{n,m}$ converges absolutely provided $k,m\to \infty$, and hence, the Fibonacci wavelet series given by (14) converges uniformly to $u\left(\eta \right)$.    □

Towards the culmination, we provide an Algorithm 1 of the Fibonacci wavelet method to obtain a numerical solution of the Hunter-Saxton Equation (27).

Algorithm 1: Algorithm for the proposed Fibonacci wavelet method

Input: The level of resolution $k=1,2,\dots$ and $m=0,1,\dots ,M-1$, $0\le \eta \le 1$. Define the Fibonacci wavelet ${\varphi }_{n,m}\left(\eta \right)$ by Equation (10). Construct the vector $\Phi \left(\eta \right)$ from (18). Construct the Fibonacci wavelet basis matrix $\Phi \left(\eta \right)$ using collocation points (20). Compute the operational matrices of integration ${\mathbf{S}}_1$ and ${\mathbf{S}}_2$. Define unknown coefficient vectors $\mathbf{H}=[{\mathbf{h}}_{\mathbf{1},\mathbf{0}},\dots ,{\mathbf{h}}_{\mathbf{1},\mathbf{M}-\mathbf{1}},{\mathbf{h}}_{\mathbf{2},\mathbf{0}},\dots ,{\mathbf{h}}_{\mathbf{2},\mathbf{M}-\mathbf{1}},\dots ,$${\mathbf{h}}_{{\mathbf{2}}^{\mathbf{k}-\mathbf{1}},\mathbf{0}},\dots ,{\mathbf{h}}_{{\mathbf{2}}^{\mathbf{k}-\mathbf{1}},\mathbf{M}-\mathbf{1}}{]}^{\mathbf{T}}.$ Convert the given problem (2) into a linearized differential equation by using the quasi-linearization technique. Approximate the highest time derivative function in (29) by Fibonacci wavelets. Establish the system of algebraic equations (38). Solve the system of algebraic equations in the previous step by any classical method or the fsolve command in the MATLAB software. Substitute the obtained wavelet coefficients $\mathbf{H}$ into (37). The approximate solution $u(\eta ,\zeta )$ on $[0,1]$.

5. Numerical Examples and Discussion

This section constitutes the centerpiece of this article: the operational matrices of integration as constructed in Section 2 based on the Fibonacci wavelets are utilized for obtaining the approximate solution of the non-linear Hunter–Saxton Equation (27) under certain initial and boundary conditions. To facilitate the narrative, we take into account some examples whose exact solutions are available in the open literature. This allows us to compare the obtained results with exact solutions and the solutions acquired through other numerical techniques. The accuracy of the proposed method is determined by the absolute error:

$$\begin{array}{c}\hfill E_{abs}=|u(\eta ,\zeta )-u_{n,m}(\eta ,\zeta )|,\end{array}$$

(44)

where $u(\eta ,\zeta )$ and $u_{n,m}(\eta ,\zeta )$, respectively, denote the exact and approximate solutions.

Example 1.

Consider Equation (29) subject to the initial condition:

$$\begin{array}{c}\hfill u(\eta ,0)=2\eta ,{\displaystyle \frac{\partial u(\eta ,0)}{\partial \zeta }}=-2\eta ,0\le \eta \le 1,\end{array}$$

(45)

and the boundary condition:

$$\begin{array}{c}\hfill u(0,\zeta )=0,{\displaystyle \frac{\partial u(0,\zeta )}{\partial \eta }}={\displaystyle \frac{2}{1+\zeta }},0<\zeta \le 1.\end{array}$$

(46)

The analytic solution of the problem (29) with respect to the initial and boundary conditions (45) and (46) is

$$\begin{array}{c}\hfill u(\eta ,\zeta )={\displaystyle \frac{2\eta }{1+\zeta }}.\end{array}$$

(47)

The initial guess is given by

$$\begin{array}{c}\hfill f_0(\eta ,\zeta )=2\eta -2\zeta \eta .\end{array}$$

(48)

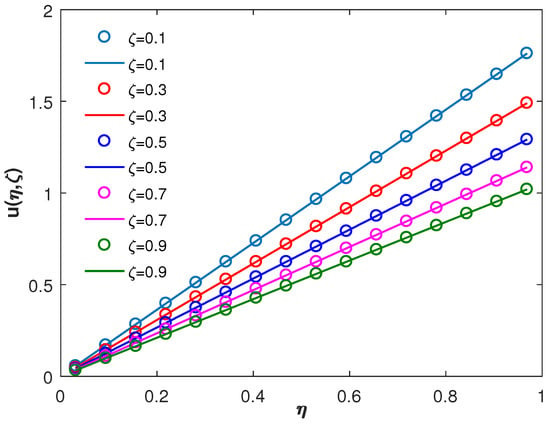
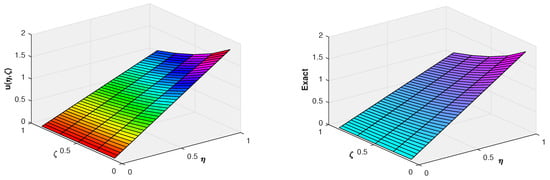
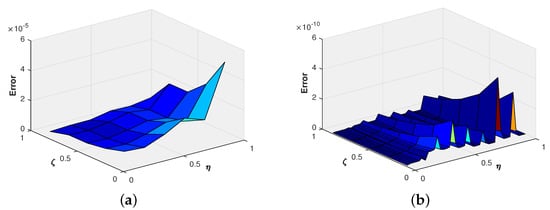
The comparison of the exact solution and the approximate solution for $k=3,M=4$ and $k=4,M=5$ is depicted in Figure 1 and Figure 2, respectively. From Figure 3, the absolute error for $k=2,M=3$ and $k=4,M=5$ is represented via three-dimensional plots, from which we infer that as we increase the wavelet parameters k and M, the absolute error decreases. To show the legitimacy of the proposed method, we compare the obtained absolute error with the absolute error of the trigonometric B-spline [9] and the Haar wavelet methods [23] in

Table 1. Comparison of the proposed method’s absolute error with the HWM and B-spline methods of Example 1 for $\zeta$ = 0.1.

$\mathit{\eta }$	Present Method	Haar Wavelet Method [23]	B-Spline [9]
0.1	$1.1052\times {10}^{-11}$	$1.00\times {10}^{-11}$	$5.0871\times {10}^{-8}$
0.2	$4.5815\times {10}^{-11}$	$5.00\times {10}^{-11}$	$5.8416\times {10}^{-8}$
0.3	$4.5253\times {10}^{-11}$	$7.00\times {10}^{-11}$	$7.1641\times {10}^{-8}$
0.4	$6.6008\times {10}^{-11}$	$1.10\times {10}^{-9}$	$5.9301\times {10}^{-8}$
0.5	$1.6400\times {10}^{-11}$	$2.00\times {10}^{-10}$	$5.8624\times {10}^{-8}$
0.6	$1.4383\times {10}^{-11}$	$4.00\times {10}^{-10}$	$5.7901\times {10}^{-8}$
0.7	$5.5616\times {10}^{-12}$	$4.00\times {10}^{-10}$	$7.4068\times {10}^{-9}$
0.8	$1.2655\times {10}^{-11}$	$4.00\times {10}^{-10}$	$4.5148\times {10}^{-9}$
0.9	$3.9552\times {10}^{-11}$	$4.00\times {10}^{-10}$	$1.5287\times {10}^{-9}$

,

Table 2. Comparison of the proposed method’s absolute error with the HWM and B-spline methods of Example 1 for $\zeta$ = 0.01.

$\mathit{\eta }$	Present Method	Haar Wavelet Method [23]	B-Spline [9]
0.1	$4.0590\times {10}^{-13}$	$7.36\times {10}^{-9}$	$7.3711\times {10}^{-10}$
0.2	$2.0500\times {10}^{-12}$	$5.21\times {10}^{-8}$	$5.3433\times {10}^{-9}$
0.3	$1.6620\times {10}^{-12}$	$6.91\times {10}^{-8}$	$9.6802\times {10}^{-9}$
0.4	$2.4243\times {10}^{-12}$	$8.88\times {10}^{-7}$	$8.2694\times {10}^{-9}$
0.5	$6.0234\times {10}^{-12}$	$9.16\times {10}^{-7}$	$8.1740\times {10}^{-9}$
0.6	$5.2824\times {10}^{-13}$	$9.46\times {10}^{-7}$	$8.0728\times {10}^{-9}$
0.7	$1.3101\times {10}^{-13}$	$1.85\times {10}^{-6}$	$1.0326\times {10}^{-9}$
0.8	$4.6474\times {10}^{-13}$	$1.88\times {10}^{-6}$	$6.2946\times {10}^{-10}$
0.9	$4.4524\times {10}^{-12}$	$1.91\times {10}^{-6}$	$2.1314\times {10}^{-10}$

and

Table 3. Comparison of the proposed method’s absolute error with the HWM and B-spline methods of Example 1 for $\zeta$ = 0.001.

$\mathit{\eta }$	Present Method	Haar Wavelet Method [23]	B-Spline [9]
0.1	$1.4482\times {10}^{-11}$	$4.61\times {10}^{-6}$	$7.6083\times {10}^{-12}$
0.2	$7.3141\times {10}^{-11}$	$3.43\times {10}^{-5}$	$6.7013\times {10}^{-11}$
0.3	$5.9300\times {10}^{-11}$	$5.40\times {10}^{-5}$	$1.7831\times {10}^{-10}$
0.4	$8.6497\times {10}^{-11}$	$6.35\times {10}^{-4}$	$8.4624\times {10}^{-10}$
0.5	$2.1490\times {10}^{-11}$	$6.56\times {10}^{-4}$	$8.3696\times {10}^{-10}$
0.6	$1.8847\times {10}^{-11}$	$6.78\times {10}^{-4}$	$8.3225\times {10}^{-10}$
0.7	$4.6660\times {10}^{-12}$	$1.32\times {10}^{-3}$	$1.0256\times {10}^{-11}$
0.8	$1.6583\times {10}^{-11}$	$1.34\times {10}^{-3}$	$6.2168\times {10}^{-11}$
0.9	$5.1833\times {10}^{-11}$	$1.37\times {10}^{-3}$	$2.0828\times {10}^{-11}$

for different values of ζ, from which one can easily infer that the results achieved through the Fibonacci wavelets are reasonably effective in comparison to the other existing numerical methods.

Example 2.

Consider Equation (29) subject to the initial conditions:

$$\begin{array}{c}\hfill u(\eta ,0)={\left(2+3\eta \right)}^{2/3}+2\eta +2,{\displaystyle \frac{\partial u(\eta ,0)}{\partial \zeta }}=2\eta +{\displaystyle \frac{2\eta }{{\left(3\eta +2\right)}^{1/3}}},0\le \eta \le 1,\end{array}$$

(49)

and the boundary conditions:

$$\begin{array}{c}\hfill u(0,\zeta )={\displaystyle \frac{2^{2/3}+2}{{\left(1+\zeta \right)}^2}},{\displaystyle \frac{\partial u(0,\zeta )}{\partial \eta }}={\displaystyle \frac{2^{2/3}\left(\zeta +2^{1/3}(\zeta +1)+1\right)}{{(1+\zeta )}^2}},0<\zeta \le 1.\end{array}$$

(50)

The analytic solution of the problem (29) together with the initial and boundary conditions (49) and (50) is

$$\begin{array}{c}\hfill u(\eta ,\zeta )={\displaystyle \frac{{\left(2+3\eta (1+\zeta )\right)}^{2/3}+2\eta (1+\zeta )+2}{{\left(1+\zeta \right)}^2}}.\end{array}$$

(51)

The initial guess is given by

$$\begin{array}{c}\hfill u_0(\eta ,\zeta )={\left(2+3\eta \right)}^{2/3}+2\eta +2+\zeta \left(2\eta +{\displaystyle \frac{2\eta }{{\left(3\eta +2\right)}^{1/3}}}\right).\end{array}$$

(52)

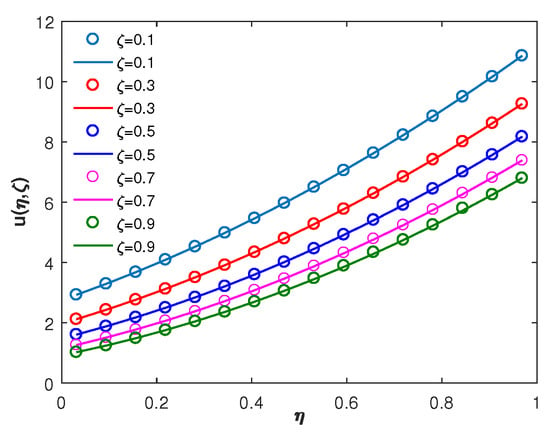
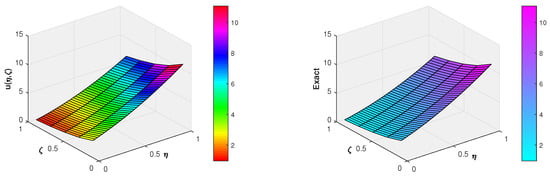
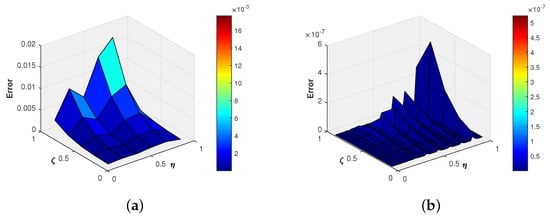
Figure 4 and Figure 5 depict the graphical comparison of the proposed method with the exact solution for $k=3,M=4$ and $k=4,M=5$, respectively, which suggests that the Fibonacci wavelets are in good agreement with the analytic solution of the problem. Moreover, in Figure 6, the absolute error for different $k=2,M=3$ and $k=4,M=5$ is shown via a three-dimensional plot, which elucidates that, upon increasing the wavelet parameters k and M, the absolute error decreases. Finally, a comparison of the absolute error of the proposed method with the trigonometric B-spline [9] and the Laguerre wavelet methods [24] is given in

Table 4. Comparison of the proposed method’s absolute error with the HWM and B-spline methods of Example 2 for $\zeta$ = 0.1.

$\mathit{\eta }$	Present Method	Laguerre Wavelet Method [24]	B-Spline [9]
0.1	$1.0628\times {10}^{-10}$	$1.8010\times {10}^{-10}$	$1.3312\times {10}^{-9}$
0.2	$4.0301\times {10}^{-10}$	$1.5112\times {10}^{-10}$	$5.7990\times {10}^{-9}$
0.3	$2.5753\times {10}^{-10}$	$3.9270\times {10}^{-9}$	$1.0590\times {10}^{-8}$
0.4	$2.5521\times {10}^{-10}$	$1.4702\times {10}^{-8}$	$5.6427\times {10}^{-7}$
0.5	$1.1001\times {10}^{-9}$	$1.6749\times {10}^{-8}$	$5.4550\times {10}^{-7}$
0.6	$2.2703\times {10}^{-11}$	$1.9008\times {10}^{-8}$	$5.3513\times {10}^{-7}$
0.7	$1.9953\times {10}^{-10}$	$3.5397\times {10}^{-8}$	$5.8207\times {10}^{-8}$
0.8	$2.1422\times {10}^{-10}$	$8.8317\times {10}^{-8}$	$3.5256\times {10}^{-8}$
0.9	$1.0988\times {10}^{-9}$	$2.4388\times {10}^{-8}$	$1.1877\times {10}^{-8}$

,

Table 5. Comparison of the proposed method’s absolute error with the HWM and B-spline methods of Example 2 for $\zeta$ = 0.01.

$\mathit{\eta }$	Present Method	Laguerre Wavelet Method [24]	B-Spline [9]
0.1	$8.8795\times {10}^{-11}$	$2.5810\times {10}^{-10}$	$3.8198\times {10}^{-9}$
0.2	$3.3756\times {10}^{-10}$	$3.9875\times {10}^{-10}$	$8.6529\times {10}^{-8}$
0.3	$2.2081\times {10}^{-10}$	$2.6958\times {10}^{-9}$	$8.0389\times {10}^{-8}$
0.4	$2.4009\times {10}^{-10}$	$7.1080\times {10}^{-9}$	$3.2713\times {10}^{-8}$
0.5	$6.3429\times {10}^{-10}$	$8.9865\times {10}^{-9}$	$8.1837\times {10}^{-8}$
0.6	$1.9034\times {10}^{-11}$	$2.0586\times {10}^{-10}$	$8.7400\times {10}^{-9}$
0.7	$1.4141\times {10}^{-10}$	$2.4610\times {10}^{-9}$	$9.4588\times {10}^{-9}$
0.8	$1.6486\times {10}^{-10}$	$1.5601\times {10}^{-9}$	$5.7392\times {10}^{-9}$
0.9	$7.0159\times {10}^{-10}$	$8.6593\times {10}^{-9}$	$1.9343\times {10}^{-9}$

and

Table 6. Comparison of the proposed method’s absolute error with the HWM and B-spline methods of Example 2 for $\zeta$ = 0.001.

$\mathit{\eta }$	Present Method	Laguerre Wavelet Method [24]	B-Spline [9]
0.1	$8.7724\times {10}^{-11}$	$1.3562\times {10}^{-10}$	$7.2964\times {10}^{-9}$
0.2	$3.3357\times {10}^{-10}$	$5.3152\times {10}^{-10}$	$6.1501\times {10}^{-9}$
0.3	$2.1867\times {10}^{-10}$	$8.2561\times {10}^{-10}$	$7.0557\times {10}^{-9}$
0.4	$2.3968\times {10}^{-10}$	$1.0520\times {10}^{-10}$	$8.9905\times {10}^{-9}$
0.5	$6.0037\times {10}^{-10}$	$1.3694\times {10}^{-10}$	$8.8754\times {10}^{-9}$
0.6	$1.9034\times {10}^{-11}$	$2.0586\times {10}^{-10}$	$8.7400\times {10}^{-9}$
0.7	$1.3737\times {10}^{-10}$	$6.2059\times {10}^{-11}$	$9.9712\times {10}^{-10}$
0.8	$1.6157\times {10}^{-10}$	$1.2536\times {10}^{-11}$	$6.0609\times {10}^{-10}$
0.9	$6.7317\times {10}^{-10}$	$1.8010\times {10}^{-10}$	$2.0468\times {10}^{-10}$

for different values of ζ. From these tables, we conclude that the proposed method is more accurate than the other existing numerical methods.

6. Conclusions and Future Work

In the present paper, we formulated a new and efficient collocation method based on the Fibonacci wavelets for obtaining the numerical solution of the non-linear Hunter–Saxton equation. The efficacy of the proposed method was demonstrated via certain test problems. The absolute error due to the proposed scheme was compared with the absolute error of the trigonometric B-spline method, Laguerre wavelet method, and Haar wavelet method. In conclusion, we inferred that the proposed wavelet-based numerical technique yields a much more stable solution and a better approximation than the existing ones. The present work can be extended across diverse fields of physical and biological sciences, in particular obtaining the solution of higher-dimensional time-fractional differential equations.