Solving the Container Relocation Problem by Using a Metaheuristic Genetic Algorithm

Abstract

Maritime transport is the backbone of international trade of goods. Therefore, seaports are of great importance for maritime transport. Container transport plays an important role in maritime transport and is increasing year by year. Containers transported to a container terminal are stored in container yards side by side and on top of each other, forming blocks. If a container that is not on top of the block has to be retrieved, the containers that are above the required container must be relocated before the required container is retrieved. These additional container relocations, which block the retrieval of the required container, slow down the entire retrieval process. The container relocation problem, also known as the block relocation problem, is an optimization problem that involves finding an optimal sequence of operations for retrieving blocks (containers) from a container yard in a given order, minimizing additional relocations of blocking containers. In this paper, the focus is on the two-dimensional, static, offline and the restricted container relocation problem of real-size yard container bays. A new method for resolving the container relocation problem that uses a genetic algorithm is proposed to minimize the number of relocations within the bay. The method is evaluated on well-known test instances, and the obtained results are compared with the results of various relevant models for resolving the container relocation problem. The results show that the proposed method achieves the best or the second-best result for each test instance within the test set.

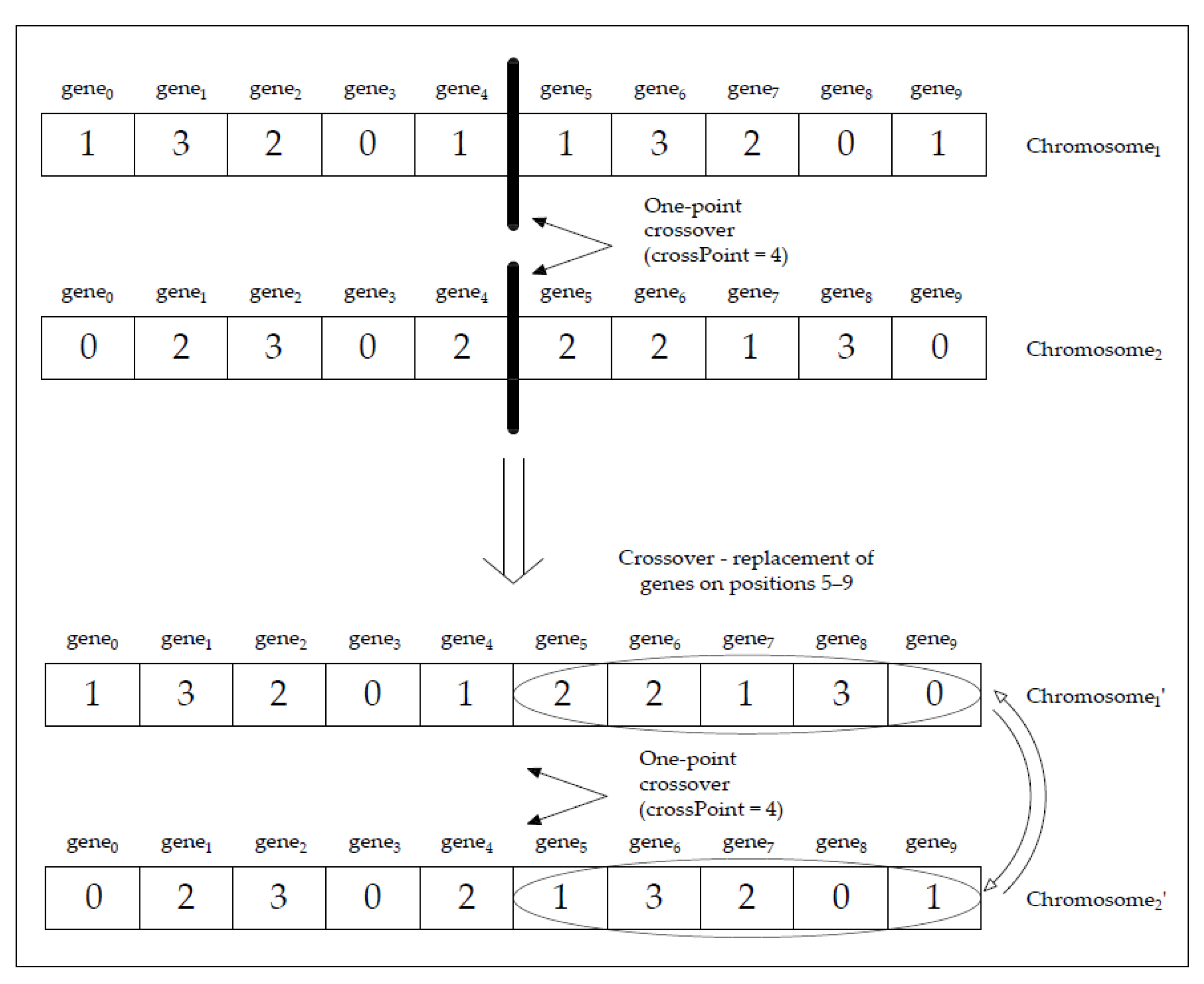
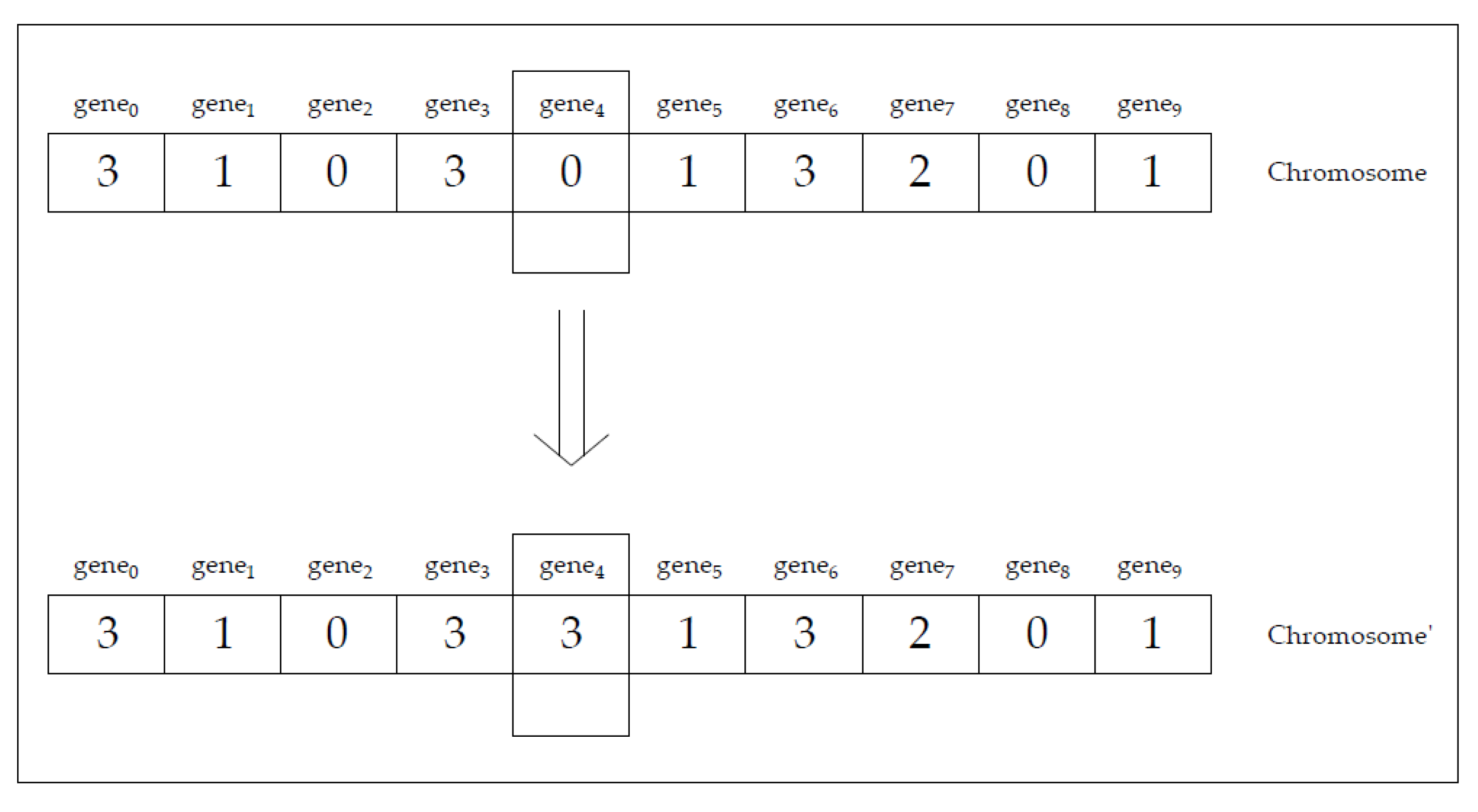
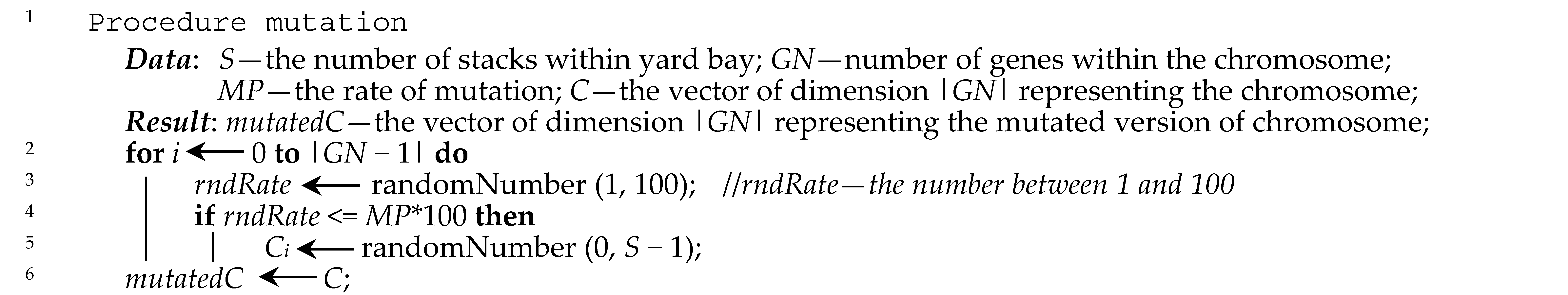1. Introduction

These days, maritime transport plays a very important role in global transport, as more than 90% of global trade is carried out by sea [1]. Considering various transport modes of maritime transportation, more than 15% refers to container transport [2]. Therefore, container transportation plays an essential role in world trade, and consequently container terminals have become a very important hub of global trade. An increasing number of container shipments leads to higher demands on the seaport container terminals, container logistics, and management, as well as on technical equipment [3]. Therefore, container transportation requires almost perfect coordination between all stakeholders, work resources and processes within the entire container transport system [4].

There are a large number of logistics problems inside container terminals (berth allocation, stacking, transport optimization, crane split, etc.) that have to be optimized and mutually integrated to improve and speed up the overall container transfer through the terminal in order to reduce the waiting time of the transfer means (vessels, trains and trucks) when loading and unloading containers and thus to increase the total container traffic within the terminal. According to [5], one of the most important optimization problems at the container terminal is the stacking of containers in the stacking area (the part of a storage yard). On average, 80% of the containers are transferred to the stacking area before being transferring from the container terminal [5]. Thus, the optimization of the stacking logistics problems has become one of the most important research areas with respect to the optimization of container terminal processes.

In the storage area, containers are stacked side by side and on top of each other, forming blocks. When a target container is to be retrieved, there is a high probability that one or more containers are stacked above it and blocking its retrieval. Moving blocking containers adds additional cost to the retrieval of a target container due to the additional crane running time and increased retrieval time. Therefore, containers must be stacked in such a way that there is a minimum number of additional container movements within the stacking area [6]. These additional unproductive movements are called reshuffles. As mentioned earlier, reshuffling slows down the retrieval time of the target container and thus the total container shipment time between the stacking area and other areas of the container terminal. Therefore, the crane operation schedule needs to be optimized to minimize the number of reshuffles, i.e., to minimize the time of retrieving the blocking containers, as well as to maximize the utility of each crane operating in the stacking area.

One of the well-known post-stacking optimization problems within the stacking area is the Container Relocation Problem (CRP), also known as Block Relocation Problem (BRP) [7]. In CRP, the operations of reshuffling the blocking containers and retrieving the next container that has to be shipped are performed in parallel. Each container must be retrieved with a minimum amount of reshuffling of the blocking containers. Within the CRP, there are two main sub-problems: restricted and unrestricted CRP [8]. In the restricted CRP, when the desired (target) container is retrieved, only the containers that block the retrieval of the desired (target) container can be relocated. In contrast to the restricted CRP, in the unrestricted CRP, all containers can be relocated to facilitate the reach of containers that must be retrieved later. Therefore, solving restricted CRP is much more complex and demanding with respect to the unrestricted CRP. The restricted CRP is NP-hard [5], so it is difficult to determine a good solution for retrieving all containers with a minimum number of unproductive reshuffles.

One of the possible solutions to solve the restricted CRP is to implement nature-inspired metaheuristic algorithms that solve various NP-hard real-life problems very effectively. Metaheuristics are becoming very popular over the last decade due to their simplicity, flexibility, derivation-free mechanism and local optima avoidance capability [9]. According to [6], the term metaheuristics is defined in computer science and mathematical optimization as a higher-level process or heuristics designed to find, generate or select heuristics that can find a sufficiently good solution for some optimization problem, especially when the available information in the optimization problem is incorrect or incomplete, or the computational capacity is limited. Although it was invented a long time ago [10], the genetic algorithm is still one of the most used nature-inspired metaheuristics in solving different optimization problems. In [11], an overview of the use of nature-inspired metaheuristics for optimization problems in a container terminal is presented. Thus far, the genetic algorithm has been used in [7,12,13,14,15,16,17,18,19]. Only the solutions in [17,18,19] use a genetic algorithm to solve restricted CRP. Besides [17,18,19], which use a genetic algorithm to solve restricted CRP, there are only two solutions for restricted CRP [20,21] that use nature-inspired metaheuristics. In [20], the ant colony optimization algorithm [22] was used, while in [21], simulation annealing [23] is used for restricted CRP solving. Considering the excellent results of [17,18] obtained in resolving the most complex test set of restricted CRPs [24], we assume that there is a great potential for using nature inspired metaheuristics to solve restricted CRP. The test set described in [24] consists of a huge set of CRPs considering different bay sizes. All CRPs within this test set have a maximum occupancy capacity, which makes it more difficult to solve the problem given the large number of blocking containers.

In [17,18], for solving restricted CRP, the use of a genetic algorithm is proposed, to determine the order of executing one of the four relocation rules (based on stacks occupancy) for blocked containers on the terminal stacking area. These rules prefer to perform the reshuffle of the blocking container to the nearest possible stack (column) that satisfies the restrictions set within a particular relocation rule. Along with minimizing the number of relocations in CRP, these four rules of relocation optimize the horizontal movement of reshuffled containers. The main objective of CRP is to minimize the number of reshuffles. When applying these four rules of relocation to solve CRP, the focus is sometimes on optimizing the horizontal distance (relocate to the nearest stack) rather than the number of relocations. In certain situations, the total number of relocations ends up being lower if the reshuffled container is not relocated to the nearest possible stack (column). Therefore, it is necessary to improve the method described above, which uses a genetic algorithm.

The list of contributions of this paper is as follows. We have studied in the literature review only the methods and models that have been used to solve the most complex test instances of restricted CRPs [24]. We believe that these methods and models are the most appropriate for comparison with our new method. In this paper, we propose a new genetic algorithm-based solution in order to minimize the number of relocations within the bay. Using the genetic algorithm, the method finds an optimal sequence of container relocations to determine a minimum number of total relocations. Considering a certain container that has to be relocated, the best current stack (column) position is not determined, but the stack position that will optimize the total number of relocations at the end. We also implement the linear programming model to resolve CRP as well as to get optimal results for small bay sizes. As stated before, CRP is NP-hard problem. Hence, using the linear programming model, it cannot only resolve CRPs for large bay sizes. Nevertheless, the obtained optimal results for small bay sizes confirm that our new method also obtains optimal results for small sizes. The complete results of our new optimization technique, compared with the results of different best models obtained on the most complex test instances of restricted CRPs [24], have shown that our proposed method achieves optimal (for small test instances) or the best possible solutions (for large test instances) for most test instances. In addition, we created a statistical t-test to compare the results between our previous method [17] and our new method to demonstrate the difference between these results. Due to the very high t-value that is obtained, a large difference between the two sample groups can be confirmed.

The paper is organized in five interdependent sections. Section 2 introduces the basic terminology of restricted CRP. In Section 3, we discuss the literature review. The proposed genetic algorithm-based method for solving the CRP is presented in Section 4. In Section 5, the evaluation of our new method is presented with respect to the most complex test instances of restricted CRPs [24]. Finally, a conclusion is given in Section 6.

2. Container Relocation Problem—Model Set Up

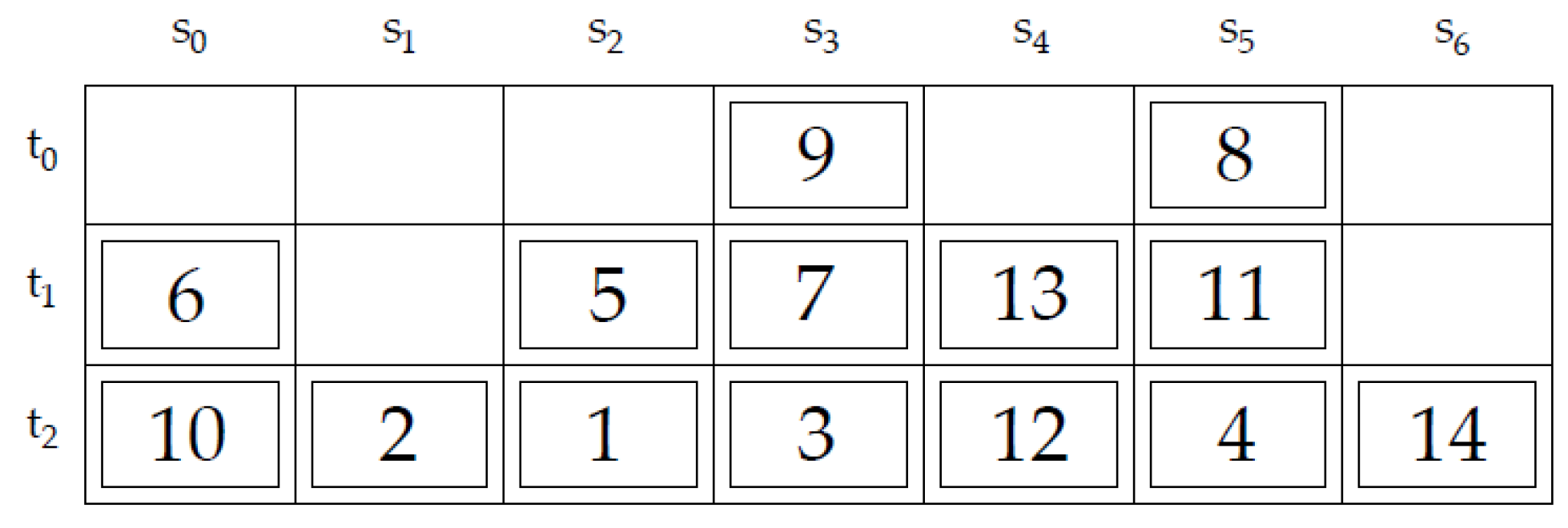
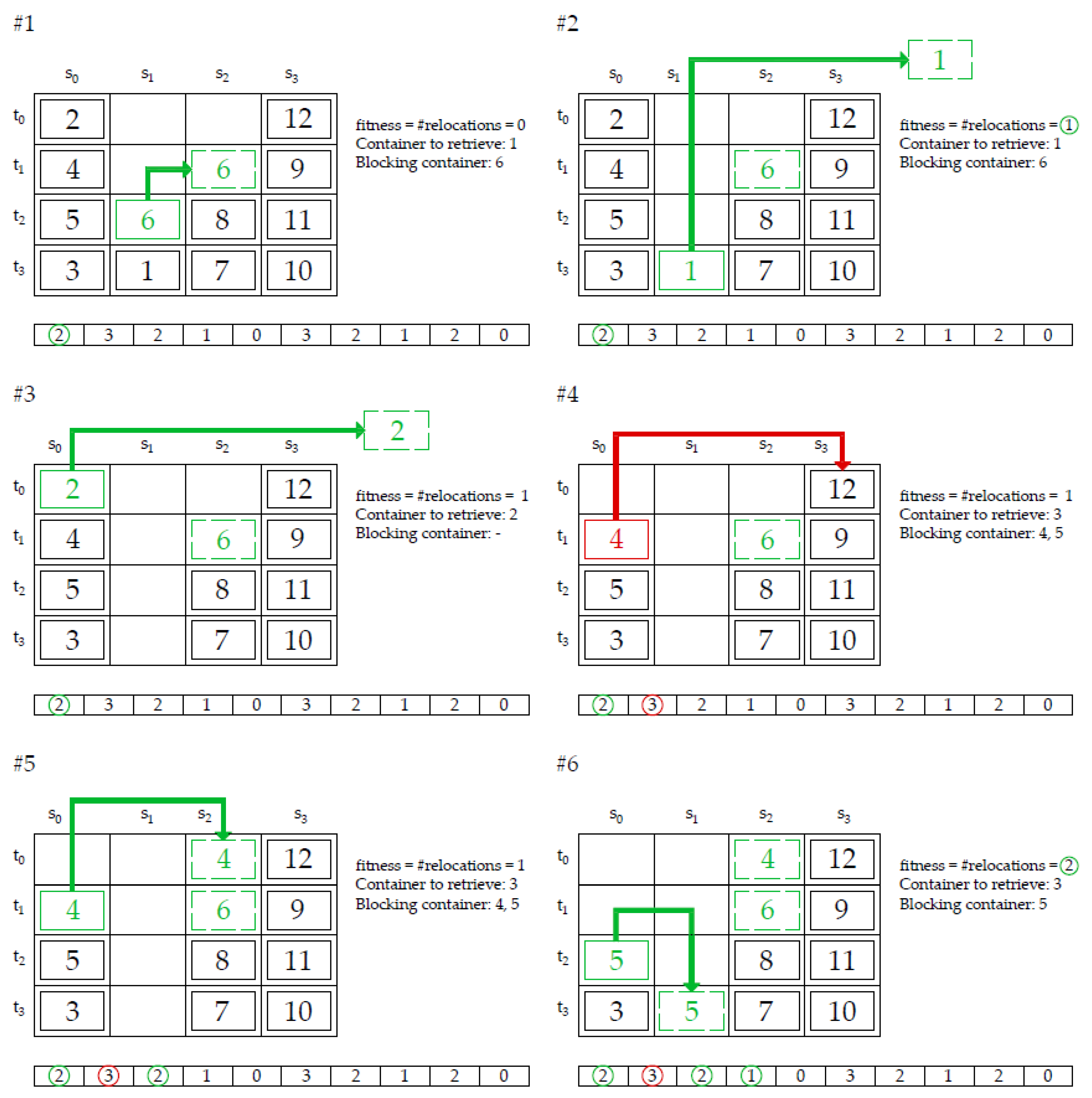
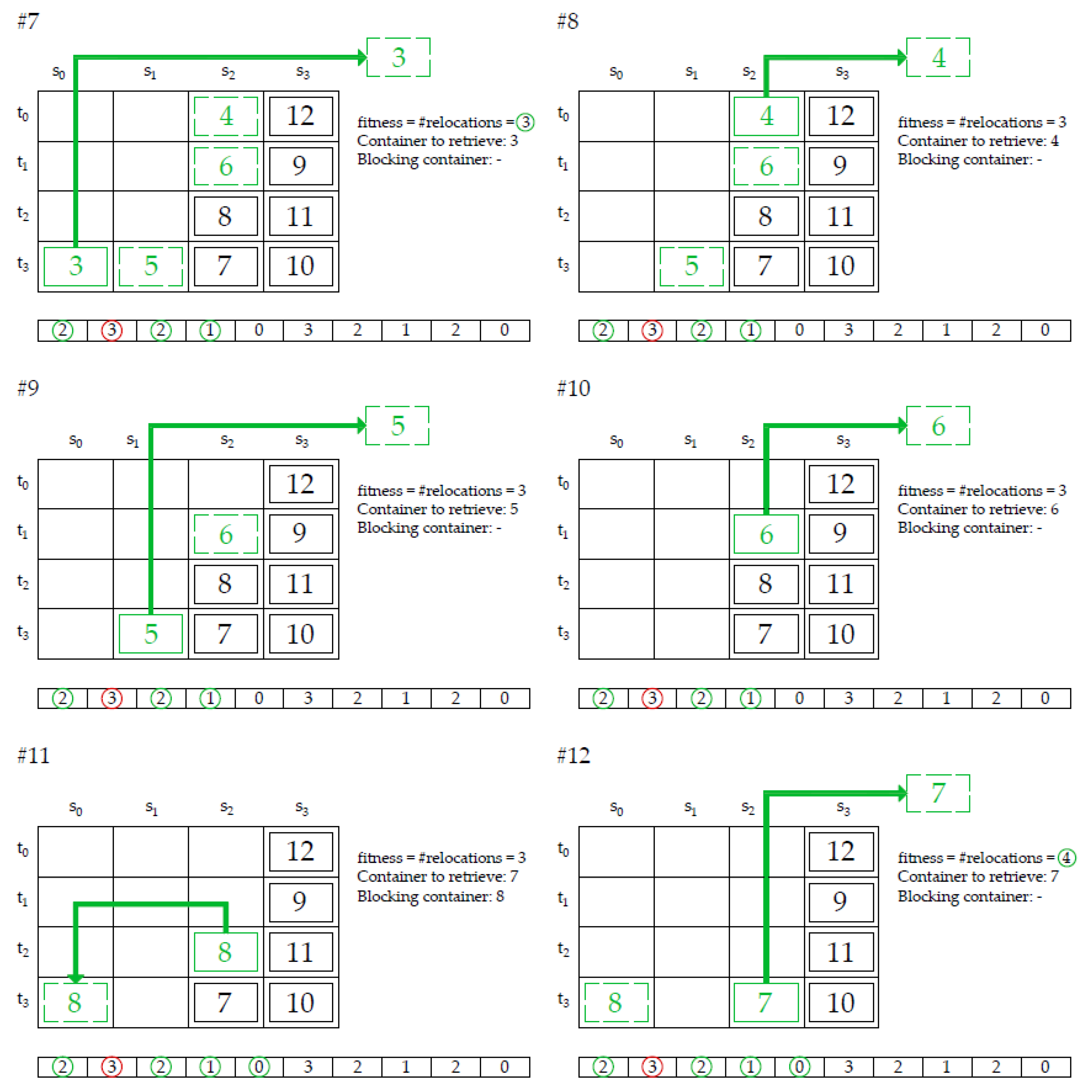
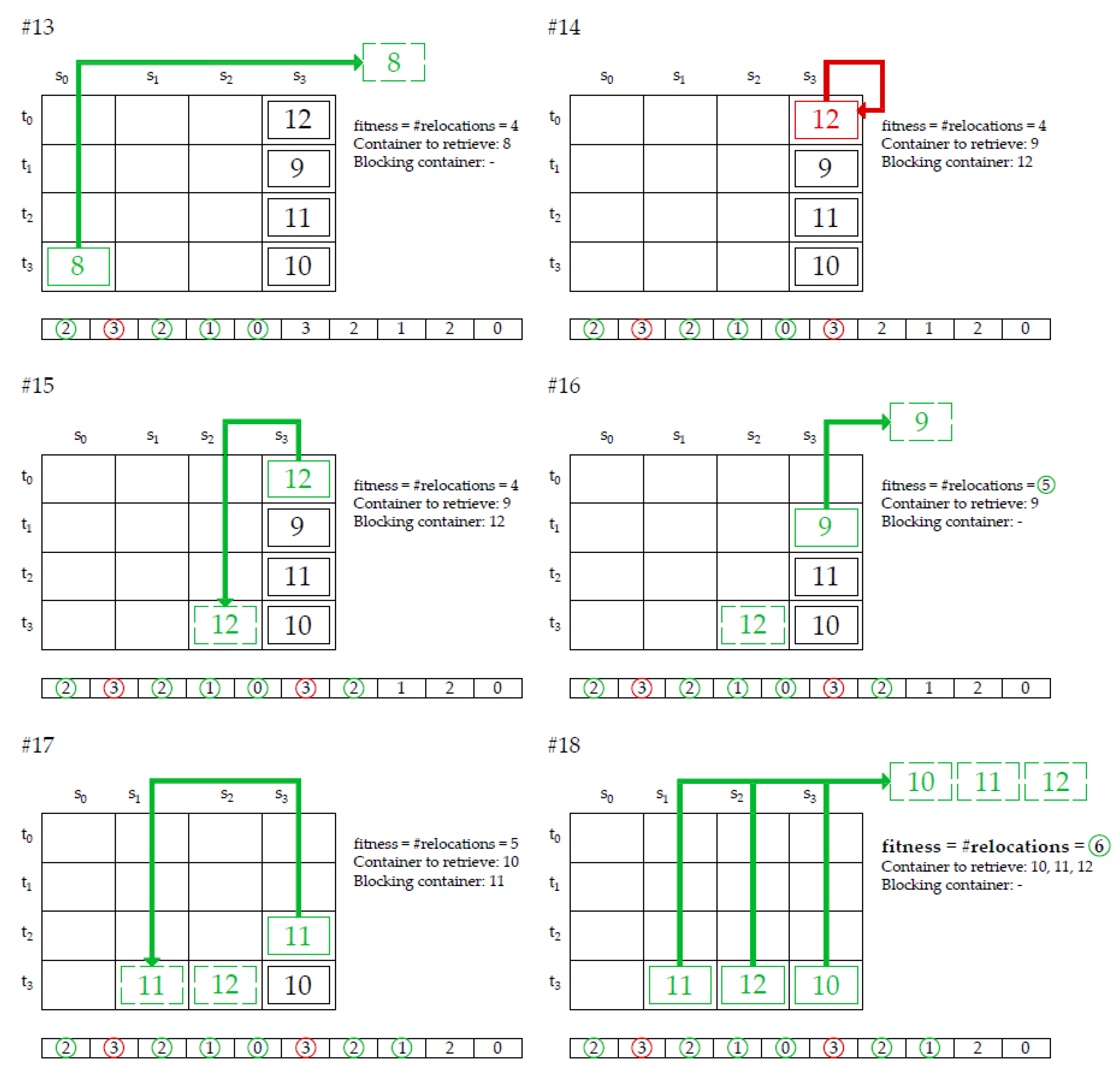
In this paper, we focus on solving the two-dimensional, static, offline, and restricted container relocation problem. A two-dimensional problem means that the container relocation problem is solved for one bay with certain numbers of stacks and tiers (Figure 1).

As can be seen in Figure 1, the containers are marked with a different retrieval priority (ordinal numbers) based on the transport documentation that specifies the departure order. The retrieval represents the lifting of the target container and loading it onto a truck or other internal transport unit [17]. Therefore, the retrieval time for each container is known in advance (offline variant). A container with a smaller number has a higher priority and must be retrieved earlier. If some container blocks access to a particular container that needs to be retrieved next, it must be relocated to another free stack within the bay. These relocations of blocking containers, called “reshuffles”, slow down the entire process of retrieving and shipping containers from the bay. The CRP focuses on finding the best sequence of relocation positions to retrieve all containers within the given bay (respecting their priority) with a minimum number of relocations [17]. The retrieval and relocation of containers is performed by a yard stacking crane called a rubber tired gantry crane (RTG), as shown in Figure 2.

During the retrieval and shipping of containers within/from the bay, no new containers arrive in that bay. This is the static variant of the CRP. As mentioned earlier, the restricted CRP is limited to moving only the blocking containers and retrieving the container that is currently being shipped. Therefore, containers that are not blocking the next shipping container cannot be moved to optimize the number of additional relocations. Thus, this restricted CRP is much more complicated than the unrestricted CRP.

The definition of the problem can be formalized and relies on the assumptions A1 to A13 and constraints C1 to C4 according to [17].

3. Literature Review

The CRP was first mentioned in [25]. In the research paper, the simulation model has been used in order to analyze the impact of the number of stacks and tiers in a bay with respect to the total number of crane operations. A similar approach for solving CRP has been proposed in [26,27], where certain heuristic rules were applied for the first time in order to reduce the total number of additional container relocations at a container stacking area. In [28], an equation, which explains the relation between stacks’ height within a bay and the expected number of container relocations within that bay with respect to the number of containers, is proposed. Thereby, the corresponding maximum height of the stacks (the number of containers that can stack above each other) is determined within the bay to minimize additional container relocation operations. The integer linear programming method has been used in [29,30,31] for solving these small data sets. However, for real restricted CRP, where there is a large number of containers in one bay, linear programming does not meet the requirements for efficiently solving restricted CRP.

Newer solutions usually use heuristic methods based on branching and bounding method (B&B) with diverse searching and branching strategies [24,32,33,34,35,36,37]. In [32], for the first time, the B&B and heuristic rule was proposed for determining the optimal positions for blocking containers to minimize the amount of container reshuffling. Additionally, the specific equation was proposed to estimate the number of reshuffles within a bay. The A* (A-star) method, a path search algorithm implemented in [36], was used to minimize additional reshuffles in restricted CRP together with a heuristic algorithm that shortened the time for solving the problem. In [35,37], a new improved A* (A-star) method, which is based on iterative execution procedure, was proposed for solving restricted CRP. The new heuristic approach, which considers in account the characteristics of the next relocating container when deciding on the position of this container, is proposed in [27]. The new heuristic approach is an improvement of the min–max approach for solving restricted CRP. The improved search algorithm was applied to restricted CRP by reducing the complexity of the search space for quicker obtaining the requested solution. In addition to the proposed solutions, based on the B&B method, several models use other methods [24,34]. In [24], the beam search algorithm was proposed for the same purpose. The improved beam search algorithm was proposed in [34]. The Decision Support System (DSS) has been implemented in order to optimize the entire Hong Kong container terminal [38]. To minimize the amount of container reshuffling at a container stacking area, a rule Reshuffle Index (RI) was defined specifying the stack with the smallest RI (a stack that contains the smallest number of containers that must be retrieved before the blocking container being relocated) into which the blocking container will be relocated in order to retrieve the desired (target) container within the stacking area. Several authors introduce metaheuristic algorithms inspired by nature to solve restricted CRP. According to [6], the term metaheuristics in computer science and mathematical optimization is defined as a higher-level process or heuristics designed to find, generate or select heuristics that can find a sufficiently good solution for some optimization problem, especially when available information in the optimization problem is incorrect or incomplete, or there is a limited computational capacity. Nature-inspired metaheuristics algorithms have been applied to solve a large number of real-life optimizing problems. These algorithms imitate various natural systems and processes using mathematical models and algorithms.

As stated in the Introduction section, for solving restricted CRP, the use of the genetic algorithm [10] is proposed in [17,18], which determines the order of execution of one of the four relocation rules (based on the stacks occupancy) for blocked containers on the terminal stacking area. These rules prefer to make the reshuffling of blocking containers to the nearest possible stack (column), which satisfies the restrictions set within a particular relocation rule. In this way, a minimum number of relocations is not obtained for each CRP. Thus, in this paper, we propose a new method based on the genetic algorithm in order to minimize the number of relocations within the bay for each CRP test problem. In addition of using a genetic algorithm, some other nature-inspired metaheuristic algorithms have been used in solving CRPs. Simulation annealing [23] is used for restricted CRP solving in [21]. In [20], the Ant Colony algorithm [22] was used for restricted CRP resolving. In [17], a method that implements a genetic algorithm is proposed for solving restricted CRP with containers that are grouped by the retrieval time window. This problem is much easier to solve than classic restricted CRP because more containers are retrieved in a common time window. Containers within the same window do not always have to be retrieved in the same order, but in such a way that the number of additional movements is minimal. Although this method is used for the easier (simple) restricted CRP, it is interesting insofar as the only solution, along with [17,18,20,21], that uses metaheuristic algorithms inspired by nature for resolving restricted CRP.

In continuation, the focus will be on related papers dealing with the solution of restricted CRP of the currently most complex test set in the literature, which was presented in [24]. As stated before, this test set consists of different restricted CRPs in which the bays are maximally occupied with containers. For the bay, consisting of W stacks and H tiers (maximum stacking height), the maximum number of N containers that such a bay can store is N = W × H − (H − 1). We assumed that the models proposed for finding the solution of this test set are more referenced for being presented here. For this testing data set, the best results were achieved by the methods proposed in [17,24,33,34]. As stated before, in [17], the genetic algorithm is implemented within the proposed solution so that it finds the best order to execute the container relocating rules by minimizing the number of container reshuffling. The method in [17] is the only method that uses nature inspired metaheuristic algorithm for resolving the most complex test set presented in [24]. Considering the very good results obtained when solving the CRP and possible improvements in the method, we assume that there is a great room for improvement in restricted CRP solving with the usage of nature-inspired metaheuristic algorithms.

Furthermore, there is a large number of newly proposed methods for solving CRP, and some of them are described in [39,40,41,42,43]. However, the authors do not test out the methods on this highly complex test set [24]. Therefore, we did not compare our new method with these methods because we believe that the test set from [24] is the most relevant test set for comparing methods for solving CRP. As mentioned earlier, the test set from [24] consists of several restricted CRPs where the bays are maximally occupied by containers.

4. A New Method for CRP Resolving Based on Genetic Algorithm

4.1. Genetic Algorithm

As mentioned earlier, the genetic algorithm is a nature-inspired metaheuristic algorithm based on a process of natural selection. Nature-inspired metaheuristic algorithms generally find a solution to a given problem that is close to the optimum in a short time, thus speeding up the process of finding a good enough solution. It cannot be said with certainty that the solution is the best, since these algorithms have not searched the entire solution space given the speed at which a solution is found. However, the relationship between the speed at which a solution is found and the goodness of the solution found argues for the use of these algorithms in solving NP-hard problems such as the CRP. As stated before, the genetic algorithm finds a solution to a given problem by imitating the process of natural selection. At the beginning of the solution finding process, a sample set of potential solutions (chromosomes) is randomly generated. This set is called the initial population. Each solution in the population is called a chromosome. A chromosome consists of a set of genes. A gene is part of an overall solution that represents the chromosome. To evaluate how well each chromosome (i.e., its genes) represents the solution to the optimization problem, a fitness function must be defined to determine the goodness of each chromosome (solution). To have the process of natural selection work, each chromosome contains the same genes and the same number of genes [10]. In order to obtain better solutions in the next population of chromosomes, the basic operators of the genetic algorithm must be applied to the chromosomes of the previous generation. Selection, crossover and mutation are the basic operators of genetic algorithm. Selection selects better chromosomes from the previous population that will be part of the next generation. The operator crossover crosses two chromosomes from the previous population to create a better chromosome (solution) for the next generation. Crossing of two good chromosomes promotes the creation of child chromosomes that are better than their parent chromosomes. Mutation involves changing one or more genes within a chromosome to eventually find a better chromosome. The pseudo code of the genetic algorithm is shown in Algorithm 1.

Algorithm 1. Pseudo code of genetic algorithm.

4.2. A New Method for CRP Resolving

As mentioned earlier, the focus is on solving the two-dimensional, static, offline, and restricted CRP. Figure 3 shows an example of a CRP on a bay with four tiers (t represents the numbers of tiers, i.e., the height of the stacks) and four stacks (s represents the number of stacks, i.e., the width of the bay). A bay consists of 12 containers.

The stacks are indexed from left to right with number values from 0 to 3, similarly with the height of the stacks, i.e., tiers. The uppermost tier has index 0 (tier ${\mathrm{t}}_0$), and the lowermost tier has index 3 (tier ${\mathrm{t}}_3$). The position of the containers is determined by an ordered pair (t, s). For example, container 4 is located at position (1, 0). Each container has a priority retrieving number according to which it is shipped from the bay. The smaller the number, the sooner the container is shipped from the bay. The goal is to retrieve all containers from the bay with the minimum number of reshuffles (relocations of blocking containers) [17]. Only containers blocking the container currently being retrieved can be relocated to another stack. Containers can be relocated to a particular stack only if the stack is not fully occupied (the number of containers in the stack is 4). As mentioned earlier, we propose a new method based on a genetic algorithm to minimize the number of relocations within the bay. The genetic algorithm finds an optimal sequence of positions for relocating blocking containers. The process of determining an optimal sequence of container relocations using a genetic algorithm is described in detail below.

4.2.1. The Chromosome

Before starting the genetic algorithm, the chromosome that represents the solution to the optimization problem must be defined. In our procedure for solving CRP, the chromosome consists of a sequence of integer numerical values (genes) whose values depend on the total number of stacks. Each numerical value represents the position (stack) to which the next blocking container must be relocated. Thus, the values of the genes within the chromosome are equal to the indices of the stacks. The example of a chromosome solving the CRP on a bay with four tiers and four stacks (Figure 3) can be seen in Figure 4.

The first value (gene) is equal to 2, indicating that the first blocking container must be relocated in the stack with index 2 (s₂). Applying this chromosome to solve the problem in Figure 3, the first blocking container is container 6 because it blocks the retrieval of the container with priority 1. Therefore, as shown in Figure 5, the container with priority 6 must be relocated in stack 2 (s₂). Then, the container with priority 1 can be retrieved and shipped to the next transport location. It can be seen that the container with priority 2 can be retrieved immediately because it is located on the top of the stack with index 0 (s₀).

It may happen that the next blocking container cannot be moved to the position defined in the solution (chromosome). There are two situations in which this can happen: when the stack into which the blocking container must be relocated is completely full, and when the position of relocating the blocking container is equal to the current position of that container.

Considering the situation in Figure 6 (after the retrieval of the containers 1 and 2 in the example showed in Figure 5), the next container to be retrieved is the container with priority 3. The first blocking container is the container with priority 4 and the first unused gene within the chromosome is number 3. It means that the container with priority 4 must be moved to the stack with index 3. Stack 3 is fully occupied, so the second gene (number 3) within the chromosome (potential solution) is skipped and does not apply to the relocation of container 4. Therefore, container 4 is relocated to stack 2, because the first valid gene within the chromosome is the gene with the value 2.

Similarly, if the next gene within the chromosome that represents the next location for the current blocking container has the value of the stack in which the current blocking container is already located, as in the fully occupied stack above, the first valid gene within the chromosome is used to perform the relocation of the blocking container. Considering the possibility of genes appearing within chromosomes that are not valid, it is assumed that the length of the chromosome (the number of genes) must be slightly longer relative to the number of containers within the bay. Experiments have shown that the number of genes in a chromosome is determined by multiplying the number of containers stacked in the bay by the number 10. Thus, if the bay consists of five containers, the number of genes in a chromosome is 50. With this chromosome length, each CRP within the test set was successfully resolved. When talking about the quality of an individual solution (chromosome), only the number of applied genes represents the number of reshuffles (container relocations) within the bay, i.e., the value of the fitness function. The complete process of fitness function calculation for this problem is presented in the next subsection.

4.2.2. The Fitness Function

As earlier mentioned, the fitness function is the most important part of the genetic algorithm because it represents the optimization problem that has to be solved. The quality of each chromosome in the genetic algorithm process is evaluated with the fitness function. In terms of the CRP, the fitness function is defined by the following equation:

$$fitness=\#relocations$$

(1)

where $\#relocations$ is the number of all relocations of blocking containers while retrieving the containers based on their priorities. The smaller the value of the fitness function, the better the potential solution (chromosome). The pseudo code for the fitness function calculation of our method is shown in Algorithm 2.

Algorithm 2. Pseudo code of fitness function calculation.

An example of the fitness function calculation for CRP and particular chromosomes can be seen in Figure 7, Figure 8 and Figure 9. First, the container with priority 1 must be retrieved. Container 6 blocks container 1, so it must be relocated. Container 6 would be relocated on the position corresponding to the value of the first gene in the chromosome. The value of the first gene is 2, so container 6 is relocated to stack 2 (Figure 7, part #2). The value of the fitness function is now equal to 1. Container 1 can be retrieved and shipped further (Figure 7, part #2) after the relocation of container 6. Container 2 is next for retrieving. Since this container is not blocked by any container, it can be retrieved immediately (Figure 7, part #3). Now, the container with priority 3 must be retrieved. Containers 4 and 5 block container 3, thus they must be relocated. First, the relocation of container 4 must be performed. The next not used gene within the chromosome has value 3 indicating that the following relocation must be made on stack 3. As stack 3 is fully occupied, this relocation cannot be made thus this gene is skipped (Figure 7, part #4). The next available gene has value 2, thus container 4 is relocated to stack 2 (Figure 7, part #5). The blocking container 5 is relocated to stack 1 (Figure 7, part #6). Now, the fitness function is equal to 3. Currently, there are no containers blocking the retrieval of containers with priorities 3, 4, 5, and 6, so they can be shipped further without making any relocations (Figure 8, parts #7, #8, #9, and #10).

Container 8 blocks container 7 and therefore must be relocated. Container 8 is moved to the position corresponding to the value of the first unused gene within the chromosome. The value of the first unused gene is 0, so container 8 is relocated in stack 0 (Figure 8, part #11). The value of the fitness function is now equal to 4. Containers 7 and 8 can now be retrieved and shipped further (Figure 8, part #12 and Figure 9. Part #13). The container with priority 12 blocks the retrieval of container 9, and so has to be relocated according to the value of the next available gene.

The value of the next available gene is 3, so the relocation cannot be performed because container 12 is already positioned in stack 3 (Figure 9, part #14). The next gene is equal to 2, so container 12 is relocated into stack 2 (Figure 9, part #15). The fitness function value is now equal to 5, and container 9 can now be retrieved and shipped further (Figure 9, part #16). The container with priority 11 blocks the retrieval of container 10, so it must be relocated according to the value of the next available gene, which equals 1. Consequently, container 11 is relocated to stack 1 (Figure 9, part #17), and the value of the fitness function is increased by 1 (equal to 6). Now, all remaining stacked containers (10, 11 and 12) can be retrieved according to their priorities (Figure 9, part #18).

In the end, the fitness function is equal to 6 for this example chromosome. In order to obtain better and better chromosomes during the evolution process within the genetic algorithm, selection, crossover and mutation must be performed.

4.2.3. Selection

As stated before, selection is the process of choosing the better chromosomes from the previous generation that will be part of the next generation. On those selected chromosomes, the genetic operators (crossover and mutation) are performed in order to obtain even better chromosomes, which are a possible solution to the optimization problem. In this way, natural selection is simulated, where the better individuals survive. During the selection process, the best chromosomes of the previous generation are largely selected. However, it is useful to select a smaller percentage of less good chromosomes. There is always a possibility that such chromosomes contain some good genes (a good part of the solution) that can help to create better chromosomes in the future through crossover and mutation processes. There are different types of selection [44], but in this optimization problem of determining the sequence of the best relocation positions to minimize the number of relocations, deterministic tournament selection is chosen. In deterministic tournament selection, k chromosomes are randomly selected from the existing chromosomes. The chromosome with the highest fitness function value is selected in the next generation. This process is repeated n times since the next generation consists of n chromosomes. When deterministic tournament selection is used, the chromosome with the highest fitness function value in the previous generation may not be included in the next generation. Therefore, the elitism rule is applied in this selection procedure. The elitism rule always selects the chromosome with the highest fitness function for the next generation.

4.2.4. Genetic Operators

The genetic operators, crossover and mutation, are applied to the chromosomes selected in the selection procedure. The crossover operator crosses the genes of two selected chromosomes. In this way, two new chromosomes are created, each consisting of mixed genes from their parents. In this paper, the crossover with one crossover point is used, because it performs faster than any other type of crossover. Before performing the crossover, the crossover point must be determined. If the chromosome consists of n genes, the crossover point has a value in the range between 2 and n − 1. The value of the crossover point is determined by a random function. The pseudo code for the crossover process of our method is shown in Algorithm 3.

Algorithm 3. Pseudo code of crossover process.

An example of the crossover procedure is shown in Figure 10.

At the beginning, chromosome₁ has the values (3, 1, 0, 3, 0, 1, 3, 2, 0, 1) and chromosome₂ has the values (0, 2, 3, 0, 2, 2, 2, 1, 3, 0). The crossover point is assigned the value of 4 (crossover is performed for genes on indices 5 to 9) by using a random number function. After performing the crossover operator between these chromosomes, the genes at indices 5 to 9 are interchanged, resulting in two new chromosomes: chromosome_1′ with values (3, 1, 0, 3, 0, 2, 2, 1, 3, 0) and chromosome_2′ with values (0, 2, 3, 0, 2, 1, 3, 2, 0, 1).

The mutation operator mutates the genes of a chromosome (solution), i.e., changes the values of some genes within the chromosome to obtain a better chromosome than the original one. Before the mutation is performed, the index of the gene(s) that will be mutated must be defined. If the chromosome consists of n genes, the index can have a value between 1 and n. In addition, the probability of mutation must be defined (usually the probability is less than 5%). The pseudo code for the mutation process of our method is shown in Algorithm 4.

Algorithm 4. Pseudo code of mutation process.

Figure 11 shows an example of a mutation process. At the beginning, the chromosome has the values (3, 1, 0, 3, 0, 1, 3, 2, 0, 1). The index of the mutated gene gets the value 4 by using random number function. After performing the mutation operator on the mutated gene, the chromosome’ has the values (3, 1, 0, 3, 3, 1, 3, 2, 0, 1).

What is important to emphasize, after mutation and crossover, is that all generated chromosomes remain feasible as potential solutions for the current CRP that is being solved. As stated before, the length of the chromosome (the number of genes) must be slightly longer relative to the number of containers within the bay considering the possibility of genes appearing within chromosomes that are not valid. In this way, any chromosome obtained by mutation, crossover or random generation remains feasible as a potential solution to the current CRP.

5. Results and Discussion

The experiment was run on a 64-bit Windows 10 operating system with an Intel^® Core™ i5-8265U CPU 1.60 GHz processor and 8 GB of RAM. The method described above was implemented in Java using the integrated development environment (IDE) NetBeans 11.3. Additionally, the Java Genetic Algorithm and Programming (JGAP) library [45] was used to implement the genetic algorithm in this programming procedure. The method was tested with different parameter values within the genetic algorithm to find the best possible setup of the genetic algorithm to obtain the highest quality solutions in the shortest possible time. The best possible setting of the genetic algorithm had the following parameter values: the number of generations was 300, the size of the population of each generation was 100, the mutation probability was 0.05, and elitism (the best possible solution from the previous generation is automatically included in the next generation) was set, and the percentage of chromosomes from the previous generation that is included in the next generation was 0.5. The small number of chromosomes in each population (100) allows very fast execution of the genetic algorithm. However, to obtain high quality solutions (chromosomes), the number of generations must be increased, as well as the percentage of the crossover probability which, in addition to mutation, allows a diverse searching of solution space for CRP. Half of the chromosomes (solutions) of the previous generation are included in the process of the next generation of genetic algorithm, so such selection ensures that quality solutions are included in the search process along with the newly randomly generated solutions of the next generation. All parameters of genetic algorithm and their values are given in

Table 1. The genetic algorithm setup for resolving CRPs.

Parameter	Value
Number of generations	300
Size of population	100
Mutation rate	0.05
Number of genes within the chromosome	10 × number of containers in CRP
Percentage of selected chromosomes from previous generation	0.5
Elitism	set

.

The method was tested on a test set of restricted CRPs described in [24]. As mentioned before, this test set consists of a large set of CRPs considering different bay sizes. All CRPs in this test set contain the maximum possible number of containers (maximum occupancy) within the bay considering the bay size of a given CRP. The maximum occupancy makes it difficult to solve the problem given the large number of blocking containers, so this test set is the most relevant test set for evaluating models that solve the CRP. The total number of containers stacked in the bay is obtained from the expression in [24]:

N = W × H − (H − 1)

(2)

where N is the total number of containers stacked within a bay, W is the total number of stacks (columns) in a bay, and H is the total number of tiers in a bay. The maximum occupancy is obtained by subtracting the (H − 1) from W × H. The value (H − 1) is the largest number of relocations to retrieve one container if a stack is full (contains H containers) and the container, that needs to be retrieved, is blocked by (H − 1) containers within that stack, i.e., it is positioned at the bottom of the stack. In this way, there is always a sufficient number of free container positions (slots) to which blocking containers can be relocated.

The experiment was performed for the following bay sizes: 3 × 7–6 × 7, 3 × 6–6 × 6, 3 × 5–6 × 5, 3 × 4–6 × 4, 3 × 3–6 × 3. The test set in [24] consists of 40 different problem instances for each bay size. The maximum tested bay size (6 × 7) corresponds to the specifications of the latest technological RTG cranes in regard to the actual sizes of bays. Therefore, the tiers’ parameter assumes a value from 3 to 6 while the stacks’ parameter assumes a value from 3 to 7. The results obtained with the proposed method were compared with the other best models applied to this test set. In

Table 2. The results of the CRP test set [24] on real sizes of bays achieved by the proposed method and the other best models of different authors.

Tiers × Stacks	No. of Containers	A* (A-Star) Method [35,37]	Decision Support System [38]	Min-Max [29]	Chain [33]	Chain F [33]	BSA [24]	GA with Rules [17]	New GA Method	Linear Programming
3 × 3	7	3.58	3.42	3.42	3.42	3.38	3.38	3.38	3.30	3.30
4 × 3	9	6.67	6.10	5.82	5.82	5.95	5.67	5.85	5.67	5.67
5 × 3	11	10.60	9.80	9.10	9.10	8.70	8.40	8.93	8.40	8.40
6 × 3	13	15.40	13.60	12.97	12.77	12.30	11.50	12.30	11.50	-
3 × 4	10	5.67	5.03	4.95	4.95	4.95	4.85	4.98	4.85	4.85
4 × 4	13	10.50	9.05	8.75	8.72	8.57	8.43	8.55	8.42	8.42
5 × 4	16	16.30	14.50	13.12	13.02	13.17	12.20	12.63	12.25	-
6 × 4	19	23.20	19.10	17.15	17.05	16.92	15.60	16.93	15.62	-
3 × 5	13	6.95	5.90	5.75	5.75	5.80	5.75	5.80	5.75	5.75
4 × 5	17	14.40	12.20	11.40	11.35	11.40	11.00	11.35	10.98	-
5 × 5	21	21.00	18.10	17.07	16.95	16.65	15.60	16.75	15.60	-
6 × 5	25	31.80	25.60	23.92	23.52	23.57	21.10	22.60	21.15	-
3 × 6	16	8.95	7.92	7.72	7.72	7.85	7.65	7.88	7.65	-
4 × 6	21	16.00	13.20	12.67	12.55	12.60	12.00	12.48	12.02	-
5 × 6	26	26.90	22.60	20.60	20.42	20.52	19.30	20.32	19.35	-
6 × 6	31	41.20	32.60	29.02	28.77	28.57	26.10	28.50	26.15	-
3 × 7	19	11.50	10.10	9.02	9.05	9.17	8.95	9.15	8.95	-
4 × 7	25	19.40	20.10	16.35	16.45	16.07	15.50	16.13	15.48	-
5 × 7	31	33.00	30.90	23.15	22.92	22.70	21.40	22.60	21.42	-
6 × 7	37	45.80	45.00	34.40	34.07	34.07	31.00	33.55	31.62	-
Total sum of average relocations		368.82	324.82	286.35	284.37	282.91	265.38	280.66	266.04

, the results obtained by the proposed method are compared with those obtained by the other authors who achieved the most significant results with this test set. Furthermore, we have implemented the linear programming model for CRP to get optimal results for small bay sizes (last column in Table 2). As stated before, CRP is NP-hard problem. Hence, using the linear programming model to resolve CRP, we managed to get results for bay sizes 3 × 3, 4 × 3, 3 × 4, 4 × 4, 3 × 5, and 5 × 3 in which there are no more than 15 containers inside the bay. The obtained results are the optimal results for these bay sizes. Additionally, the process of obtaining the results with linear programming model was very slow even for such small bay sizes.

The highlighted results (emboldened) indicate the best results obtained for each test instance considering the different sizes of the bay. It can be seen that the proposed method achieves the best or the second best results for each test instance along with the solution proposed in [24]. For the bay sizes 3 × 3, 4 × 4, 4 × 5 and 4 × 7, the proposed method achieved the best results, even better than [24]. By introducing the linear programming model, we also proved that our method gives optimal results for small bay sizes. Considering that for large bay sizes, where linear programming cannot be used, there are currently no better results than those obtained by the method from [24] or our new method, we can conclude that our method solves CRPs very successfully.

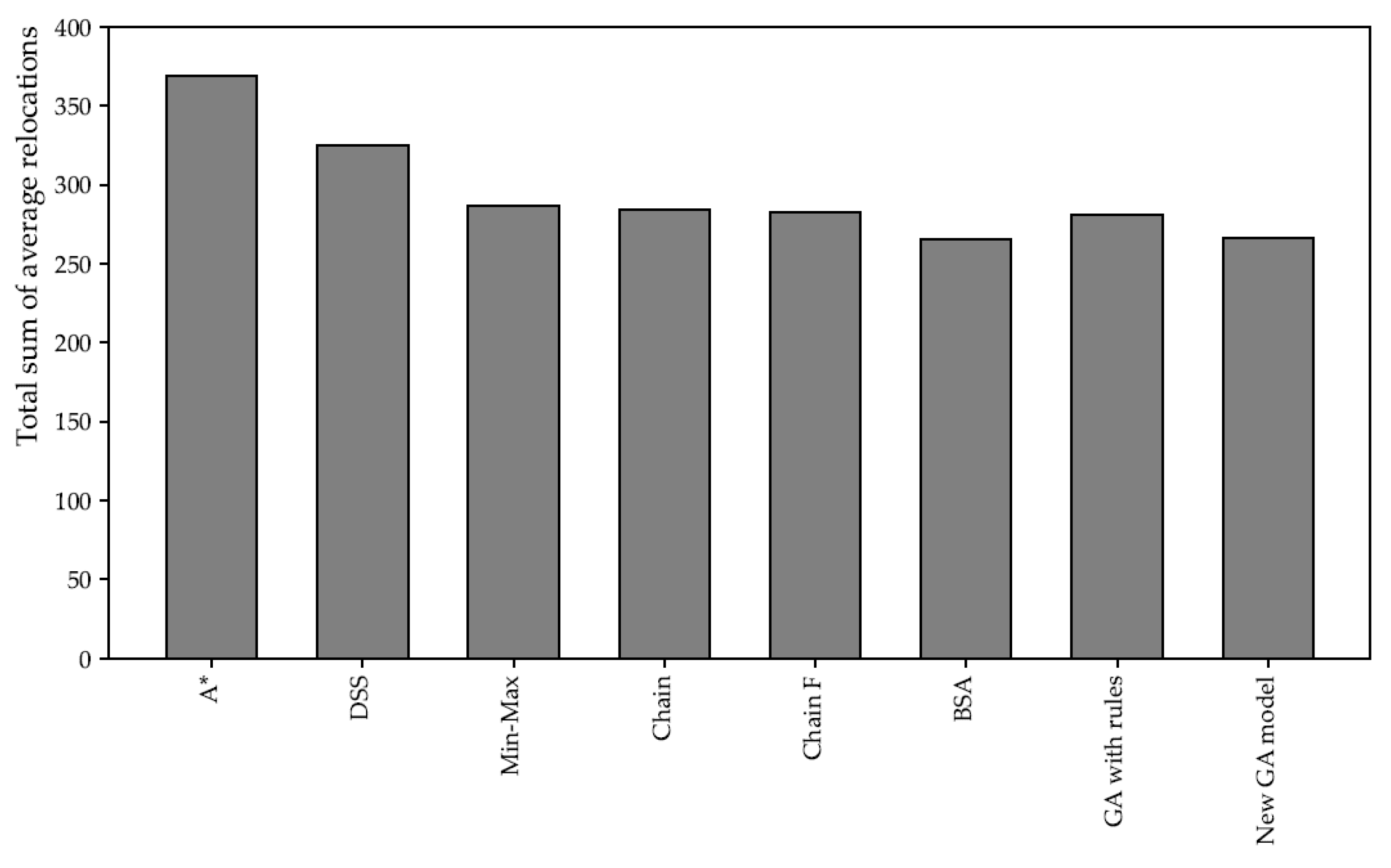
Although the overall results (total sum of average relocations) achieved by the proposed method (266.04) are slightly worse than the method in [24] (265.38), these overall results are very close to each other (Table 2 and Figure 12). Compared to the results obtained in [24], the proposed method is worse by 0.3%. Therefore, approximately less than 1 additional container relocation were performed considering all solutions detected by our method and comparing these solutions to the best model solutions. Considering that there are 20 different test sets with 40 test instances, the total increase of only one additional container relocation is negligible. Moreover, the results of these two techniques are much better than the results of other best methods [17,29,33,35,37,38]. Considering the obtained results, the best third method was our previous model proposed in [17] with an overall result of 280.66. It can be seen that the method proposed in this paper has significantly improved the quality of the solutions found for the CRP test set [24] compared to the previous method. Our new method is for 5.5% better than the previous method, which favored the relocation of blocking containers to the nearest available stacks.

We also confirmed this claim using the statistical t-test, which is used to compare the means of two sample groups. We ran 50 simulations for all test sets of CRP for our previous method [17] and the method proposed in this paper. The null hypothesis (H0) for these two sample groups was that the difference between the means of these groups is zero. Since the t-value was 2218.5, the null hypothesis is definitely rejected. Higher values of the t-value indicate that there is a large difference between the two sample groups, as shown by the results in Table 1 (266.04 vs. 280.66).

As mentioned earlier, our previous method introduces four rules for container relocation, one of which applies to the relocation of the next blocking container depending on the random selection process within the genetic algorithm. The drawback of this method was favoring container relocation to the nearest possible stack satisfying the applied relocation rule, thus optimizing the horizontal movement of reshuffled containers. Since the main objective of the CRP test set in [24] is to minimize the number of reshuffles (relocations of blocking containers), in certain situations, if the reshuffled container is not relocated to the nearest possible stack (column), the total number of relocations will be smaller at the end. 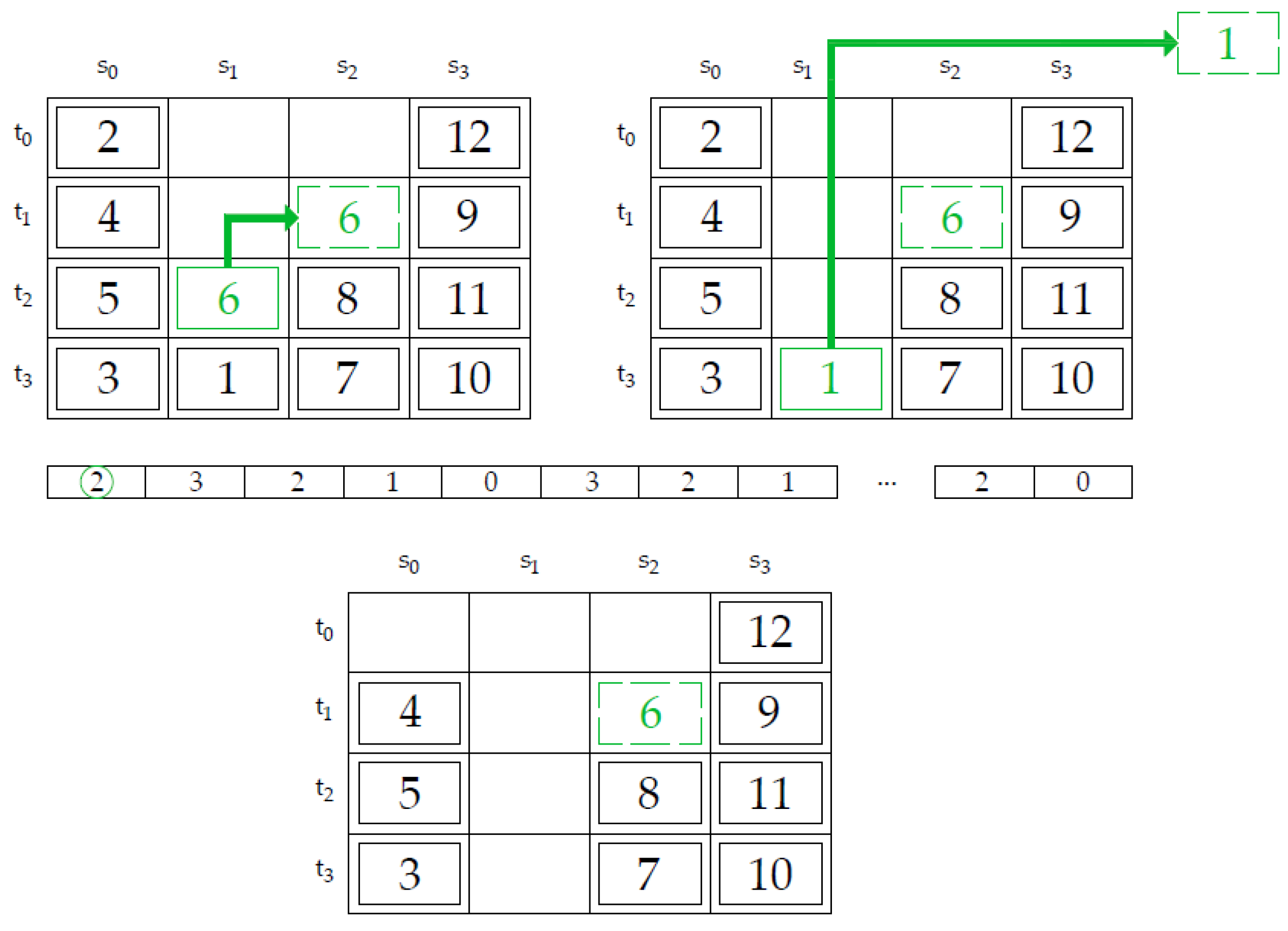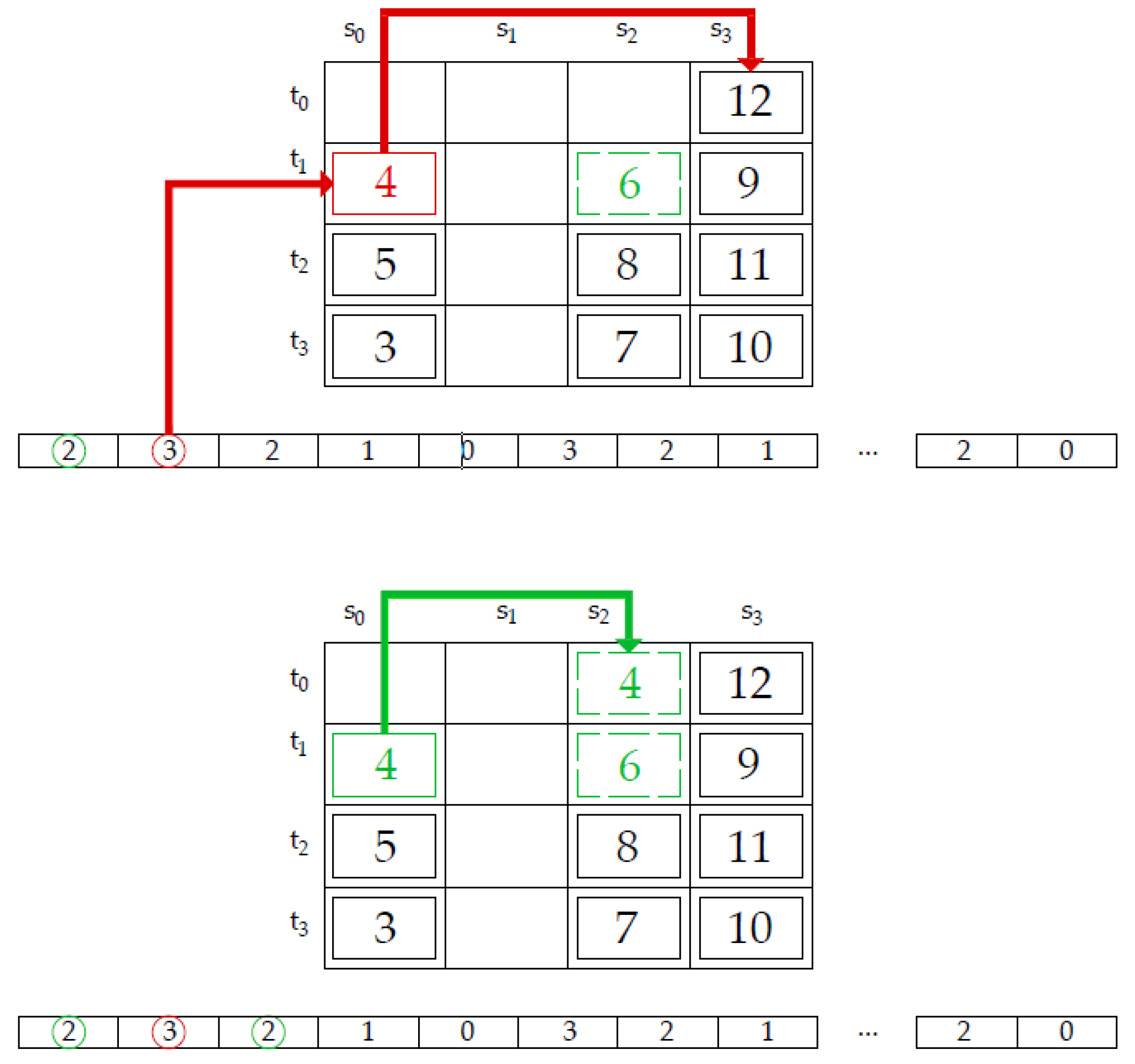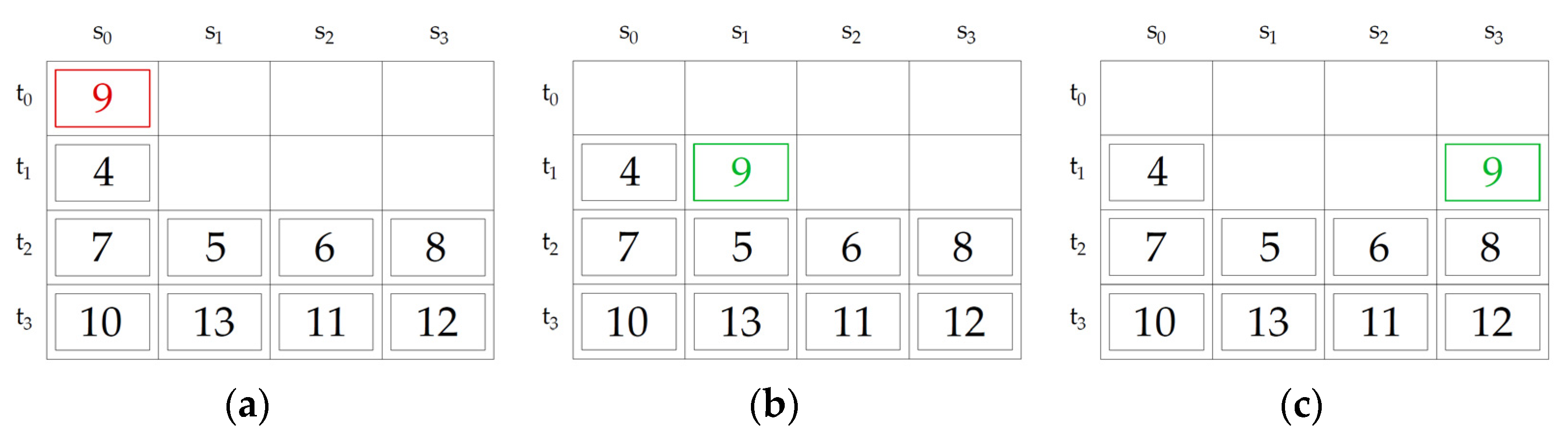In Figure 13, an example of a different solution of container relocation, between our previous method [17] and the proposed method, is shown. As stated before, our previous method proposes four different relocation rules of blocking containers (Rule R1—relocate the container to the nearest stack in which all containers will be retrieved later than the blocking container, Rule R2—relocate the container to the nearest empty stack, Rule R3—relocate the container to the nearest and the lowest stack, and Rule R4—Relocate the container to the nearest stack that is not full to the maximum stacking height). According to Figure 13, the container with priority 4 must be retrieved next. Given that container 9 blocks container 4, it must be relocated. Considering four rules proposed in [17], only rules R3 and R4 are applicable for relocation of the container 9. As the method favors the nearest possible stack, the container with priority 9 will be relocated in stack with index 1 (s₁) (Figure 13b). However, this is not the best possible option because, when the container 5 would have to be retrieved, the container 9 should be relocated over the container 7 or container 6 (i.e., the nearest stack). Thus, there is an additional relocation move that slows down the process of retrieving containers. Our newly proposed method is not restricted with any rule, so the genetic algorithm can randomly determine the stack with index 3 as the position for relocating container 9 (Figure 13c). In this way, containers 4, 5, 6, and 7 can be retrieved without making additional relocations resulting in a faster retrieval process.

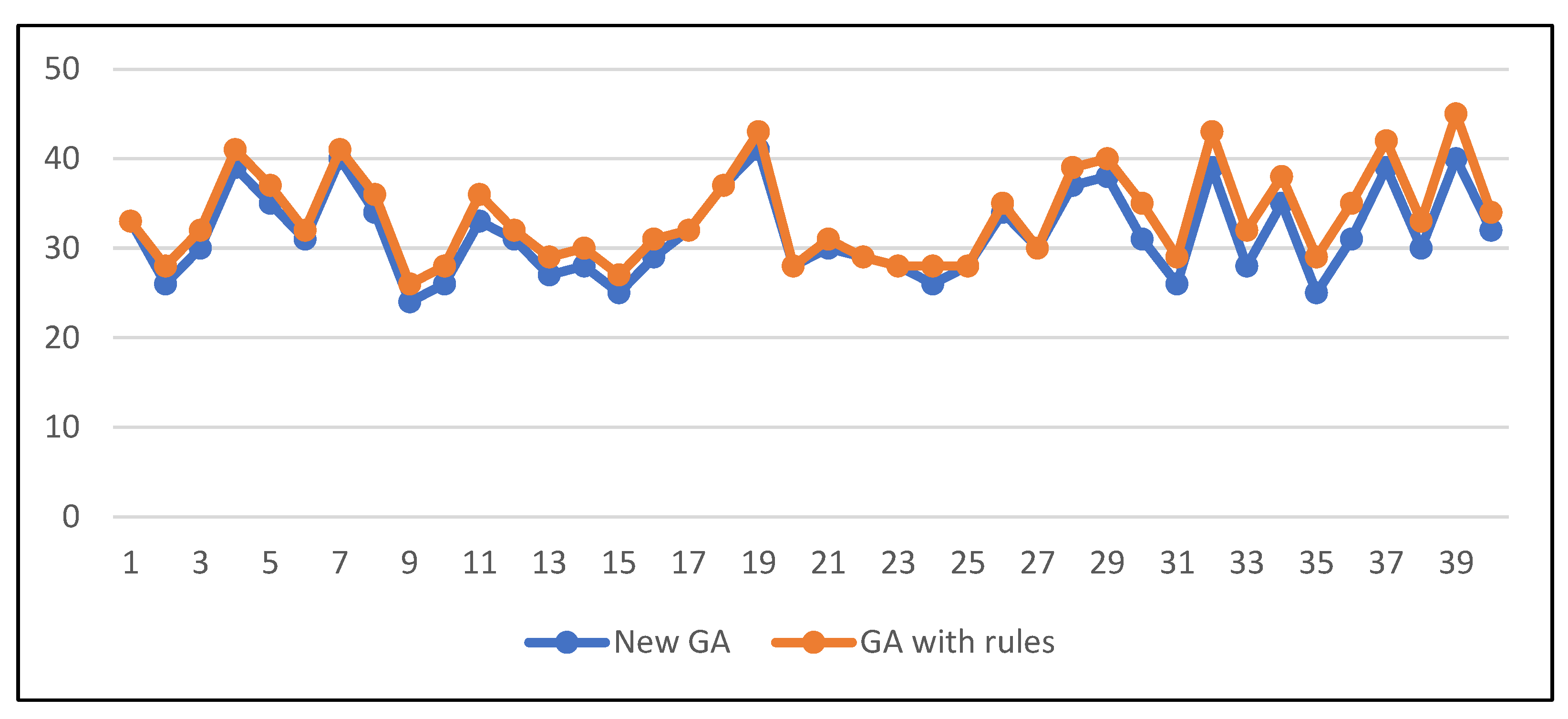
In addition, a comparison of the results of our previous method (GA with rules) and our new method was performed for all 40 instances of the large test set for bay size 6 × 7 (Figure 14). It can be seen that for each instance of the test set, the new method (blue line) finds a solution with less additional relocations than our previous method (orange line). Finally, this is already clear in Table 2, which shows the overall result for the 6 × 7 test set (new method—31.62 vs. GA with rules—33.55).

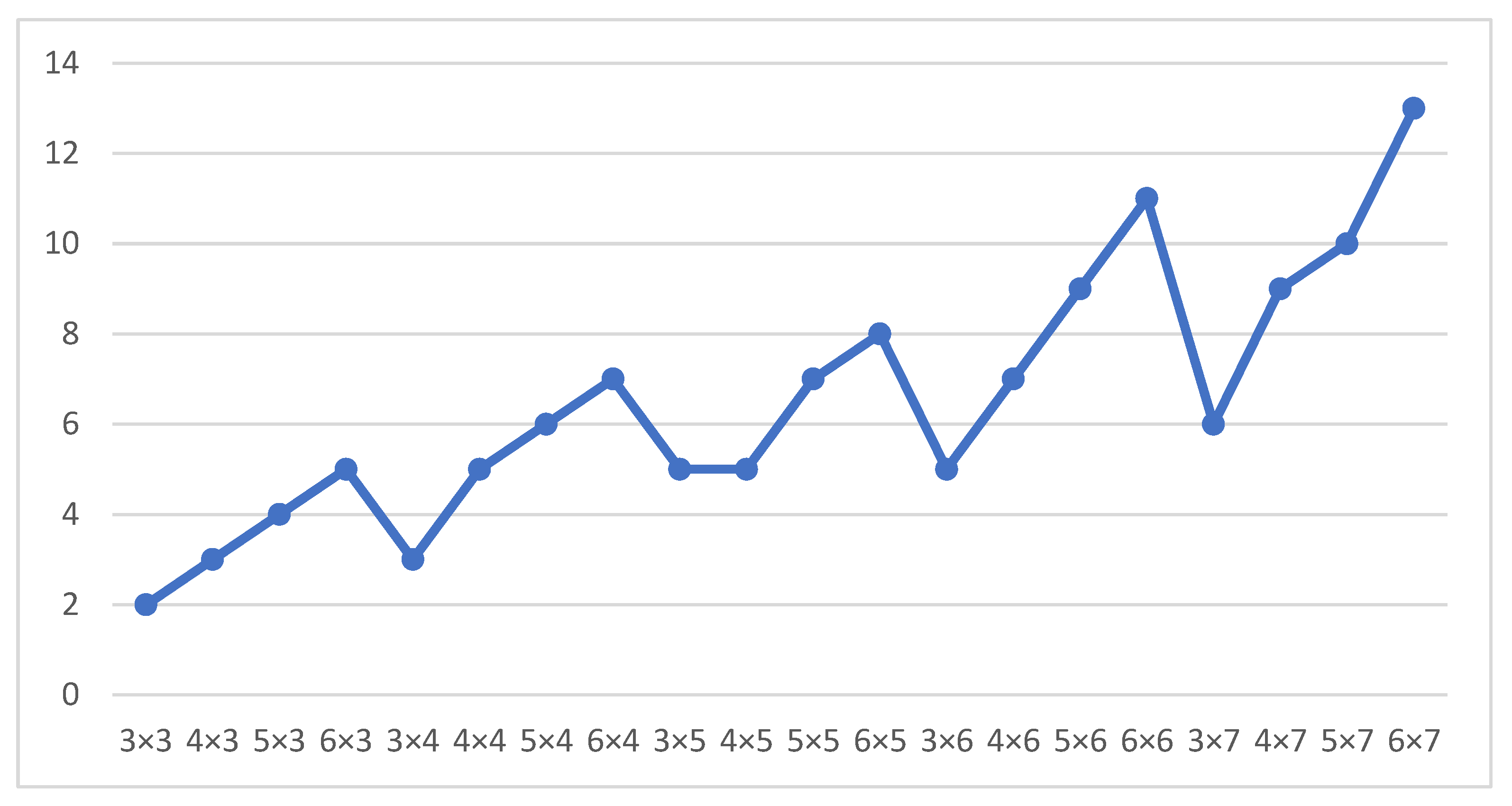
Figure 15 shows the average computational results (in seconds) of our new method for solving CRP of different bay sizes (from 3 × 3 to 6 × 7). Our method determines the solutions fast enough. Of course, the longest time needed to determine the solution was for the 6 × 7 dock size and was 13 s on average. From this we can conclude that the dock size does not affect the performance of our new method too much.

Considering the results obtained with the method proposed in this paper, we proved that the quality of resolving CRP can be further improved.

6. Conclusions

Today, more than 90% of global trade is carried out by sea, which is why seaports play a very important role in world transport. Container transport is one of the most important modes in maritime transportation. As container traffic increases every year, container transportation requires near perfect coordination between all stakeholders, working resources and processes within the entire container transportation system to minimize transit time, delivery time reliability and consequently cost as the main factor for efficient container transportation.

This paper deals with the restricted CRP, which is one of the most important optimization problems in the stacking area of the port container terminal. There is an increasing number of containers that need be stacked in seaports before further shipping. In order to minimize the retrieval time of all containers, that need to be shipped from the stack in the specified order, the relocation of blocking containers must be done in a way that minimizes the number of additional movements (reshuffles) of these blocking containers that stay in the stacking area (it is not yet their turn to ship). Therefore, the crane operation schedule must be optimized to minimize the number of reshuffles, i.e., shorten the time to retrieve the blocking containers, as well as to maximize the utility of each crane operating in the stacking area. Since the restricted CRP optimization problem is NP-hard, it is difficult to find a good solution for retrieving all containers with a minimum number of unproductive reshuffles.

In this paper, a new method based on genetic algorithm was proposed to resolve the restricted CRP at the stacking area of a port container terminal. The experiment of the proposed method was conducted on test cases with 20 various bay sizes (different numbers of tiers and stacks), each of which consists of 40 different test instances. These test instances are the most complex test instances that exist for evaluating models for solving restricted CRPs, since all instances of this test set contain the maximum possible number of containers (maximum occupancy) within the bay considering the bay size of particular CRP test case.

The experimental results prove that the proposed method successfully determines the optimal relocation of blocking containers in order to minimize the total number of relocations within the bay. For all test cases, regardless of the size of the bay, the proposed method proved to be the best or second best solution compared to the well-known solutions of other authors in this field of research.

The only limitation of this method is that it is not possible to verify the quality of the solutions obtained for large test sets (e.g., yard bay with a size of 6 tiers and 6 stacks). Nevertheless, we can assume that the method finds excellent solutions since it has been proven that it gives optimal results for small test sets. For large test sets, this method achieves the best or second-best results compared to other relevant models or methods that solve CRP.

Considering the excellent results obtained by using a genetic algorithm as a major component of the proposed method, we assume that there is a great potential for using nature inspired metaheuristics to solve the restricted CRP. Therefore, in future work, we will focus on improving the method by using other nature-inspired algorithms such as Lion Optimization algorithm [46] or Red deer algorithm [47]. We will try to improve the proposed method so that it is capable of solving 3D CRPs.