Stray Light Nonuniform Background Elimination Method Based on Image Block Self-Adaptive Gray-Scale Morphology for Wide-Field Surveillance
Abstract
:1. Introduction
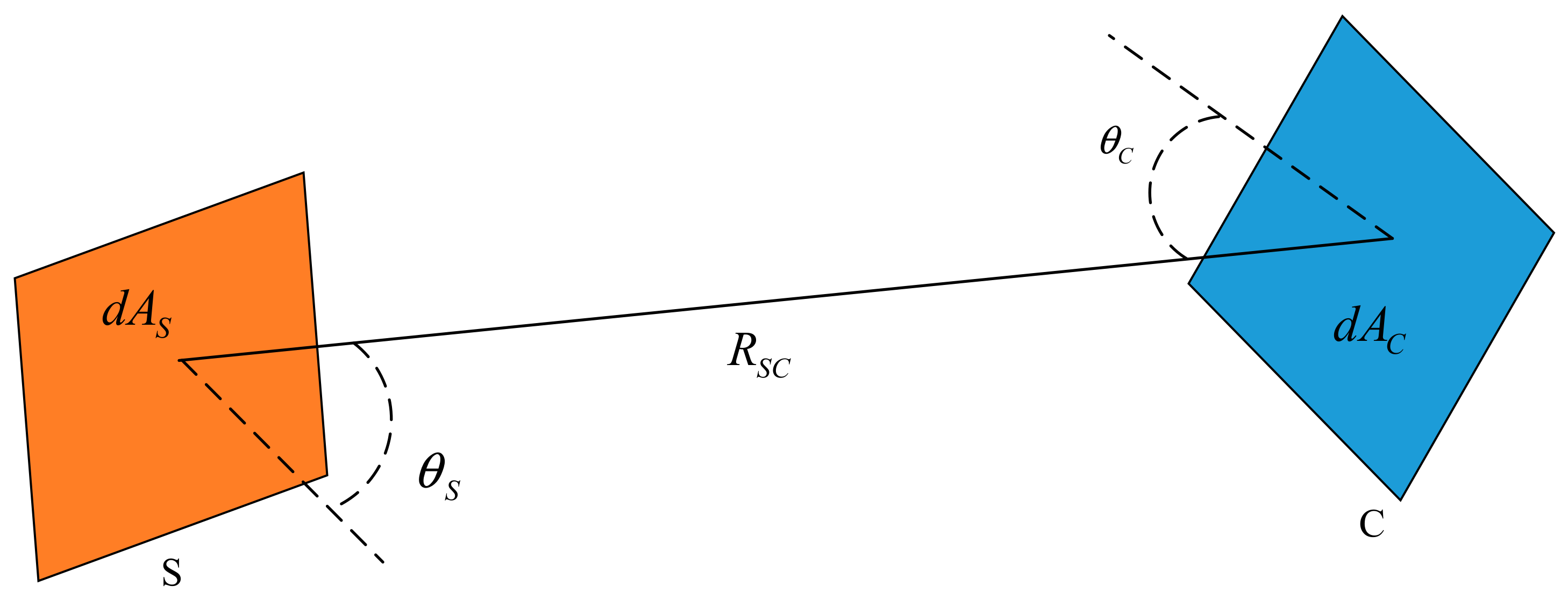
2. Principles of the Formation and Elimination of Stray Light Backgrounds
3. Nonuniform Background Elimination
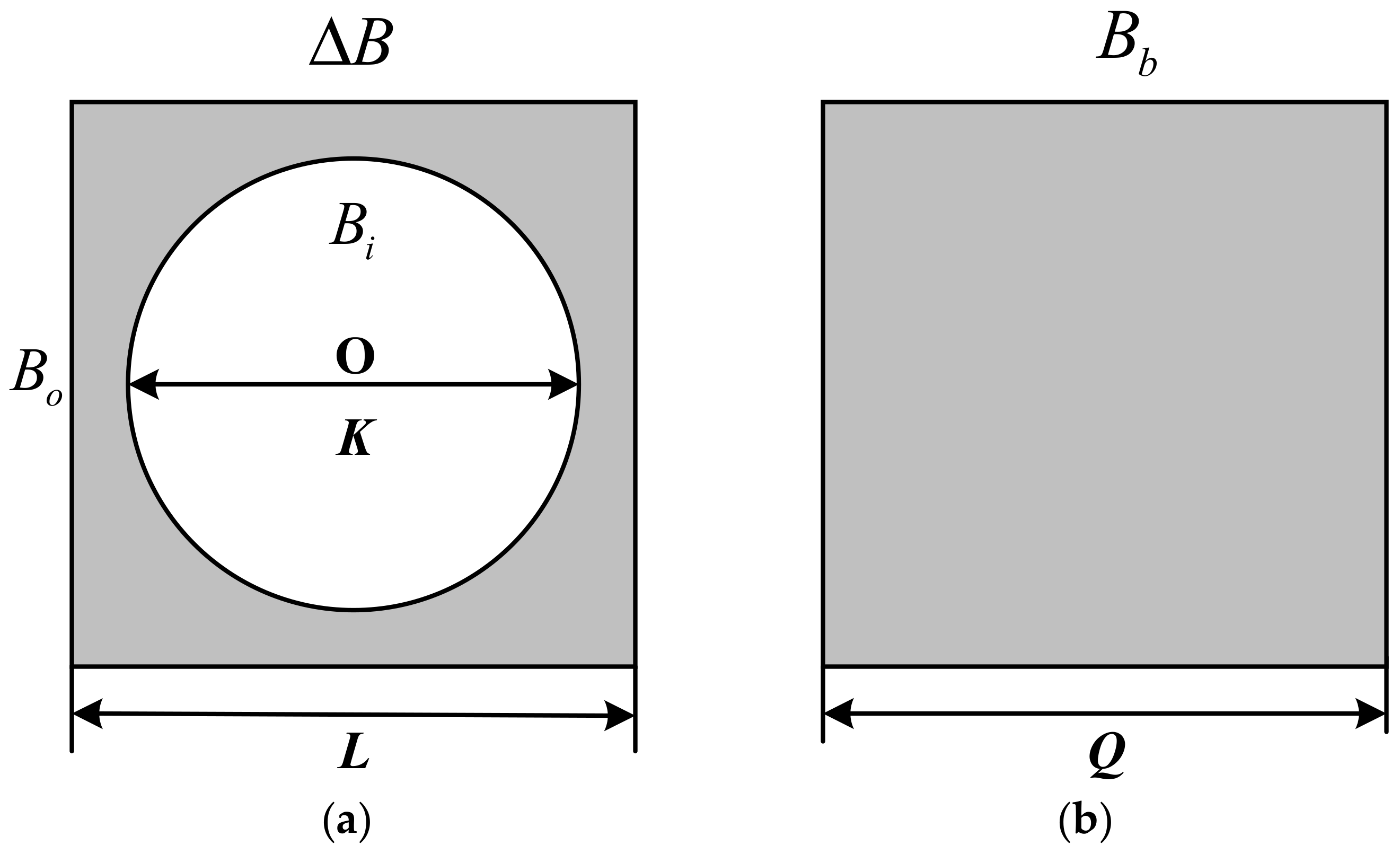
3.1. Definition of Structural Operators
3.2. Self-Adaptive Size Adjustment
3.3. Gray-Scale Morphological Operation
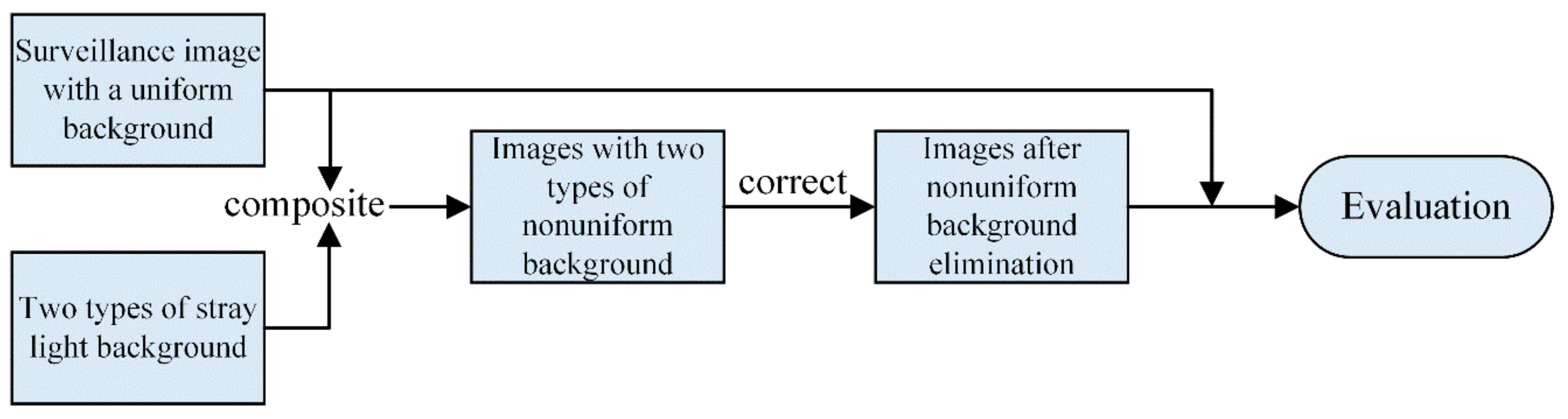
4. Experiments and Discussion
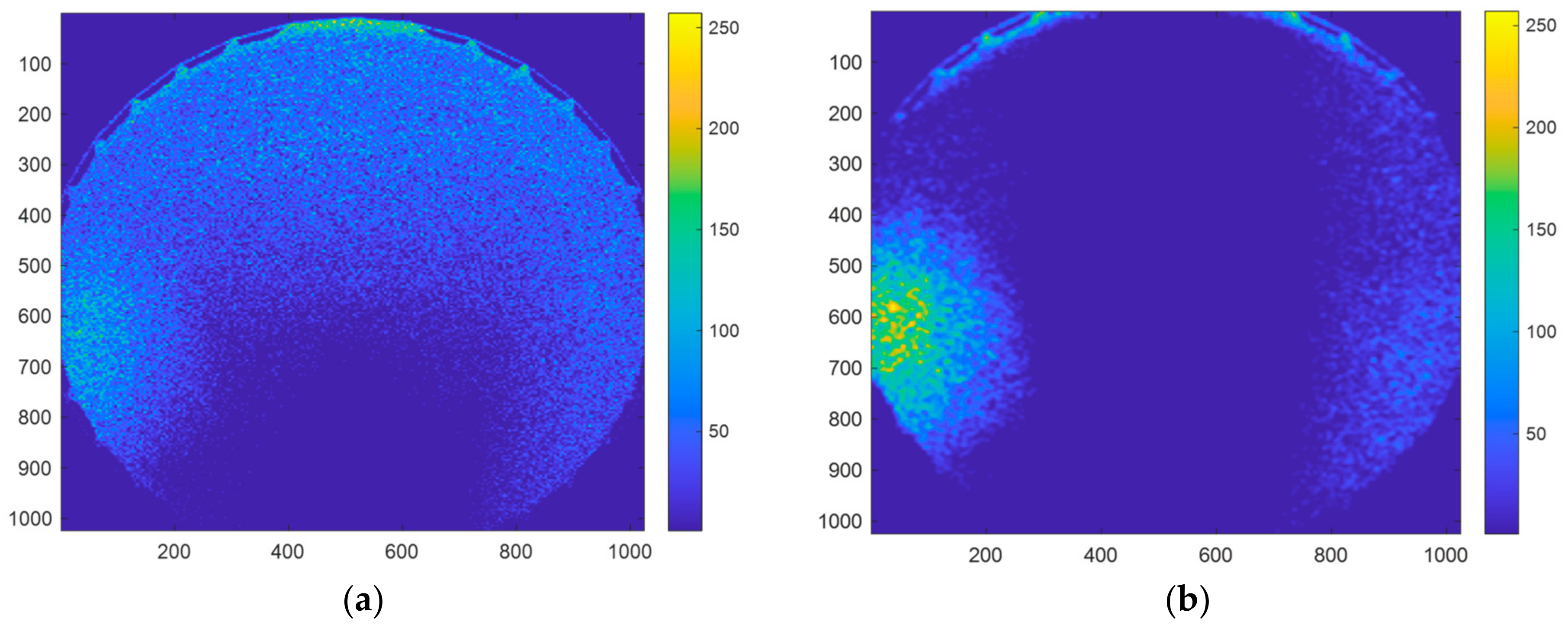
4.1. Simulation Experimental Principles and Results
4.2. Real Image Experimental Results and Discussion
4.2.1. Accuracy of Nonuniform Background Elimination
4.2.2. Accuracy of Target Retention
4.2.3. Computation Time
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xie, D.; Huang, Y.; Yan, C.; Wang, H.; Xu, A. Research on Space-Based Visible Detection for Conical Space Targets. Appl. Sci. 2022, 12, 4426. [Google Scholar] [CrossRef]
- Castronuovo, M.M. Active space debris removal—A preliminary mission analysis and design. Acta Astronaut. 2011, 69, 848–859. [Google Scholar] [CrossRef]
- Muntoni, G.; Montisci, G.; Pisanu, T.; Andronico, P.; Valente, G. Crowded Space: A Review on Radar Measurements for Space Debris Monitoring and Tracking. Appl. Sci. 2021, 11, 1364. [Google Scholar] [CrossRef]
- Ren, S.; Yang, X.; Wang, R.; Liu, S.; Sun, X. The Interaction between the LEO Satellite Constellation and the Space Debris Environment. Appl. Sci. 2021, 11, 9490. [Google Scholar] [CrossRef]
- Garrett, H.B.; Pike, C.P. Collision Frequency of Artificial Satellites: Creation of a Debris Belt. Space Syst. Their Interact. Earth’s Space Environ. 2015, 707–736. [Google Scholar]
- Murtaza, A.; Pirzada, S.; Xu, T.; Liu, J. Orbital Debris Threat for Space Sustainability and Way Forward. IEEE Access 2020, 8, 61000–61019. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, B.; He, F.; Song, K.; He, L. Wide-field auroral imager onboard the fengyun satellite. Light Sci. Appl. 2019, 8, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Brinton, T. SBSS Satellite On Track To Enter Operations in Spring. Space News. 2011, 22, 7. [Google Scholar]
- Sharma, J.; Stokes, G.; von Braun, C. Toward operational space-based space surveillance. Lincoln Lab. J. 2002, 13, 309–334. [Google Scholar]
- Li, S.; Li, C.; Yang, X.; Zhang, K.; Yin, J.F. Infrared Dim Target Detection Method Inspired by Human Vision System. Opt. Int. J. Light Electron Opt. 2020, 206, 164167. [Google Scholar] [CrossRef]
- Yue, W.; Emmett, I. A Practical Approach to Landsat 8 TIRS Stray Light Correction Using Multi-Sensor Measurements. Remote Sens. 2018, 10, 589. [Google Scholar]
- Hardy, T.; Cain, S.; Jeon, J.; Blake, T. Improving space domain awareness through unequal-cost multiple hypothesis testing in the space surveillance telescope. Appl. Opt. 2015, 54, 5481–5494. [Google Scholar] [CrossRef]
- Hardy, T.; Cain, S.; Blake, T. Unequal a priori probability multiple hypothesis testing in space domain awareness with the space surveillance telescope. Appl. Opt. 2016, 55, 4036–4046. [Google Scholar] [CrossRef]
- Liu, D.; Wang, X.; Li, Y.; Xu, Z.M.; Wang, J.N.; Mao, Z.H. Space target detection in optical image sequences for wide-field surveillance. Int. J. Remote Sens. 2020, 41, 1–12. [Google Scholar] [CrossRef]
- Cao, X.; Rong, S.; Liu, Y.; Li, T.Y.; Wang, Q.; He, B. Non-uniform illumination correction for underwater image using fully convolutional network. IEEE Access 2020, 8, 109989–110002. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Peng, L.; Zhang, T.; Liu, Y.; Li, M.; Peng, Z. Infrared Dim Target Detection Using Shearlet’s Kurtosis Maximization under Non-Uniform Background. Symmetry 2019, 11, 723. [Google Scholar] [CrossRef] [Green Version]
- Wen, J.; Li, S.; Sun, J. A new binarization method for non-uniform illuminated document images. Pattern Recogn. 2013, 46, 1670–1690. [Google Scholar] [CrossRef]
- Liu, N.; Xie, J. Interframe phase-correlated registration scene-based nonuniformity correction technology. Infrared Phys. Technol. 2015, 69, 198–205. [Google Scholar] [CrossRef]
- Bai, X.; Zhang, B.; Du, Z.; Liu, T.; Jin, T.; Xue, B.D.; Zhou, F.G. Survey on dim small target detection in clutter background: Wavelet, inter-frame and filter based algorithms. Procedia Eng. 2011, 15, 479–483. [Google Scholar] [CrossRef] [Green Version]
- Xi, J.; Wen, D.; Ersoy, O.; Yi, H.W.; Yao, D.L.; Song, Z.X.; Xi, S.B. Space debris detection in optical image sequences. Appl. Opt. 2016, 55, 7929–7940. [Google Scholar] [CrossRef]
- Mustafa, W.A.; Yazid, H. Background correction using average filtering and gradient based thresholding. J. Telecommun. Electron. Comput. Eng. 2016, 5, 81–88. [Google Scholar]
- Jiang, J.; Li, L.; Zhang, G. Robust and accurate star segmentation algorithm based on morphology. Opt. Eng. 2016, 55, 6. [Google Scholar] [CrossRef] [Green Version]
- Sun, T.; Xing, F.; Bao, J.; Ji, S.; Li, J. Suppression of stray light based on energy information mining. Appl. Opt. 2018, 57, 9239–9245. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Liu, D.; Yan, C.; Hu, C.H. Stray light nonuniform background correction for a wide-field surveillance system. Appl. Opt. 2020, 59, 10719–10728. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Liu, D.; Yan, C.; Hu, C.H. Stray Light Elimination Method Based on Recursion Multi-Scale Gray-Scale Morphology for Wide-Field Surveillance. IEEE Access 2021, 9, 16928–16936. [Google Scholar] [CrossRef]
- Bennett, H.E. Scattering characteristics of optical materials. Opt. Eng. 1978, 17, 480–488. [Google Scholar] [CrossRef]
- Li, J.; Yang, Y.; Qu, X.; Jiang, C. Stray Light Analysis and Elimination of an Optical System Based on the Structural Optimization Design of an Airborne Camera. Appl. Sci. 2022, 12, 1935. [Google Scholar] [CrossRef]
- Wei, L.; Yang, L.; Fan, Y.-P.; Cong, S.-S.; Wang, Y.-S. Research on Stray-Light Suppression Method for Large Off-Axis Three-Mirror Anastigmatic Space Camera. Sensors 2022, 22, 4772. [Google Scholar] [CrossRef]
- Xu, Z.; Hu, C.; Yan, C. Vane structure optimization method for stray light suppression in a space-based optical system with wide field of view. Opt. Eng. 2019, 58, 1. [Google Scholar] [CrossRef]








| Stray Light Background | THT | MIF | INTHT | IBSGM |
|---|---|---|---|---|
| First type | 8.4982 | 12.4052 | 5.0044 | 4.8320 |
| Second type | 4.7121 | 7.2477 | 3.1371 | 2.6711 |
| Figure 11a | Figure 11b | Figure 11c | ||||
|---|---|---|---|---|---|---|
| Background Residual | Mean | Standard Deviation | Mean | Standard Deviation | Mean | Standard Deviation |
| THT | 21.2518 | 9.3417 | 21.7236 | 9.1999 | 21.8202 | 9.3119 |
| MIF | 3.1559 | 3.0220 | 2.1904 | 2.4297 | 2.4088 | 2.5845 |
| INTHT | 0.4408 | 0.4983 | 0.4270 | 0.4077 | 0.5071 | 0.5887 |
| IBSGM | 0.0231 | 0.1502 | 0.0249 | 0.1559 | 0.0245 | 0.1736 |
| Method | Figure 12a | Figure 12b | Figure 12c |
|---|---|---|---|
| THT | 83% | 85% | 81% |
| MIF | 86% | 88% | 85% |
| INTHT | 93% | 96% | 92% |
| IBSGM | 98% | 99% | 97% |
| Method | Computation Time (s) |
|---|---|
| THT | 0.517 |
| MIF | 3.521 |
| INTHT | 0.436 |
| IBSGM | 6.934 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Wang, X.; Li, Y. Stray Light Nonuniform Background Elimination Method Based on Image Block Self-Adaptive Gray-Scale Morphology for Wide-Field Surveillance. Appl. Sci. 2022, 12, 7299. https://doi.org/10.3390/app12147299
Wang J, Wang X, Li Y. Stray Light Nonuniform Background Elimination Method Based on Image Block Self-Adaptive Gray-Scale Morphology for Wide-Field Surveillance. Applied Sciences. 2022; 12(14):7299. https://doi.org/10.3390/app12147299
Chicago/Turabian StyleWang, Jianing, Xiaodong Wang, and Yunhui Li. 2022. "Stray Light Nonuniform Background Elimination Method Based on Image Block Self-Adaptive Gray-Scale Morphology for Wide-Field Surveillance" Applied Sciences 12, no. 14: 7299. https://doi.org/10.3390/app12147299
APA StyleWang, J., Wang, X., & Li, Y. (2022). Stray Light Nonuniform Background Elimination Method Based on Image Block Self-Adaptive Gray-Scale Morphology for Wide-Field Surveillance. Applied Sciences, 12(14), 7299. https://doi.org/10.3390/app12147299





