Abstract
Movable object type wave power generators produce energy through the process of primary energy conversion, which converts the potential and kinetic energy of the waves into mechanical energy, secondary energy conversion that converts it into energy for generator operation using a mechanical system or hydraulic system, and final energy conversion, the last step in power generation. The secondary energy conversion system that transmits and amplifies energy according to the primary energy conversion needs to secure durability while power generation performance varies greatly depending on how the secondary energy conversion system is built. As a result, reliability assessment of systems based on system engineering are a very important issue. Therefore, in this study, for the conceptual design based on reliability assessment of the secondary energy conversion system, the system concept was established using the integrated computer-aided manufacturing (ICAM) definition for function modeling (IDEF0), a system analysis method, while necessary equipment and process flow diagrams (PFD) were derived. In addition, the database (DB) and formula of the secondary energy conversion system were constructed, and reliability assessment algorithms and programs were developed. Finally, the PFD and reliability assessment program were verified by applying them to a representative movable object type wave power generator.
1. Introduction
Through the Paris Climate Change Accord in 2015, it became mandatory to reduce the emission of carbon dioxide worldwide. The government of the Republic of Korea also announced a significant reduction in greenhouse gas emissions by 37% compared to business as usual (BAU) by 2030 [1]. As a result, the era of decarbonization, which resolves the emission of carbon dioxide, the main cause of environmental pollution, has begun, and interest in carbon-free, pollution-free renewable energy is increasing significantly. Energy decarbonization means that the amount of carbon per unit mass of the main energy source (coal, oil, natural gas, etc.) decreases. Energy decarbonization can be achieved if renewable energy becomes the main energy source.
Among the various renewable energy sources, wave energy is one of the most popular sources of energy due to the geographical characteristics of Korea, which has three sides open to the sea. The amount of wave energy in Korea is about 5.5 million kW [2], and it is important to utilize it well. However, converting this energy into electricity is not easy. Although it has been attempted from the late 19th century, it took a long time to commercialize it due to low power conversion efficiency, while compared to other renewable energy power generation devices that have already been formalized, various types of wave power generators are still being researched and developed.
Wave power generators creating power by using the energy of waves produce energy through the process of primary energy conversion converting from the potential and kinetic energy of the waves to mechanical energy, secondary energy conversion converting energy for generator operation using a mechanical system or hydraulic system, and final energy conversion for power generation.
The primary energy conversion is classified according to differences in the method of absorbing wave energy such as rotational displacement, horizontal or vertical displacement when absorbing energy from waves. Representatively, there are oscillating water column (OWC), overtopping, and movable object type wave power generators according to the primary energy conversion method as shown in Figure 1. Among them, the movable object type wave power generator is very advantageous in terms of energy-absorbing efficiency because wave energy directly affects the floating body. In addition, the point absorber wave power generator having a smaller floating body size than the wavelength is advantageous for applying to multiple generations using the same sized structures or installing in parallel with other energy sources. Therefore, many studies have been conducted recently.
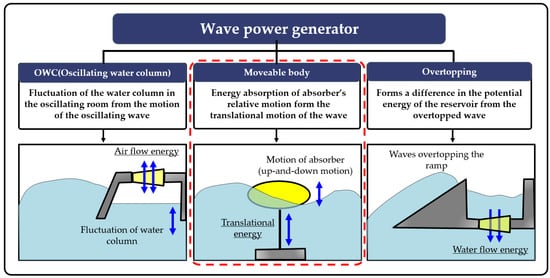
Figure 1.
Classification of wave power generators.
The whole process of energy conversion of primary energy conversion, secondary energy conversion, and final energy conversion through movable object type wave power generators can be expressed as shown in Figure 2. In the primary energy conversion, the vertical or horizontal reciprocating motion of the waves is transferred to the vertical or horizontal reciprocating motion of the floating body. In the second energy conversion, this motion is transmitted to a rotational motion using mechanical systems such as gears, pulleys, gearboxes, or hydraulic system elements such as hydraulic cylinders, hydraulic pumps, and hydraulic motors. This rotational motion is transmitted through the shaft to drive a generator. In the final energy conversion, this motion is converted into electrical energy through a generator.

Figure 2.
Step-by-step process of energy conversion through movable object type wave power generator.
Until now, for the primary energy conversion system of the movable object type wave power generator, studies such as comparing and verifying the performance by changing the shape or angle of incidence of the floating body have been actively conducted [3,4,5,6,7,8,9]. In addition, many studies on efficiency analysis using experiments and simulation techniques have been performed on the movable object type wave power generator [10,11,12,13,14].
The secondary energy conversion system of a movable object type wave power generator is typically a mechanical system type that transmits energy transmitted from the motion of a floating body in rotational motion using various gear systems, pulleys, and gearboxes. The wave power generator applying Salter’s duck type WEC is a representative movable object type wave power generator to which the secondary energy conversion mechanical system is applied [15]. In addition, there is a wave power generator to which a secondary energy conversion hydraulic system is attached that operates a hydraulic pump and motor by generating a pressure difference of a fluid through a hydraulic cylinder, or operates a turbine with a flow of fluid using energy transmitted from the motion of a floating body. Representatively, the generators that apply wavestar type WEC belong to this category [16]. In addition, there are hybrid generators that use both secondary energy conversion mechanical and hydraulic systems in combination.
Many studies have previously been conducted on the efficiency analysis of these secondary energy conversion systems. With the theme of the secondary energy conversion mechanical system, a system that can amplify or reduce the final efficiency by combining the mechanism of the gear system was constructed [17]. The system consists of 12 sets of parallel gears that transmit torque to a sun gear through a bevel gear, one-way gear. A system using a double rack and pinion gear system and a shaft were applied. This system converts the horizontal reciprocating motion of the wave into the reciprocating motion of the arm and rack gear and converts it into the rotational motion of the pinion gear [18]. In addition, a multi-level secondary energy conversion system was developed that converts bidirectional rotational motion into unidirectional motion using bearings and bevel gears, and then applies a power transmission system to increase the rotational speed [19]. A complex system was constructed in which the toothed gear rack attached to the buoy rotates the pinion gear, and the other pinion gear rotates in the opposite direction to generate power. This system is attached with a revolution per minute (RPM) multiplier to improve the RPM of the output shaft [20]. For pulleys, not gears, a bidirectional driven float-type wave power generator with six pulleys and two ratchet wheels was designed [21].
As the theme of the secondary energy conversion hydraulic system, a power take-off (PTO) system using a discrete displacement cylinder was constructed. It transfers energy by changing the flow of oil or gas and converts the flow energy into rotational energy using a hydraulic motor [22]. Additionally, a hydraulic pump with secondary control hydrostatic transmission was applied. This system produces pulley torque using buoy and counterweight, increases the pulley torque produced using the gearbox, and uses the increased torque for the hydraulic pump and motor [23].
As a result of previous research analysis, various types of secondary energy conversion systems can be applied. However, contrary to the diversity of the configuration of the secondary energy conversion system, it is difficult to find a study for the conceptual design of the system through system analysis and generalization. Since the power generation performance of the system varies depending on the form of the secondary energy conversion system, the reliability assessment of the system in the conceptual design stage is a very important issue. For this, it is necessary to generalize the power transmission form of the secondary energy conversion system by assessing the reliability of the system using appropriate methods. Regarding the reliability assessment of the engineering structure, various techniques considering uncertainty have been actively studied [24,25,26,27], and studies related to reliability assessment of wave power generator systems have been conducted [28,29].
Therefore, in this study, for the conceptual design of the secondary energy conversion system used in the movable object type wave power generator, first, the system concept is established using the integrated computer-aided manufacturing (ICAM) definition for function modeling (IDEF0) system analysis method for the secondary energy conversion system, and the process flow diagrams (PFD) were derived. Second, the algorithm for estimating the efficiency of the secondary energy conversion system was formed by applying the derived PFD, and based on this, a reliability assessment program was developed. Finally, verification was performed by applying the PFD and program developed in this study to a representative movable object type wave power generator applying Salter’s duck type WEC. Ultimately, this study focused on the establishment of the conceptual design process of the movable object type wave power generator by developing the reliability assessment algorithm and program of the secondary energy conversion system. By using the conceptual design algorithm derived through system generalization in this study, it is judged that the appropriate conceptual design based on reliability assessment can be performed no matter what type of secondary energy conversion system is configured, while the presentation of a conceptual design guideline based on reliability assessment is of great value. Furthermore, through a software update, the reliability assessment algorithm of all other equipment included in the secondary energy conversion system of the wave power generator will be included, and the DB of other equipment will be additionally secured. Updating the software developed in this study and securing additional DB, will be used as the basis for the development of the secondary energy conversion system of the actual wave power generator.
2. System Analysis of Secondary Energy Conversion System
2.1. System Generalization Using IDEF0
IDEF0 is the first functional modeling method developed in the 1970s to model the relationship between the functions and roles of systems in the United States Air Force’s ICAM project [30]. This model structurally depicts the functions of the system environment and information or objects related to those functions using a graphical representation.
The IDEF0 model consists of graphics for relational data modeling, as shown in Figure 3. The middle box represents the function performed by the role elements. In addition, according to the role, four arrows called input, control, output, mechanism (ICOM) define the relationship between the functions of the system and additionally express auxiliary information through text and description. Input arrow means data or object that is converted into output by function. Control arrow means a condition or environment for controlling the performance of a function. Output arrow means data or objects produced by a function. Mechanism arrow means a means or program for performing a function [31]. Multiple inputs, controls, and mechanisms are entered for a single box, and multiple outputs are generated, but not all of these inputs, controls, and mechanisms work simultaneously for all outputs. That is, a combination of input, control, and mechanism produces a combination of different outputs.
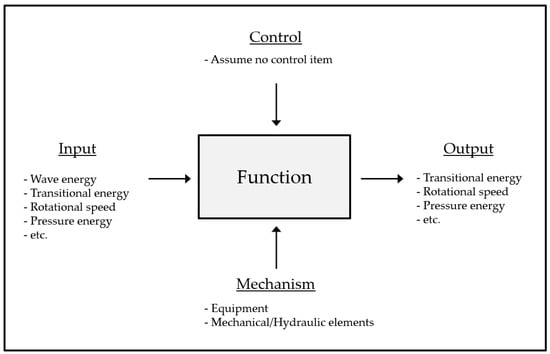
Figure 3.
IDEF0 basic formalism.
For the conceptual design of the secondary energy conversion systems, based on the system analysis of representative types of the movable object type wave power generator performed in the previous section, in this section, the energy conversion type of the system is expressed and generalized by IDEF0 modeling method. It is shown in Figure 4.
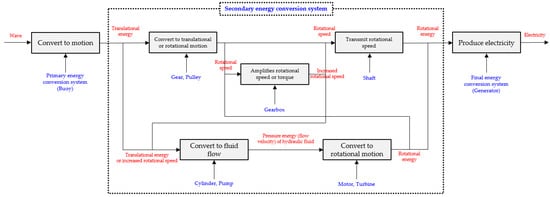
Figure 4.
IDEF0 modeling of secondary energy conversion system.
The input is given the motion of the movable body by wave energy, and thus the displacement is derived by output according to the transmission as a function. Control includes rules and procedures for control. However, in this study, because it is a modeling of functions for one system, control items were not considered. The mechanism on the lower side represents a means to perform a function, in the system of this study, the means for performing the function is the mechanical equipment, so the IDEF0 model was constructed using equipment as a means. For example, for the conversion to rotational motion, gear and pulley were set as the mechanism, and accordingly, the output derived by applying the mechanism to the input transmitted in the previous step was provided as the input of the function in the next step.
Finally, in this paper, the energy conversion process was verified through the functional analysis of the secondary energy conversion system of the movable object type wave power generator using the IDEF0 modeling method. In addition, through the functional analysis results, eight equipment-pieces necessary for the configuration of the system were derived. The derived equipment is shown in Table 1.

Table 1.
Equipment and each input/output obtained through IDEF0 modeling.
2.2. Process Flow Diagram (PFD)
Through the functional analysis using the IDEF0 method in the previous section, the necessary equipment for performing each function was derived. According to the function of the derived equipment, the gear or pulley of the mechanical system is in charge of translation of translational or rotational motion, the gearbox amplifies the number of revolutions using the gear ratio, and the shaft is responsible for the transmission function of the rotation axis. The hydraulic system is also responsible for converting translational motion using a cylinder and generating rotational energy using a motor or turbine. Accordingly, in this section, based on the logic of secondary energy conversion, secondary energy conversion systems are constructed as an appropriate combination of each derived equipment.
Therefore, the case of each representative secondary energy conversion system constructed by applying mechanical and hydraulic system equipment is shown in Figure 5 and Figure 6 as a process flow diagram. If the input and output components of the equipment before and after, such as Figure 5 and Figure 6, are matched, it is possible to diversify the system configuration with a combination of various equipment, but the autonomy for arrangement must be guaranteed. In this study, for the secondary energy conversion mechanical system and hydraulic system, the eight most representative PFDs were derived based on the literature review results of the existing secondary energy conversion system. More various PFDs can be derived, but in general, the more the equipment of the system, the lower the efficiency. Therefore, the PFD according to the combination of more equipment was not derived in this study.
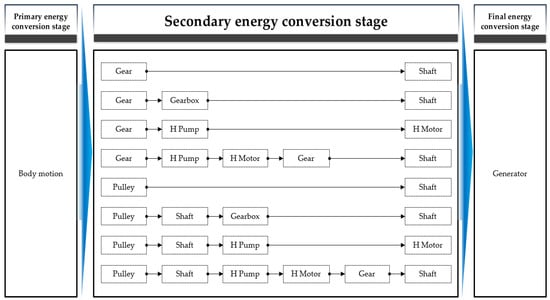
Figure 5.
PFD of secondary energy conversion system started with the mechanical system.
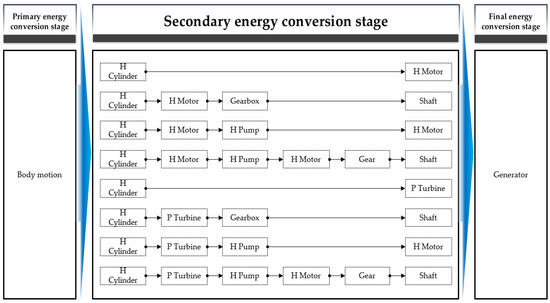
Figure 6.
PFD of secondary energy conversion system started with the hydraulic system.
3. Development of Reliability Assessment Program
In this chapter, according to the system configuration of the PFD derived in the previous chapter, a program was developed to assess the reliability when each equipment of the secondary energy conversion mechanical system transmits energy. The RPM generated by the primary energy conversion is the input to the secondary energy conversion formula, and the RPM by the secondary energy conversion is the output. To express this, a DB and a formula for reliability assessment of gears and pulleys, which are the equipment of the mechanical system, were constructed. Additionally, when evaluating the performance of secondary energy conversion including the hydraulic system, the efficiency at each stage was assumed to be 85% for the hydraulic pump [32] and 90% for the hydraulic motor [33].
3.1. DB and Formula for Reliability Assessment of Gear
The efficiency DB of the gear, which is the main mechanical equipment of the secondary energy conversion system, was built, and the energy conversion formula for reliability assessment was built using this DB. In the gear system, power loss does not occur in the shaft and oil, while power loss due to gear friction is the most significant part. Therefore, assuming that there is no loss due to friction of the gear system, efficiency can be calculated by considering only the loss of the gear itself depending on the shape, size, and material of the gear. In this study, the transmission efficiency DB of the gear system was built based on the commercial products of KHK Gears and is shown in Table 2. It is classified according to category and type [34]. The efficiency value can be calculated through the DB of the table. For reference, in general, as the gear stage increases, more energy loss occurs, and thus efficiency decreases. In addition, the formula for applying the efficiency of the gear system is as shown in the below Equation (1).
where, is the revolution per minute (RPM) of the rotor shaft (rpm); is the RPM of the output shaft (rpm); is the number of teeth in the gear 1; is the number of teeth in gear 2; η is the efficiency of the gear (%).

Table 2.
Efficiency DB for each type of gear [34].
The ratio of the number of teeth of the gear becomes the ratio of the rotational speed. Accordingly, the performance formula by secondary energy conversion using gears, theoretically without loss, is derived as in Equation (1).
3.2. DB and Formula for Reliability Assessment of Pulley
For the pulley, which is the main mechanical equipment of the secondary energy conversion system, an efficiency DB and formula were built. First, the efficiency of the pulley system is determined by the performance of the belt. Therefore, the transmission efficiency DB of the pulley system is built on the basis of commercial products and is shown in Table 3. The items are company, belt type, and model. The reliability assessment program was configured to use DB by selecting the type of classical V-belts, cogged V-belts, timing belts, etc., from the pulley list. In addition, the formula for evaluating the performance to apply the efficiency of the pulley system is given Equation (2). As shown below, the pulley system uses the same performance formulas as the gear, and only the expression of the ratio is different.
where, is the RPM of the rotor (rpm); is the RPM of the output shaft (rpm); is the diameter of the rotor (m); is the diameter of the output shaft (m); η is efficiency of the pulley (%).

Table 3.
Efficiency DB for each type of belt [35,36].
Since the circumferential speeds of the rotor and shaft are the same, the ratio of the diameter between the pulleys is the ratio of the rotational speed. Accordingly, the performance formula by secondary energy conversion using pulleys without loss is derived as in Equation (2). Finally, in this study, the efficiency DB and formula of the gear and pulley were constructed, and a program was developed to assess the reliability of the secondary energy conversion mechanical system using these.
3.3. Reliability Assessment Algorithms & Program
The algorithm for assessing the reliability of the secondary energy conversion using the DB and formula of the gear and pulley built in the previous section is shown in Figure 7. As in the algorithm, according to the type and specifications of the equipment, the corresponding efficiency DB and formula were constructed. Accordingly, the RPM generated by the primary energy conversion is the input to the secondary energy conversion formula, and the RPM by the secondary energy conversion is the output.
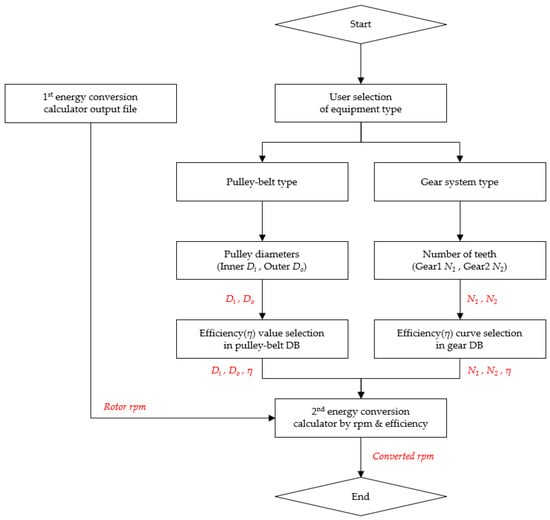
Figure 7.
Reliability assessment algorithm of secondary energy conversion mechanical system.
The graphical user interface (GUI) of the reliability assessment program developed by applying the efficiency DB based on the commercial products according to the algorithm is shown in Figure 8. For example, if the gear and pulley systems are selected, and the transmission efficiency and basic properties of the selected system are input, the efficiency and RPM are derived using the built-in performance formula. On the GUI, the weight factor of RPM () is a factor that applies the amount of change in RPM when there is an RPM converter such as a pump or gearbox system, not a gear or pulley system. In addition, the weight factor of efficiency () is a factor that applies the efficiency change when there is an efficiency converter other than a gear and pulley system. Weight factor is used to account for the variation in each stage when assessing the reliability of the multi-stage system. Finally, using the reliability assessment program developed in this study, the performances of each type of equipment that make up the system are derived, and the guideline can be presented when designing the model. In the future, through the continuous update of the program, the reliability assessment algorithm of all other equipment included in the secondary energy conversion system of the wave power generator will be included, and the DB of other equipment will be additionally secured. Accordingly, it will be used as the basis for the development of the secondary energy conversion system of the actual wave power system.
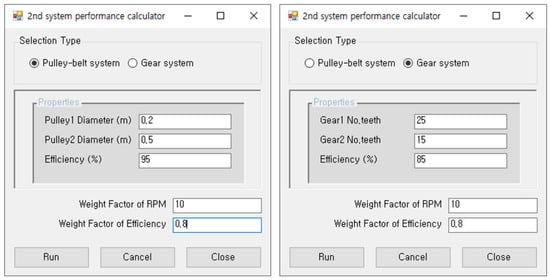
Figure 8.
GUI of reliability assessment program of secondary energy conversion mechanical system.
4. Verification
4.1. Movable Object Type Wave Power Generator Applying Salter’s Duck Type WEC
In this chapter, verifications and applications of the derived PFD and the developed reliability assessment programs for conceptual design were performed. Since there is a limit in verifying all derived PFDs, the movable object type wave power generator applying Salter’s duck type WEC was selected as a verification example. This is composed of a gear or pulley system and is applied with a secondary energy conversion mechanical system that is as easy to design as a basic shape. First, the mechanism of the Salter’s duck type WEC was analyzed to assess the reliability of the wave power generator applying it.
The movable object type wave power generator applying Salter’s duck type WEC was invented by Scottish physicist Stephen Salter and presented in the Nature Journal in 1974 [15]. After development, the system was extensively verified through model experiments [37,38] and theoretical analyses [39,40,41] in the late 70s and early 80s. The duck-type rotor drives the generator based on the rotational motion by waves and is designed to perform only one-way motion by applying a ratchet mechanism. The representative Salter’s duck type WEC is the WEPTOS WEC developed in Denmark [42]. The WEPTOS WEC applied Salter’s duck type primary energy conversion system, which consists of two sets of V-spaced structures that absorb the wave energy through a line of rotors, each of which transmits energy directly to the generator. In the end, the line of rotor of these two sets of V-shaped structures was designed to reduce the wave load by turret mooring and rotating at an angle between 13 and 120 degrees around the point [43,44].
4.2. Verification of PFD and Reliability Assessment Program
The Salter’s duck type WEC converts the rotational energy absorbed by the rotor from the wave by the transmission principle of gear or pulley, a secondary energy conversion equipment, and transmits it to another axis through the shaft, so that the generator develops. In the meantime, the rotation can be amplified by equipment such as gearbox, hydraulic pump, and hydraulic motor. In this study, reliability assessment was performed for each of the three systems consisting of gear and pulley in the first stage of the secondary energy conversion mechanical system in the derived PFDs of Figure 5 and Figure 6 for the Salter′s duck type WEC. Table 4 shows the assumptions of specifications and efficiency for each equipment constituting the secondary energy conversion system, the efficiency of the output to the input, and the ratio of the RPM without loss [32,33,45,46,47]. The evaluated parameters for each stage of the system using the performance formula-based reliability assessment program developed in the previous chapter are as shown in Table 5. For reference, the input RPM delivered in stage 1 was assumed to be 1.0, because it is intended to assess the ratio of RPM and the efficiency at the final stage.

Table 4.
Assumptions and RPM ratio and efficiency ratio of input/output for each equipment.

Table 5.
Parameter for each stage according to the PFDs.
As shown in Table 5, when a secondary energy conversion system is constructed including only pulleys or gears, the final RPM is low, but the efficiency is the highest. As the number of equipment-pieces of the system increases, RPM gradually increases, but the efficiency gradually decreases. Moreover, the hydraulic system generally does not exceed 90% in efficiency for both pump and motor, so it can be seen that the efficiency drops up to about 75% for systems including the hydraulic system. For this reason, it can be determined that a combination of mechanical systems is more suitable as a secondary energy conversion system of the existing Salter’s duck type WEC. In the reliability assessment using the developed program, if reliability is assessed based on the specifications and efficiency of equipment, it is judged that reliability of various PFDs can be assessed at the conceptual design stage, and the most suitable energy conversion system can be constructed. Accordingly, difficulties in deriving an optimal energy conversion system may be solved through various applied PFDs.
In addition, to compare the results when the ideal RPM of the final stage is the same due to the same rotational increase rate of the system, Table 6 shows the results of comparing four systems composed of equipment with different specifications so that the final RPM in the no loss state is derived identically. As shown in Table 6, the RPMs without loss of the final stage on the four PFDs are all the same at 8.0, but the final efficiency × RPM value is different due to the difference in efficiency of the equipment constituting each system. The results of efficiency × RPM show that PFD 1 is the highest, followed by PFD 4. From these results, it can be judged that PFD 1 composed only of gears and shafts is the most efficient system with low loss. However, an efficient system does not necessarily mean efficiency in terms of economics [48]. In terms of system performance, RPM increases gradually as the number of equipment-pieces in the system increases. Therefore, when using the conceptual design process in this study, it is essential to improve the design more cost-effectively by evaluating economic viewpoints such as CAPEX and OPEX related to the system efficiency in the early development stages of the system [49].

Table 6.
Efficiency and RPM of the system having the same rotational increase rate.
Finally, for the generators with different types of secondary energy conversion systems, it is judged that a more efficient design is possible if design is performed according to the conceptual design process suggested in this study. The process proceeds in the order of constructing the system based on the PFD derived through system analysis through IDEF0 while assessing the reliability of the constructed system using the performance formula of the equipment constituting the system. In addition, as in this study, if a hybrid system that applies both a mechanical system and a hydraulic system is designed based on reliability assessment using a DB of equipment, it is expected that a more seamless conceptual design and reliability assessment will be possible. However, since the expression of the performance formula varies depending on the equipment of the system, the efficiency curve or DB of the equipment must be constructed separately.
In addition, the purpose of this study is to provide the basis for conceptual design based on reliability assessment through system analysis of the secondary energy conversion system, so it does not perform accurate reliability assessment based on a physical model considering the factors attributable to the efficiency of the system equipment. For example, in the case of a secondary energy conversion mechanical system with a pulley system, when assessing reliability based on a physical model, it should be modeled considering various deterioration factors such as belt characteristics and friction. However, in this study, factors affecting efficiency were not considered, and efficiency DB based on commercial products was used. In future studies, physical models are to be developed and more accurate reliability assessments performed by considering factors attributable to performance deterioration.
5. Conclusions
Although a lot of research studies have been conducted on the viewpoint of energy conversion of the wave power generator, among them, research on the system analysis and concept design based on reliability assessment for the secondary energy conversion system has not. Accordingly, in this study, the secondary energy conversion system was analyzed and generalized using the IDEF0 method, and equipment and PFD needed for the design of the system were derived. Therefore, the efficiency DB and formula of the mechanical equipment were built, and a program for reliability assessment was developed and verified using this. The main results are summarized as follows:
- In this study, verification of the derived PFD and the developed reliability assessment programs for conceptual design were performed by using Salter’s duck type WEC. As a result of the analysis based on the assessed reliability, it can be seen that as the number of components in the system increases, the final efficiency gradually decreases. In addition, in the case of a system including a hydraulic system, the efficiency decreases to about 75%. For this reason, it can be determined that the mechanical system is more suitable as a secondary energy conversion system of the existing Salter’s duck type WEC. In conclusion, it is judged that reliability of various PFDs can be assessed at the conceptual design stage, and the most suitable energy conversion system can be constructed.
- In addition, PFDs having the same rotational increase rate were compared. As for system performance, RPM increases gradually as the number of equipment-pieces in the system increases. Therefore, for the systems used in other movable object type WEC, it is judged that more efficient design is possible if the design is performed by combining the conceptual design process suggested in this study and economic evaluation such as CAPEX and OPEX related to the system efficiency.
- As a result, the conceptual design process derived from this study is shown in Figure 9. The process proceeds in the order of constructing the system based on the PFD derived through system analysis through IDEF0 and assessing the reliability of the constructed system using the performance formula of the equipment constituting the system. In addition, if a hybrid system that applies both a mechanical system and a hydraulic system is designed based on reliability assessment using a DB of equipment, it is expected that a more seamless conceptual design and reliability assessment will be possible.
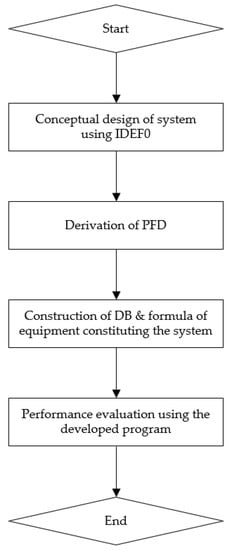 Figure 9. Conceptual design process based on reliability assessment of secondary energy conversion system.
Figure 9. Conceptual design process based on reliability assessment of secondary energy conversion system.
Finally, the subject of this study is in the unique field of wave power systems. In this field, system analysis and generalization for conceptual design are performed, and the presentation of the guidelines for conceptual design based on reliability assessment is considered to be of great value. However, the purpose of this study is to provide guidelines for conceptual design through system analysis of the secondary energy conversion system, it is judged that accurate results based on physical models cannot be obtained. Accordingly, in future studies, physical models will be developed and more accurate reliability assessments performed by considering factors attributable to performance deterioration.
Author Contributions
Conceptualization, T.-W.K. and J.-W.O.; Funding acquisition, K.-H.K.; Investigation, J.-H.L. and H.-W.K.; Project administration, J.-Y.P. and K.-H.K.; Software, J.-W.O.; Supervision, J.-W.O.; Validation, T.-W.K. and J.-W.O.; Visualization, T.-W.K. and J.-W.O.; Writing—original draft, T.-W.K.; Writing—review and editing, T.-W.K. and J.-W.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by a grant from the Endowment Project of “Development of WECAN for the Establishment of Integrated Performance and Structural Safety Analytical Tools of Wave Energy Converter” funded by the Korea Research Institute of Ships and Ocean engineering (PES4350).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Park, S.W. Post-2020 Climate Regime and Paris Agreement. Environ. Law Policy 2016, 16, 285–322. [Google Scholar]
- Park, S.K.; Kim, Y.J. A Comparative Study on Korea and United States Sea Grant Program. Ocean Polar Res. 2008, 30, 59–77. [Google Scholar] [CrossRef]
- Song, R.; Zhang, M.; Qian, X.; Wang, X.; Dai, Y.M.; Chen, J. A Floating Ocean Energy Conversion Device and Numerical Study on Buoy Shape and Performance. J. Mar. Sci. Eng. 2016, 4, 35. [Google Scholar] [CrossRef]
- Sjökvist, L.; Krishna, R.; Rahm, M.; Castellucci, V.; Anders, H.; Leijon, M. On the optimization of point absorber buoys. J. Mar. Sci. Eng. 2014, 2, 477–492. [Google Scholar] [CrossRef]
- Dai, Y.; Chen, Y.; Xie, L. A study on a novel two-body floating wave energy converter. Ocean Eng. 2017, 130, 407–416. [Google Scholar] [CrossRef]
- Cho, I.H.; Koh, C.H.; Bae, Y.H. Performance Analysis of a Horizontal Cylinder Wave Energy Converter with off-centered Rotational Axis. J. Korean Soc. Mar. Environ. Energy 2018, 21, 10–22. [Google Scholar] [CrossRef]
- Do, H.T.; Dang, T.D.; Ahn, K.K. A multi-point-absorber wave-energy converter for the stabilization of output power. Ocean Eng. 2018, 161, 337–349. [Google Scholar] [CrossRef]
- Do, H.T.; Dinh, Q.T.; Nguyen, M.T.; Phan, C.B.; Dang, T.D.; Lee, S.; Park, H.G.; Ahn, K.K. Effects of non-vertical linear motions of a hemispherical-float wave energy converter. Ocean Eng. 2015, 109, 430–438. [Google Scholar] [CrossRef]
- Hu, Y.; Yang, S.; He, H.; Chen, H. Influence of Central Platform on Hydrodynamic Performance of Semi-Submerged Multi-Buoy Wave Energy Converter. J. Mar. Sci. Eng. 2020, 8, 12. [Google Scholar] [CrossRef]
- Kim, M.S.; Sohn, J.H.; Kim, J.H.; Sung, Y.J. Efficiency Analysis of a Wave Power Generation System by Using Multibody Dynamics. Trans. Korean Soc. Mech. Eng. A 2016, 40, 557–563. [Google Scholar] [CrossRef]
- De Andrés, A.D.; Guanche, R.; Armesto, J.A.; Del Jesus, F.; Vidal, C.; Losada, I.J. Time domain model for a two-body heave converter: Model and applications. Ocean Eng. 2013, 72, 116–123. [Google Scholar] [CrossRef]
- Rahmati, M.T.; Aggidis, G.A. Numerical and experimental analysis of the power output of a point absorber wave energy converter in irregular waves. Ocean Eng. 2016, 111, 483–492. [Google Scholar] [CrossRef]
- Song, S.K.; Sung, Y.J.; Park, J.B. Modeling and simulation of a wave energy converter INWAVE. Appl. Sci. 2017, 7, 99. [Google Scholar] [CrossRef]
- Cho, Y.H.; Nakamura, T.; Mizutani, N.; Lee, K.H. An Experimental Study of a Bottom-Hinged Wave Energy Converter with a Reflection Wall in Regular Waves—Focusing on Behavioral Characteristics. Appl. Sci. 2020, 10, 6734. [Google Scholar] [CrossRef]
- Salter, S.H. Wave power. Nature 1974, 249, 720–724. [Google Scholar] [CrossRef]
- Kramer, M.; Marquis, L.; Frigaard, P. Performance evaluation of the wavestar prototype. In Proceedings of the 9th European Wave and Tidal Energy Conference, Southampton, UK, 5–9 September 2011. [Google Scholar]
- Jang, J.S.; Sohn, J.H. Dynamic Analysis of Wave Energy Generation System by Using Multibody Dynamics. Trans. Korean Soc. Mech. Eng. A 2011, 35, 1579–1584. [Google Scholar] [CrossRef][Green Version]
- Hwang, S.S.; Lee, D.S.; Yang, K.U.; Byun, J.H.; Park, I.H. Development of a Moving Body Type Wave Power Generator using Wave Horizontal Motions and Hydraulic Experiment for Electric Power Production. J. Korean Soc. Coast. Ocean Eng. 2016, 28, 73–80. [Google Scholar] [CrossRef]
- Sim, K.H.; Park, J.S.; Jung, S.J. Elector-Mechanical Modeling and Performance Analysis of Floating Wave Energy Converts Utilizing Yo-Yo Vibration System. Trans. Korean Soc. Mech. Eng. A 2015, 39, 79–87. [Google Scholar] [CrossRef][Green Version]
- Chandrasekaran, S.; Harender. Power Generation Using Mechanical Wave Energy Converter. Int. J. Ocean Clim. Syst. 2012, 3, 57–70. [Google Scholar] [CrossRef]
- Fang, H.; Tao, Y.; Zhang, S.; Xiao, Z. Design and analysis of bidirectional driven float-type wave power generation system. J. Mod. Power Syst. Clean Energy 2018, 6, 50–60. [Google Scholar] [CrossRef]
- Hansen, R.H.; Kramer, M.M.; Vidal, E. Discrete displacement hydraulic power take-off system for the wavestar wave energy converter. Energies 2013, 6, 4001–4044. [Google Scholar] [CrossRef]
- Do, H.T.; Ahn, K.K. Application of Secondary Control Hydrostatic Transmission in A Multi-Point Absorbing Wave Energy Converter. J. Drive Control 2014, 11, 1–7. [Google Scholar] [CrossRef][Green Version]
- Wang, L.; Liu, Y.; Li, M. Time-dependent reliability-based optimization for structural-topological configuration design under convex-bounded uncertain modeling. Reliab. Eng. Syst. Saf. 2022, 221, 108361. [Google Scholar] [CrossRef]
- Wang, L.; Liu, J.; Yang, C.; Wu, D. A novel interval dynamic reliability computation approach for the risk evaluation of vibration active control systems based on PID controllers. Appl. Math. Model. 2021, 92, 422–446. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, L.; Gu, K.; Li, M. Artificial Neural Network (ANN)-Bayesian Probability Framework (BPF) based method of dynamic force reconstruction under multi-source uncertainties. Knowl.-Based Syst. 2022, 237, 107796. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, X.; Wu, Z.; Chen, W. Evidence theory-based reliability optimization for cross-scale topological structures with global stress, local displacement, and micro-manufacturing constraints. Struct. Multidiscip. Optim. 2022, 65, 23. [Google Scholar] [CrossRef]
- Kolios, A.; Di Maio, L.F.; Wang, L.; Cui, L.; Sheng, Q. Reliability assessment of point-absorber wave energy converters. Ocean Eng. 2018, 163, 40–50. [Google Scholar] [CrossRef]
- Heikkilä, E.; Välisalo, T.; Tiusanen, R.; Sarsama, J.; Räikkönen, M. Reliability modelling and analysis of the power take-off system of an oscillating wave surge converter. J. Mar. Sci. Eng. 2021, 9, 552. [Google Scholar] [CrossRef]
- National Institute of Standards and Technology (NIST) Draft Federal Information Processing Standards Publication 183: Announcing the Standard for Integration Definition for Function Modeling (IDEF0). Available online: https://www.idef.com/wp-content/uploads/2016/02/idef0.pdf (accessed on 16 April 2020).
- Ismail, H.S.; Rashid, M.; Zhu, P.; Poolton, J. A IDEF0-Based Methodology for Project Reliability Assessment. In Proceedings of the 2010 IEEE International Conference on Industrial Engineering and Engineering Management, Macao, China, 7–10 December 2010. [Google Scholar]
- Minav, T.A.; Heikkinen, J.E.; Pietola, M. Direct driven hydraulic drive for new powertrain topologies for non-road mobile machinery. Electr. Power Syst. Res. 2017, 152, 390–400. [Google Scholar] [CrossRef]
- Zhang, Q. Basics of Hydraulic Systems; CRC Press–Taylor & Francis Group: Boca Raton, FL, USA, 2019. [Google Scholar]
- KHK Gears. The ABC’s of Gears Basic Guide–B; Kohara Gear Industry Co., Ltd.: Toshiharu Kohara, Japan, 2007. [Google Scholar]
- Breig, W.F.; Oliver, L.R. Energy loss and efficiency of power transmission belts. In Proceedings of the 3rd World Energy Engineering Congress, The Association of Energy Engineers, Atlanta, GA, USA, 13–16 October 1980. [Google Scholar]
- Arntz Optibelt Gmbh. Technical Manual V-Belt Drives; Arntz Optibelt Group: Höxter, Germany, 2018. [Google Scholar]
- Salter, S.H.; Jeffrey, D.C.; Taylor, J.R.M. First Year Interim Report on Edinburgh Wave Power Project: Study of Mechanisms for Extracting Power from Sea Waves; University of Edinburgh: Edinburgh, UK, 1975. [Google Scholar]
- Jeffrey, D.C.; Richmond, D.J.E.; Salter, S.H.; Taylor, J.R.M. Second Year Interim Report on Edinburgh Wave Power Project: Study of Mechanisms for Extracting Power from Sea Waves; University of Edinburgh: Edinburgh, UK, 1976. [Google Scholar]
- Evans, D.V. A Theory for Wave-power Absorption by Oscillating Bodies. J. Fluid Mech. 1976, 77, 1–25. [Google Scholar] [CrossRef]
- Count, B.M. On the Dynamics of Wave-power Devices. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1978, 363, 559–579. [Google Scholar]
- Mynett, A.E.; Serman, D.D.; Mei, C.C. Characteristics of Salter’s Cam for Extracting Energy from Ocean Waves. Appl. Ocean Res. 1979, 1, 13–20. [Google Scholar] [CrossRef]
- Pecher, A.; Kofoed, J.P.; Larsen, T. Design Specifications for the Hanstholm WEPTOS Wave Energy Converter. Energies 2012, 5, 1001–1017. [Google Scholar] [CrossRef]
- Pecher, A.; Kofoed, J.P. Experimental Study on the Updated PTO System of the WEPTOS Wave Energy Converter; (DCE Contract Reports; No. 138); Department of Civil Engineering, Aalborg University: Aalborg, Denmark, 2013. [Google Scholar]
- Pecher, A.; Kofoed, J.P. Experimental Study on the Structural and Mooring Loads of the WEPTOS Wave Energy Converter; (DCE Contract Reports; No. 142); Department of Civil Engineering, Aalborg University: Aalborg, Denmark, 2014. [Google Scholar]
- Kapelevich, A. High gear ratio epicyclic drives analysis. Gear Technol. 2014, 3, 62–67. [Google Scholar]
- Hearle, J.W.S.; Sultan, M.A.I.; Govender, S. The Form Taken by Threads Laid on a Moving Belt. Part I: Experimental Study. J. Text. Inst. 1976, 67, 373. [Google Scholar] [CrossRef]
- Eaton Corporation Inc. DuraForceTM HMV/HMR/HMF/HMA Catalog; Eaton Corporation Inc.: Dublin, Ireland, 2011. [Google Scholar]
- De Andres, A.; Maillet, J.; Hals Todalshaug, J.; Möller, P.; Bould, D.; Jeffrey, H. Techno-economic related metrics for a wave energy converters feasibility assessment. Sustainability 2016, 8, 1109. [Google Scholar] [CrossRef]
- Weber, J. WEC Technology Readiness and Performance Matrix–finding the best research technology development trajectory. In Proceedings of the 4th International Conference on Ocean Energy, Dublin, Ireland, 17–19 October 2012. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).