Intelligent Black–Litterman Portfolio Optimization Using a Decomposition-Based Multi-Objective DIRECT Algorithm
Abstract
:1. Introduction
- We develop a new random forest-based BL portfolio optimization model in which a novel method for generating investor views on the basis of random forests is adopted. In this method, a view vector is generated based on the predicted asset returns obtained by random forests, and the confidence matrix which contains the uncertainty of each view is measured by the differences in the predicted values of multiple trees.
- We propose a decomposition-based multi-objective DIRECT algorithm, named multiDecompose, to handle the random forest-based BL model mentioned above in a short time while maintaining high accuracy, in which an indicator is explored to encourage potentially optimal hyperrectangles to be chosen in all directions. With this indicator, the algorithm can provide a better exploration of the search space of an MOP, especially when stuck in a local optimal Pareto set or a part of the global Pareto set.
- We demonstrate the superiority of the proposed algorithm over NSGA-II and MOEA/D on the MOP and DTLZ benchmark problems as well as the effectiveness of solving random forest-based BL model. Moreover, we also test the performance of random forest-based BL model by a comparison with the MV model using the real-world data.
2. Related Work
3. Preliminaries
3.1. Classical Black–Litterman Model
- Q is a K-dimensional view vector which maintains K subjective returns of certain assets.
- refers to a matrix that reflects the confidence in views.
- P is a mapping matrix, representing the correspondence between K views and corresponding assets.
- is the covariance matrix of asset returns.
- is the market equilibrium return calculated by the Formula (3), where is the market-cap weights, and denotes the risk aversion coefficient which is obtained by dividing the market excess return by its variance .
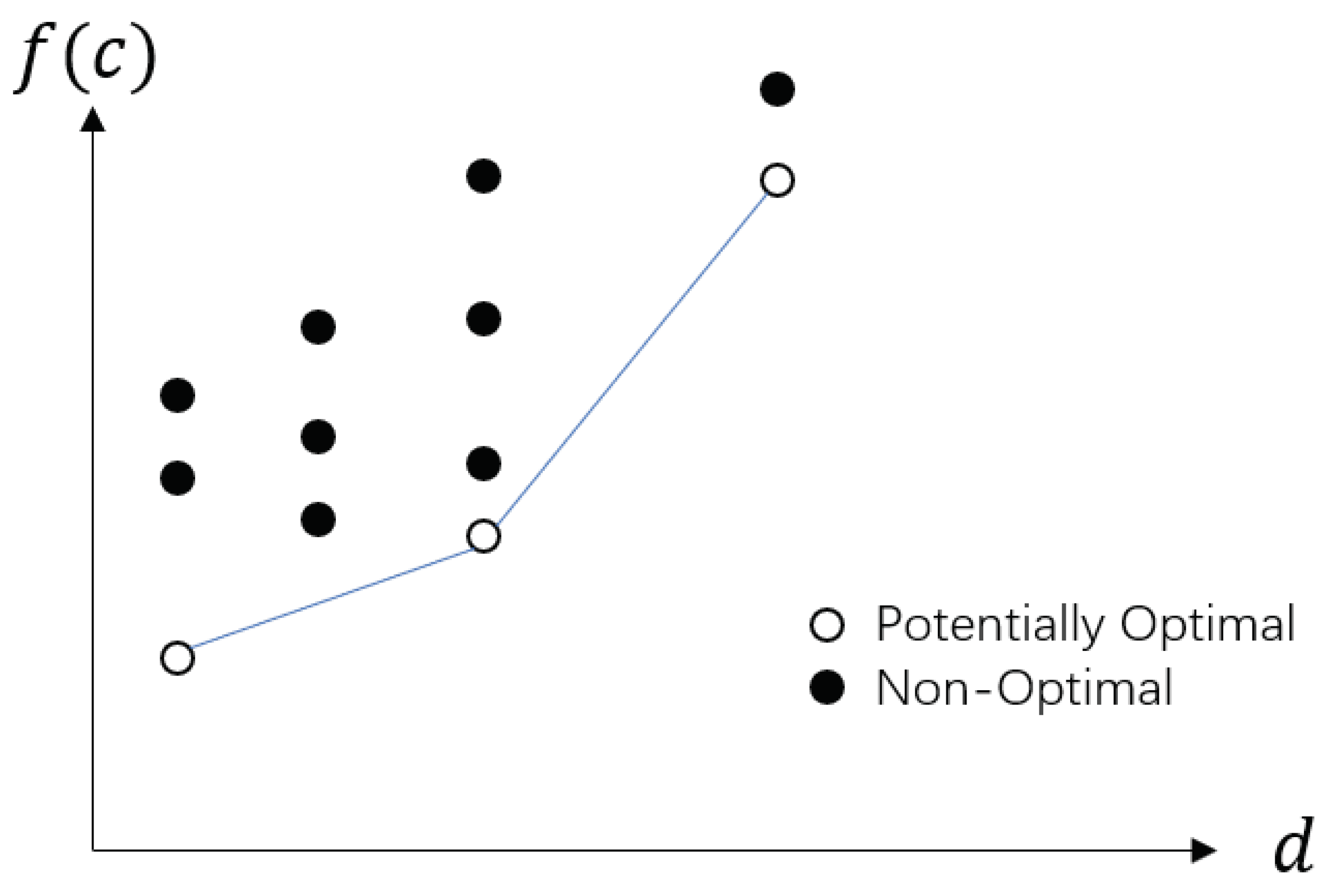
3.2. DIRECT Framework
| Algorithm 1 Procedure for hyperrectangle partition |
| Input: Function to be minimized f, the current potentially optimal hyperrectangle i Output: Newly acquired hyperrectangles from i
|
| Algorithm 2 DIRECT algorithm |
| Input: Function to be minimized f, evaluation budget t Output: Approximate minimum of function f
|
4. Materials and Methods
4.1. Random Forest-Based Black–Litterman Portfolio Optimization Model
4.1.1. Generating Views Using Random Forests
| Algorithm 3 Main training steps of random forests |
| Input:S data samples Output: M decision trees
|
- Construct a random forest model based on the historical return data to predict asset returns, and use the model output as an absolute view.
- Calculate the maximum absolute deviation between the output of M decision trees and the model output .
- Calculate the proportion of subtrees whose absolute deviation from is less than and take it as the uncertainty of the corresponding view.
- Repeat the above process until the K views and corresponding uncertainty are constructed.
4.1.2. Random Forest-Based Black–Litterman Model
4.2. DIRECT Algorithm for Multi-Objective Optimization
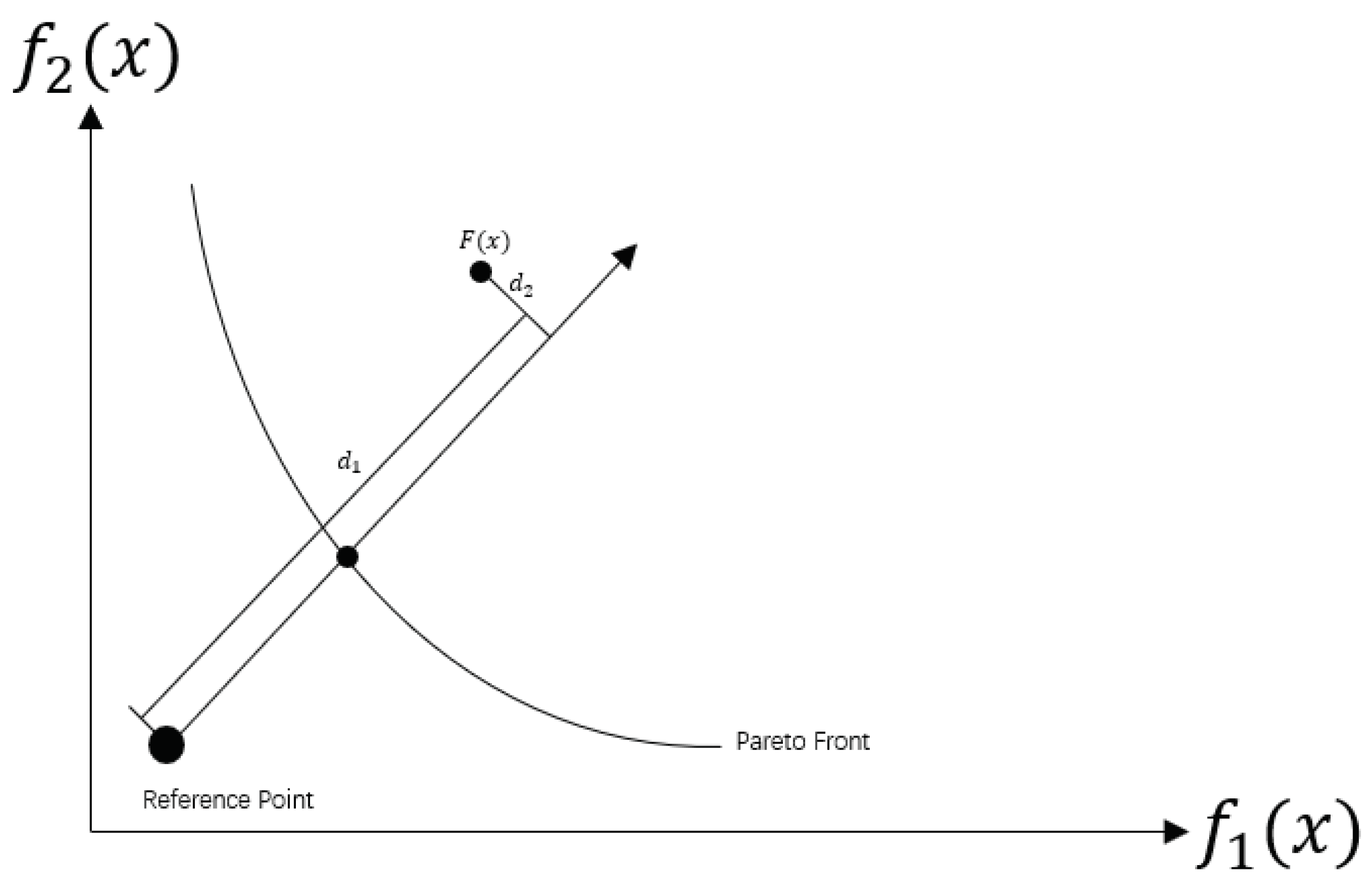
4.2.1. Decomposition Based Strategy for Potentially Optimal Hyperrectangles Selecting
| Algorithm 4 Generation procedure of the decomposition based indicator |
| Input:H weight vectors , N objective function vectors at the center of N hyperrectangles and reference point Output: for N hyperrectangles
|
4.2.2. Decomposition Based Partition Procedure
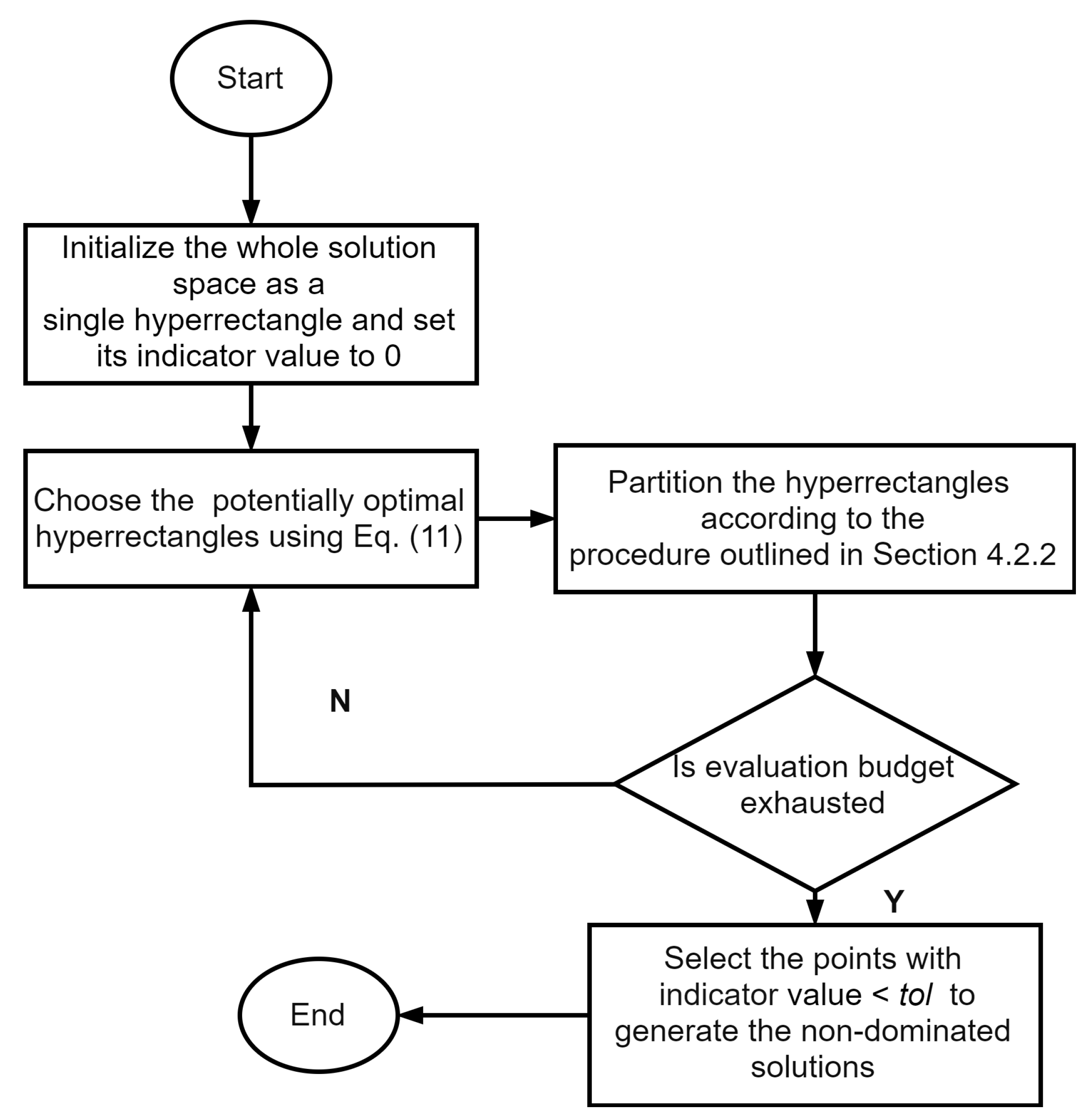
4.2.3. Decomposition Based Multi-Objective DIRECT Algorithm
5. Results
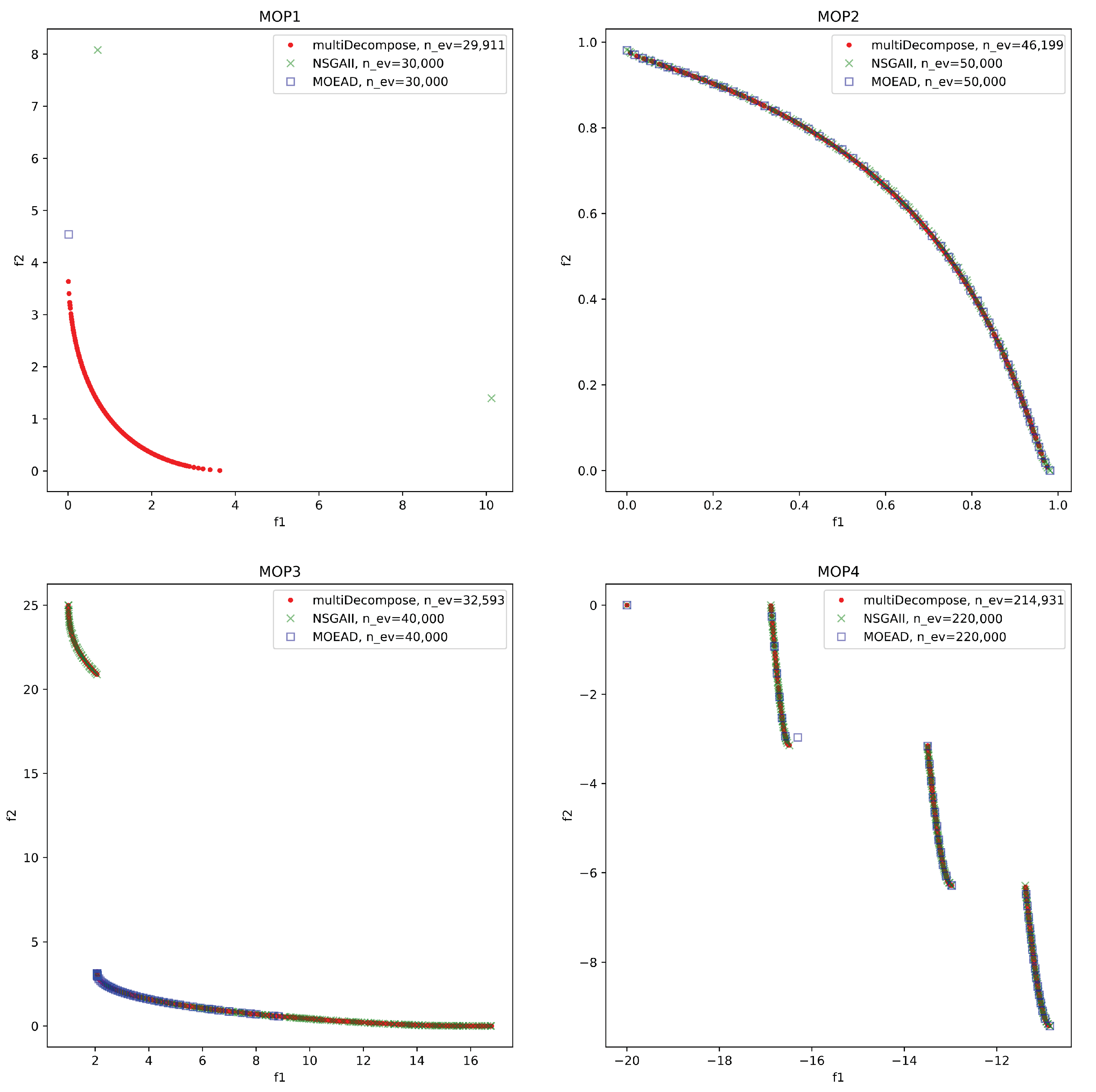
5.1. Performance of multiDecompose on Benchmark Problems
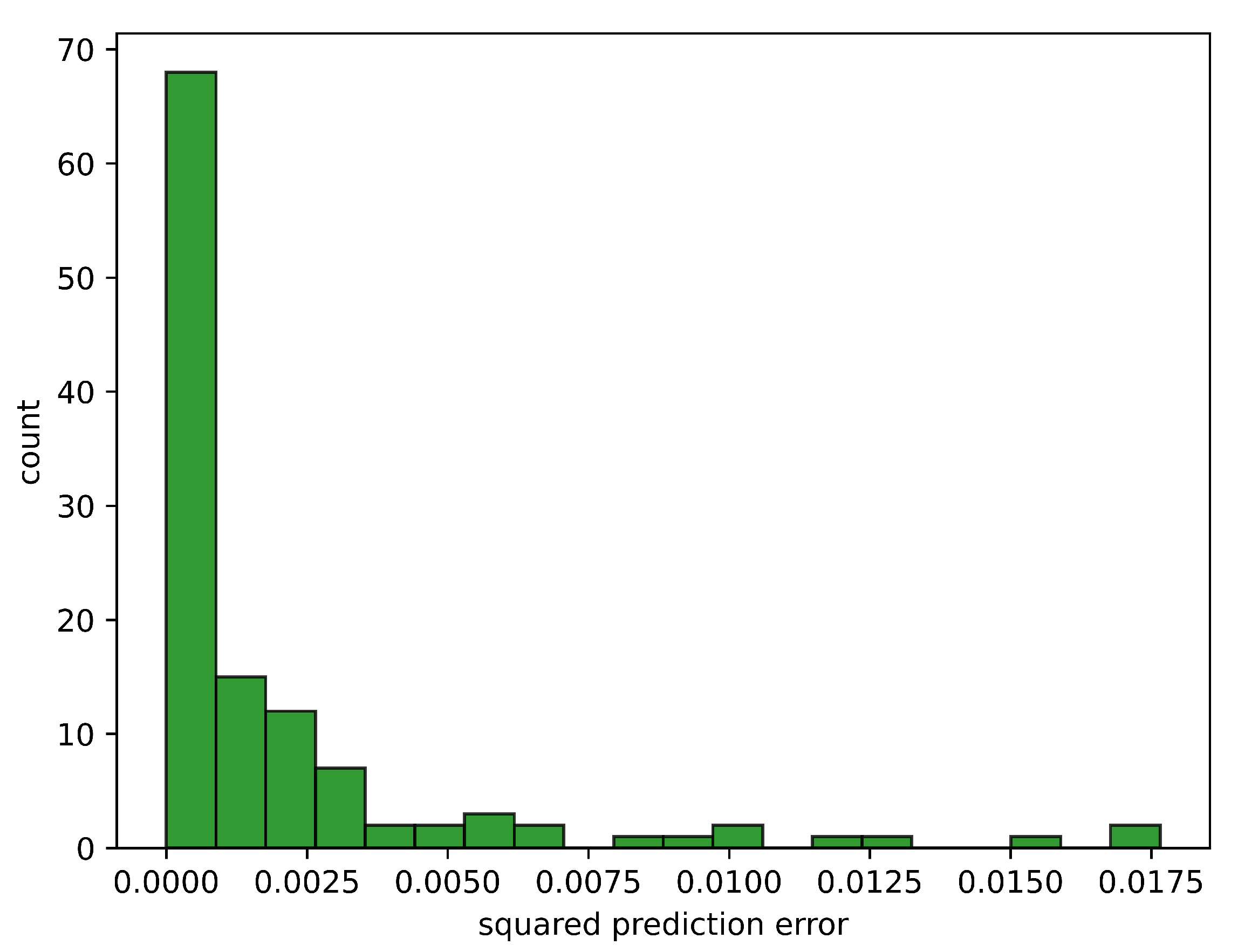
5.2. Portfolio Performance of the Random Forest-Based BL Model
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Markowitz, H. Portfolio Selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Li, C.; Wu, Y.; Lu, Z.; Wang, J.; Hu, Y. A Multiperiod Multiobjective Portfolio Selection Model With Fuzzy Random Returns for Large Scale Securities Data. IEEE Trans. Fuzzy Syst. 2021, 29, 59–74. [Google Scholar] [CrossRef]
- Greiner, S.P. Investment Risk and Uncertainty: Advanced Risk Awareness Techniques for the Intelligent Investor; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Black, F.; Litterman, R. Global asset allocation with equities, bonds, and currencies. Fixed Income Res. 1991, 2, 1–44. [Google Scholar]
- Black, F.; Litterman, R. Global portfolio optimization. Financ. Anal. J. 1992, 48, 28–43. [Google Scholar] [CrossRef]
- Caliskan, T. Comparing Black Litterman Model and Markowitz Mean Variance Model with Beta Factor, Unsystematic Risk and Total Risk. Bus. Econ. Res. J. 2012, 3, 1–43. [Google Scholar]
- Cheung, W. The black–litterman model explained. J. Asset Manag. 2010, 11, 229–243. [Google Scholar] [CrossRef]
- Jia, X.; Gao, J. Extensions of black-litterman portfolio optimization model with downside risk measure. In Proceedings of the 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; pp. 1114–1119. [Google Scholar]
- Palczewski, A.; Palczewski, J. Black–Litterman model for continuous distributions. Eur. J. Oper. Res. 2019, 273, 708–720. [Google Scholar] [CrossRef]
- Simos, T.E.; Mourtas, S.D.; Katsikis, V.N. Time-varying Black–Litterman portfolio optimization using a bio-inspired approach and neuronets. Appl. Soft Comput. 2021, 112, 107767. [Google Scholar] [CrossRef]
- Stoilov, T.; Stoilova, K.; Vladimirov, M. Application of modified Black-Litterman model for active portfolio management. Expert Syst. Appl. 2021, 186, 115719. [Google Scholar] [CrossRef]
- Alexander, D.; Svetlana, D. Application of Ensemble learning for views generation in Meucci Portfolio Optimization Framework. Rev. Bus. Econ. Stud. 2013, 1, 100–110. [Google Scholar]
- Asad, M. Optimized stock market prediction using ensemble learning. In Proceedings of the 2015 9Th International Conference on Application of Information and Communication Technologies (AICT), Rostov-on-Don, Russia, 14–16 October 2015; pp. 263–268. [Google Scholar]
- Kim, H.Y.; Won, C.H. Forecasting the volatility of stock price index: A hybrid model integrating LSTM with multiple GARCH-type models. Expert Syst. Appl. 2018, 103, 25–37. [Google Scholar] [CrossRef]
- Min, L.; Dong, J.; Liu, D.; Kong, X. A Black-Litterman Portfolio Selection Model with Investor Opinions Generating from Machine Learning Algorithms. Eng. Lett. 2021, 29, 710–721. [Google Scholar]
- Zhang, Q.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, Part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2013, 18, 577–601. [Google Scholar] [CrossRef]
- Piyavskii, S. An algorithm for finding the absolute extremum of a function. USSR Comput. Math. Math. Phys. 1972, 12, 57–67. [Google Scholar] [CrossRef]
- Shubert, B.O. A sequential method seeking the global maximum of a function. SIAM J. Numer. Anal. 1972, 9, 379–388. [Google Scholar] [CrossRef]
- Jones, D.R.; Perttunen, C.D.; Stuckman, B.E. Lipschitzian optimization without the Lipschitz constant. J. Optim. Theory Appl. 1993, 79, 157–181. [Google Scholar] [CrossRef]
- Jones, D.R.; Martins, J.R. The DIRECT algorithm: 25 years Later. J. Glob. Optim. 2021, 79, 521–566. [Google Scholar] [CrossRef]
- Markowitz, H. Portfolio Selection, Efficent Diversification of Investments; John Wiley and Son: New York, NY, USA, 1959. [Google Scholar]
- Müjdecı, S.Y.; Alnahas, D.; Öcal, M.; Duru, N.; Tüccar, B. Hyperparameter Optimization for Black-Litterman Model via Genetic Algorithms. In Proceedings of the 2021 International Conference on INnovations in Intelligent Systems and Applications (INISTA), Kocaeli, Turkey, 25–27 August 2021; pp. 1–5. [Google Scholar]
- Satchell, S.; Scowcroft, A. A demystification of the Black–Litterman model: Managing quantitative and traditional portfolio construction. J. Asset Manag. 2000, 1, 138–150. [Google Scholar] [CrossRef]
- Martellini, L.; Ziemann, V. Extending Black-Litterman analysis beyond the mean-variance framework. J. Portf. Manag. 2007, 33, 33–44. [Google Scholar] [CrossRef]
- Figelman, I. Black–Litterman with a Factor Structure Applied to Multi-Asset Portfolios. J. Portf. Manag. 2017, 44, 136–155. [Google Scholar] [CrossRef]
- Chen, S.D.; Lim, A.E. A Generalized black–litterman model. Oper. Res. 2020, 68, 381–410. [Google Scholar] [CrossRef] [Green Version]
- Donthireddy, P. Black-Litterman Portfolios with Machine Learning Derived Views. 2018. Available online: https://www.researchgate.net/publication/326489143_Black-Litterman_Portfolios_with_Machine_Learning_derived_Views (accessed on 25 July 2018).
- Kara, M.; Ulucan, A.; Atici, K.B. A hybrid approach for generating investor views in Black–Litterman model. Expert Syst. Appl. 2019, 128, 256–270. [Google Scholar] [CrossRef]
- Wang, L.; Ishida, H.; Hiroyasu, T.; Miki, M. Examination of multi-objective optimization method for global search using DIRECT and GA. In Proceedings of the 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008; pp. 2446–2451. [Google Scholar]
- Al-Dujaili, A.; Suresh, S. Dividing rectangles attack multi-objective optimization. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 3606–3613. [Google Scholar] [CrossRef]
- Wong, C.S.Y.; Al-Dujaili, A.; Sundaram, S. Hypervolume-based DIRECT for multi-objective optimisation. In Proceedings of the 2016 on Genetic and Evolutionary Computation Conference Companion, Denver, CO, USA, 20–24 July 2016; pp. 1201–1208. [Google Scholar]
- Best, M.J.; Grauer, R.R. On the sensitivity of mean-variance-efficient portfolios to changes in asset means: Some analytical and computational results. Rev. Financ. Stud. 1991, 4, 315–342. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Sequential model-based optimization for general algorithm configuration. In International Conference on Learning and Intelligent Optimization; Springer: Berlin/Heidelberg, Germany, 2011; pp. 507–523. [Google Scholar]
- Blank, J.; Deb, K. pymoo: Multi-objective optimization in python. IEEE Access 2020, 8, 89497–89509. [Google Scholar] [CrossRef]
- Brockhoff, D.; Tran, T.D.; Hansen, N. Benchmarking numerical multiobjective optimizers revisited. In Proceedings of the 2015 Annual Conference on Genetic and Evolutionary Computation, Madrid, Spain, 11–15 July 2015; pp. 639–646. [Google Scholar]
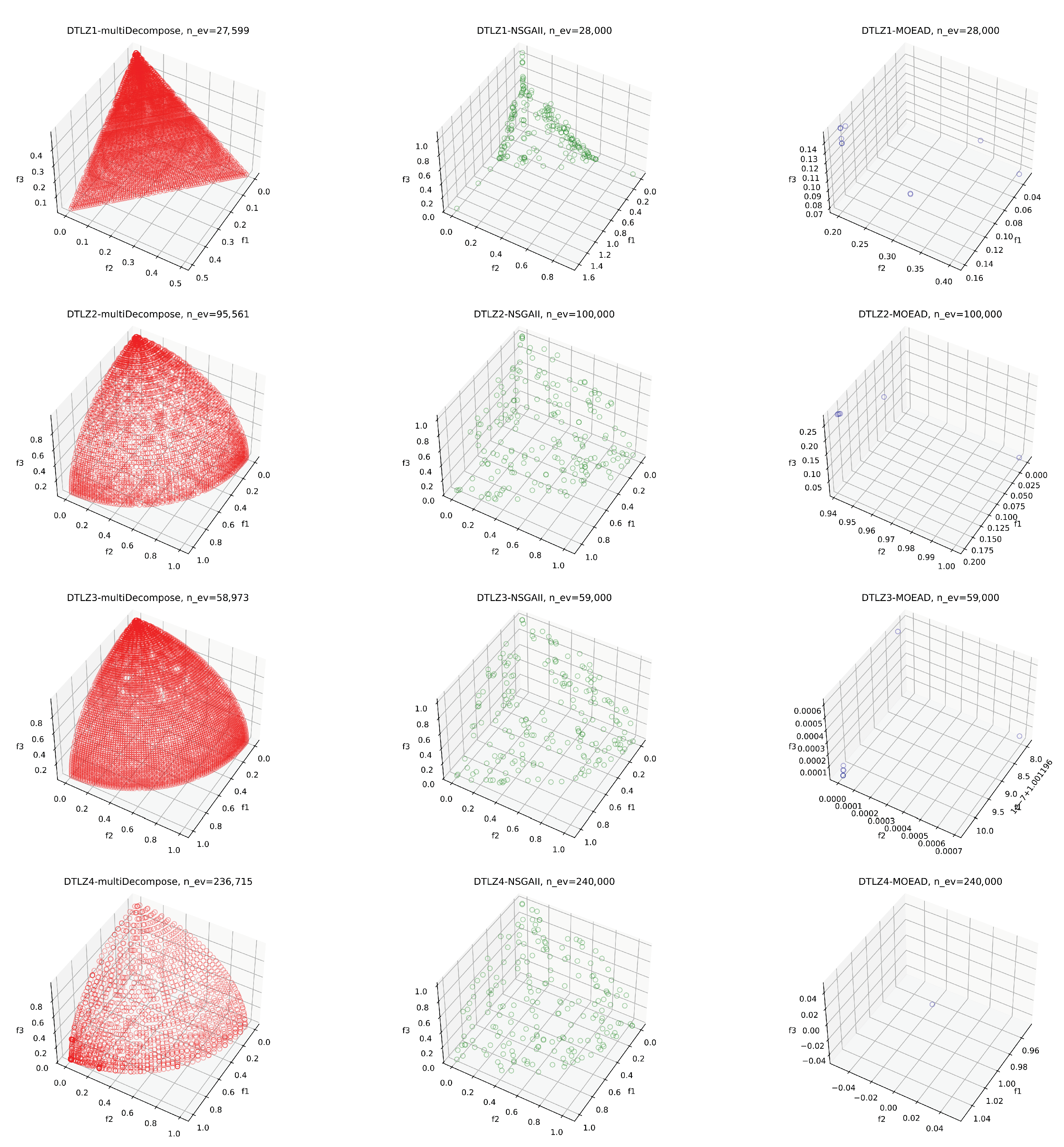

| Test Instance | Number of Objectives | Solution Space Dimension |
|---|---|---|
| MOP1 | 2 | 1 |
| MOP2 | 2 | 3 |
| MOP3 | 2 | 2 |
| MOP4 | 2 | 3 |
| DTLZ1 | 3 | 7 |
| DTLZ2 | 3 | 10 |
| DTLZ3 | 3 | 10 |
| DTLZ4 | 3 | 10 |
| multiDecompose | NSGA-II | MOEA/D | |
|---|---|---|---|
| MOP1 | 13494.20024 | 12157.93554 | 8265.419011 |
| MOP2 | 0.304549570 | 0.302570066 | 0.296286100 |
| MOP3 | 360.3988959 | 360.3714609 | 354.1858850 |
| MOP4 | 27.37042078 | 27.35540827 | 26.62617847 |
| DTLZ1 | 4.947239949 | 4.937894772 | 4.071856060 |
| DTLZ2 | 0.506487643 | 0.447724955 | 0.123985535 |
| DTLZ3 | 31.63621196 | 30.60244867 | 23.59450020 |
| DTLZ4 | 0.547895448 | 0.506647045 | 0.073129642 |
| Code | Name | Location | |
|---|---|---|---|
| 1 | 600519 | Kweichow Moutai Co., Ltd. | Renhuai, China |
| 2 | 601318 | Ping An Insurance (Group) Co., Ltd. | Shenzhen, China |
| 3 | 600036 | China Merchants Bank | Shenzhen, China |
| 4 | 601398 | Industrial and Commercial Bank of China | Beijing, China |
| 5 | 602276 | Jiangsu Hengrui Medicine Co., Ltd. | Lianyungang, China |
| 6 | 601186 | China Railway Construction | Beijing, China |
| 7 | 601288 | Agricultural Bank of China | Beijing, China |
| 8 | 603288 | Foshan Haitian Flavouring and Food Co., Ltd. | Foshan, China |
| 9 | 601012 | Longi Green Energy Technology Co., ltd. | Xi’an, China |
| 10 | 600031 | Sany Heavy Industry Co., ltd. | Beijing, China |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Chen, Y.; Yang, X.; Wang, Z.; Lu, Z.; Chi, X. Intelligent Black–Litterman Portfolio Optimization Using a Decomposition-Based Multi-Objective DIRECT Algorithm. Appl. Sci. 2022, 12, 7089. https://doi.org/10.3390/app12147089
Li C, Chen Y, Yang X, Wang Z, Lu Z, Chi X. Intelligent Black–Litterman Portfolio Optimization Using a Decomposition-Based Multi-Objective DIRECT Algorithm. Applied Sciences. 2022; 12(14):7089. https://doi.org/10.3390/app12147089
Chicago/Turabian StyleLi, Chen, Yidong Chen, Xueying Yang, Zitian Wang, Zhonghua Lu, and Xuebin Chi. 2022. "Intelligent Black–Litterman Portfolio Optimization Using a Decomposition-Based Multi-Objective DIRECT Algorithm" Applied Sciences 12, no. 14: 7089. https://doi.org/10.3390/app12147089
APA StyleLi, C., Chen, Y., Yang, X., Wang, Z., Lu, Z., & Chi, X. (2022). Intelligent Black–Litterman Portfolio Optimization Using a Decomposition-Based Multi-Objective DIRECT Algorithm. Applied Sciences, 12(14), 7089. https://doi.org/10.3390/app12147089







