Abstract
This paper presents a channel-wise average pooling and one dimension pixel-shuffle architecture for a denoising autoencoder (CPDAE) design that can be applied to efficiently remove electrode motion (EM) artifacts in an electrocardiogram (ECG) signal. The three advantages of the proposed design are as follows: (1) In the skip connection layer, less memory is needed to transfer the features extracted by the neural network; (2) Pixel shuffle and pixel unshuffle techniques with point-wise convolution are used to effectively reserve the key features generated from each layer in both the encoder and decoder; (3) Overall, fewer parameters are required to reconstruct the ECG signal. This paper describes three deep neural network models, namely CPDAELite, CPDAERegular, and CPDAEFull, which support various computational capacity and hardware arrangements. The three proposed structures involve an encoder and decoder with six, seven, and eight layers, respectively. Furthermore, the CPDAELite, CPDAERegular, and CPDAEFull structures require fewer multiply-accumulate operations—355.01, 56.96, and 14.69 million, respectively—and less parameter usage—2.69 million, 149.7 thousand, and 55.5 thousand, respectively. To evaluate the denoising performance, the MIT–BIH noise stress test database containing six signal-to-noise ratios (SNRs) of noisy ECGs was employed. The results demonstrated that the proposed models had a higher improvement of SNR and lower percentage root-mean-square difference than other state-of-the-art methods under various conditions of SNR.
1. Introduction
According to the Global Burden of Disease report, cases of cardiovascular disease (CVD) doubled from 271 million in 1990 to 523 million in 2019 [1]. A proportion of these patients are diagnosed with cardiac arrhythmias. Some cardiac arrhythmias, such as ventricular fibrillation and ventricular tachycardia, can lead to sudden cardiac arrest, which results in death if first aid cannot be performed within several minutes [2]. One of the diagnostic tools for CVDs is the electrocardiogram (ECG), which is recorded from a biosignal acquisition system [3,4]. An ECG represents the electrical activity of heart tissue. Portable products that feature ECG acquisition systems include Holter monitors, automated external defibrillators, and pacemakers. These products record an ECG and diagnose abnormal heart rhythms in real-time. However, not only the patient’s ECG but also baseline wander (BW) noise, muscle artifacts (MA), electrode motion (EM) artifacts [5], and powerline interference (PLI) [6] are recorded during measurements [3]. BW noise is a low-frequency artifact that occurs during breathing and can have a substantial influence on the diagnosis of an ST segment in lead I [7]; MA noise is a high-frequency noise that occurs when muscle activates continuously, as when the patient feels cold or nervous [8]; EM artifacts are generated from the stretching of the Ag/AgCl electrode barrier layer in the skin [5]. Because EM artifacts are similar in appearance to ectopic beats, they are regarded as the most challenging noise to eliminate; PLI is a 50-Hz or 60-Hz artifact influenced by the ac in recording equipment [6]. Recorded ECGs are invariably accompanied by noise of diverse intensities, which affect the accuracy of the instrument and can affect the doctor’s judgment. Therefore, a suitable denoising algorithm to reconstruct a clean ECG from a noisy ECG can aid in CVD diagnosis.
Several denoising approaches based on different techniques have been developed; examples include adaptive filtering [9,10,11], the wavelet method [12,13,14], empirical mode decomposition (EMD) [15,16,17,18], and denoising autoencoder (DAE) algorithms [19,20,21,22,23,24,25,26,27,28]. An adaptive filter updates its weight according to the error between the noisy ECG signal and the noise reference signal. In [9], various least-mean squares (LMS)-based adaptive filter algorithms were proposed. An adaptive filter uses a noise reference to only eliminate the noise in a noisy ECG and produce a clean ECG. The experimental results demonstrated that most noise was removed after 200 iterations. The QRS segment in an ECG is a complex wave, and it is difficult to denoise efficiently in this short segment because the LMS filter cannot update the weight coefficients immediately. In [10], the noisy ECG signal and the noise reference signal were transferred from the time domain into the frequency domain by using the fast Fourier transform, and then the LMS algorithm was used to calculate weights to the minimum mean-square error (MSE) between two input signals. The adaptive filter adjusts the magnitude in the frequency domain directly so that the filtered ECG approaches a clean ECG. In complexity computation, LMS-based approaches are simpler than other denoising techniques and can be easily implemented in digital circuits. In [11], a delayed error normalized LMS (DENLMS) adaptive filter was proposed and implemented on FPGAs to reduce Gaussian white noise in a wireless ECG monitoring system. WT is another popular technique for reducing noise. WT is a capable tool that divides a noisy signal into numerous frequency subbands with different wavelet coefficients; subsequently, the threshold function limits the frequency magnitude for the reconstruction of the clean ECG signal. In [12], a nonlocal WT (NLWT) that combines nonlocal means (NLM) and WT was proposed. In a noisy ECG, the NLWT separates samples into several similar blocks by using the reference block in the similarity data matrix (SDM) extraction stage. Subsequently, these similar blocks are transferred into the wavelet domain, and the threshold function only retains the ECG magnitude to reconstruct the clean ECG signal.
EMD-based approaches decompose the noisy ECG signal into several intrinsic mode functions (IMFs) using a Hilbert–Huang transform (HHT, [29]), and the denoising ECG signal can be reconstructed by removing the noise IMFs. In [15], a real-time 2-stage motion noise (MN) artifact cancelation method based on EMD was proposed. The EMD isolates high-frequency components of the signal under the assumption that most of the MN artifacts are contained in the first stage, and the MN artifacts are eliminated by the high-pass filter in the first EMD (F-EMD) in the second stage. Although the aforementioned denoising approaches have been widely and successfully applied, they have several limitations. In adaptive filtering approaches, a noise reference signal for BW, EM, and MA must be measured, necessitating the use of additional electrodes. In the wavelet approaches, the software and hardware thresholds to satisfy various scenarios are challenging to define. In the EMD approach, because the frequencies of P waves and T waves in lead I, II, and III are similar to some of the noise, they may be classified as noise IMFs after HHT [29]. The detailed pros and cons for various strategies are listed as Table 1. A DAE algorithm for ECG biosignal noise removal was proposed in [19,20,21,22,23]. In [19,20], the DAE was improved to extract the features of a clean ECG in the wavelet domain. Because these approaches use the DAE for adjusting the threshold, they have greater denoising performance than do wavelet methods. In [21], a deep neural network (DNN)–DAE outperformed an adaptive filtering approach, EMD, and wavelet approaches with a superior signal-to-noise ratio (SNRimp). In [22], a fully convolutional denoising autoencoder (FCN-based DAE) surpassed a DNN–DAE and convolutional neural network (CNN)–DAE. However, the QRS segment was distorted because fully connected layers averaged out the neighboring samples in the QRS segment. Reference [23] reports that denoising performance was improved by adding long short-term memory (LSTM) to a DAE. The LSTM cell learns the time series orders of ECG waves, which enhances the reconstruction quality. However, LSTM involves the use of numerous parameters and exhibits high computing complexity. Therefore, a CUDA accelerator was recommended to be used during the influence stage. In the studied DAE network, denoising performance was evaluated by calculating the SNRimp, root-mean-square error (RMSE), and percentage root-mean-square difference (PRD) for a noisy ECG with different SNRs.

Table 1.
Comparison of Advantages and Disadvantages of Various Strategies.
In contrast to various datasets widely used in computer vision, few datasets are available for ECG signal enhancement. Therefore, most noisy ECG signals are mixed manually using one of the following two methods: (1) adding Gaussian noise into the recorded ECG from patients (MIT–BIH arrhythmia database [30], MITDB); (2) adding EM, BW, and MA noise recorded from physically active volunteers (MIT–BIH Noise Stress Test Database [31], NSTDB) into a clean ECG. Recently, refs. [20,23,24,32] added Gaussian noise into a clean ECG and then successfully eliminated this white noise.
However, this approach is limited because the noisy ECGs used are not realistic. In [19,21,22,25,27,28], the ratios of BW, EM, and MA artifacts in the noisy ECG were not mentioned, which indicates that the noisy ECGs may be different even if the same signal segments of noise and ECG are employed. Therefore, evaluating the denoising performance of each approach is not possible. As illustrated in Figure 1, the waves of (a)–(d) are different when the composition ratio of noise is adjusted, but the SNRs of these four situations are identical.
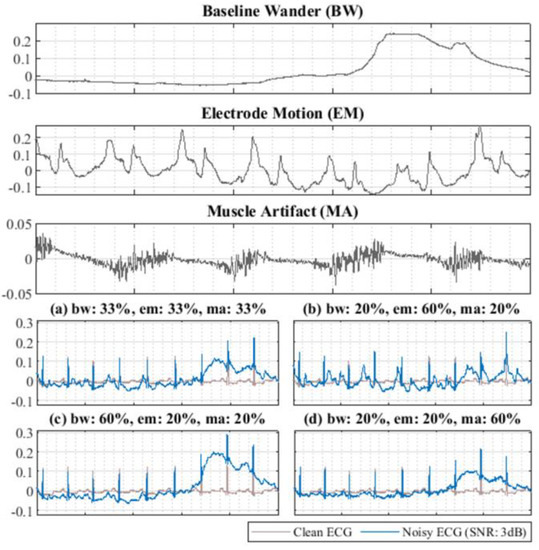
Figure 1.
Noisy ECG signal mixed with different component ratios of BW, EM, and MA. (a–d) illustrate the noisy ECG with 3 dB SNR and clean ECG signal, BW, EM, and MA artifacts in the same segment.
To objectively evaluate the denoising performance, we used NSTDB_118e [–6, 0, 6, 12, 18, and 24 dB] and NSTDB_119e [–6, 0, 6, 12, 18, and 24 dB] from PhysioNet as noisy ECG signals [33]. The experimental results demonstrated that the proposed approach is highly capable of suppressing different intensities of noise. In this paper, a high-quality channel-wise average pooling and 1D pixel-shuffle DAE (CPDAE) is proposed. The proposed CPDAE deploys residual block, pixel shuffle, global average pooling, and skip connection to extract a clean ECG. Here, skip connection is widely applied in deep learning, which can remedy the lost information with dimensionality reduction in the encoder and combines the features in deep and shallow layers [34,35,36]. However, all of the features have to be recorded in every encoder layer on computation if the feature information is directly transmitted from encoder to decoder. This requires a great amount of memory for additional data storage in the architecture. Hence, channel-wise average pooling (CWAP) and point-wise convolution (PW Conv.) are proposed to mitigate the issue of excessive memory requirements caused by original skip-connection. CWAP is calculated by averaging the features in every channel so that the memory requirement is substantially reduced. To provide information of the encoder layer effectively, point-wise convolution (PW Conv.) is applied to restore the features into the same shape as the encoder features, and then, the features are merged into the decoder layer, which achieves memory saving and provides information received from the encoder layer to the decoder layer. Based on the above design concept, the key contributions of the proposed method can be summarized as follows:
- The schemes of the residual block, pixel shuffle, and CWAP layer are utilized in the proposed DAE for enhancing the feature extracting capability, and the results show that the proposed CPDAE, which uses fewer parameters, can achieve better denoising performance than state-of-the-art approaches.
- The proposed CWAP layer between encoder and decoder not only avoids the ECG features disappearing through the deeper encoder layer, but also uses less memory than the shortcut connection. Furthermore, the key features are all averaged in the
- CWAP layer so that the number of channels is greatly reduced to one channel, and this also implies that it only takes 1/C times the memory size in implementation.
- The noisy ECG dataset obtained from NSTDB dataset is adopted to evaluate the denoising performance for various algorithms under the same conditions to ensure the same experimental environment can be completely rebuilt.
- To test the generalizability of various DAE models, the other noisy ECG dataset with six noise-level inputs is generated by randomly mixing the first 30 min section of the ECG signal in NSRDB with the 30 min section of EM noise in NSTDB. The experimental results demonstrate that the proposed CPDAE has better noise suppression than other approaches.
2. Methodology
2.1. Review of AE and DAE
A DAE is a variation of an autoencoder (AE) that is widely used in lossy data compression [37]. An AE aims to make the output equal to the input x, as depicted in Figure 2a. An AE has two main parts: (1) The encoder maps the high-dimension input into a low-dimension code z via neural network layers (NNs); (2) The decoder reconstructs the high-dimension signal from the low-dimension code. The formulas of these two parts can be expressed as Equations (1) and (2), where w and b are the weight and bias of NNs in the encoder, respectively, and and represent the weight and bias matrices of NNs in the decoder, respectively. ϕ and ψ are the nonlinear activation functions of the encoder and the decoder, respectively.
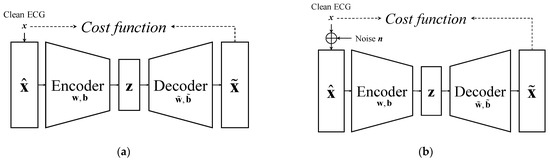
Figure 2.
Architecture of (a) AE and (b) DAE.
To make x and be as similar as possible, the MSE is used as the cost function (3) in AE, where N and i are the number of input data and the data sample index, respectively.
The DAE, an extension of the AE, is employed to reconstruct a clean signal from a corrupted signal [38]. It is commonly used in signal denoising and enhancement [39,40]. As illustrated in Figure 2b, the input of a DAE is a corrupted signal , which consists of a clean signal x and a noise signal n, and the denoised signal is reconstructed from . In the encoder layer, NNs attempt to isolate the features of the clean signal into code z, and is further reconstructed from z by the decoder. During the training phase, a DAE can learn the features of a clean ECG by updating the weights according to the cost function computed according to the MSE between the clean signal and the reconstructed signal.
2.2. Residual Block
The residual block [41] has been widely applied to avoid the vanishing gradient problem in deeper neural network layers. During the training phase, the optimizer updates every NN’s parameters by calculating the gradient from the cost function [42]. However, the vanishing gradient in the lower layers is more evident than that in the upper layers; therefore, the accuracy cannot be increased even if more NNs are added. To solve this problem, the residual block adds identity mapping between the start and the end of the NNs in Equation (4). This is evident in Figure 3, where zn+1 and zn are, respectively, the input and output of the residual block, ReLU σ is the activation function, and F (zn) represents the NNs.
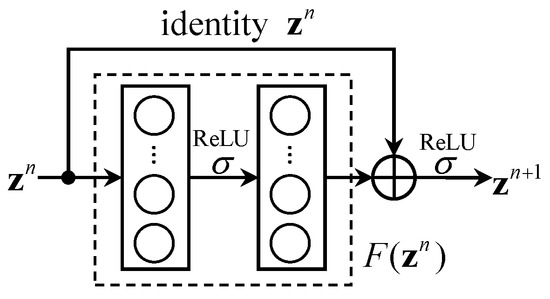
Figure 3.
Block diagram of the residual block.
2.3. Pixel Shuffle (Subpixel)
The pixel-shuffle (PS) layer was first applied for increasing the image resolution in [43]; the goal of PS is to map the image from low resolution to high resolution. The PS is an operation of data arrangement without any parameters and is used to generate one high-resolution feature from four low-resolution features. In [44], checkerboard artifacts were avoided by adding the PS operation before the deconvolution operation. In this study, we applied PS to preserve the features in an up-sampling process instead of using the general method of transposed convolution with stride = 2. PS converted the features in p from two channels into one channel, as illustrated in Figure 4. Similarly, pixel unshuffle was adopted to separate the features in from one channel into two channels in a down-sampling process. In various architectures of autoencoders for ECG signal noise cancellation, the ECG features in different layers are extracted from high-dimension information through multiple neural layers via an encoder. Finally, only precious few features are retained as ECG (as Z in Figure 2). Afterward, the clean ECG is reconstructed from precious few features (Z) via the decoder. This procedure reveals that the reduction in the number of neurons is essential in the encoder, so all of the available methods adopt max-pooling or convolution with stride = 2 to attain the number of neurons dropped by half. At max-pooling, the maximum features are retained, and the rest features are discarded. If the adjacent feature values are great, only the maximum value can be preserved, and the other significant features also have to be scrapped. If the stride in convolution is set to 2, the movement of the kernel is shifted by two grids, which lessens the computational cost and the number of output features is dropped by half. However, the precision of feature extraction with stride = 2 is not more exact compared to stride = 1. For this reason, this work not only adopts un-pixel shuffle and pixel shuffle methods to preserve the information but also deploys convolution with stride = 1 to extract the detail features as much as possible so that more precise information can be acquired.

Figure 4.
Workflow of the modified 1D pixel−shuffle and 1D pixel−unshuffle.
3. Proposed CPDAE
In this study, a CPDAE network architecture was proposed for ECG noise cancelation. The proposed structure consists of several encoder and decoder layers. The noisy ECG is fed into the input layer first, and the clean ECG feature code z is extracted in the encoding stage. The signal is reconstructed in the decoding stage. Moreover, channel-wise average pooling (CWAP) between the corresponding encoder and decoder layers is added to compensate for the decreased feature content layer by layer.
To test the denoising performance, three models were proposed and implemented in this study. The proposed CPDAELite attempts to minimize the amount of parameter usage and the number of multiply–accumulate operations (MACs); the proposed CPDAEFull exhibits the greatest denoising capability; the proposed CPDAERegular is the median version between the lite and full versions. In the remainder of this paper, only CPDAERegular is discussed for simplicity. The CPDAERegular consists of seven encoders, seven decoders, and six CWAP blocks. The overall architecture is illustrated in Figure 5. The detailed procedures of the encoder, decoder, and CWAP are described in the following sections.
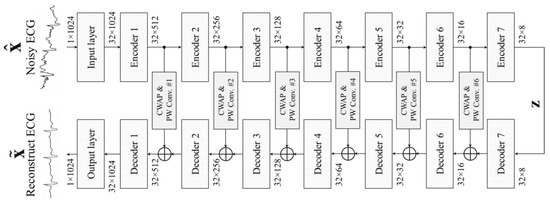
Figure 5.
Architecture of the regular version of the proposed CPDAE.
3.1. Encoder Layer
Initially, the input (1 × 1024) noisy ECG () is fed into the convolution operation to extend the channel to 32. Subsequently, seven encoder layers are used to extract the clean ECG features from the input signal. Finally, a 32 × 8 dimensional feature map z is obtained after the noisy ECG proceeds through the seven encoder layers. The structure of encoders 1–7 is illustrated in Figure 6; the input (an) is fed into the 1D residual block (1D Res) to extract the ECG features. After 1D-PUS rearranges the features, the dimension is converted from C × N to 2C × N/2. No parameters need to be learned in 1D-PUS. Finally, the output of the encoder layer (an+1) is obtained after the point-wise convolution operation, which combines with the channel features [45]. In detail, the kernel size of 1D convolution is set to 5 in 1D Res, and that of point-wise convolution is set to 1 in Figure 6. Moreover, the ReLU is used as the activation function (σ) in 1D Res.
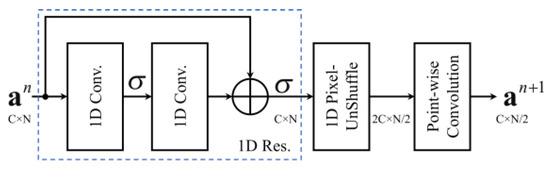
Figure 6.
Layer structure of encoders 1–7; C and N are the numbers of input channels and features, respectively.
3.2. Channel-Wise Average Pooling in Skip Connection
When the encoder layer maps features into low-dimensional z from the input layer, certain tiny but key features disappear as the network deepens. This results in the reconstructed features being unable to perfectly represent the features of the ECG signal [36]. To solve this problem, a skip connection between the corresponding encoder and decoder was added in [34,35,36]. However, this requires substantial memory use to hold the output of the encoder layer [46]. In this study, CWAP was proposed as a trade-off between denoising quality and memory requirements. The CWAP passes the average feature of channels from the encoder to the corresponding decoder and reduces the amount of memory usage in the skip connection as follows in Equation (5):
where and a are the CWAP output and input from the encoder, respectively. In addition, C is the number of input channels, and N represents the number of features. The CWAP averages the input channels into one channel () to reduce C times the memory usage of the skip connection. The memory size of the output of point-wise convolution takes the same dimension as a, and the output can be fed into the decoder layer, as depicted in Figure 7. To minimize gradient vanishing, a nonlinear activation function, such as a ReLU or sigmoid function, is not available in the skip connection.
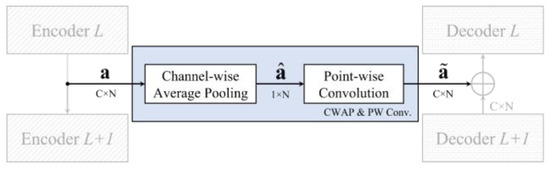
Figure 7.
Channel-wise average pooling layer structure and point-wise convolution operation.
3.3. Decoder Layer
The decoder layer is almost inversely symmetrical to the encoder part. Seven decoders are mapped to the high-dimensional features from the code z, as illustrated in Figure 5. Except for the last layer (decoder 7), the input of each decoder is the sum of both the skip connection and the output of the upper decoder layer, calculated through element-wise addition. Each decoder reconstructs the features from an by using the 1D residual block. Subsequently, the point-wise convolution (PW Conv) increases two times the channels that are required before up-sampling the 1D PS operation, and the features (an+1) are rearranged to be the output features in the decoder layer, as illustrated in Figure 8. With the same configuration as the encoder layer, the kernel size of the 1D convolution in the 1D residual block is set to 5, and that of the point-wise convolution in the encoder layer is set to 1.
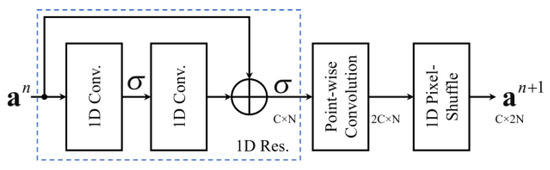
Figure 8.
Layer structure of decoders 1–7.
After passing through decoders 1–7, the features of the clean ECG are distributed in 32 channels, where the features are mapped from low dimensions to high dimensions. The reconstructed ECG signal () is obtained after the data pass through the output layer, which diminishes the 32 channels into 1 channel by convolution operations.
The detailed layer information of the proposed regular model and its submodule is listed in Table 2 and Table 3, respectively. Initially, the noisy ECG with the size of 1 × 1024 is fed into the Input Layer. Then, the ECG signal is extracted by 7 layers of the Encoder, and it is further compressed into the Code z with the size of 32 × 8. Subsequentially, the clean ECG can be reconstructed by 7 layers of the Decoder and an Output Layer. In addition, to enhance the quality of the reconstructed signal, the key features are transmitted by 6 layers of CWAP inserting between Encoder Layers 1–6 and Decoder Layers 1–6. The total number of parameters of CPDAERegular is 194,753, and the proposed model can be real-time run on certain low-cost CUDA devices. The number of encoders and decoders in the proposed model can be arbitrarily increased or decreased as long as the number of the feature code z is a natural number.

Table 2.
Layer Information for the Regular Version of Proposed CPDAE.

Table 3.
Layer Information of the Submodule for the Regular Version of the Proposed CPDAE.
4. Experimental Results
4.1. Evaluation Criteria
In this study, the quantitative performance of the denoising technique was evaluated using RMSE, PRD, and SNRimp.
SNRimp compares the SNR between the noisy ECG (SNRin) and the reconstructed signal (SNRout). A higher SNRimp value indicates superior denoising performance, defined as follows. The aforementioned variables are defined as follows:
where M is the strength of the signal, and xi is the amplitude of each sampling point in a clean ECG. Similarly, and are the amplitudes of the sampling in the reconstructed ECG and noisy ECG, respectively.
RMSE represents the variance between the reconstructed ECG () and the clean ECG (x). A smaller RMSE value represents a more favorable denoising performance. RMSE is formulated as follows:
PRD represents the reconstructed signal quality between the clean signal and the reconstructed signal. A lower PRD value, defined in Equation (10), indicates higher quality. Because of the original dc offset that exists in the clean ECG dataset, the mean of the input signal was considered in this work, consistent with the approach in [47].
4.2. Dataset Selection and Experiment Preprocessing
To evaluate the proposed system, a noisy ECG signal and a clean ECG signal were acquired from the nstdb [31] and the mitdb [30], respectively. The mitdb contains 48 half-hour excerpts of two-channel ambulatory ECG recordings, which were recorded at a 360 Hz sampling rate with 11-bit resolution using an analog/digital converter [33]. The mitdb includes several types of arrhythmia, and it has been widely used as the dataset for heartbeat classification [48]. The nstdb provides twelve 30 min ECG recordings (two leads per recording) and three 30 min recordings of noise typical in ambulatory ECGs [49]. The noisy ECG was created by mixing six levels (–6 dB, 0 dB, 6 dB, 12 dB, 18 dB, and 24 dB) of EM noise into the clean ECG recordings from mitdb_118 and mitdb_119 [50]. First, the noise was added to the recordings after the first 5 min. Subsequently, 2 min noise segments with 2 min noise-free segments were alternated until the end.
In this study, the noisy ECG signal was acquired from the noise segment of 24 ECG leads in the nstdb, which can be found in 5–7, 9–11, 13–15, 17–19, 21–23, 25–27, and 29–30 min in every ECG lead. Subsequently, each segment was further separated into several nonoverlap fragments with a length of 1024 samples. Finally, 6888 noisy ECGs were used to evaluate the denoising performance. For the clean ECG signal, the corresponding indices of the clean ECG in mitdb-118 and mitdb-119 were used. The 6888 fragments were split into a training set and testing set, with 80% and 20% of the fragments, respectively. The dc offset was removed from all fragments in the preprocessing phase in consideration of the effect of the dc offset on PRD. Moreover, the 11-bit digitized ECG signal was divided by 2048 to normalize the input data within 0 and 1.
4.3. Experimental Results and Comparison
The artificial intelligence framework of this study was PyTorch 1.9, and the adopted CPU, RAM, and GPU in our experiment were an AMD R9-5950x, 96 GB, and Nvidia RTX3090 24 GB, respectively. To train the models efficiently, suitable hyperparameters were selected and set to accelerate the training convergence speed. Table 4 demonstrates the six hyperparameters used in this study. The cost function using MSE was the same as in previous studies [21,22,23,24,28]. The epochs were set to 1000 to ensure that each model would converge during the training phase. The learning rate was set to 10−4 and decayed by one-half every 200 epochs. This implied that the weights could be updated rapidly in the early training stage, and finetuned at the final training stage [51]. For optimization, an Adam optimizer was employed instead of stochastic gradient descent because it could locate the gradient more accurately.

Table 4.
Hyperparameters for the Experiment.
To evaluate the denoising performance with various parameters and MACs, we implemented CPDAELite, CPDAERegular, and CPDAEFull with different combinations, as displayed in Table 5. CPDAELite is highly suitable for implementation on an embedded platform. CPDAEFull has the highest denoising performance and the greatest number of MACs. This implies that a powerful GPU would be needed to realize this highly complex algorithm. CPDAERegular balances denoising performance and lightweight computational capability. For the testing phases of Lite, Regular, and Full versions, the average run-time per frame was 0.1154 ms, 0.1424 ms, and 0.1327 ms, respectively. Conceptually, the MACs can be reduced by decreasing the number of encoder and decoder layers and the number of channels for each layer, but the denoising capability of DAE would drop down. However, deeper layers have the ability to learn data representations with multiple levels of abstraction. This method compensates for the lack of features when a low number of channels in each encoder/decoder layer is used (e.g., CPDAELite). By contrast, when more channels are available in each encoder/decoder layer (e.g., CPDAEFull), the denoising performance is not substantially improved by adding more layers.

Table 5.
Components of the Proposed Models.
To evaluate the performance of the proposed CPDAE more clearly, the channel numbers were, respectively set to 16, 32, 48, 64, and 128 with the corresponding numbers of layers set to 5, 6, 7, 8, and 9 for the usage of encoder and decoder. Here, the average of SNRimp was utilized to measure the performance. Figure 9 shows that the more layers, the higher SNRimp attained under the fixed numbers of channels. In addition, a better average of SNRimp would be obtained with the adjustment of the numbers of channels and layers. The design goal of CPDAELite aims to decrease the number of parameters and achieved performance similar to that of FCN [22]. The desired average of SNRimp in CPDAELite has to be more than 10 dB, so the numbers of channels and layers were set to 16 and 8, respectively. The result with CPDAERegular attained a curve with the greatest improvement, where the numbers of channels and layers were respectively set to 32 and 7. The model of CPDAFull achieved the best denoising results, where the numbers of channels and layers were respectively set to 128 and 6. Although each additional encoder and decoder layer could improve the performance slightly, it also led to a significant increase in the number of parameters.
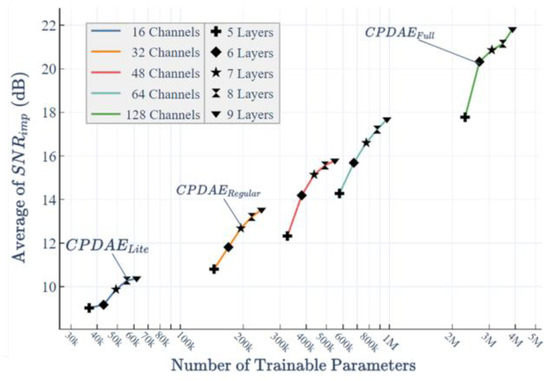
Figure 9.
A performance comparison of CPDAE models with various channels and encoder/decoder layers.
The proposed models were compared with the following four existing approaches: (1) DNN–DAE, (2) CNN–DAE, (3) FCN–DAE [22], and (4) CNN–LSTM–DAE [23]. The DNN–DAE has 10 fully connected layers with 512, 256, 128, 64, 32, 64, 128, 256, 512, and 1024 nodes. The CNN–DAE uses the same structure as the FCN–DAE [22] in layers 1–13, and two fully connected layers are added in layers 14 and 15. Moreover, ReLU and batch normalization are used at the end of each layer. The model architectures of the FCN–DAE [22] and CNN–LSTM–DAE [23] are state-of-the-art. The FCN–DAE [22] has six convolution layers in the encoder and seven transposed convolutions in the decoder. The CNN–LSTM–DAE [23] uses eight convolution layers and five max-pooling layers to extract the features of the clean ECG in the encoder. In contrast with previous works, LSTM cells at the end of the encoder were added to learn the relevant information in the sequential data. To recover the original clean ECG signal, eight convolution layers, six up-sampling layers, and one fully connected layer are used in the decoder.
The average loss curves for various DAEs under the testing and training sets are depicted in Figure 10. In the training phase (Figure 10a), the loss value of every DAE was an obvious decrease in the first 500 epochs, ensuring that all DAEs could effectively obtain the trainable parameters. After the DAEs had been trained over 800 epochs, the trend of the loss curve for all DAEs became flat, so we stopped training at epoch 1000. In the last epoch, DNN–DAE showed the highest loss value; however, the FCN–DAE and CNN–LSTM–DAE had very similar loss values. It is worth noting that the proposed CPDAEFull had the lowest loss value in this experiment, and the loss value almost had no changes after 300 times of epochs. This result shows that the proposed CPDAEFull learns ECG features very well compared with other methods by using fewer training times. In the testing phase, the DNN–DAE had the worst MSE. The loss curves of the proposed CPDAE models (Lite, Regular, and Full version) had a significant improvement compared with other approaches.
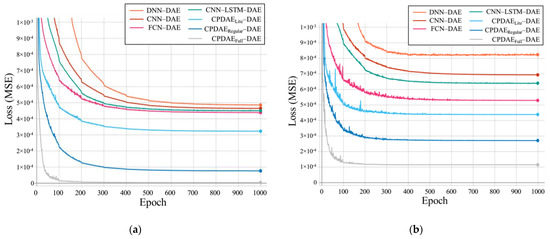
Figure 10.
The loss curves in training and testing phases: (a) training phase; (b) testing phase.
The criteria for the improvement of SNR are reported in Figure 11. We used box plots to display the SNRimp distribution under certain SNRin. All of the models exhibited favorable improvement in low SNRin (−6 dB, 0 dB, and 6 dB). When the SNRin was −6, the DNN–DAE, CNN–DAE, FCN–DAE, CNN–LSTM–DAE, and CPDAELite exhibited a similar SNRimp distribution. According to our results, CPDAERegular and CPDAEFull were ranked first (23.68 dB) and second (20.05 dB) in terms of average SNRimp. However, when the SNRin was increased to 12, 18, and 24 dB, the proposed CPDAE methods were superior to the other approaches. Moreover, because the noise was not always at a high-intensity level, performance had to be tested under low-intensity noise. The state-of-the-art approaches were only tested under the condition of SNRin > 10 dB; higher SNRin was essential for validation. The SNRimp values of the DNN–DAE, CNN–DAE, FCN–DAE, and CNN–LSTM–DAE methods decreased under the conditions of 12, 18, and 24 dB SNRin.
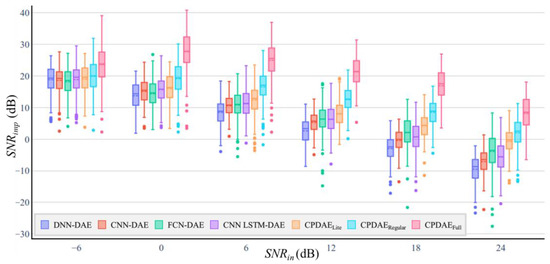
Figure 11.
Box plots for SNRimp comparison of the denoising criteria of all of the evaluated methods under six SNRin for the testing phase of NSTDB; the box plots include outliers (dot), minimum, interquartile range, median, maximum, and average (dotted line).
Figure 12 and Figure 13 demonstrate the average PRD and RMSE, respectively. Lower PRD and RMSE values imply that the reconstructed ECG is closer to a clean ECG. EM noise is the most difficult to remove because it has waves similar to a clean ECG. The models treated the ECG signal as noise in some cases, which resulted in higher PRD values. Under the –6 dB condition of SNRin, the CNN-LSTM-DAE approach exhibited the widest interquartile range (IQR), which indicates that the denoising performance was the most unstable. The FCN method had the lowest IQR, but its average PRD was higher than that of the other methods. Although the proposed CPDAELite did not exhibit any obvious difference in SNRimp, the reconstructed ECG was more similar to a clean ECG than those obtained with the other methods. However, the PRD and RMSE values of the proposed CPDAEFull were much lower than the values of the other methods in all situations.
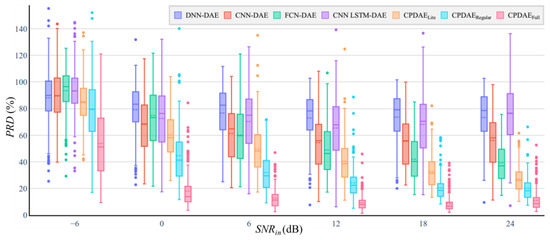
Figure 12.
Box plots for PRD comparison of the denoising criteria of all of the evaluated methods under six SNRin for the testing phase of NSTDB; the box plots include outliers (dot), minimum, interquartile range, median, maximum, and average (dotted line).
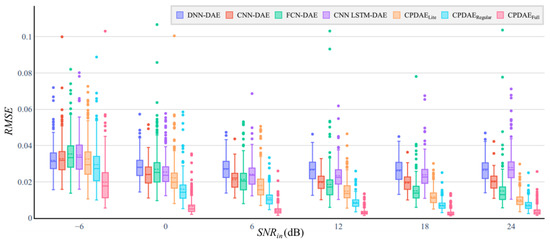
Figure 13.
Box plots for RMSE comparison of the denoising criteria of all of the evaluated methods under six SNRin for the testing phase of NSTDB; the box plots include outliers (dot), minimum, interquartile range, median, maximum, and average (dotted line).
Table 6 reports the total numbers of trainable parameters and MACs for various methods with the two criteria of average SNRimp and average PRD. The DNN–DAE, CNN–DAE, and CNN–LSTM–DAE used several fully connected layers, which necessitated the use of numerous parameters and resulted in ineffective processing of complex noise. For the comparison of MACs, the DNN–DAE consists of the fully connected layer so that it only costs 1.4 M MACs. The proposed CPDAEFull costs the highest MACs because the number of channels is higher than others. For the performance comparison of the SNRimp and PRD, the proposed CPDAELite uses fewer parameters and MACs than FCN–DAE and achieves better denoising performance. Here, CPDAEFull is the best version of the proposed models, and it exhibits outstanding denoising performance under different SNRin values, although it would take 344.01 M MACs. To ensure the generalizability of the proposed method, EM noise was further added into a clean ECG in MIT-BIH Normal Sinus Rhythm Database (NSRDB, [52]), where the data include the ECG signals from 16 subjects. Twelve minutes of ECG signals were taken from each subject to be evaluated in experiments. Six levels of noisy ECG signals were mixed into ECG signals, i.e., −6, 0, 6, 12, 18, and 24 dB. Finally, there were a total of 59,400 untrained noisy ECG data to be tested in the testing phase. To evaluate the various algorithms by SNRimp and PRD, a box plot was deployed as shown in Figure 14 and Figure 15. The results show that the three proposed CPDAE models had superior noise suppression compared to the other algorithms.

Table 6.
Comparison of the Proposed Models with State-of-the-art Methods.
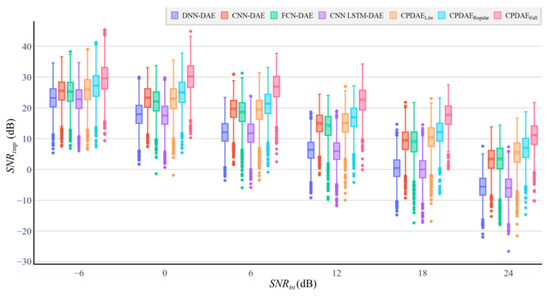
Figure 14.
Box plots for SNRimp comparison of the denoising criteria of all of the evaluated methods under six SNRin for the testing phase of NSRDB with EM noise; the box plots include outliers (dot), minimum, interquartile range, median, maximum, and average (dotted line).
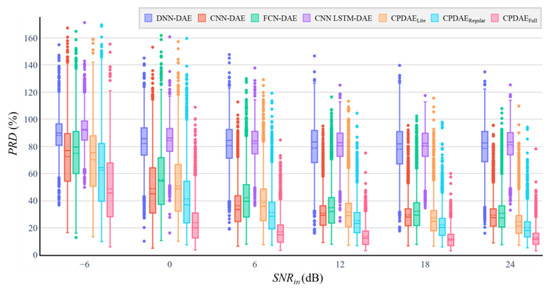
Figure 15.
Box plots for PRD comparison of the denoising criteria of all of the evaluated methods under six SNRin for the testing phase of NSRDB with EM noise; the box plots include outliers (dot), minimum, interquartile range, median, maximum, and average (dotted line).
Two noisy signals are displayed in Figure 16a,j, and the corresponding clean signals are displayed in Figure 16b,k. The ECG filtered with the CNN–DAE (Figure 16c,d) and DNN–DAE (Figure 16l,m) could eliminate most noise well, but the ECG signals were also destroyed. In the FCN–DAE, the reconstructed ECG retained most information of the ECG wave; however, one QRS segment was misjudged as noise (Figure 16e). The CNN–LSTM–DAE exhibited a similar result in Figure 16o. The proposed CPDAELite removed the most noise, but the amplitude of the T wave was slightly decreased, as seen in Figure 16g,p. The proposed CPDAERegular retained the most significant ECG features. Moreover, the proposed CPDAEFull retained the complete ECG features and produced the clearest ECG. In addition, we also tested the proposed DAE on self-recorded ECG, and the experimental results in Figure 17 demonstrate that the proposed models can extract a clear ECG signal from corrupted ECGs. Since these ECG and noise signals had never been seen in the training set, the reconstructed ECGs would have some distortion. However, it still shows that the proposed framework is able to restore important features such as the P wave, the QRS complex, and the T wave. Therefore, we believe that the generalizability of the proposed method exists and can stand the test of other datasets. Although the proposed CPDAE had outstanding performance, there were still some outliers in the statistical analysis. This result indicates some limitations existing in the proposed CPDAE. Here, we revealed three scenarios for the case of impairment as shown in Figure 18. Figure 18a demonstrates that the reconstructed ECG located at the boundary received a little distortion if a fragment of a ECG signal containing any one of the P wave, QRS complex, or T wave was cut at the boundary. Figure 18b shows that if the original ECG signal contained more high-frequency noise, it was difficult to reconstruct a perfect denoising ECG for both CPDAELite and CPDAERegular under this situation. Because the proposed CPDAEFull had the strongest computing ability, it obtained much better reconstructed ECG signals than the others. Figure 18c shows that the intermediate ECG signal was disappearing, and the proposed CPDAE could not render a properly reconstructed ECG. It is interesting in the position of the intermediate reconstructed ECG for the proposed CPDAE. The position of the reconstructed ECG signal for CPDAELite was later than that for the original clean ECG, and the position of the reconstructed ECG signal for CPDAERegular was earlier than that for the original clean ECG. The proposed CPDAEFull misjudged the original ECG signal, resulting in the wrong reconstruction location because of the strong noise interference.
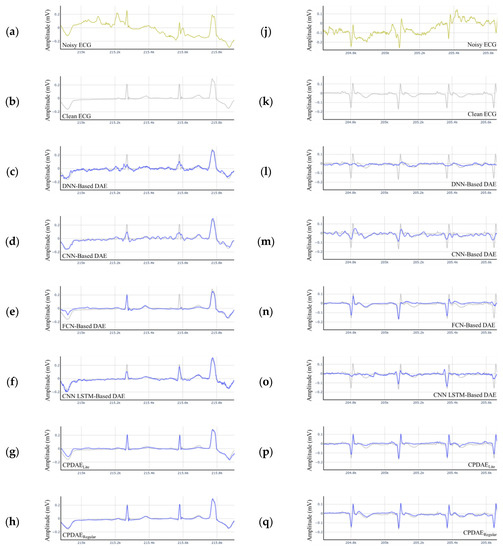

Figure 16.
Comparison of the reconstructed results for various evaluated models in MLII of NSTDB_119e06 (a–i), and V1 of NSTDB_118e06 (j–r).
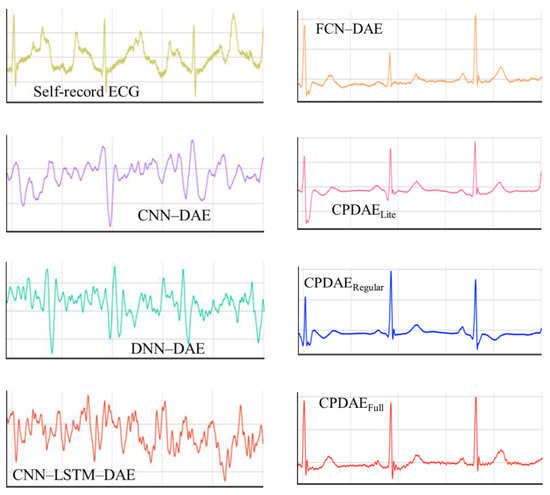
Figure 17.
Reconstructed ECGs of various DAEs in self-recorded ECG.
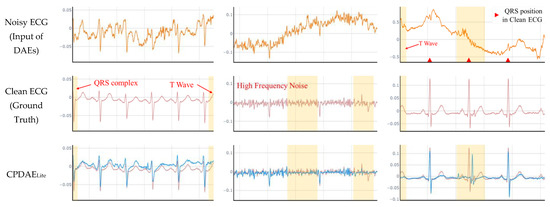
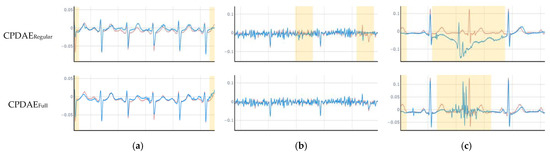
Figure 18.
Three scenarios for the limitations of the proposed CPDAE algorithm. (a) Boundary effect; (b) high-frequency interference; (c) strong high-frequency noise interference with boundary effect.
5. Conclusions
In this study, a CPDAE was proposed to effectively eliminate the electrode EM artifacts in a noisy ECG. The three proposed models of the CPDAE, namely CPDAELite, CPDAERegular, and CPDAEFull, can be implemented on devices and platforms with different computational capabilities. The purpose of designing CWAP is to reduce memory usage while feature transfers are needed. Therefore, it can be applied to any network that involves a shortcut layer or combines with an attention mechanism to selectively transfer features. The source code can be found in the Supplementary Materials. Considering that EM is the hardest noise to remove and causes PRD to be higher under the condition of −6 dB SNRin, removing the EM signal without losing ECG features remains a challenge. To compare with state-of-the-art methods, the proposed models provided higher SNR with less computational complexity. The MAC and SNR results demonstrate that the proposed methods are suitable for future ECG instrumentation applications. However, among the limitations, it is worth noting that there were a small number of outliers in the boxplots of the three CPDAE models, which means the proposed method can not suppress the noise in some parts of all scenarios. Because the integrity of ECG segments in noisy ECGs cannot be ensured, the CPDAE misjudged ECG features as noise when the ECG features were not complete in noisy ECGs In addition, our studies can be extended to investigation of the following subjects: (1) The significant ECG features are kept completely or not; (2) Adding BW and MA noise to the evaluation; (3) The dataset should be re-checked because we found some ECGs containing noise in some fragments, which reduces the denoising performance during the training phase; (4) Using other loss function instead of MSE; (5) The information of RR intervals can be involved in the proposed CPDAE; (6) Considering that each ECG signal has highly similar and significant features, the generative adversarial networks (GAN) architecture can be a good solution to improve the quality of the reconstructed ECG; (7) Although the three proposed CPDAE models demonstrate very outstanding reconstructed quality, it is necessary to verify the usability of reconstructed ECGs via the doctor.
Supplementary Materials
The following are available online at: https://github.com/MagnusJhang/Channel-wise-Average-Pooling-and-1D-Pixel-Shuffle-Denoising-Autoencoder (accessed on 8 July 2022).
Author Contributions
Conceptualization, Y.-S.J. and S.-C.L.; methodology, Y.-S.J. and S.-T.W.; software, Y.-S.J.; validation, S.-H.W. and S.-C.L.; formal analysis, Y.-S.J. and M.-H.S.; investigation, M.-H.S.; resources, S.-T.W.; data curation, Y.-S.J. and S.-T.W.; writing—original draft preparation, Y.-S.J., Wang, S.-T, and S.-C.L.; writing—review and editing, S.-C.L. and Wang, S.-T; visualization, Y.-S.J.; supervision, M.-H.S. and S.-H.W.; project administration, M.-H.S., S.-H.W., and S.-C.L.; funding acquisition, M.-H.S., S.-C.L., and S.-H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by Ministry of Science and Technology, Taiwan, under Grant MOST 110-2622-E-224-006, 110-2221-E-150-045, and 109-2221-E-150-043, in part by Smart Machinery and Intelligent Manufacturing Research Center, and Higher Education SPROUT Project, National Formosa University, Yunlin, Taiwan, in part by Ministry of Education (MOE) Female Researching Talent Cultivation Project for STEM field, and in part by Intelligent Recognition Industry Service Center from the Featured Areas Research Center Program within the framework of the Higher Education Sprout Project by the Ministry of Education (MOE) in Taiwan.
Informed Consent Statement
Not applicable.
Data Availability Statement
The dataset of NSRDB with EM noise can be downloaded at https://www.kaggle.com/datasets/yusyuanjhang/mitbih-nsrdb-with-nstdb-em-noise (accessed on 1 February 2020).; The dataset of NSTDB can be downloaded at https://physionet.org/content/nstdb/1.0.0/ (accessed on 1 February 2020).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Roth, G.A.; Mensah, G.A.; Johnson, C.O.; Addolorato, G.; Ammirati, E.; Baddour, L.M.; Barengo, N.C.; Beaton, A.; Benjamin, E.J.; Benziger, C.P.; et al. Global Burden of Cardiovascular Diseases and Risk Factors, 1990–2019: Update from the GBD 2019 Study. J. Am. Coll. Cardiol. 2020, 76, 2982–3021. [Google Scholar] [CrossRef] [PubMed]
- Al-Khatib, S.M.; Stevenson, W.G.; Ackerman, M.J.; Bryant, W.J.; Callans, D.J.; Curtis, A.B.; Deal, B.J.; Dickfeld, T.; Field, M.E.; Fonarow, G.C.; et al. 2017 AHA/ACC/HRS Guideline for Management of Patients with Ventricular Arrhythmias and the Prevention of Sudden Cardiac Death. Circulation 2018, 138, e272–e391. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salinet, J.L.; Luppi Silva, O. ECG Signal Acquisition Systems. In Developments and Applications for ECG Signal Processing: Modeling, Segmentation, and Pattern Recognition; Academic Press: Cambridge, MA, USA, 2019; pp. 29–51. [Google Scholar] [CrossRef]
- Sun, C.; Liao, J.; Wang, G.; Li, B.; Meng, M.Q.H. A portable 12-lead ECG acquisition system. In Proceedings of the 2013 IEEE International Conference on Information and Automation, ICIA, Yinchuan, China, 26–28 August 2013; pp. 368–373. [Google Scholar] [CrossRef]
- Webster, J.G. Reducing Motion Artifacts and Interference in Biopotential Recording. IEEE Trans. Biomed. Eng. 1984, BME-31, 823–826. [Google Scholar] [CrossRef]
- Huhta, J.C.; Webster, J.G. 60-Hz Interference in Electrocardiography. IEEE Trans. Biomed. Eng. 1973, BME-20, 91–101. [Google Scholar] [CrossRef] [PubMed]
- Lenis, G.; Pilia, N.; Loewe, A.; Schulze, W.H.W.; Dössel, O. Comparison of Baseline Wander Removal Techniques considering the Preservation of ST Changes in the Ischemic ECG: A Simulation Study. Comput. Math. Methods Med. 2017, 2017, 1–13. [Google Scholar] [CrossRef]
- Hesar, H.D.; Mohebbi, M. Muscle artifact cancellation in ECG signal using a dynamical model and particle filter. In Proceedings of the 2015 22nd Iranian Conference on Biomedical Engineering, ICBME 2015, Tehran, Iran, 25–27 November 2015; pp. 178–183. [Google Scholar] [CrossRef]
- Rahman, M.Z.U.; Shaik, R.A.; Reddy, D.V.R.K. Efficient and simplified adaptive noise cancelers for ecg sensor based remote health monitoring. IEEE Sens. J. 2012, 12, 566–573. [Google Scholar] [CrossRef]
- Rahman, M.Z.U.; Karthik, G.V.S.; Fathima, S.Y.; Lay-Ekuakille, A. An efficient cardiac signal enhancement using time–frequency realization of leaky adaptive noise cancelers for remote health monitoring systems. Measurement 2013, 46, 3815–3835. [Google Scholar] [CrossRef]
- Venkatesan, C.; Karthigaikumar, P.; Varatharajan, R. FPGA implementation of modified error normalized LMS adaptive filter for ECG noise removal. Clust. Comput. 2019, 22, 12233–12241. [Google Scholar] [CrossRef]
- Yadav, S.K.; Sinha, R.; Bora, P.K. Electrocardiogram signal denoising using non-local wavelet transform domain filtering. IET Signal Process. 2015, 9, 88–96. [Google Scholar] [CrossRef] [Green Version]
- Prashar, N.; Sood, M.; Jain, S. Design and implementation of a robust noise removal system in ECG signals using dual-tree complex wavelet transform. Biomed. Signal Process. Control 2021, 63, 102212. [Google Scholar] [CrossRef]
- Mourad, T. ECG Denoising Based on 1-D Double-Density Complex DWT and SBWT. In The Stationary Bionic Wavelet Transform and its Applications for ECG and Speech Processing; Mourad, T., Ed.; Springer International Publishing: Cham, Switzerland, 2022; pp. 31–50. ISBN 978-3-030-93405-7. [Google Scholar] [CrossRef]
- Lee, J.; McManus, D.D.; Merchant, S.; Chon, K.H. Automatic motion and noise artifact detection in holter ECG data using empirical mode decomposition and statistical approaches. IEEE Trans. Biomed. Eng. 2012, 59, 1499–1506. [Google Scholar] [CrossRef] [PubMed]
- Boda, S.; Mahadevappa, M.; Dutta, P.K. A hybrid method for removal of power line interference and baseline wander in ECG signals using EMD and EWT. Biomed. Signal Process. Control 2021, 67, 102466. [Google Scholar] [CrossRef]
- Patro, K.K.; Jaya Manmadha Rao, M.; Jadav, A.; Rajesh Kumar, P. Noise Removal in Long-Term ECG Signals Using EMD-Based Threshold Method. Lect. Notes Data Eng. Commun. Technol. 2021, 63, 461–469. [Google Scholar] [CrossRef]
- Blanco-Velasco, M.; Weng, B.; Barner, K.E. ECG signal denoising and baseline wander correction based on the empirical mode decomposition. Comput. Biol. Med. 2008, 38, 1–13. [Google Scholar] [CrossRef]
- Xiong, P.; Wang, H.; Liu, M.; Zhou, S.; Hou, Z.; Liu, X. ECG signal enhancement based on improved denoising auto-encoder. Eng. Appl. Artif. Intell. 2016, 52, 194–202. [Google Scholar] [CrossRef]
- Hao, H.; Liu, M.; Xiong, P.; Du, H.; Zhang, H.; Lin, F.; Hou, Z.; Liu, X. Multi-lead model-based ECG signal denoising by guided filter. Eng. Appl. Artif. Intell. 2019, 79, 34–44. [Google Scholar] [CrossRef]
- Xiong, P.; Wang, H.; Liu, M.; Liu, X. Denoising autoencoder for eletrocardiogram signal enhancement. J. Med. Imaging Health Inform. 2015, 5, 1804–1810. [Google Scholar] [CrossRef]
- Chiang, H.T.; Hsieh, Y.Y.; Fu, S.W.; Hung, K.H.; Tsao, Y.; Chien, S.Y. Noise Reduction in ECG Signals Using Fully Convolutional Denoising Autoencoders. IEEE Access 2019, 7, 60806–60813. [Google Scholar] [CrossRef]
- Dasan, E.; Panneerselvam, I. A novel dimensionality reduction approach for ECG signal via convolutional denoising autoencoder with LSTM. Biomed. Signal Process. Control 2021, 63, 102225. [Google Scholar] [CrossRef]
- El Bouny, L.; Khalil, M.; Adib, A. Convolutional Denoising Auto-Encoder Based AWGN Removal from ECG Signal. In Proceedings of the 2021 International Conference on INnovations in Intelligent SysTems and Applications, INISTA 2021, Kocaeli, Turkey, 25–27 August 2021. [Google Scholar]
- Bing, P.; Liu, W.; Zhang, Z. DeepCEDNet: An Efficient Deep Convolutional Encoder-Decoder Networks for ECG Signal Enhancement. IEEE Access 2021, 9, 56699–56708. [Google Scholar] [CrossRef]
- Nurmaini, S.; Darmawahyuni, A.; Sakti Mukti, A.N.; Rachmatullah, M.N.; Firdaus, F.; Tutuko, B.; Mukti, A.N.S.; Rachmatullah, M.N.; Firdaus, F.; Tutuko, B. Deep Learning-Based Stacked Denoising and Autoencoder for ECG Heartbeat Classification. Electronics 2020, 9, 135. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Yang, L.; Liu, M.; Yuan, X.; Xiong, P.; Lin, F.; Liu, X. ECG signal denoising based on deep factor analysis. Biomed. Signal Process. Control 2020, 57, 101824. [Google Scholar] [CrossRef]
- He, Z.; Liu, X.; He, H.; Wang, H. Dual Attention Convolutional Neural Network Based on Adaptive Parametric ReLU for Denoising ECG Signals with Strong Noise. In Proceedings of the 2021 43rd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Guadalajara, Mexico, 1–5 November 2021; pp. 779–782. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Snin, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Moody, G.B.; Mark, R.G. The impact of the MIT-BIH arrhythmia database. IEEE Eng. Med. Biol. Mag. 2001, 20, 45–50. [Google Scholar] [CrossRef]
- George, M.; Warren, M.; Roger, M. A noise stress test for arrhythmia detectors. Comput. Cardiol. 1984, 11, 381–384. [Google Scholar]
- Singh, P.; Pradhan, G. A New ECG Denoising Framework Using Generative Adversarial Network. IEEE/ACM Trans. Comput. Biol. Bioinform. 2021, 18, 759–764. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.Y.; Yang, Y.H. Denoising Auto-Encoder with Recurrent Skip Connections and Residual Regression for Music Source Separation. In Proceedings of the 17th IEEE International Conference on Machine Learning and Applications, ICMLA 2018, Orlando, FL, USA, 17–20 December 2018; pp. 773–778. [Google Scholar] [CrossRef] [Green Version]
- Peng, Y.; Zhang, L.; Liu, S.; Wu, X.; Zhang, Y.; Wang, X. Dilated Residual Networks with Symmetric Skip Connection for image denoising. Neurocomputing 2019, 345, 67–76. [Google Scholar] [CrossRef]
- Dong, L.F.; Gan, Y.Z.; Mao, X.L.; Yang, Y.B.; Shen, C. Learning Deep Representations Using Convolutional Auto-encoders with Symmetric Skip Connections. In Proceedings of the ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing, Calgary, AB, Canada, 15–20 April 2018; pp. 3006–3010. [Google Scholar] [CrossRef] [Green Version]
- Liu, T.; Wang, J.; Liu, Q.; Alibhai, S.; Lu, T. High-Ratio Lossy Compression: Exploring the Autoencoder to Compress Scientific Data; High-Ratio Lossy Compression: Exploring the Autoencoder to Compress Scientific Data. IEEE Trans. Big Data 2021, PP, 2332–7790. [Google Scholar] [CrossRef]
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P.A. Extracting and composing robust features with denoising autoencoders. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 1096–1103. [Google Scholar] [CrossRef] [Green Version]
- Lee, D.; Choi, S.; Kim, H.J. Performance evaluation of image denoising developed using convolutional denoising autoencoders in chest radiography. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2018, 884, 97–104. [Google Scholar] [CrossRef]
- Lu, X.; Tsao, Y.; Matsuda, S.; Hori, C. Speech enhancement based on deep denoising autoencoder. In Proceedings of the Annual Conference of the International Speech Communication Association, Interspeech, Lyon, France, 25–29 August 2013; pp. 436–440. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef] [Green Version]
- Werbos, P. Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Science. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, 1974. [Google Scholar]
- Shi, W.; Caballero, J.; Huszar, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar] [CrossRef] [Green Version]
- Aitken, A.; Ledig, C.; Theis, L.; Caballero, J.; Wang, Z.; Shi, W. Checkerboard artifact free sub-pixel convolution: A note on sub-pixel convolution, resize convolution and convolution resize. arXiv 2017, arXiv:1707.02937. [Google Scholar]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, 21–26 July 2017; pp. 1800–1807. [Google Scholar] [CrossRef] [Green Version]
- Hascoet, T.; Zhuang, W.; Febvre, Q.; Ariki, Y.; Takiguchi, T.; Hascoet, T.; Zhuang, W.; Febvre, Q.; Ariki, Y.; Takiguchi, T. Reducing the Memory Cost of Training Convolutional Neural Networks by CPU Offloading. J. Softw. Eng. Appl. 2019, 12, 307–320. [Google Scholar] [CrossRef]
- Němcová, A.; Smíšek, R.; Maršánová, L.; Smital, L.; Vítek, M. A comparative analysis of methods for evaluation of ECG signal quality after compression. BioMed Res. Int. 2018, 2018, 1–26. [Google Scholar] [CrossRef] [PubMed]
- Luz, E.J.d.S.; Schwartz, W.R.; Cámara-Chávez, G.; Menotti, D. ECG-based heartbeat classification for arrhythmia detection: A survey. Comput. Methods Programs Biomed. 2016, 127, 144–164. [Google Scholar] [CrossRef] [PubMed]
- Moody, G.; Mark, R. MIT-BIH Noise Stress Test Database v1.0.0. Available online: https://physionet.org/content/nstdb/1.0.0/ (accessed on 1 February 2020).
- Moody, G.; Mark, R. MIT-BIH Arrhythmia Database v1.0.0. Available online: https://physionet.org/content/mitdb/1.0.0/ (accessed on 1 February 2020).
- Senior, A.; Heigold, G.; Ranzato, M.; Yang, K. An empirical study of learning rates in deep neural networks for speech recognition. In Proceedings of the ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 6724–6728. [Google Scholar]
- Moody, G.; Mark, R. MIT-BIH Normal Sinus Rhythm Database v1.0.0. Available online: https://physionet.org/content/nsrdb/1.0.0/ (accessed on 1 February 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).