Next Article in Journal
A New Approach to the Allocation of Multidimensional Resources in Production Processes
Previous Article in Journal
Coping with Access Difficulties and Absenteeism through Data Visualization: A Case Study from a Rural Vocational School in Northern Greece
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 12
Issue 14
10.3390/app12146939
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Effect of Side Wall Cutout Sizes on Corrugated Box Compression Strength in the Function of Length-to-Width Ratios—An Experimental Study

by
Renáta Pidl
1,
Lajos Fehér
1 and
Péter Böröcz
2,*
1
Department of Applied Mechanics, Széchenyi István University, Egyetem tér 1, 9026 Győr, Hungary
2
Department of Logistics and Forwarding, Széchenyi István University, Egyetem tér 1, 9026 Győr, Hungary
*
Author to whom correspondence should be addressed.
Appl. Sci. 2022, 12(14), 6939; https://doi.org/10.3390/app12146939
Submission received: 24 June 2022 / Revised: 6 July 2022 / Accepted: 7 July 2022 / Published: 8 July 2022
(This article belongs to the Section Mechanical Engineering)
Browse Figures
Versions Notes

Abstract

:
Packaging made from corrugated cardboard is a widely used solution in modern supply chains for the handling, storage and distribution of goods. These packages are required to maintain adequate protection conditions; however, in many cases, the cardboard box dimensions, handles and/or ventilation holes, quality and their configuration could compromise its protection strength. This study observes and evaluates the performance of corrugated cardboard boxes made with B-flute boards by considering different cutout sizes from the side walls (0%, 20%, 40%, 60% and 80%) in various box length–width ratios of 200 mm, 300 mm, 400 mm, 500 mm and 600 mm in length and a constant 300 mm width and height. Box compression tests were performed in a laboratory, and results were compared with mathematical statistics. In each cutout case, the maximum compression force was observed with the box with dimensions of 400 × 300 × 300 mm. The measurement results showed that the 1.33 length-to-width ratio has the best maximum compression force result. The statistical tests showed that there is no significant difference between the 0% and 20% cutout groups.

1. Introduction

In both production and distribution logistics, the packaging of products is essential [1,2,3,4,5]. Packaging’s basic functions include facilitating the storage, handling and transportation of products. In many cases, packaging also includes product descriptions, promotional graphics and product protection labels. In today’s widespread internet commerce, consumer packages are also provided with external protective packaging to standardize handling [6]. In production and distribution logistics, filled and sealed packages are subjected to various mechanical and climatic stresses during transport, storage and loading processes. Mechanical loads can be static or dynamic [7]. In logistics, product packaging systems are stacked. In warehousing, stack heights are high but static, while vehicles have lower stack heights, and their static and dynamic loads act simultaneously. Dynamic loads are caused by shocks and vibrations to the packaging during transportation [8]. Static and dynamic loads act together on the packaging and can damage the packaging or even the packaged product. Damage to the outer packaging can disrupt logistics chains, as the receiver may suspect that the packaged product may also be damaged [9,10,11].
A significant part of logistics packaging can consist of fully enclosed boxes made of corrugated cardboard, partially open compartments or even frames without side walls. The main advantages of paper-based packaging are that it is an economic, reliable protection of products, its relatively low unit packaging costs, its recyclability and its biodegradability [12,13]. The structure of corrugated cardboard is always composed of odd layers. The number of layers is usually three or five. The inner and outer surfaces of the cardboard are made up of a flat paper layer with a corrugated layer in between to provide rigidity. In the case of three-ply corrugated cardboard, a corrugated layer is placed between inner and outer flat layers, while in the case of five-ply cardboard, the two corrugated layers in the middle are separated by another flat layer. There are also several types of corrugated layers according to flute height and flute length. Corrugated and flat plies are made of base papers with different properties, mainly because the corrugating technology requires different paper properties compared to flat plies. The individual layers are bonded together by glue. The flat corrugated cardboards are cut out according to the flattened pattern of the box body, and in the same phase, the cardboard is folded along the folding lines (so-called “creasing”), so that box bodies can be folded precisely when the boxes are made.
For the production of corrugated cardboard, the flat plies can be classified into the following quality categories according to their fiber content and the resulting strength properties:
  • Kraftliner, which contains only primary cellulose fibers;
  • Testliner or duplex, which contains partly primary fiber and partly recycled secondary fiber;
  • Srenc, which contains only secondary fibers or fibers from other waste paper processing in which contaminants are unavoidably introduced during processing (e.g., plastic residues, ink residues, etc.).
The papers that form the corrugated layer can be divided into two categories:
  • Fluting, which contains primary fibers with low fiber length and density;
  • Wellenstoff, which is practically identical to the base material of srenc but contains additives that make it suitable for corrugating technology.
The thickness of the corrugated cardboards depends on the type of corrugating medium used for the corrugated cardboard. In the paper industry, the highest flute is A, followed by flute C; the lowest normal flute is B; and the so-called microflute is increasingly being used, with the letters E and F (FEFCO, European Federation of Corrugated Board Manufacturers). The structure of the corrugated board is shown in Figure 1 [14].
In box production, FEFCO assigns a numerical code to each box type. The simplest and most commonly used box variant is the so-called slotted-type boxes consisting of basically one piece with a glued or taped manufacturing joint and top and bottom flaps, code FEFCO 0201 [14], shown in Figure 2.
After being filled and sealed, the finished boxes are usually stacked, placed on a flat pallet and transported through the logistics chain to their destination. During this time, bottom box layers are subject to considerable stacking load. In practice, the boxes must be dimensioned for this expected stacking load [15,16,17].
The primary consideration for designers is that the compressive strength of the bottom box, which is expected to receive the largest compressive load, should be such that it can support the loads of the other layers placed on it, without significant compression or sidewall buckling in order to form a relatively rigid unit load. Since in both the manufacturing of base papers and corrugated cardboards and during the erection, filling and closing of the boxes, a number of random strength-reducing effects can affect the box, therefore, the final results will generally result in a significant strength variation. Optimal package design for corrugated boxes remains a major challenge [18,19]. When trying to ensure product-packaging integrity the situation is further complicated by environmental conditions that can affect the mechanical behavior of corrugated board, such as temperature and relative humidity changes [20,21], which can decrease the resilience of the integrity of packaged product to damages [1,3,5,11].
The best known semi-empirical formula for stacked load sizing is McKee’s equation [11,22]. The equation has been modified for different conditions, e.g., Kawanishi 1989, to predict the compressive strength of packages. Kellicutt and Landt [23] have also developed a model for compressive load sizing based on the principle of annular compressive strength. Beldie et al. 2001 modeled the mechanical behavior of corrugated cardboard packages subjected to static compressive loading. Corrugated cardboard was modeled as an orthotropic, linearly elastic-plastic laminate. An attempt was made to determine the load-carrying capacity of a box by determining the initial resistance of the package to bending caused by a given applied force. Biancolini and Brutti [24] developed a numerical model to account for splitting properties of the boxes in strength calculations.
The side walls of the box shown in Figure 2 are often weakened by cutouts for various purposes. There can be several reasons for cutouts:
  • Tab-like cutouts used to grip the box;
  • Ventilation openings, mainly used to increase the shelf life of agricultural products (vegetables, fruit);
  • Products requiring cold storage;
  • Window-like cutouts to identify and view the product (e.g., to read the product’s barcode or QR code);
  • Creating window-like cutouts to reduce the amount of corrugated cardboard used.
The effect of sidewall cutouts for different purposes on reducing compressive strength has been investigated by several authors [25,26,27,28,29,30,31].
Garbowski et al. [32] showed that the box strength is greater if the hole is smaller and its location is closer to the center of the wall, and the McKee formula cannot give accurate results in the aspect of the cutout independently from its position, shape and size. However, their study presented a mixed analytical/numerical method to reduce the error of estimation of compression strength calculated by a simplified McKee formula for boxes with different ventilation openings and holes.
Furthermore, the aspect ratio is another important factor that impacts corrugated box compression strength [27,33,34], in which the results showed that when the aspect ratio changes from 1 to 3, the compression strength increases at first, and then decreases; the compression strength reaches a maximum when the aspect ratio was 1.6 or so.
This paper attempts to measure and analyze the effects of the various cutout sizes of corrugated cardboard boxes to mechanical strength with different kinds of length-to-width aspect ratios. In reviewing the literature on this subject discussed above, the authors could not find any published research that measures and analyzes the interconnection of these variables. Additionally, the authors could not find any papers focused on analyzing the dimensions of cutout sizes to box dimensions. Therefore, this paper can provide a novel insight into circumstances for packaging engineers to design boxes based on experimental data.

2. Materials and Methods

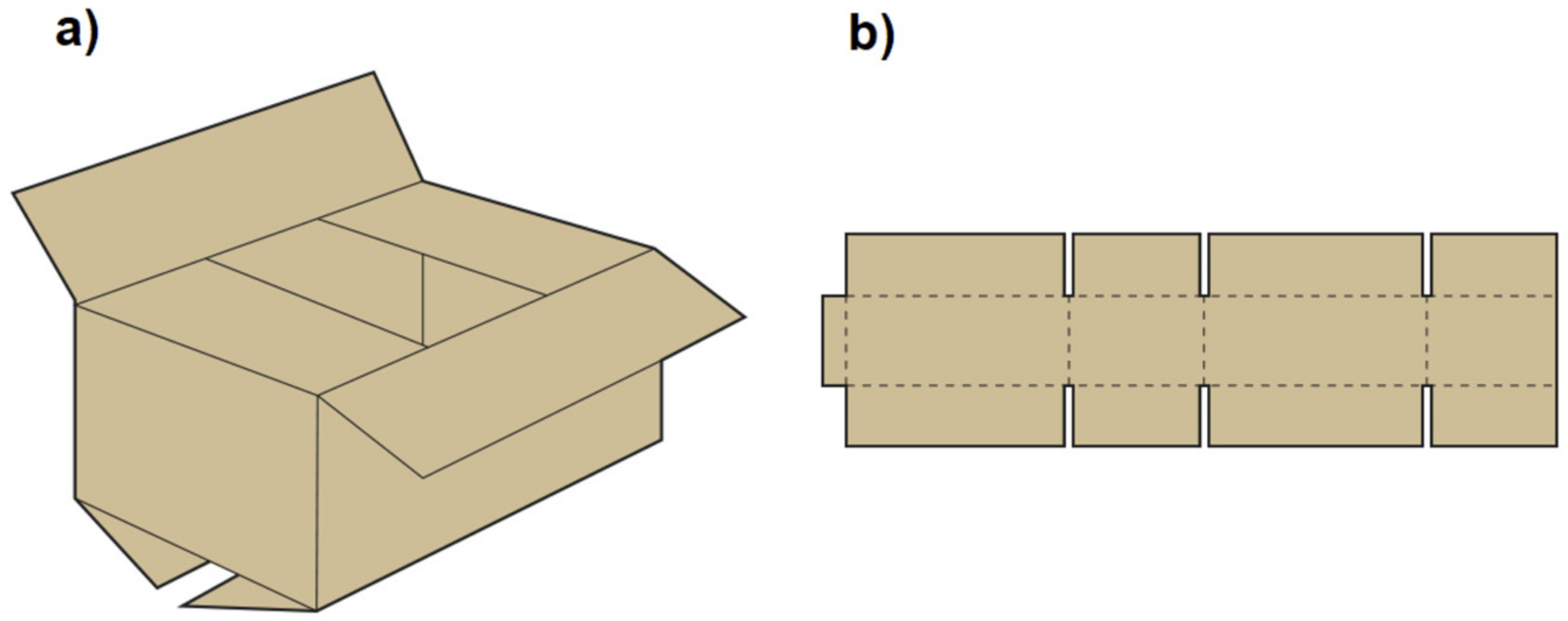
2.1. Sample Design and Geometrical Sizes

B-flute corrugated boxes with different cutouts were evaluated in this study. Each box was made from the same cardboard material. The corrugated cardboard material composition was as follows:
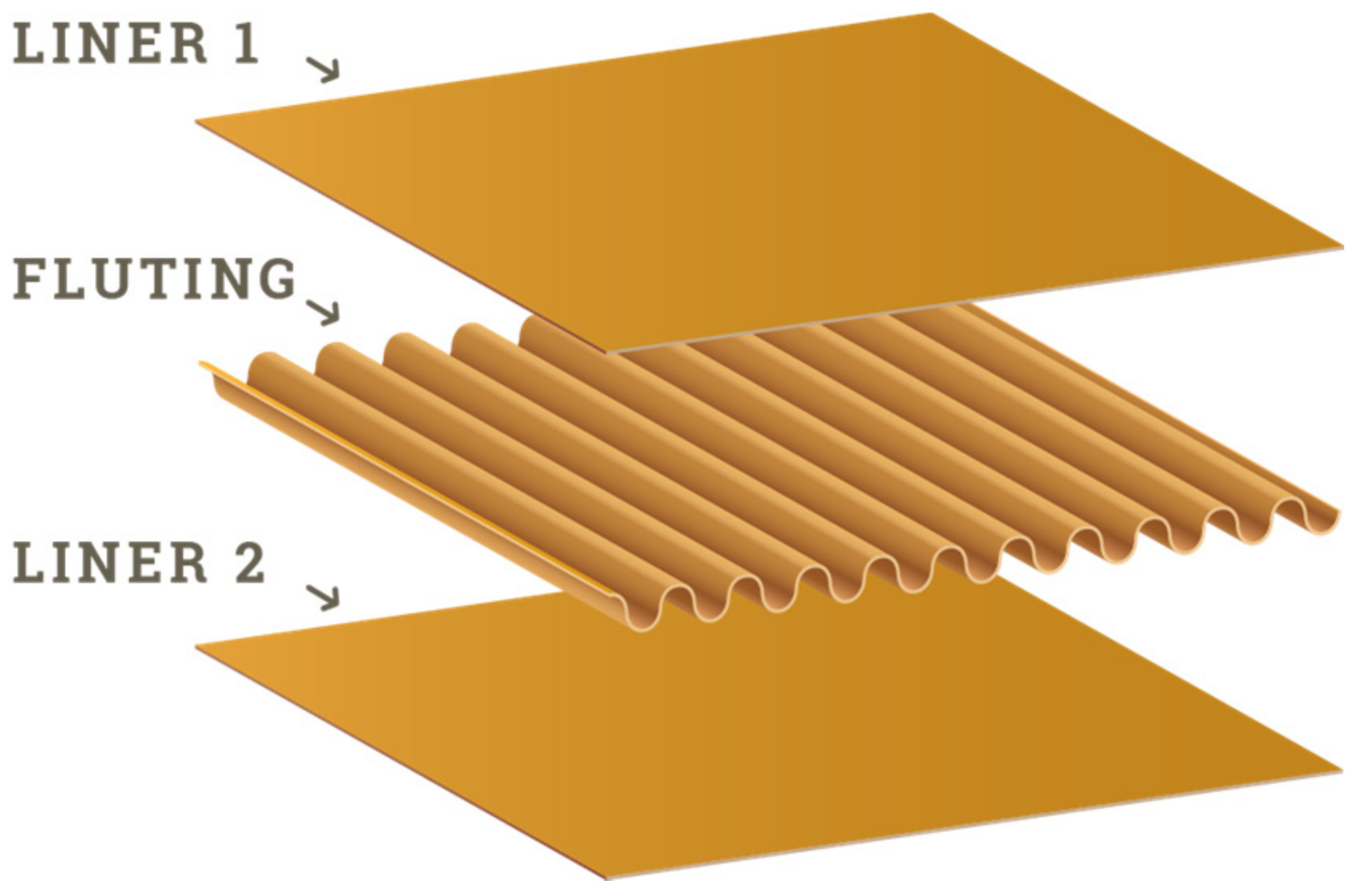
  • Number of layers: three (single wall design);
  • Parts of the corrugated cardboard material:
    ○
    Outer liner: 210 GD2 (weight 210 g/m2, coated white lined chipboard with grey back, quality class 2);
    ○
    Fluting medium: 120 HC (weight 120 g/m2, high-compression wellenstoff);
    ○
    Inner liner: 130 TL 3 (weight 130 g/m2, Testliner, quality class 3).
The properties of this B-flute corrugated cardboard are shown in Table 1. The cardboards of the boxes were manufactured by DS Smith (Hungary, Győr) using a corrugated cardboard cutting machine (Kongsberg XL20). Each box was made from two cardboard halves that were glued together. The assembly of the boxes and the gluing process was made by hand.
Figure 3 shows the samples that were used for this study. The widths and heights of the boxes were the same. For the measurements, five types of boxes with different length sizes (shown in Figure 4) and five further subtypes with different cutouts were used. The sizes of the boxes and the cutouts are shown in Table 2. The five subtypes were defined by the ratio of the cutouts to the given box’s edge lengths. These ratios were 0%, 20%, 40%, 60% and 80%. The sample with 0% cutouts can considered as the control sample. The dimensions of the cutouts can be calculated from the dimensions of the lengths of the edges of the boxes. In each sample, the cutouts were positioned in the middle of the sides of the boxes, as shown in Figure 3.
The box bodies were cut out of the available plates, and the bending line was formed using a plotter. The reason for using a plotter is that this procedure avoids accidental errors that can occur during the cutting process, both with the cutting tools and with the in-process transfer and feeding systems. Practical experience has shown that the strength of the plotter samples exceeds the strength of the boxes coming off the production lines by about 10 to 15%. The type of plotter, characteristics and blades used is the Kongsberg XL20.
For the test, 5 different box sizes were selected that had a uniform box width and height of 300 mm and a variation in box length, as shown in Table 2. The procedure for cutting out the side walls was to cut out 20–80% of the side wall length and height in relation to the geometric center of the side wall. A plotter was used so as to not damage the structure of the plate by manual intervention. The cutouts were made on all four sidewalls as described above. In Table 2, the size and cutout data for holes and their surface percentages were summarized for all five versions. From each of the variants, 10-10 pieces were investigated (Figure 4).

2.2. Experimental Design

Box compression test (BCT) was performed to determine the differences of the box parameters. Before the BCT, the boxes were preconditioned at 30 °C ± 1 °C and 20–30% relative humidity for 24 h and then conditioned at 23 °C ± 1 °C and 50% ± 2% relative humidity for 24 h in a climate-testing chamber. The conditioning process was followed by the ASTM D4332 standard [35]. The testing speed of the BCTs was 12.7 mm/min ± 2.5 mm/min in accordance with the ASTM D642 standard [36]. The setup of the BCTs is shown in Figure 5.
Ten samples were tested for each package design with two hundred and fifty samples in total. The compression force and deformation were recorded. A typical BCT force–deformation diagram is shown in Figure 6.

2.3. Data Analysis

Recorded data from the BCTs went through a statistical evaluation. Average maximum compression force values were calculated from the BCT recorded data for each type of box and cutout. These average maximum compression force values were the basis to determine the differences between the groups. For comparison, a factorial ANOVA (analysis of variance) analysis and Tukey post hoc test were executed. The independent variables were the lengths of the boxes and sizes of the cutouts. The average maximum compression force was the dependent variable. The significance level was determined at p < 0.05 for the statistical analysis. For the statistical evaluations, Matlab R2021b (MathWorks Inc., Natick, MA, USA) and JASP 0.16.3 (University of Amsterdam, Amsterdam, The Netherlands) were used. Whiskers represent the standard errors (SE) of means.

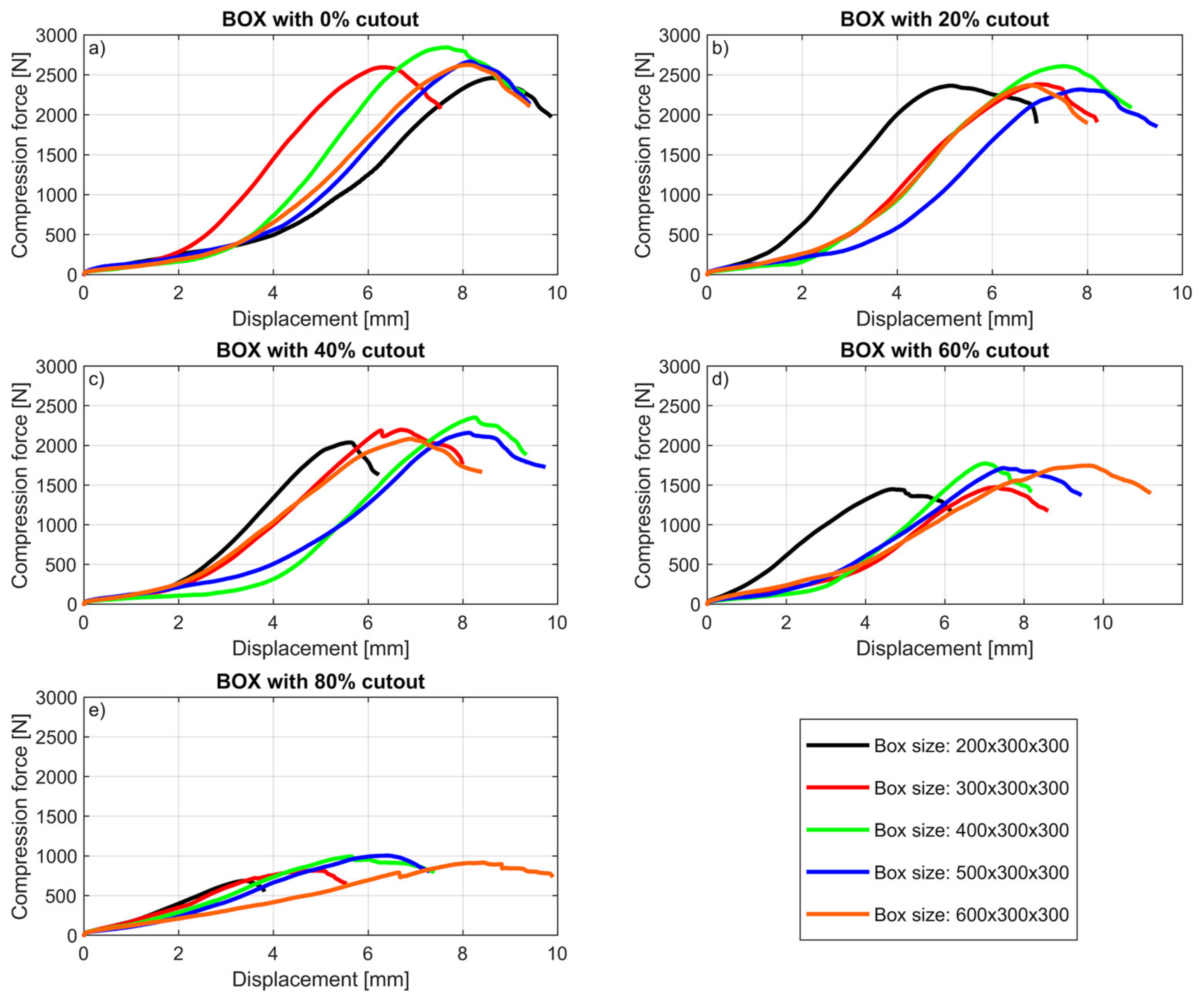
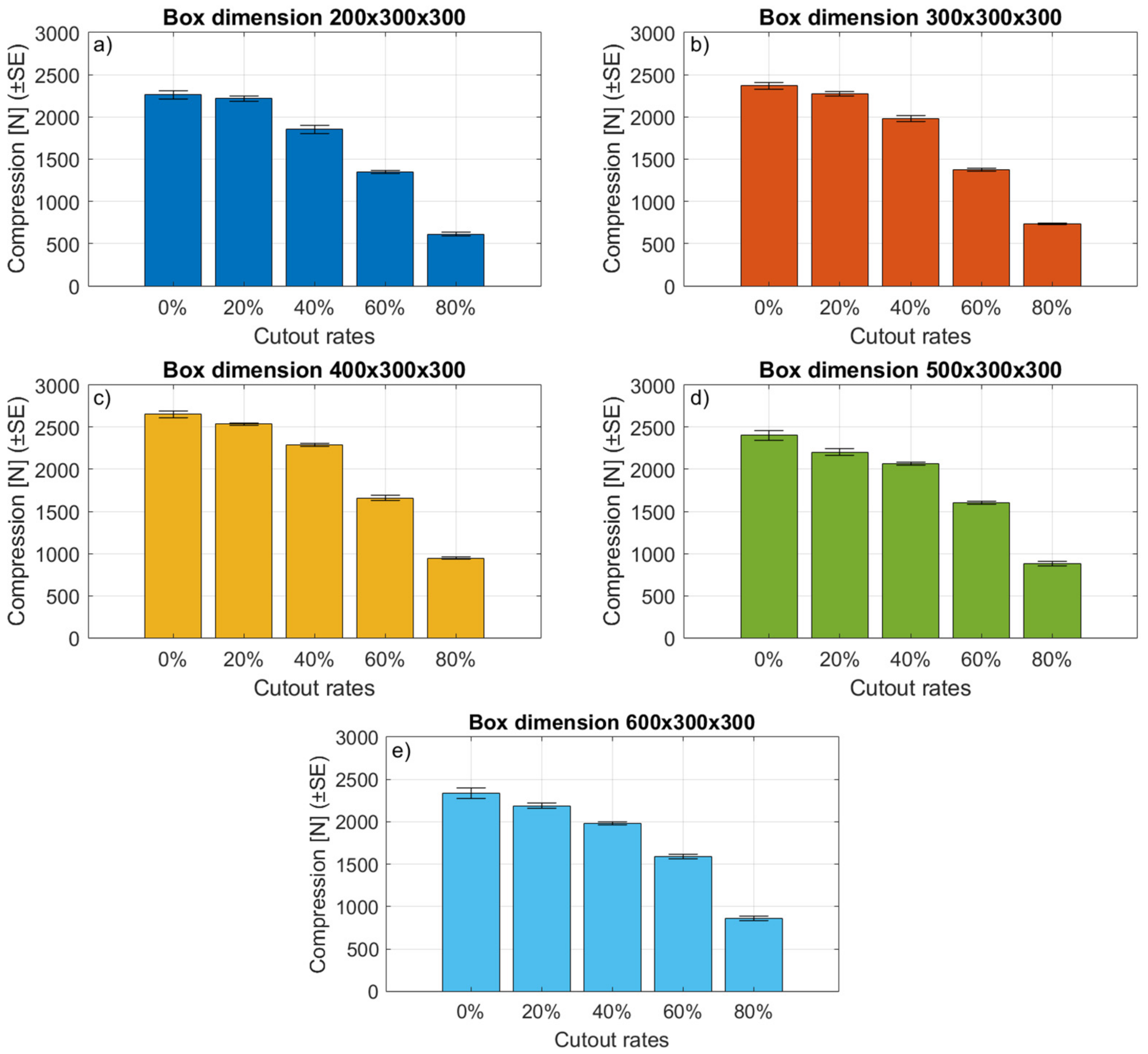
3. Results

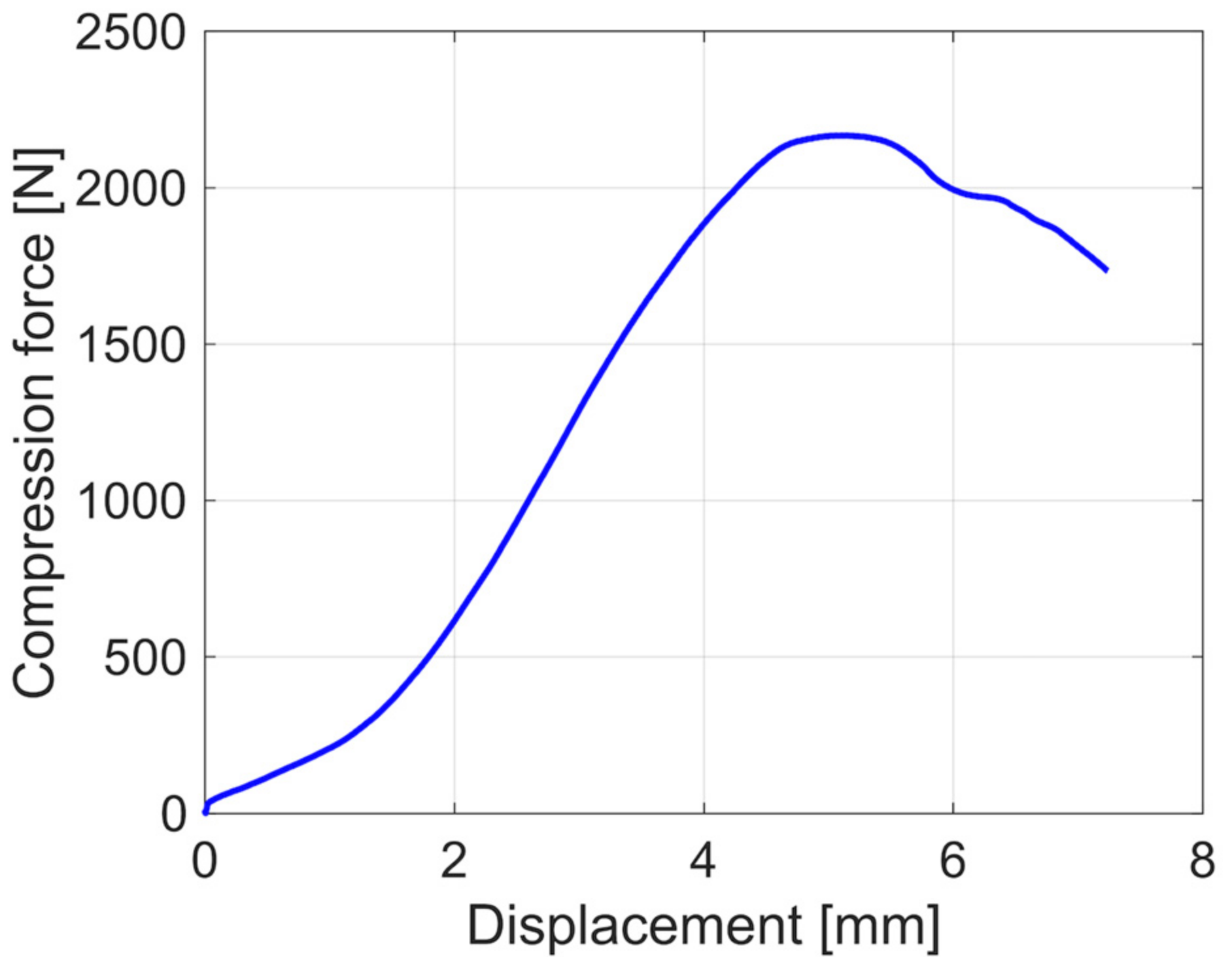
3.1. Results of the BCT Tests

The results of the BCT tests are presented in Table 3 and Figure 7. Table 3 shows the maximum and average of compression force for each cutout size. The table shows the length-to-width ratio for each box type as well. The maximum compression force was 2842 N for the box with dimensions of 400 × 300 × 300 mm and 0% cutout. In each cutout case, the maximum compression force was observed for the box with dimensions of 400 × 300 × 300 mm.
Figure 7 shows those curves for the samples where the maximum force was observed on different box sizes during the compression tests. Observing the compression force as a function of the length-to-width ratio, the maximum compression force occurred for the box size with a ratio of 1.33. This length-to-width ratio exceeded the values of the other specimens for all sizes, regardless of the cutout. The values of maximum compression forces for the other samples were, in decreasing order, 1.66, 2, 1 and 0.66, so the worst result in all cases was obtained by the box with a base size of 200 × 300 mm. The maximum compression force decreases as the cutout area increases. A significant decrease in compressive force occurs at a cut-off ratio of 80% (Data from all measurements are available from the authors).

3.2. ANOVA Analysis

Figure 8 shows the average values of the maximum compression forces for the sample’s series in each box dimension group. It can be seen that the 400 × 300 × 300 sized box with a 1.33 length-to-width ratio performed the best in every cutout group. The 400 × 300 × 300 with 0% cutout had on average a maximum compression force of 2651 N ± 39 N (shown in Table 3). The 200 × 300 × 300 sized box with an 80% cutout was the least stiff with a 614 N ± 19 N average compression force. The lowest average compression forces appeared in the 200 × 300 × 300 sized group with 0%, 40%, 60% and 80% cutouts. In the 20% cutout group the 600 × 300 × 300 box was shown to have the lowest average compression force (shown in Table 3).
The ANOVA analysis and the Tukey post hoc test showed there was significant difference (p < 0.05) between the strongest and weakest boxes in each group. In 0%, 20% and 40% cutout groups, the 400 × 300 × 300 sized boxes were shown to have significantly higher average compression strength than the other ones. The difference in the average maximum compression forces between the 0% and 20% cutout groups were not statistically significant in any size group except the 500 × 300 mm length-to-width ratio group.

4. Discussion

This study can be compared only partially with previous literature [1,22,28,33]. The reason for this is that those studies used cutouts for ventilation purposes in standard locations and sizes generally used in practice. Based on this, the role of the sidewall cutouts in influencing the strength cannot be determined. Study of Garbowski et al. [32] would be a point of reference partly due to the same FEFCO 0201 box type samples, but it did not observe the effect of the length-to-width ratio and the cutout size together. That study used only a 1.5 (300 × 200 mm) length-to-width ratio.
In our study, starting from the geometric center of the box sidewalls, the cutout area of the sidewall was continuously increased in cases with the same manufacture and design, so that a clear observation between the sidewall cutout area and associated maximum compression strength can be obtained.
In ref. [34], where the effect of the aspect ratio on box compression strength was investigated, the authors showed that the compressive strength increases at first and then decreases, and the maximum compression strength appeared when the length-to-width ratio was about 1.6. The results of this study have shown a good correlation with [33], but in our case, the optimal length-to-width ratio was 1.33. It should be noted here that in [33], the material of the tested corrugated box was a BC flute corrugated cardboard with five layers, but in our tests, a B flute corrugated cardboard with a single wall design was applied. So, it can be presumed that the different optimal length-to-width ratio in our case came from the different corrugated box material. Based on our study, a corrugated box with a 1.33 length-to-width ratio made from B flute corrugated cardboard with three layers showed the best result; therefore, it can be assumed that this is the most suitable ratio for logistics usage if other conditions are met.
Here, it has to be mentioned that the scientific literature examines many variables compared to our study, such as the quality of the corrugated cardboard, the number of layers, the shape and position of the cutouts or ventilation holes, temperature and/or humidity changes and box height. Our study reduced the number of variables to two in order to be able to clearly examine the effect of the length-to-width ratio (by keeping the height constant) and cutout sizes. The shape of the cutouts was perfectly square, and these are placed precisely in the center of the sidewalls. No such study has presented this before. Of course, these cutouts reduced the sidewall surface area; thereby, it logically changed the mechanical behavior of the box structure. Further research is needed to determine the correlation between the reduction in compression strength and different cutout sizes involving more cardboard types and quality. However, the results of this study can give better guidance on the placement of the handle and ventilation holes, taking into account the factor of the box length-to-width ratio.
It can be assumed that the average of maximum compression force decreases when the cutout rate increases. The 400 × 300 × 300 sized box was strongest in each group. So, in this study, the results showed that the optimal box size with or without cutouts has a 1.33 length-to-width ratio. The statistical tests showed that there is no significant difference between the 0% and 20% cutout groups, so the compression strength of the boxes was not changed significantly if a 20% cutout was used.
The preliminary results presented in this study make a reasonable first approximation of interconnection within the base length-to-width ratio and cutout sizes of the boxes. The authors would like to draw the attention to additional ongoing research involving more variables that focus on such variables as cardboard quality with different layer numbers, flute heights and grammage per square meter. The laboratory experiments utilizing these variables will more carefully address the correlation between decreasing compression and material reduction possibilities, which are generally difficult to deal with. One aspect of additional research that will be examined is the prediction of compression forces when the cutout sizes increase. The aim of these future experiments is to develop a possible numerical model for predicted compression forces from laboratory-measured compression forces.

Limitations for Practice

  • The applied experimental method for the data of this study uses only one B-flute corrugated cardboard quality, so the results can only show a narrow range of interest based on corrugated cardboard box area. In reality, boxes made of corrugated cardboard have an extremely wide range and variation, such as A, B, C and others, along with different flute-heights with variations in the numbers of layers; therefore, data from this study may be limited for general use but covers an important issue for possible materials reduction and packaging engineering design.
  • In addition, there are some environmental conditions that significantly affect the possible box compression strength. It has been proven that the changes in temperature and relative humidity or the difference between the dynamic and static loads will affect the expected compression strength of the boxes. This study did not investigate these phenomena.
  • Last but not least, the theoretical dynamics of compression strength require more experimental results with a varied selection of corrugated cardboard quality to show the exact correlation with compression strength in the function of the length-to-width ratio and cutout sizes together.

5. Conclusions

The measured maximum compression force for this study was 2 842 N for the box with dimensions of 400 × 300 × 300 mm and 0% sidewall cutout made from B-flute corrugated cardboard. In regard to the cutout ratios of 20%, 40% 60% and 80%, the highest maximum compression force could be observed for the box with dimensions of 400 × 300 × 300 mm when the base length-to-width ratio of the box was 1.33. The differences in the average maximum compression forces between 0% and 20% cutout groups were not statistically significant in any base-size group, except the 500 × 300 mm length-to-width group.
Based on the results of our study, the following broader context can also be drawn. The relationship between the material reduction achieved by 20% cutout and the expected compressive force of B-flute single-wall (three layers) corrugated cardboard can result in a more favorable packaging waste mechanism (decreased secondary and increased primary waste) and material cost reduction.

Author Contributions

Conceptualization, R.P. and L.F.; formal analysis, R.P. and L.F.; funding acquisition, R.P. and P.B.; investigation, R.P., L.F. and P.B.; methodology, R.P. and L.F.; supervision, P.B.; visualization, R.P. and L.F.; writing—original draft, R.P.; writing—review and editing, R.P. and P.B. All authors have read and agreed to the published version of the manuscript.

Funding

The APC was funded by Széchenyi István University.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

The data published in this research are available on request from the first author and corresponding authors.

Acknowledgments

We would like to acknowledge DS SMITH, who made the samples for measurements available free of charge for this study. We would also like to thank Zoltán Pánczél for his personal support and guidance in this study.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Fadiji, T.; Coetzee, C.; Opara, U.L. Compression strength of ventilated corrugated paperboard packages: Numerical modelling, experimental validation and effects of vent geometric design. Biosyst. Eng. 2016, 151, 231–247. [Google Scholar] [CrossRef]
  2. Fadiji, T.; Berry, T.; Coetzee, C.; Opara, U.L. Investigating the mechanical properties of paperboard packaging material for handling fresh produce under different environmental conditions: Experimental analysis and finite element modelling. J. Appl. Packag. Res. 2017, 9, 20–34. [Google Scholar]
  3. Opara, U.L.; Fadiji, T. Compression damage susceptibility of apple fruit packed inside ventilated corrugated paperboard package. Sci. Hortic. 2018, 227, 154–161. [Google Scholar] [CrossRef]
  4. Fadiji, T.; Coetzee, C.; Chen, L.; Chukwu, O.; Opara, U.L. Susceptibility of apples to bruising inside ventilated corrugated paperboard packages during simulated transport damage. Postharvest Biol. Technol. 2016, 118, 111–119. [Google Scholar] [CrossRef]
  5. Fadiji, T.; Coetzee, C.; Pathare, P.; Opara, U.L. Susceptibility to impact damage of apples inside ventilated corrugated paperboard packages: Effects of package design. Postharvest Biol. Technol. 2016, 111, 286–296. [Google Scholar] [CrossRef]
  6. Marsh, K.; Bugusu, B. Food packaging—Roles, materials, and environmental issues. J. Food Sci. 2007, 72, R39–R55. [Google Scholar] [CrossRef]
  7. Singh, S.P.; Singh, J.; Paek, Y. New pressure sensitive device to measure and predict package drops. J. Appl. Packag. Res. 2009, 3, 149–160. [Google Scholar]
  8. Beldie, L.; Sandberg, G.; Sandberg, L. Paperboard packages exposed to static loads–finite element modelling and experiments. Packag. Technol. Sci. 2001, 14, 171–178. [Google Scholar] [CrossRef]
  9. Lu, F.; Ishikawa, Y.; Kitazawa, H.; Satake, T. Measurement of impact pressure and bruising of apple fruit using pressure-sensitive film technique. J. Food Eng. 2010, 96, 614–620. [Google Scholar] [CrossRef] [Green Version]
  10. Lu, F.; Ishikawa, Y.; Kitazawa, H.; Satake, T. Assessment and prediction of repetitive impact damage to apple fruit using pressure-sensitive film technique. J. Food Agric. Environ. 2012, 10, 156–160. [Google Scholar]
  11. Pathare, P.B.; Opara, U.L. Structural design of corrugated boxes for horticultural produce: A review. Biosyst. Eng. 2014, 125, 128–140. [Google Scholar] [CrossRef]
  12. Fadiji, T.; Berry, T.M.; Coetzee, C.J.; Opara, U.L. Mechanical design and performance testing of corrugated paperboard packaging for the postharvest handling of horticultural produce. Biosyst. Eng. 2018, 171, 220–244. [Google Scholar] [CrossRef]
  13. Talbi, N.; Batti, A.; Ayad, R.; Guo, Y.Q. An analytical homogenization model for finite element modelling of corrugated cardboard. Compos. Struct. 2009, 88, 280–289. [Google Scholar] [CrossRef]
  14. FEFCO Code. Design Style Library for Corrugated, Board Products, 12th ed.; FEFCO: Brussels, Belgium, 2022; Available online: https://www.fefco.org/sites/default/files/files/2022–04–21_FEFCO%20Code_WEB_unprotected.pdf (accessed on 14 June 2022).
  15. Garbowski, T.; Gajewski, T.; Grabski, J.K. The role of buckling in the estimation of compressive strength of corrugated cardboard boxes. Materials 2020, 13, 4578. [Google Scholar] [CrossRef]
  16. Garbowski, T.; Gajewski, T.; Grabski, J.K. Role of transverse shear modulus in the performance of corrugated materials. Materials 2020, 13, 3791. [Google Scholar] [CrossRef]
  17. Garbowski, T.; Gajewski, T.; Grabski, J.K. Torsional and transversal stiffness of orthotropic sandwich panels. Materials 2020, 13, 5016. [Google Scholar] [CrossRef]
  18. Bartolozzi, G.; Pierini, M.; Orrenius, U.L.F.; Baldanzini, N. An equivalent material formulation for sinusoidal corrugated cores of structural sandwich panels. Compos. Struct. 2013, 100, 173–185. [Google Scholar] [CrossRef]
  19. Biancolini, M.E.; Brutti, C.; Mottola, E.; Porziani, S. Numerical Evaluation of Buckling and Post-Buckling Behaviour of Corrugated Board Containers. Presented at the XXXIV Convegno Nazionale Associazione Italiana Per L’Analisi Delle Sollecitazioni. Presented at the XXXIV Convegno Nazionale Associazione Italiana Per L’Analisi Delle Sollecitazioni, Milan, Italy, 14–17 September; 14–17 September 2005. [Google Scholar]
  20. Defraeye, T.; Cronje, P.; Berry, T.; Opara, U.L.; East, A.; Hertog, M.; Verbovenc, P.; Nicolaich, B. Towards integrated performance evaluation of future packaging for fresh produce in the cold chain. Trends Food Sci. Technol. 2015, 44, 201–225. [Google Scholar] [CrossRef]
  21. Zaghloul, M.M.Y.; Mohamed, Y.S.; El-Gamal, H. Fatigue and tensile behaviors of fiber-reinforced thermosetting composites embedded with nanoparticles. J. Compos. Mater. 2019, 53, 709–718. [Google Scholar] [CrossRef]
  22. McKee, R.C.; Gander, J.W.; Wachuta, J.R. Compression strength formula for corrugated boxes. Paperboard Packag. 1963, 48, 149–159. [Google Scholar]
  23. Kellicutt, K.; Landt, E. Development of design data for corrugated fiberboard shipping containers. Tappi. J. 1952, 35, 398–402. [Google Scholar]
  24. Biancolini, B.M.E.; Brutti, C. Numerical and experimental investigation of the strength of corrugated board packages. Packag. Technol. Sci. 2003, 16, 47–60. [Google Scholar] [CrossRef]
  25. Han, J.; Park, J.M. Finite element analysis of vent/hand hole designs for corrugated fibreboard boxes. Packag. Technol. Sci. 2007, 20, 39–47. [Google Scholar] [CrossRef]
  26. Singh, J.; Olsen, E.; Singh, S.P.; Manley, J.; Wallace, F. The effect of ventilation, and hand holes on loss of compression strength in corrugated boxes. J. Appl. Packag. Res. 2008, 2, 227–238. [Google Scholar]
  27. Fadiji, T.; Coetzee, C.J.; Berry, T.M.; Opara, U.L. Investigating the role of geometrical configurations of ventilated fresh produce packaging to improve the mechanical strength–Experimental and numerical approaches. Food Packag. Shelf Life 2019, 20, 100–312. [Google Scholar] [CrossRef]
  28. Fadiji, T.; Coetzee, C.J.; Opara, U.L. Analysis of the creep behaviour of ventilated corrugated paperboard packaging for handling fresh produce—An experimental study. Food Bioprod. Process. 2019, 117, 126–137. [Google Scholar] [CrossRef]
  29. Czechowski, L.; Kmita-Fudalej, G.; Szewczyk, W.; Gralewski, J.; Bienkowska, M. Numerical and experimental study of five-layer non-symmetrical paperboard panel stiffness. Materials 2021, 14, 7453. [Google Scholar] [CrossRef]
  30. Berry, T.M.; Defraeye, T.; Shrivastava, C.; Ambaw, A.; Coetzee, C.; Opara, U.L. Designing ventilated packaging for the fresh produce cold chain. Food Bioprod. Process. 2022, 134, 121–149. [Google Scholar] [CrossRef]
  31. Archaviboonyobul, T.; Chaveesuk, R.; Singh, J.; Jinkarn, T. An analysis of the influence of hand hole and ventilation hole design on compressive strength of corrugated fiberboard boxes by an artificial neural network model. Packag. Technol. Sci. 2020, 33, 171–181. [Google Scholar] [CrossRef]
  32. Garbowski, T.; Gajewski, T.; Grabski, J.K. Estimation of the compressive strength of corrugated cardboard boxes with various openings. Energies 2020, 14, 155. [Google Scholar] [CrossRef]
  33. Wei, Z.; Hua, G.J.; Zhao, D.J. Testing Research of Aspect Ratio on Corrugated Box Compression Strength. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Bach, Switzerland , 2011; Volume 48, pp. Volume 1213–1216. [Google Scholar] [CrossRef]
  34. Ambaw, A.; Fadiji, T.; Opara, U.L. Thermo-mechanical analysis in the fresh fruit cold chain: A review on recent advances. Foods 2021, 10, 1357. [Google Scholar] [CrossRef] [PubMed]
  35. ASTM D4332–01; Standard Practice for Conditioning Containers, Packages, or Packaging Components for Testing. American Society of Testing and Materials International: West Conshohocken, PA, USA, 2006.
  36. ASTM ASTM D642; Standard Test Method for Determining Compressive Resistance of Shipping Containers, Components, and Unit Loads. American Society of Testing and Materials International: West Conshohocken, PA, USA, 2010.
Applsci 12 06939 g001 550
Figure 1. The structure of corrugated board [14].
Figure 1. The structure of corrugated board [14].
Applsci 12 06939 g001
Applsci 12 06939 g002 550
Figure 2. Box type FEFCO 0201 [14]: (a) finished box body; (b) extended drawing of the box body.
Figure 2. Box type FEFCO 0201 [14]: (a) finished box body; (b) extended drawing of the box body.
Applsci 12 06939 g002
Applsci 12 06939 g003 550
Figure 3. Five types of cutouts used on samples with different dimensions.
Figure 3. Five types of cutouts used on samples with different dimensions.
Applsci 12 06939 g003
Applsci 12 06939 g004 550
Figure 4. Corrugated cardboard box samples used for this study.
Figure 4. Corrugated cardboard box samples used for this study.
Applsci 12 06939 g004
Applsci 12 06939 g005 550
Figure 5. Setup of the box compression tests (BCTs): (a) control sample and (b) cutout sample.
Figure 5. Setup of the box compression tests (BCTs): (a) control sample and (b) cutout sample.
Applsci 12 06939 g005
Applsci 12 06939 g006 550
Figure 6. Typical BCT force–deformation diagram.
Figure 6. Typical BCT force–deformation diagram.
Applsci 12 06939 g006
Applsci 12 06939 g007 550
Figure 7. Maximum force–compression diagrams according to cutout ratios: (a) 0% cutout ratio; (b) 20% cutout ratio; (c) 40% cutout ratio; (d) 60% cutout ratio; (e) 80% cutout ratio.
Figure 7. Maximum force–compression diagrams according to cutout ratios: (a) 0% cutout ratio; (b) 20% cutout ratio; (c) 40% cutout ratio; (d) 60% cutout ratio; (e) 80% cutout ratio.
Applsci 12 06939 g007
Applsci 12 06939 g008 550
Figure 8. Averages of maximum compression forces and its standard errors (SE): (a) 200 × 300 × 300 mm box; (b) 300 × 300 × 300 mm box; (c) 400 × 300 × 300 mm box; (d) 500 × 300 × 300 mm box; (e) 600 × 300 × 300 mm box.
Figure 8. Averages of maximum compression forces and its standard errors (SE): (a) 200 × 300 × 300 mm box; (b) 300 × 300 × 300 mm box; (c) 400 × 300 × 300 mm box; (d) 500 × 300 × 300 mm box; (e) 600 × 300 × 300 mm box.
Applsci 12 06939 g008
Table
Table 1. Material properties of the B-flute corrugated cardboard.
Table 1. Material properties of the B-flute corrugated cardboard.
PropertiesSpecificationStandard
Board Thickness2.8 mm (±10%)ISO 3034 (FEFCO no.3)
Grammage512 g/m2 (±10%)ISO 536:1995
Edge Crush Test (ECT)5.1 kN/m (±15%)ISO 3037 (FEFCO no.8)
Bursting Strength (BST)676 kPa (±15%)ISO 2759 (FEFCO no.4)
Table
Table 2. Configurations for dimensions of samples for this study (width and height of 300 mm).
Table 2. Configurations for dimensions of samples for this study (width and height of 300 mm).
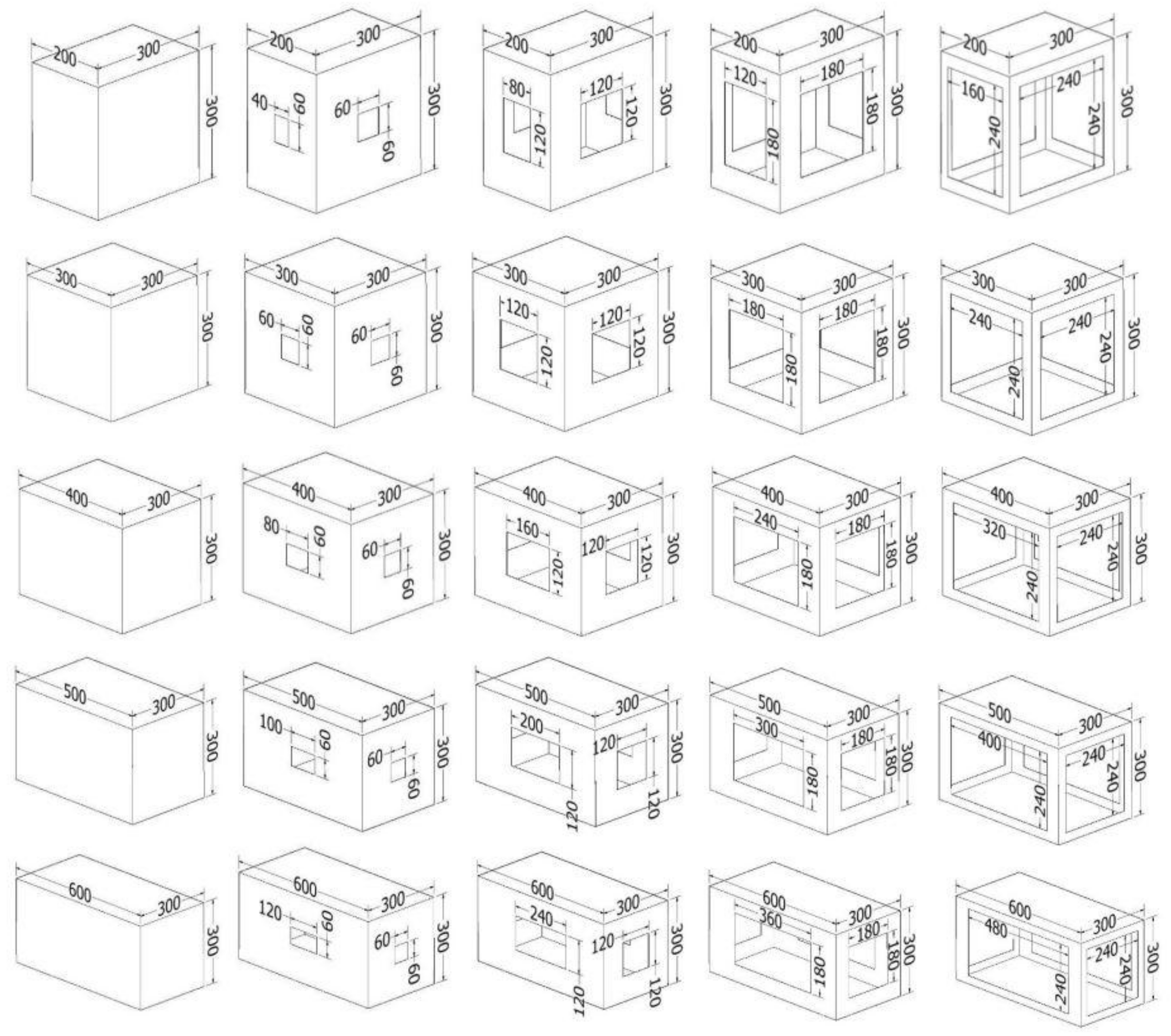
Length (mm)Perimeter (mm)Area without Top and Bottom (mm2)Cutout Rates(%)Sizes of Cutouts (mm)
2001000300,0000-
2040 × 60/60 × 60
4080 × 120/120 × 120
60120 × 180/180 × 180
80160 × 240/240 × 240
3001200360,0000-
2060 × 60/60 × 60
40120 × 120/120 × 120
60180 × 180/180 × 180
80240 × 240/240 × 240
4001400420,0000-
2080 × 60/60 × 60
40160 × 120/120 × 120
60240 × 180/180 × 180
80320 × 240/240 × 240
5001600480,0000-
20100 × 60/60 × 60
40200 × 120/120 × 120
60300 × 180/180 × 180
80400 × 240/240 × 240
6001800540,0000-
20120 × 60/60 × 60
40240 × 120/120 × 120
60360 × 180/180 × 180
80480 × 240/240 × 240
Table
Table 3. Summary table of measurement results.
Table 3. Summary table of measurement results.
Length (mm)Width (mm)Length-to-Width RatioCutout(%)Maximum Compression Force (N)Average Compression Force (N)
2003000.66024612261
2023642217
4020371851
6014471346
80685614
3003001025942367
2023822275
4021971981
6014701373
80814734
4003001.33028422651
2026082537
4023512291
6017711656
80993946
5003001.66026662402
2023162203
4021582066
6017131603
801003877
6003002026242339
2023712189
4020821980
6017451591
80915862
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Pidl, R.; Fehér, L.; Böröcz, P. The Effect of Side Wall Cutout Sizes on Corrugated Box Compression Strength in the Function of Length-to-Width Ratios—An Experimental Study. Appl. Sci. 2022, 12, 6939. https://doi.org/10.3390/app12146939

AMA Style

Pidl R, Fehér L, Böröcz P. The Effect of Side Wall Cutout Sizes on Corrugated Box Compression Strength in the Function of Length-to-Width Ratios—An Experimental Study. Applied Sciences. 2022; 12(14):6939. https://doi.org/10.3390/app12146939

Chicago/Turabian Style

Pidl, Renáta, Lajos Fehér, and Péter Böröcz. 2022. "The Effect of Side Wall Cutout Sizes on Corrugated Box Compression Strength in the Function of Length-to-Width Ratios—An Experimental Study" Applied Sciences 12, no. 14: 6939. https://doi.org/10.3390/app12146939

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop