Abstract
This paper focuses on the implementation of an accurate meshless scheme for the simulation of the advection–diffusion of non-active pollutant in a two-dimensional depth-averaged flow. The depth-averaged flow model includes the shallow water system and the pollutant propagation described by the advection–diffusion equation with diffusion tensor. The mathematical model was implemented by using a meshless method based on local radial basis functions. This method was used to numerically evaluate the spatial derivatives and complemented with the second-order Runge–Kutta method for the time evolution. To remove the non-physical oscillations, which appear at the discontinuity, a filter based on a hyperviscosity operator was applied. To investigate the effectiveness and accuracy of the proposed scheme, a number of tests are presented, including the dam break problem, and the pure transport of a pollutant in a long channel. Finally, a hypothetical example of a pollutant transport in the Strait of Gibraltar is modeled. The results obtained are compared both with analytical solutions and with simulation results obtained by a finite volume method based on the Roe-MUSCL scheme. The main advantages of the proposed method are: (i) the simplicity of implementation, (ii) the ability to handle calculations of slowly varying flows or concentrations, as well as rapidly varying flows containing shocks or discontinuities, and (iii) the ability to satisfy the C-property and guarantee positive values of both water level and pollutant concentration.
1. Introduction
Understanding flows in shallow natural environments is a fundamental issue for human society. These flows are not always thoroughly understood. Indeed, the modeling of flooding by river overflow, the identification of flood-prone areas, tsunami waves, hydraulic jumps and tidal bore have been topics of research for several decades. Modeling such flows becomes more complex if we want to account for the flow of discharge. Many of these pollutants adversely effect the ecology and environment and pose a threat to human health and to the local economy. Effective and reliable estimates of the damage to water quality caused by pollution could play an important role in establishing strategies for environmental protection. Mathematical models and computer simulations are very useful tools for analyzing water flow and pollutant transport. Most of these models employ numerical techniques for the solution of the shallow water equations and the advection–diffusion equation, which are still widely used [1,2,3]. In shallow water flows, pollutant transport is determined by the nature of the flow. In rivers, estuaries, and coastal areas, flows are generally characterized by high topographic complexity, very open flow boundaries, variable scales in space and time and strong advection, and sometimes even pure advection in the case of hydraulic jumps. As a consequence, when developing a numerical model of shallow water flows, one encounters major difficulties that result as much from the physical complexity of the environment as from the numerical complications. Thus, the geomorphological complexity of rivers, estuaries, and coastal areas often requires narrow computational meshes. Numerical stability then requires a small computational time step, proportional to the size of the space step. The strongly convective flow, possibly with a shock front, causes numerical oscillations or artificial diffusion. These are due to the treatment of the advection terms in the governing equations of the water mass transport, by standard approximation methods. Several methods have been used for solving shallow water equations coupled with the transport–diffusion equation. Most of these were mesh-based methods such as finite differences, finite volumes or finite elements [4,5,6]. However, these methods have proven problematic when dealing with high flow or concentration gradients and tend to produce numerical oscillations or numerical diffusion. To deal with these challenges, there are also semi-analytical or mesoscopic approximation methods for the solution of time-dependent partial differential equations [7,8,9].
Historically, the Roe scheme was among the first schemes to be adapted to conservation law problems [10,11], including shallow water flow problems [12]. The Roe scheme has been used for solving the Riemann problem, which naturally arises when applying mesh-based methods. Over the years, several authors have developed new schemes that use the same concepts. These schemes differ either in the way they incorporate the other source terms or in the technique used to increase the order of precision. Among the methods used were the Essentially Non-Oscillatory (ENO) [13] or Weighted Essentially Non-Oscillatory (WENO) [14] methods, which reconstruct the solution using polynomials of arbitrary degree. Some authors have also developed centrally weighted essential non oscillatory (CWENO) schemes [15]. Another approach is the Multi-dimensional Optimal Order Detection method, originally developed in [16]. This method also uses polynomial reconstruction of the solution, with polynomials of as high a degree as desired. Since its introduction, it has been extended by its authors in [17,18]. A revised entropy criterion for the detection of oscillations has been developed to choose the most optimal numerical solution. Additionally, some researchers applied the finite element method [18,19]. The discontinuous Galerkin method has also been applied to solve the shallow water equations coupled with the diffusion transport equation. All these methods are known for their high accuracy, but in practice they are still very complex. In addition, their results are dependent on the mesh quality, particularly for unstructured meshes, and the computation costs are generally high.
In this paper, we develop a meshless local method based on radial basis functions (LRBFs) for the transport of non-active pollutants by shallow water. Typically, in the references mentioned above, LRBF methods are implemented for the simulation of water flows. Due to their flexibility and simplicity of implementation, these methods can be very useful in treating cases of high geometric and bathymetric complexity. Our objective in the present study is to extend the LRBF method for the numerical simulation of two-dimensional pollutant transport problems to real geometries. The main advantages of the proposed LRBF method are (i) the simplicity of implementation for the system of shallow water equations coupled with the advection–diffusion equation, (ii) the simultaneous resolution of both problems in time with the same accuracy, (iii) the ability to handle calculations of slowly varying flows or concentrations, as well as rapidly varying flows containing shocks or discontinuities, (iv) the ability to satisfy the C-property, and (v) guaranteeing positive values of both water level and pollutant concentration in transient simulations. The results presented in this paper demonstrate the high resolution of the proposed method and confirm its ability to provide accurate and efficient simulations for the transport of pollutants by shallow water flows, including complex topography and geometry.
The rest of the paper is structured as follows: in Section 2, the mathematical model is presented. In Section 3, the numerical tools, including the LRBF method and its implementation, are developed. Section 4 discusses one-dimensional and two-dimensional experiments, demonstrating excellent results.
2. Pollutant Transport by Shallow Water Flow
Pollutant transport by shallow water flow can be modeled by shallow water equations coupled with the advection–diffusion equation. The system of shallow water equations is obtained by integrating the Navier–Stokes equations over the depth of the water. This system of equations is used to describe the flow of water in cases where the depth is much smaller than the horizontal scale of motion. These equations are used to model flows in shallow coastal zone, lakes, and rivers, among other phenomena. They are also used in simulating river flooding. Whenever shallow water transports non-reactive pollutants, the shallow water equations are coupled with the advection–diffusion equation, with the resulting global system written in a conservative form, being as follows:
where and are the flow discharge, u and v being the average velocities in the horizontal x, y plane. Gravity is taken along the z axis with acceleration g. We define as the bottom of the river and as the elevation of the free surface, where h is the water height. The quantities and are forces that represent the Coriolis acceleration or the drag force due to wind, and and are the bottom frictional stresses defined by Manning’s law:
where is the Manning coefficient.
In the advection–diffusion equation, represents the concentration of the pollutant and and are the elements of the diagonal diffusion tensor of the pollutant. It should be noted that the diffusion coefficients depend on the flow velocity, the water depth, the wind and also the vertical turbulence. In this paper, the calculation of these terms is not considered. For more details on how to calculate the diffusion tensor elements in the context of shallow water flows, refer to the work of Toro [1]. We simplify the system of Equation (1) by rewriting it as:
with
The source term , including differential and scalar terms, is expressed as follows:
where is the bed-slope term, is the bottom friction term, and is the other scalar forces described in the system (1). It should be noted that the terms , , and contain differential operators, so their numerical approximations would require the approximation of these operators. In the following, we present the procedure adopted in this work.
3. Numerical Solution by Meshless Method
3.1. Formulation of the Local RBF Differentiation
We employ the radial basis functions method, which is a meshless method originally proposed by Kansa [19], for the numerical solution of pollutant transport by the shallow water model. In the following, we outline the main features of this method.
Radial basis function interpolation approximates the solution function by an expansion. According to the Kansa method, the solution is approximated on a set of N collocation nodes by a linear combination of local radial basis functions, as follows [20]:
where represents the unknown coefficients to be calculated, is a radial basis function, is the distance between the nodes and , and is a stencil that contains the index i and indices of the n nearest neighbor of the node . The stencil consists of the indices of node points falling within three times the distance to the nearest node. Thus, the number of nodes indexed by the stencil is variable, as it depends on the distribution of nodes in the computational domain.
Many radial basis functions have been proposed in the literature. In the current study, we use the infinitely smooth multiquadric radial basis function defined as , where is a shape parameter that plays a substantial role in the resulting accuracy. Generally, the determination of the range of shape values can be obtained by using numerical tests. In this study, we also use the procedure proposed by Sarra in [21]. Therefore, an optimal shape parameter has been identified. In all simulations, , in which is the minimum distance between two nodes and 2 ×10.
The numerical solution of an equation involving partial derivatives can be approximated by using the linear approximation of the partial derivatives at the nodes, based on local radial basis functions as follows:
This can be rewritten in a more concise form as
where is an vector of unknown coefficients to be calculated and is an matrix containing linear differentiation of the radial basis function . Using Equation (6), the coefficient can be expressed in terms of the function F as follows:
where is the inverse of the matrix . By removing the dependence on the expansion coefficients, the equation in (8) becomes:
Note that in the governing equations the first and second derivatives are calculated for each node by using several matrix operations on matrices, which slows down the computations. In order to overcome the problem of the successive inversion of many matrices, Yao et al. [20] reformulated the local interpolation and differentiation matrices in terms of a global sparse matrix by appending zeros to the proper entries. This reformulation was also used by [22] for the space–time derivatives. The entries of the global differentiation matrix are then defined as follows:
Using this approach, the first and second spatial derivatives of a function can be expressed as follows:
where and are first and second derivative matrices with respect to x and y.
3.2. Numerical Procedure
In this section, we will describe the implementation of the LRBF method for shallow water equations coupled with the advection–diffusion equation of a non-active pollutant.
First, a set N of distinct points, , are considered in the study area. The system (3) is approximated by the following equivalent system:
where and are the convective flux and is the term due to bottom variation. Using the local radial basis function meshless method to perform numerical evaluation, we obtain:
and
Thus, the numerical solution consists of the numerical evaluation of all the derivatives involved, and this is performed several times during the same time step. So, for reasons of computational efficiency, we first evaluate the derivation matrices Dx, Dy, Dxx and Dyy, then the numerical fluxes.
For time progression, the second-order Runge–Kutta scheme was employed and found to be reasonably stable. The formula used for the solution at the time level is as follows:
In the above formula, represents the time step; this needs to be chosen carefully to guarantee the stability of the scheme. In all our simulations, we chose using the following formula:
where is the smallest distance node and is the current number taken equal .
At the beginning of each step of the RK scheme, the friction effect is evaluated and used implicitly by the splitting scheme proposed in [23]. Keeping only the local acceleration and bed friction terms, the momentum equation is approximated as follows:
Since the friction term is only involved in the momentum equation, only the flow rates need to be evaluated. Thus, the following implicit scheme is used [24]:
This updated flux is used as an initial condition for the operators in Equation (17).
3.3. Hyperviscosity-Based LRBF Stabilization
It is well known that the discretization of shallow water equations, where the convection term dominates, leads to non-physical oscillations. As demonstrated in several works [25,26,27], it is possible to overcome this problem by adding hyperviscosity to the second member of the system, which acts as a filter as follows:
where k is the order of the Laplacian operator. Using the LRBF approximation described above, the hyperviscosity operator is given by the following expression:
In the above expression, represents the amount of hyperviscosity to be added, also known as the damping coefficient. As mentioned in [25], there are several ways to identify the optimal value of gamma. For proper stability and accuracy, the gamma values are directly proportional to the resolution of the grid, as well as the order k [28]. However, the simplest method is trial and error using very short tests. The lower cut-off quickly becomes apparent. For the dam break problem, Dehgham and Abbaszadeh [27] used a value of to stabilize their method, while values ranging from to 1 were used by Flyer et al. [26] to solve the shallow water equations on a sphere. In [25], the author proposed that values of are to scale with . In our simulations, depending on the number of points used, the gamma values range between and and the order k is taken to be one.
4. Numerical Results
4.1. Numerical Demonstration of C-Property
The first verification of our method was in simulating the lake at rest or C-property (a scheme that is exact in the stationary case is said to satisfy the C-property). This property was introduced by [29] to check the balance between convective flow and flow due to bed variations. This means that the scheme is exact when applied to the stationary case . Numerical schemes satisfying this property are called balanced schemes. We model the bed of the lake as a channel of length 10 m, described by the following function:
We compute the numerical solution for 200 points within 1 s under the following initial conditions:
In Figure 1, we present the numerical results obtained in terms of water level h and free surface , as well as the variation in error along the free surface. The results show that the maximum error is always lower than , satisfying the C-property.
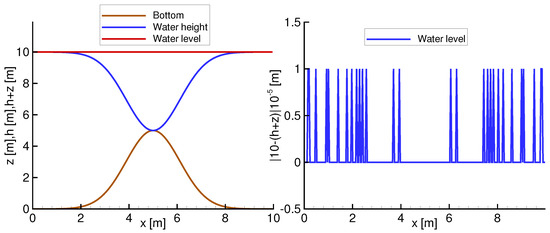
Figure 1.
Numerical solution of water height and depth of the lake at rest with an overview of the error.
4.2. Circular Dam Break Problem
This problem is a numerical study of symmetrical flow due to a circular dam break. An interesting aspect of this example is that it is solved by a shock wave that propagates downstream by increasing water height. In contrast, a depression wave propagates upstream by decreasing the water height. Several authors have investigated numerical solutions to this problem. Their investigations resulted in numerous research reports in the literature, such as [30,31,32]. Here, we propose a channel of 10 m × 10 m dimensions, with a flat, smooth bottom, enabling us to neglect the friction between the bottom and the water. The water is retained in a column 4 m in diameter placed at the center of the domain. This column is assumed to break suddenly at an initial time. The initial conditions of this problem are described as follows:
For boundary conditions, we assume that the basin is closed on all sides, and that the no-slip condition applies to all sides. The problem is solved at a density containing 4000 nodes.
Figure 2 and Figure 3 show the results obtained by the proposed method at different times and in different formats. A three-dimensional view and contour lines of water height are shown in Figure 2 for times s, s and s at the left and right range, respectively. In practice, the propagation speed and the shape of the flood wave are accurately calculated in order to set up intervention plans. In this case, the calculations show that the wave front develops symmetrically and propagates towards the sides of the basin. The sections also show that the wave front is well captured. This method appears to reproduce the flow behavior correctly, and the results obtained are similar to those reported in the references mentioned above.
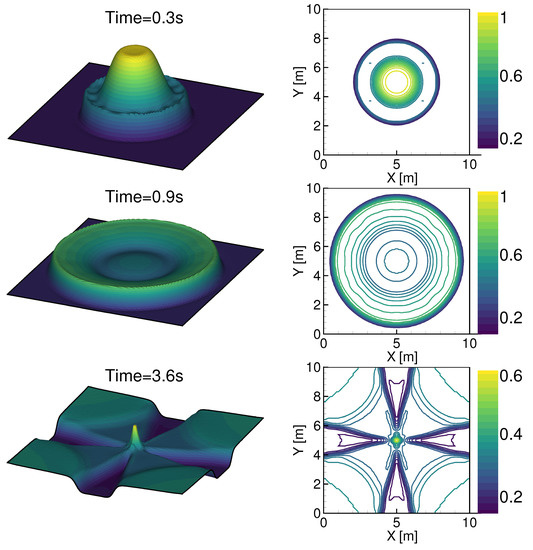
Figure 2.
Water level calculated after the dam break at times s, s and s. On the right, a three-dimensional view, and on the left, the water level contours.
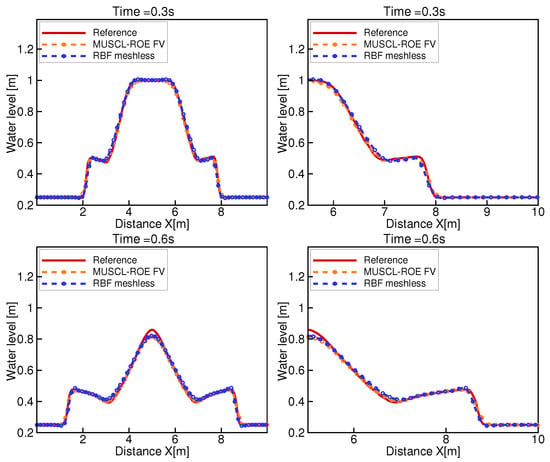
Figure 3.
Comparisons of water level cross-sections at x = 5 m calculated using the Roe-MUSCL finite volumes method and the present LRBF meshless method at times t = 0.3 s and 0.6 s.
In order to make a quantitative comparison, we compared the results obtained by the meshless method and those obtained by a mesh-based method, namely, second-order finite volumes. The method is a second-order augmented Riemann using the MUSCL scheme [33] with a mesh of 4000 nodes allowing for the generation of 15,678 volumes.
Figure 3 shows a cross section of pollutant concentration at the water height m in the instants s and s.
The numerical results obtained by our method are in reasonable agreement with those of previous studies. Our results are clearly seen to be close to the reference results, and to be comparable to those obtained by the finite volume method. Since meshless methods based on RBFs are easy to implement, they represent suitable approaches for the simulation of shallow water flows creating shock waves.
4.3. Pollutant Advection in a Uniform Flow Field
We next model the pure advection of a pollutant, in which all the diffusion tensor elements are zero (). Transport occurs longitudinally along a 30 m-long channel with a flat bottom. The flow is taken to be uniform with a velocity m/s and . The initial condition for the pollutant concentration is taken to be Gaussian, placed at the point ( m, m),
where we take and . Once in the flow, the pollutant moves along the x axis at a constant speed of m/s. Figure 4 depicts the plume transport and displays the pollutant concentration at times , 12 and 20 s. It is seen from the figure that the shape of the pollutant is correctly preserved. Furthermore, the correct position of the plume is reflected by an accurate calculation of the propagation speed of the concentration wave. Nevertheless, the calculation of the maximum concentration is affected by numerical diffusion when the number of points used is small. We also provide the maximum and minimum concentration values in the same figure. These values indicate that the concentration is preserved positively, as well as the maximum concentration being accurate.
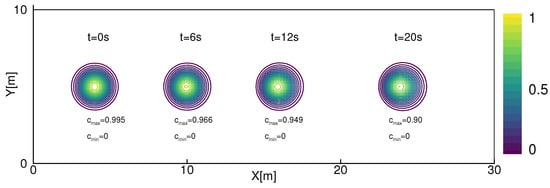
Figure 4.
Pollutant concentration distribution in the channel at times s, 6 s, 12 s, and 20 s.
In Table 1, we present the errors obtained for the concentration c at times s, 12 s, and 20 s for the same point distribution, using the Roe-MUSCL finite volume scheme and the LRBF methods. By examining the values of the and errors, it is clear that the LRBF method is much more accurate.

Table 1.
Results for the accuracy of the pollutant advection example using the LRBF and finite volume methods.
We performed a comparison between our simulation results, those obtained by the Roe-MUSCL finite volume scheme, and the analytical solution. We present in Figure 5 a longitudinal section at m of the pollutant concentration for the same simulation times as those in Figure 4. This figure shows the results of numerical analysis performed on distributions with 8000 points for the present meshless method; a mesh contained 8000 points and 15,680 volumes. Clearly, the results obtained by our numerical method agree very well with those of the analytical method.
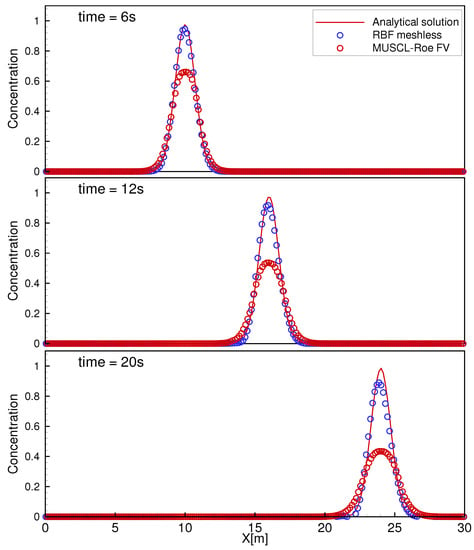
Figure 5.
Cross-section of the pollutant concentration in the straits at times s, 12 s, and 20 s at m.
4.4. Pollutant Transport in the Strait of Gibraltar
The Strait of Gibraltar, located between Spain (north) and Morocco (south), links the Mediterranean Sea and the Atlantic Ocean. It has an approximate length of 60 km between its western section, Barbate–Tangier and its eastern section, Gibraltar–Sebta. Its width varies from a minimum of about 14 km in the section Tarifa–Punta Cires to a maximum of 44 km in the section Barbate–Tangier. The Strait of Gibraltar contains two large bays, the Bay of Algeciras, which is located in the east of the strait, and the Bay of Tangier, located in the west (see Figure 6).
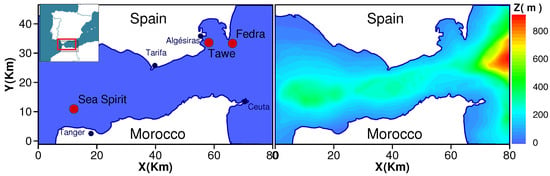
Figure 6.
Location (left) and bathymetry (right) of the Strait of Gibraltar with details showing the initial location of oil spills from the Sea Spirit, Fedra, and Tawe accidents (red circles).
The Strait of Gibraltar is one of the most used maritime ways in the world. More than 100,000 merchant vessels transit the strait every year [34]. In particular, oil vessels pose a threat to the ecological safety of the strait due to the serious consequences of oil spills. Indeed, historically, the Strait of Gibraltar has witnessed several oil spill accidents, for example, the accident of the Sea Spirit on the western side of the Strait of Gibraltar in 1990, and the accident of the Fedra-Tawe in Algeciras Bay in 2008 [34]. This is all the more concerning since the Strait of Gibraltar serves as the conduit through which surface water flows from the Atlantic to the Mediterranean sea [35]. With this in mind, it is clear that protecting the environment of the strait is crucial. An understanding of the hydrodynamics and pollutant transport in the Strait of Gibraltar is essential for the construction of intervention strategies.
In this study, the dynamics and transport of a pollutant plume in the Strait of Gibraltar are simulated numerically. The main objective is to test the ability of the LRBF method to handle the complexities of the Strait of Gibraltar, including geometric and topographic complexity.
The bathymetry used in this simulation is shown in Figure 6. The Strait of Gibraltar has an irregular bathymetry, exceeding a depth of 800 m on the eastern coast. The hydrodynamics of the strait are generated through the open boundaries by a difference in water height, producing the main component of the tide [36]. The Spanish and Moroccan coasts are assumed to be impermeable; hence, a no-slip condition is used for the velocity field. The present study examines the effects of releasing a non-active pollutant at the inlet of the strait. Thus, at an initial time, an injection of a pollutant in the form of the following function is made:
and indicate the initial position of the release. The point distributions adopted for the strait consist of 7690 points. This distribution, as well as the initial location of the pollutant, is presented in Figure 7. Finally, we summarize in Table 2 all the physical and numerical parameters necessary to implement the numerical model.
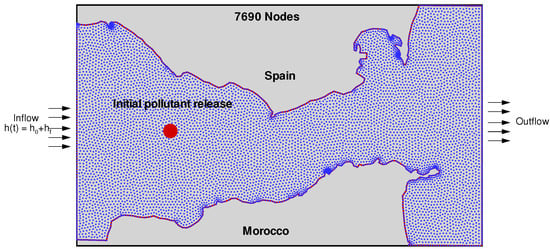
Figure 7.
Computational nodes used for the Strait of Gibraltar simulations.

Table 2.
Numerical and physical parameters of the model.
The simulation resulted in a velocity field at the water surface, as presented in Figure 8. This field is extremely important, as it shows the trajectory of the water masses. It also allows us to study the way in which an emitted particle is transported, and to distinguish regions that are free of any pollution from areas where pollution is possible. Analysis of the results reveals a high speed in the central line of the strait, with the formation of vortices and reverse currents near the coast. This is especially true in the Bay of Algeciras. Overall, the behavior found is comparable with that simulated previously in [2,36,37,38].
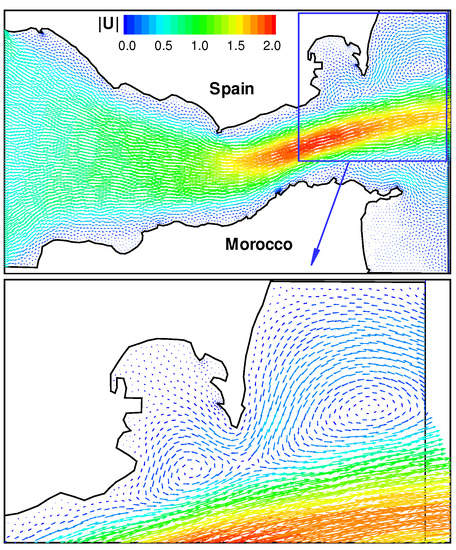
Figure 8.
Velocity field of the flow in the Strait of Gibraltar.
In Figure 9, we present the results of the pollutant transport at five different times, 2 h 7 min, 3 h 20 min, 5 h, 7 h 30 min, and 9 h 35 min, corresponding to the time needed for the pollutant to exit the strait if wind effects are not taken into account. In general, these calculations provide an estimate of the time required for the pollutant to be transported out of the study area. The first of these periods is the most relevant from a decision-making perspective, since, during this period, the concentrations are higher and, therefore, so are the risks. However, if the accident occurs near the coastline, the time required for the contaminants to be removed increases. From the numerical point of view, the results show that the LRBF method can correctly simulate the behavior of the pollutant transport, as well as its interaction with the flow. Moreover, the positivity of the concentration is maintained throughout the displacement.
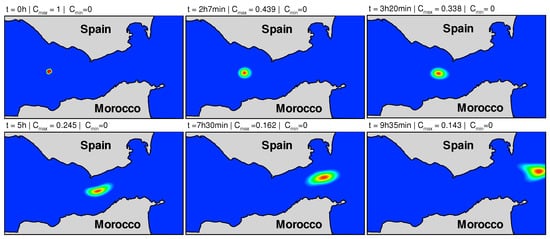
Figure 9.
Position and concentration of the pollutant released in the Strait of Gibraltar at different times.
In Figure 10, we show a comparison of the evolution of the maximum concentration calculated by the LRBF method and the finite volume method featuring the Roe-MUSCL scheme. Under the conditions used, the meshless method clearly minimizes numerical dissipation, even over long periods.
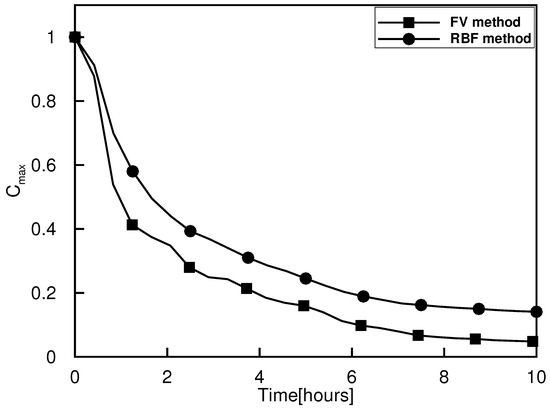
Figure 10.
Evolution of the maximum pollutant concentration against time.
5. Conclusions
In this work, the shallow water equations coupled with the advection–diffusion equation are presented to simulate pollutant transport in shallow water flows. The resulting system is solved numerically using a meshless method based on local radial basis functions. To stabilize the method and eliminate the non-physical oscillations that occur in the vicinity of the discontinuities, a hyperviscosity technique is implemented. Subsequently, the meshless model is successfully applied using several tests with satisfactory results, confirming its numerical stability and computational accuracy. Numerical computations demonstrate: (i) the simplicity of the implementation of the method for the shallow water system, (ii) the ability of the method to handle calculations of slowly varying flows or concentrations, as well as rapidly varying flows containing shocks or discontinuities, and (iii) the preservation of the C-property and the positivity of the water height and pollutant concentration. Moreover, this study shows that the model works well for the propagation of pollution in a shallow water flow. Finally, findings concerning pollutant transport within the Strait of Gibraltar show that the presented method can be implemented for large species transport systems in a flow field driven by water flows.
Author Contributions
Conceptualization, M.A.N. and E.C.; methodology, M.A.N. and E.C.; software, M.A.N. and E.C.; validation, M.A.N.and E.C.; formal analysis, M.A.N. and E.C.; investigation, M.A.N. and E.C.; resources, M.A.N. and E.C.; data curation, E.C.; writing—original draft preparation, E.C.; writing—review and editing, M.A.N.; visualization, M.A.N. and E.C.; supervision, M.A.N. and E.C.; project administration, M.A.N.; funding acquisition, M.A.N.; All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported through the Annual Funding track by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia [Project No. AN000674].
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
The authors acknowledge the Deanship of Scientific Research at King Faisal University for the financial support, [Project No. AN000674].
Conflicts of Interest
The author declares that the research was conducted in the absence of any conflict of interest.
References
- Aizinger, V.; Dawson, C. A discontinuous Galerkin method for two-dimensional flow and transport in shallow water. Adv. Water Resour. 2002, 25, 67–84. [Google Scholar] [CrossRef]
- Benkhaldoun, F.; Elmahi, I.; Seaı, M. Well-balanced finite volume schemes for pollutant transport by shallow water equations on unstructured meshes. J. Comput. Phys. 2007, 226, 180–203. [Google Scholar] [CrossRef][Green Version]
- Vanzo, D.; Siviglia, A.; Toro, E.F. Pollutant transport by shallow water equations on unstructured meshes: Hyperbolization of the model and numerical solution via a novel flux splitting scheme. J. Comput. Phys. 2016, 311, 1–20. [Google Scholar] [CrossRef]
- Bouchut, F. Efficient numerical finite volume schemes for shallow water models. Ed. Ser. Adv. Nonlinear Sci. Complex. 2007, 2, 189–256. [Google Scholar]
- Hanert, E.; Legat, V.; Deleersnijder, E. A comparison of three finite elements to solve the linear shallow water equations. Ocean Model. 2003, 5, 17–35. [Google Scholar] [CrossRef]
- Lundgren, L.; Mattsson, K. An efficient finite difference method for the shallow water equations. J. Comput. Phys. 2020, 422, 109784. [Google Scholar] [CrossRef]
- Arifeen, S.U.; Haq, S.; Ghafoor, A.; Ullah, A.; Kumam, P.; Chaipanya, P. Numerical solutions of higher order boundary value problems via wavelet approach. Adv. Differ. Equ. 2021, 2021, 347. [Google Scholar] [CrossRef]
- Hussain, Z.; Khan, S.; Ullah, A.; Ayaz, M.; Ahmad, I.; Mashwani, W.K.; Chu, Y.M. Extension of optimal homotopy asymptotic method with use of Daftardar–Jeffery polynomials to Hirota–Satsuma coupled system of Korteweg–de Vries equations. Open Phys. 2020, 18, 916–924. [Google Scholar] [CrossRef]
- Shah, Z.; Kumam, P.; Ullah, A.; Khan, S.N.; Selim, M.M. Mesoscopic Simulation for Magnetized Nanofluid Flow within a Permeable 3D Tank. IEEE 2021, 9, 135234–135244. [Google Scholar] [CrossRef]
- Roe, P.L. Characteristic-based schemes for the euler equations. Annu. Rev. Fluid Mech. 1986, 18, 337–365. [Google Scholar] [CrossRef]
- Chen, S.; Yan, C.; Lou, S.; Lin, B. An improved entropy-consistent euler flux in low mach number. J. Comput. Sci. 2018, 27, 271–283. [Google Scholar] [CrossRef]
- Alcrudo, F.; Garcia-Navarro, P. A high-resolution godunov-type scheme in finite volumes for the 2d shallow-water equations. Int. J. Numer. Methods Fluids 1993, 16, 489–505. [Google Scholar] [CrossRef]
- Zhao, F.; Pan, L.; Wang, S. Weighted essentially non-oscillatory scheme on unstructured quadrilateral and triangular meshes for hyperbolic conservation laws. J. Comput. Phys. 2018, 374, 605–624. [Google Scholar] [CrossRef]
- Shu, C.W. Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws. In Advanced Numerical Approximation of Nonlinear Hyperbolic Equations; Quarteroni, A., Ed.; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1998; Volume 1697, pp. 325–432. [Google Scholar]
- Caleffi, V.; Valiani, A.; Bernini, A. High-order balanced cweno scheme for movable bed shallow water equations. Adv. Water Resour. 2007, 30, 730–741. [Google Scholar] [CrossRef]
- Clain, S.; Diot, S.; Loubère, R. A high-order finite volume method for systems of conservation laws—Multi-dimensional optimal order detection (mood). J. Comput. Phys. 2011, 230, 4028–4050. [Google Scholar] [CrossRef]
- Diot, S.; Clain, S.; Loubère, R. Improved detection criteria for the multi-dimensional optimal order detection (mood) on unstructured meshes with very high-order polynomials. Comput. Fluids 2012, 64, 43–63. [Google Scholar] [CrossRef]
- Diot, S.; Loubère, R.; Clain, S. The multidimensional optimal order detection method in the three-dimensional case: Very high-order finite volume method for hyperbolic systems. Int. J. Numer. Methods Fluids 2013, 73, 362–392. [Google Scholar] [CrossRef]
- Kansa, E.J. Multiquadrics—A scattered data approximation scheme with applications to computational fluid-dynamics—I surface approximations and partial derivative estimates. Comput. Math. Appl. 1990, 19, 127–145. [Google Scholar] [CrossRef]
- Yao, G.; Kolibal, J.; Chen, C.S. A localized approach for the method of approximate particular solutions. Comput. Math. Appl. 2011, 61, 2376–2387. [Google Scholar] [CrossRef]
- Sarra, S. A local radial basis function method for advection–diffusion–reaction equations on complexly shaped domains. Appl. Math. Comput. 2012, 218, 9853–9865. [Google Scholar] [CrossRef]
- Tabbakh, Z.; Seaid, M.; Ellaia, R.; Ouazar, D.; Benkhaldoun, F. A local radial basis function projection method for incompressible flows in water eutrophication. Eng. Anal. Bound. Elem. 2019, 106, 528–540. [Google Scholar] [CrossRef]
- Kesserwani, G.; Liang, Q. Locally limited and fully conserved rkdg2 shallow water solutions with wetting and drying. J. Sci. Comput. 2012, 50, 120–144. [Google Scholar] [CrossRef]
- Chaabelasri, E. Numerical simulation of dam break flows using a radial basis function meshless method with artificial viscosity. Model. Simul. Eng. 2018, 2018, 4245658. [Google Scholar] [CrossRef]
- Fornberg, B.; Lehto, E. Stabilization of rbf-generated finite difference methods for convective pdes. J. Comput. Phys. 2011, 230, 2270–2285. [Google Scholar] [CrossRef]
- Flyer, N.; Lehto, E.; Blaise, S.; Wright, G.B.; St-Cyr, A. A guide to rbf-generated finite differences for nonlinear transport: Shallow water simulations on a sphere. J. Comput. Phys. 2012, 231, 4078–4095. [Google Scholar] [CrossRef]
- Dehghan, M.; Abbaszadeh, M. The use of proper orthogonal decomposition (pod) meshless rbf-fd technique to simulate the shallow water equations. J. Comput. Phys. 2017, 351, 478–510. [Google Scholar] [CrossRef]
- Flyer, N.; Barnett, G.A.; Wicker, L.J. Enhancing finite differences with radial basis functions: Experiments on the navier–stokes equations. J. Comput. Phys. 2016, 316, 39–62. [Google Scholar] [CrossRef]
- Bermudez, A.; Vazquez, M.E. Upwind methods for hyperbolic conservation laws with source terms. Comput. Fluids 1994, 23, 1049–1071. [Google Scholar] [CrossRef]
- Amiri, S.M.; Talebbeydokhti, N.; Baghlani, A. A two-dimensional well-balanced numerical model for shallow water equations. Sci. Iran. 2013, 20, 97–107. [Google Scholar] [CrossRef]
- Touma, R.; Kanbar, F. Well-balanced central schemes for two-dimensional systems of shallow water equations with wet and dry states. Appl. Math. Model. 2018, 62, 728–750. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, J.; Zhao, N. A new fifth-order finite difference well-balanced multi-resolution WENO scheme for solving shallow water equations. Comput. Math. Appl. 2020, 80, 1387–1404. [Google Scholar] [CrossRef]
- Chaabelasri, E.; Jeyar, M. Salhi, N.; Elmahi, I. A simple unstructured finite volume scheme for solving shallow water equations with wet/dry interface. Int. J. Mech. Eng. Technol. 2019, 10, 1849–1861. [Google Scholar]
- González, C.J.; Reyes, E.; Álvarez, O.; Izquierdo, A.; Bruno, M.; Mañanes, R. Surface currents and transport processes in the strait of gibraltar: Implications for modeling and management of pollutant spills. Ocean. Coast. Manag. 2019, 179, 104869. [Google Scholar] [CrossRef]
- Periáñez, R.; Pascual-Granged, A. Modelling surface radioactive, chemical and oil spills in the strait of gibraltar. Comput. Geosci. 2008, 34, 163–180. [Google Scholar] [CrossRef]
- Banda, M.K.; Seaïd, M.; Thömmes, G. Lattice boltzmann simulation of dispersion in two-dimensional tidal flows. Int. J. Numer. Methods Eng. 2009, 77, 878–900. [Google Scholar] [CrossRef]
- Benkhaldoun, F.; Elmahi, I.; Seaïd, M. Application of mesh-adaptation for pollutant transport by water flow. Math. Comput. Simul. 2009, 79, 3415–3423. [Google Scholar] [CrossRef]
- Talbi, H.; Chaabelasri, E.; Jeyar, M.; Salhi, N. Random walk particle tracking for convection-diffusion dominated problems in shallow water flows. J. Appl. Comput. Mech. 2021, 7, 486–495. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).