Investigation of Classification and Anomalies Based on Machine Learning Methods Applied to Large Scale Building Information Modeling
Abstract
:1. Introduction
2. Data Extraction
2.1. Introduction of the Data
2.2. Data Extraction
3. Feature Engineering
3.1. Feature Standardization
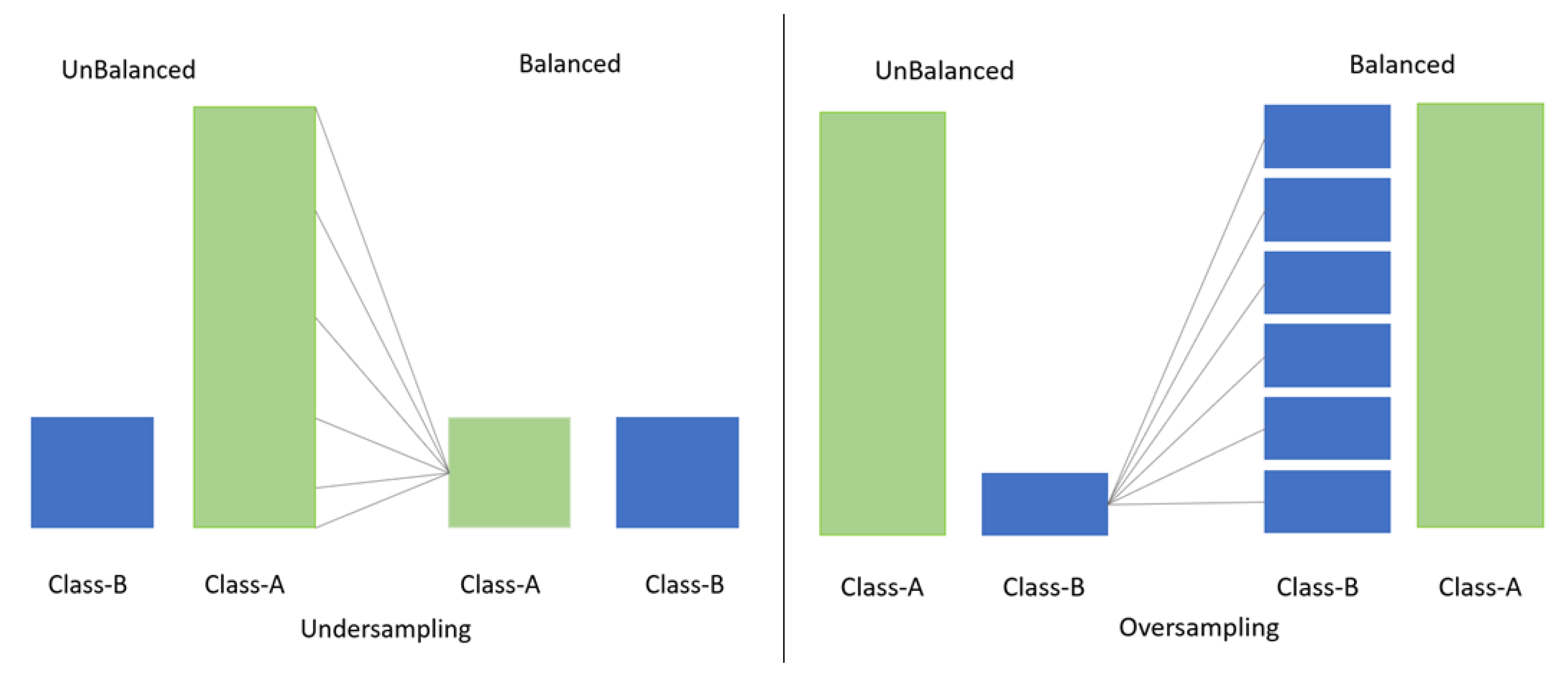
3.2. Imbalance between Classes
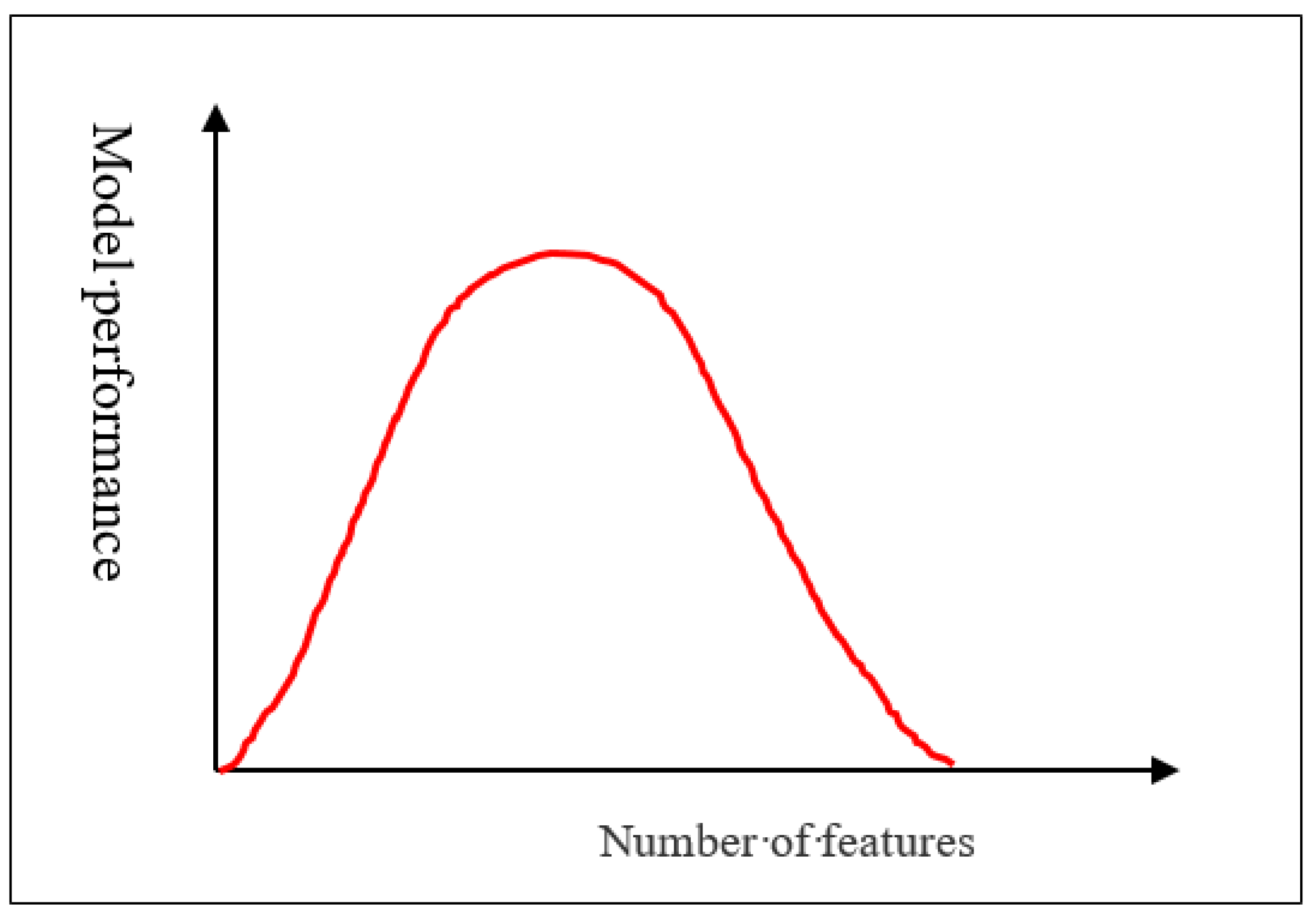
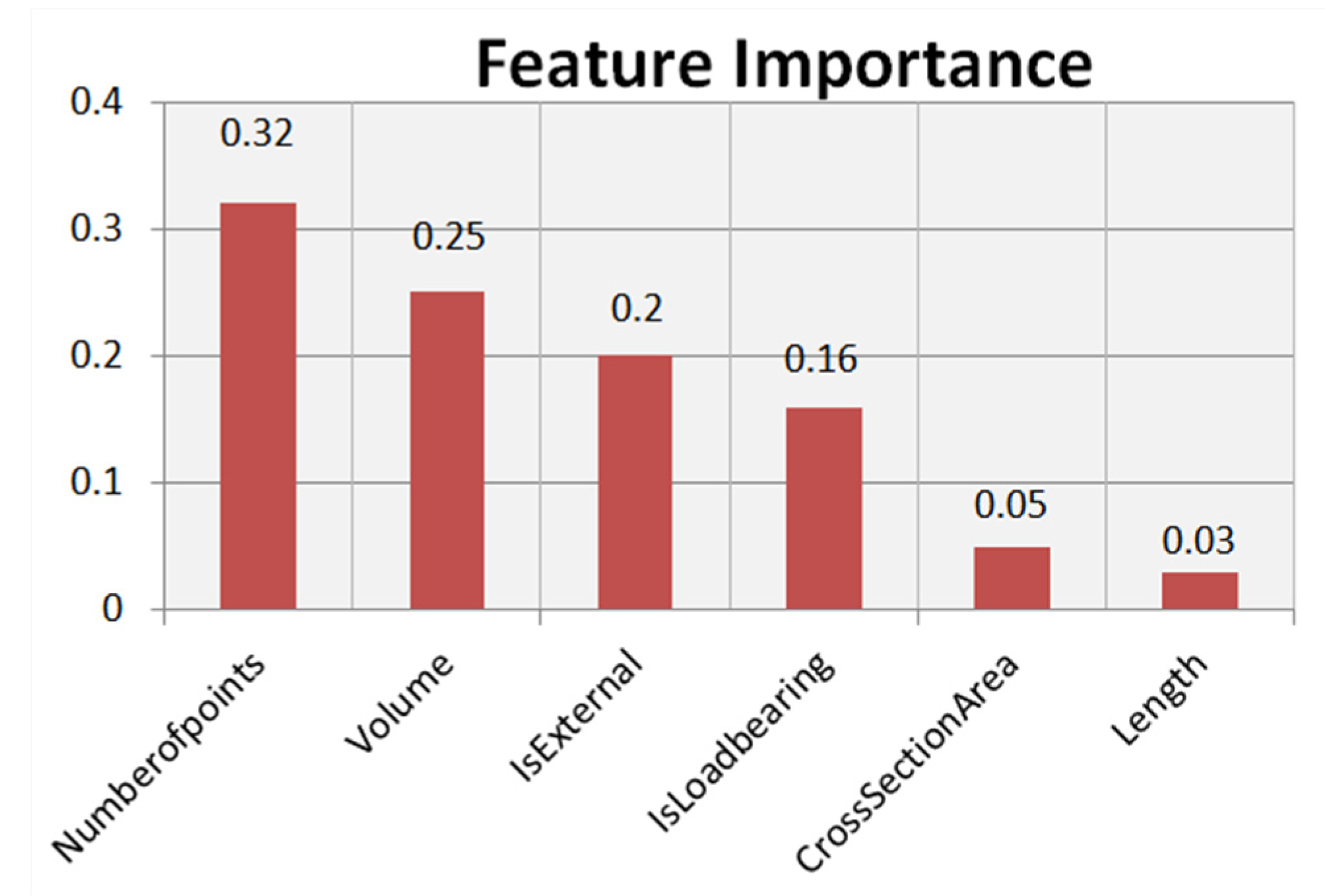
3.3. Feature Selection
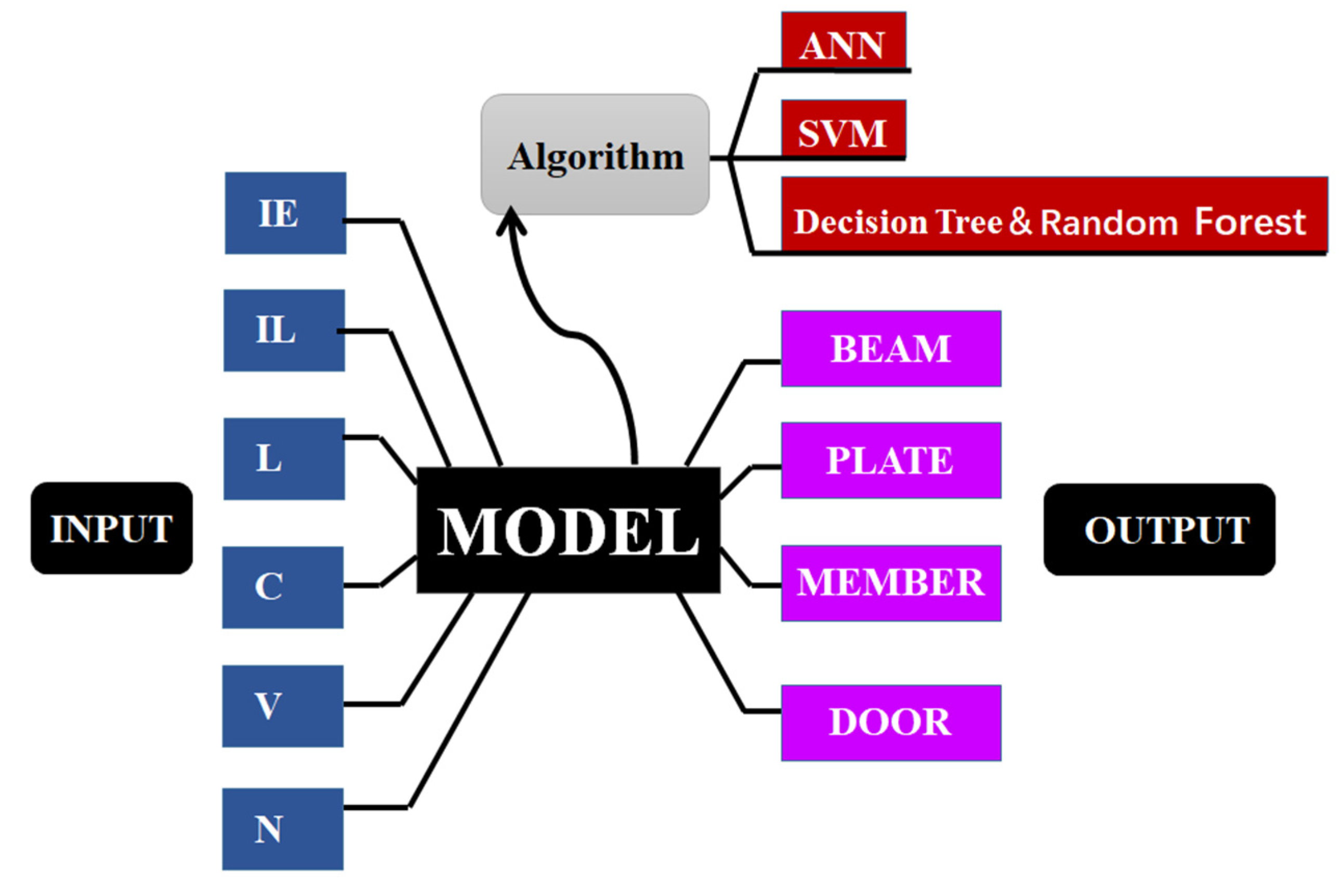
4. BIM Element Classification
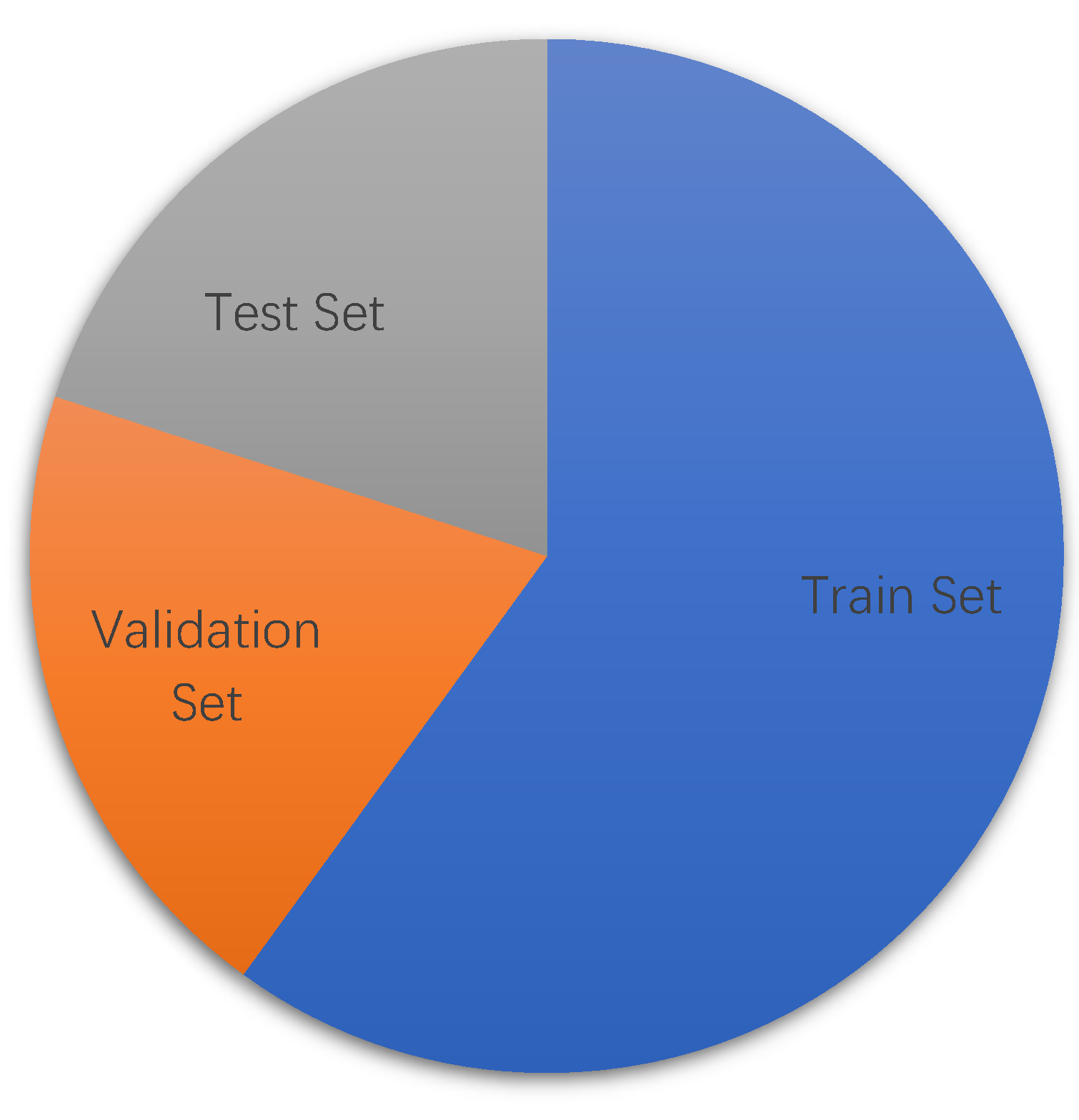
4.1. Data Set and Overall Thinking
4.2. BIM Element Classification Experiment
4.2.1. BIM Element Classification Based on Support Vector Machine
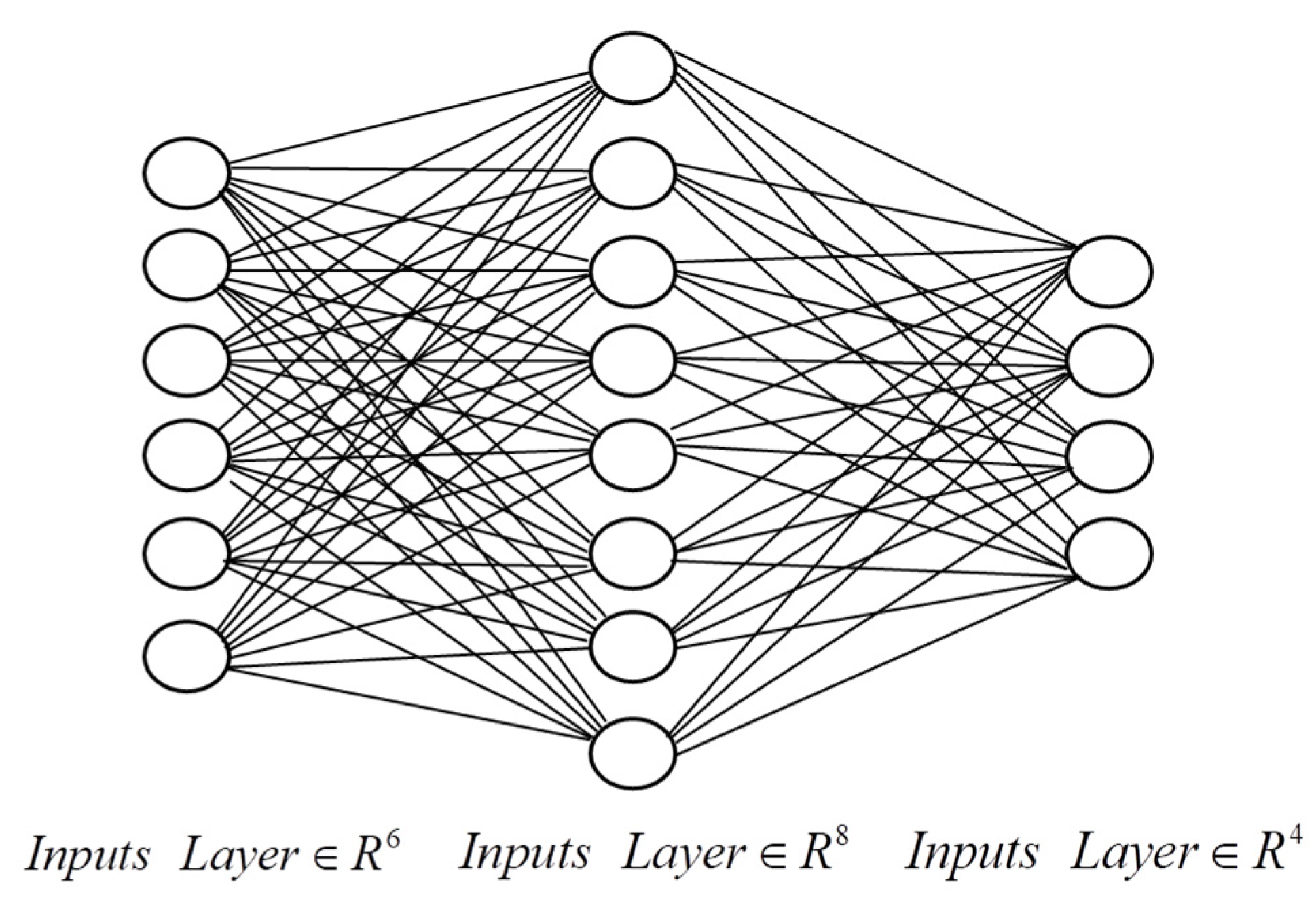
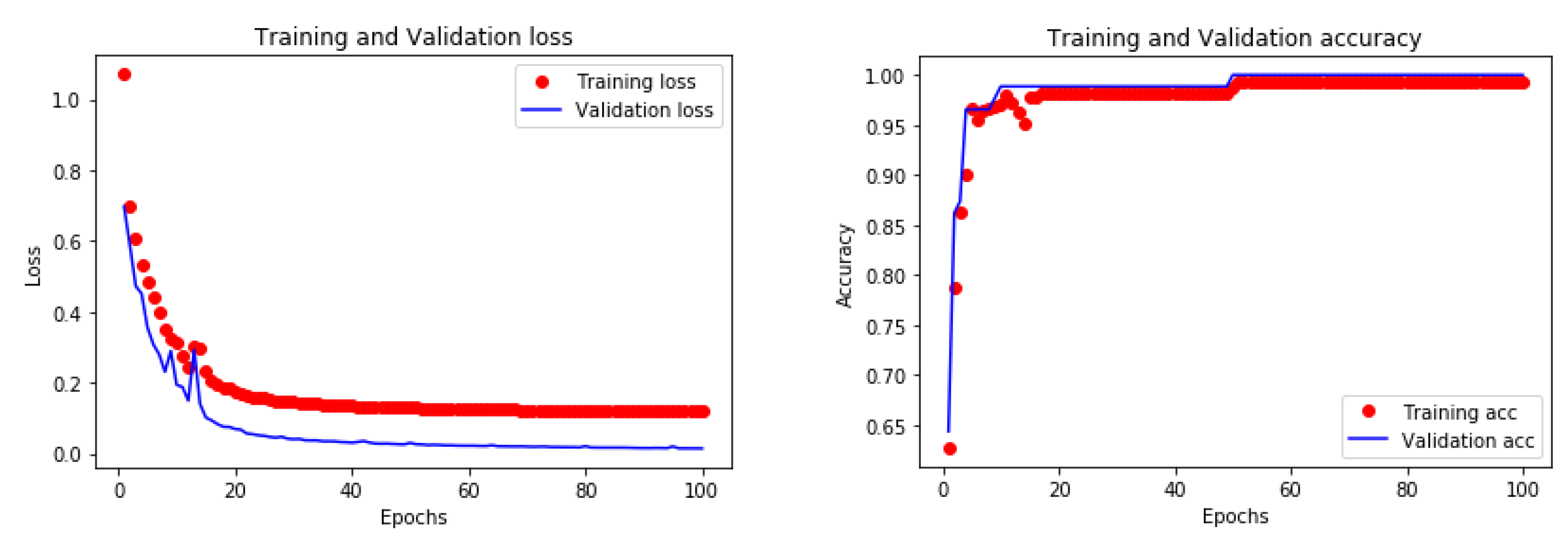
4.2.2. BIM Element Classification Based on Artificial Neural Network
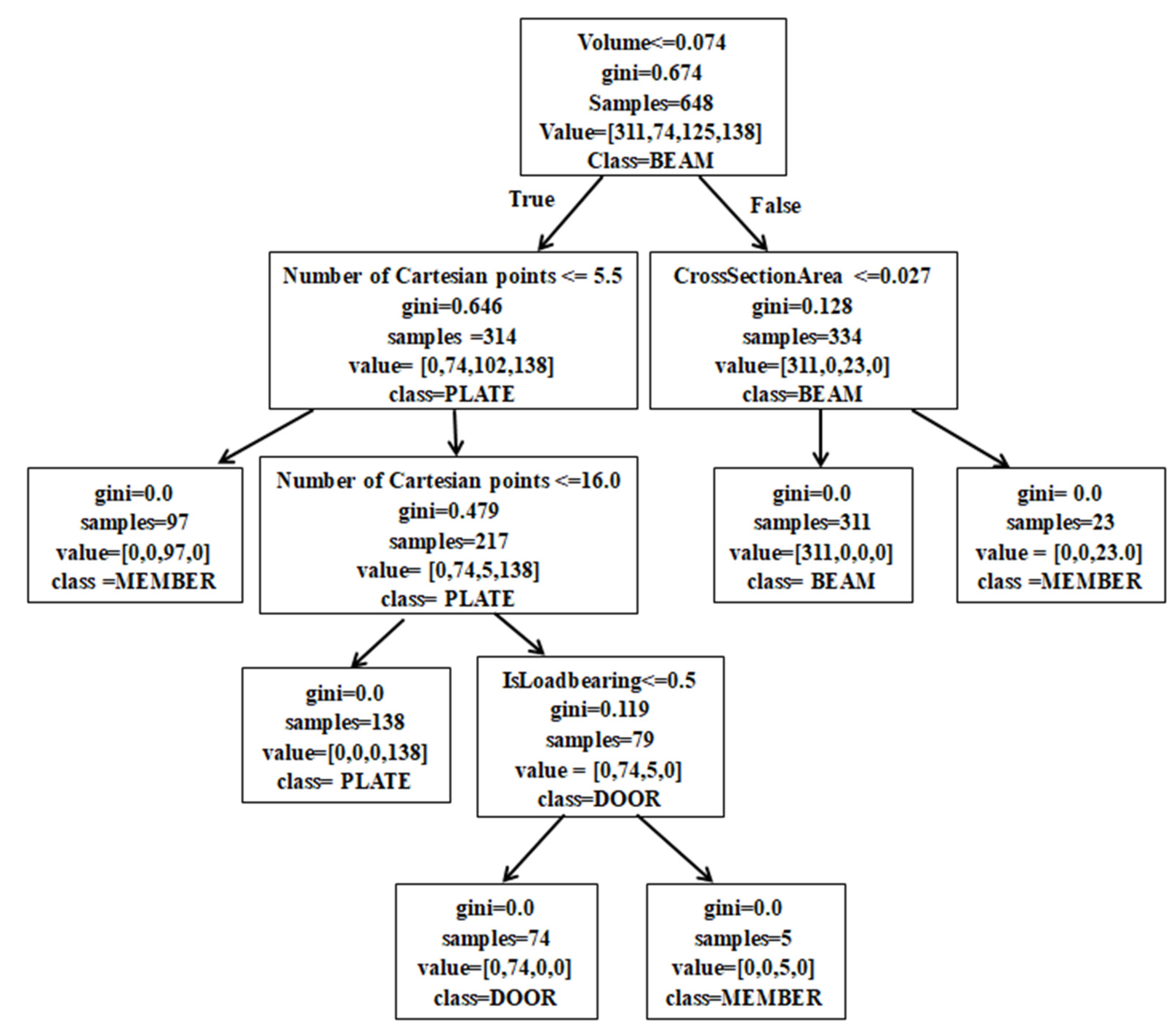
4.2.3. BIM Element Classification Based on Decision Tree and Random Forest
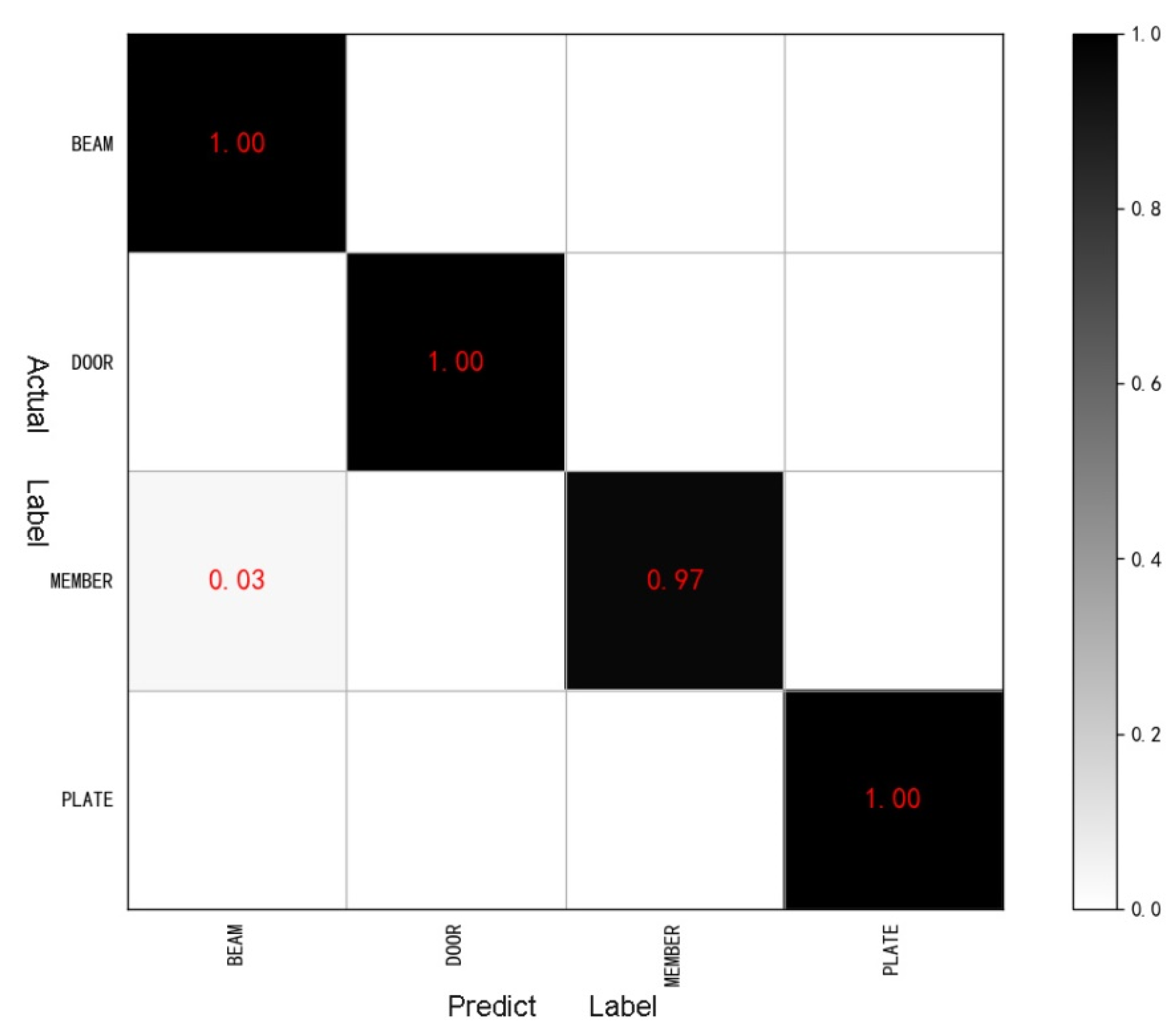
4.3. Results and Discussion
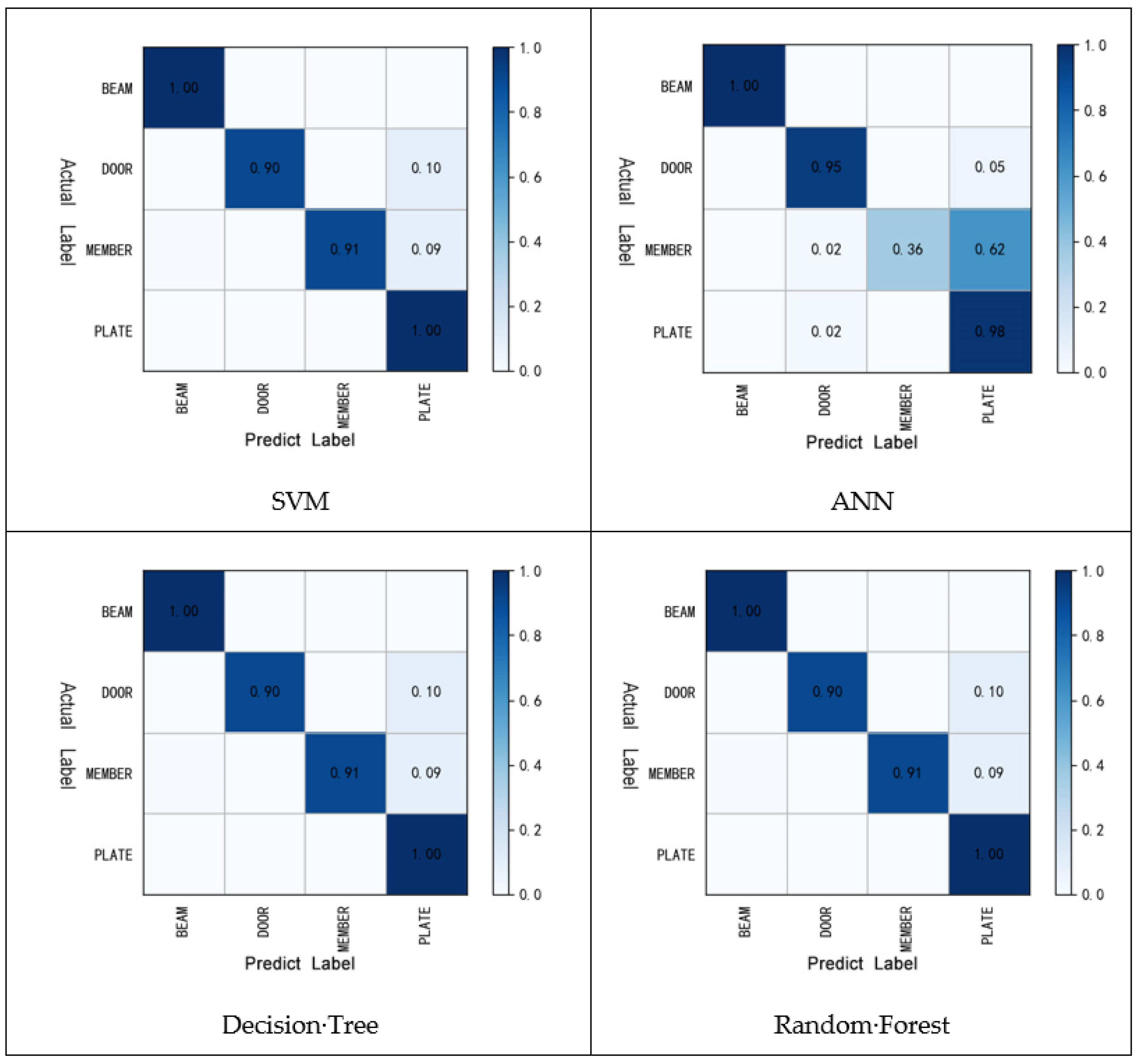
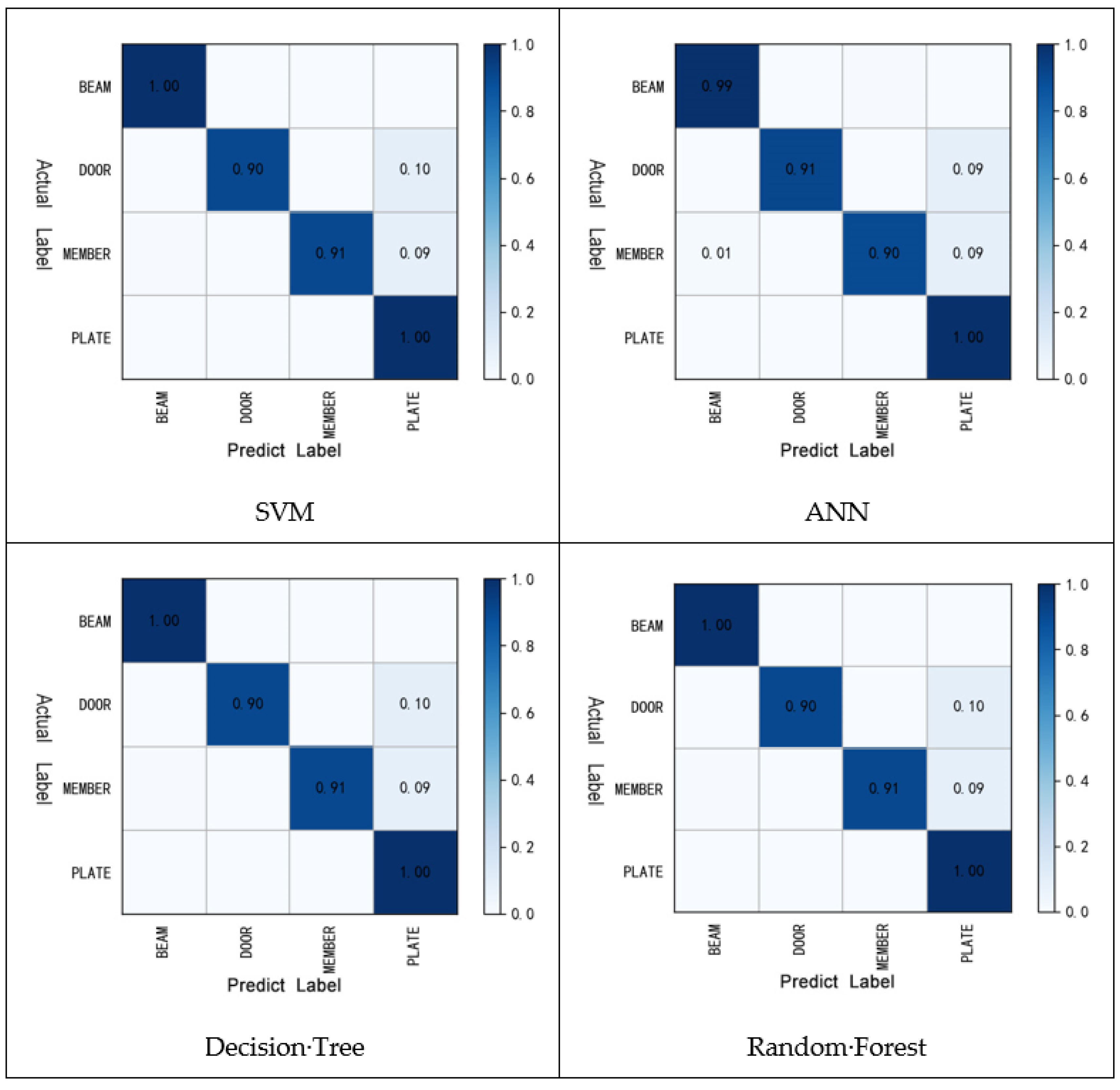
4.3.1. Comparison of Optimal Classification Results
4.3.2. Comparison of Classification Results in Single Different Dataset
4.3.3. Comparison of Classification Results on Mixed Data Sets
5. Abnormal Data Detection
5.1. Abnormal Data and Evaluation Indexes
5.2. Abnormal Data Detection Experiment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Bradley, A.; Li, H.; Lark, R.; Dunn, S. BIM for infrastructure: An overall review and constructor perspective. Autom. Constr. 2016, 71, 139–152. [Google Scholar] [CrossRef]
- Tamke, M.; Myrup, M.; Evers, H.L. D7.7.1-Current State of 3D Object Processing in Architectural Research and Practice. Available online: http://duraark.eu/wp-content/uploads/2014/06/duraark_d7.7.1.pdf (accessed on 15 June 2022).
- Tamke, M.; Jensen, M.M.; Beetz, J.; Krijnen, T.; Edvardsen, D.F. Building Information Deduced: State and Potentials for Information Query in Building Information Modelling. In Proceedings of the Fusion: Proceedings of the 32nd eCAADe Conference, Newcastle upon Tyne, UK, 10–12 October 2014; Thompson, E.M., Ed.; 2014; pp. 375–384. [Google Scholar]
- Krijnen, T.; Tamke, M. Assessing implicit knowledge in BIM models with machine learning. In Design Modelling Sympoisum: Modelling Behaviour; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Howell, S.; Rezgui, Y. Beyond BIM: Knowledge Management for a Smarter Built Environment; BRE Electronic Publications: Garston, UK, 2018. [Google Scholar]
- Kubicki, S.; Guerriero, A.; Schwartz, L.; Daher, E.; Idris, B. Assessment of synchronous interactive devices for BIM project coordination: Prospective ergonomics approach. Autom. Constr. 2019, 101, 160–178. [Google Scholar] [CrossRef]
- Leggieri, V.; Ruggieri, S.; Zagari, G.; Uva, G. Appraising seismic vulnerability of masonry aggregates through an automated mechanical-typological approach. Autom. Constr. 2021, 132, 103972. [Google Scholar] [CrossRef]
- Batty, M. Digital twins, Environment and Planning B: Urban Analytics and City Science. SAGE J. 2018, 45, 817–820. [Google Scholar]
- Boje, C.; Guerriero, A.; Kubicki, S.; Rezgui, Y. Towards a semantic Construction Digital Twin: Directions for future research. Autom. Constr. 2020, 114, 103179. [Google Scholar] [CrossRef]
- Lomio, F.; Farinha, R.; Laasonen, M.; Huttunen, H. Classification of Building Information Model (BIM) Structures with Deep Learning. arXiv 2018, arXiv:1808.00601. [Google Scholar]
- Valero, E.; Forster, A.; Bosché, F.; Renier, C.; Hyslop, E.; Wilson, L. High Level-of-Detail BIM and Machine Learning for Auto-mated Masonry Wall Defect Surveying. In Proceedings of the 35th International Symposium on Automation and Robotics in Construction, Berlin, Germany, 25–28 July 2018. [Google Scholar]
- Zhang, H.; Gu, M. Research and Application of Intelligent BIM Model Checking Tools. J. Inf. Technol. Civ. Eng. Archit. 2018, 10, 1–6. [Google Scholar]
- Romero-Jarén, R.; Arranz, J. Automatic segmentation and classification of BIM elements from point clouds. Autom. Constr. 2021, 124, 103576. [Google Scholar] [CrossRef]
- Jung, N.; Lee, G. Automated classification of building information modeling (BIM) case studies by BIM use based on natural language processing (NLP) and unsupervised learning. Adv. Eng. Inform. 2019, 41, 100917. [Google Scholar] [CrossRef]
- McArthur, J.; Shahbazi, N.; Fok, R.; Raghubar, C.; Bortoluzzi, B.; An, A. Machine learning and BIM visualization for maintenance issue classification and enhanced data collection. Adv. Eng. Inform. 2018, 38, 101–112. [Google Scholar] [CrossRef]
- Koo, B.; Shin, B. Applying novelty detection to identify model element to IFC class misclassifications on architectural and infrastructure Building Information Models. J. Comput. Des. Eng. 2018, 5, 391–400. [Google Scholar] [CrossRef]
- Bloch, T.; Sacks, R. Comparing machine learning and rule-based inferencing for semantic enrichment of BIM models. Autom. Constr. 2018, 91, 256–272. [Google Scholar] [CrossRef]
- Donoho, D.L. High-Dimensional Data Analysis: The Curses and Blessings of Dimensionality. AMS Math Chall. Lect. 2000, 1, 32. [Google Scholar] [CrossRef]
- Nagler, T.; Czado, C. Evading the curse of dimensionality in nonparametric density estimation with simplified vine copulas. J. Multivar. Anal. 2016, 151, 69–89. [Google Scholar] [CrossRef] [Green Version]
- Salimi, A.; Ziaii, M.; Amiri, A.; Hosseinjanizadeh, M.; Karimpouli, S.; Moradkhani, M. Using a Feature Subset Selection method and Support Vector Machine to address curse of dimensionality and redundancy in Hyperion hyperspectral data classification. Egypt. J. Remote. Sens. Space Sci. 2017, 21, 27–36. [Google Scholar] [CrossRef]
- Fernández-Martínez, J.L.; Fernández-Muñiz, Z. The curse of dimensionality in inverse problems. J. Comput. Appl. Math. 2020, 369, 112571. [Google Scholar] [CrossRef]
- Grüne, L. Overcoming the curse of dimensionality for approximating Lyapunov functions with deep neural networks under a small-gain condition. IFAC-PapersOnLine 2021, 54, 317–322. [Google Scholar] [CrossRef]


| Visualization | Name | Standard | Num.of Ele |
|---|---|---|---|
 | 20160125_Existing_Trapelo_Design_Intent | IFC2X3 | 1479 |
 | 210_King_Toronto | IFC2X3 | 8820 |
 | Wyandotte_Lofts | IFC2X3 | 2887 |
 | 20190104WestRiverSide_ Hospital_Architecture | IFC4 | 14,440 |
| Characteristics of the Name | Type | Choose |
|---|---|---|
| Representation Type (R) | STRING | ⊠ |
| Is External (IE) | STRING | ☑ |
| Is Load bearing (IL) | STRING | ☑ |
| Length (L) | FLOAT | ☑ |
| Perimeter (P) | FLOAT | ⊠ |
| Area (A) | FLOAT | ⊠ |
| Cross Section Area (C) | FLOAT | ☑ |
| Volume (V) | FLOAT | ☑ |
| Number of Cartesian points (N) | INT | ☑ |
| File Name | Number of Elements | Total | Mark | ||||
|---|---|---|---|---|---|---|---|
| BEAM | DOOR | PLATE | MEMBER | SUM | |||
| ETDI.IFC | 512 | 122 | 230 | 218 | 1082 | 1479 | ON |
| 11…15.IFC | 0 | 0 | 0 | 0 | 0 | 78 | TW |
| 21…to.IFC | 0 | 211 | 375 | 1037 | 1623 | 2750 | TH |
| 20…re.IFC | 0 | 440 | 2211 | 7122 | 9773 | 11,328 | FO |
| A…FC.IFC | 0 | 77 | 0 | 0 | 77 | 327 | FI |
| Co…ng.IFC | 0 | 0 | 0 | 0 | 0 | 270 | SI |
| Re…ct.IFC | 137 | 0 | 0 | 22 | 159 | 231 | SE |
| Sim…le.IFC | 0 | 0 | 0 | 0 | 0 | 0 | EI |
| Te…ol.IFC | 14 | 100 | 1349 | 3294 | 4757 | 5284 | NI |
| Ur…15.IFC | 0 | 0 | 0 | 0 | 0 | 23 | TE |
| Wa…ts.IFC | 63 | 203 | 483 | 21 | 770 | 1471 | EL |
| Data | Source | Total | Element | |||
|---|---|---|---|---|---|---|
| BEAM | DOOR | PLATE | MEMBER | |||
| Data1 | ON | 1082 | 512 | 122 | 230 | 218 |
| Data2 | ON | 2048 | 512 | 512 | 512 | 512 |
| Data3 | ON+TH+FO+NI+EL | 18,005 | 589 | 1076 | 4848 | 11,692 |
| Data4 | ON+NI+EL | 6609 | 589 | 425 | 2062 | 3533 |
| σ | 0.01 | 0.1 | 1 | 10 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Training | Test | Training | Test | Training | Test | Training | Test | ||
| 0.01 | 0.4878 | 0.4147 | 0.7676 | 0.7051 | 0.6971 | 0.6505 | 0.6971 | 0.6405 | |
| 0.1 | 0.8462 | 0.7880 | 0.8520 | 0.7926 | 0.9850 | 0.9585 | 0.9791 | 0.8341 | |
| 1 | 0.8520 | 0.7926 | 0.9850 | 0.9677 | 0.9988 | 0.9769 | 0.9988 | 0.8479 | |
| C | 10 | 0.8520 | 0.7926 | 0.9988 | 0.9723 | 0.9988 | 0.9862 | 1.000 | 0.8479 |
| 20 | 0.9849 | 0.9677 | 0.9988 | 0.9816 | 0.9988 | 0.9862 | 1.000 | 0.8479 | |
| 50 | 0.9942 | 0.9908 | 0.9988 | 0.9816 | 0.9988 | 0.9862 | 1.000 | 0.8479 | |
| 100 | 0.9988 | 0.9908 | 0.9988 | 0.9769 | 1.000 | 0.9862 | 1.000 | 0.8479 | |
| Hyperparameter | Optimal Value |
|---|---|
| Network Structure | N(6,8,4) |
| Max Iteration | 100 |
| Optimization method | SDG |
| Learning rate | 0.03 |
| Momentum | 0.5 |
| Target | Result |
|---|---|
| Accuracy | 0.9816 |
| Loss | 0.1509 |
| Training Accuracy | Test Accuracy | |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1 | 1 |
| … | 1 | 1 |
| 10 | 1 | 1 |
| Optimization | SVM | ANN | Decision Tree | Random Forest |
|---|---|---|---|---|
| Training Accuracy | 0.9988 | 1 | 1 | 1 |
| Test Accuracy | 0.9908 | 0.9816 | 0.9908 | 1 |
| ON(2048) | NI(13176) | EL(1932) | ||||
|---|---|---|---|---|---|---|
| Training | Test | Training | Test | Training | Test | |
| SVM | 0.9988 | 0.9908 | 0.9461 | 0.9453 | 0.9784 | 0.9767 |
| ANN | 1 | 0.9816 | 0.9456 | 0.9450 | 0.9672 | 0.9587 |
| DT | 1 | 0.9908 | 0.9461 | 0.9454 | 0.9784 | 0.9767 |
| RF | 1 | 1 | 0.9461 | 0.9454 | 0.9784 | 0.9767 |
| SVM | ANN | DT | RF | |
|---|---|---|---|---|
| Hyperparameter | DEFAULT | |||
| Train Accuracy | 0.8255 | 0.8221 | 0.8252 | 0.8252 |
| Test Accuracy | 0.8224 | 0.8215 | 0.8241 | 0.8241 |
| SVM | ANN | DT | RF | |
|---|---|---|---|---|
| Hyperparameter | DEFAULT | |||
| Training Accuracy | 0.9542 | 0.9510 | 0.9558 | 0.9558 |
| Test Accuracy | 0.9522 | 0.9508 | 0.9558 | 0.9558 |
| normal data | BEAM W-Wide F SweptSoli False True 0.261838 3 0 0 0 0 BEAM C-Channe SwptSoli False True 0.103896 16 0 0 0 0 | Normal |
| Abnormal data | BEAM W-Wide F SwptSoli False True 0.266505 3 0 0 1 0 BEAM W-Wide F SwptSoli False True 0.261838 6 0 0 1 0 | Abnormal properties |
| BEAM Exit Door MappedR False True 0.266505 28 0 0 0 0 BEAM Stair: Steel Brep False True 0.261838 95 0 0 0 0 | Abnormal label |
| Data Set | Number | Data Set Composition | |
|---|---|---|---|
| Normal | Abnormal | ||
| DATA_L | 278 | 239 | 39 |
| DATA_F | 1082 | 973 | 109 |
| DATA_LF | 1360 | 1223 | 137 |
| DATA_L | DATA_F | DATA_LF | ||||
|---|---|---|---|---|---|---|
| ANN | RF | ANN | RF | ANN | RF | |
| Accuracy | 1 | 1 | 0.9641 | 0.9590 | 0.9463 | 0.9587 |
| Precision | 1 | 1 | 1 | 0.9898 | 0.9669 | 0.9616 |
| Recall | 1 | 1 | 0.9327 | 0.9327 | 0.9286 | 0.9512 |
| F1 Score | 1 | 1 | 0.9652 | 0.9604 | 0.9474 | 0.9590 |
| Hyperparameter | Adagrad r = 0.08 iter = 100 6-8-1 r-si | Adagrad r = 0.07 iter = 200 6-32-16-2 r-r-so | Adagrad r = 0.08 iter = 200 6-36-64-8-1 r-si-r-si | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, M.; Chao, Z.; Coelho, R.F.; Tian, S. Investigation of Classification and Anomalies Based on Machine Learning Methods Applied to Large Scale Building Information Modeling. Appl. Sci. 2022, 12, 6382. https://doi.org/10.3390/app12136382
Xiao M, Chao Z, Coelho RF, Tian S. Investigation of Classification and Anomalies Based on Machine Learning Methods Applied to Large Scale Building Information Modeling. Applied Sciences. 2022; 12(13):6382. https://doi.org/10.3390/app12136382
Chicago/Turabian StyleXiao, Manyu, Zhiqin Chao, Rajan Filomeno Coelho, and Shaobo Tian. 2022. "Investigation of Classification and Anomalies Based on Machine Learning Methods Applied to Large Scale Building Information Modeling" Applied Sciences 12, no. 13: 6382. https://doi.org/10.3390/app12136382
APA StyleXiao, M., Chao, Z., Coelho, R. F., & Tian, S. (2022). Investigation of Classification and Anomalies Based on Machine Learning Methods Applied to Large Scale Building Information Modeling. Applied Sciences, 12(13), 6382. https://doi.org/10.3390/app12136382





