A Bayesian Dynamic Inference Approach Based on Extracted Gray Level Co-Occurrence (GLCM) Features for the Dynamical Analysis of Congestive Heart Failure
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset
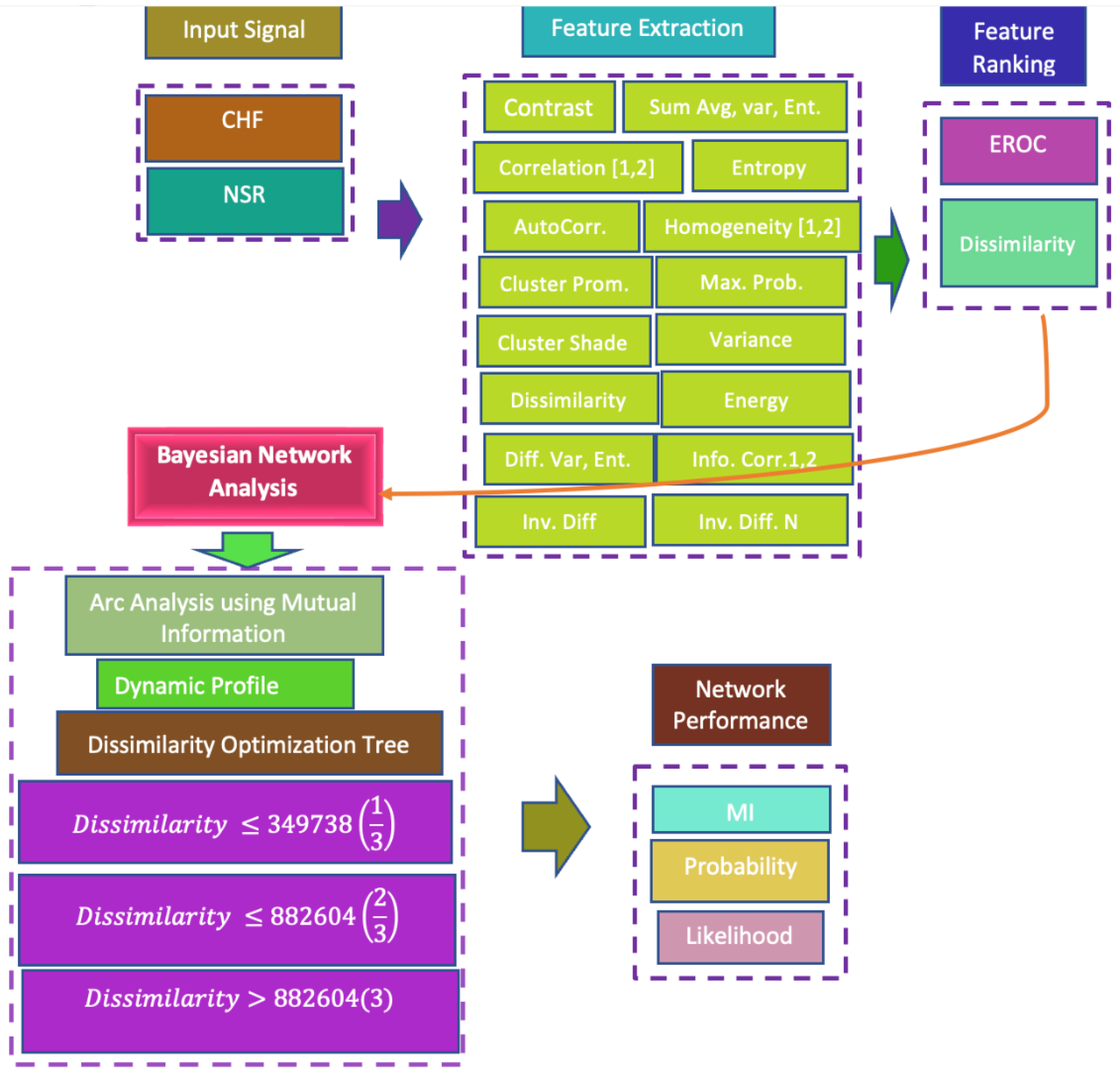
2.2. Features Extraction
2.3. Gray-Level Co-Occurrence Matrix (GLCM)
2.4. Feature Ranking Algorithms
2.5. Bayesian Inference Approach
2.6. Mutual Information (MI)
2.7. Exploratory Analysis of the Unsupervised Network
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GLCM | Gray level co-occurrence |
| HRV | Heart rate variability |
| PC | Pearson’s correlation |
| CHF | Congestive heart failure |
| NSR | Normal sinus rhythm |
| MI | Myocardial infarction |
| SCD | Sudden cardiac death |
| CAD | Computed aided diagnostic |
| ECG | Electrocardiogram |
| EMD | Empirical mode decomposition |
| LF | Low frequency |
| VLF | Very low frequency |
| HF | High frequency |
| SDNN | Standard deviation of normal-to-normal beat interval |
| LRP | Low risk patients |
| AF | Atrial fibrillation |
| RMSSD | Root mean square of successive RR differences |
| FAWT | Flexible analytic wavelet transforms |
| APEnt | Accumulated permutation entropy |
| MI | Mutual information |
| PC | Pearson’s correlation |
| KL | Kullback–Leibler |
| EROC | Empirical receiver operating characteristic curve |
| NYHA | New York Heart Association |
| MFCC | Mel frequency cepstral Coefficients |
| SIFT | Scale invariant Feature transform |
| EFDs | Elliptic Fourier descriptors |
| WPC | Wavelet phase coherence |
| DAG | Directed acyclic graph |
References
- Stein, P.K.; Kleiger, R.E.; Domitrovich, P.P.; Schechtman, K.B.; Rottman, J.N. Clinical and demographic determinants of heart rate variability in patients post myocardial infarction: Insights from the cardiac arrhythmia suppression trial (CAST). Clin. Cardiol. 2000, 23, 187–194. [Google Scholar] [CrossRef] [PubMed]
- Malliani, A.; Lombardi, F.; Pagani, M.; Cerutti, S. Power spectral analysis of cardiovascular variability in patients at risk for sudden cardiac death. J. Cardiovasc. Electrophysiol. 1994, 5, 274–286. [Google Scholar] [CrossRef] [PubMed]
- Pagani, M. Heart rate variability and autonomic diabetic neuropathy. Diabetes. Nutr. Metab. 2000, 13, 341–346. [Google Scholar] [PubMed]
- Sajadieh, A. Increased heart rate and reduced heart-rate variability are associated with subclinical inflammation in middle-aged and elderly subjects with no apparent heart disease. Eur. Heart J. 2004, 25, 363–370. [Google Scholar] [CrossRef]
- Hu, J.; Gao, J.; Tung, W.; Cao, Y. Multiscale analysis of heart rate variability: A comparison of different complexity measures. Ann. Biomed. Eng. 2010, 38, 854–864. [Google Scholar] [CrossRef]
- Liu, G.-Z.; Huang, B.-Y.; Wang, L. A wearable respiratory biofeedback system based on generalized body sensor network. Telemed. e-Health 2011, 17, 348–357. [Google Scholar] [CrossRef]
- Liu, G.-Z.; Guo, Y.-W.; Zhu, Q.-S.; Huang, B.-Y.; Wang, L. Estimation of respiration rate from three-dimensional acceleration data based on body sensor network. Telemed. e-Health 2011, 17, 705–711. [Google Scholar] [CrossRef]
- Budi Siswanto, B.; Shimokawa, H.; Samal, U.C.; Ponikowski, P.; Cowie, M.R.; Hu, S.; Rastogi, V.; AlHabib, K.F.; Anker, S.D.; Krum, H.; et al. Heart failure: Preventing disease and death worldwide. ESC Heart Fail. 2014, 1, 4–25. [Google Scholar] [CrossRef]
- Peteiro, J.; Peteiro-Vázquez, J.; Gacía-Campos, A.; García-Bueno, L.; Abugattás-de-Torres, J.P.; Castro-Beiras, A. The causes, consequences, and treatment of left or right heart failure. Vasc. Health Risk Manag. 2011, 7, 237. [Google Scholar] [CrossRef]
- Jong, T.-L.; Chang, B.; Kuo, C.-D. Optimal timing in screening patients with congestive heart failure and healthy subjects during circadian observation. Ann. Biomed. Eng. 2011, 39, 835–849. [Google Scholar] [CrossRef]
- Khaled, A.; Owis, M.I.; Mohamed, A.S.A. Detection of congestive heart failure using time-domain methods and poincar.e plot of heart rate variability signals. In Proceedings of the 3rd Cairo International Biomedical Engineering Conference, CIBEC 2006, Cairo, Egypt, 21–24 December 2006. [Google Scholar]
- Soni, J.; Ansari, U.; Sharma, D.; Soni, S. Predictive data mining for medical diagnosis: An overview of heart disease prediction. Int. J. Comput. Appl. 2011, 17, 43–48. [Google Scholar] [CrossRef]
- Falsey, A.R.; Walsh, E.E.; Esser, M.T.; Shoemaker, K.; Yu, L.; Griffin, M.P. Respiratory syncytial virus-associated illness in adults with advanced chronic obstructive pulmonary disease and/or congestive heart failure. J. Med. Virol. 2019, 91, 65–71. [Google Scholar] [CrossRef] [PubMed]
- Kaikkonen, L.; Parviainen, T.; Rahikainen, M.; Uusitalo, L.; Lehikoinen, A. Bayesian networks in environmental risk assessment: A review. Integr. Environ. Assess. Manag. 2021, 17, 62–78. [Google Scholar] [CrossRef] [PubMed]
- Kocian, A.; Massa, D.; Cannazzaro, S.; Incrocci, L.; Di Lonardo, S.; Milazzo, P.; Chessa, S. Dynamic Bayesian network for crop growth prediction in greenhouses. Comput. Electron. Agric. 2020, 169, 105167. [Google Scholar] [CrossRef]
- Amaral, C.B.D.; Oliveira, G.H.F.D.; Eghrari, K.; Buzinaro, R.; Môro, G.V. Bayesian network: A simplified approach for environmental similarity studies on maize. Crop Breed. Appl. Biotechnol. 2019, 19, 70–76. [Google Scholar] [CrossRef]
- Laurila-Pant, M.; Mäntyniemi, S.; Venesjärvi, R.; Lehikoinen, A. Incorporating stakeholders’ values into environmental decision support: A Bayesian Belief Network approach. Sci. Total Environ. 2019, 697, 134026. [Google Scholar] [CrossRef]
- Zhang, L.; Pan, Q.; Wang, Y.; Wu, X.; Shi, X. Bayesian network construction and genotype-phenotype inference using GWAS Statistics. IEEE/ACM Trans. Comput. Biol. Bioinforma. 2019, 16, 475–489. [Google Scholar] [CrossRef] [PubMed]
- Corrales, D.C.; Corrales, J.C.; Figueroa-Casas, A. Toward detecting crop diseases and pest by supervised learning. Ing. Univ. 2015, 19, 207–228. [Google Scholar] [CrossRef]
- Gandhi, N.; Armstrong, L.J.; Petkar, O. PredictingRice crop yield using Bayesian networks. In Proceedings of the 2016 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Jaipur, India, 21–24 September 2016; pp. 795–799. [Google Scholar]
- Musango, J.K.; Peter, C. A Bayesian approach towards facilitating climate change adaptation research on the South African agricultural sector. Agrekon 2007, 46, 245–259. [Google Scholar] [CrossRef]
- Ershadi, M.M.; Seifi, A. An efficient Bayesian network for differential diagnosis using experts’ knowledge. Int. J. Intell. Comput. Cybern. 2020, 13, 103–126. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.N.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.-K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [PubMed]
- Rathore, S.; Hussain, M.; Aksam Iftikhar, M.; Jalil, A. Ensemble classification of colon biopsy images based on information rich hybrid features. Comput. Biol. Med. 2014, 47, 76–92. [Google Scholar] [CrossRef]
- Ferland-McCollough, D.; Slater, S.; Richard, J.; Reni, C.; Mangialardi, G. Pericytes, an overlooked player in vascular pathobiology. Pharmacol. Ther. 2017, 171, 30–42. [Google Scholar] [CrossRef] [PubMed]
- Dheeba, J.; Albert Singh, N.; Tamil Selvi, S. Computer-aided detection of breast cancer on mammograms: A swarm intelligence optimized wavelet neural network approach. J. Biomed. Inform. 2014, 49, 45–52. [Google Scholar] [CrossRef]
- Hussain, L.; Saeed, S.; Awan, I.A.; Idris, A.; Nadeem, M.S.A.; Chaudhary, Q.-A. Detecting brain tumor using machine learning techniques based on different features extracting strategies. Curr. Med. Imaging Rev. 2019, 15, 595–606. [Google Scholar] [CrossRef] [PubMed]
- Hussain, L.; Ali, A.; Rathore, S.; Saeed, S.; Idris, A.; Usman, M.U.; Iftikhar, M.A.; Suh, D.Y. Applying Bayesian Network approach to determine the association between morphological features extracted from prostate cancer images. IEEE Access 2019, 7, 1586–1601. [Google Scholar] [CrossRef]
- Hussain, L.; Huang, P.; Nguyen, T.; Lone, K.J.; Ali, A.; Khan, M.S.; Li, H.; Suh, D.Y.; Duong, T.Q. Machine learning classification of texture features of MRI breast tumor and peri-tumor of combined pre- and early treatment predicts pathologic complete response. Biomed. Eng. Online 2021, 20, 1–23. [Google Scholar] [CrossRef]
- Hussain, L.; Ahmed, A.; Saeed, S.; Rathore, S.; Awan, I.A.; Shah, S.A.; Majid, A.; Idris, A.; Awan, A.A. Prostate cancer detection using machine learning techniques by employing combination of features extracting strategies. Cancer Biomarkers 2018, 21, 393–413. [Google Scholar] [CrossRef]
- Anjum, S.; Hussain, L.; Ali, M.; Alkinani, M.H.; Aziz, W.; Gheller, S.; Duong, T.Q. Detecting brain tumors using deep learning convolutional neural network with transfer learning approach. Int. J. Imag. Sys. Tech. 2022, 32, 307–323. [Google Scholar] [CrossRef]
- Rathore, S.; Hussain, M.; Khan, A. Automated colon cancer detection using hybrid of novel geometric features and some traditional features. Comput. Biol. Med. 2015, 65, 279–296. [Google Scholar] [CrossRef]
- Baim, D.S.; Colucci, W.S.; Monrad, E.S.; Smith, H.S.; Wright, R.F.; Lanoue, A.; Gauthier, D.F.; Ransil, B.J.; Grossman, W.; Braunwald, E. Survival of patients with severe congestive heart failure treated with oral milrinone. J. Am. Coll. Cardiol. 1986, 7, 661–670. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual comparisons by ranking methods. In Biometrics Bulletin; Springer: New York, NY, USA, 1992; Volume 1, p. 80. [Google Scholar]
- Acharya, U.R.; Fujita, H.; Sudarshan, V.K.; Bhat, S.; Koh, J.E. Application of entropies for automated diagnosis of epilepsy using EEG signals: A review. Knowl. -Based Syst. 2015, 88, 85–96. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Parvez, A.; Phadke, A.C. Efficient implementation of GLCM based texture feature computation using CUDA platform. In Proceedings of the 2017 International Conference on Trends in Electronics and Informatics (ICEI), Tirunelveli, India, 11–12 May 2017; pp. 296–300. [Google Scholar]
- Singh, G.A.P.; Gupta, P.K. Performance analysis of various machine learning-based approaches for detection and classification of lung cancer in humans. Neural Comput. Appl. 2019, 31, 6863–6877. [Google Scholar] [CrossRef]
- Nithya, R. Comparative Study on Feature Extraction. J. Theor. Appl. Infrormation Technol. 2011, 33, 7. [Google Scholar]
- Wang, H.; Khoshgoftaar, T.M.; Gao, K. A comparative study of filter-based feature ranking techniques. In Proceedings of the 2010 IEEE International Conference on Information Reuse & Integration, Las Vegas, NV, USA, 4–6 August 2010; Volume 1, pp. 43–48. [Google Scholar]
- Yu, S.; Zhang, Z.; Liang, X.; Wu, J.; Zhang, E.; Qin, W.; Xie, Y. A matlab toolbox for feature importance ranking. In Proceedings of the 2019 International Conference on Medical Imaging Physics and Engineering (ICMIPE), Shenzhen, China, 22–24 November 2019; 2019; pp. 1–6. [Google Scholar]
- Pearl, J. Fusion, propagation, and structuring in belief networks. Artif. Intell. 1986, 29, 241–288. [Google Scholar] [CrossRef]
- Bayesia, S.C. BayesiaLab7. Bayesia USA: Franklin, TN, USA, 2017. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Xiao, F.; Gao, L.; Ye, Y.; Hu, Y.; He, R. Inferring gene regulatory networks using conditional regulation pattern to guide candidate genes. PLoS ONE 2016, 11, e0154953. [Google Scholar] [CrossRef][Green Version]
- Moreno-Jiménez, E.; García-Gómez, C.; Oropesa, A.L.; Esteban, E.; Haro, A.; Carpena-Ruiz, R.; Tarazona, J.V.; Peñalosa, J.M.; Fernández, M.D. Screening risk assessment tools for assessing the environmental impact in an abandoned pyritic mine in Spain. Sci. Total Environ. 2011, 409, 692–703. [Google Scholar] [CrossRef]
- Wilhere, G.F. Using Bayesian networks to incorporate uncertainty in habitat suitability index models. J. Wildl. Manag. 2012, 76, 1298–1309. [Google Scholar] [CrossRef]

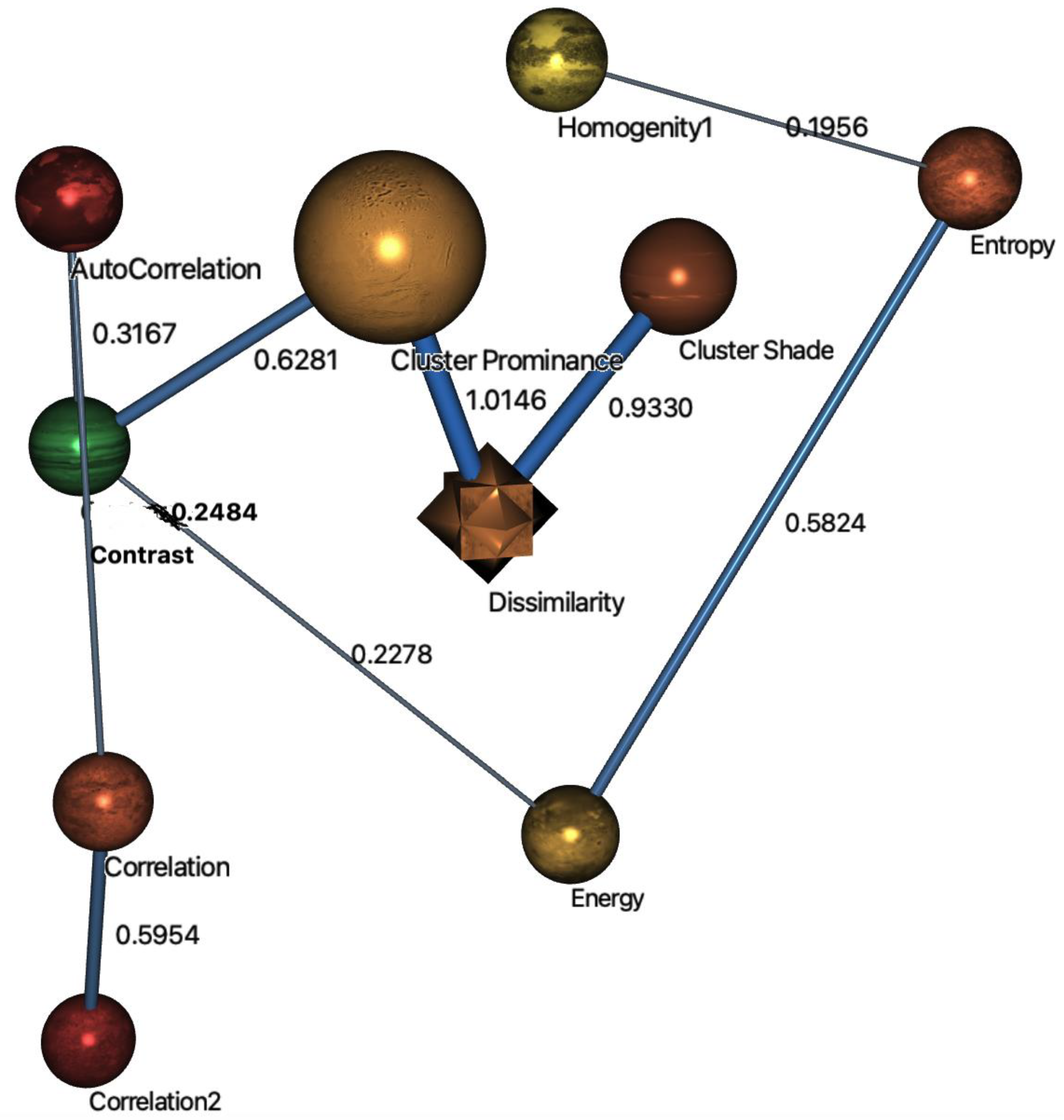

| Node | Outgoing Force | Incoming Force | Total Force |
|---|---|---|---|
| Dissimilarity | 0.9330 | 1.0146 | 1.9477 |
| Cluster prominance | 1.6428 | 0.0000 | 1.6428 |
| Contrast | 0.5446 | 0.6281 | 1.1727 |
| Cluster shade | 0.0000 | 0.9330 | 0.9330 |
| Correlation | 0.5954 | 0.2848 | 0.8802 |
| Energy | 0.5824 | 0.2278 | 0.8102 |
| Entropy | 0.1956 | 0.5824 | 0.7779 |
| Autocorrelation | 0.2848 | 0.3167 | 0.6015 |
| Correlation2 | 0.0000 | 0.5954 | 0.5954 |
| Homogenity1 | 0.0000 | 0.1956 | 0.1956 |
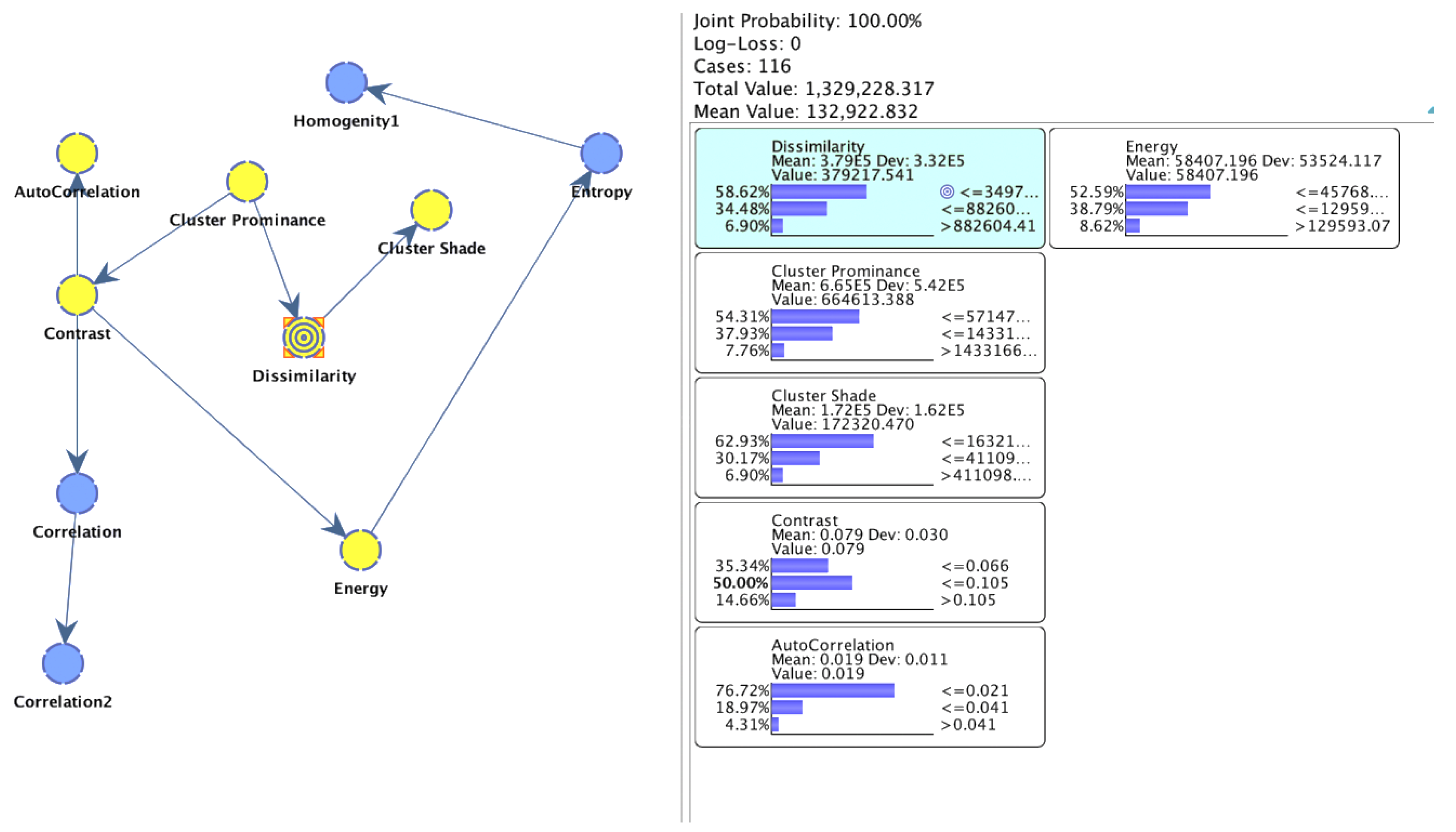
| Node | Mutual Information (MI) | Normalized MI | Relative MI | Relative Significance | p-Value |
|---|---|---|---|---|---|
| Cluster prominence | 1.0146 | 64.01% | 81.33% | 1.0000 | 0.0000 |
| Cluster shade | 0.9330 | 58.86% | 74.79% | 0.9196 | 0.0000 |
| Contrast | 0.5425 | 34.22% | 43.48% | 0.5347 | 0.0000 |
| Autocorrelation | 0.1329 | 8.38% | 10.65% | 0.1310 | 0.00026 |
| Energy | 0.0895 | 5.64% | 7.17% | 0.0882 | 0.006164 |
| Entropy | 0.0519 | 3.72% | 4.16% | 0.0512 | 0.0795 |
| Correlation | 0.0394 | 2.48% | 3.15% | 0.0388 | 0.176 |
| Correlation2 | 0.0291 | 1.83% | 2.33% | 0.0287 | 0.3218 |
| Homogenity1 | 0.0118 | 0.74% | 0.94% | 0.0116 | 0.7549 |
| Node | Binary MI | Relative Binary Significance | Binary Relative Significance | Maximum Bayes Factor | ||
|---|---|---|---|---|---|---|
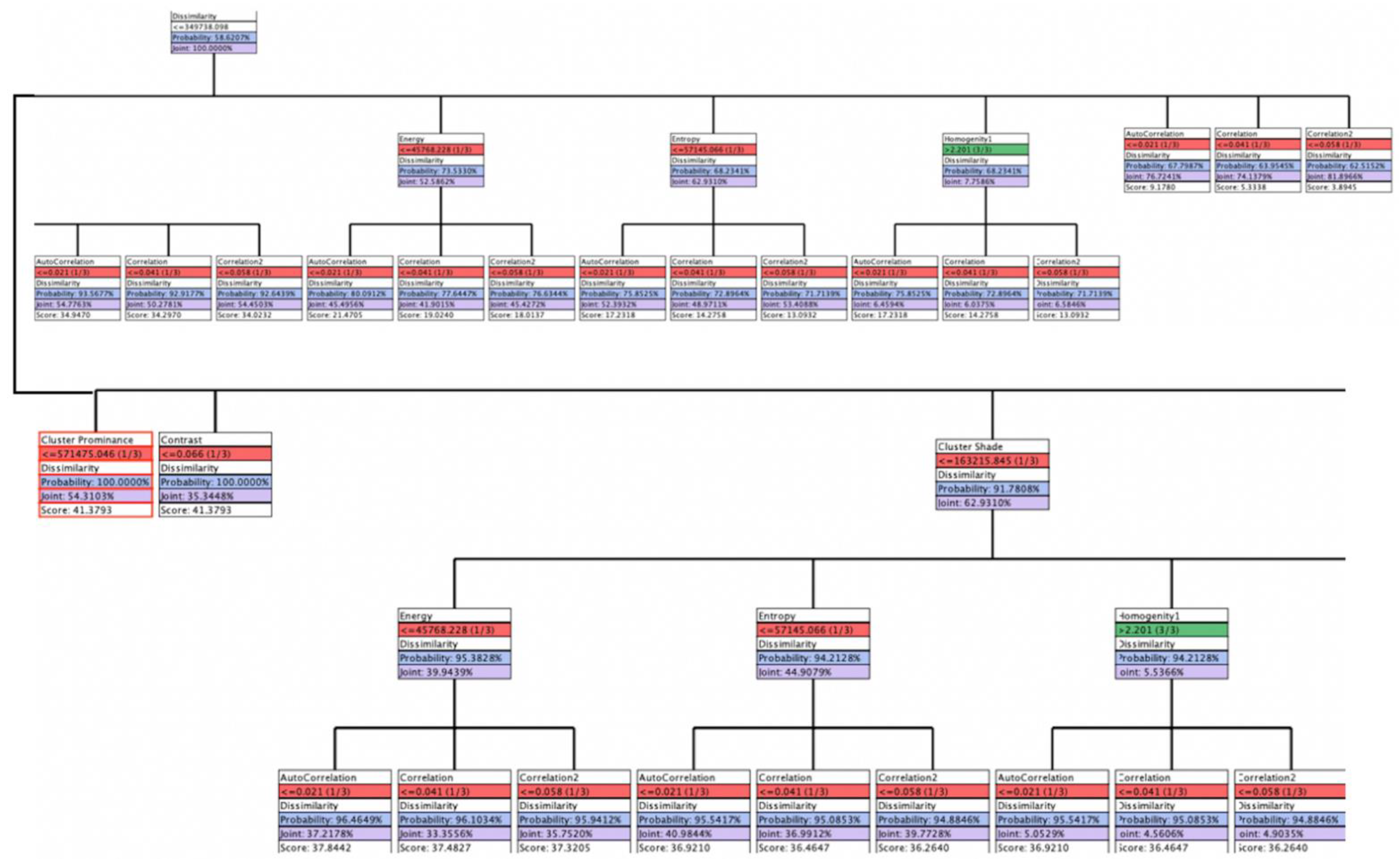
| Cluster prominence | 0.7847 | 80.19% | 1.000 | ≤571,475 (1/3) | 92.64% | 1.7059 |
| Cluster shade | 0.6640 | 67.86% | 0.8462 | ≤163,215 (1/3) | 98.52% | 1.5657 |
| Contrast | 0.3957 | 40.44% | 0.5043 | ≤0.068 (1/3) | 60.29% | 1.7059 |
| Autocorrelation | 0.0839 | 8.57% | 0.1069 | ≤0.021 (1/3) | 88.73% | 1.1566 |
| Energy | 0.0802 | 8.19% | 0.1021 | ≤45,768 (1/3) | 65.96% | 1.2544 |
| Entropy | 0.0481 | 4.92% | 0.0614 | ≤57,145 (1/3) | 73.25% | 1.1640 |
| Correlation | 0.0279 | 2.85% | 0.0356 | ≤0.041 (1/3) | 80.88% | 1.0910 |
| Correlation2 | 0.0215 | 2.19% | 0.0274 | ≤0.058 (1/3) | 87.33% | 1.0664 |
| Homogenity1 | 0.0112 | 1.14% | 0.0143 | >2.201 (1/3) | 9.03% | 1.1640 |
| Node | Binary MI | Relative Binary Significance | Binary Relative Significance | Maximum Bayes Factor | ||
|---|---|---|---|---|---|---|
| Cluster prominence | 0.6966 | 74.95% | 1.000 | ≤1,433,166.15 (2/3) | 97.50% | 2.5705 |
| Cluster shade | 0.6150 | 66.17% | 0.84828 | ≤411,098.14 (2/3) | 85.00% | 2.8171 |
| Contrast | 0.2993 | 32.20% | 0.4297 | ≤0.105 (2/3) | 84.20% | 1.6841 |
| Energy | 0.0441 | 4.74% | 0.0633 | >129,593.07 (2/3) | 11.90% | 1.3809 |
| Entropy | 0.0259 | 2.78% | 0.0372 | >156,446.10 (3/3) | 5.92% | 1.3751 |
| Autocorrelation | 0.0160 | 1.71% | 0.0229 | >0.041 (3/3) | 6.73% | 1.5628 |
| Correlation | 0.0069 | 0.74% | 0.0100 | >0.089 (2/3) | 13.01% | 1.3722 |
| Homogenity1 | 0.0063 | 0.67% | 0.0090 | ≤1.241 (1/3) | 56.32 | 1.1265 |
| Correlation2 | 0.0055 | 0.58% | 0.0078 | >0.124 (3/3) | 8.28% | 1.3722 |
| Node | Binary MI | Relative Binary Significance | Binary Relative Significance | Maximum Bayes Factor | ||
|---|---|---|---|---|---|---|
| Cluster shade | 0.3621 | 100% | 1.000 | >411,098 (3/3) | 100% | 14.500 |
| Cluster prominence | 0.3230 | 89.21% | 0.8922 | >1,433,166 (3/3) | 100% | 12.888 |
| Contrast | 0.2159 | 59.62% | 0.5962 | >0.105 (3/3) | 100% | 6.8235 |
| Autocorrelation | 0.0907 | 25.06% | 0.2506 | ≤0.041 (2/3) | 76.47% | 4.032 |
| Energy | 0.0287 | 7.94% | 0.0794 | >129,593 (3/3) | 29.41% | 3.411 |
| Correlation | 0.0241 | 6.65% | 0.0665 | >0.089 (3/3) | 25.75% | 2.716 |
| Correlation2 | 0.0171 | 4.73% | 0.0473 | >0.124 (3/3) | 16.39% | 2.716 |
| Entropy | 0.0154 | 4.25% | 0.0426 | >156,446 (3/3) | 12.81% | 2.972 |
| Homogenity1 | 0.0033 | 0.90% | 0.0090 | ≤1.241 (1/3) | 62.03% | 1.240 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eltahir, M.M.; Hussain, L.; Malibari, A.A.; K. Nour, M.; Obayya, M.; Mohsen, H.; Yousif, A.; Ahmed Hamza, M. A Bayesian Dynamic Inference Approach Based on Extracted Gray Level Co-Occurrence (GLCM) Features for the Dynamical Analysis of Congestive Heart Failure. Appl. Sci. 2022, 12, 6350. https://doi.org/10.3390/app12136350
Eltahir MM, Hussain L, Malibari AA, K. Nour M, Obayya M, Mohsen H, Yousif A, Ahmed Hamza M. A Bayesian Dynamic Inference Approach Based on Extracted Gray Level Co-Occurrence (GLCM) Features for the Dynamical Analysis of Congestive Heart Failure. Applied Sciences. 2022; 12(13):6350. https://doi.org/10.3390/app12136350
Chicago/Turabian StyleEltahir, Majdy M., Lal Hussain, Areej A. Malibari, Mohamed K. Nour, Marwa Obayya, Heba Mohsen, Adil Yousif, and Manar Ahmed Hamza. 2022. "A Bayesian Dynamic Inference Approach Based on Extracted Gray Level Co-Occurrence (GLCM) Features for the Dynamical Analysis of Congestive Heart Failure" Applied Sciences 12, no. 13: 6350. https://doi.org/10.3390/app12136350
APA StyleEltahir, M. M., Hussain, L., Malibari, A. A., K. Nour, M., Obayya, M., Mohsen, H., Yousif, A., & Ahmed Hamza, M. (2022). A Bayesian Dynamic Inference Approach Based on Extracted Gray Level Co-Occurrence (GLCM) Features for the Dynamical Analysis of Congestive Heart Failure. Applied Sciences, 12(13), 6350. https://doi.org/10.3390/app12136350






