A Method of Multi-Objective Optimization and Multi-Attribute Decision-Making for Huangjinxia Reservoir

Abstract

The objectives of flood control, power generation, water supply and ecology for reservoir operation are neither completely coordinated nor completely opposed, and its optimal operation and decision-making is very complicated. This study proposed a method of multi-objective optimization and multi-attribute decision making for reservoir operation (MODRO). The correlation analysis method was used to analyze the competitive relationship among the extracted objectives, and the multi-objective optimal operation model was constructed. The NSGA-II-SEABODE algorithm was applied to solve the MODRO problem. The objective extraction, model construction, optimization solution and scheme selection were coupled to form a multi-objective optimization and multi-attribute decision making method with the whole process of “Objective-Modeling-Optimization-Selection”. Huangjinxia Reservoir, which is located in Shaanxi, China, was selected as the case study. The results show that: (1) Quantifying the degree of conflict among objectives makes the construction of the multi-objective optimal operation model more reasonable. (2) The NSGA-II-SEABODE algorithm are used to obtain the decision-making scheme, which provides decision-making basis for managers. (3) For Huangjinxia Reservoir, water diversion is negatively related to power generation and ecology, and power generation is positively related to ecology. The results can promote the efficient utilization of water resources, improve the comprehensive benefits of reservoirs, and provide decision-making support for actual reservoir operation.

1. Introduction

Water resources are indispensable basic resources for the development of economy, society and ecology. To fully develop, utilize and effectively manage water resources, more than 58,000 reservoirs with dam height of more than 15 m had been built in the world by 2020, of which China accounts for about 40.6% of the total reservoirs in the world [1]. Reservoirs, as the core of the natural water cycle and social water cycle, play an increasingly important role in the complex water resources system. However, with the rapid development of social economy and the continuous improvement of the development and utilization of water resources, the competition among industrial water use, agricultural water use, power generation water use and eco-environmental water use in the river is more and more fierce, and the contradiction among multi-objectives is very prominent. More and more water conservancy authorities and researchers have begun to study reservoir operation modes that not only meet the benefits of flood control and prospering, but also meet the ecological benefits, so as to achieve a balance of interests in water supply, power generation, ecology, etc., and make the comprehensive benefits of water resources the best [2,3]. However, for reservoir operation, the objectives are neither completely coordinated nor completely opposed. Regardless of the number of objectives, the ultimate purpose is to obtain the decision-making scheme and provide decision support for the management department. Therefore, its essence is a multi-objective optimization and decision-making for the reservoir operation (MODRO) problem.

At present, multi-objective optimization and decision-making for reservoir operation generally includes three parts: model construction, optimization solution and scheme selection. Among them, model construction is the carrier and framework system for realizing the operation objectives and constraints, which provides mathematical possibilities for seeking multi-objective optimal solutions. In recent years, most studies have focused on two-objective and three-objectives model construction, such as water supply and power generation [4,5], power generation and ecology [6,7], flood control and power generation [8,9], water supply and power generation and ecology [10,11,12]. For the MODRO problem, there are often three possible relationships between objectives: negative correlation, positive correlation and uncorrelation. As the number of objectives increases, there may be more conflicts among objectives, and the difficulty of the problem increases. However, the existing research methods are too subjective and arbitrary for the selection of objectives, which cannot objectively reflect the correlation among objectives. For multi-objective optimization problems with three or more objectives, the results are not satisfactory.

Optimization solution is a necessary means to complete functions of the model described above. At present, optimization algorithms mainly include traditional optimization algorithms and modern intelligent algorithms. Among them, traditional optimization algorithms include linear programming (LP) [13,14], nonlinear programming (NP) [15], dynamic programming (DP) [16,17] and large-scale system decomposition coordination (LSSDC) [18]. These methods can quickly solve small-scale optimization problems, but are not ideal for large-scale optimization problems. With the development of economy and society, the degree of exploitation and utilization of water resources is getting higher and higher, and the scale of water resources regulation and storage projects is getting bigger and bigger, which puts forward higher requirements for reservoir optimal operation. Modern intelligent optimization algorithms are widely used in reservoir optimal operation, such as genetic algorithm (GA) [19,20], particle swarm optimization (PSO) [21,22], artificial neural network (ANN) [23], simulated annealing algorithm (SA) [24] and ant colony optimization (ACO) [25,26]. In addition, new swarm intelligence optimization algorithms continue to emerge, such as wolf pack algorithm (WPA) [27], differential evolution algorithm (DEA) [28,29] and artificial bee colony algorithm (ABCA) [30]. In view of the flexibility of intelligent algorithms to solve optimization problems, many researchers have combined different intelligent algorithms and achieved good results in reservoir operation [31,32,33]. It can be seen that the current research on the optimization solution method has been relatively mature, and due to the complexity of the MODRO problem, there is no universal solution method, and each method has its applicable conditions.

After solving by multi-objective optimization algorithm, it is no longer a single optimal solution, but a series of alternative schemes. For decision makers, it is necessary to make a quick judgment on the current operation situation and select the decision-making scheme that is most in line with the actual reservoir operation. Scheme selection belongs to the decision-making problem. Currently, the most widely used methods are entropy weight method [34], fuzzy set theory [35], TOPSIS decision-making method [36], vague set theory [37], interval-valued [38] and grey relational decision-making [39]. All these methods need to normalize the alternative set to obtain the initial weight coefficients or membership degrees of evaluation indexes. Considering the subjective preferences of decision makers, the objective weights or membership degrees are corrected and processed. In the decision-making process, decision makers are often affected by subjective factors, of which it is difficult to make scientific judgments. To solve this problem, Kang et al. [40] proposed an approach of successive elimination of alternative schemes based on the k-order and p-degree of efficiency (SEACODE). Compared with the traditional methods, SEABODE method can directly select the scheme from the decision matrix and gradually eliminate the inferior scheme. There is no need to standardize the decision matrix or calculate the attribute weight, thus reducing the influence of subjective factors.

The existing studies have made significant achievements in model construction, optimization solution and scheme selection. However, when constructing the model, the degree of conflict between objectives is not quantified, and there are redundant objectives, resulting in a large number of false non-dominated solutions; Secondly, it is ignored that the essence of reservoir operation is a complex decision-making problem with multi-objectives, multi-stages and multi-attributes, which needs to be studied from the perspective of decision-making and obtain a reasonable and feasible decision-making scheme through scientific methods. Therefore, this study proposed a method of multi-objective optimization and multi-attribute decision making for reservoir operation coupling the whole process of “Objective-Modeling-Optimization-Selection”. Taking Huangjinxia Reservoir as an example, the multi-objective optimal operation and decision-making is carried out to verify the scientificity and feasibility of the proposed method.

The rest of this paper is organized as follows. Section 2 describes the general situation of the Huangjinxia Reservoir, selection of typical years and water demand. Section 3 analyzes the objective correlation, determines the objective functions and constructs the multi-objective optimal operation model. Section 4 introduces the NSGA-II-SEABODE algorithm, presents the procedure of application of NSGA-II-SEABODE for the MODRO problem and selects the evaluation indexes of schemes. Section 5 compares the Pareto solution sets in different typical years and analyzes and discusses the decision-making schemes in different typical years. Section 6 concludes the paper.

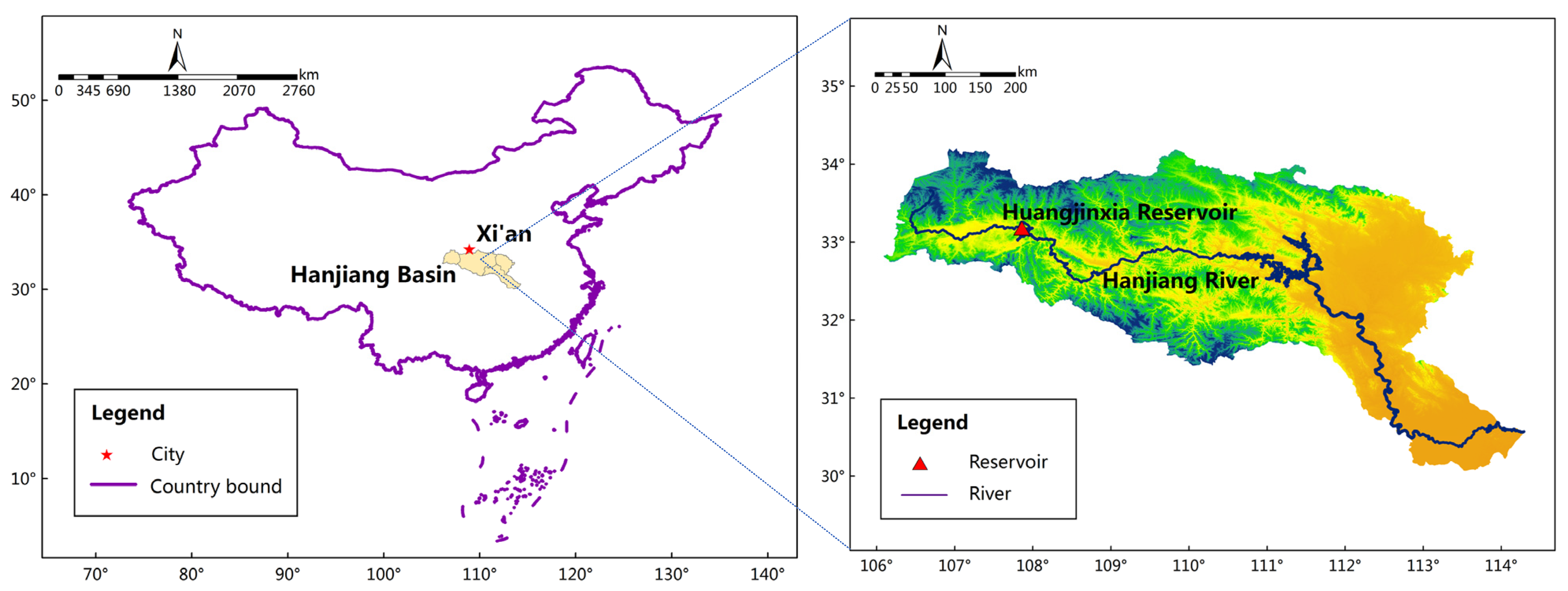
2. Study Area

2.1. Project Overview

Shaanxi province in China straddles the Yellow River and the Yangtze River. The North of Qinling Mountains is the Yellow River and the South is the Yangtze River. The Hanjiang River, the largest tributary of the Yangtze River, originates from the south of Qinling Mountains in Shaanxi Province, flows through Shaanxi and Hubei provinces and flows into the Yangtze River in Wuhan City, with a total length of 1577 km and a drainage area of 159,000 km². The annual average rainfall of the basin is 600~1300 mm, the annual average runoff is about 60 billion m³ and the total water resources are abundant. The Weihe River, the largest tributary of the Yellow River, originates in Weiyuan County, Gansu province, flowing through Gansu, Ningxia and Shaanxi provinces, and flows into the Yellow River in Tongguan. The total length of the Weihe River is 818 km, of which the length in Shaanxi is 502 km. The total area of the basin is 135,000 km², of which the area in Shaanxi is 67,100 km². The Weihe River is located in arid and semi-arid areas of China, the total amount of water resources is scarce. However, the population of the region is dense, and the economy is developed. To meet the water demand for life and production, the water diversion along the Weihe River is increasing, resulting in the contradiction between supply and demand of water resources.

The Hanjiang-to-Weihe River water diversion project is a cross-basin water diversion project in Shaanxi province. The water quantity of Hanjiang River is transferred to the Weihe River in Guanzhong area through the super-long water-conveyance tunnel through Qinling Mountains, which is an important engineering measure to alleviate the water shortage problems in cities and industries along the Weihe River in Guanzhong area. The Hanjiang-to-Weihe River water diversion project includes the Huangjinxia Reservoir and the Sanhekou reservoir. The Huangjinxia Reservoir is the main water source of the water diversion project, which is responsible for alleviating the water shortage in the Weihe River, improving the ecological environment in the middle and lower reaches of the Weihe River, and supporting the economic and social development of the Guanzhong Plain.

This paper took the Huangjinxia Reservoir as the research object. The reservoir is located in the upper reaches of the Hanjiang River, as shown in Figure 1. The main characteristic parameters are shown in

Table 1. Characteristic parameters of Huangjinxia Reservoir and pump station.

Parameter Category	Numerical Value
Dead water level/m	440
Normal pool level/m	450
Flood control level/m	448
Total reservoir storage/108 m3	2.29
Effective storage capacity/108 m3	0.92
Installed capacity/MW	135
Guaranteed output/MW	8.6
Installed capacity of pump station/MW	129.5
Pumping flow of pump station/(m3/s)	70
Ecological flow/(m3/s)	25
Design flow of fishway/(m3/s)	1.5 1

¹ The operation time of fishway is from April to July, and the design flow of fishway is included in the ecological flow.

. After the impoundment of the Huangjinxia Reservoir, the water is extracted from the reservoir by the Huangjinxia pump station to supply water for the Weihe River. The Huangjinxia Reservoir is a typical multi-objective reservoir, which not only undertakes the water diversion task, but also takes into account the power generation and the ecological water demand of the downstream river. The operation period of the reservoir is from July to June the next year. According to the water diversion plan, the short-term water diversion in 2025 is 1 billion m³ and the long-term water diversion in 2030 is 1.5 billion m³. This paper only discusses the scenario of water diversion of 1.5 billion m³ in 2030.

2.2. Selection of Typical Years and Water Demand Analysis

There are no measured hydrological data at the Huangjinxia dam site of Hanjiang River. Yangxian hydrological station is located at 72 km upstream of the dam, with a controlled watershed area of 14,192 km². In this paper, the section flow of Yangxian hydrological station was taken as the inflow of Huangjinxia Reservoir. Through the hydrologic frequency analysis of the monthly average flow data of Yangxian hydrological station from 1967 to 2014, the designed runoff under 95%, 75%, 50%, 25% and 5% inflow frequencies were 1.299 billion m³, 3.327 billion m³, 4.799 billion m³, 7.449 billion m³ and 11.007 billion m³, respectively.

According to the principle of minimum root mean square error between designed runoff and measured runoff, July 1967 to June 1968 was selected as an extraordinarily dry year under 95% inflow frequency, July 1972 to June 1973 as a dry year under 75% inflow frequency, July 2001 to June 2002 as a normal year with 50% inflow frequency, July 1984 to June 1985 as a wet year under 25% inflow frequency and July 1983 to June 1984 as an extraordinarily wet year under 5% inflow frequency. The natural runoff processes in different typical years are shown in Figure 2. According to the water diversion plan, the water diversion volume of the Hanjiang-to-Weihe water diversion project will be 1.5 billion m³ by 2030. The water demand processes in the water receiving area are relatively stable, and are mainly urban domestic water use, industrial and commercial enterprises water use. Therefore, the monthly average water demand flow is 47.53 m³/s.

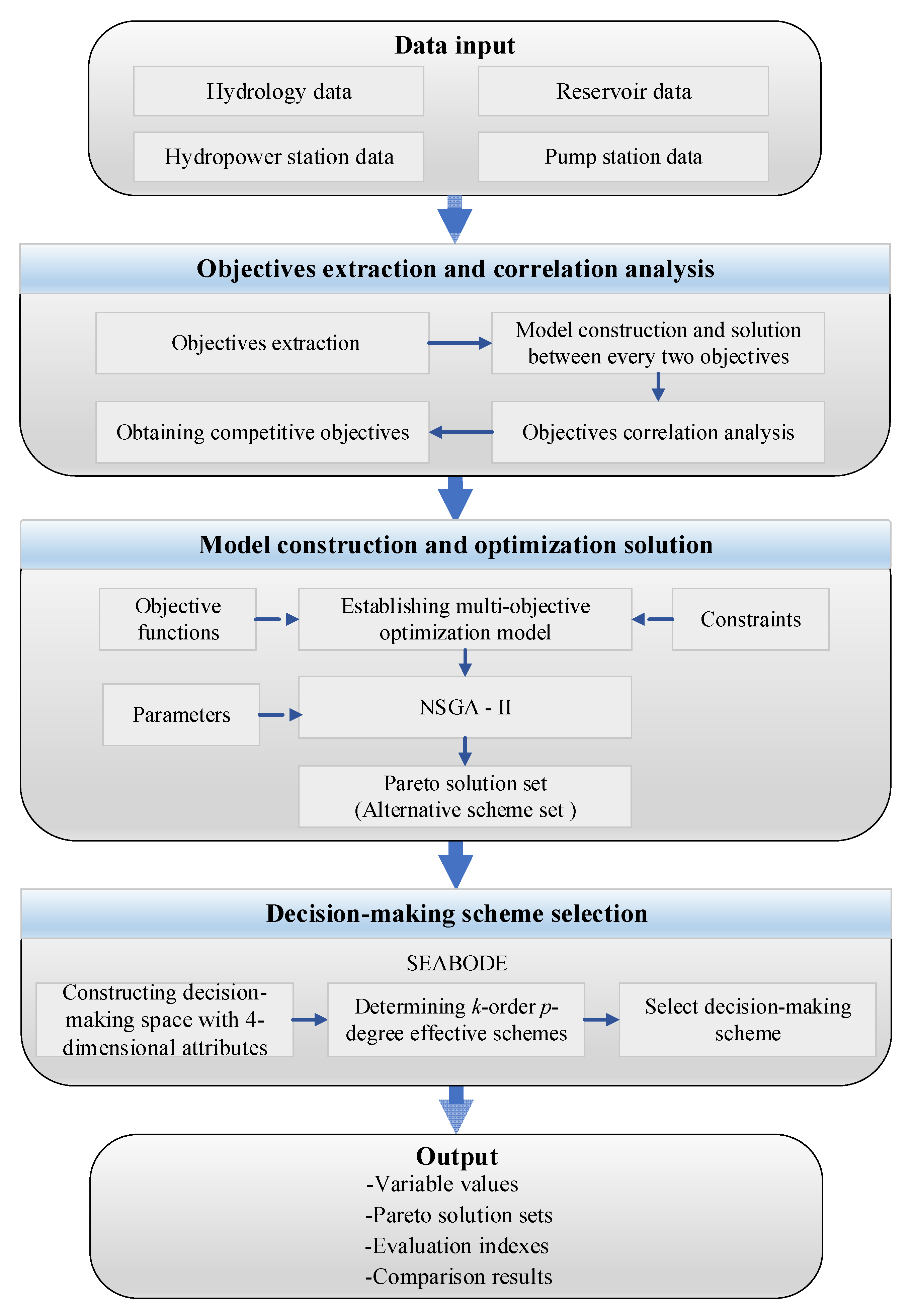
3. Model Construction

3.1. Objective Functions

3.1.1. Objective Extraction

The Huangjinxia Reservoir undertakes multi-objective such as water diversion, power generation, flood control and ecology, among which the flood control objective can be met by the water level constraints of the reservoir in flood season. This paper mainly extracted the water diversion objective, power generation objective and ecology objective and analyzed the correlation between these three objectives before constructing the multi-objective optimal operation model.

1. Water diversion objective: maximum water diversion (Equation (1))

$$MaxW={{\displaystyle \sum }}_{t=1}^T{Q}_g\left(t\right)\Delta t,t=1, 2,\dots ,T$$

(1)

where W is the total water diversion; t is the index of operational periods; Δt is the duration of each period; Q_g(t) is the water diversion flow during each period Δt; T is the total number of operational periods.

2. Power generation objective: maximum power generation (Equation (2))

$$MaxE={{\displaystyle \sum }}_{t=1}^{T}K{Q}_f\left(t\right)H\left(t\right)\Delta t,t=1, 2,\dots ,T$$

(2)

where E is the total power generation; K is the power output coefficient; Q_f(t) is the flow passing through the hydraulic turbine during each period; H (t) is the power generation head during each period.

3. Ecology objective: minimum ecological AAPFD value (Equation (3))

It is generally believed that the river ecosystem is in the best state under the condition of natural inflow. For the river affected by reservoir operation, the degree of ecological damage downstream of the river is usually measured by the difference between outflow of reservoir and natural inflow [41]. At present, the most used method is to calculate the amended annual proportion flow deviation (ecological AAPFD value). The smaller the AAPFD value, the better the river ecological environment [42]. The AAPFD value is calculated as follows in Equation (3):

$$MinR={\left[{{\displaystyle \sum }}_{t=1}^T{\left(\frac{Q_t-Q_t^n}{ \overline{Q_t^n}}\right)}^2\right]}^{0.5}, t=1, 2,\dots ,T$$

(3)

where R is the ecological AAPFD value; Q_t is the outflow of the reservoir after operation during each period; $Q_t^n$ is the natural inflow during each period; $\overline{Q_t^n}$ is the average of natural inflow during the operational period.

The constraints mainly include water balance constraint, pumping flow constraint of pump station, reservoir water level constraint, power output constraint and variable non-negative constraint.

3.1.2. Correlation Analysis

The multi-objective optimization problem is a competitive game among objectives in essence. Therefore, when constructing the model, it is necessary to analyze the correlation between every two objectives, judge the competitive relationship between objectives and eliminate the objectives that do not meet the conditions or transform them into constraints. In this paper, the inflow data of the extraordinarily dry year under 95% inflow frequency and dry year under 75% inflow frequency were selected, and the NSGA-II was used to solve the double-objective optimal operation model with water diversion and power generation, water diversion and ecology, power generation and ecology as the objective functions, respectively, so as to explore the competitive relationship between every two objectives. The results are shown in Figure 3 and Figure 4.

It can be seen that there was an obvious competitive relationship between the water diversion objective and the power generation objective. The relationship between total water diversion and total power generation was approximately nonlinear in extraordinarily dry year: y = −0.0205x² + 0.1355x + 0.5996. The relationship between total water diversion and total power generation was approximately nonlinear in dry year: y = −0.0133x² + 0.1357x + 1.9398. In addition, the correlation coefficients of total water diversion and total power generation in extraordinarily dry year and dry year were −0.968 and −0.989, respectively, and their absolute values were both greater than the critical correlation coefficient 0.267 under the reliability level of 0.01. Therefore, the water diversion objective has a negative correlation with the power generation objective. Further analysis showed that the total water diversion and the ecological AAPFD value were positively correlated in the extraordinarily year and dry year, and the correlation coefficients were 0.984 and 0.972, respectively. The larger the ecological AAPFD value, the worse the river ecology. Therefore, the water diversion objective and the ecological objective were negatively correlated. Similarly, the power generation objective was positively correlated with the ecological objective.

Compared with the power generation objective, the ecological objective of Huangjinxia Reservoir is secondary. Therefore, this paper selected the maximum water diversion and the maximum power generation as the objective functions and constructed the multi-objective optimal operation model for Huangjinxia Reservoir.

3.1.3. Objective Determination

According to the correlation analysis results of the above operation objectives, the objective functions of multi-objective optimal operation model for Huangjinxia Reservoir can be constructed as follows:

4. Water diversion objective: maximum water diversion (Equation (4))

$$MaxW={{\displaystyle \sum }}_{t=1}^T{Q}_g\left(t\right)\Delta t,t=1, 2,\dots ,T$$

(4)

where W is the total water diversion; $t$ is the index of operational periods; $\Delta t$ is the duration of each period; $Q_g\left(t\right)$ is the water diversion flow during each period $\Delta t$; $T$ is the total number of operational periods.

5. Power generation objective: maximum power generation (Equation (5))

$$MaxE={{\displaystyle \sum }}_{t=1}^{T}K{Q}_f\left(t\right)H\left(t\right)\Delta t,t=1, 2,\dots ,T$$

(5)

where $E$ is the total power generation; $K$ is the power output coefficient; $Q_f\left(t\right)$ is the flow passing through the hydraulic turbine during each period; $H\left(t\right)$ is the power generation head during each period.

3.2. Constraints

6. Water balance constraint (Equation (6)):

$$V_{t+1}=V_t+\left(I_t-Q_t\right)\mathsf{\Delta }t$$

(6)

where $V_{t+1}$ and $V_t$ are the final and initial reservoir storage during each period $\Delta t$; $I_t$ is the inflow of the reservoir during each period; $Q_t$ is the outflow of the reservoir during each period.

7. Water level constraint (Equation (7)):

$$Z_{t+1,min}\le Z_{t+1}\le Z_{t+1,max}$$

(7)

where $Z_{t+1,min}$ and $Z_{t+1,max}$ are the lower limit and upper limit of water levels allowed during each period; $Z_{t+1,min}$ corresponds to the dead water level of the reservoir; $Z_{t+1,max}$ corresponds to the flood control water level of the reservoir in the flood periods, while it is the normal pool level in other periods.

8. Power output constraint (Equation (8)):

$$N_{t,min}\le N_t\le N_{t,max}$$

(8)

where $N_{t,min}$ is the minimum output during each period; $N_{t,max}$ is the maximum output during each period; $N_t$ is the output during each period.

9. Pumping flow constraint of pump station (Equation (9)):

$$Q_{g,t}\le Q_{g,max}$$

(9)

where $Q_{g,t}$ is the pumping flow of the pump station during each period; $Q_{g,max}$ is the maximum pumping flow of the pump station.

10. Ecological flow constraint (Equation (10)):

$$Q_t\ge Q_{e,t}$$

(10)

where $Q_t$ is the outflow of reservoir during each period; Q_e,t is the ecological water demand during each period.

11. Non-negative constraint: all variables mentioned above are positive.

4. Model Solving

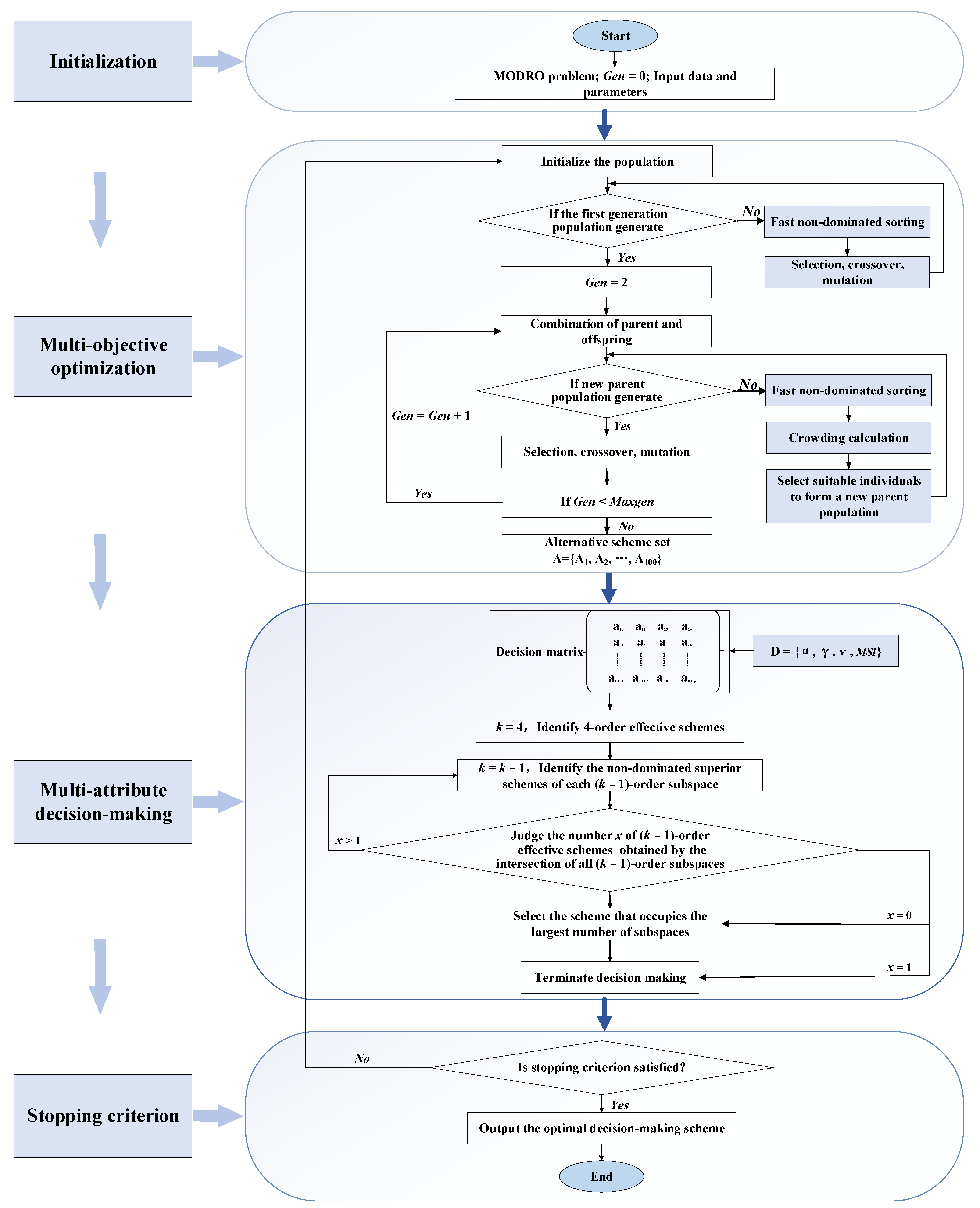
4.1. NSGA-II-SEABODE

In order to solve the MODRO problem, this paper established a solution algorithm of multi-objective optimization and multi-attribute decision making (NSGA-II-SEABODE) which coupled the classical multi-objective optimization algorithm with the approach of multi-attribute decision making. The general idea of the NSGA-II-SEABODE algorithm is: firstly, the non-dominated sorting genetic algorithm II (NSGA-II) is used to solve the multi-objective optimization problem to obtain the alternative scheme set (Pareto solution set). Then, the approach of successive elimination of alternative schemes based on the k-order and p-degree of efficiency (SEABODE) is used to seek the optimal decision-making scheme in the alternative scheme set. In general, multi-attribute decision making processes need to normalize the decision matrix and determine the weight coefficient of the evaluation indexes, which is more or less subjective, and the final decision scheme is greatly affected by the subjectivity of the decision-maker. To solve this problem, the approach of SEABODE adopted in this paper does not need to normalize the decision matrix or determine the weight of attributes, thus reducing the influence of subjective factors.

The simplified flow chart of the NSGA-II-SEABODE algorithm is shown in Figure 5. In the initialization stage, the data, parameters and studied problem are input. In the multi-objective optimization stage, the NSGA-II is used to solve the above model, and alternative scheme set A is obtained through the main steps of fast non-dominated sorting, crowding calculation and elite selection strategy and so on. In the multi-attribute decision stage, the decision-making space with 4-dimensional attributes (denoted by D = {$\alpha$, $\gamma$, $\nu$, $WSI$}) is constructed to make decision on alternative scheme set A. Among them, $\alpha$ is reliability of water diversion, $\gamma$ is recoverability of insufficient water diversion, $\nu$ is water shortage depth, and $WSI$ is water shortage index. Starting from k = 4, identify 4-order effective schemes in decision-making space with 4-dimensional attributes. By that analogy, k = k − 1, identify the non-dominated superior schemes of each (k − 1)-order subspace, and the intersection of all subspaces is the (k − 1)-order effective schemes. Judge whether the program terminates or not according to the number of the effective schemes x. The terminate condition is finally satisfied and the decision-making completed.

4.2. Application of NSGA-II-SEABODE for the MODRO Problem

The NSGA-II-SEABODE algorithm was applied to the MODRO problem of Huangjinxia Reservoir, the established objective functions and constraints of the MODRO problem were added into the algorithm. This paper selected five typical years for calculation, i.e., extraordinarily dry year (p = 95%), dry year (p = 75%), normal year (p = 50%), wet year (p = 25%) and extraordinarily wet year (p = 5%). The basic parameters of the algorithm are set as follows: the population size is N, the maximum iteration times is Maxgen, the crossover probability is pc, the mutation probability is pm, the crossover distribution index is ${\eta }_c$, the mutation distribution index is ${\eta }_m$, and the operational periods are 12 months. Taking water levels as the decision variables, $N$ individuals are randomly generated within the feasible ranges of water levels (upper and lower limits of water level). Through a series of steps, mainly including initialization, multi-objective optimization, multi-attribute decision making and stopping criteria, so repeatedly, until the stopping criterion is satisfied. The specific steps of NSGA-II-SEABODE are shown in Algorithm 1.

Algorithm 1: NSGA-II-SEABODE

Input: The MODRO problem, constraints, decision variables (water levels), population size $N$, maximum iteration times $Maxgen$, crossover probability $pc$, mutation probability $pm$, cross distribution index ${\eta }_c$, mutation distribution index ${\eta }_m$.

Output:$\left\{X^1,\cdots ,X^N\right\}$ and $\left\{S^1,\cdots ,S^N\right\}\leftarrow$ Final water levels and decision-making scheme.

Step 1: Initialization

1.1 Setting parameters: N = 100, Maxgen = 2000, pc = 0.9, pm = 0.08, ${\eta }_c$ = 20, ${\eta }_m$ = 20, Gen = 0. 1.2 $\left\{X^1,\cdots ,X^N\right\}\leftarrow$ Initialization population $P_0$ randomly.

Step 2: Multi-objective optimization

2.1 Non-dominated sorting of initialized population $P_0$, select individuals with good fitness. Perform genetic operations to generate the first-generation subgroup $Q_0$.

2.2 Gen = 2, intermediate population $R_t=P_t\cup Q_t \leftarrow$ Combine parent population with offspring population.

2.3 New parent population $P_{t+1}=R_t\left[0:N\right]\leftarrow$ Fast non-dominated sorting and congestion calculation for $R_t$, select individuals with good fitness. 2.4 New offspring population $\leftarrow$ Perform genetic operations. 2.5 If $Gen=Maxgen$, $A=\left\{A_1,\cdots ,A_{100}\right\}\leftarrow$ Obtain alternative scheme set; else $Gen=Gen+1$, go to Step 2.2.

Step 3: Multi-attribute decision making

3.1 Decision matrix $\leftarrow D=\left\{\alpha ,\gamma ,\nu ,MSI\right\}$ and $A=\left\{A_1,\cdots ,A_{100}\right\}$.

3.2 $k$ = 4, identify 4-order effective scheme set in the 4-dimensional attribute space {$\alpha ,\gamma ,\nu ,MSI$}.

3.3 $k$ = $k$ − 1, identify non-dominated superior schemes in each ($k$ − 1)-order subspace; then identify the number $x$ of (k − 1)-order effective schemes obtained by the intersection of all ($k$ − 1)-order subspaces.

3.4 If x > 1, go to Step 3.3; else if $x$ = 1, the scheme is directly output as the final decision-making scheme $\left\{S^1,\cdots ,S^N\right\}$; else $x$ = 0, then the scheme that occupies the largest number of subspaces is selected. 3.5 Terminate decision making. Step 4: Stopping criteria If the stopping criterion is satisfied, stop; else go to Step 2.

4.3. Evaluation Indexes Selection

In order to seek the optimal decision-making scheme, four evaluation indexes are selected to construct the decision-making space with 4-dimensional attributes and evaluate the alternative schemes in different typical years, which includes reliability of water diversion ($\alpha$), recoverability of insufficient water diversion ($\gamma$), water shortage depth (ν) and water shortage index ($WSI$). The calculation method of each index is as follows:

(1) Reliability of water diversion ($\alpha$): The index represents the ratio of the number of periods in which the water diversion meets the user’s needs to the total number of operational periods, and reflects the guaranteed degree of water diversion. The index is a maximized type index. The greater the value, the better. The calculation formula is as follows in Equations (11) and (12):

$$\alpha =\frac{{{\displaystyle \sum }}_{t=1}^T{K}_t}{T}$$

(11)

$$\{\begin{array}{c}{K}_t=1,Q_g\left(t\right)\ge Q_{need}\left(t\right)\\ K_t=0,Q_g\left(t\right)<Q_{need}\left(t\right)\end{array}$$

(12)

where $\alpha$ is the reliability of water diversion; Q_g(t) is the water diversion during each period; $Q_{need}\left(t\right)$ is the water demand during each period; $K_t$ is the discrimination coefficient of whether the water supply meets the water demand. When $Q_g\left(t\right)\ge Q_{need}\left(t\right)$, $K_t$ = 1; Otherwise, $K_t$ = 0.

(2) Recoverability of insufficient water diversion ($\gamma$): The index indicates the average probability of the water diversion recovering from the failure state ($Q_g\left(t\right)<Q_{need}\left(t\right)$) to the normal state during the reservoir operational periods, which is a maximized type index. The greater the value, the better. The calculation formula is as follows in Equation (13):

$$\gamma =\frac{{{\displaystyle \sum }}_{t=1}^T\left(K_t=1|K_{t-1}=0\right)}{T-{{\displaystyle \sum }}_{t=1}^T{K}_t}$$

(13)

where γ is the recoverability of insufficient water diversion.

(3) Water shortage depth ($\nu$): The index indicates the degree of water shortage during the periods of insufficient water supply, and is represented by the maximum of relative water shortage in each period. The index is a minimized type index. The smaller the value, the better. The calculation formula is as follows in Equation (14):

$$\nu =\max \left\{D{R}_1,D{R}_2,\dots ,D{R}_t\right\}, {DR}_t=1-\frac{Q_g\left(t\right)}{Q_{need}\left(t\right)}.$$

(14)

where ν is the depth of water shortage; $D{R}_t$ is the relative water shortage during each period.

(4) Water shortage index ($WSI$): The index reflects the loss degree of reservoir water supply benefits, which is a minimized type index. The smaller the value, the better. The calculation formula is as follows in Equation (15):

$$WSI=\frac{100}{T}{\displaystyle \sum }_{t=1}^{T}D{R}_t{}^2$$

(15)

where $WSI$ is the water shortage index.

The method of multi-objective optimization and multi-attribute decision making for reservoir operation includes four steps: objectives extraction, model construction, optimization solution and decision-making scheme selection. The specific process is shown in Figure 6.

Step 1: Data input. The basic parameters of the reservoir, hydropower station, pump station and monthly inflow data are input.

Step 2: Objectives extraction and correlation analysis. The objectives are extracted according to the reservoir operation task. By analyzing the correlation of every two objectives, the competitive objectives are obtained.

Step 3: Model construction. The multi-objective optimal operation model is constructed through competitive objectives obtained by Step 2 and related constraints.

Step 4: Optimization solution. The Pareto solution set or the alternative scheme set is obtained by the NSGA-II.

Step 5: Decision-making scheme selection. The evaluation indexes are selected to form a decision-making space with 4-dimensional attributes. The approach of SEABODE is used to optimize the scheme set obtained by Step 4, and the final decision-making scheme is obtained.

Step 6: Output the Pareto solution set, the variable values, the evaluation indexes and the comparison results.

5. Results and Discussion

5.1. Pareto Solution Set

The Pareto solution sets under different inflow frequencies were obtained by solving the above model through NSGA-II, as shown in Figure 7. The Pareto solution sets under different inflow frequencies had different shapes, but the whole was smooth and continuous. There was an obvious negative correlation between total power generation and total water diversion, which further explained the competitive relationship between the two objectives. With the continuous increase in natural inflow, the total power generation and total water diversion were also increasing. For example, the maximum of total power generation and total water diversion in extraordinarily dry year were 0.775 × 10⁸ kW·h and 5.27 × 10⁸ m³, the maximum of total power generation and total water diversion in extraordinarily wet year were 5.75 × 10⁸ kW·h and 14.45 × 10⁸ m³, with an increase of 4.975 × 10⁸ kW·h and 9.18 × 10⁸ m³, respectively. It showed that the amount of natural inflow had a significant impact on the benefits of the reservoir. For the Pareto solution sets under different inflow frequencies, the increasing range of power generation was less than that of water diversion, indicating that the water diversion was more sensitive to the amount of natural inflow. In other words, power generation objective was more sensitive to water diversion objective.

5.2. Multi-Attribute Decision making Results

The above Pareto solution sets under different inflow frequencies were used as the alternative scheme sets for multi-attribute decision making. The 100 schemes in the Pareto solution set were numbered as 1~100, respectively. The 4-dimensional decision-making attribute values of 100 schemes in each scheme set were calculated. The variation range and standard deviation were shown in

Table 2. Variation range and standard deviation of 4-dimensional decision-making attribute values in different typical years.

Typical Years		$\mathit{\alpha }$	$\mathit{\gamma }$	$\mathit{\nu }$	WSI
Extraordinarily dry year	Variation range	[0, 0.083]	[0, 0.090]	[0.92, 1.00]	[48.03, 51.38]
	Standard deviation	0.008	0.009	0.03	1.084
Dry year	Variation range	[0.50, 0.66]	[0.2, 0.33]	[0.71, 1.00]	[15.78, 30.21]
	Standard deviation	0.047	0.063	0.093	3.99
Normal year	Variation range	[0.583, 0.75]	[0.2, 0.4]	[0.68, 0.99]	[9.13, 18.53]
	Standard deviation	0.038	0.064	0.064	2.66
Wet year	Variation range	[0.66, 0.83]	[0.25, 0.50]	[0.24, 0.86]	[0.86, 8.20]
	Standard deviation	0.063	0.265	0.179	1.85
Extraordinarily wet year	Variation range	[0.67, 0.91]	[0.25, 1.00]	[0.31, 0.99]	[0.91, 14.00]
	Standard deviation	0.049	0.087	0.259	4.06

. It can be seen that the 4-dimensional decision-making attribute values of each scheme set for different typical years were different. Therefore, the approach of SEACODE was used to sort, eliminate and select the scheme set to obtain the final decision-making scheme.

The number of 4-order effective schemes, non-dominated superior schemes in 3-order subspaces and 3-order effective schemes of the alternative scheme sets under different inflow frequencies were shown in

Table 3. Number of 4-order and 3-order effective schemes in different typical years.

Typical Years	{$\mathit{\alpha }$, $\mathit{\gamma }$, $\mathit{\nu }$, $\mathit{W}\mathit{S}\mathit{I}$}	{$\mathit{\alpha }$, $\mathit{\gamma }$, $\mathit{\nu }$}	{$\mathit{\alpha }$, $\mathit{\gamma }$, $\mathit{W}\mathit{S}\mathit{I}$}	{$\mathit{\alpha }$, $\mathit{\nu }$, $\mathit{W}\mathit{S}\mathit{I}$}	{$\mathit{\gamma }$, $\mathit{\nu }$, $\mathit{W}\mathit{S}\mathit{I}$}	Number of 3-Order Effective Schemes
Extraordinarily dry year	6	1	2	6	6	1
Dry year	6	3	3	3	5	0
Normal year	5	3	3	4	3	1
Wet year	6	4	4	3	5	2
Extraordinarily wet year	6	2	2	3	3	2

. When k = 4, the numbers of 4-order effective schemes in each typical year were 6, 6, 5, 6 and 6 by the first-round sorting of the alternative scheme sets, which reduced the preferred range of schemes by 94%, 94%, 95%, 94% and 94%, and greatly reduced the number of alternative schemes. When k = 3, the 4-order effective scheme sets were sorted in the second-round, that is, the non-dominated superior schemes of each 3-order subspace were obtained from the 4-order effective scheme sets. Then the numbers of 3-order effective schemes obtained by the intersection of all 3-order subspaces were 1, 0, 1, 2 and 2, of which the number of 3-order effective schemes in extraordinarily dry year and normal year was 1. The schemes could be used as the final decision-making schemes of extraordinarily dry year, normal year and wet year, and the scheme numbers were 32 and 63, respectively.

The number of 3-order effective schemes in dry year was 0. The scheme that occupied the largest number of subspaces need to be determined as the final decision-making scheme.

Table 4. Optimization processes of 3-order effective schemes in dry year.

Scheme No.	$\mathit{\alpha }$	$\mathit{\gamma }$	$\mathit{\nu }$	$\mathit{W}\mathit{S}\mathit{I}$	{$\mathit{\alpha }$, $\mathit{\gamma }$, $\mathit{\nu }$}	{$\mathit{\alpha }$, $\mathit{\gamma }$, $\mathit{W}\mathit{S}\mathit{I}$}	{$\mathit{\alpha }$, $\mathit{\nu }$, $\mathit{W}\mathit{S}\mathit{I}$}	{$\mathit{\gamma }$, $\mathit{\nu }$, $\mathit{W}\mathit{S}\mathit{I}$}
13	0.583	0.2	0.718	15.873		√ 1	√	√
51	0.583	0.2	0.716	16.273	√		√	√
85	0.667	0.25	0.887	19.991	√	√	√
35	0.500	0.33	0.770	18.257		√		√
49	0.500	0.33	0.760	18.678	√			√
15	0.500	0.33	0.769	18.535				√

¹ “√” represents that the scheme is non-dominated in the corresponding 3-order subspace.

showed the optimization processes of 4-order effective schemes to 3-order effective schemes in dry year. It can be seen that No. 13 scheme, No. 51 scheme and No. 85 scheme occupied three subspaces. The total water diversion and total power generation of No. 13 scheme were 11.01 × 10⁸ m³ and 1.814 × 10⁸ kW·h, respectively, No. 51 scheme were 11.005 × 10⁸ m³ and 1.817 × 10⁸ kW·h, and No. 85 scheme were 11.067 × 10⁸ m³ and 1.804 × 10⁸ kW·h, respectively. As the main task of Huangjinxia Reservoir is water supply and considering power generation and ecology at the same time. Therefore, No. 85 scheme with a large total water diversion was selected as the final decision-making scheme in dry year.

The number of 3-order effective schemes in extraordinarily wet year and wet year was greater than 1, so it is necessary to sort the 3rd-order effective scheme set to obtain the 2nd-order effective scheme. The final decision-making schemes in extraordinarily wet year and wet year were No. 44 scheme and No.52 scheme.

Table 5. Decision-making schemes in different typical years.

Typical Years	Scheme No.	$\mathit{\alpha }$	$\mathit{\gamma }$	$\mathit{\nu }$	$\mathit{W}\mathit{S}\mathit{I}$
Extraordinarily dry year	32	0	0.090	0.931	48.038
Dry year	85	0.583	0.20	0.718	15.879
Normal year	63	0.667	0.25	0.689	9.130
Wet year	52	0.833	0.50	0.6224	3.976
Extraordinarily wet year	44	0.916	1	0.577	2.770

showed the final decision-making schemes of different typical years. It can be seen that the 4-dimensional decision-making attribute values of each typical year were very different. With the increase in water inflow, the reliability of water diversion $\alpha$ and the recoverability of insufficient water diversion $\gamma$ increased, and the water shortage depth $\nu$ and the water shortage index WSI decreased. This paper focused on the analysis of attribute values in the dry year and extraordinarily dry year. It can be seen that the evaluation indexes in the dry year were better than those in the extraordinarily dry year. The reliability of water diversion $\alpha$ in dry year was 0.583, that is, 7 months of the year could meet the normal water demand in the Guanzhong plain. While the reliability of water diversion $\alpha$ in the extraordinarily dry year was 0, that is, decreased by 0.583 compared with the dry year, there was no month in the extraordinarily dry year that could meet the water demand in the Guanzhong plain. The recoverability of insufficient water diversion $\gamma$ in dry year was 0.11 higher than that in the extraordinarily dry year. The water shortage depth $\nu$ in the dry year decreased by 0.213 compared with the extraordinarily dry year. The water shortage index $WSI$ in the dry year was 32.159 lower than that in the extraordinarily dry year, and the decreasing range was much larger than that in other typical years. In general, the water diversion capacity of the reservoir was greatly weakened in the dry year, especially in the extraordinarily dry year. In view of this situation, the staff should make emergency preparations in advance in the actual operation.

5.3. Decision-Making Scheme Analysis

According to the above decision-making schemes, the processes of monthly water diversion and power generation in different typical years were shown in Figure 8. It can be seen that the total water diversion was smallest in the extraordinarily dry year, due to the little water inflow from the upper reaches of the Han River. The water diversion of each month was below the water demand line, and no month could meet the water demand. In addition, the water diversion in October was the smallest, and the power generation also dropped to the lowest level. The water inflow from December to April in dry year was relatively low, and the water diversion of Huangjinxia Reservoir was below the water demand line. The maximum water shortage occurred in March, and the power generation in these months was relatively low. The water inflow from December to March next year in normal year was relatively low, and the water diversion struggled to meet the water demand of the Guanzhong plain. In other months, the water diversion was above the water demand line, and the power generation head was higher, so the power generation was larger. The water demand could be met in the wet year and the extraordinarily wet year except for January and February, and the reservoir could maintain a high head for power generation.

6. Conclusions

The multi-objective optimization and decision-making for reservoir operation is of great significance to realize efficient utilization of water energy resources and improve the operation and management level of reservoir. This paper coupled objective extraction, model construction, optimization solution and scheme selection, and put forward a multi-objective optimization and multi-attribute decision making method for reservoir operation with the whole process of “Objective-Modeling-Optimization-Selection”. Taking Huangjinxia Reservoir as an example, and the main conclusions are summarized as follows:

(1) By extracting reservoir operation objectives, analyzing the correlation among objectives, and quantifying the degree of conflict among objectives, the competing operation objectives can be obtained, which makes the construction of the multi-objective optimal operation model more reasonable.

(2) The NSGA-II-SEABODE algorithm can solve the model to obtain the alternative scheme set and obtain the final decision-making scheme in the scheme set, which provides decision-making basis for managers.

(3) The implementation of the multi-objective optimization and multi-attribute decision making method in Huangjinxia Reservoir explores the competitive relationship among water supply, power generation and ecology. The results provide a theoretical basis for the efficient utilization of water resources of Huangjinxia Reservoir.

Although some results have been made in this study, due to the complexity of MODRO problems, there are still many shortcomings, which should be further explored. Under the influence of global climate change and human activities, the consistency of hydrological series has changed, and the existing decision-making schemes are difficult to cope with the changes of future hydrological regime. We will explore the MODRO problems under changing environment. In addition, we will carry out research on multi-objective optimization and multi-attribute decision-making for reservoir group and establish multi-objective optimal operation model of reservoir group. The alternative scheme set will be obtained by using the solving algorithm with high computational efficiency, and the decision-making scheme will be selected by multi-attribute decision-making method with strong optimization ability.