Investigation of the Effect of Capillary Barrier on Water–Oil Movement in Water Flooding
Abstract
:1. Introduction
2. Oil–Water Two-Phase Flow Dynamics
2.1. Continuity Equation
2.2. Momentum Conservation Equation
2.3. Oil–Water Interfacial Tension
2.4. Volume of Fluid Method
2.5. Rock Wettability
2.6. Averaging Properties of Oil–Water Flow
3. Capillary Barrier Phenomenon
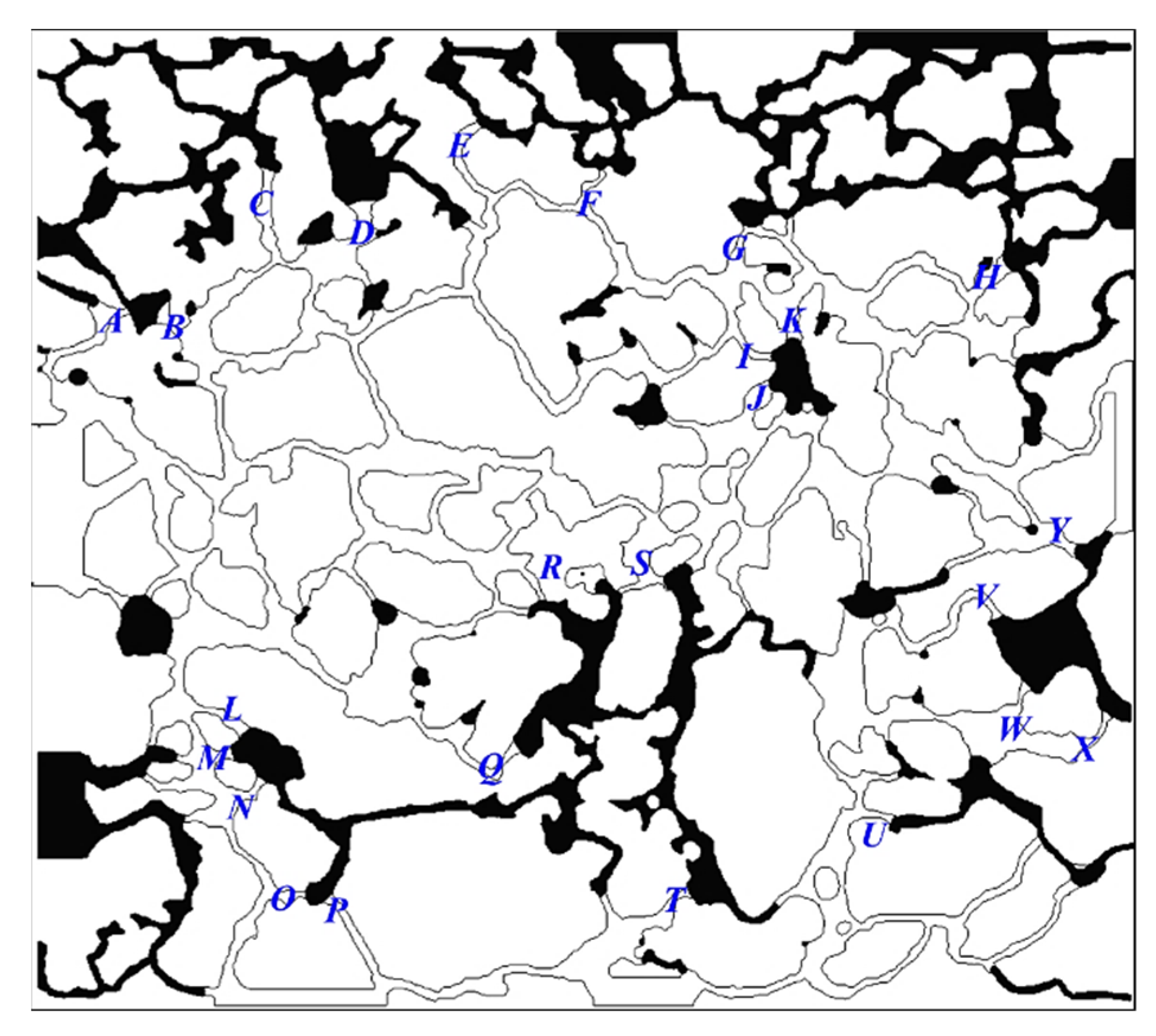
3.1. Remaining Oil Formation during the Water-Flooding Process
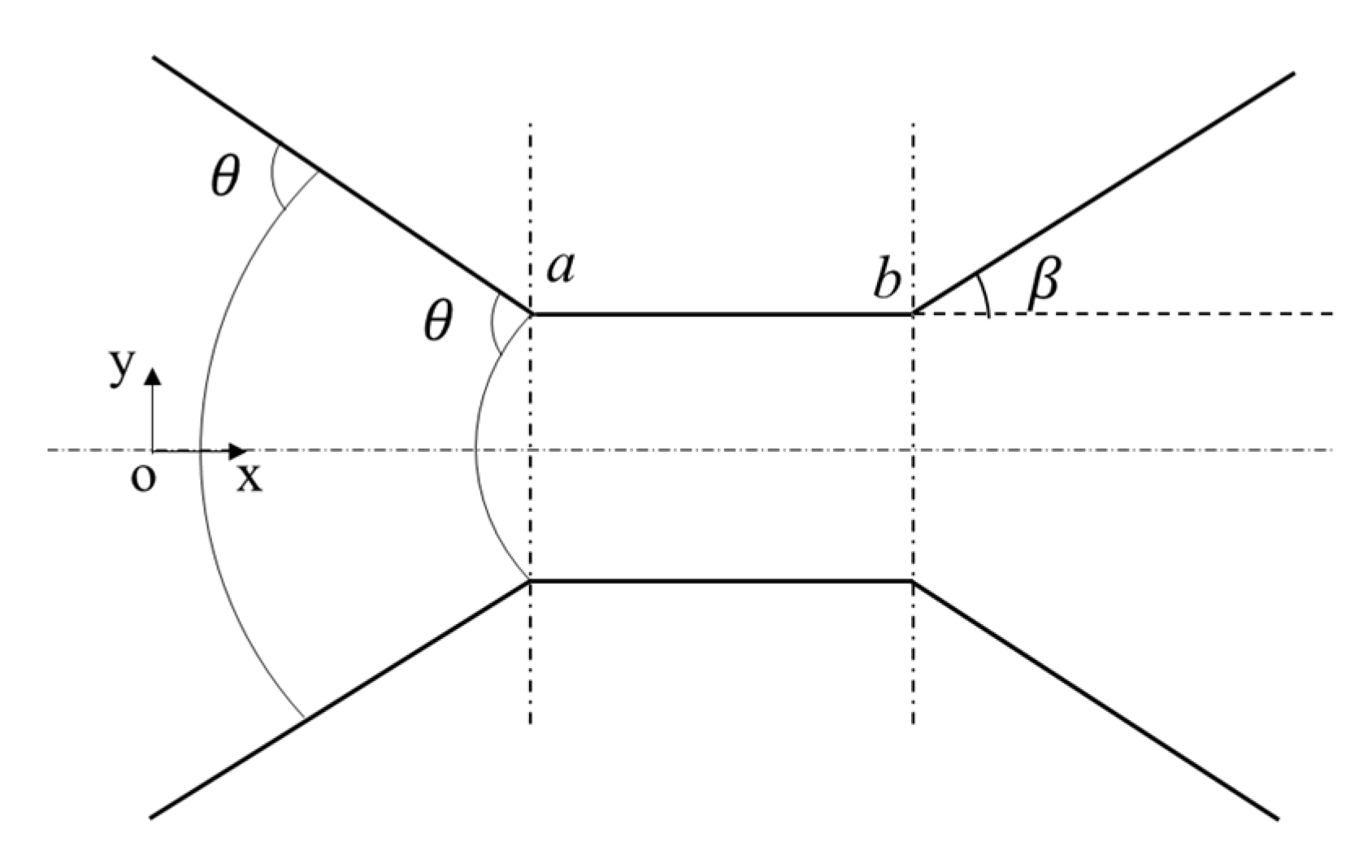
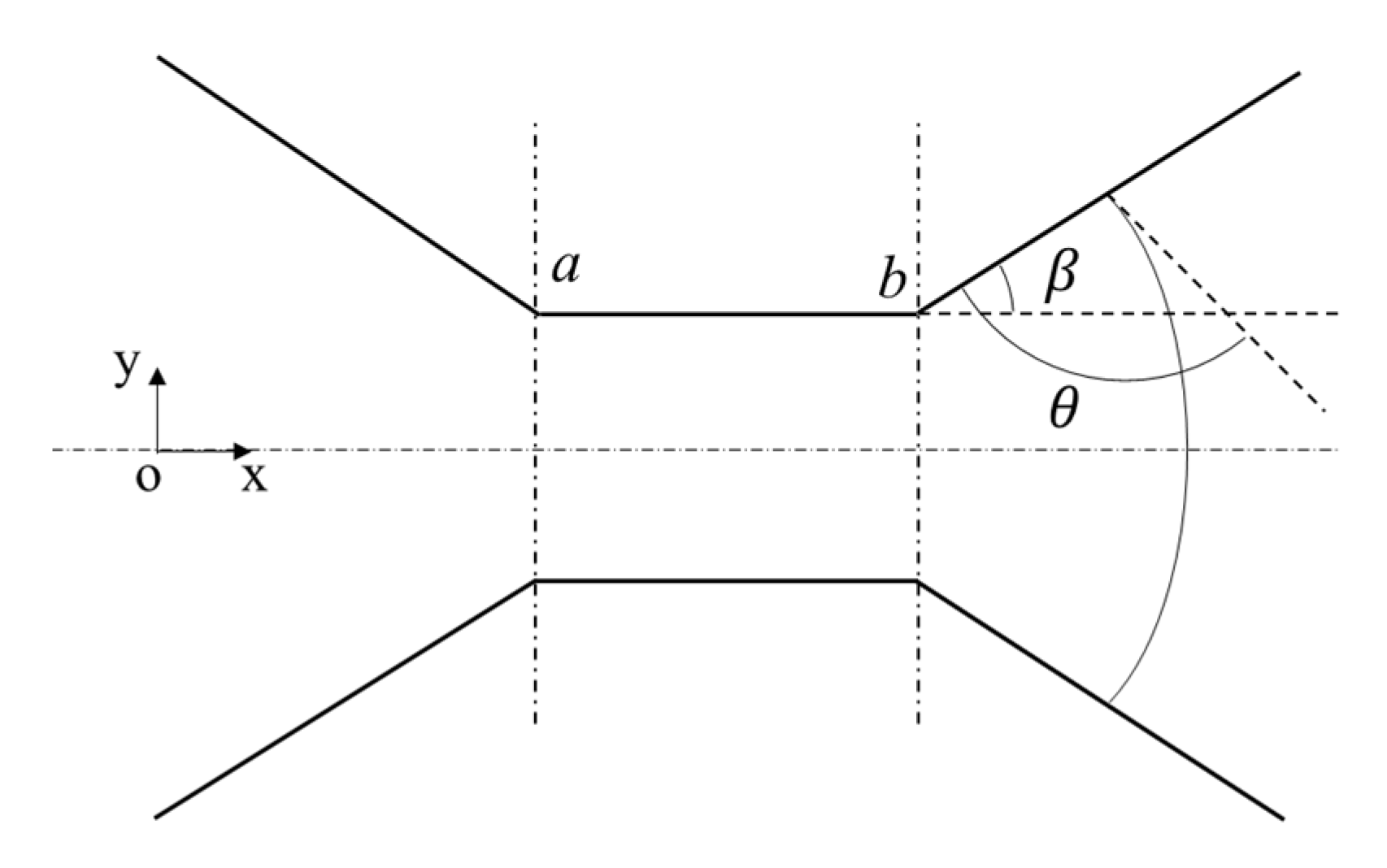
3.2. Conceptual Physical Model of Capillary Barrier
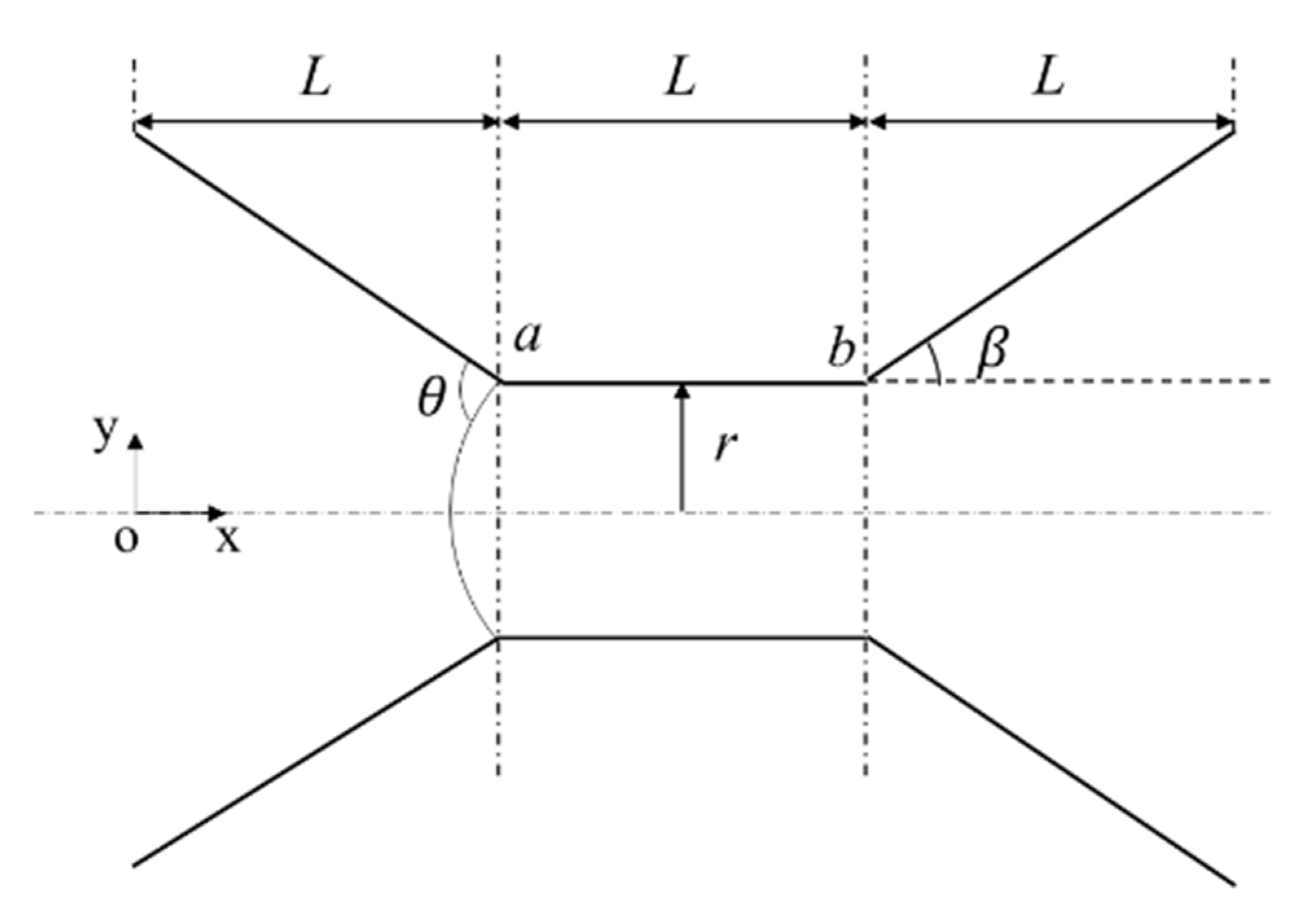
3.3. Variation of the Capillary Force along the Central Axis
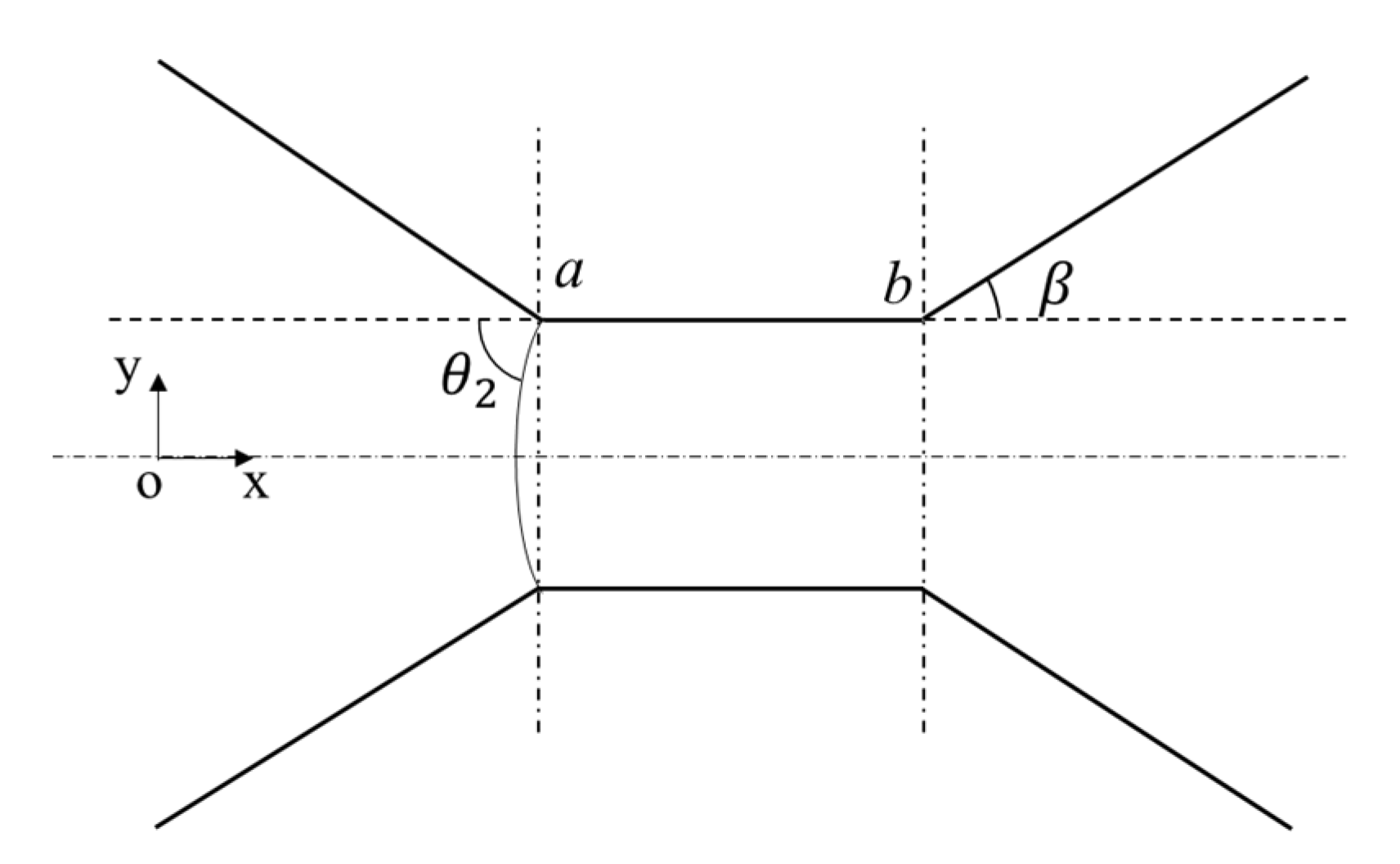
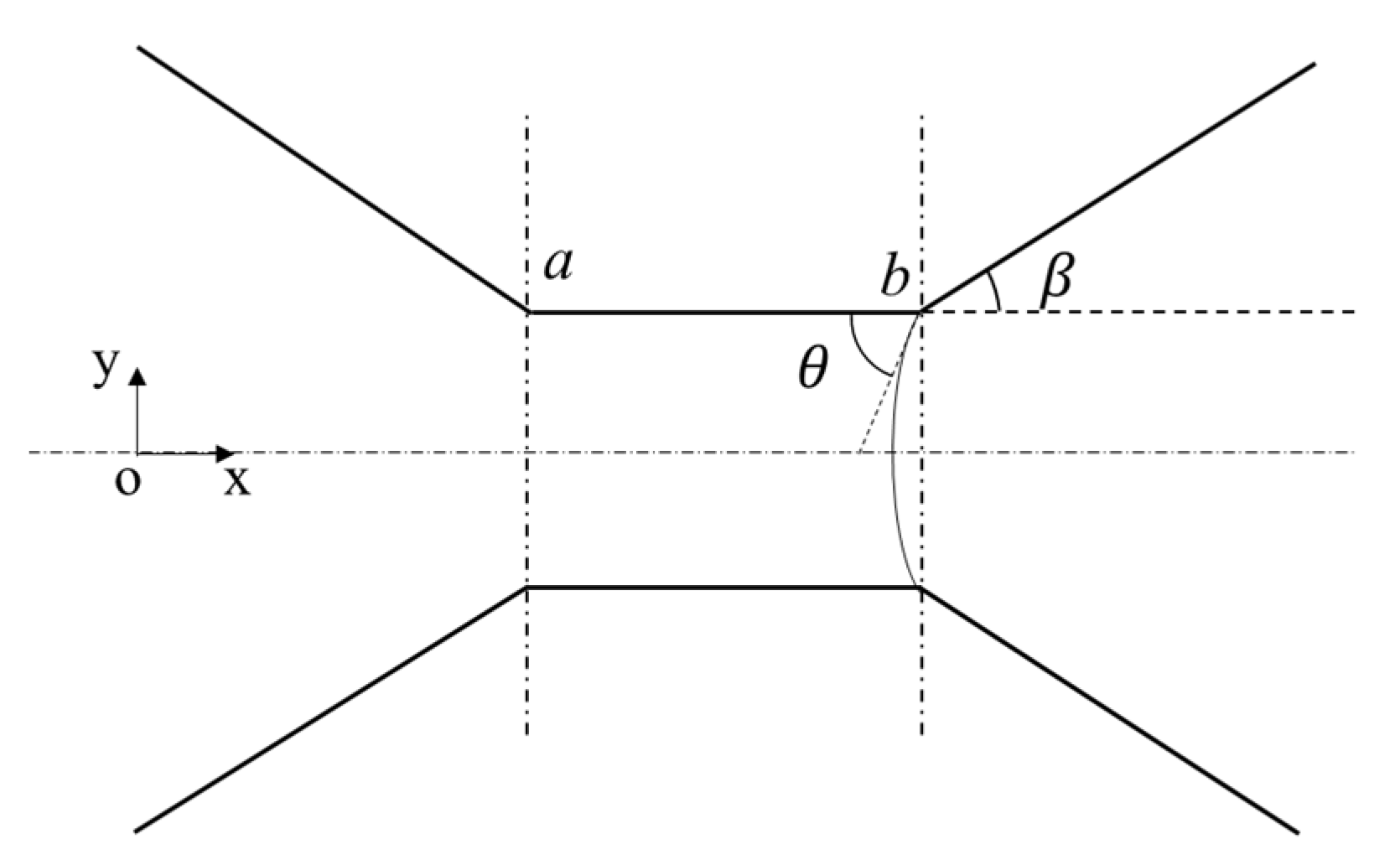
3.3.1. Analysis of the Capillary Force at Different Stages
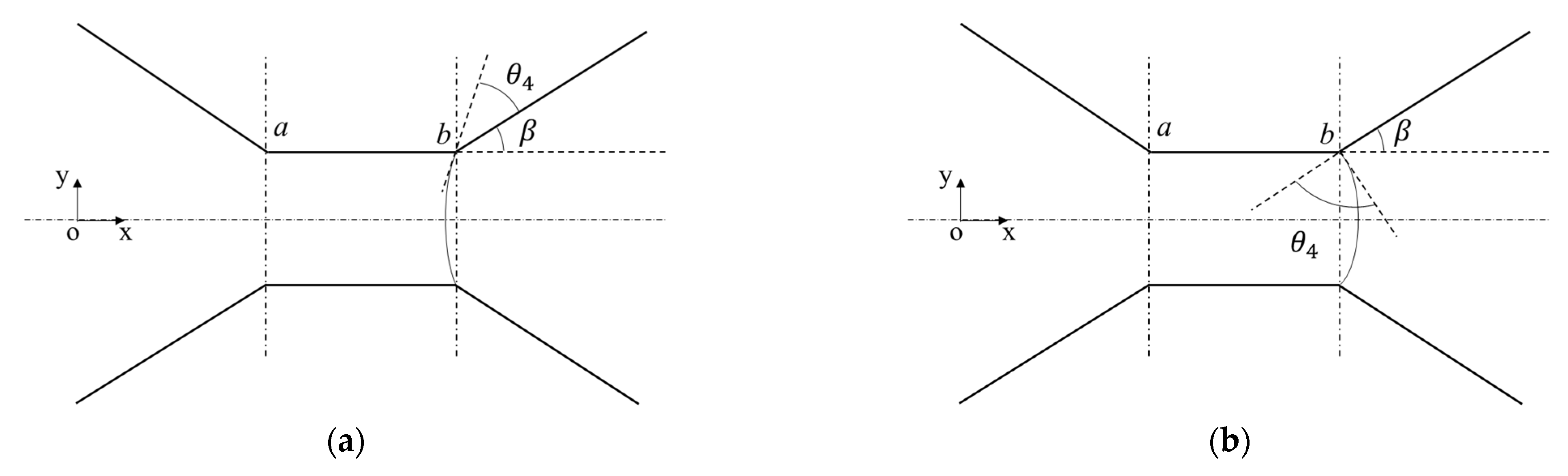
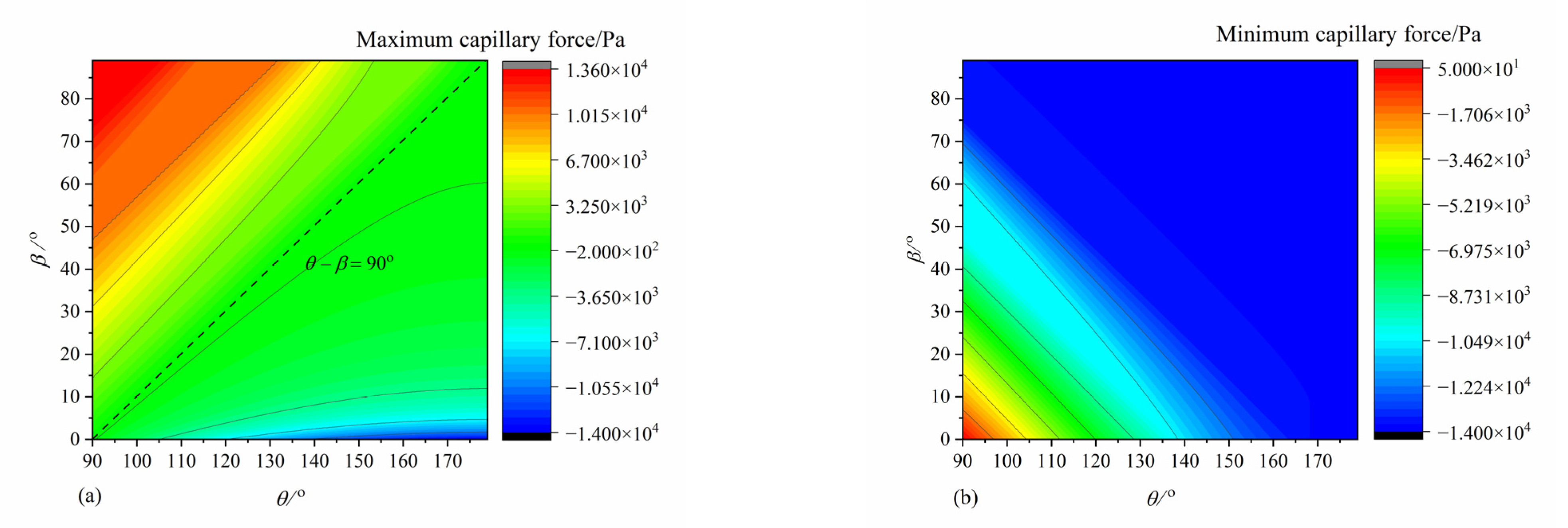
3.3.2. The Maximal Value and Minimal Value of the Capillary Force and Its Corresponding Conditions
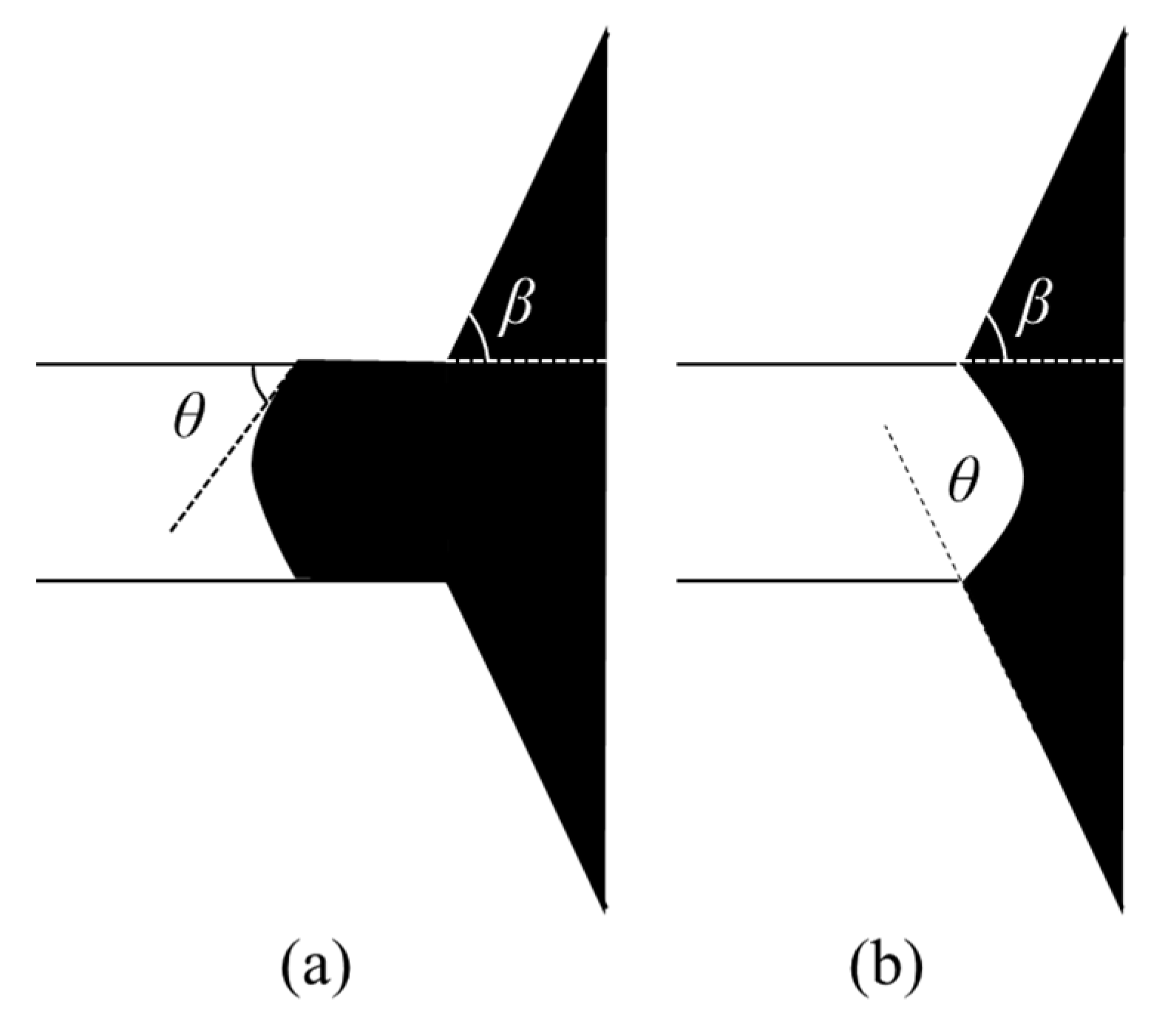
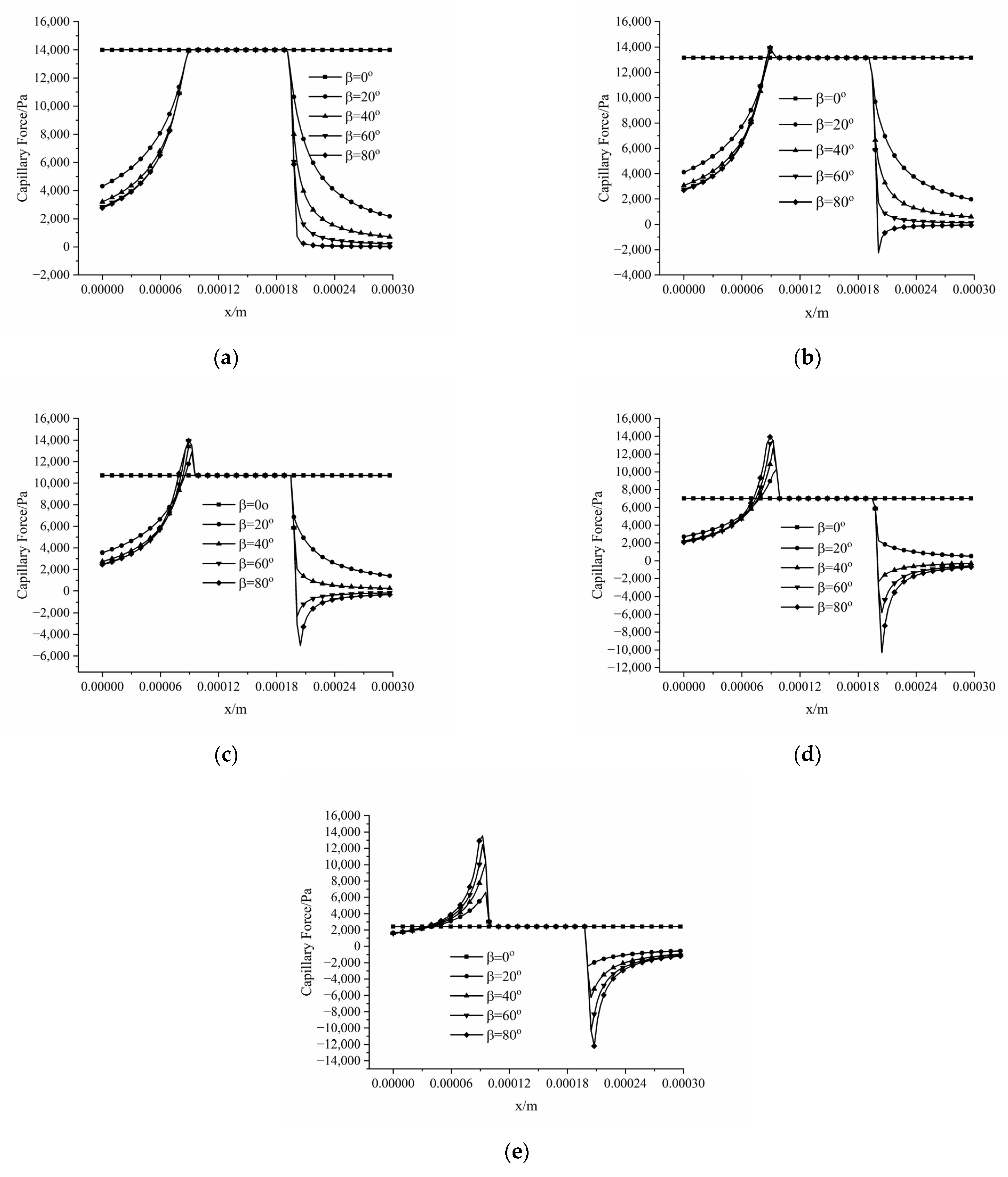
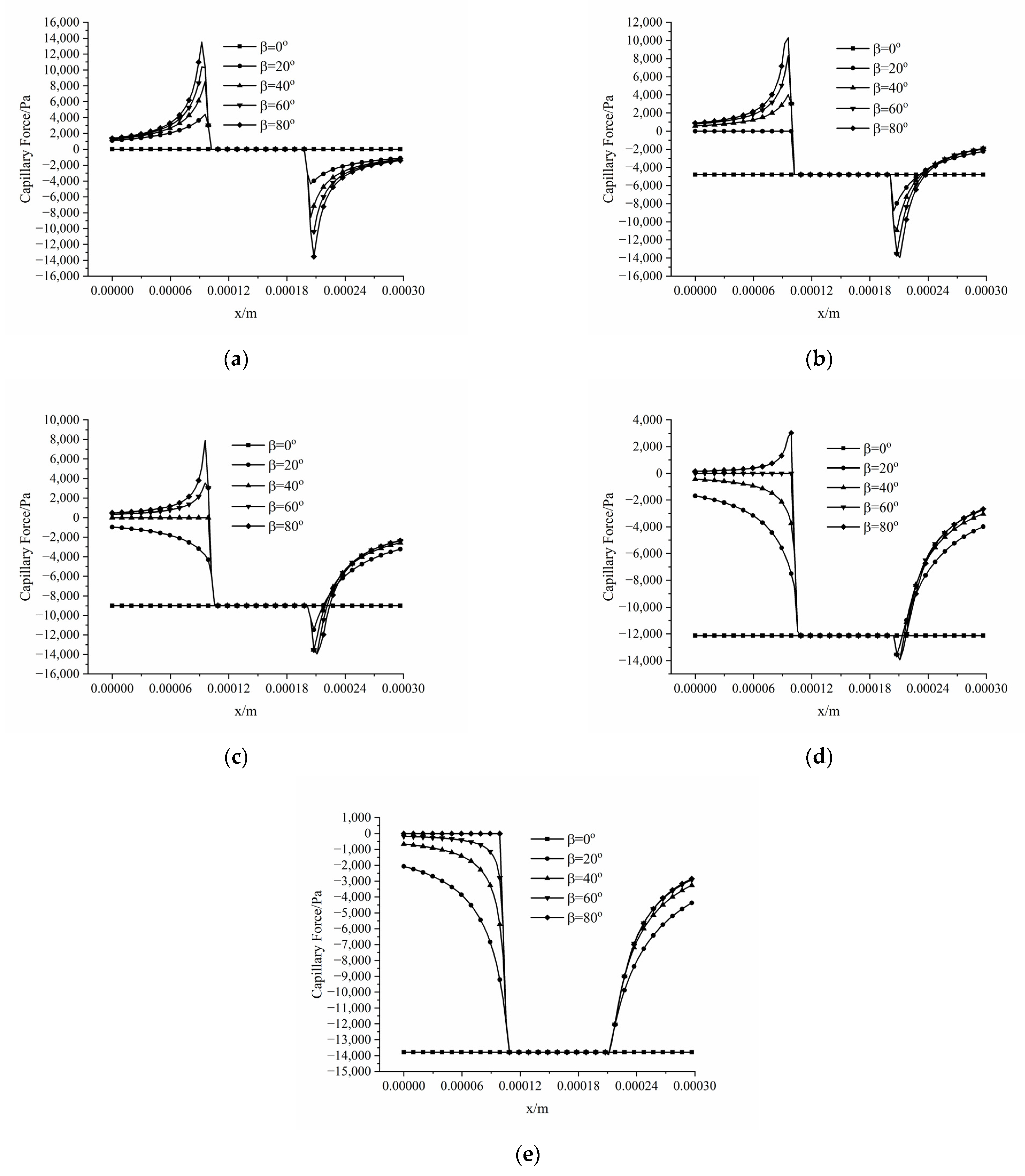
3.4. Effect of Different Contact Angles and Opening Angles on the Capillary Force
3.4.1. Water-Wet Conditions
3.4.2. Oil-Wet Conditions
4. Effect of the Capillary Barrier on Oil–Water Two-Phase Flow in Porous Media Model
4.1. Physical Model and Case Setup
4.2. Numerical Conditions
4.3. Results and Discussion
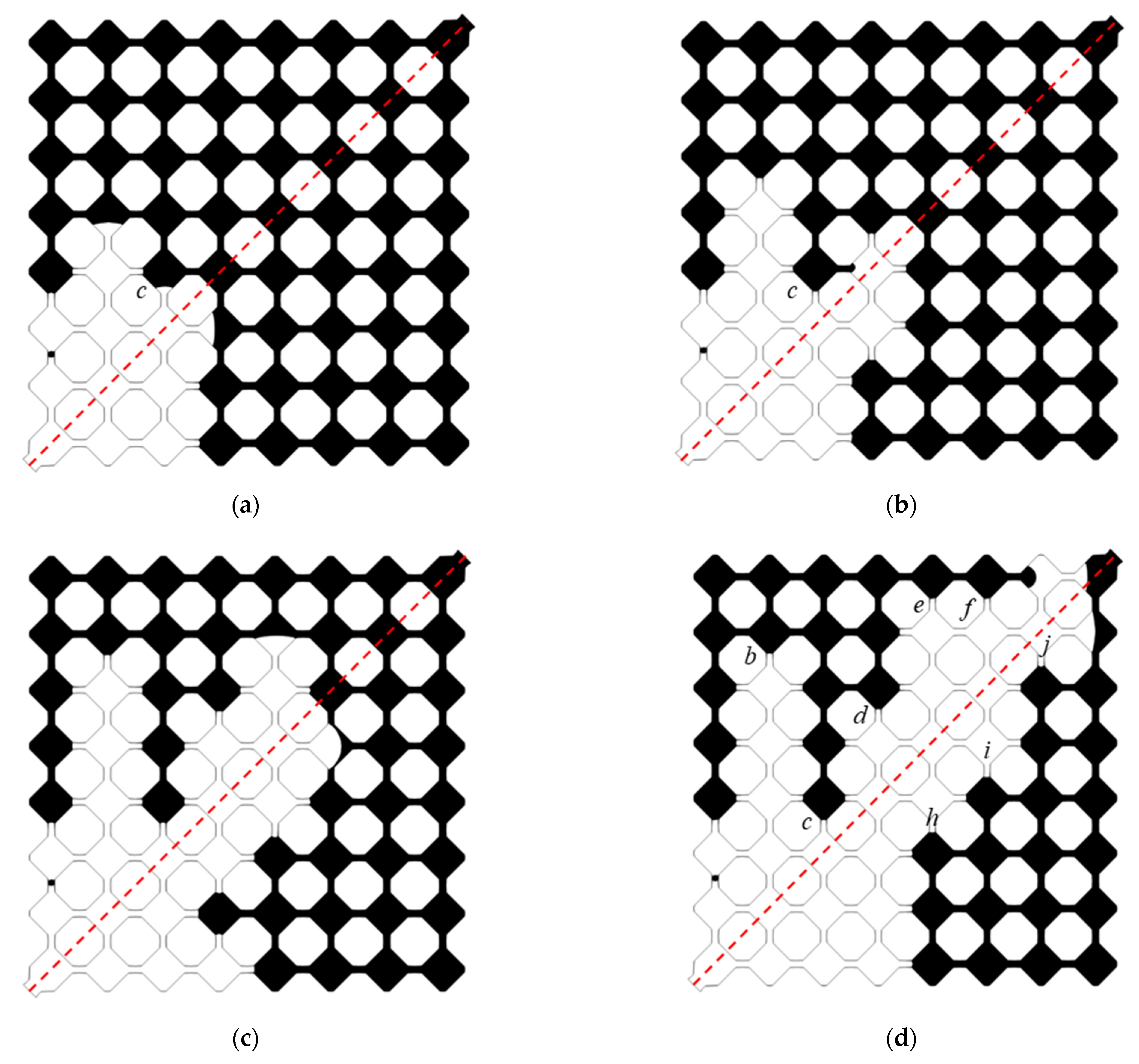
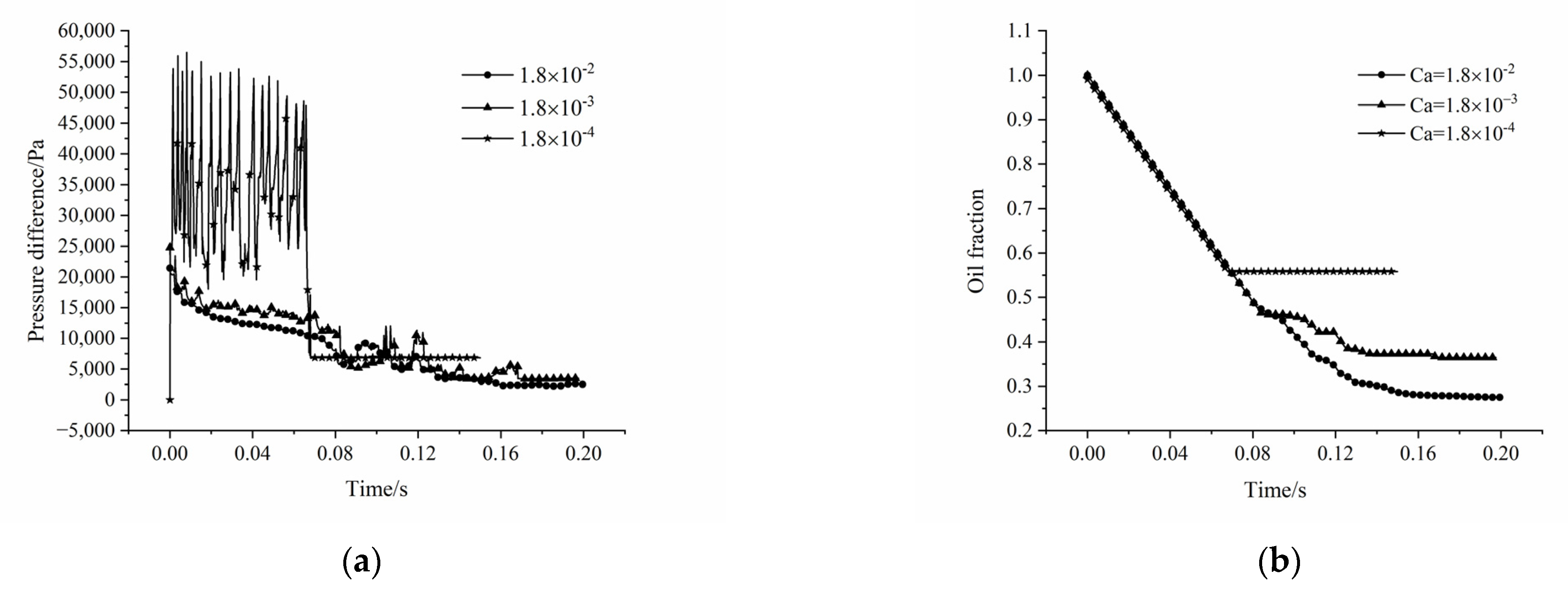
4.3.1. Water-Wet Condition
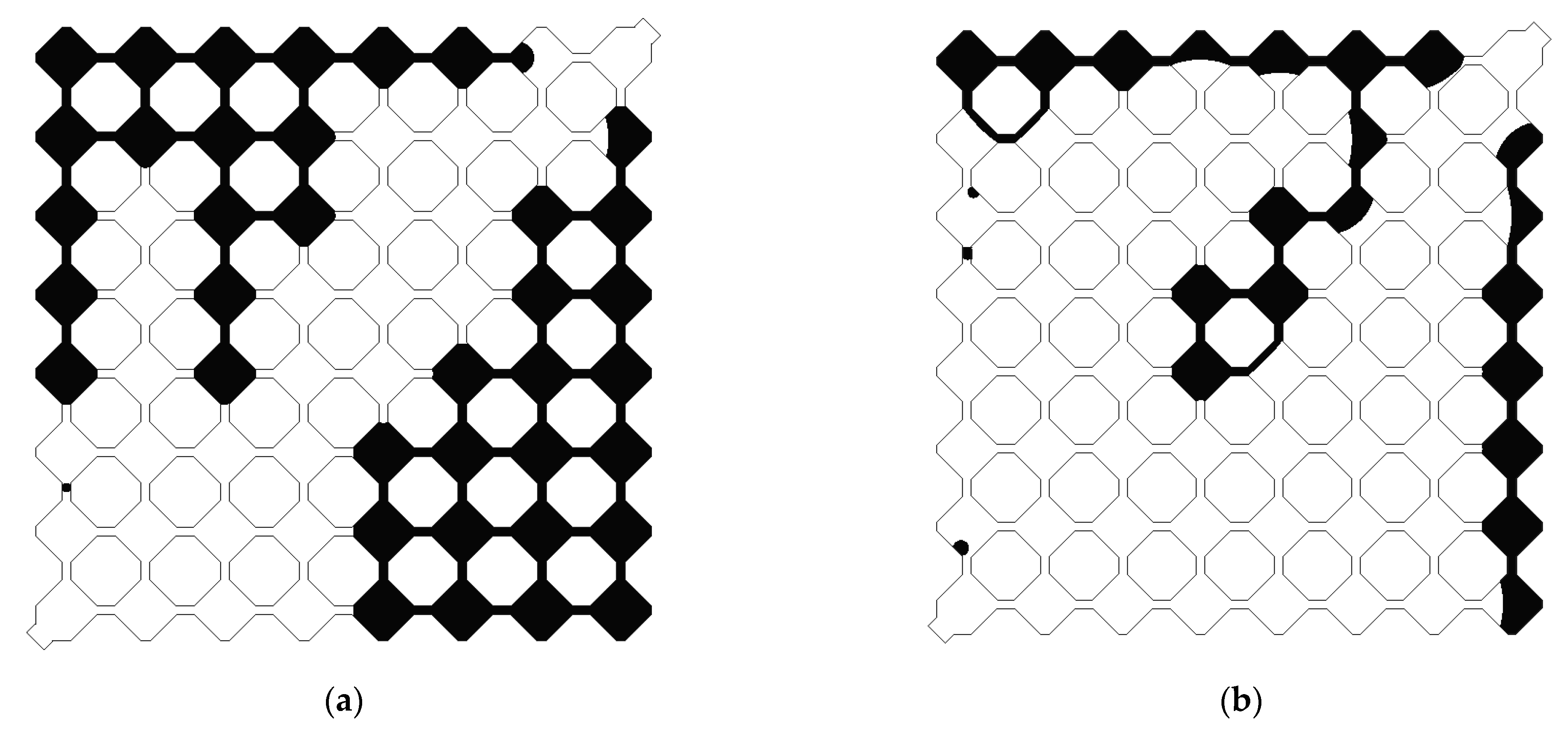
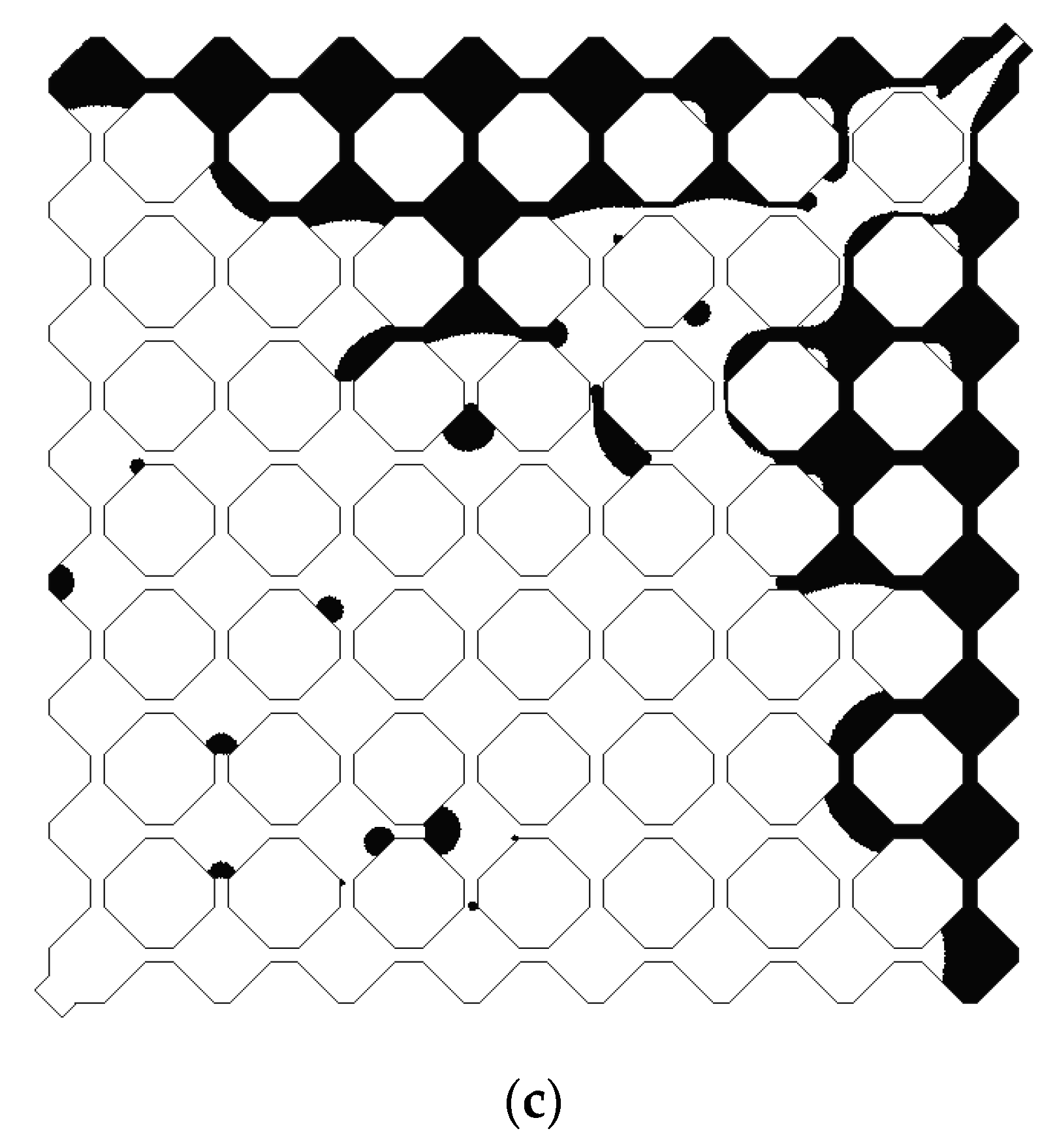
4.3.2. Oil-Wet Condition
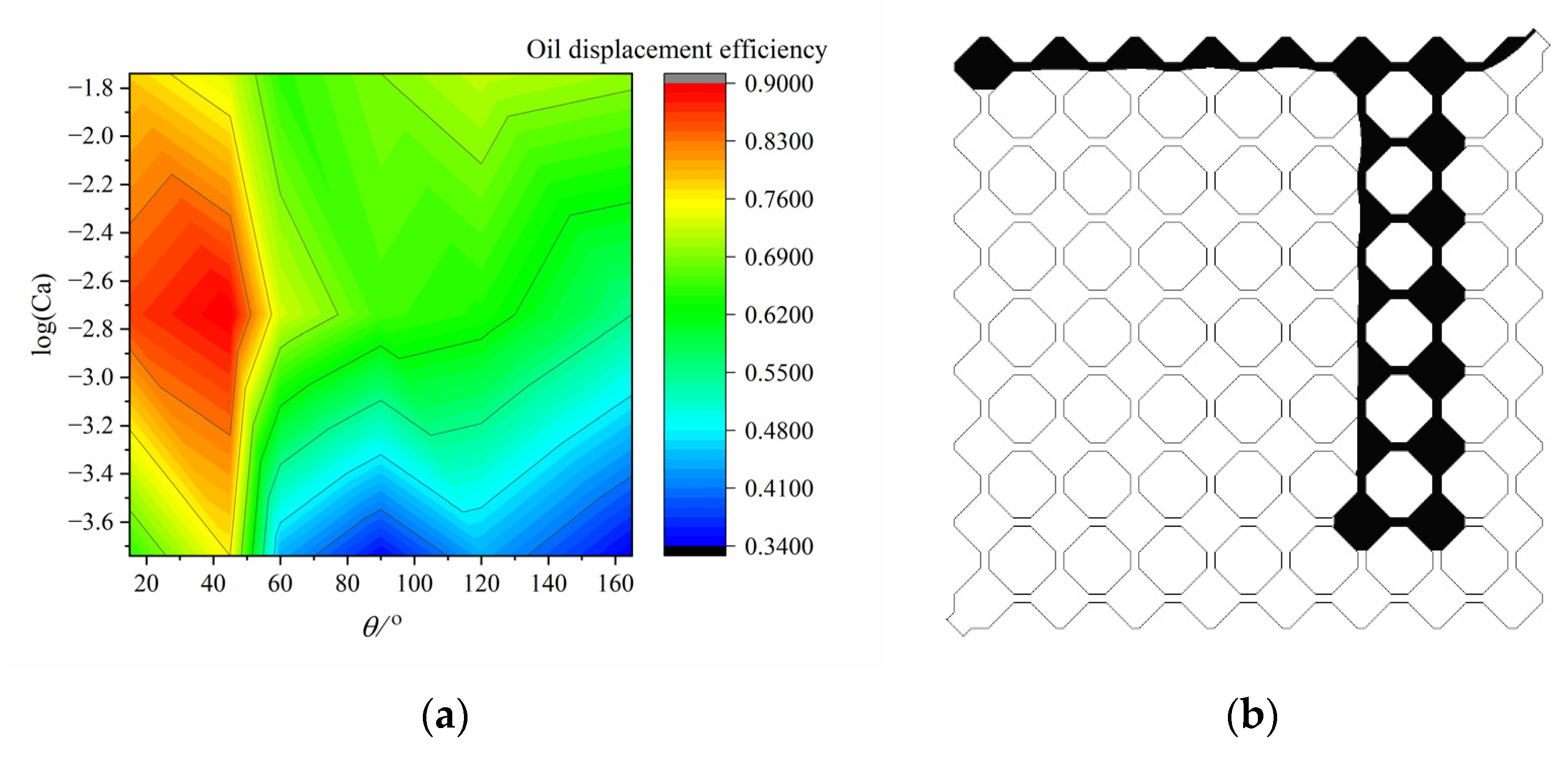
4.3.3. The Change of Oil Displacement Efficiency
5. Conclusions
- The capillary barrier effect is largely responsible for the formation of the residual oil in the reservoir rock. The interplay between the capillary force and viscous force determines the oil–water two-phase flow in the porous media; and the capillary barrier effect is caused by a geometric structure; even in the water-wet conditions, capillary force can still present resistance characteristics. The negative values of capillary force indicate the occurrence of the capillary barrier phenomenon. The capillary force is a type of driving force when the interface enters the throat section if the condition is satisfied. The capillary force presents resistance characteristics if the condition is satisfied. When θ + β > 90°, the oil–water interface will reverse, and the direction of the capillary force will point to the side of the water phase.
- The occurrence of capillary barrier phenomena under different wettability regimes are mainly dominated by the contact angle and the opening angle during the oil displacement process. Under water-wet conditions, the capillary force is positive in the process of the liquid entering the throat section. The capillary force is negative, and the occurrence of the capillary barrier phenomenon can be observed in the process of the liquid leaving the throat section when β + θ > 90°; while under oil-wet conditions, the capillary force is negative when the liquid is leaving the throat section, and there is a positive peak capillary pressure when the oil–water interface enters the throat from the pore once the condition θ − β < 90° is satisfied.
- The highest oil displacement efficiency under water-wet conditions is obtained at the intermediate capillary number of 1.8 × 10−3 and obvious fluctuations of the pressure difference before and after the breakthrough of the water phase are observed; while the highest oil displacement efficiency under oil-wet conditions is obtained at the large capillary number of 1.8 × 10−2 and the occurrence of the capillary barrier effect facilitates the mobilization of the fluid phase and the increase of the sweep area when θ − β ≤ 90°.
- Under oil-wet conditions, the larger the capillary number, the higher the oil displace-mint efficiency; while under water-wet conditions, the optimal oil displacement efficiency is obtained under intermediate capillary numbers and at the contact angles at which the capillary barrier phenomenon cannot be observed.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Solution Scheme and Solution Procedures
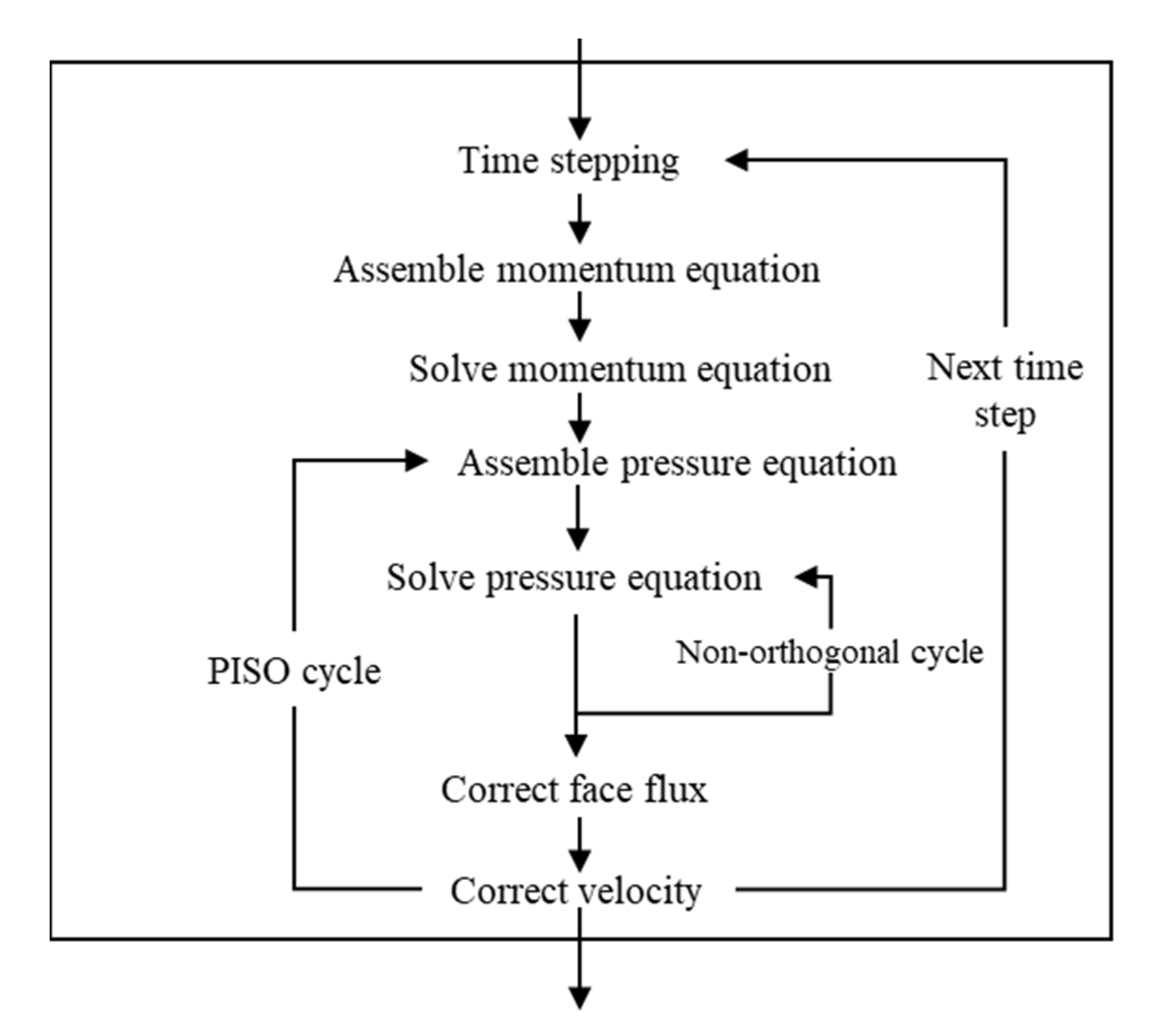
Appendix B. Model Validation

References
- BP. Statistical Review of World Energy, 69th ed.; BP: London, UK, 2020. [Google Scholar]
- Chai, R.; Liu, Y.; He, Y.; Liu, Q.; Xue, L. Dynamic behaviors and mechanisms of fluid-fluid interaction in low salinity waterflooding of carbonate reservoirs. J. Pet. Sci. Eng. 2021, 208, 109256. [Google Scholar] [CrossRef]
- Zallaghi, M.; Khazali, A.R. Experimental and modeling study of enhanced oil recovery from carbonate reservoirs with smart water and surfactant injection. Fuel 2021, 304, 121516. [Google Scholar] [CrossRef]
- Jamaloei, B.Y.; Kharrat, R. Analysis of microscopic displacement mechanisms of dilute surfactant flooding in oil-wet and water-wet porous media. Transp. Porous Media 2010, 81, 1–19. [Google Scholar] [CrossRef]
- Jamaloei, B.Y.; Kharrat, R.; Asghari, K.; Torabi, F. The influence of pore wettability on the microstructure of residual oil in surfactant-enhanced water flooding in heavy oil reservoirs: Implications for pore-scale flow characterization. J. Pet. Sci. Eng. 2011, 77, 121–134. [Google Scholar] [CrossRef]
- Moore, T.F.; Slobod, R.L. Displacement of oil by water-effect of wettability, rate, and viscosity on recovery. In Proceedings of the SPE-502-G Presented at the Fall Meeting of the Petroleum Branch of AIME, New Orleans, LA, USA, 2–5 October 1955. [Google Scholar]
- Vivas, F.J.A.; Babadagli, T. Drainage type oil and heavy-oil displacement in circular tubes: Two- and three-phase flow characteristics and residual oil saturation development in the form of film at different temperatures. J. Pet. Sci. Eng. 2014, 118, 61–73. [Google Scholar] [CrossRef]
- Sohrabi, M.; Danesh, A.; Jamiolahmady, M. Visualisation of residual oil recovery by near-miscible gas and SWAG injection using high-pressure micromodels. Transp. Porous Media 2008, 74, 239–257. [Google Scholar] [CrossRef]
- Ning, T.; Xi, M.; Hu, B.; Wang, L.; Huang, C.; Su, J. Effect of viscosity action and capillarity on pore-scale oil-water flowing behaviors in a low-permeability sandstone waterflood. Energies 2021, 14, 8200. [Google Scholar] [CrossRef]
- Saha, R.; Tiwari, P.; Uppaluri, R.V.S. Chemical Nanofluids in Enhanced Oil Recovery: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Khoramian, R.; Kharrat, R.; Golshokooh, S. The development of novel nanofluid for enhanced oil recovery application. Fuel 2022, 311, 122558. [Google Scholar] [CrossRef]
- Mariyate, J.; Bera, A. Recent progresses of microemulsions-based nanofluids as a potential tool for enhanced oil recovery. Fuel 2021, 306, 121640. [Google Scholar] [CrossRef]
- Sagala, F.; Hethnawi, A.; Nassar, N.N. Hydroxyl-functionalized silicate-based nanofluids for enhanced oil recovery. Fuel 2020, 269, 117462. [Google Scholar] [CrossRef]
- Minakov, A.V.; Guzei, D.V.; Pryazhnikov, M.I.; Filimonov, S.A.Y.; Voronenkova, Y.O. 3D pore-scale modelling of nanofluids-enhanced oil recovery. Pet. Explor. Dev. 2021, 48, 956–967. [Google Scholar] [CrossRef]
- Rabbani, H.S.; Zhao, B.; Juanes, R.; Shokri, N. Pore geometry control of apparent wetting in porous media. Sci. Rep. 2018, 8, 15729. [Google Scholar] [CrossRef] [PubMed]
- Galkin, S.V.; Martyushev, D.A.; Osovetsky, B.M.; Kazymov, K.P.; Song, H. Evaluation of void space of complicated potentially oil-bearing carbonate formation using X-ray tomography and electron microscopy methods. Energy Rep. 2022, 8, 6245–6257. [Google Scholar] [CrossRef]
- Silva, G.O.M.; Lamas, L.F.; Soares, A.P. Characterization of carbonate facies and study of their relationship with dissolution and wettability in CO2 injection. J. Pet. Sci. Eng. 2021, 206, 108938. [Google Scholar] [CrossRef]
- Adegbite, J.O.; Belhaj, H.; Bera, A. Investigation on the relationship among the porosity, permeability and pore throat size of transition zone samples in carbonate reservoirs using multiple regression analysis, artificial neural network and adaptive neuro-fuzzy interface system. Pet. Res. 2021, 6, 321–332. [Google Scholar] [CrossRef]
- Wei, H.; Zhu, X.; Liu, X.; Yang, H.; Tao, W.-Q.; Chen, L. Pore-scale study of drainage processes in porous media with various structural heterogeneity. Int. Commun. Heat Mass Transf. 2022, 132, 105914. [Google Scholar] [CrossRef]
- Ho, C.K.; Webb, S.W. Capillary barrier performance in heterogeneous porous media. Water Resour. Res. 1998, 34, 603–609. [Google Scholar] [CrossRef]
- Tami, D.; Rahardjo, H.; Leong, E.-C.; Fredlund, D.G. Design and laboratory verification of a physical model of sloping capillary barrier. Can. Geotech. J. 2004, 41, 814–830. [Google Scholar] [CrossRef]
- Avanzi, F.; Hirashima, H.; Yamaguchi, S.; Katsushima, T.; De Michele, C. Observations of capillary barriers and preferential flow in layered snow during cold laboratory experiments. Cryosphere 2016, 10, 2012–2026. [Google Scholar] [CrossRef] [Green Version]
- Man, P.; Mastrangelo, C.; Burns, M.; Burke, D. Microfabricated capillarity-driven stop valve and sample injector. In Proceedings of the Eleventh International Workshop on Micro Electro Mechanical Systems, Heidelberg, Germany, 25–29 January 1998; IEEE Xplore: Piscataway, NJ, USA, 1998. [Google Scholar]
- Glière, A.; Delattre, C. Modeling and fabrication of capillary stop valves for planar microfluidic systems. Sens. Actuators A Phys. 2006, 130, 601–608. [Google Scholar] [CrossRef]
- Leu, T.S.; Chang, P.Y. Pressure barrier of capillary stop valves in micro sample separators. Sens. Actuators A Phys. 2004, 115, 508–515. [Google Scholar] [CrossRef]
- Arab, D.; Kantzas, A.; Bryant, S.L. Water flooding of oil reservoirs: Effect of oil viscosity and injection velocity on the interplay between capillary and viscous forces. J. Pet. Sci. Eng. 2020, 186, 106691. [Google Scholar] [CrossRef]
- Jin, X.; Chao, C.; Edlmann, K.; Fan, X. Understanding the interplay of capillary and viscous forces in CO2 core flooding experiments. J. Hydrol. 2022, 606, 127411. [Google Scholar] [CrossRef]
- Suo, S.; Gan, Y.X. Tuning capillary flow in porous media with hierarchical structures. Phys. Fluids 2021, 33, 034107. [Google Scholar] [CrossRef]
- Lin, Q.; Bijeljic, B.; Raeini, A.Q.; Rieke, H.; Blunt, M.J. Drainage Capillary Pressure Distribution and Fluid Displacement in a Heterogeneous Laminated Sandstone. Geophys. Res. Lett. 2021, 48, e2021GL093604. [Google Scholar] [CrossRef]
- Pavuluri, S.; Maes, J.; Yang, J.; Regaieg, M.; Moncorgé, A.; Doster, F. Towards pore network modelling of spontaneous imbibition: Contact angle dependent invasion patterns and the occurrence of dynamic capillary barriers. Comput. Geosci. 2020, 24, 951–969. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Mao, Y.; Yang, L.; Wei, W.; Meng, Q.; Cai, J. A comprehensive review of factors affecting dynamic capillary effect in two-phase flow. Transp. Porous Media 2022, 1–22. [Google Scholar] [CrossRef]
- Ubbink, O. Numerical Prediction of Two Fluid Systems with Sharp Interfaces; University of London: London, UK, 1997. [Google Scholar]
- Jasak, H.; Weller, H.G.; Gosman, A.D. High resolution NVD differencing scheme for arbitrarily unstructured meshes. Int. J. Numer. Methods Fluids 1999, 31, 431–449. [Google Scholar] [CrossRef]
- Crank, J.; Phyllis, N. A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type. Math. Proc. Camb. Philos. Soc. 1947, 43, 431–449. [Google Scholar] [CrossRef]
- Su, J.; Chai, G.; Wang, L.; Cao, W.; Gu, Z.; Chen, C.; Xu, X.Y. Pore-scale direct numerical simulation of particle transport in porous media. Chem. Eng. Sci. 2019, 199, 613–627. [Google Scholar] [CrossRef]
- Blunt, M.J. Multiphase Flow in Permeable Media: A Pore-Scale Perspective; Imperial College London: London, UK, 2017. [Google Scholar]
- Ambekar, A.S.; Mattey, P.; Buwa, V.V. Pore-resolved two-phase flow in a pseudo-3D porous medium: Measurements and volume-of-fluid simulations. Chem. Eng. Sci. 2021, 230, 116128. [Google Scholar] [CrossRef]
- Tian, Y.; Ju, B.; Chen, X.; Chen, Z.; Dong, Y.; Wu, D. Pore-scale Investigation of Waterflooding Based on Experiments and Numerical Simulations Considering the Change in Geometry and Wettability. Energy Fuels 2021, 35, 17617–17628. [Google Scholar] [CrossRef]
- Patankar, S.V.; Spalding, D.B. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int. J. Heat Mass Transf. 1972, 15, 1787–1806. [Google Scholar] [CrossRef]
- van Doormaal, J.P.; Raithby, G.D. Enhancement of the SIMPLE method for predicting incompressible fluid flow. Numer. Heat Transf. Appl. 1984, 7, 147–163. [Google Scholar]
- Issa, R.I. Solution of implicitly discretized fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Sun, H.X.; Su, J.W. A sub-grid interface locating algorithm for free surface two-phase flows. J. Xi’an Jiaotong Univ. 2017, 51, 79–87. [Google Scholar]
- Su, J.; Chai, G.; Wang, L.; Cao, W.; Yu, J.; Gu, Z.; Chen, C. Direct numerical simulation of pore scale particle-water-oil transport in porous media. J. Pet. Sci. Eng. 2019, 180, 159–175. [Google Scholar] [CrossRef]







| Wettability | Conditions | Maximal Value | Minimal Value |
|---|---|---|---|
| 0 < θ < 90° (water-wet) 90° < θ < 180° (oil-wet) | 0 < β − θ < 90° | r (driving force) | r/cosθ (driving force) |
| −90° < β − θ < 0 | r/cos(θ − β) (driving force) | r/cosθ (driving force) | |
| −180° < β − θ < 0 | r/cos(θ − β) (driving force, resistance) | r/cosθ (resistance) |
| Wettability | Conditions | Maximal Value | Minimal Value |
|---|---|---|---|
| 0 < θ < 90° (water-wet) 90° < θ < 180° (oil-wet) | 0 < β + θ < 180° | r/cosθ (driving force) | r/cos(θ + β) (driving force, resistance) |
| 90° < β + θ < 180° | r/cosθ (resistance) | r/cos(θ + β) (resistance) | |
| 180° < β + θ < 270° | r/cosθ (resistance) | −r (resistance) |
| Wettability | Conditions | Maximal Value | Minimal Value |
|---|---|---|---|
| 0 < θ < 180° | 0 < β + θ < 90° | r/cos(θ + β) (driving force) | (Lsinβ + rcosβ)/(cosθ – sinβ) |
| 90° < β + θ < 270° | (Lsinβ + rcosβ)/(cosθ – sinβ) | r/cos(θ + β) (resistance) |
| Items | Value |
|---|---|
| |v|/m·s−1 | 0.1 |
| vx, vy/m·s−1 | 0.0707 |
| σ1~3/N·m−1 | 0.5, 0.05, 0.005 |
| θ1~7 | 15°, 30°, 45°, 60°, 90°, 120°, 165° |
| ρoil/g·cm−3 | 0.8498 |
| ρwater/g·cm−3 | 1 |
| μoil/m2 s−1 | 1.89 × 10−5 |
| μwater/m2 s−1 | 1.0 × 10−6 |
| Physical Quantity | Boundaries | ||
|---|---|---|---|
| Inlet | Outlet | Wall | |
| velocity | fixed value | zero gradient | fixed value |
| pressure | zero gradient | fixed value | zero gradient |
| water volume fraction | fixed value | zero gradient | constant contact angle |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, B.; Gu, Z.; Zhou, C.; Wang, L.; Huang, C.; Su, J. Investigation of the Effect of Capillary Barrier on Water–Oil Movement in Water Flooding. Appl. Sci. 2022, 12, 6285. https://doi.org/10.3390/app12126285
Hu B, Gu Z, Zhou C, Wang L, Huang C, Su J. Investigation of the Effect of Capillary Barrier on Water–Oil Movement in Water Flooding. Applied Sciences. 2022; 12(12):6285. https://doi.org/10.3390/app12126285
Chicago/Turabian StyleHu, Bingtao, Zhaolin Gu, Chenxing Zhou, Le Wang, Chuanqing Huang, and Junwei Su. 2022. "Investigation of the Effect of Capillary Barrier on Water–Oil Movement in Water Flooding" Applied Sciences 12, no. 12: 6285. https://doi.org/10.3390/app12126285
APA StyleHu, B., Gu, Z., Zhou, C., Wang, L., Huang, C., & Su, J. (2022). Investigation of the Effect of Capillary Barrier on Water–Oil Movement in Water Flooding. Applied Sciences, 12(12), 6285. https://doi.org/10.3390/app12126285







