Joint Communication–Motion Planning in Networked Robotic Systems

Abstract

In the recent decade, many research efforts in robotic society have considered motion planning for maintaining connectivity in networked robotic system (NRS) by exploiting robotic autonomous mobility. On the other hand, cognitive radio (CR) in the communication society aims at fully exploiting the spectrum in a wireless network, while the motion planning is seldom considered, as a wireless device itself may not decide where to go. In this article, joint communication–motion planning (JCMP) is proposed to boost the capability of NRS by exploiting both the adaptive communications and mobility control of autonomous robots. Specifically, we propose a JCMP framework for NRS, which aims at jointly exploiting the degree-of-freedom in mobility, space, time, frequency and power dimensions from both the motion and communication components. Afterward, we design and evaluate JCMP in a conventional and a CR-relay-assisted robot system, which shows the capability of JCMP in improving the performance of NRS. Finally, we summarize the proposed JCMP-enabled NRS framework and provide a series of future research directions.

1. Introduction and Related Works

In recent years, researchers have witnessed the development of robot technology and great industrial/academic efforts. With the interaction between the robot and physical and social environment, people have made considerable research contributions in robotic sensing, cognition, motion/path planning and control [1]. Compared with a single robot, the goal of the multi-robot system is to complete challenging tasks or significantly improve task performance, which requires consensus and cooperation among robots [2]. Therefore, it is very important to maintain the connection quality of information exchange between robots. Since mobile robots are unlikely to be connected by wire, wireless communication, network and infrastructure between robots will play a key role. The wireless connected robot network (WCRN) is likely to be included in the next generation communication network.

There is an increasing interest in integrating autonomous robots into wireless communication networks [3,4,5,6,7,8,9,10,11,12,13], which is the method in which the robot utilizes its own degrees of freedom (mostly transmission power and mobility) to improve the communication quality of the system. For example, refs. [3,4,5,6,7,11,12] all improve the communication quality through the location of mobile communication equipment, while most of the remaining research is through the joint optimization of transmission power and location. In terms of optimization objectives, some research takes traditional communication performance indicators as optimization objectives, such as minimizing the total energy consumption [4,5,11,13], bandwidth usage [9], communication rate [10], etc. There are also a few studies that use some novel indicators, such as maximizing the throughput guarantees to the video streaming [7].

As for contributions, most of the contributions above focus on designing communication-aware motion planning (CAMP) for different applications, as shown in

Table 1. Contributions on communication-aware motion planning (CAMP) in networked robotic system (NRS).

Ref.	Network Topology	Design Objective	Exploited DoF
[3]	Multi-hop	Maximizing communication quality of service	Mobility
[4]	Point-to-Point	Minimizing the total energy consumption	Mobility
[5]	Point-to-Point	Minimizing the total energy consumption	Mobility
[6]	Point-to-Point	Maximizing the strength of receiving signal	Mobility
[7]	Point-to-Point	Maximizing the throughput guarantees to the video streaming	Mobility
[8]	Multi-hop	Maximizing the long-term throughput	Mobility, Trans-mit Power
[9]	Multi-Unicast	Maximizing the bandwidth-usage	Topology
[10]	Multi-hop	Maximizing the communication rate	Transmit Power, Phase-shift
[11]	Point-to-Point	Minimizing the total energy consumption	Mobility
[12]	Multi-Unicast	Minimizing the service discrepancy among all pairs of robots	Mobility
[13]	Point-to-Point	Minimizing the total energy consumption	Mobility, Trans-mit Power

. Based on the above contributions, CAMP can be summarized as using the knowledge of connection quality to plan motion, so as to satisfy some communication constraints and improve specific task-oriented performance. Therefore, CAMP focuses on using mobile resources to optimize the communication quality, and the communication scheme is fixed or has limited adaptive ability, so the communication quality must be guaranteed through motion planning [11]. Although some works have considered adaptive transmission schemes, such as adaptive transmission power [11], they can be summarized as making full use of the degrees of freedom (DoF) in time, frequency and power to optimize communication quality to support mission objectives. Let us give two examples of robot monitoring to illustrate the above assertion. The scenario is shown in Figure 1. In this scenario, the sensing robot explores the area and tracks any interested target, and then transmits the sensing data to the base station.

We may conclude that the CAMP proposals have not fully considered the degree-of-freedom exhibited in motion planning and communication planning. Against this background, we propose the joint communication–motion planning (JCMP), which aims at jointly exploiting the DoF in mobility, space time, frequency and power (MSTFP) dimensions from both the motion and communication components equipped by the robots, which also leads to much more fertilized interplays between different dimensions in communication and motion. As a result, the NRS adopting JCMP will be capable of covering a wider range of application scenarios that involve holistic energy control, dynamic access and interference control.

In this paper, a robot-assisted surveillance model is considered as shown in Figure 1. The sensing robot, the relay robot as well as the base station are secondary users (SUs) and form a secondary relay system, and a primary user (PU) exists in the same area. If the underlay approach is adopted, the SUs are allowed to use the spectrum of the PU only when the interference generated by the SUs does not exceed the tolerance level of the PU. Hence, when the sensing robot is moving closer to the PU, it has to reduce its transmit power to avoid over-high interference, while the relay robot should strike a trade-off between motion and communication planning. Specifically, moving the relay robot closer to the sensing robot may help improve the source-relay link quality; however, the relay robot is also moving closer to the PU, which not only incurs a higher motion energy consumption, but also leads to a more stringent relay transmit power that degrades the link quality spanning from the relay robot to the base station. Hence, a more sophisticated design on the mobility/communication tradeoff is required, which is as will be shown quantitatively in Section 2 and Section 3.

The contributions of this paper are as follows:

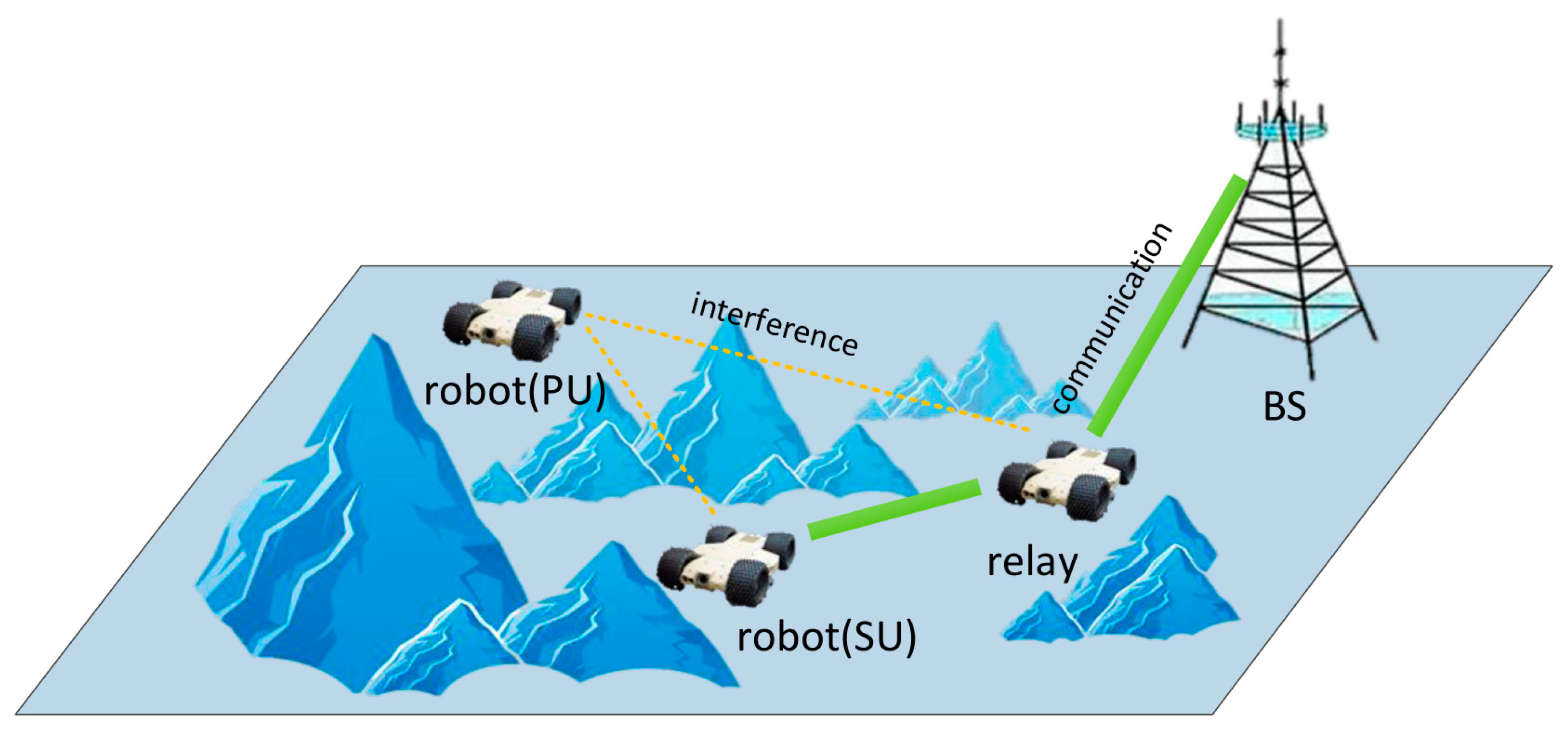
• Based on the OODA loop, we propose a relay-assisted robot surveillance prototype and a cognitive-relay-assisted robot system with interference constraints. We establish the communication system modeling considering the influence of path loss and multi-path fading.
• Under these two systems, we designed JCMP algorithms and jointly optimized the power and motion of the relay robot and the power of the sensing robot.
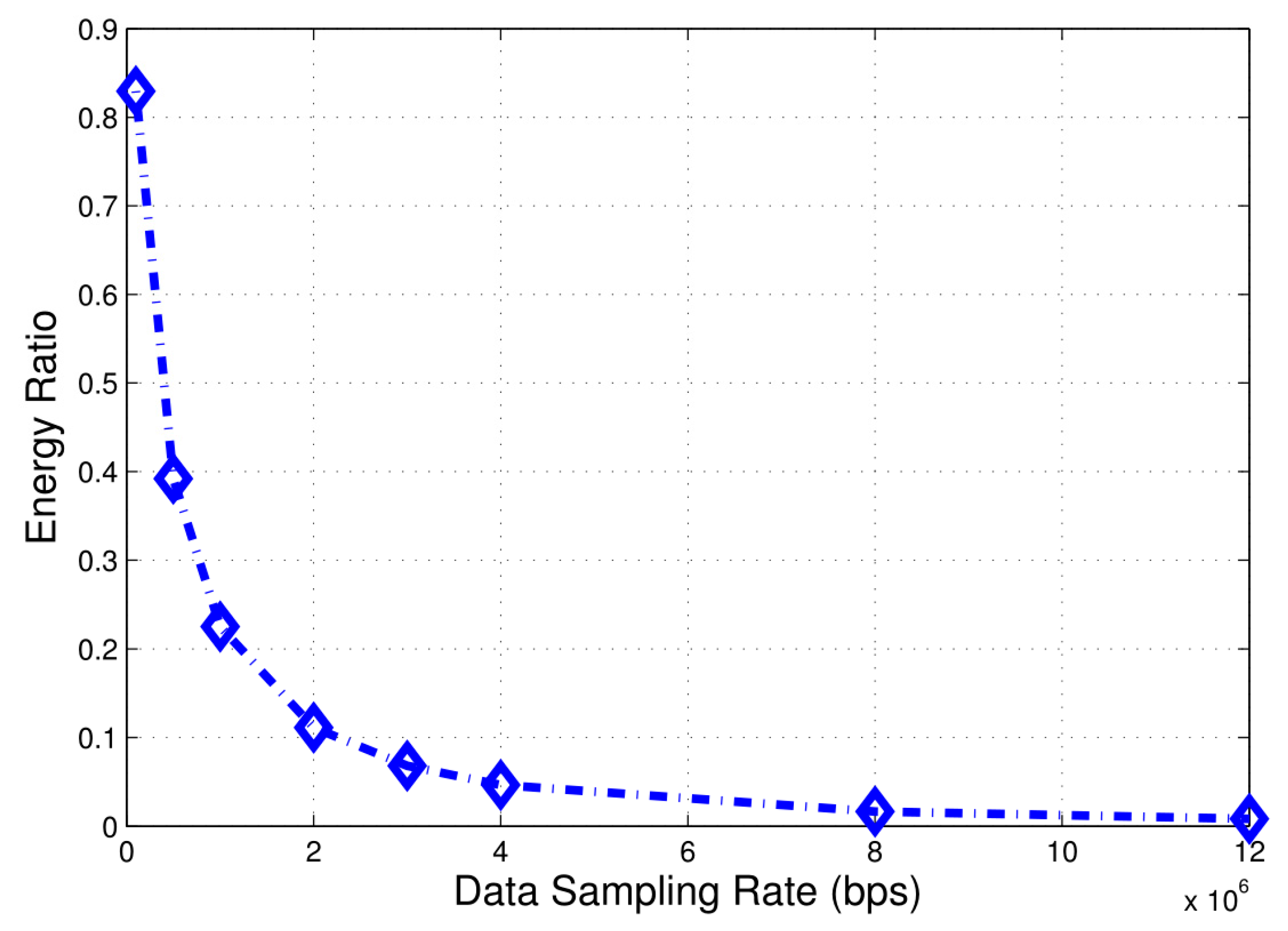
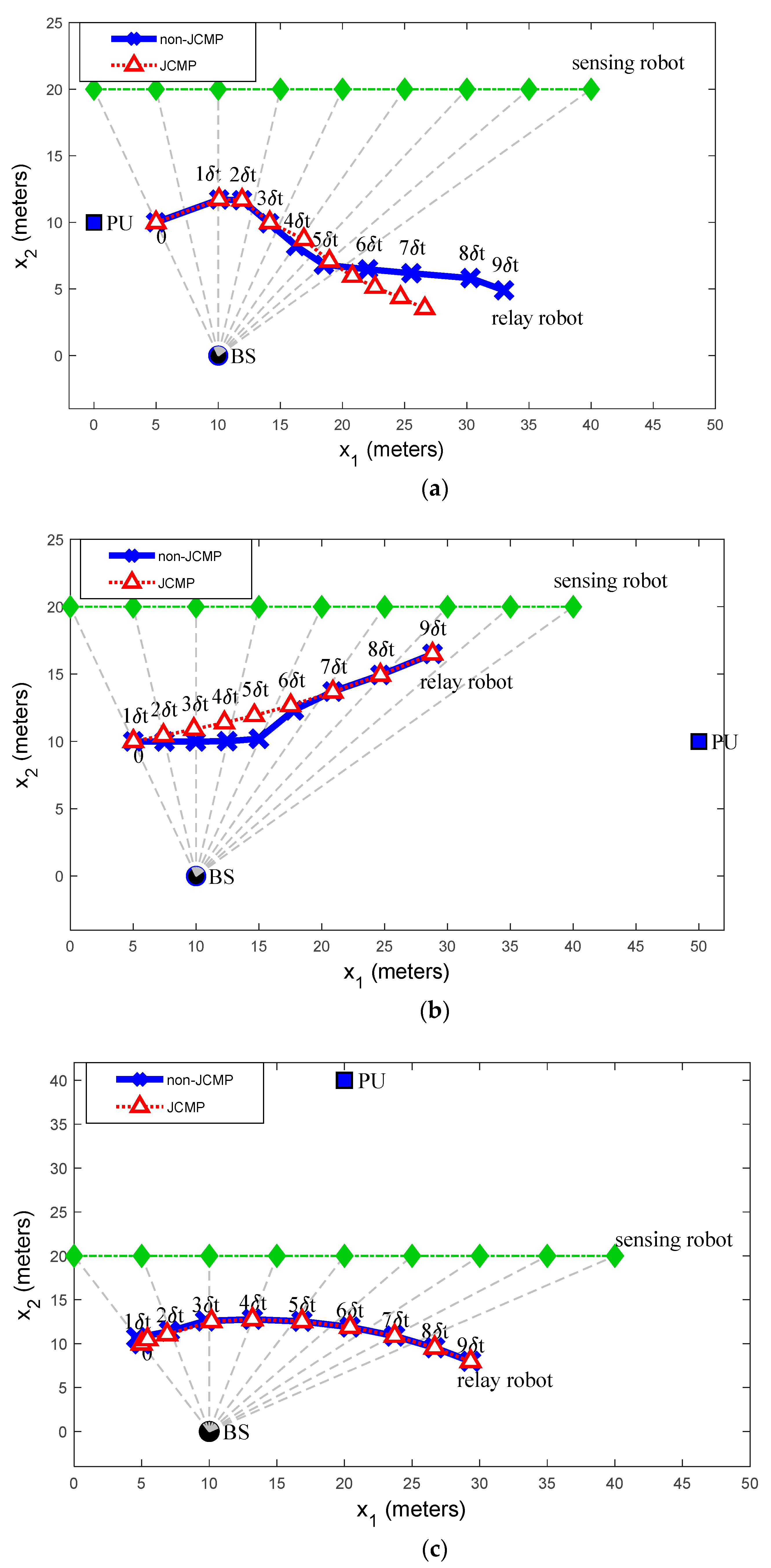
• Numerical results show that the joint planning method using JCMP can save more power than non-JCMP.

The rest of the paper is organized as follows: A conventional relay-assisted system and a CR-relay-assisted system are proposed in Section 2 and Section 3, respectively. In Section 2, the energy-saving ratio and the optimal trajectory of the relay robot are presented by numerical simulation. It is verified that, compared with non-JCMP, the JCMP model can significantly save the total energy consumption of the system. On this basis, Section 3 continues to add CR-relay to the communication model and discusses the relationship between the location of the primary user (PU) with the optimal trajectory and energy-saving ratio. Finally, several open problems and research directions are put forward along with the conclusions in Section 4.

2. Conventional Relay-Assisted Robot System

In order to present a comprehensive description of the algorithm design for both this section and Section 3, we give a cognitive-relay-assisted robot system scheme based on the OODA loop in Figure 2. Based on the basic theory of the OODA loop, the interaction between the robot and external environment can be divided into four parts: observe, orient, decide and act. Specific to the algorithm solution in this section: the first part in this scheme corresponds to resource sensing, that is, sensing the external wireless communication environment, which is based on the Rayleigh fading channel. We also consider the impact of path loss and other factors on communication performance. The second part corresponds to performance evaluation, which is divided into communication energy consumption evaluation and motion energy consumption evaluation. The third part corresponds to the JCMP, which jointly optimizes the position of the relay robot, transmit powers of the relay robot and transmit powers of the sensing robot in order to minimize the overall energy consumption of the system. The fourth part corresponds to task execution, which is divided into task execution in communication domain (i.e., power optimization) and task execution in geographic domain (i.e., location optimization). After the actions of these four parts are executed, they will have an effect on the environment and the next round of OODA loop starts.

In this section, we propose a relay-assisted robot surveillance prototype, and illustrate the benefit of JCMP. We consider a single-sensing-robot surveillance system depicted in Figure 1. We may still follow the OODA procedure in [14] to design the cognitive-relay-assisted robot surveillance example, with the emphasis on the JCMP procedure for minimizing the energy consumption.

The sensing robot is responsible for collecting monitored data with fixed sampling rate $\eta$ (bit/s) along a predefined route. After operating data collection for a period of $T$, the robots stop and send the monitored data to the base station through the relay robot. In this example, time division multiple access (TDMA) and decode-and-forward (DaF) relaying are adopted, where a transmission period is divided into two time slots (TSs). In the first TS, the sensing robot transmits the monitored data to the relay robot, while in the second TS, the relay decodes the data, re-encodes and forwards to the base station using same modulation and coding. We define a step, which comprises the data collection period $T$ plus the transmission period of 2 TSs. The surveillance tasks may endure multiple steps, and our objective is to minimize the total energy consumption which may contain two main parts: the communication and motion energy consumption.

Let us follow the OODA procedure in [14] to design the relay-assisted robot surveillance example, with an emphasis on the JCMP module.

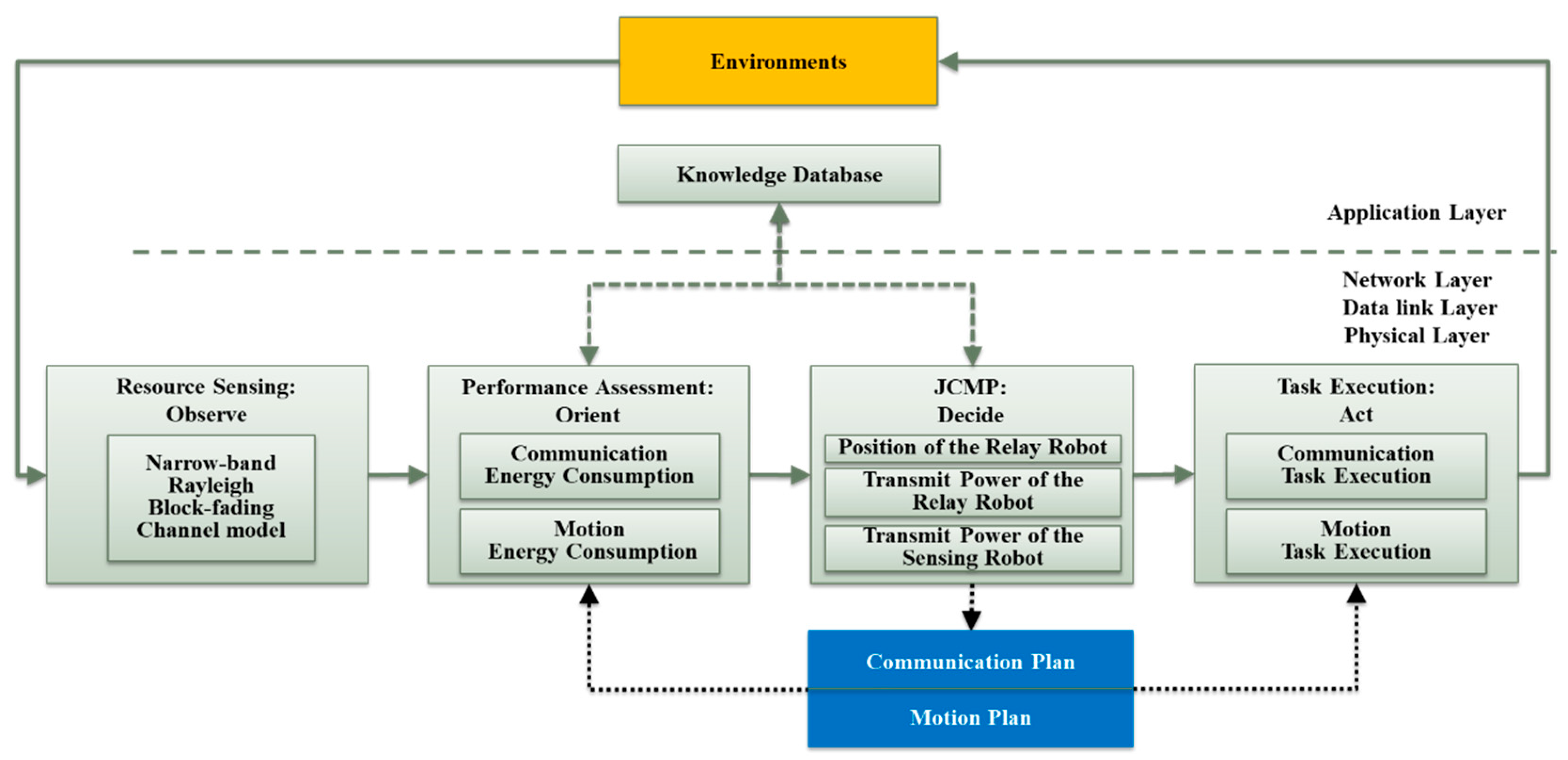
2.1. Resource Sensing: Observe

In order to enable effective JCMP, the prediction on the achievable communication quality is vital, which relies on the associated wireless channel measurement in the actual environment. We consider a realistic communication channel model, including both the path loss and the multipath fading.

As the wireless channel measurement is heavily reliant on the actual environment, in order to emphasize the JCMP procedure, let us now consider a universally adopted narrow-band block-fading channel model, where the fading coefficients remain constant for the duration of a transmission packet and then they are faded independently from one packet to another over the time dimension. We assume the wireless fading channel is Rayleigh distributed.

The channel bandwidth is $B$, and $N_0$ is the additive white Gaussian noise (AWGN) power spectral density. Given the transmit power $P_i$, the distance $d_{i,j}=\Vert x_i-x_j\Vert$ between the transmitter $i$ and the receiver $j$ and the pathloss exponent $\beta$. The instantaneous received signal-to-noise power ratio (SNR) is expressed as ${\gamma }_{ij}=\frac{P_i{d}_{ij}^{-\beta }{\left|h_{ij}\right|}^2}{N_{0}B}$, where the instantaneous channel coefficient $h_{ij}$ captures the small-scale fading effect of the channel spanning from the transmitter $i$ to the receiver $j$. In this paper, we assume that each robot is capable of measuring the instantaneous received SNR.

2.2. Performance Assessment: Orient

As the JCMP aims at minimizing the total energy consumption, including both the communication energy consumption and the motion energy consumption, which would be assessed in the orient procedure.

2.2.1. Communication Performance Assessment

As discussed in [14], the realistic channel model (RCM)-based connectivity quality metric (CQM) may better capture the communication performance of the NRSs in realistic environments. Hence, we adopt the packet error ratio (PER) as the metric for quantifying the communication performance.

Next, we quantify the relationship between the communication energy and PER. According to [15], then, the instantaneous per-hop PER between node $i$ and $j$ is given by [15].

$${\mathrm{PER}}_n\left({\gamma }_{ij}\right)\approx \{\begin{array}{cc}1,& \mathrm{if}\\ a_n\exp \left(-g_n{\gamma }_{ij}\right),& \mathrm{if}\end{array}\begin{array}{c}0<{\gamma }_{ij}<{\gamma }_{pn}\\ {\gamma }_{ij}\ge {\gamma }_{pn}\end{array}$$

(1)

where ${\gamma }_{ij}$ is the received signal-to-noise ratio (SNR) at node $j$ received from node $i$, ${\gamma }_{pn}$, $a_n$ and $g_n$ are relative to the transmission mode index $n$, which represents the specific modulation and channel coding rate as shown in Table II of [15]. We may select a mode from a set of six modes for different scenarios. As the channel is Rayleigh-faded, the resulted per-hop PER is

$$\begin{array}{ll}{\mathrm{PER}}_{\mathrm{n}}\left({\overline{\gamma }}_{ij}\right)\hfill & ={\displaystyle {\int }_0^{+\infty }{\mathrm{PER}}_{\mathrm{n}}}\left({\gamma }_{ij}\right)\frac{1}{{\overline{\gamma }}_{ij}}\exp \left(-\frac{{\gamma }_{ij}}{{\overline{\gamma }}_{ij}}\right)d\gamma \hfill \\ \hfill & =1-\exp \left(-\frac{{\gamma }_{pn}}{{\overline{\gamma }}_{ij}}\right)+\frac{a_n}{g_n{\overline{\gamma }}_{ij}+1}\exp \left(-g_n{\gamma }_{pn}\right)\exp \left(-\frac{{\gamma }_{pn}}{{\overline{\gamma }}_{ij}}\right)\hfill \end{array}$$

(2)

where $\overline{\gamma }$ is the average received SNR. As the channel coefficients over the two hops are mutually independent and the relay is decode-and-forward, we can obtain the end-to-end PER of the relay-assisted channel.

$$\begin{array}{ll}\hfill & {\mathrm{PER}}_{srd}^{\mathrm{e}2\mathrm{e}}\hfill \\ =\hfill & 1-\left[1-{\mathrm{PER}}_{\mathrm{n}}\left({\overline{\gamma }}_{sr}\right)\right]\left[1-{\mathrm{PER}}_{\mathrm{n}}\left({\overline{\gamma }}_{rd}\right)\right]\hfill \\ =\hfill & 1-\left[\exp \left(-\frac{{\gamma }_{pn}}{{\overline{\gamma }}_{sr}}\right)-\frac{a_n}{{\overline{\gamma }}_{sr}{g}_n+1}\exp \left(-g_n{\gamma }_{pn}\right)\exp \left(-\frac{{\gamma }_{pn}}{{\overline{\gamma }}_{sr}}\right)\right]\hfill \\ \times \hfill & \left[\exp \left(-\frac{{\gamma }_{pn}}{{\overline{\gamma }}_{rd}}\right)-\frac{a_n}{{\overline{\gamma }}_{rd}{g}_n+1}\exp \left(-g_n{\gamma }_{pn}\right)\exp \left(-\frac{{\gamma }_{pn}}{{\overline{\gamma }}_{rd}}\right)\right]\hfill \\ =\hfill & {\alpha }_n\left(\frac{1}{G_{sr}{P}_s}+\frac{1}{G_{rd}{P}_r}\right)+o\left(\frac{1}{\overline{\gamma }}\right)\simeq {\alpha }_n\left(\frac{1}{G_{sr}{P}_s}+\frac{1}{G_{rd}{P}_r}\right)\hfill \end{array}$$

(3)

where $P_s$ and $P_r$ are the transmit power of the sensing robot and of the relay robot, respectively. ${\alpha }_n$ is only relative to the mode index $n$ and defined as ${\alpha }_n=\left[{\gamma }_{pn}+\frac{a_n}{g_n}\exp \left(-g_n{\gamma }_{pn}\right)\right]$, while the average channel gains are defined as $G_{sr}=\frac{{\Vert x_s-x_r\Vert }^{-\beta }}{N_{0}B},\hspace{0.17em}{G}_{rd}=\frac{{\Vert x_r-x_d\Vert }^{-\beta }}{N_{0}B},\hspace{0.17em}i=1,\dots ,N.$ As shown in our previous works in [16], the full expression of Equation (3) is too complex for minimizing the transmit energy. Instead, the high SNR asymptotic expression is tight for medium-to-low PER for guaranteeing communication quality and also effective in power allocation. Hence, we opt for the asymptotic expression of Equation (3) by omitting the $o\left(\frac{1}{\overline{\gamma }}\right)$ components.

2.2.2. Motion Performance Assessment

In order to accurately evaluate the motion performance, we take the robot energy consumption model provided in [17] as a reference. Ref. [17] is committed to providing a more accurate energy consumption model of robot. They believed that the energy consumption of robots mainly came from motion, sensing of the external environment, microcontrollers and embedded computers. In terms of the relationship between motion and energy consumption, they pointed out that the motor carried by the robot converted electrical energy into mechanical energy. Therefore, the motion energy consumption was equal to the motor power consumption. The motor power consumption included the mechanical output power and the energy conversion loss. Let the mass of the robot be $m$ and the friction coefficient be $\mu$. If the velocity of the robot at a certain time is $v$, the acceleration is $a$, the gravity constant is $g$, and the energy conversion loss is $p_l$, then according to the laws related to physics, it can be concluded that the traction force required by the robot at this time is $m(a+g\mu )$, and the corresponding output power is $m(a+g\mu )v$. Based on the above conclusion, the motion power $p_m$ can be expressed as $p_m\left(m,v,a\right)=p_l+m\left(a+g\mu \right)v$. This conclusion was verified in the form of measured experiments in [17], so this model is accurate and reliable. If we let ${\kappa }_1=m\left(a+g\mu \right)$, ${\kappa }_2=p_l$, and $P_{mo}=p_m\left(m,v,a\right)$, we can adopt the linear motion power consumption model as in

$$P_{\mathrm{mo}}=\{\begin{array}{c}{\kappa }_{1}v+{\kappa }_2\\ 0\end{array}\begin{array}{c}\mathrm{if}\\ \mathrm{if}\end{array}\begin{array}{c}0<v\le v_{\max }\\ v=0\end{array}$$

(4)

and obviously, we only need to integrate (4) in time to obtain the corresponding energy consumption

$$E_{\mathrm{mo}}={\kappa }_1{l}_{\mathrm{R}}+{\kappa }_2{t}_{\mathrm{mo}}$$

(5)

where ${\kappa }_1$, ${\kappa }_2$ are constants, $v_{\max }$ is the maximum velocity of the mobile robot, and $l_{\mathrm{R}}$ is the trajectory length during $t_{\mathrm{mo}}$. It is assumed that the trajectory is a straight line connecting the current position and the next position of the mobile robot, while no physical obstacle is in between. It may be verified that when adopting the maximum velocity $v_{\max }$, the motion time $t_{\mathrm{mo}}$ ($t_{\mathrm{mo}}=l_{\mathrm{R}}/v_{\max }$) is minimized. With a specific trajectory length, the motion energy consumption $E_{\mathrm{mo}}$ is also minimized when adopting $v_{\max }$. Therefore, we use $v_{\max }$ as the velocity of the mobile robot.

2.3. Joint Communication-Motion Planning: Decide

2.3.1. Problem Formulation

After the performance assessment, the JCMP aims at minimizing the total energy consumption. Considering that the surveillance routes are predefined, the motion costs of the sensing robots may not be optimized. Hence, in each step, the energy consumption $E$ may contain three parts: the motion and communication costs of the relay robot, and the communication costs of the sensing robots, which can be formulated as an optimization problem given by Equation (6).

$$\begin{gathered} \underset{x_{\mathrm{R},k},P_{\mathrm{S},k},P_{\mathrm{R},\mathrm{k}}}{\min }J={\displaystyle \sum _{k=1}^K{P}_{\mathrm{s},\mathrm{k}}}{t}_s+P_{\mathrm{r},\mathrm{k}}{t}_{\mathrm{r}}+\omega l_{\mathrm{R}}\left(x_{\mathrm{r},\mathrm{k}},x_{\mathrm{r},\mathrm{k}-1}\right) \\ \mathrm{s}.\hspace{0.17em}\mathrm{t}.\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{l}_{\mathrm{R}}\left(x_{\mathrm{r},\mathrm{k}},x_{\mathrm{r},\mathrm{k}-1}\right)\le v_{\max }T,\hspace{0.17em}\forall k\in [1,K] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{p}_{srd}^{\mathrm{e}2\mathrm{e}}\left(P_{\mathrm{s},\mathrm{k}},P_{\mathrm{r},\mathrm{k}},x_{\mathrm{r},k}\right)\le p_{ub},\hspace{0.17em}\forall k\in [1,K] \end{gathered}$$

(6)

In Equation (6), $x_{\mathrm{r},k}$, $P_{\mathrm{s},\mathrm{k}}$ and $P_{\mathrm{r},\mathrm{k}}$ are the optimization variables. $x_{\mathrm{r},k}$ represents the position of the relay robot at the end of the $k$-th time step. $P_{\mathrm{s},\mathrm{k}}$ and $P_{\mathrm{r},\mathrm{k}}$ are the transmit power of the sensing robot and of the relay robot during their individual transmission duration, respectively. It is noted that the transmission during each time step initiates after the robots finish the movements, becoming stationary and synchronized. $t_{\mathrm{s}}$ and $t_{\mathrm{r}}$ represent the time duration of the sensing robot and of the relay robot for transmitting $T\eta$ bits of data samples, respectively, which are given by $t_s=T\eta /B{R}_{\mathrm{s}}$ and $t_r=T\eta /B{R}_{\mathrm{r}}$, where Rs and Rr are the spectral efficiency (bit/s/Hz) of the sensing robot and of the relay robot. In addition, $\omega l_{\mathrm{R}}\left(x_{\mathrm{r},\mathrm{k}},x_{\mathrm{r},\mathrm{k}-1}\right)$ is the motion energy consumption of the relay robot, where $l_{\mathrm{R}}\left(x_{\mathrm{r},\mathrm{k}},x_{\mathrm{r},\mathrm{k}-1}\right)=\Vert x_{\mathrm{r},\mathrm{k}}-x_{\mathrm{r},\mathrm{k}-1}\Vert$ is the distance traveled by the relay robot from the current position $x_{\mathrm{r},\mathrm{k}-1}$ to the goal position $x_{\mathrm{r},\mathrm{k}}$ in the $k$-th time step. The coefficient $\omega$ is expressed as $\omega ={\kappa }_1+{\kappa }_2/v_{\max }$. Finally, $p_{srd}^{\mathrm{e}2\mathrm{e}}\left(P_{\mathrm{s},\mathrm{k}},P_{\mathrm{r},\mathrm{k}},x_{\mathrm{r},k}\right)$ is the required end-to-end PER of the two-hop link from the sensing robot to the base station via the relay robot, and $p_{\mathrm{ub}}$ is the upper bound.

2.3.2. JCMP Solutions

Equation (6) involves the joint optimization of the motion (position of the relay robot) and communication (transmit powers of the relay robot and sensing robot), where the variables are $x_{\mathrm{r},\mathrm{k}}$, $P_{\mathrm{s},\mathrm{k}}$, and $P_{\mathrm{r},\mathrm{k}}$. Solving Equation (6) directly may incur a relative high computation complexity. Therefore, we first consider a simpler and classical communication planning problem, namely, given the positions of the sensing robots, the relay robot and the base station, how do we minimize the total communication energy consumption given the PER constraint? As will be shown below, we may obtain the closed-form expression of the optimal transmit power of the sensing robots and the relay robot. Based on these closed-form optimal power expressions, the original problem in Equation (6) is transformed into a motion planning problem, namely, given the optimal communication energy consumption for each possible position of the relay robot, how do we optimize the motion of the relay robot for minimizing the total energy consumption?

Hence, during the $k$-th time step, if the position of the relay robot $x_{\mathrm{r},\mathrm{k}}$ is given, the motion energy is fixed, and we may formulate the communication planning problem according to Equation (6) as

$$\begin{array}{l}\underset{P_{\mathrm{s},k,}{P}_{\mathrm{r},\mathrm{k}}}{\min }{J}_k=P_{\mathrm{s},\mathrm{k}}{t}_{\mathrm{s}}+P_{\mathrm{r},\mathrm{k}}{t}_{\mathrm{r}}\hfill \\ \hspace{0.17em}\mathrm{s}.\hspace{0.17em}\mathrm{t}.\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{p}_{\mathrm{srd}}^{\mathrm{e}2\mathrm{e}}\left(P_{\mathrm{s},\mathrm{k}},P_{\mathrm{r},\mathrm{k}}\right)\le p_{\mathrm{ub}}.\hfill \end{array}\forall k\in [1,K]$$

(7)

By analyzing Equation (7), we may find that the objective function is linear, which is convex. For the constraint, we define the function $h=p_{\mathrm{srd}}^{\mathrm{e}2\mathrm{e}}\left(P_{\mathrm{s},\mathrm{k}},P_{\mathrm{r},\mathrm{k}}\right)-p_{\mathrm{ub}}$, and calculate its Hessian matrix. The results show that the Hessian matrix $H$ is positive definite, which confirms the communication planning problem of Equation (7) is convex, and we may obtain an optimal solution with Karush–Kuhn–Tucker (KKT) conditions. Using the Lagrange function and by applying KKT conditions, we may derive the expressions of the optimal transmit powers in closed-form:

$$\begin{array}{l}{P}_{\mathrm{s},\mathrm{k}}^{*}\left(x_{\mathrm{r},\mathrm{k}}\right)=\frac{\sqrt{t_{\mathrm{r}}{t}_{\mathrm{s}}{u}_k{v}_k}+t_{\mathrm{s}}{u}_k}{t_{\mathrm{s}}{p}_{\mathrm{ub}}}\\ P_{\mathrm{r},\mathrm{k}}^{*}\left(x_{\mathrm{r},\mathrm{k}}\right)=\frac{\sqrt{t_{\mathrm{r}}{t}_{\mathrm{s}}{u}_k{v}_k}+t_{\mathrm{r}}{v}_k}{t_{\mathrm{r}}{p}_{\mathrm{ub}}}\end{array}$$

(8)

where we have $u_k={\alpha }_n/G_{sr,k}$, $v_k={\alpha }_n/G_{rd,k}$, $G_{sr,k}={\Vert x_{\mathrm{s},\mathrm{k}}-x_{\mathrm{r},\mathrm{k}}\Vert }^{-\beta }/N_{0}B$, and $G_{rd,k}={\Vert x_{\mathrm{r},\mathrm{k}}-x_{\mathrm{d},\mathrm{k}}\Vert }^{-\beta }/N_{0}B$ with $x_{\mathrm{s},\mathrm{k}}$ being the position of the sensing robot during the $k$-th time step. By substituting Equation (8) into Equation (6), we may transform the original problem into a motion planning problem, which is only relative to the positions $x_r=\left\{x_{r,1},x_{r,2},\dots ,x_{r,K}\right\}$ of the relay robot.

$$\begin{array}{l}\underset{x_r}{\min }\hspace{0.17em}\hspace{0.17em}J={\displaystyle \sum _{k=1}^K{P}_{\mathrm{s},\mathrm{k}}^{*}}\left(x_{\mathrm{r},\mathrm{k}}\right)t_s+P_{\mathrm{r},\mathrm{k}}^{*}\left(x_{\mathrm{r},\mathrm{k}}\right)t_r+\omega l_{\mathrm{R}}\left(x_{\mathrm{r},\mathrm{k}},x_{\mathrm{r},\mathrm{k}-1}\right)\hfill \\ \hspace{0.17em}\mathrm{s}.\hspace{0.17em}\mathrm{t}.\hspace{0.17em}\hspace{0.17em}{l}_{\mathrm{R}}\left(x_{\mathrm{r},\mathrm{k}},x_{\mathrm{r},\mathrm{k}-1}\right)\le v_{\max }T,\hspace{0.17em}\forall k\in [1,K]\hfill \end{array}.$$

(9)

Letting ${\xi }_k\left(x_{\mathrm{r},k}\right)=P_{\mathrm{s},k}^{*}\left(x_{\mathrm{r},k}\right)t_{\mathrm{s}}+P_{\mathrm{r},k}^{*}\left(x_{\mathrm{r},k}\right)t_{\mathrm{r}}$, we have

$$\begin{array}{l}{\xi }_k\left(x_{\mathrm{r},k}\right)=P_{\mathrm{s},k}^{*}\left(x_{\mathrm{r},k}\right)t_{\mathrm{s}}+P_{\mathrm{r},k}^{*}\left(x_{\mathrm{r},k}\right)t_{\mathrm{r}}\hfill \\ ={\left({\kappa }_{\mathrm{s}}{\Vert x_{\mathrm{r},k}-x_{\mathrm{s},k}\Vert }^{\frac{\beta }{2}}+{\kappa }_{\mathrm{r}}{\Vert x_{\mathrm{r},k}-x_{\mathrm{bs}}\Vert }^{\frac{\beta }{2}}\right)}^2\hfill \\ ={\left({\kappa }_{\mathrm{s}}{\Vert {\mathrm{A}}_k{x}_r+\left(-x_{\mathrm{s},k}\right)\Vert }^{\frac{\beta }{2}}+{\kappa }_{\mathrm{r}}{\Vert {\mathrm{A}}_k{x}_r+\left(-x_{\mathrm{bs}}\right)\Vert }^{\frac{\beta }{2}}\right)}^2\hfill \\ ={\left[f_1\left(x_r\right)+f_2\left(x_r\right)\right]}^2={\left[g\left(x_r\right)\right]}^2.\hfill \end{array}$$

(10)

Both ${\mathrm{A}}_k{x}_r+\left(-x_{\mathrm{s},k}\right)$ and ${\mathrm{A}}_k{x}_r+\left(-x_{\mathrm{bs}}\right)$ are affine mappings of $x_r$, which guarantees the convexity of $f_1\left(x_r\right)$, $f_2\left(x_r\right)$ and $g\left(x_r\right)$. Considering $g\left(x_r\right)$ is a nonnegative convex function, ${\left[g\left(x_r\right)\right]}^2$ is also convex. Similarly, $w\Vert x_{r,k}-x_{r,k-1}\Vert$ is convex, so the function $J$ is also convex. Therefore, the motion planning problem of Equation (9) is a convex optimization problem; hence, we may obtain the optimal position of the relay robot in each time step by using the interior point method.

2.4. Task Execution: Act

2.4.1. Implementation

In the considered surveillance scenario, two kinds of data should be exchanged between the sensing robot and the relay robot, namely the monitored data sampled by the sensors on the sensing robot, and the control information, e.g., the goal positions of the sensing robot $x_{\mathrm{s},\mathrm{k}}$, the transmit powers that the sensing robots may adopt $P_{s,k}$. The motion planning algorithm may be operated on the relay robot. In the beginning of each time step, the sensing robot sends the monitored data $T\eta$ and its goal positions $x_s=\left\{x_{s,1},x_{s,2},\dots ,x_{s,K}\right\}$ during the next $K$ time steps to the relay robot. After the computation of Equation (6), the relay robot sends the allocated transmit power $P_s=\left\{P_{s,1},P_{s,2},\dots ,P_{s,K}\right\}$ to the sensing robot, which is used during the communication between the sensing robot and the relay robot.

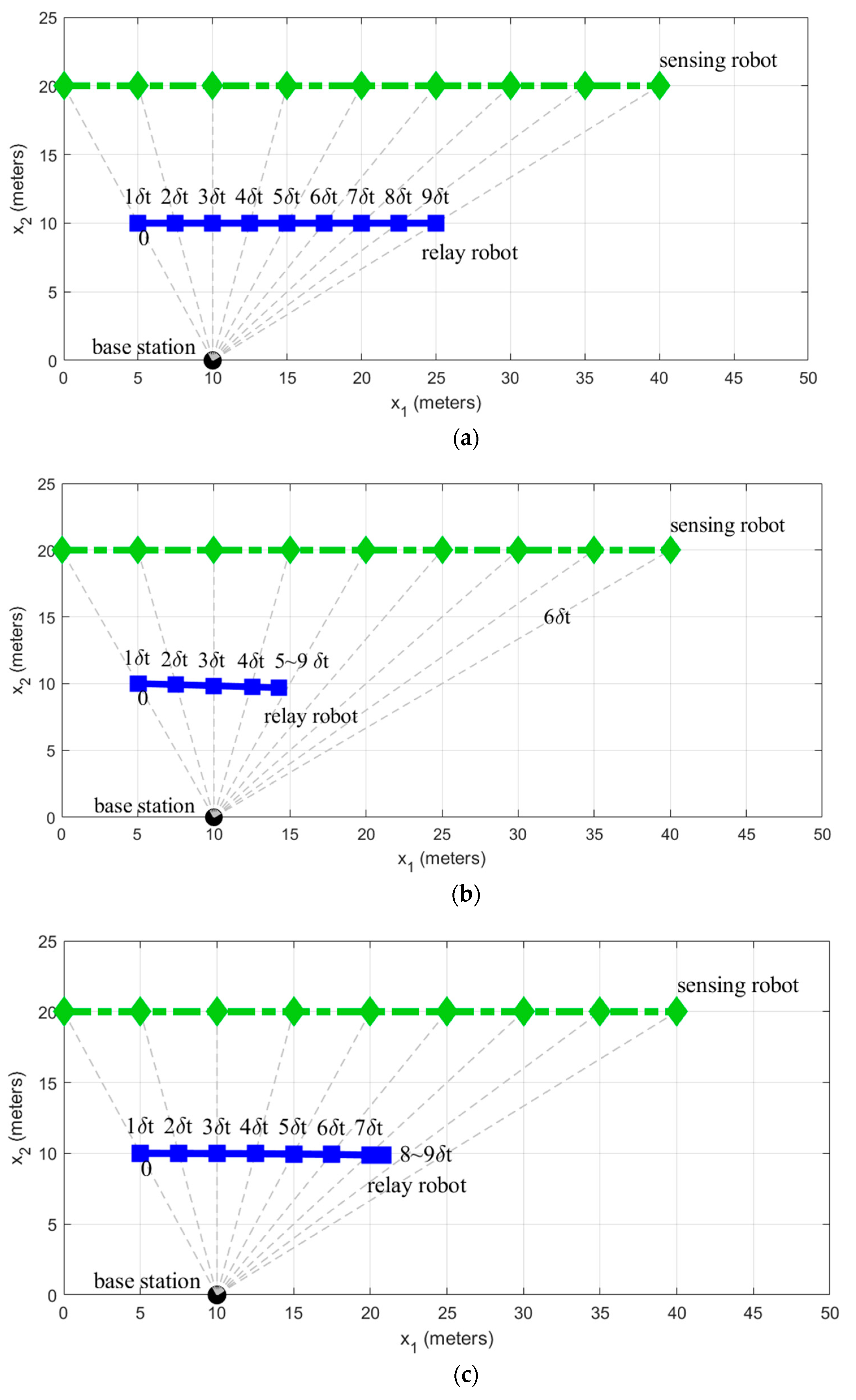
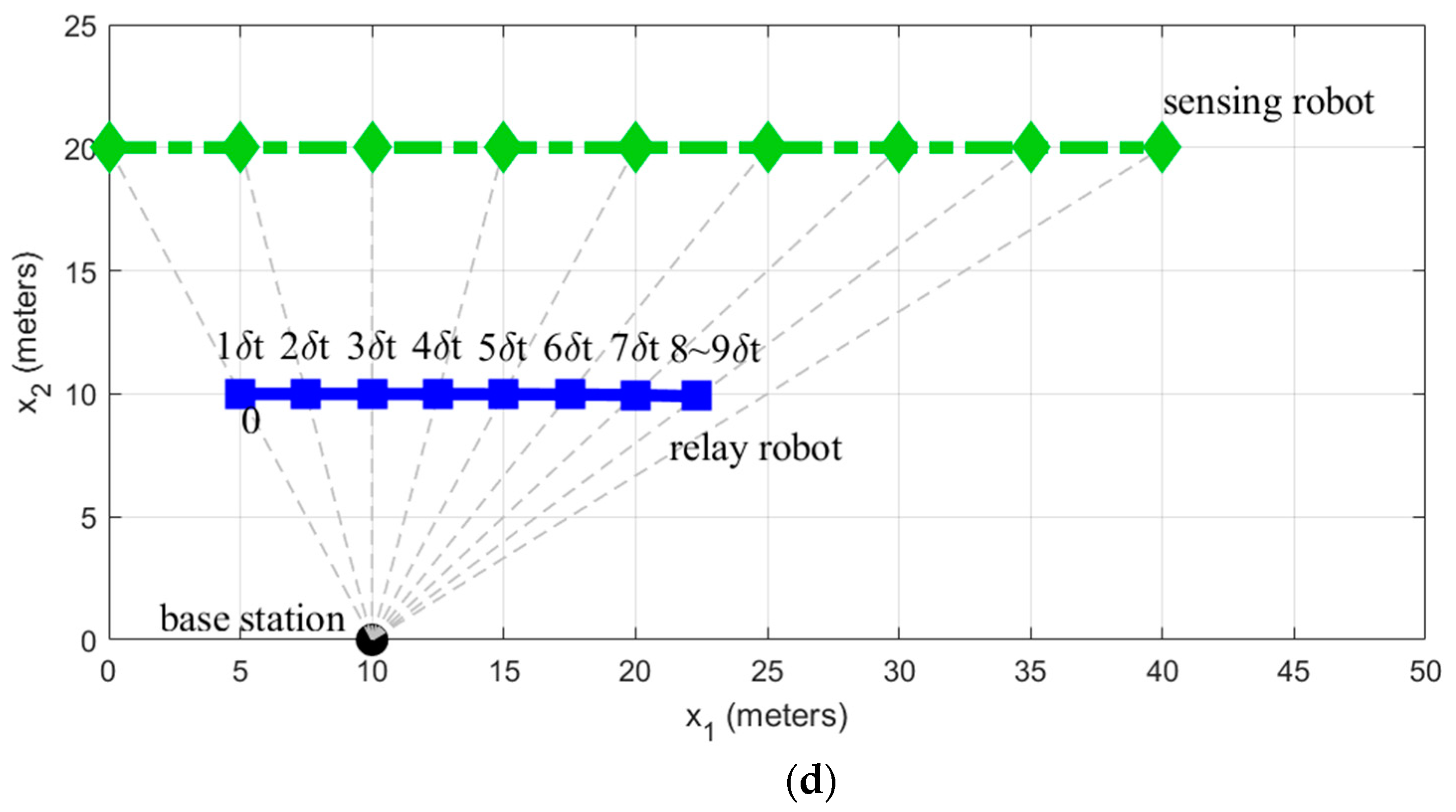
2.4.2. Results

We consider a workspace of a 50 m × 25 m region, and the remote base station is located at a fixed position $x_d=\left(10,0\right)$. We adopt the 802.11 g protocol and the corresponding bandwidth $B=20$MHz. Moreover, $\beta$ is often obtained from empirical measurements, here we set $\beta =3.68$. Furthermore, the noise power spectral density $N_0$ is set to −100 dBm/Hz. For the end-to-end PER upper bound, we use an accepted value 0.01, and adopt the transmission-mode index $n=2$ [15]. The motion parameters are measured for a Pioneer 3DX robot as follows: ${\kappa }_1=7.4$, ${\kappa }_2=0.29$ and $v_{\max }=1$ [17].

We assume the trajectory of the sensing robot travels along a straight line from $x_{\mathrm{s},1}=(0,20)$ to $x_{s,9}=(40,20)$. The JCMP-optimized trajectories of the relay robot at different data sampling rates are shown by the square lines in Figure 3. In each time step, the relay robot aims at moving to the position where the total energy cost is minimal.

If we only take the communication quality into account for motion planning, namely, adopting the non-JCMP philosophy that just optimizes communication performance, during each period of time $T$, the optimal position of the relay robot is located on the straight line between the base station and the sensing robot, as shown by Figure 3a and serve it as our benchmark. As we increase the data sampling rate of the sensing robot with several separate values, ${\eta }_{\mathrm{s}}=1$, 5, 10 Mbit/s. The results demonstrate that at a lower data sampling rate, the relay robot may prefer staying at the same place to moving, as shown in Figure 3. At a higher data sampling rate, e.g., ${\eta }_{\mathrm{s}}=10$ Mbit/s, it is preferred that the relay robot moves to the position with better wireless communication quality instead of staying at the same place, and gets closer to the trajectory of the benchmark. The reason is that when the data sampling rate increases, the weight of the communication terms in the objective function of (8) increases. In order to minimize the total energy consumption of the system, the optimization algorithm tends to minimize those terms with larger weights.

We compare the total energy consumption of the JCMP with that of the benchmark during the whole period, and the results are shown in Figure 4. The data sampling rates evaluated are from ${\eta }_{\mathrm{s}}=$100 kbit/s to 12 Mbit/s. When the motion energy of the sensing robot is not considered, the corresponding total energy consumption of the JCMP to the benchmark ranges from 89.16% to 2.01%, and this ratio is defined as the energy saving of the JCMP. On the other hand, considering that the motion of the sensing robot cannot be optimized, when the constant motion energy of the sensing robot is included, the corresponding total energy saving ratio will decrease. Based on the results of Figure 4, we may conclude that at relatively low data sampling rates, the JCMP is capable of saving more energy than the benchmark, which only optimizes the communication energy. At high data sampling rates, e.g., ${\eta }_{\mathrm{s}}=12$Mbit/s, the communication term becomes the dominant component in the objective function, and hence the solution may get closer to that of the CAMP benchmark.

3. Cognitive-Relay-Assisted Robot System with Interference Constraints

In this section, we enhance the robot surveillance prototype by incorporating cognitive relaying and illustrate the benefit of JCMP. We consider a system, where the sensing robot, the relay robot and the base station are secondary users (SUs), and a primary user (PU) coexists. The underlay approach is considered and the interference constraint on the primary user should be satisfied, namely, a limited amount of interference emitted by the SUs can be tolerated at the PU. The system settings are identical to those in the system model of the previous section, except that the transmit power of the sensing robot and the relay robot should satisfy the interference constraints, while the design objective is minimizing the total energy consumption of the SUs.

3.1. Resource Sensing: Observe

We consider the narrow-band Rayleigh block-fading channel model as in the previous section, and the instantaneous received signal-to-noise power ratio (SNR) is expressed as ${\gamma }_{ij}=\frac{P_i{d}_{ij}^{-\beta }{\left|h_{ij}\right|}^2}{N_{0}B}$, where the channel bandwidth is $B$, and $N_0$ is the additive white Gaussian noise (AWGN) power spectral density, the distance $d_{i,j}=\Vert x_i-x_j\Vert$ between the transmitter $i$ and the receiver $j$ and the pathloss exponent $\beta$. In this paper, we assume that each robot is capable of measuring the instantaneous received SNR.

3.2. Performance Assessment: Orient

We aim at minimizing the total energy consumption, including both the communication energy consumption and the motion energy consumption. The communication energy depends on the transmit powers of the sensing robot and the relay robot, which should satisfy both the PER constraint and the interference constraint. The PER formulation is given by Equation (2). During the $k$-th time step, the transmit power $P_{i,k}$ emitted by the sensing robot and the relay robot should satisfy the interference constraints. Specifically, the average received signal-to-noise power ratio at the PU is ${\overline{\gamma }}_{ip,k}(P_{i,k})=\frac{P_{i,k}{d}_{ip,k}^{-\beta }}{N_{0}B}$ should be smaller than the pre-defined threshold ${\gamma }_{p,th}$, namely, ${\overline{\gamma }}_{sp,k}<{\gamma }_{p,th}$ and ${\overline{\gamma }}_{rp,k}<{\gamma }_{p,th}$. Finally, the motion energy consumption is quantified by Equation (5).

3.3. Joint Communication-Motion Planning: Decide

3.3.1. Problem Formulation

After the performance assessment, the JCMP aims at minimizing the total energy consumption. In each step, the energy consumption may contain three parts: the motion and communication costs of the relay robot, and the communication costs of the sensing robots, which can be formulated as an optimization problem given by Equation (11).

$$\begin{gathered} \underset{x_{\mathrm{r},k},P_{\mathrm{S},k},P_{\mathrm{R},\mathrm{k}}}{\min }J={\displaystyle \sum _{k=1}^K{P}_{\mathrm{s},\mathrm{k}}}{t}_s+P_{\mathrm{r},\mathrm{k}}{t}_{\mathrm{r}}+\omega l_{\mathrm{R}}\left(x_{\mathrm{r},\mathrm{k}},x_{\mathrm{r},\mathrm{k}-1}\right) \\ \mathrm{s}.\hspace{0.17em}\mathrm{t}.\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{l}_{\mathrm{R}}\left(x_{\mathrm{r},\mathrm{k}},x_{\mathrm{r},\mathrm{k}-1}\right)\le v_{\max }T,\hspace{0.17em}\forall k\in [1,K] \\ \hspace{1em}\hspace{1em}\hspace{1em}{p}_{srd}^{\mathrm{e}2\mathrm{e}}\left(P_{\mathrm{s},\mathrm{k}},P_{\mathrm{r},\mathrm{k}},x_{\mathrm{r},k}\right)\le p_{ub},\hspace{0.17em}\forall k\in [1,K] \\ {\overline{\gamma }}_{ip,k}(P_{s,k})\le {\gamma }_{p,th},\hspace{0.17em}\forall k\in [1,K] \\ \hspace{1em}\hspace{1em}{\overline{\gamma }}_{ip,k}(P_{\mathrm{r},\mathrm{k}},x_{\mathrm{r},k})\le {\gamma }_{p,th},\hspace{0.17em}\forall k\in [1,K] \end{gathered}$$

(11)

In Equation (11), $x_{\mathrm{r},k}$, $P_{\mathrm{s},\mathrm{k}}$ and $P_{\mathrm{r},\mathrm{k}}$ are the optimization variables, which represent the position of the relay robot during the $k$-th time step, as well as the transmit power of the sensing robot and of the relay robot during their individual transmission duration, respectively. Besides the motion constraints and the PER constraints as given in Equation (6), the third constraint defines the interference constraints imposed on the transmit power $P_{s,k}$ of the sensing robot, while the fourth constraint represents the interference constraints imposed on both the transmit power $P_{r,k}$ and the motion strategy $x_{r,k}$ of the relay robot.

3.3.2. JCMP Solutions

Equation (11) involves the joint optimization of the motion (position of the relay robot $x_{\mathrm{r},\mathrm{k}}$) and communication (transmit powers of the relay robot $P_{\mathrm{r},\mathrm{k}}$ and of the sensing robot $P_{\mathrm{s},\mathrm{k}}$). Firstly, we formulate the same communication planning problem as in Equation (7) and the optimal transmit power is given by Equation (8). By substituting Equation (8) into Equation (11), we may transform the original problem into a motion planning problem, which is only relative to the positions $x_r=\left\{x_{r,1},x_{r,2},\dots ,x_{r,K}\right\}$ of the relay robot and its formulation is similar to that in Equation (9), except that the selected $x_r$ should also satisfy the interference constraints.

$$\begin{gathered} \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\underset{x_r}{\min }\hspace{0.17em}\hspace{0.17em}J={\displaystyle \sum _{k=1}^K{P}_{\mathrm{s},\mathrm{k}}^{*}}\left(x_{\mathrm{r},\mathrm{k}}\right)t_s+P_{\mathrm{r},\mathrm{k}}^{*}\left(x_{\mathrm{r},\mathrm{k}}\right)t_r+\omega l_{\mathrm{R}}\left(x_{\mathrm{r},\mathrm{k}},x_{\mathrm{r},\mathrm{k}-1}\right) \\ \mathrm{s}.\hspace{0.17em}\mathrm{t}.\hspace{0.17em}\hspace{0.17em}{l}_{\mathrm{R}}\left(x_{\mathrm{r},\mathrm{k}},x_{\mathrm{r},\mathrm{k}-1}\right)\le v_{\max }T,\hspace{0.17em}\forall k\in [1,K] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{P}_{\mathrm{s},\mathrm{k}}^{*}\left(x_{\mathrm{r},\mathrm{k}}\right)G_{sp,k}\le {\gamma }_{p,th},\hspace{0.17em}\forall k\in [1,K] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{P}_{\mathrm{s},\mathrm{k}}^{*}\left(x_{\mathrm{r},\mathrm{k}}\right)G_{rp,k}\left(x_{\mathrm{r},\mathrm{k}}\right)\le {\gamma }_{p,th},\hspace{0.17em}\forall k\in [1,K] \end{gathered}$$

(12)

where $G_{sp,k}={\Vert x_{s,k}-x_{p,k}\Vert }^{-\beta }/N_{0}B$ and $G_{rp,k}\left(x_{\mathrm{r},\mathrm{k}}\right)={\Vert x_{\mathrm{r},\mathrm{k}}-x_{p,k}\Vert }^{-\beta }/N_{0}B$. It may be identified that Equation (12) is nonconvex. Therefore, we may use the relay trajectory of the non-CR scenario in Equation (9) as the initial value and iteratively optimize $x_r$ using the interior point method; however, the global optimum is not guaranteed.

3.4. Task Execution: Act

3.4.1. Implementation

In the cognitive-relay-assisted robot surveillance scenario, the monitored data sampled by the sensing robot, as well as the control information should be exchanged between the sensing robot and the relay robot, where the JCMP algorithm may be operated at the relay robot.

In the beginning of each time step, the sensing robot sends the monitored data $T\eta$ and its goal positions $x_s=\left\{x_{s,1},x_{s,2},\dots ,x_{s,K}\right\}$ during the next $K$ time steps to the relay robot, it is also assumed that the positions of the PU during the next $K$ time steps are available at the cognitive relay robot, which may rely on proactive cooperation from the PUs. After solving the problem in Equation (11), the relay robot sends the allocated transmit power $P_s=\left\{P_{s,1},P_{s,2},\dots ,P_{s,K}\right\}$ to the sensing robot, which is used during the communication between the sensing robot and the relay robot.

3.4.2. Results

We still consider the same configuration as in Section 2 and assume the same trajectory of the sensing robot travels along a straight line from $x_{\mathrm{s},1}=(0,20)$, $x_{s,9}=(40,20)$. A fixed PU coexists along with a secondary relay system consisted of the sensing robot, the relay robot and the base station. In each time step, the relay robot adopting the JCMP strategy aims at moving to the position where the total energy consumption is minimal, while the relay robot adopting the non-JCMP strategy only take the communication quality into account. The sampling rate of the sensing robot is ${\eta }_{\mathrm{s}}=1$Mbit/s, while the maximum tolerable interference-to-noise ratio at the PU is 10 dB.

We may compare the behavior of the relay robot given different PU locations as seen in Figure 5. In Figure 5a, the PU is located near the start point of the sensing robot’ trajectory, while the energy saving ratio is 17.5%. Similar to the case without PU as seen in Figure 2, the JCMP relay robot may prefer staying at the same place to moving, while the non-JCMP relay robot is more inclined to follow the trace of the sensing robot. However, in order to avoid high interference at the PU, the relay robot of both planning strategies tends to move away from the PU.

In Figure 5b, the PU is located near the end point of the sensing robot’ trajectory, while the energy saving ratio is 1.45%. Either non-JCMP or JCMP is adopted, the relay robot adopting has to move close the sensing robot as the sensing robot approaches the PU, which significantly limits the transmit power of the sensing robot. Additionally, the stringent interference imposed by the PU limits the feasible trajectories of the relay robot. Hence, the achievable energy saving of JCMP is stringent.

The same situation was observed for the cases, where the PU is located in the adversarial positions near the base station or along the trajectory of the sensing robot as illustrated in the Figure 5c,d. In these scenarios, the feasible solution space is tightly constrained, hence JCMP has very limited potential to find a better trajectory than non-JCMP. As can be observed in Figure 5d, in order to pose low interference on the PU, the relay robot moves too far away from the base station and even exceeds the sensing robot, and hence the PU may prohibit the relay robot from providing effective relaying.

Some insights may already be inferred from the results of the simple system of a single PU and three SUs. Firstly, it may be found that the location of the PU has a noticeable impact on the optimal trajectories of both non-JCMP and JCMP, as well as on the achievable energy consumption. It may also be anticipated that as the maximum tolerable interference-to-noise ratio decreases or the PU is located further away from the operating area of the secondary relay system, the feasible solution space may be relaxed, and the trajectories and the energy-saving ratio may be closer to those in the cases without PU as shown in Figure 3.

As was also illustrated by the results, sophisticated interactions have emerged in a simple four-node CR system; hence, many more configurations may need to be analyzed, leading to a series of open problems and new findings. Due to the limited space of this introductory treatise, these open problems will be investigated in our future works.

4. Conclusions and Open Problems

In this paper, we first reviewed the contributions on NRSs, with a focus on the CAMP scheme and proposed that JCMP may outperform CAMP by exploiting more degrees-of-freedom. Then, we proposed the OODA-based NRS architecture that incorporates JCMP. After reviewing the SoAs in connectivity quality metric for the performance assessment module, the JCMP was discussed in more detail, and two examples were provided to show the benefits of JCMP.

The two examples in Section 2 and Section 3 may be naturally extended to more sophisticated scenarios. An NRS of multiple sensing robots, multiple relay robots along with multiple PUs allowing underlay, overlay and interleave CR approaches will be incorporated in our future works. Additionally, each SU robot may be equipped with multiple antennas for beamforming a null point toward the PUs, which may also greatly improve the communication quality [18].

Meanwhile, we also point out several problems that JCMP may face in practical application:

• The system complexity of JCMP is high. This is because JCMP needs to optimize the position and power of multiple robots simultaneously. In practice, it is necessary to reasonably design the hardware architecture of JCMP, so that it can still complete the timely adjustment of various parameters in a flexible external environment.
• Stable communication between robots. This paper is devoted to the development of a networked robot system that completely depends on wireless communication. Since the command and control of robots and the data transmission between robots all depend on wireless communication, a stable communication system is the premise for robots to perform tasks. In the actual environment (especially in the urban environment), multi-path fading, shadow fading, and path loss will affect the stability of wireless communication. Therefore, the wireless channel should be accurately evaluated and modeled before the JCMP is applied in the actual scene.