Application of Statistical Process Control for Structural Health Monitoring of a High-Speed Railway Track System
Abstract
:1. Introduction
2. Research Approach
2.1. Statistical Models
2.1.1. Multilinear Regression Model
2.1.2. Time Series Difference Equation Model
2.2. Control Charts
2.2.1. Individual Control Chart
2.2.2. Moving Range Control Chart
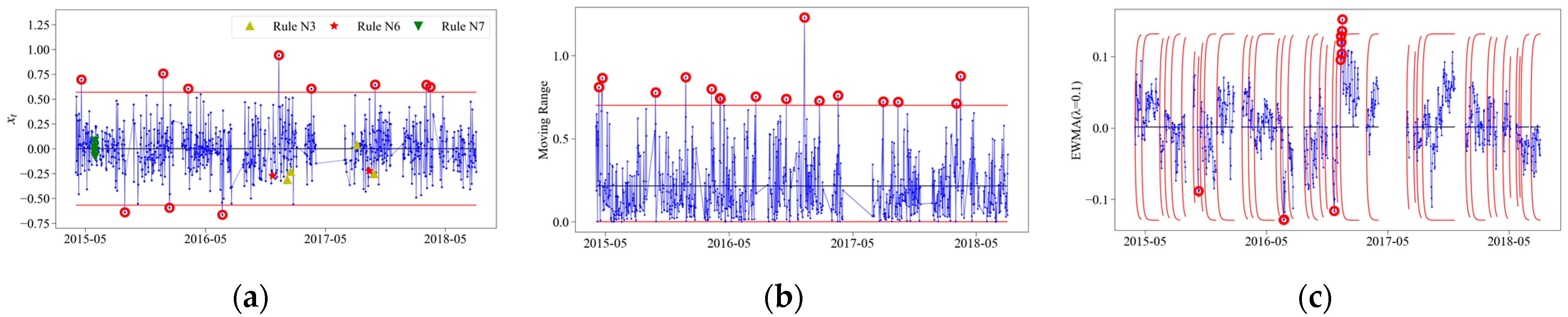
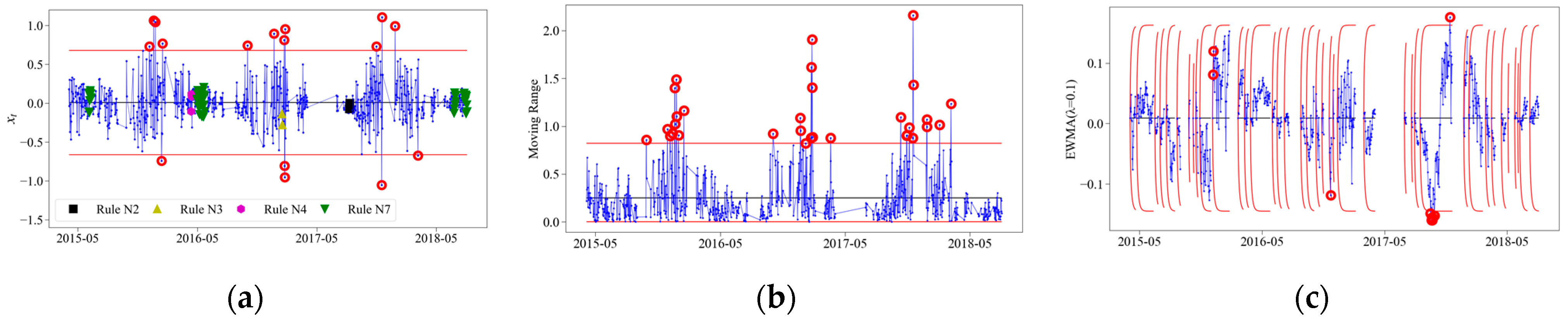
2.2.3. Supplementary Runs Rules
- Rule N1: 1 measurement above (or below) the upper (or lower) control limit.
- Rule N2: 9 consecutive measurements on one side of CL.
- Rule N3: 6 consecutive measurements increasing or decreasing.
- Rule N4: 14 consecutive measurements alternating up and down.
- Rule N5: 2 out of 3 measurements beyond CL ± on same side.
- Rule N6: 4 out of 5 measurements beyond CL ± on same side.
- Rule N7: 15 consecutive measurements between ± from CL.
- Rule N8: 8 consecutive measurements beyond CL ± on both sides.
2.2.4. EWMA Control Chart
3. Data and Analysis
3.1. Acquisition and Preprocessing of Data
3.2. Analysis of Common-Cause Variation
3.2.1. Application of Multilinear Regression Model
3.2.2. Application of Time Series Difference Equation Model
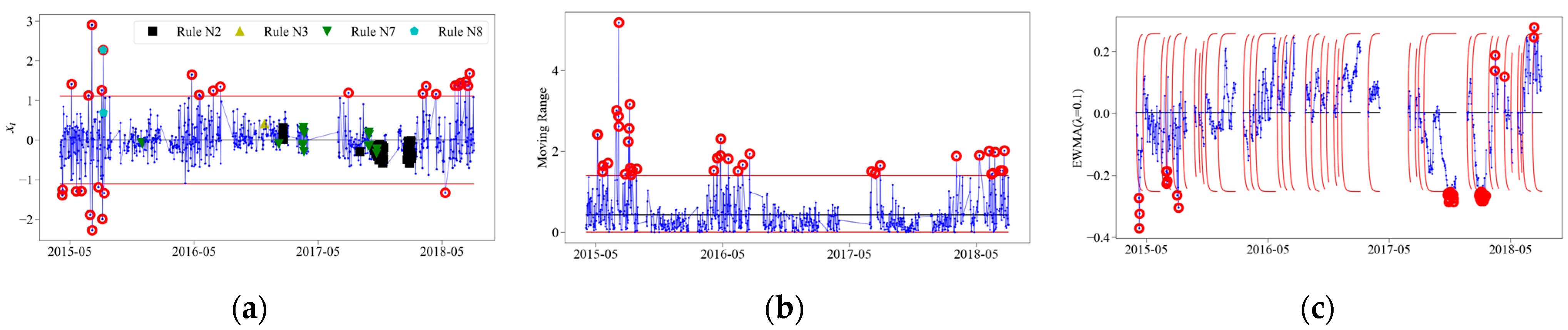
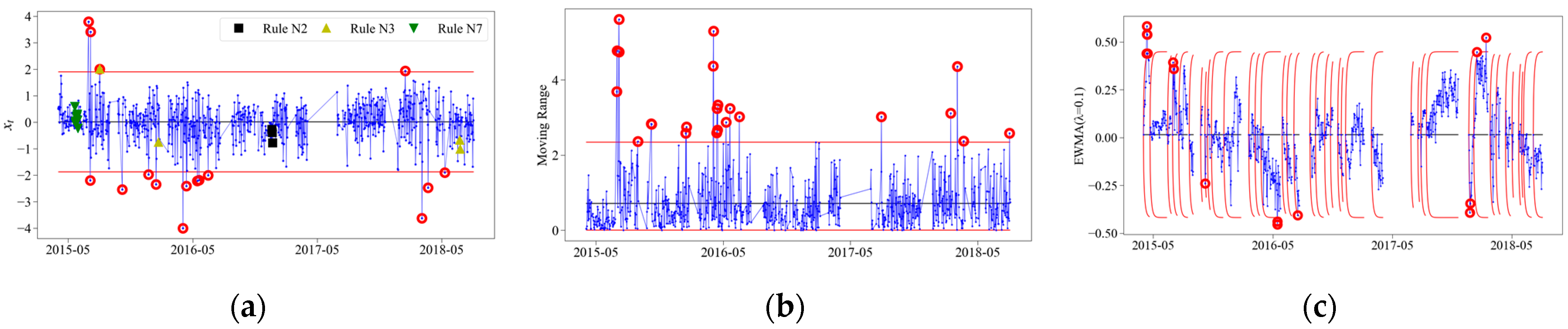
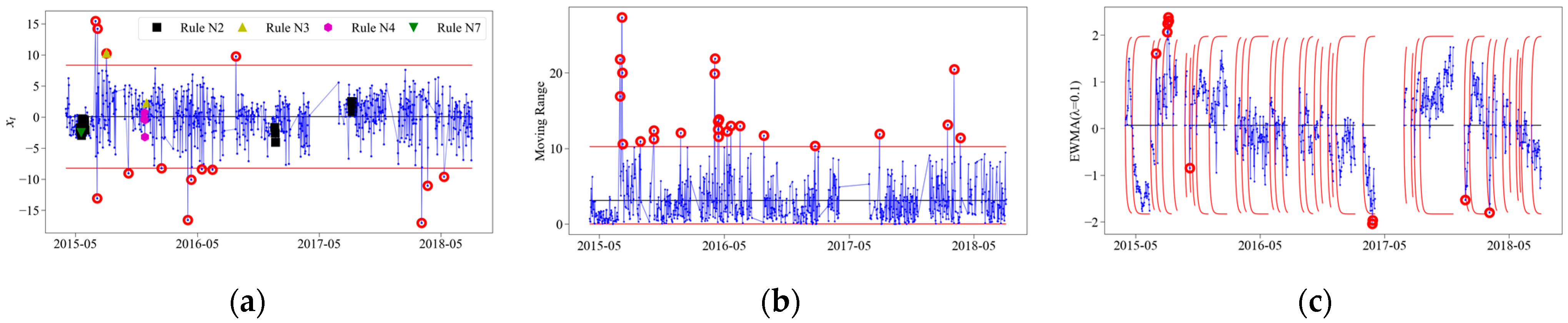
3.3. Analysis of Special-Cause Variation
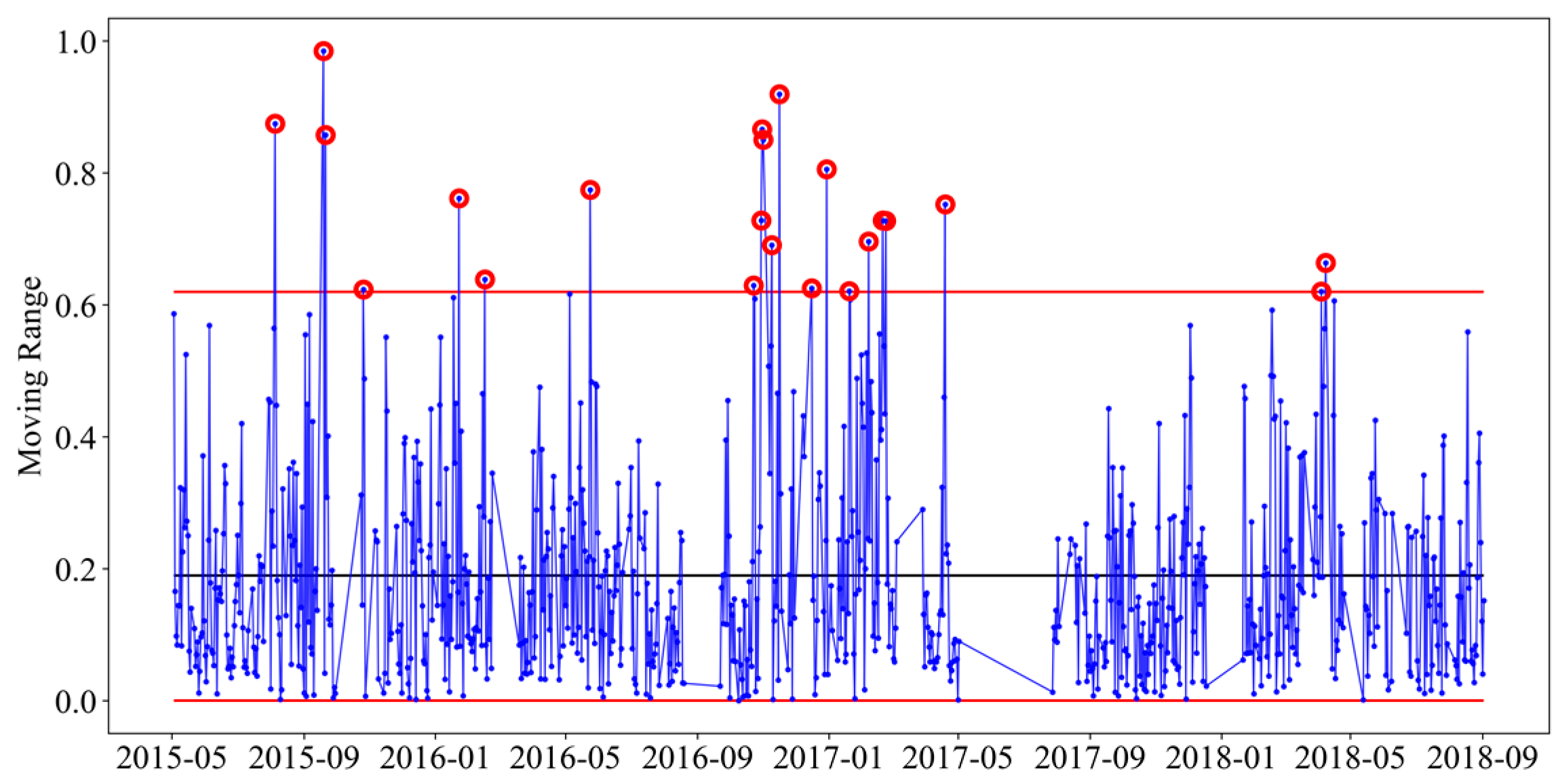
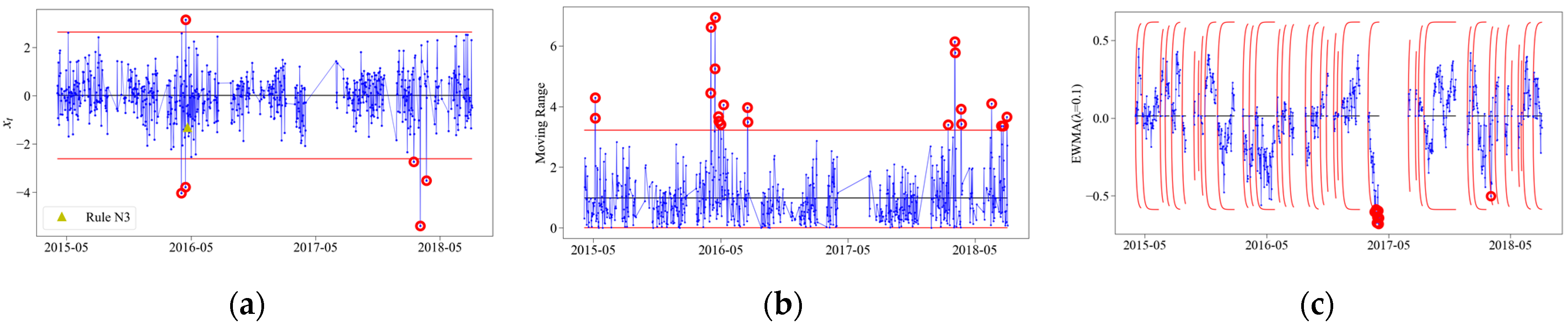
3.3.1. Example of Control Chart
3.3.2. Analysis of All Measuring Points
4. Conclusions
- (1)
- With respect to the girder displacement and track slab–girder relative displacements, the displacement variations were mainly caused by the temperature effects and linear trends. The variations of the observation were consistent with the one caused by the temperature effects, indicating that temperature is a key factor for the displacement variations. The proportions of these variations caused by the linear trends to the ones caused by the temperature effects almost exceed 10%, suggesting that linear trends were also unneglectable components in the measurement sequences.
- (2)
- The ACF values of regression residuals were large with lag ≥ 1, and vary regularly with lags, indicating the serial dependence in the discontinuous monitoring data. The ACF values of difference equation residuals showed the opposite variation rules with lags, and fell mostly in the 95% confidence interval, which validates the feasibility of the TSDE model for capturing the serial dependence.
- (3)
- As for the rail–track slab relative displacement 15 and track slab–girder relative displacement 17, numerous outliers were detected by control charts. This suggested that the track system at these two measuring points was sensitive to special causes. With regard to the special causes triggering the anomalous responses of local and overall track systems, sixteen and twenty-eight significant special events were detected, respectively. Among these events, the durations of special events from 27 June 2015 to 29 June 2015 and from 12 May 2016 to 15 May 2016 exceeded three days, which should be paid special attention.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Zhong, Y.L.; Gao, L.; Zhang, Y.R. Effect of Daily Changing Temperature on the Curling Behavior and Interface Stress of Slab Track in Construction Stage. Constr. Build. Mater. 2018, 185, 638–647. [Google Scholar] [CrossRef]
- Cai, X.P.; Luo, B.C.; Zhong, Y.L.; Zhang, Y.R.; Hou, B.W. Arching Mechanism of the Slab Joints in CRTSII Slab Track under High Temperature Conditions. Eng. Fail. Anal. 2019, 98, 95–108. [Google Scholar] [CrossRef]
- Cai, X.P.; Gao, L.; Liu, C.; Zhang, C.; Xin, T.; Sun, G.L. Monitoring Data Management Information System for Ballastless Track Turnout on Elevated Station. J. Railw. Eng. Soc. 2016, 33, 52–57. [Google Scholar]
- Ye, X.W.; Ni, Y.Q.; Yin, J.H. Safety Monitoring of Railway Tunnel Construction Using FBG Sensing Technology. Adv. Struct. Eng. 2013, 16, 1401–1409. [Google Scholar] [CrossRef]
- Ni, Y.Q.; Xia, H.W.; Ko, J.M. Structural Performance Evaluation of Tsing Ma Bridge Deck Using Long-Term Monitoring Data. Mod. Phys. Lett. B 2008, 22, 875–880. [Google Scholar] [CrossRef]
- Wang, H.P.; Gong, X.S.; Wang, X.Z.; Feng, S.Y.; Yang, T.L.; Guo, Y.X. Discrete Curvature-Based Shape Configuration of Composite Pipes for Local Buckling Detection Based on Fiber Bragg Grating Sensors. Measurement 2022, 188, 110603. [Google Scholar] [CrossRef]
- Gao, H.W.; Li, H.M.; Liu, B.; Zhang, H.; Luo, J.H.; Cao, Y.; Yuan, S.Z.; Zhang, W.G.; Kai, G.Y.; Dong, X.Y. A Novel Fiber Bragg Grating Sensors Multiplexing Technique. Opt. Commun. 2005, 251, 361–366. [Google Scholar] [CrossRef]
- Zou, Z.L.; Bao, Y.Q.; Li, H.; Spencer, B.F.; Ou, J.P. Embedding Compressive Sensing-Based Data Loss Recovery Algorithm Into Wireless Smart Sensors for Structural Health Monitoring. IEEE Sens. J. 2015, 15, 797–808. [Google Scholar] [CrossRef]
- Bao, Y.Q.; Li, H.; Sun, X.D.; Yu, Y.; Ou, J.P. Compressive Sampling–Based Data Loss Recovery for Wireless Sensor Networks Used in Civil Structural Health Monitoring. Struct. Health Monit. 2012, 12, 78–95. [Google Scholar] [CrossRef]
- RFC 3517; A Conservative Selective Acknowledgment (SACK)-based Loss Recovery Algorithm for TCP. IETF: Fremont, CA, USA, 2003.
- Kim, B.; Lee, J. Retransmission Loss Recovery by Duplicate Acknowledgment Counting. IEEE Commun. Lett. 2004, 8, 69–71. [Google Scholar] [CrossRef]
- Spyrou, E.D.; Kappatos, V. Application of Forward Error Correction (FEC) Codes in Wireless Acoustic Emission Structural Health Monitoring on Railway Infrastructures. Infrastructures 2022, 7, 41. [Google Scholar] [CrossRef]
- Fan, G.; Li, J.; Hao, H. Lost Data Recovery for Structural Health Monitoring Based on Convolutional Neural Networks. Struct. Control. Health Monit. 2019, 26, e2433. [Google Scholar] [CrossRef]
- Ma, Z.R.; Gao, L. Predicting Mechanical State of High-Speed Railway Elevated Station Track System Using a Hybrid Prediction Model. KSCE J. Civ. Eng. 2021, 25, 2474–2486. [Google Scholar] [CrossRef]
- Ma, Z.R.; Gao, L.; Zhong, Y.L.; Ma, S.; An, B.L. Arching Detection Method of Slab Track in High-Speed Railway Based on Track Geometry Data. Appl. Sci. 2020, 10, 6799. [Google Scholar] [CrossRef]
- Shewhart, W.A. Economic Control of Quality of Manufactured Products; D. Van Nostrand Company: New York, NY, USA, 1931. [Google Scholar]
- Deming, W.E. On Probability as a Basis for Action. Am. Stat. 1975, 29, 146–152. [Google Scholar] [CrossRef]
- Montgomery, D.C. Introduction to Statistical Quality Control; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Kosnik, D.E.; Zhang, W.Z.; Durango-Cohen, P.L. Application of Statistical Process Control for Structural Health Monitoring of a Historic Building. J. Infrastruct. Syst. 2014, 20, 05013002. [Google Scholar] [CrossRef]
- Sohn, H.; Czarnecki, J.A.; Farrar, C.R. Structural Health Monitoring Using Statistical Process Control. J. Struct. Eng. 2000, 126, 1356–1363. [Google Scholar] [CrossRef]
- Fugate, M.L.; Sohn, H.; Farrar, C.R. Vibration-Based Damage Detection Using Statistical Process Control. Mech. Syst. Signal Process. 2001, 15, 707–721. [Google Scholar] [CrossRef] [Green Version]
- Lu, P.; Phares, B.M.; Greimann, L.; Wipf, T.J. Bridge Structural Health–Monitoring System Using Statistical Control Chart Analysis. Transp. Res. Rec. 2010, 2172, 123–131. [Google Scholar] [CrossRef]
- Magalhães, F.; Cunha, A.; Caetano, E. Vibration Based Structural Health Monitoring of an Arch Bridge: From Automated OMA to Damage Detection. Mech. Syst. Signal Process. 2012, 28, 212–228. [Google Scholar] [CrossRef]
- Chen, Y.K.; Corr, D.J.; Durango-Cohen, P.L. Analysis of Common-Cause and Special-Cause Variation in the Deterioration of Transportation Infrastructure: A Field Application of Statistical Process Control for Structural Health Monitoring. Transp. Res. Part B Methodol. 2014, 59, 96–116. [Google Scholar] [CrossRef]
- Chen, Y.K.; Durango-Cohen, P.L. Development and Field Application of a Multivariate Statistical Process Control Framework for Health-Monitoring of Transportation Infrastructure. Transp. Res. Part B Methodol. 2015, 81, 78–102. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, P.; Zhao, W. Dynamic Responses Due to Irregularity of No. 38 Turnout for High-Speed Railway. In Proceedings of the ICTE, Chengdu, China, 23–25 July 2011; pp. 2544–2549. [Google Scholar] [CrossRef]
- Worden, K.; Sohn, H.; Farrar, C.R. Novelty Detection in a Changing Environment: Regression and Interpolation Approaches. J. Sound Vib. 2002, 258, 741–761. [Google Scholar] [CrossRef]
- Peeters, B.; De Roeck, G. One-Year Monitoring of the Z24-Bridge: Environmental Effects Versus Damage Events. Earthq. Engng. Struct. Dyn. 2001, 30, 149–171. [Google Scholar] [CrossRef]
- Ni, Y.Q.; Hua, X.G.; Fan, K.Q.; Ko, J.M. Correlating Modal Properties with Temperature Using Long-Term Monitoring Data and Support Vector Machine Technique. Eng. Struct. 2005, 27, 1762–1773. [Google Scholar] [CrossRef]
- Nelson, L.S. The Shewhart Control Chart—Tests for Special Causes. J. Qual. Technol. 2018, 16, 237–239. [Google Scholar] [CrossRef]
- Yun, C.B.; Min, J. Smart sensing, Monitoring, and Damage Detection for Civil Infrastructures. KSCE J. Civ. Eng. 2010, 15, 1–14. [Google Scholar] [CrossRef]
- Xu, Y.L.; Chen, B.; Ng, C.L.; Wong, K.Y.; Chan, W.Y. Monitoring Temperature Effect on a Long Suspension Bridge. Struct. Control. Health Monit. 2010, 17, 632–653. [Google Scholar] [CrossRef]
- Griffiths, D.; Bunder, M.; Gulati, C.; Onizawa, T. The Probability of an Out of Control Signal from Nelson’s Supplementary Zig-Zag Test. J. Stat. Theory Pract. 2010, 4, 609–615. [Google Scholar] [CrossRef] [Green Version]
- Domaneschi, M.; Niccolini, G.; Lacidogna, G.; Cimellaro, G.P. Nondestructive Monitoring Techniques for Crack Detection and Localization in RC Elements. Appl. Sci. 2020, 10, 3248. [Google Scholar] [CrossRef]
- Domaneschi, M.; Sigurdardottir, D.; Glisic, B. Damage Detection on Output-Only Monitoring of Dynamic Curvature in Composite Decks. Struct. Monit. Maint. 2017, 4, 1–15. [Google Scholar] [CrossRef]
- Morgese, M.; Domaneschi, M.; Ansari, F.; Cimellaro, G.P.; Inaudi, D. Improving Distributed Fiber-Optic Sensor Measures by Digital Image Correlation: Two-Stage Structural Health Monitoring. ACI Struct. J. 2021, 118, 91–102. [Google Scholar] [CrossRef]

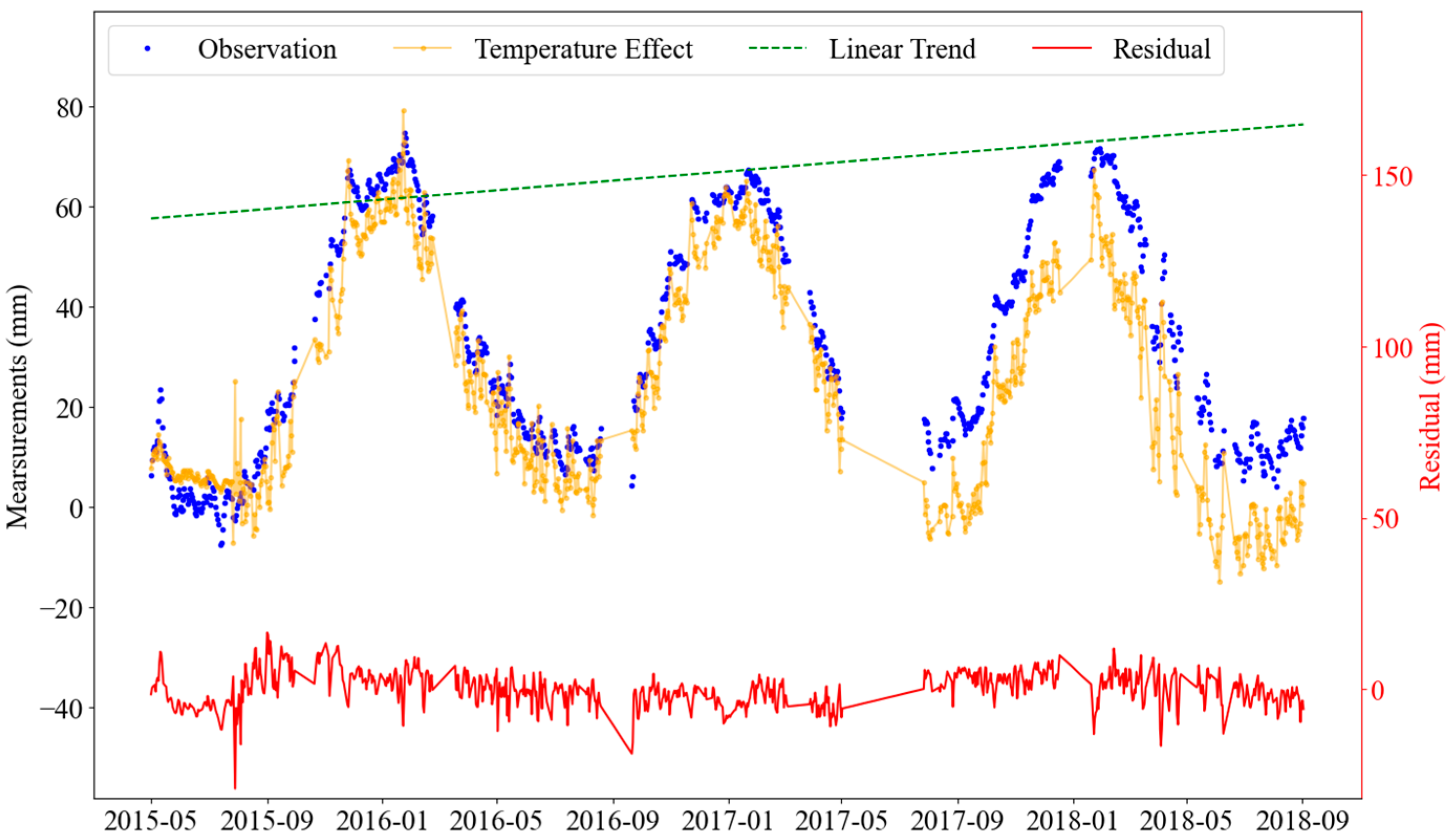
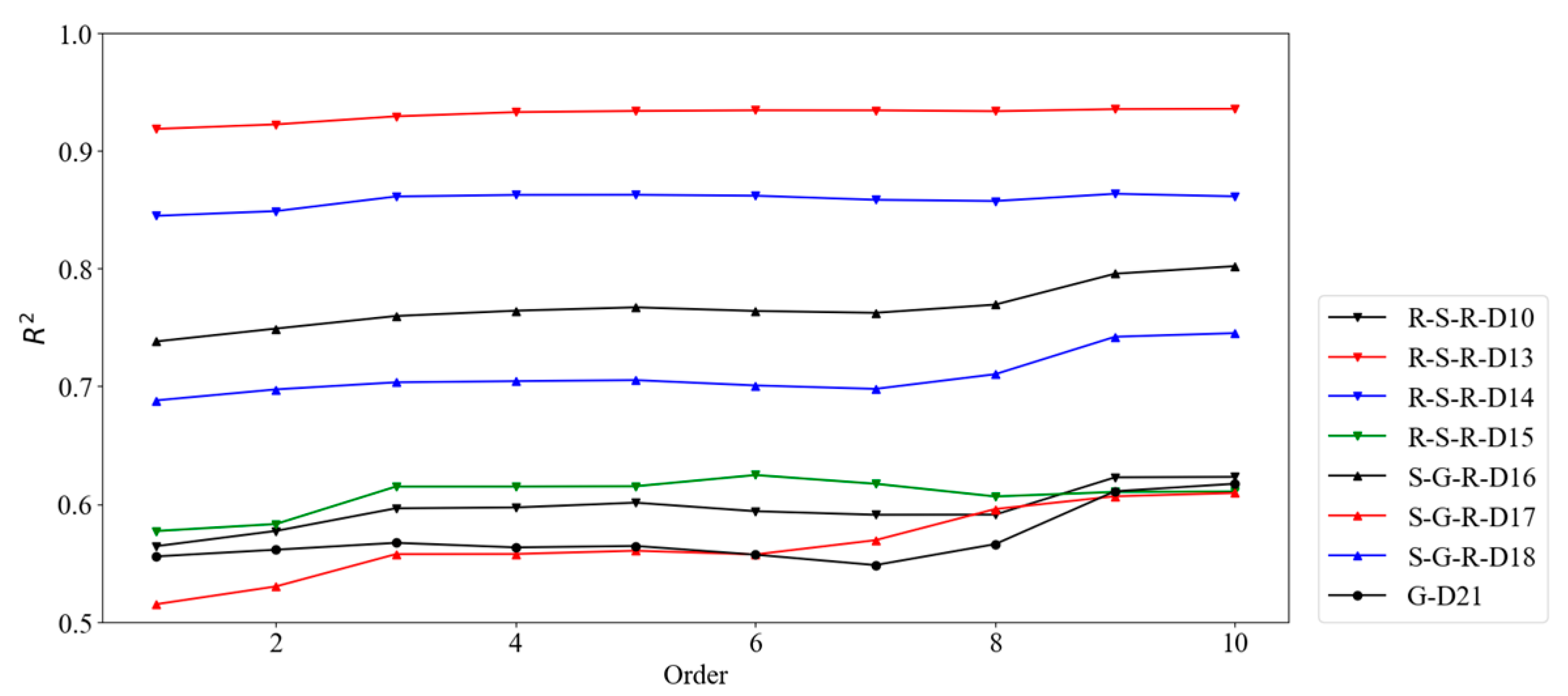
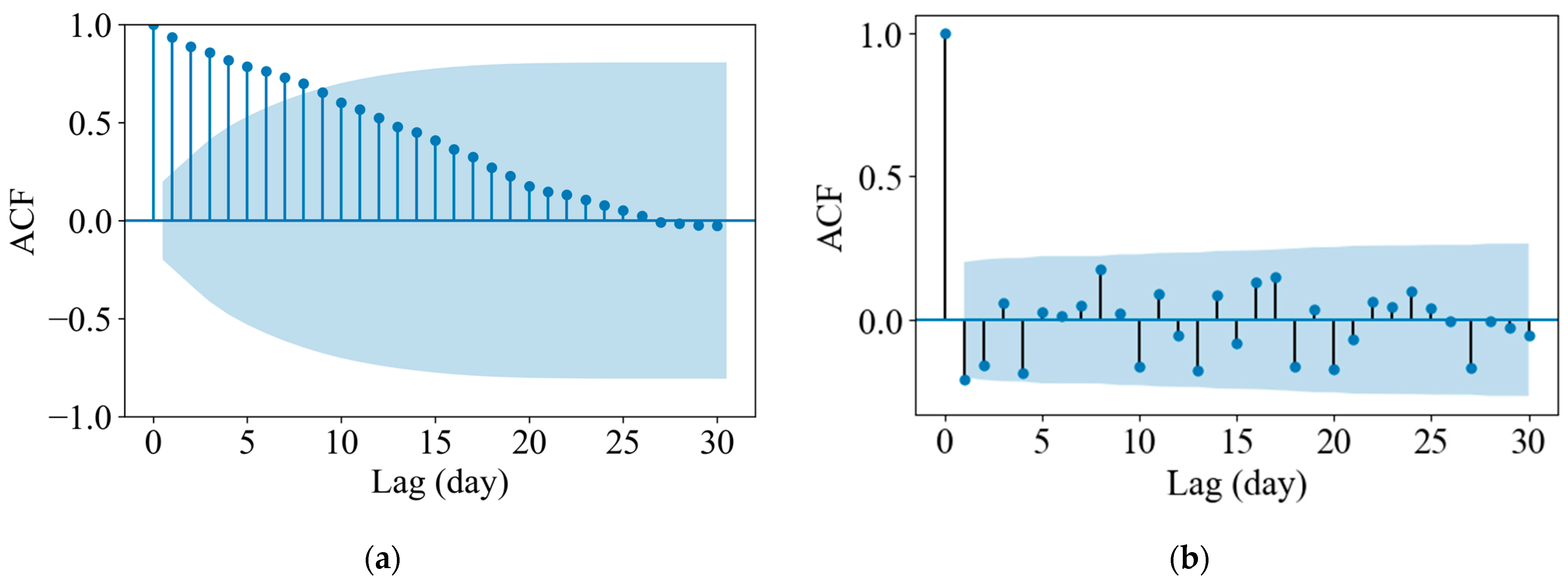
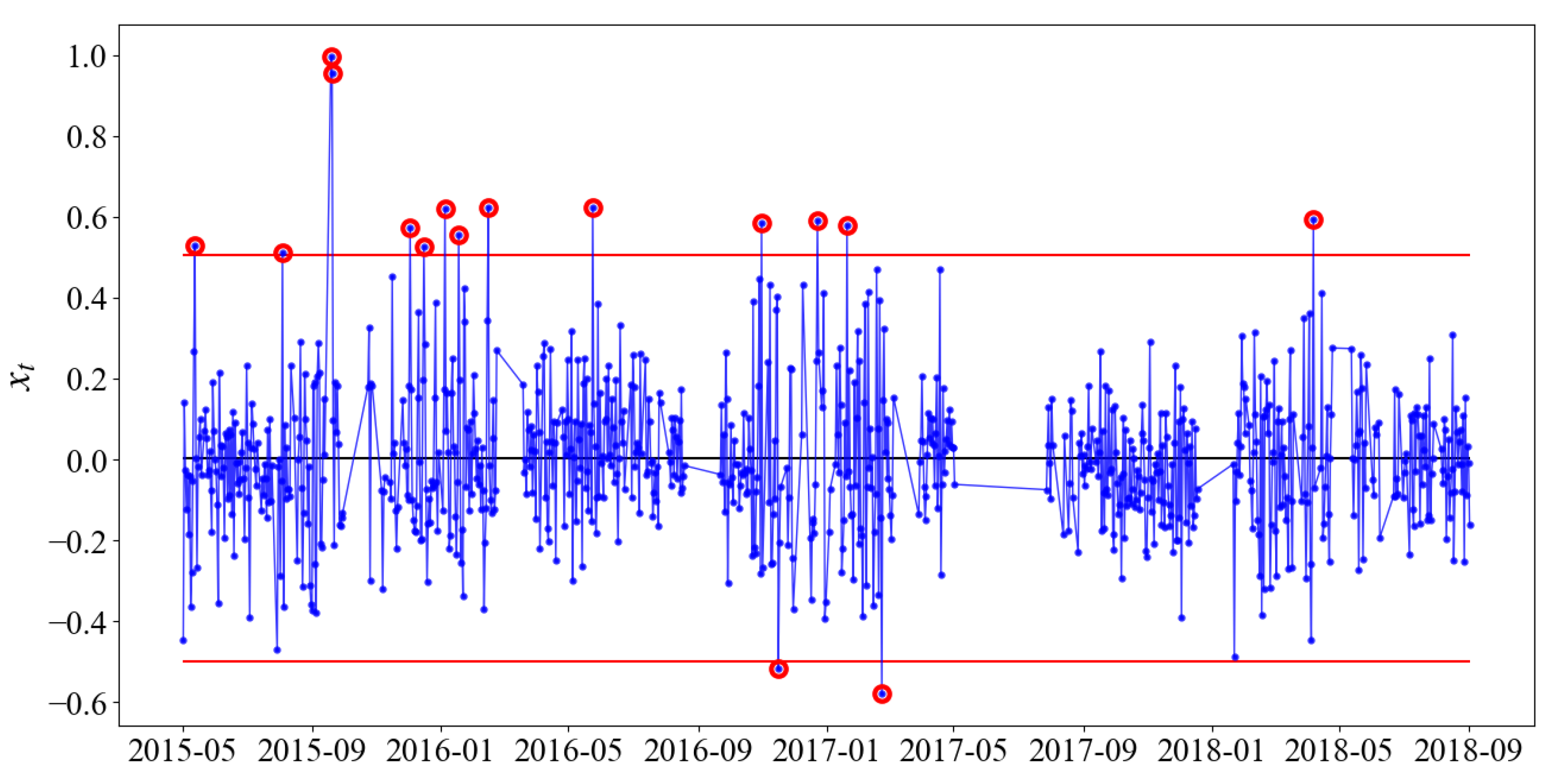



| Measuring Point | Abbreviation | Intercept | Linear Trend | Air Temperature | R2 | |||
|---|---|---|---|---|---|---|---|---|
| t-stat | t-stat | t-stat | ||||||
| Rail–track slab relative displacement 10 | R-S-R-D10 | 6.3372 | 55.5 | 0.0025 | 18.4 | −0.2355 | −51.8 | 0.767 |
| Rail–track slab relative displacement 13 | R-S-R-D13 | −0.5130 | −10.2 | −0.0001 | −2.3 | 0.0394 | 19.7 | 0.308 |
| Rail–track slab relative displacement 14 | R-S-R-D14 | −1.0387 | −24.4 | −0.0002 | −4.3 | −0.0228 | −13.5 | 0.196 |
| Rail–track slab relative displacement 15 | R-S-R-D15 | −0.6734 | −20.1 | −0.0011 | −26.8 | 0.0341 | 25.6 | 0.591 |
| Track slab–girder relative displacement 16 | S-G-R-D16 | −23.0683 | −91.5 | −0.0040 | −13.5 | 0.9166 | 91.4 | 0.906 |
| Track slab–girder relative displacement 17 | S-G-R-D17 | −6.4153 | −123.9 | −0.0009 | −15.5 | 0.2408 | 117.0 | 0.940 |
| Track slab–girder relative displacement 18 | S-G-R-D18 | 10.2280 | 98.2 | 0.0017 | 13.7 | −0.4057 | −97.9 | 0.917 |
| Girder displacement 21 | G-D21 | 57.5937 | 145.6 | 0.0154 | 33.2 | −2.0303 | −129.1 | 0.952 |
| Measuring Point | Data Variation Caused by the Linear Trend (mm) | Data Variation Caused by the Temperature Effect (mm) | Proportion (%) |
|---|---|---|---|
| S-G-R-D16 | 4.884 | 42.426 | 11.51% |
| S-G-R-D17 | 1.099 | 11.146 | 9.86% |
| S-G-R-D18 | 2.076 | 18.778 | 11.05% |
| G-D21 | 18.803 | 93.975 | 20.01% |
| Measuring Point | t-stat | t-stat | t-stat | R2 | |||
|---|---|---|---|---|---|---|---|
| R-S-R-D10 | 0.8562 | 23.943 | −0.2224 | −4.854 | 0.1348 | 3.813 | 0.596 |
| R-S-R-D13 | 0.9586 | 96.654 | - | - | - | - | 0.919 |
| R-S-R-D14 | 0.9233 | 67.120 | - | - | - | - | 0.845 |
| R-S-R-D15 | 0.8964 | 25.545 | −0.3436 | −7.484 | 0.2429 | 7.156 | 0.616 |
| S-G-R-D16 | 0.8565 | 48.274 | - | - | - | - | 0.738 |
| S-G-R-D17 | 0.7028 | 29.630 | - | - | - | - | 0.515 |
| S-G-R-D18 | 0.8159 | 42.707 | - | - | - | - | 0.688 |
| G-D21 | 0.7227 | 32.142 | - | - | - | - | 0.555 |
| Measuring Point | Individual Control Chart | Supplementary Runs Rules | Moving Range Control Chart | EWMA Control Chart | Total |
|---|---|---|---|---|---|
| R-S-R-D10 | 6 | 1 | 21 | 10 | 38 |
| R-S-R-D13 | 16 | 18 | 22 | 8 | 64 |
| R-S-R-D14 | 11 | 10 | 16 | 10 | 47 |
| R-S-R-D15 | 16 | 64 | 31 | 10 | 121 |
| S-G-R-D16 | 13 | 7 | 21 | 15 | 56 |
| S-G-R-D17 | 29 | 67 | 37 | 43 | 176 |
| S-G-R-D18 | 16 | 17 | 23 | 15 | 71 |
| G-D21 | 14 | 31 | 24 | 10 | 79 |
| Total | 121 | 215 | 195 | 121 | 652 |
| Measuring Point | Date | Control Charts | Measuring Point | Date | Control Charts |
|---|---|---|---|---|---|
| R-S-R-D10 | 2018.4.3 | I, MR, EWMA | S-G-R-D17 | 2017.11.19 | I, N2, N7 |
| R-S-R-D13 | 2015.9.19 | I, MR, EWMA | 2017.11.20 | I, N2, N7 | |
| R-S-R-D14 | 2017.1.9 | I, MR, EWMA | 2018.8.9 | I, MR, EWMA | |
| R-S-R-D15 | 2016.1.5 | I, MR, EWMA | S-G-R-D18 | 2015.7.30 | I, MR, EWMA |
| S-G-R-D16 | 2015.7.30 | I, MR, EWMA | 2015.11.6 | I, MR, EWMA | |
| 2015.8.5 | I, MR, EWMA | G-D21 | 2015.7.30 | I, MR, EWMA | |
| R-S-R-D10 | 2015.7.30 | I, MR, EWMA | 2015.9.1 | I, N3, EWMA | |
| 2015.9.6 | I, N8, MR | 2015.11.6 | I, MR, EWMA |
| Date | Measuring Points with Outliers Detected | Number of Measuring Points | Date | Measuring Points with Outliers Detected | Number of Measuring Points |
|---|---|---|---|---|---|
| 2015.6.27~2015.6.29 | R-S-R-D14, S-G-R-D16, S-G-R-D18, G-D21 | 4 | 2016.6.8 | R-S-R-D10, R-S-R-D15, S-G-R-D16, S-G-R-D18, G-D21 | 5 |
| 2015.7.30~2015.7.31 | S-G-R-D16, S-G-R-D17, S-G-R-D18, G-D21 | 4 | 2016.6.19 | R-S-R-D15, S-G-R-D16, S-G-R-D18, G-D21 | 4 |
| 2015.8.4~2015.8.5 | R-S-R-D13, S-G-R-D16, S-G-R-D17, S-G-R-D18, G-D21 | 5 | 2017.1.20 | R-S-R-D13, R-S-R-D15, S-G-R-D18, G-D21 | 4 |
| 2015.8.6 | S-G-R-D16, S-G-R-D17, S-G-R-D18, G-D21 | 4 | 2017.2.20 | R-S-R-D13, R-S-R-D15, S-G-R-D16, G-D21 | 4 |
| 2015.9.1 | S-G-R-D16, S-G-R-D17, S-G-R-D18, G-D21 | 4 | 2017.4.19 | R-S-R-D10, R-S-R-D13, R-S-R-D15, S-G-R-D17 | 4 |
| 2016.1.23 | R-S-R-D13, R-S-R-D14, R-S-R-D15, S-G-R-D16 | 4 | 2017.8.28 | S-G-R-D16, S-G-R-D17, S-G-R-D17, G-D21 | 4 |
| 2016.1.24 | R-S-R-D14, R-S-R-D15, S-G-R-D16, G-D21 | 4 | 2018.3.15 | R-S-R-D10, S-G-R-D16, S-G-R-D17, S-G-R-D18, G-D21 | 5 |
| 2016.5.2~2016.5.3 | R-S-R-D10, S-G-R-D16, S-G-R-D18, G-D21 | 4 | 2018.4.3 | R-S-R-D10, R-S-R-D14, S-G-R-D16, S-G-R-D18, G-D21 | 5 |
| 2016.5.12~2016.5.13 | R-S-R-D15, S-G-R-D16, S-G-R-D18, G-D21 | 4 | 2018.4.4 | R-S-R-D10, R-S-R-D13, S-G-R-D16, S-G-R-D17, G-D21 | 5 |
| 2016.5.14 | R-S-R-D10, S-G-R-D16, S-G-R-D18, G-D21 | 4 | 2018.4.21 | R-S-R-D10, S-G-R-D16, S-G-R-D18, G-D21 | 4 |
| 2016.5.15 | R-S-R-D10, S-G-R-D16, S-G-R-D17, S-G-R-D18, G-D21 | 5 | 2018.7.24 | R-S-R-D13, R-S-R-D15, S-G-R-D17, S-G-R-D18 | 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wu, K.; Yu, C.; Zhang, S.; Cai, X. Application of Statistical Process Control for Structural Health Monitoring of a High-Speed Railway Track System. Appl. Sci. 2022, 12, 6046. https://doi.org/10.3390/app12126046
Zhang Y, Wu K, Yu C, Zhang S, Cai X. Application of Statistical Process Control for Structural Health Monitoring of a High-Speed Railway Track System. Applied Sciences. 2022; 12(12):6046. https://doi.org/10.3390/app12126046
Chicago/Turabian StyleZhang, Yanrong, Kai Wu, Chao Yu, Shuang Zhang, and Xiaopei Cai. 2022. "Application of Statistical Process Control for Structural Health Monitoring of a High-Speed Railway Track System" Applied Sciences 12, no. 12: 6046. https://doi.org/10.3390/app12126046
APA StyleZhang, Y., Wu, K., Yu, C., Zhang, S., & Cai, X. (2022). Application of Statistical Process Control for Structural Health Monitoring of a High-Speed Railway Track System. Applied Sciences, 12(12), 6046. https://doi.org/10.3390/app12126046







