Thermoelastic Analysis in Poro-Elastic Materials Using a TPL Model
Abstract
:1. Introduction
2. Basic Equations
- (i)
- The three-phase-lag model is denoted by (TPL)
- (ii)
- (GNIII) indicate the Green−Naghdi type III model
- , , , , , ,
- , , , , ,
- , , , , ,
- , , as in [23].
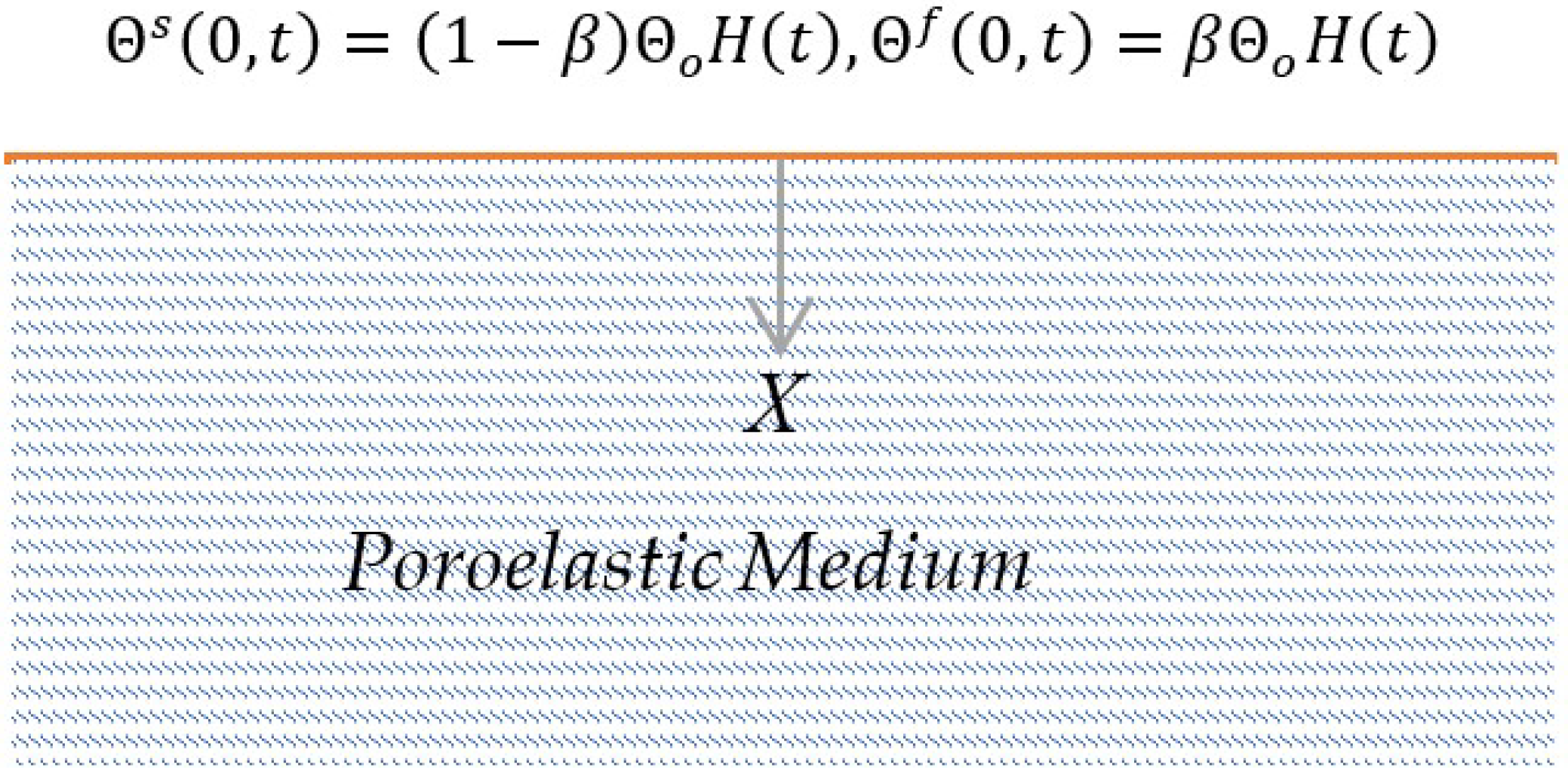
3. Application
- (1)
- The thermal boundary conditions
- (2)
- The mechanical boundary conditions
4. Finite Element Method
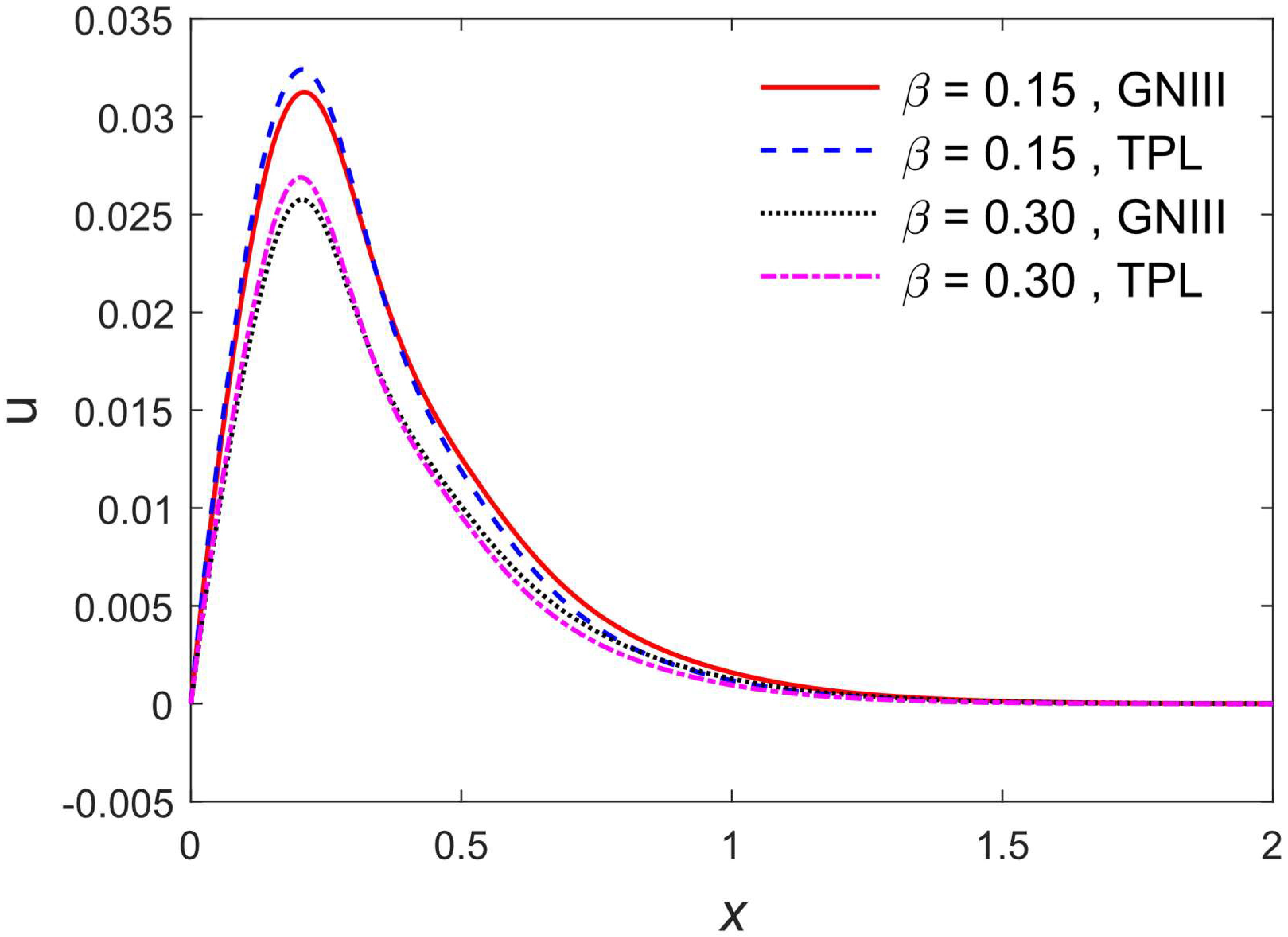
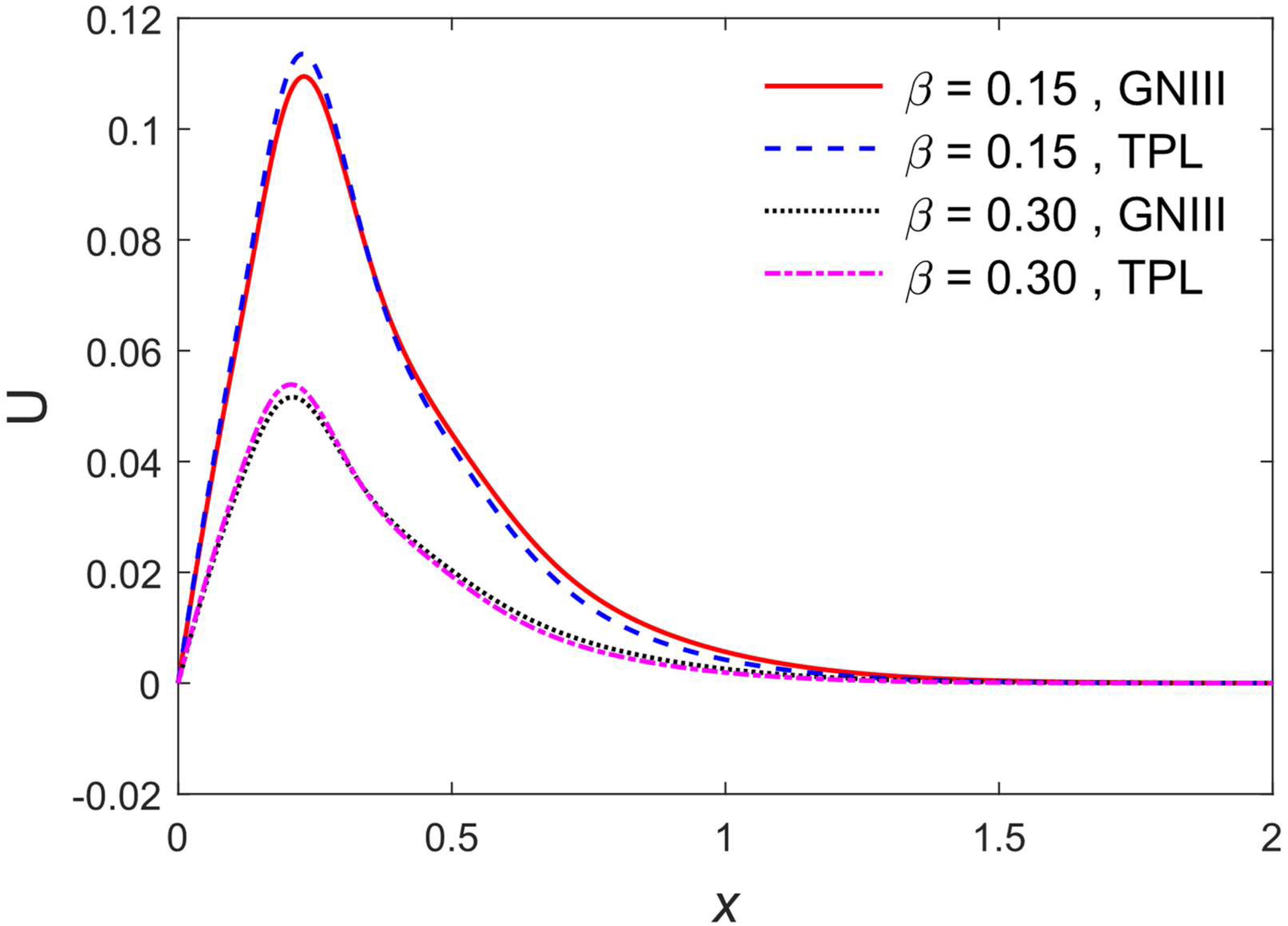
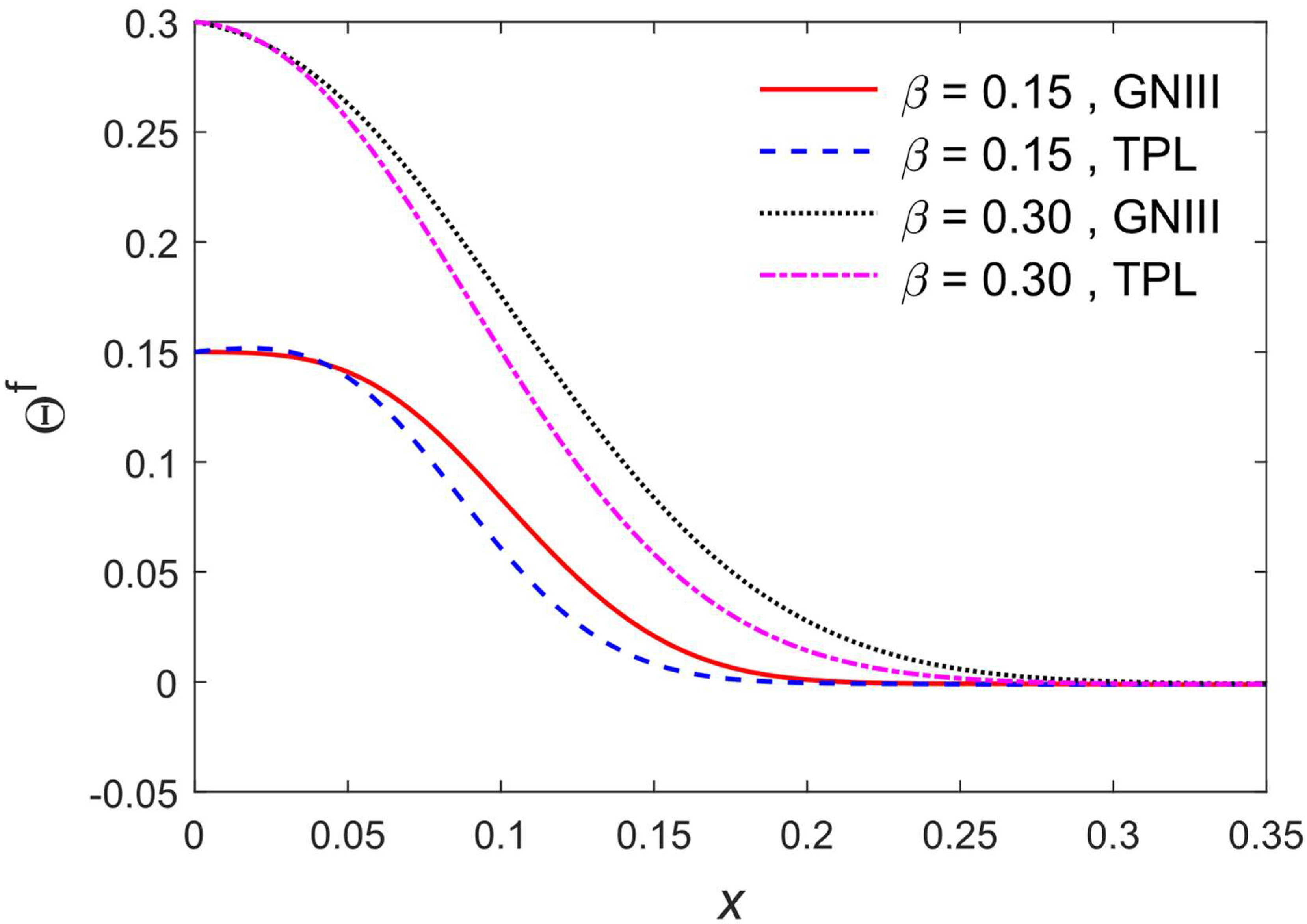
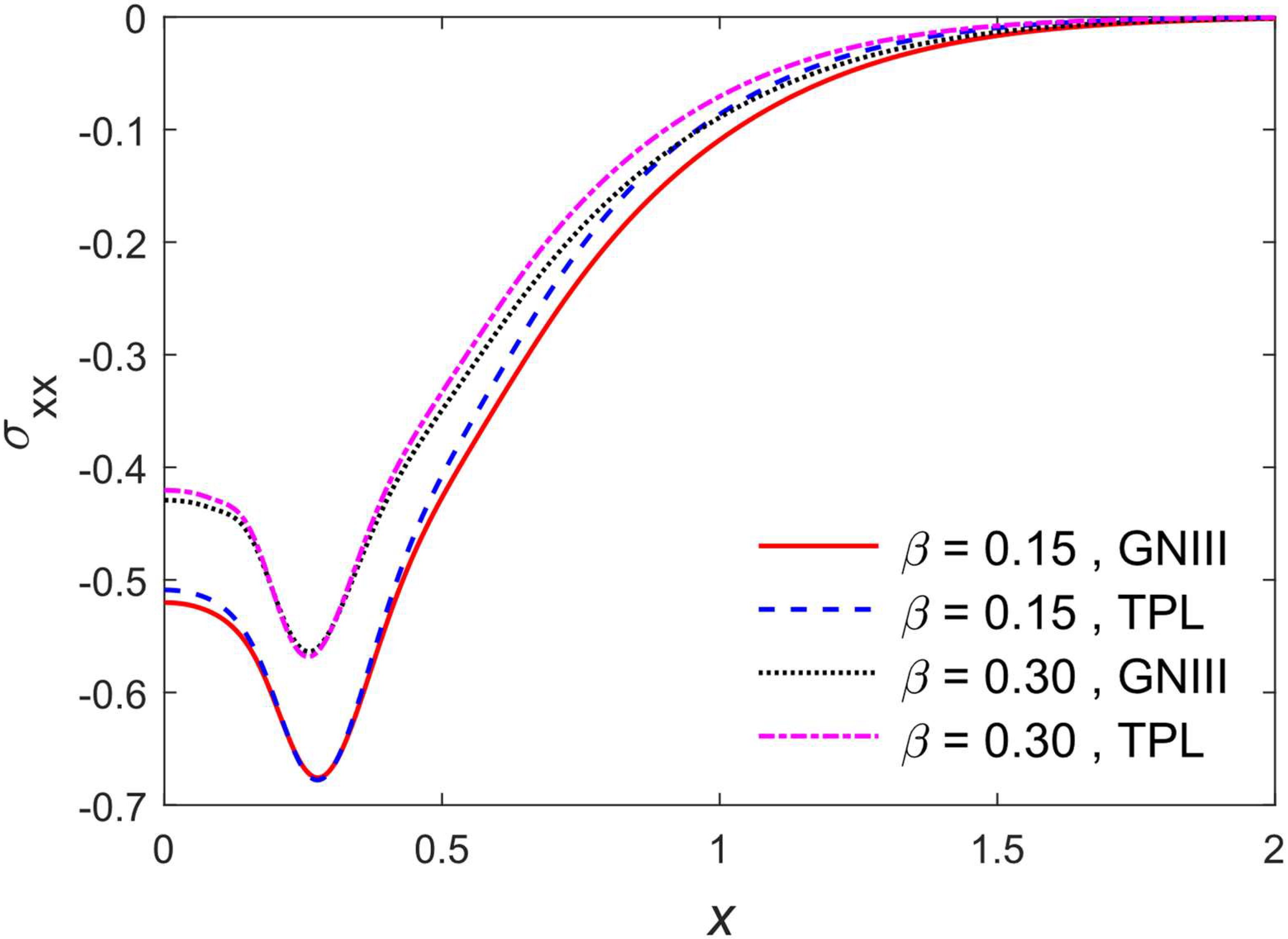
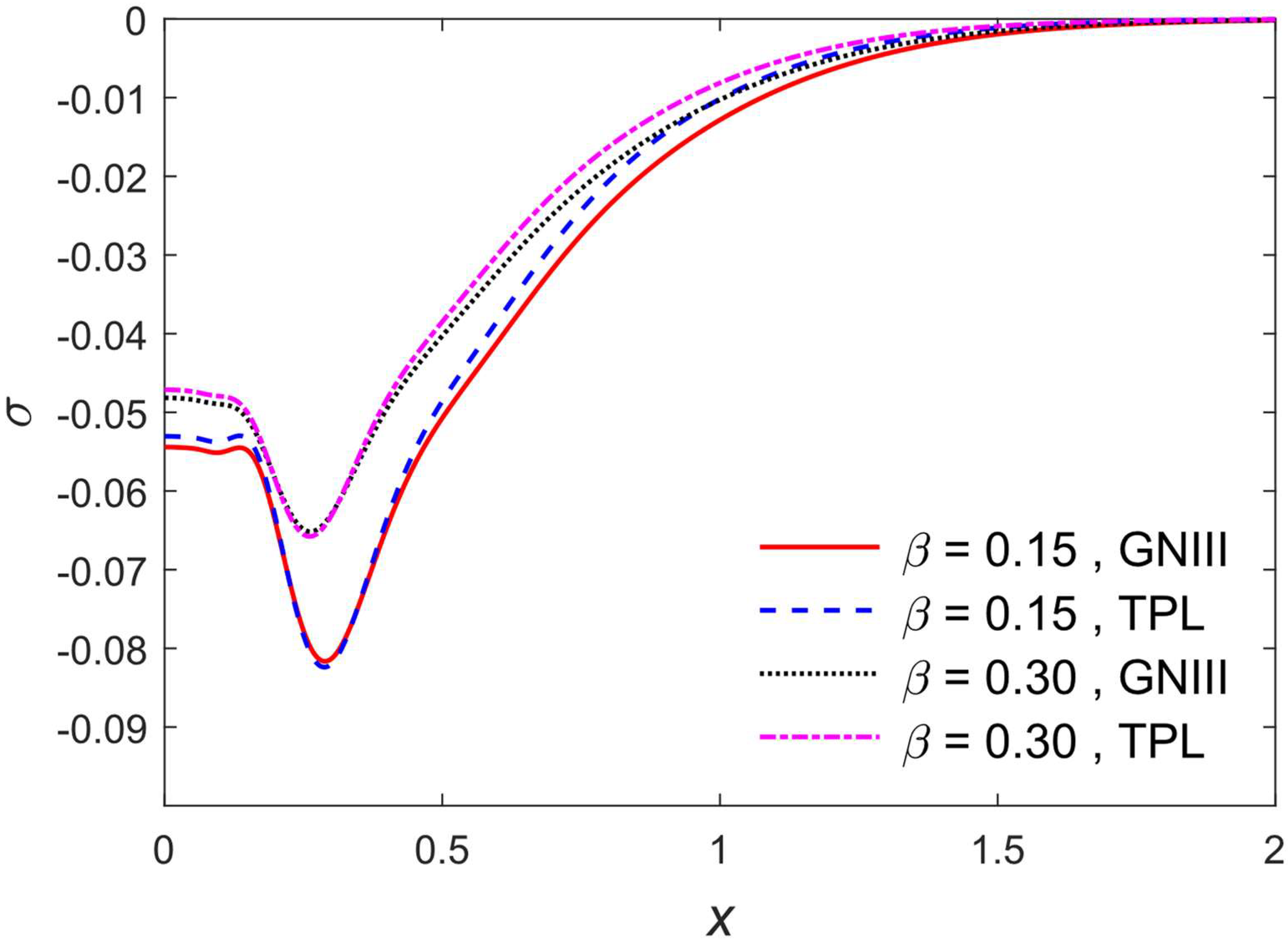
5. Results and Discussions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Biot, M.A. General solutions of the equations of elasticity and consolidation for a porous material. J. Appl. Mech. 1956, 23, 91–96. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher frequency range. J. Acoust. Soc. Am. 1956, 28, 179–191. [Google Scholar] [CrossRef]
- Biot, M.A. Thermoelasticity and irreversible thermodynamics. J. Appl. Phys. 1956, 27, 240–253. [Google Scholar] [CrossRef]
- Green, A.E.; Naghdi, P.M. A re-examination of the basic postulates of thermomechanics. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1991, 432, 171–194. [Google Scholar]
- Green, A.; Naghdi, P. On undamped heat waves in an elastic solid. J. Therm. Stresses 1992, 15, 253–264. [Google Scholar] [CrossRef]
- Green, A.; Naghdi, P. Thermoelasticity without energy dissipation. J. Elast. 1993, 31, 189–208. [Google Scholar] [CrossRef]
- Tzou, D.Y. Unified field approach for heat conduction from macro- to micro-scales. J. Heat Transf. 1995, 117, 8–16. [Google Scholar] [CrossRef]
- Tzou, D.Y. Experimental support for the lagging behavior in heat propagation. J. Thermophys. Heat Transf. 1995, 9, 686–693. [Google Scholar] [CrossRef]
- Choudhuri, S.R. On a thermoelastic three-phase-lag model. J. Therm. Stresses 2007, 30, 231–238. [Google Scholar] [CrossRef]
- McTigue, D. Thermoelastic response of fluid-saturated porous rock. J. Geophys. Res. Solid Earth 1986, 91, 9533–9542. [Google Scholar] [CrossRef]
- Singh, B. On propagation of plane waves in generalized porothermoelasticity. Bull. Seismol. Soc. Am. 2011, 101, 756–762. [Google Scholar] [CrossRef]
- Singh, B. Rayleigh surface wave in a porothermoelastic solid half-space. In Proceedings of the Poromechanics 2017-Proceedings of the 6th Biot Conference on Poromechanics, Paris, France, 9–13 July 2017; pp. 1706–1713. [Google Scholar]
- Youssef, H.M. Theory of generalized porothermoelasticity. Int. J. Rock Mech. Min. Sci. 2007, 44, 222–227. [Google Scholar] [CrossRef]
- El-Naggar, A.; Kishka, Z.; Abd-Alla, A.; Abbas, I.; Abo-Dahab, S.; Elsagheer, M. On the initial stress, magnetic field, voids and rotation effects on plane waves in generalized thermoelasticity. J. Comput. Theor. Nanosci. 2013, 10, 1408–1417. [Google Scholar] [CrossRef]
- Abbas, I. Natural frequencies of a poroelastic hollow cylinder. Acta Mech. 2006, 186, 229–237. [Google Scholar] [CrossRef]
- Schanz, M.; Cheng, A.-D. Transient wave propagation in a one-dimensional poroelastic column. Acta Mech. 2000, 145, 1–18. [Google Scholar] [CrossRef]
- Abbas, I.A.; El-Amin, M.; Salama, A. Effect of thermal dispersion on free convection in a fluid saturated porous medium. Int. J. Heat Fluid Flow 2009, 30, 229–236. [Google Scholar] [CrossRef]
- Saeed, T.; Abbas, I.; Marin, M. A GL model on thermo-elastic interaction in a poroelastic material using finite element method. Symmetry 2020, 12, 488. [Google Scholar] [CrossRef] [Green Version]
- Sur, A.; Kanoria, M. Memory response on thermal wave propagation in an elastic solid with voids. Mech. Based Des. Struct. Mach. 2019, 48, 326–347. [Google Scholar] [CrossRef]
- Carcione, J.M.; Cavallini, F.; Wang, E.; Ba, J.; Fu, L.Y. Physics and Simulation of Wave Propagation in Linear Thermoporoelastic Media. J. Geophys. Res. Solid Earth 2019, 124, 8147–8166. [Google Scholar] [CrossRef]
- Zhou, F.; Liu, H.; Li, S. Propagation of thermoelastic waves in unsaturated porothermoelastic media. J. Therm. Stresses 2019, 42, 1256–1271. [Google Scholar] [CrossRef]
- Wen, M.; Xu, J.; Xiong, H. Thermo-hydro-mechanical dynamic response of a cylindrical lined tunnel in a poroelastic medium with fractional thermoelastic theory. Soil Dyn. Earthq. Eng. 2020, 130, 105960. [Google Scholar] [CrossRef]
- Ezzat, M.; Ezzat, S. Fractional thermoelasticity applications for porous asphaltic materials. Pet. Sci. 2016, 13, 550–560. [Google Scholar] [CrossRef] [Green Version]
- Singh, B. Elastic wave propagation and attenuation in a generalized thermoporoelastic model. Multidiscip. Model. Mater. Struct. 2013, 9, 256–267. [Google Scholar] [CrossRef]
- Hussein, E.M. Effect of the porosity on a porous plate saturated with a liquid and subjected to a sudden change in temperature. Acta Mech. 2018, 229, 2431–2444. [Google Scholar] [CrossRef]
- Sur, A. Wave propagation analysis of porous asphalts on account of memory responses. Mech. Based Des. Struct. Mach. 2020, 49, 1109–1127. [Google Scholar] [CrossRef]
- Alawi, M.H. Generalized Porothermoelasticity of Asphaltic Material. Engineering 2011, 3, 1102. [Google Scholar] [CrossRef] [Green Version]
- Alawi, M.H. Asphaltic material in the context of generalized porothermoelasticity. Int. J. Soft Comput. 2017, 8, 1–17. [Google Scholar] [CrossRef]
- Jangid, K.; Mukhopadhyay, S. Variational principle and continuous dependence results on the generalized poro-thermoelasticity theory with one relaxation parameter. Continuum. Mech. Thermodyn. 2022, 34, 867–881. [Google Scholar] [CrossRef]
- Kumar, M.; Liu, X.; Kumari, M.; Yadav, P. Wave propagation at the welded interface of an elastic solid and unsaturated poro-thermoelastic solid. Int. J. Numer. Methods Heat Fluid Flow 2022. [Google Scholar] [CrossRef]
- Mirparizi, M.; Zhang, C.; Amiri, M.J. One-dimensional electro-magneto-poro-thermoelastic wave propagation in a functionally graded medium with energy dissipation. Phys. Scr. 2022, 97, 045203. [Google Scholar] [CrossRef]
- Abbas, I.; Hobiny, A. The thermomechanical response of a poroelastic medium with two thermal relaxation times. Multidiscip. Model. Mater. Struct. 2020, 17, 493–506. [Google Scholar] [CrossRef]
- Abbas, I.A.; Alzahrani, F.S.; Elaiw, A. A DPL model of photothermal interaction in a semiconductor material. Waves Random Complex Media 2019, 29, 328–343. [Google Scholar] [CrossRef]
- Hobiny, A.D.; Abbas, I.A. Theoretical analysis of thermal damages in skin tissue induced by intense moving heat source. Int. J. Heat Mass Transf. 2018, 124, 1011–1014. [Google Scholar] [CrossRef]
- Abbas, I.A. Eigenvalue approach on fractional order theory of thermoelastic diffusion problem for an infinite elastic medium with a spherical cavity. Appl. Math. Model. 2015, 39, 6196–6206. [Google Scholar] [CrossRef]
- Abo-Dahab, S.M.; Abbas, I.A. LS model on thermal shock problem of generalized magneto-thermoelasticity for an infinitely long annular cylinder with variable thermal conductivity. Appl. Math. Model. 2011, 35, 3759–3768. [Google Scholar] [CrossRef]
- Zeeshan, A.; Ellahi, R.; Mabood, F.; Hussain, F. Numerical study on bi-phase coupled stress fluid in the presence of Hafnium and metallic nanoparticles over an inclined plane. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 2854–2869. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ellahi, R.; Shafee, A.; Li, Z. Numerical investigation for second law analysis of ferrofluid inside a porous semi annulus: An application of entropy generation and exergy loss. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 1079–1102. [Google Scholar] [CrossRef]
- Marin, M.; Vlase, S.; Ellahi, R.; Bhatti, M. On the partition of energies for the backward in time problem of thermoelastic materials with a dipolar structure. Symmetry 2019, 11, 863. [Google Scholar] [CrossRef] [Green Version]
- Ellahi, R.; Sait, S.M.; Shehzad, N.; Ayaz, Z. A hybrid investigation on numerical and analytical solutions of electro-magnetohydrodynamics flow of nanofluid through porous media with entropy generation. Int. J. Numer. Methods Heat Fluid Flow 2019, 30, 834–854. [Google Scholar] [CrossRef]
- Milani Shirvan, K.; Mamourian, M.; Mirzakhanlari, S.; Rahimi, A.; Ellahi, R. Numerical study of surface radiation and combined natural convection heat transfer in a solar cavity receiver. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 2385–2399. [Google Scholar] [CrossRef]
- Milani Shirvan, K.; Mamourian, M.; Ellahi, R. Numerical investigation and optimization of mixed convection in ventilated square cavity filled with nanofluid of different inlet and outlet port. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 2053–2069. [Google Scholar] [CrossRef]
- Marin, M.; Hobiny, A.; Abbas, I. The effects of fractional time derivatives in porothermoelastic materials using finite element method. Mathematics 2021, 9, 1606. [Google Scholar] [CrossRef]
- Alzahrani, F.; Hobiny, A.; Abbas, I.; Marin, M. An eigenvalues approach for a two-dimensional porous medium based upon weak, normal and strong thermal conductivities. Symmetry 2020, 12, 848. [Google Scholar] [CrossRef]
- Marin, M.; Othman, M.I.A.; Abbas, I.A. An extension of the domain of influence theorem for generalized thermoelasticity of anisotropic material with voids. J. Comput. Theor. Nanosci. 2015, 12, 1594–1598. [Google Scholar] [CrossRef]
- Marin, M.; Lupu, M. On harmonic vibrations in thermoelasticity of micropolar bodies. JVC/J. Vib. Control. 1998, 4, 507–518. [Google Scholar] [CrossRef]
- Marin, M.; Stan, G. Weak solutions in Elasticity of dipolar bodies with stretch. Carpathian J. Math. 2013, 29, 33–40. [Google Scholar] [CrossRef]
- Othman, M.I.A.; Said, S.; Marin, M. A novel model of plane waves of two-temperature fiber-reinforced thermoelastic medium under the effect of gravity with three-phase-lag model. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 4788–4806. [Google Scholar] [CrossRef]
- Tiwari, R.; Abouelregal, A.E. Memory response on magneto-thermoelastic vibrations on a viscoelastic micro-beam exposed to a laser pulse heat source. Appl. Math. Model. 2021, 99, 328–345. [Google Scholar] [CrossRef]
- Tiwari, R. Magneto-thermoelastic interactions in generalized thermoelastic half-space for varying thermal and electrical conductivity. Waves Random Complex Media 2021, 1–17. [Google Scholar] [CrossRef]
- Abbas, I.A.; Kumar, R. Deformation due to thermal source in micropolar generalized thermoelastic half-space by finite element method. J. Comput. Theor. Nanosci. 2014, 11, 185–190. [Google Scholar] [CrossRef]
- Mohamed, R.; Abbas, I.A.; Abo-Dahab, S. Finite element analysis of hydromagnetic flow and heat transfer of a heat generation fluid over a surface embedded in a non-Darcian porous medium in the presence of chemical reaction. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1385–1395. [Google Scholar] [CrossRef]
- Singh, B. Reflection of plane waves from a free surface of a porothermoelastic solid half-space. J. Porous Media 2013, 16, 945–957. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hobiny, A.; Abbas, I.; Alshehri, H.; Vlase, S.; Marin, M. Thermoelastic Analysis in Poro-Elastic Materials Using a TPL Model. Appl. Sci. 2022, 12, 5914. https://doi.org/10.3390/app12125914
Hobiny A, Abbas I, Alshehri H, Vlase S, Marin M. Thermoelastic Analysis in Poro-Elastic Materials Using a TPL Model. Applied Sciences. 2022; 12(12):5914. https://doi.org/10.3390/app12125914
Chicago/Turabian StyleHobiny, Aatef, Ibrahim Abbas, Hashim Alshehri, Sorin Vlase, and Marin Marin. 2022. "Thermoelastic Analysis in Poro-Elastic Materials Using a TPL Model" Applied Sciences 12, no. 12: 5914. https://doi.org/10.3390/app12125914
APA StyleHobiny, A., Abbas, I., Alshehri, H., Vlase, S., & Marin, M. (2022). Thermoelastic Analysis in Poro-Elastic Materials Using a TPL Model. Applied Sciences, 12(12), 5914. https://doi.org/10.3390/app12125914







