Improvement and Verification of One-Dimensional Numerical Algorithm for Reservoir Water Temperature at the Front of Dams
Abstract
:1. Introduction
2. Simulation Method
2.1. Numerical Analysis Model
2.2. Inflow Simulation Model
2.3. Improved 1D Numerical Model (I1DM) for Reservoir Water Temperature
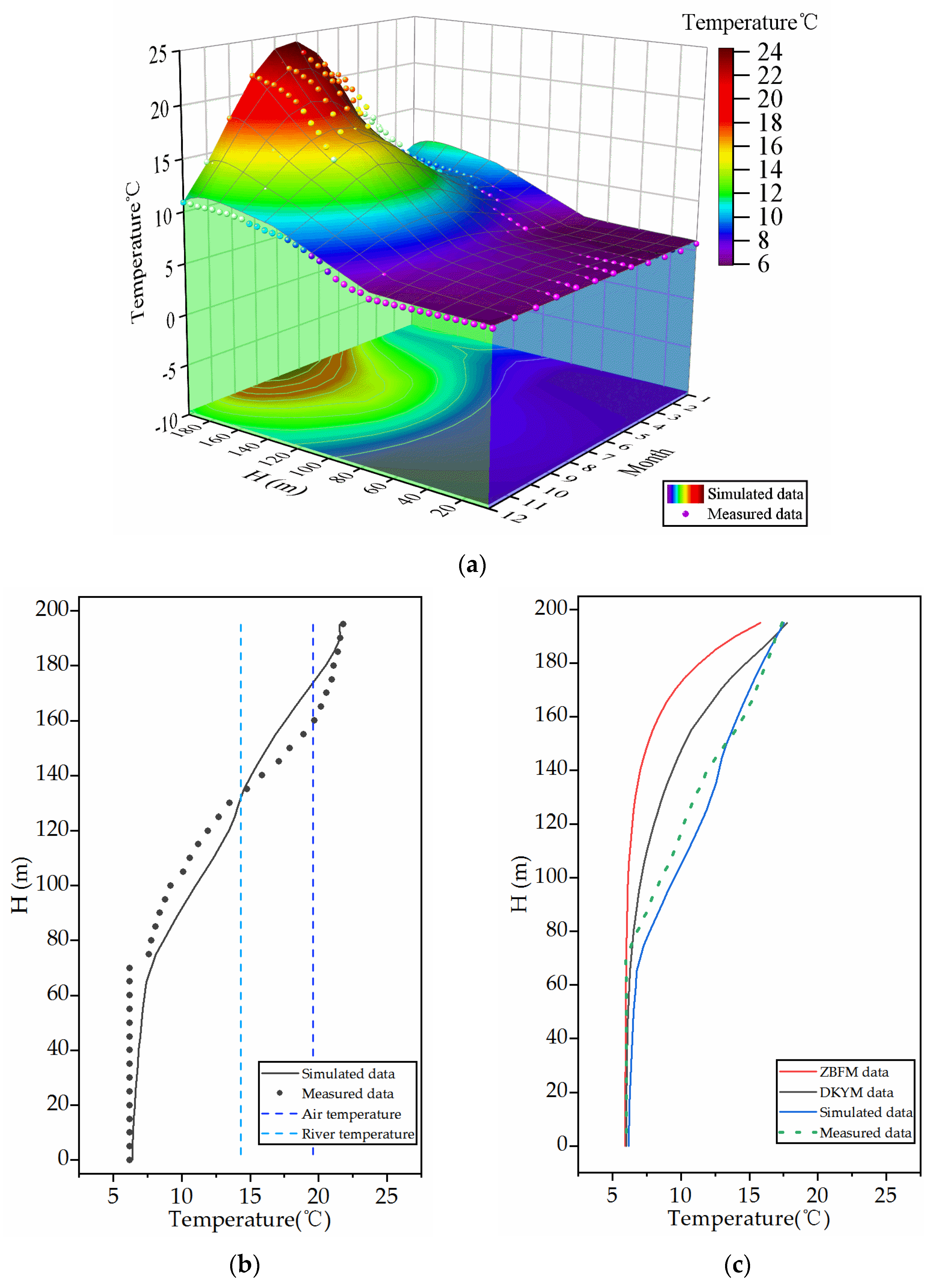
3. Validation of the Model
3.1. Parameters of the Model
3.2. Analysis of Model Results
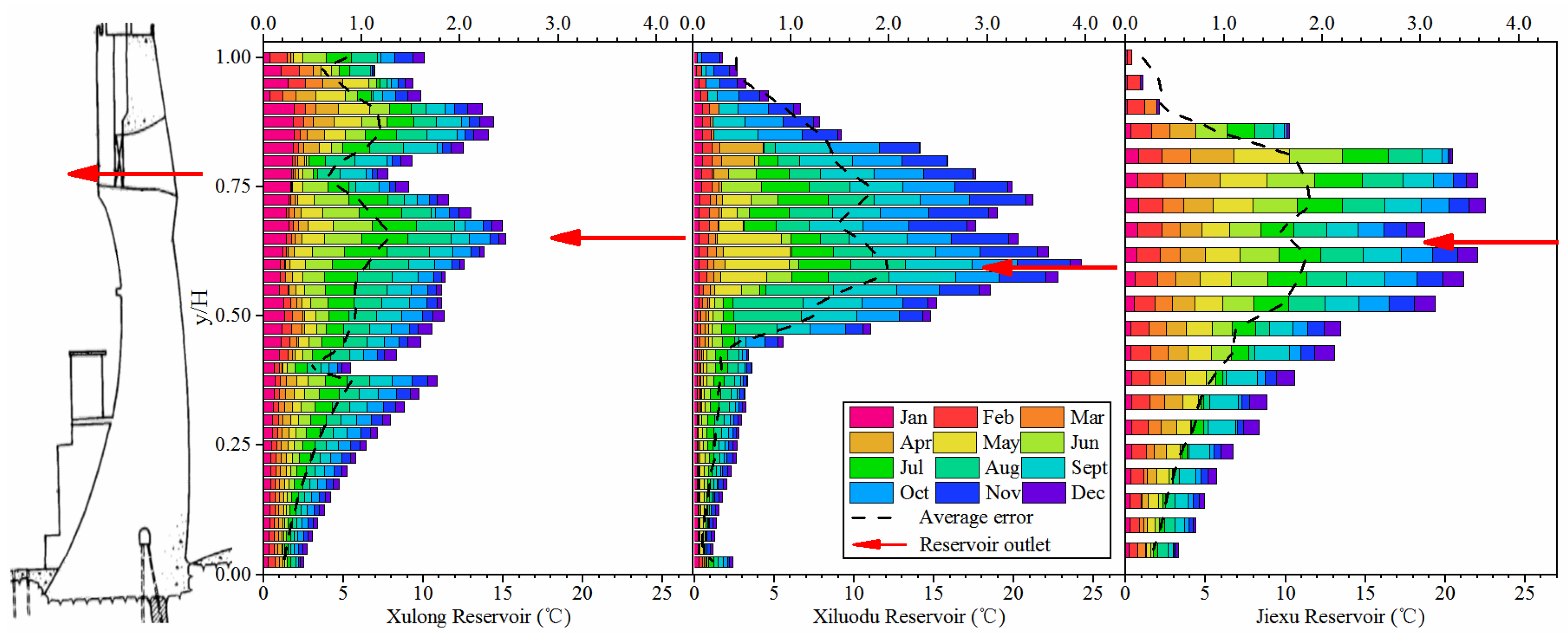
3.3. Simulation of the Bottom Slag
4. Analysis of Different Water Temperature Models
4.1. Characteristics of Each Water Temperature Method
4.2. Comparison of Simulation Results
4.3. Analysis of the Error in Vertical Direction of I1DM
5. Conclusions
- The NSE of the water temperature simulation results of the three different reservoirs are all above 0.85, and the average difference is below 1.0 °C, which has a high reliability. It can be concluded that the algorithm is suitable for predicting the water temperature at the front of the dam for reservoirs in various scales and modes of operation.
- Compared with the empirical method, this algorithm is more thorough in theory, considers more working conditions, and has more accurate simulation results. Compared with the three-dimensional numerical algorithm, this algorithm is more efficient and easier to use.
- The model proposed in this paper can be seamlessly embedded in the simulation program for concrete dam temperature control. More accurate temperature boundary conditions are provided for the simulation program without affecting the overall efficiency. The reliability of the simulation results of stress state in the crack-prone areas of the upstream surface is further improved, and it has important engineering significance for the temperature control and crack prevention design of large concrete dams.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DKYM | Dongkanyuan method |
| ZBFM | Zhu Bofang method |
| 1D/2D/3D | One-dimensional/Two-dimensional/Three-dimensional |
| NSE | The Nash–Sutcliffe efficiency coefficient |
| LBM | Lattice Boltzmann method |
| THM | Thermal-water-mechanical |
| I1DM | Improved 1D numerical model |
References
- Aniskin, N.; Nguyen, T.C. Influence factors on the temperature field in a mass concrete. E3S Web Conf. 2019, 97, 05021. [Google Scholar] [CrossRef]
- Briffaut, M.; Benboudjema, F.; Torrenti, J.M. Numerical analysis of the thermal active restrained shrinkage ring test to study the early age behavior of massive concrete structures. Eng. Struct. 2011, 33, 1390–1401. [Google Scholar] [CrossRef]
- Silva, C.M.; Castro, L.M. Hybrid-mixed stress model for the nonlinear analysis of concrete structures. Comput. Struct. 2005, 83, 2381–2394. [Google Scholar] [CrossRef]
- Wang, H.B.; Qiang, S.; Sun, X. Dynamic Simulation Analysis of Temperature Field and Thermal Stress of Concrete Gravity Dam during Construction Period. Appl. Mech. Mater. 2011, 90–93, 2677–2681. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, Y.; Yang, P. Analysis on the causes of crack formation and the methods of temperature control and crack prevention during construction of super-high arch dams. J. Hydroelectr. Eng. 2010, 29, 45–51. [Google Scholar] [CrossRef]
- Morrison, J.; Quick, M.C.; Foreman, M. Climate change in the Fraser River watershed: Flow and temperature projections. J. Hydrol. 2002, 263, 230–244. [Google Scholar] [CrossRef]
- Nsiri, I.; Tarhouni, J.; Irie, M. Modeling of Thermal Stratification and the Effect on Water Quality in Four Reservoirs in Tunisia. Hydrogeol. Hydrol. Eng. 2016, 5, 1. [Google Scholar] [CrossRef]
- Huber, W.C.; Harleman, D.R.; Ryan, P.J. Temperature prediction in stratified reservoirs. J. Hydraul. Div. 1972, 98, 645–666. [Google Scholar] [CrossRef]
- Haag, I.; Luce, A. The integrated water balance and water temperature model LARSIM-WT. Hydrol. Processes 2010, 22, 1046–1056. [Google Scholar] [CrossRef]
- Kong, Y.; Deng, Y.; Tuo, Y. Application of one-dimensional vertical temperature model in Dongjiang Reservoir. Yangtze River 2017, 48, 97–102. [Google Scholar] [CrossRef]
- Lindenschmidt, K.E.; Carr, M.K.; Sadeghian, A. CE-QUAL-W2 model of dam outflow elevation impact on temperature, dissolved oxygen and nutrients in a reservoir. Sci. Data 2019, 6, 312. [Google Scholar] [CrossRef]
- Diao, W.; Cheng, Y.G.; Zhang, C.Z. Three-dimensional prediction of reservoir water temperature by the lattice Boltzmann method: Validation. J. Hydrodyn. 2015, 27, 248–256. [Google Scholar] [CrossRef]
- Yin, T.; Li, Q.; Hu, Y.; Yu, S.; Liang, G. Coupled Thermo-Hydro-Mechanical Analysis of Valley Narrowing Deformation of High Arch Dam: A Case Study of the Xiluodu Project in China. Appl. Sci. 2020, 10, 524. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q. Prediction of Water Temperature as Affected by a Pre-Constructed Reservoir Project Based on MIKE11. Clean-Soil Air Water 2013, 41, 1–5. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, X.; Chen, K. Sensitivity analysis of thermal equilibrium parameters of MIKE 11 model: A case study of Wuxikou Reservoir in Jiangxi Province of China. Chin. Geogr. Sci. 2013, 23, 584–593. [Google Scholar] [CrossRef] [Green Version]
- He, W.; Lian, J.; Du, H. Source tracking and temperature prediction of discharged water in a deep reservoir based on a 3-D hydro-thermal-tracer model. J. Hydro-Environ. Res. 2018, 20, 9–21. [Google Scholar] [CrossRef]
- Park, G.G.; Schmidt, P.S. Numerical Modeling of Thermal Stratification in a Reservoir with Large Discharge-to-Volume Ratio1. Jawra J. Am. Water Resour. Assoc. 2010, 9, 932–941. [Google Scholar] [CrossRef]
- Wormleaton, P.R.; Hadjipanos, P. Flow Distribution in Compound Channels. J. Hydraul. Eng. 1985, 111, 357–361. [Google Scholar] [CrossRef]
- Lin, G.F.; Wu, M.C. An RBF network with a two-step learning algorithm for developing a reservoir inflow forecasting model. J. Hydrol. 2011, 405, 439–450. [Google Scholar] [CrossRef]
- Lin, G.F.; Wu, M.C.; Chen, G.R. An RBF-based model with an information processor for forecasting hourly reservoir inflow during typhoons. Hydrol. Processes 2010, 23, 3598–3609. [Google Scholar] [CrossRef]
- Kim, S. Analysis of the Water Circulation Structure in the Paldang Reservoir, South Korea. Appl. Sci. 2020, 10, 6822. [Google Scholar]
- Li, X.; Qiu, J.; Shang, Q. Simulation of Reservoir Sediment Flushing of the Three Gorges Reservoir Using an Artificial Neural Network. Appl. Sci. 2016, 6, 148. [Google Scholar] [CrossRef] [Green Version]
- Tomasz, G.D. Computational Fluid Mechanics and Heat Transfer. AIAA J. 2013, 51, 2751. [Google Scholar] [CrossRef]
- Ogedengbe, E. Non-inverted skew upwind scheme for numerical heat transfer and fluid flow simulations. Diss. Abstr. Int. 2006, 68, 0586. [Google Scholar]
- Zakonnova, A.V.; Litvinov, A.S. Analysis of Relation of Water Temperature in the Rubinsk Reservoir with Income of Solar Radiation. Hydrobiol. J. 2017, 53, 77–86. [Google Scholar] [CrossRef]
- Chang, J.Q. Research on Vertical Distribution of Water Temperature in Different Regulation Reservoirs. Adv. Mater. Res. 2014, 3248, 3190–3197. [Google Scholar] [CrossRef]
- Lee, H.; Chung, S.; Ryu, I. Three-dimensional modeling of thermal stratification of a deep and dendritic reservoir using ELCOM model. J. Hydro-Environ. Res. 2013, 7, 124–133. [Google Scholar] [CrossRef]
- Chen, Y.C.; Kao, S.P. Velocity distribution in open-channel flows with submerged aquatic plant. Hydrol. Processes 2011, 25, 2009–2017. [Google Scholar] [CrossRef]
- Shu, A.P.; Liu, Q.Q.; Fei, X.J. Unified laws of velocity distribution for sediment laden flow with high and low concentration. J. Hydraul. Eng. 2006, 37, 1175–1180. [Google Scholar] [CrossRef]
- Lu, J.; Zhou, Y.; Zhu, Y. Improved formulae of velocity distributions along the vertical and transverse directions in natural rivers with the sidewall effect. Environ. Fluid Mech. 2018, 18, 1491–1508. [Google Scholar] [CrossRef]
- Song, B.; Schmalz, N.F. Improved structure of vertical flow velocity distribution in natural rivers based on mean vertical profile velocity and relative water depth. Nord. Hydrol. 2018, 49, 878–892. [Google Scholar] [CrossRef]
- Li, X.; Yan, H.B.; Xu, Y. Discussion on New Formula of Velocity Distribution in Rectangular Open Channel. Yangtze River 2021, 39, 3. [Google Scholar]
- Ahmed, A.; Said, M.; Mohamed, T. Stability Criterion for Uniform Flow in Open Channel Cross Sections with Different Shapes. J. Irrig. Drain. Eng. 2020, 146, 40. [Google Scholar] [CrossRef]
- Simpson, J.J.; Paulson, C.A. Mid-ocean observations of atmospheric radiation. Q. J. R. Meteorol. Soc. 2010, 105, 487–502. [Google Scholar] [CrossRef]
- Gueymard, C.A. The sun’s total and spectral irradiance for solar energy applications and solar radiation models. Sol. Energy 2004, 76, 423–453. [Google Scholar] [CrossRef]
- Wilfried, B. On a derivable Equation for long-wave radiation from clear skies. Water Resour. Res. 2010, 32, 742–744. [Google Scholar] [CrossRef]
- Swinbank, W.C. Long-wave radiation from clear skies. Q. J. R. Meteorol. Soc. 2010, 89, 339–348. [Google Scholar] [CrossRef]
- Chang, X.; Liu, X.; Wei, B. Temperature simulation of RCC gravity dam during construction considering solar radiation. Eng. J. Wuhan Univ. 2006, 39, 26–29. [Google Scholar] [CrossRef]
- Zhu, Z.Y.; Qiang, S.; Liu, M.Z. Cracking Mechanism of Long Concrete Bedding Cushion and Prevention Method. Adv. Mater. Res. 2011, 163–167, 880–887. [Google Scholar] [CrossRef]
- Zhu, Z.Y.; Qiang, S.; Liu, M.Z. Cracking Mechanism of RCC Dam Surface and Prevention Method. Adv. Mater. Res. 2011, 295–297, 2092–2096. [Google Scholar] [CrossRef]
- Yuan, M.; Qiang, S.; Xu, Y. Research on Cracking Mechanism of Early-Age Restrained Concrete under High-Temperature and Low-Humidity Environment. Materials 2021, 14, 4084. [Google Scholar] [CrossRef]







| Altitude (m) | V (108 m3) | A (km2) | Altitude (m) | V (108 m3) | A (km2) | Altitude (m) | V (108 m3) | A (km2) |
|---|---|---|---|---|---|---|---|---|
| 2210 | 0.31 | 1.68 | 2250 | 1.87 | 6.71 | 2290 | 5.97 | 14.17 |
| 2220 | 0.52 | 2.52 | 2260 | 2.63 | 8.43 | 2300 | 7.48 | 15.86 |
| 2230 | 0.83 | 3.77 | 2270 | 3.55 | 10.10 | 2302 | 7.81 | 16.60 |
| 2240 | 1.28 | 5.20 | 2280 | 4.65 | 12.03 | 2305 | 8.29 | 17.13 |
| Parameter | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sept | Oct | Nov | Dec |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Air temperature (°C) | 6 | 9.5 | 12.3 | 14.8 | 20.2 | 23.4 | 22.3 | 20.3 | 19.6 | 15.3 | 10.2 | 6.4 |
| River temperature (°C) | 3 | 4.7 | 7.5 | 10.4 | 13.1 | 15.1 | 16.1 | 16.1 | 14.3 | 10.8 | 6.2 | 3.4 |
| Inflow rate (m3/s) | 1039 | 1423 | 1684 | 1653 | 1381 | 658 | 519 | 518 | 516 | 514 | 596 | 767 |
| Solar radiation (KJ/(m2·h)) | 1367 | 1311 | 1249 | 1151 | 929 | 791 | 642 | 715 | 947 | 1097 | 1256 | 1294 |
| Parameter | Mean Difference | Root Mean Square | NSE | Time | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Method | Xulong | Xiluodu | Jiexu | Sanhekou | Xulong | Xiluodu | Jiexu | Sanhekou | Xulong | Xiluodu | Jiexu | Sanhekou | - |
| DKYM | 1.7 | 1.1 | 2.0 | 3.0 | 2.5 | 1.7 | 2.6 | 3.6 | 0.89 | 0.81 | 0.64 | 0.20 | <1 min |
| ZBFM | 2.5 | 1.5 | 1.1 | 2.3 | 3.4 | 2.3 | 1.3 | 2.9 | 0.78 | 0.61 | 0.84 | 0.50 | <1 min |
| I1DM | 0.8 | 0.8 | 1.0 | 1.0 | 1.0 | 1.4 | 1.0 | 1.5 | 0.92 | 0.86 | 0.91 | 0.88 | <1 min |
| MIKE3 | 0.7 | 0.8 | 0.9 | 0.9 | 0.9 | 1.1 | 0.9 | 1.3 | 0.93 | 0.93 | 0.94 | 0.90 | >3 h |
| Reservoir Name | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sept | Oct | Nov | Dec |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Xulong | 2302 | 2302 | 2302 | 2302 | 2302 | 2302 | 2302 | 2302 | 2302 | 2302 | 2302 | 2302 |
| Xiluodu | 595 | 590 | 575 | 560 | 540 | 555 | 560 | 560 | 590 | 600 | 600 | 600 |
| Jiexu | 3374 | 3374 | 3370 | 3369 | 3367 | 3369 | 3369 | 3369 | 3369 | 3369 | 3370 | 3372 |
| Sanhekou | 634 | 634 | 634 | 634 | 634 | 634 | 634 | 634 | 634 | 634 | 634 | 634 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, X.; Shen, Z.; Wang, Z.; Qiang, S.; Yuan, M. Improvement and Verification of One-Dimensional Numerical Algorithm for Reservoir Water Temperature at the Front of Dams. Appl. Sci. 2022, 12, 5870. https://doi.org/10.3390/app12125870
Zheng X, Shen Z, Wang Z, Qiang S, Yuan M. Improvement and Verification of One-Dimensional Numerical Algorithm for Reservoir Water Temperature at the Front of Dams. Applied Sciences. 2022; 12(12):5870. https://doi.org/10.3390/app12125870
Chicago/Turabian StyleZheng, Xuerui, Zhenzhong Shen, Zhenhong Wang, Sheng Qiang, and Min Yuan. 2022. "Improvement and Verification of One-Dimensional Numerical Algorithm for Reservoir Water Temperature at the Front of Dams" Applied Sciences 12, no. 12: 5870. https://doi.org/10.3390/app12125870
APA StyleZheng, X., Shen, Z., Wang, Z., Qiang, S., & Yuan, M. (2022). Improvement and Verification of One-Dimensional Numerical Algorithm for Reservoir Water Temperature at the Front of Dams. Applied Sciences, 12(12), 5870. https://doi.org/10.3390/app12125870










