Pixel Resolution Imaging in Parallel Phase-Shifting Digital Holography
Abstract
:1. Introduction
2. Principles and Methods
2.1. Hologram Recording
2.2. Hologram Reconstruction
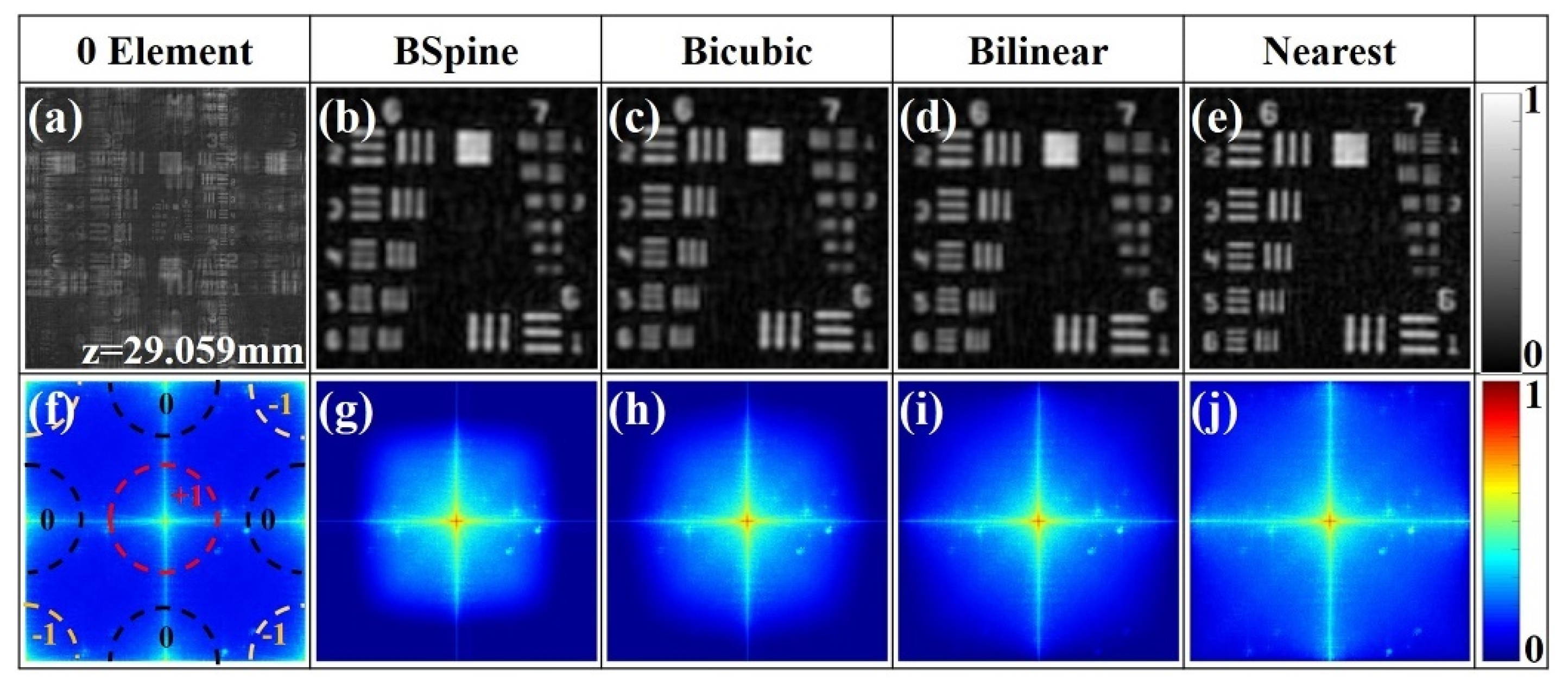
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fratz, M.; Seyler, T.; Bertz, A.; Carl, D. Digital holography in production: An overview. Light. Adv. Manuf. 2021, 2, 283–295. [Google Scholar] [CrossRef]
- Nayak, A.R.; Malkiel, E.; McFarland, M.N.; Twardowski, M.S.; Sullivan, J.M. A Review of Holography in the Aquatic Sciences: In situ Characterization of Particles, Plankton, and Small Scale Biophysical Interactions. Front. Mar. Sci. 2021, 7, 1256. [Google Scholar] [CrossRef]
- Nadeau, J.L.; Bedrossian, M.; Lindensmith, C.A. Imaging technologies and strategies for detection of extant extraterrestrial microorganisms. Adv. Phys. X 2018, 3, 1424032. [Google Scholar] [CrossRef] [Green Version]
- Javidi, B.; Carnicer, A.; Anand, A.; Barbastathis, G.; Chen, W.; Ferraro, P.; Goodman, J.; Horisaki, R.; Khare, K.; Kujawinska, M.; et al. Roadmap on digital holography [Invited]. Opt. Express 2021, 29, 35078–35118. [Google Scholar] [CrossRef]
- Yamaguchi, I.; Zhang, T. Phase-shifting digital holography. Opt. Lett. 1997, 22, 1268–1270. [Google Scholar] [CrossRef]
- Stoykova, E.; Kang, H.; Park, J. Twin-image problem in digital holography-a survey. Chin. Opt. Lett. 2014, 12, 060013. [Google Scholar] [CrossRef]
- Kimbrough, B.T. Pixelated mask spatial carrier phase shifting interferometry algorithms and associated errors. Appl. Opt. 2006, 45, 4554–4562. [Google Scholar] [CrossRef] [Green Version]
- Xia, P.; Ri, S.; Wang, Q.; Tsuda, H. Nanometer-order thermal deformation measurement by a calibrated phase-shifting digital holography system. Opt. Express 2018, 26, 12594–12604. [Google Scholar] [CrossRef]
- Awatsuji, Y.; Sasada, M.; Kubota, T. Parallel quasi-phase-shifting digital holography. Appl. Phys. Lett. 2004, 85, 1069–1071. [Google Scholar] [CrossRef]
- Xia, P.; Awatsuji, Y.; Matoba, O. One million fps phase measurement by digital holography. In Proceedings of the Selected Papers from the 31st International Congress on High-Speed Imaging and Photonics, Osaka, Japan, 7–10 November 2016; p. 103280K. [Google Scholar]
- Awatsuji, Y.; Koyama, T.; Tahara, T.; Ito, K.; Shimozato, Y.; Kaneko, A.; Nishio, K.; Ura, S.; Kubota, T.; Matoba, O. Parallel optical-path-length-shifting digital holography. Appl. Opt. 2009, 48, H160–H167. [Google Scholar] [CrossRef]
- Nomura, T.; Murata, S.; Nitanai, E.; Numata, T. Phase-shifting digital holography with a phase difference between orthogonal polarizations. Appl. Opt. 2006, 45, 4873–4877. [Google Scholar] [CrossRef] [PubMed]
- Tahara, T.; Awatsuji, Y.; Kaneko, A.; Koyama, T.; Nishio, K.; Ura, S.; Kubota, T.; Matoba, O. Parallel two-step phase-shifting digital holography using polarization. Opt. Rev. 2010, 17, 108–113. [Google Scholar] [CrossRef]
- Awatsuji, Y.; Fukuda, T.; Wang, Y.X.; Xia, P.; Kakue, T.; Nishio, K.; Matoba, O. 3D motion picture of transparent gas flow by parallel phase-shifting digital holography. In Proceedings of the Third International Conference on Photonics Solutions, Pattaya, Thailand, 8–10 November 2017; SPIE-Int Soc Optical Engineering: Bellingham, UK, 2018; Volume 10714. [Google Scholar]
- Meiling, Z.; Peng, G.; Kai, W.; Kequn, Z.; Yang, W.; Lixin, L.; Junwei, M.; Baoli, Y. A Comprehensive Review on Parallel Phase-shifting Digital Holography. Acta Photonica Sin. 2021, 50, 1. [Google Scholar]
- Millerd, J.; Brock, N.; Hayes, J.; North-Morris, M.; Kimbrough, B.; Wyant, J. Pixelated Phase-Mask Dynamic Interferometers. In Fringe 2005; Springer: Berlin/Heidelberg, Germany, 2006; pp. 640–647. [Google Scholar] [CrossRef]
- Mihoubi, S.; Lapray, P.-J.; Bigué, L. Survey of Demosaicking Methods for Polarization Filter Array Images. Sensors 2018, 18, 3688. [Google Scholar] [CrossRef] [Green Version]
- Rebhan, D.; Rosenberger, M.; Notni, G. Principle investigations on polarization image sensors. In Proceedings of the Photonics and Education in Measurement Science 2019, Jena, Germany, 17–19 September 2019; p. 111440A. [Google Scholar]
- Yamazaki, T.; Maruyama, Y.; Uesaka, Y.; Nakamura, M.; Matoba, Y.; Terada, T.; Komori, K.; Ohba, Y.; Arakawa, S.; Hirasawa, Y.; et al. Four-directional pixel-wise polarization CMOS image sensor using air-gap wire grid on 2.5-μm back-illuminated pixels. In Proceedings of the 2016 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 3–7 December 2016; pp. 8.7.1–8.7.4. [Google Scholar] [CrossRef]
- Tahara, T.; Ito, K.; Fujii, M.; Kakue, T.; Shimozato, Y.; Awatsuji, Y.; Nishio, K.; Ura, S.; Kubota, T.; Matoba, O. Experimental demonstration of parallel two-step phase-shifting digital holography. Opt. Express 2010, 18, 18975–18980. [Google Scholar] [CrossRef]
- Brock, N.J.; Crandall, C.; Millerd, J.E. Snap-shot imaging polarimeter: Performance and applications. In Polarization: Measurement, Analysis, and Remote Sensing XI.; SPIE: Bellingham, WA, USA, 2014; p. 909903. [Google Scholar] [CrossRef]
- Jiao, S.; Zou, W. High-resolution parallel phase-shifting digital holography using a low-resolution phase-shifting array device based on image inpainting. Opt. Lett. 2017, 42, 482–485. [Google Scholar] [CrossRef]
- Tahara, T.; Kanno, T.; Arai, Y.; Ozawa, T. Single-shot phase-shifting incoherent digital holography. J. Opt. 2017, 19, 065705. [Google Scholar] [CrossRef]
- Liang, D.; Zhang, Q.; Wang, J.; Liu, J. Single-shot Fresnel incoherent digital holography based on geometric phase lens. J. Mod. Opt. 2019, 67, 92–98. [Google Scholar] [CrossRef] [Green Version]
- Tahara, T.; Ito, T.; Ichihashi, Y.; Oi, R. Single-shot incoherent color digital holographic microscopy system with static polarization-sensitive optical elements. J. Opt. 2020, 22, 105702. [Google Scholar] [CrossRef]
- Tsuruta, M.; Fukuyama, T.; Tahara, T.; Takaki, Y. Fast Image Reconstruction Technique for Parallel Phase-Shifting Digital Holography. Appl. Sci. 2021, 11, 11343. [Google Scholar] [CrossRef]
- Liu, H.; V, V.R.; Ren, H.; Du, X.; Chen, Z.; Pu, J. Single-Shot On-Axis Fizeau Polarization Phase-Shifting Digital Holography for Complex-Valued Dynamic Object Imaging. Photonics 2022, 9, 126. [Google Scholar] [CrossRef]
- Liu, S.; Chen, J.; Xun, Y.; Zhao, X.; Chang, C.-H. A New Polarization Image Demosaicking Algorithm by Exploiting Inter-Channel Correlations with Guided Filtering. IEEE Trans. Image Process. 2020, 29, 7076–7089. [Google Scholar] [CrossRef]
- Xie, F.; Chen, J. A Demosaicing Algorithm Based on Local Directional Gradients for Polarization Image. In Proceedings of the 2021 International Conference on Computing, Networking, Telecommunications & Engineering Sciences Applications (CoNTESA), Tirana, Albania, 9–10 December 2021; pp. 40–44. [Google Scholar] [CrossRef]
- Xia, P.; Tahara, T.; Kakue, T.; Awatsuji, Y.; Nishio, K.; Ura, S.; Kubota, T.; Matoba, O. Performance comparison of bilinear interpolation, bicubic interpolation, and B-spline interpolation in parallel phase-shifting digital holography. Opt. Rev. 2013, 20, 193–197. [Google Scholar] [CrossRef]
- Zhaoxiang, J. Pixelated Polarization Imaging Technique and Its Application in Digital Holographic Microscopy. Ph.D. Thesis, University of Science and Technology of China, Anhui, China, 2020. [Google Scholar]
- Lane, C.; Rode, D.; Rösgen, T. Calibration of a polarization image sensor and investigation of influencing factors. Appl. Opt. 2021, 61, C37–C45. [Google Scholar] [CrossRef] [PubMed]
- Wenhui, Z.; Liangcai, C.; Guofan, J. Review on high resolution and large field of view digital holography. Infrared Laser Eng. 2019, 48, 603008. [Google Scholar] [CrossRef]
- Gao, P.; Yuan, C. Resolution enhancement of digital holographic microscopy via synthetic aperture: A review. Light. Adv. Manuf. 2022, 3, 105–120. [Google Scholar] [CrossRef]
- Liu, X.; Liu, X.; Zhang, H.; Fan, Y.; Meng, H. Research progress of digital holography in deep-sea in situ detection. In Proceedings of the Seventh Symposium on Novel Photoelectronic Detection Technology and Applications, Kunming, China, 5–7 November 2021; p. 117636J. [Google Scholar]
- LUCID VISION LABS. Available online: http://thinklucid.cn/tech-briefs/polarization-explained-sony-polarized-sensor (accessed on 5 April 2022).
- Latychevskaia, T.; Fink, H.-W. Practical algorithms for simulation and reconstruction of digital in-line holograms. Appl. Opt. 2015, 54, 2424–2434. [Google Scholar] [CrossRef] [Green Version]
- Tahara, T.; Ito, K.; Kakue, T.; Fujii, M.; Shimozato, Y.; Awatsuji, Y.; Nishio, K.; Ura, S.; Kubota, T.; Matoba, O. Parallel phase-shifting digital holographic microscopy. Biomed. Opt. Express 2010, 1, 610–616. [Google Scholar] [CrossRef]
- Tahara, T.; Shimozato, Y.; Xia, P.; Ito, Y.; Awatsuji, Y.; Nishio, K.; Ura, S.; Matoba, O.; Kubota, T. Algorithm for reconstructing wide space-bandwidth information in parallel two-step phase-shifting digital holography. Opt. Express 2012, 20, 19806–19814. [Google Scholar] [CrossRef]
- Kocsis, P.; Shevkunov, I.; Katkovnik, V.; Rekola, H.; Egiazarian, K. Single-shot pixel super-resolution phase imaging by wavefront separation approach. Opt. Express 2021, 29, 43662–43678. [Google Scholar] [CrossRef]





| Method | Size | |
|---|---|---|
| 0 elements | ||
| Nearest-neighbor | ||
| Bilinear | ||
| Bicubic | ||
| B-spline |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Meng, H.; Liu, X.; Liu, J.; Cui, X. Pixel Resolution Imaging in Parallel Phase-Shifting Digital Holography. Appl. Sci. 2022, 12, 5812. https://doi.org/10.3390/app12125812
Wang Y, Meng H, Liu X, Liu J, Cui X. Pixel Resolution Imaging in Parallel Phase-Shifting Digital Holography. Applied Sciences. 2022; 12(12):5812. https://doi.org/10.3390/app12125812
Chicago/Turabian StyleWang, Yue, Haoran Meng, Xinyue Liu, Jiahao Liu, and Xu Cui. 2022. "Pixel Resolution Imaging in Parallel Phase-Shifting Digital Holography" Applied Sciences 12, no. 12: 5812. https://doi.org/10.3390/app12125812
APA StyleWang, Y., Meng, H., Liu, X., Liu, J., & Cui, X. (2022). Pixel Resolution Imaging in Parallel Phase-Shifting Digital Holography. Applied Sciences, 12(12), 5812. https://doi.org/10.3390/app12125812






