Abstract
The electrostatic field in a nanocomposite represented by spherical nanoparticles (NPs) embedded into a dielectric between two parallel metallic electrodes is derived from first principles. The NPs are modeled by point dipoles which possess the polarizability of a sphere, and their image potential in the electrodes is found using a dyadic Green’s function. The derived field is used to obtain the parameters which characterize the electrical breakdown in a nanocomposite capacitor. It is found, in particular, that for relatively low volume fractions of NPs, the breakdown voltage linearly decreases with the volume fraction, and the slope of this dependence is explicitly found in terms of the dielectric permittivities of the NPs and the dielectric host. The corresponding decrease in the maximum energy density accumulated in the capacitor is also determined. A comparison with the experimental data on the breakdown strength in polymer films doped with BaTiO NPs available in the literature reveals a dominant role of the interface polarization at the NP-polymer interface and an existence of a nonferroelectric surface layer in NPs. This research provides a rigorous approach to the electrical breakdown phenomenon and can be used for a proper design of nanocomposite capacitors.
1. Introduction
Recently, the polymer film capacitors have received growing attention due to their advantages of a low cost, facile fabrication, excellent flexibility and high operating voltage [1]. To also attain high energy storage density, one employs nanosized inclusions with a high dielectric constant, thus increasing the effective dielectric permittivity of such polymer-based nanocomposites [2,3,4,5]. This can be performed, however, at the expense of a decrease in the capacitor breakdown strength [6,7,8] that diminishes to some extent the advantages of this approach.
To properly design nanocomposite capacitors, one needs a deep understanding of the factors which control the electrical breakdown in them. For relatively low volume fractions of inclusions, which do not create deep traps for electrons [9,10,11,12,13], the primary effect of their embedding is a modification of the electric field in the capacitor. Among different approaches which aim to account for this influence, only the Maxwell Garnett approximation [14,15] follows from first principles, while the other ones are rather phenomenological models (see, for example, a review of different models in Ref. [7]). This approximation treats the spherical inclusions as point dipoles with a dipole moment which is determined by the sphere polarizability. It is applicable, however, to composite media provided they extend throughout a space of dimensions which are much larger than the wavelength of the external field or to unbounded media in the static case. For a nanocomposite capacitor, this criterion is not fulfilled, and one must take into account the polarization of electrodes and, resulting from it, the image potential [16].
In the present paper, we develop a first-principles approach to the static electric field in a nanocomposite capacitor which is based on a rigorous account of the image potential for point dipoles between parallel metallic electrodes. The obtained results are used to find the parameters which characterize the electrical breakdown in a nanocomposite capacitor. The predicted dependencies are compared with the available experimental data on the breakdown field strength as a function of the volume fraction of inclusions and temperature.
2. Methods
2.1. Model
We consider a parallel-plate capacitor in which the gap of thickness d between the metallic electrodes is filled with a nanocomposite dielectric. The rectangular electrodes are assumed identical to each other and have the lateral dimensions and along the x and y axes, respectively. The nanocomposite is represented by identical spherical nanoparticles (NPs) of radius R with the dielectric permittivity randomly dispersed in the host dielectric with the dielectric permittivity (see Figure 1).
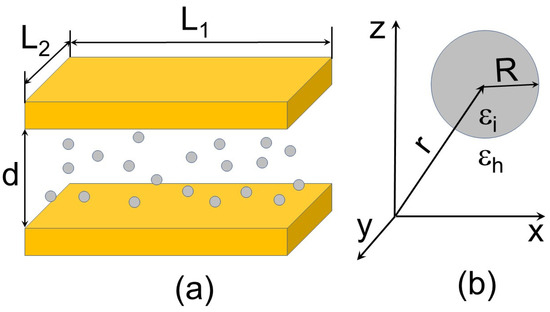
Figure 1.
(a) The model of a nanocomposite capacitor. (b) The model of an NP.
We assume that the NP radius is much less than the capacitor dimensions, i.e., , and treat the NPs as point dipoles which possess the polarizability of a dielectric sphere. Such an approach follows the assumption made by Maxwell Garnett [14] which has been widely used for the modeling of the dielectric properties of composites. The applicability of this approximation is limited to relatively small volume fractions of NPs (see Section 2.3).
2.2. Electrical Breakdown in Conventional Capacitors
We assume that the main dependencies which govern the electrical breakdown in capacitors remain valid when a small volume fraction of NPs is embedded into the host dielectric. Namely, the avalanching effect in the dielectric in a strong electric field leads to an exponential increase in the electron current density with the dielectric film thickness as follows [17]
where is the injected current density at the electrode with a negative bias (at ), the constant can be determined in terms of the electron energy sufficient for impact ionization and the recombination rate, E is the electric field strength inside the dielectric and d is the dielectric film thickness. The breakdown occurs when the electron current density reaches the critical value which is sufficient for the dielectric destruction. For a given thickness, this happens at a certain value of the field strength, , which determines the breakdown voltage .
The quantity is dictated, in its turn, by the work function of the electrode and the potential barrier for electrons formed by both the electric field potential and the image potential for an electron originating from the polarization of the electrode. Two processes contribute to this current: the quantum-mechanical tunneling through the barrier and the thermionic current above the barrier.
For relatively weak electric fields, the latter one prevails over the first one and is given by the Richardson–Schottky equation [18]
where A and B are constants, A being known as the Richardson constant, W is the work function of the electrode, E is the electric field strength inside the dielectric film, k is the Boltzmann constant and T is the temperature.
In strong electric fields, the tunneling mechanism is the dominant one and the injection current is given by the Fowler–Nordheim formula [19]
where the constants C and D are determined by the work function of the electrode and do not depend on the temperature.
2.3. Local Field in a Nanocomposite
When applying the above equations to a nanocomposite capacitor, one should regard the field strength E as the microscopic (local) field which is determined not only by the applied voltage but also by the field of the polarized NPs. For extended media and relatively small volume fractions of NPs, this field can be found in the Maxwell Garnett approximation which models the inclusions by polarizable spheres [14,15]. However, this approach is not applicable to the operating wavelengths which are comparable with or larger than the capacitor dimensions and especially for static fields which correspond to the limit [16].
A proper approach to this problem involves an account of the image potential which originates from the polarization of the electrodes and can be obtained by an infinite summation of all the induced NP dipole images in the two electrodes [20]. However, a more convenient way of calculation is using the Fourier transform of the field derived for a dipole oscillating with frequency between two reflecting surfaces and taking the limit [21].
In the adopted approximation, the induced dipole moment of an NP located at the point is given by [22]
where is the sphere polarizability and is the microscopic (local) field [23] at the position of the dipole. A random distribution of NPs allows one to formally consider their polarization, , as a continuous function of the radius vector . Then, the local field can be written in the form [23,24]
where is the external electric field applied to the capacitor and directed along the z axis and the integral term represents a collective action of the induced dipoles. Here, N is the volume number density of NPs, the quantity is the so-called field susceptibility tensor that relates the electric field at the point generated by a classical dipole, oscillating at frequency , with the dipole moment itself, located at [25], and the symbol denotes the gap volume after removal of a small volume around the NP under consideration that excludes its self-action. As far as the dipole moment in the integrand depends on the local field, Equation (5) is an integral equation which provides a self-consistent solution for the electric field in the capacitor.
The tensor can be expressed in terms of the dyadic Green’s function for Maxwell’s equations [26] and allows a decomposition into the direct contribution, which describes the field of a dipole in free space [27], and the reflected contribution, which provides the dipole field reflected from the parallel plates [21]. For a dipole near a flat surface, it is convenient to write it in the form of the 2D spatial Fourier integral as follows [28]
where is the Fourier transform of the tensor , , and are the Cartesian coordinates of the point , and are the spatial frequencies along the x and y axes, respectively.
For the purposes of the present derivation, one needs the limiting value of the tensor component when , which we denote as . This quantity determines the z-component of the local field which dictates the potential barrier for injected electrons. In this limit, the reflected field is reduced to the field originating from the images of the NP-induced dipole in the two electrodes.
Let us introduce the Fourier transform of the local field in the capacitor,
and substitute it into Equation (5). The obtained equation involves the quantity whose variation with z and is determined by the factors and with . Assuming the inequality , which will be justified in what follows, and the model of a perfect conductor for the electrodes, one obtains (see Ref. [29] for the detail)
We then obtain
where
is the Fourier transform of the applied electric field. Here, , and are the lateral dimensions of the electrodes along the x and y axes, respectively, and we have assumed that the field is zero outside the capacitor. Taking into account that the function is essentially nonzero within the range , one concludes that the essential range of integration in Equation (7) is limited to the values and . This means that the condition , which we have used above, is justified provided .
Finally, the local field, Equation (7), takes the form
with being the volume fraction of NPs and . Let us note that the applicability of this approach which models NPs by point dipoles is limited to the range [16].
3. Results
3.1. Breakdown Parameters in a Nanocomposite Capacitor
Equations (1)–(3), which describe the electrical breakdown, can be written in terms of the applied voltage, V, and the applied field strength, , as
and
respectively. Here, the new parameters
and
determine the field and temperature dependencies of the injection current in a nanocomposite capacitor.
The breakdown voltage for a nanocomposite capacitor, , is related with the one for an NPs free capacitor, , as follows
For NPs with , the quantity is positive and therefore Equation (18) describes a lowering of the breakdown voltage with an addition of NPs.
3.2. Maximum Energy Density
An important characteristic of a capacitor is the electromagnetic energy density, U, which it can accumulate. This quantity is given by
with being the permittivity of the vacuum and being an effective permittivity of the dielectric in the capacitor. The maximum value of the energy density which can be attained in a nanocomposite capacitor is determined by the breakdown field strength , i.e.,
4. Comparison with Experiments and Discussion
The above theoretical findings can be compared with the experimental results available in the literature. One should note, however, that the quantities , W and , which determine the breakdown field strength, are unknown and do not allow to calculate the absolute value of . Instead, one can consider the relative value with being the breakdown field strength in an NP-free capacitor and compare it with the predicted trend which follows from Equation (18).
First, we consider the experiments on the breakdown field in nanocomposites represented by BaTiO NPs with an average size of 100 nm dispersed in a polyvinylidene fluoride (PVDF) matrix [6]. We restrict ourselves by the range of relatively small volume fractions of BaTiO NPs () where our approach can be applied. One can see that the observed decrease with f in the breakdown strength measured at different temperatures can be well fitted by straight lines (see Figure 2) which is in agreement with Equation (18). The quantity found from the slopes of these dependencies nonmonotonically varies between 0.34 and 0.46 when the temperature changes from 20 to 120 °C which can be attributed to the error bars of the measurements.
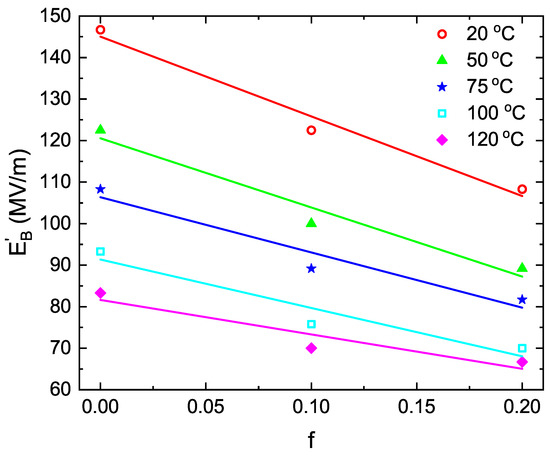
Figure 2.
The dependence of the breakdown field strength on the volume fraction of BaTiO NPs embedded in PVDF matrix for different temperatures indicated in the inset. The straight lines are the best linear fits to the experimental data shown by symbols and taken from Figure 5a in Ref. [6]. The experimental error bars are not available.
These results can be compared with the value calculated under the assumption that , which is typical for thin BaTiO films [30], and [31]. A significant difference between the calculated and fitted values of can be ascribed to the fact that the dielectric properties of BaTiO NPs are distinct from those of BaTiO films [32,33].
A remarkable temperature dependence of the breakdown field indicates that the thermionic current, Equation (13), is the dominant mechanism of the electron injection. As it follows from Equations (12) and (13), the temperature dependence of the quantity should be the same for different f. This can indeed be obtained from the experimental plots of versus T which, being recalculated to with the mean value , coincide with each other within the possible error bars (see Figure 3). Taking and the dielectric permittivity of PVDF [31], one finds for the effective dielectric permittivity of BaTiO NPs .
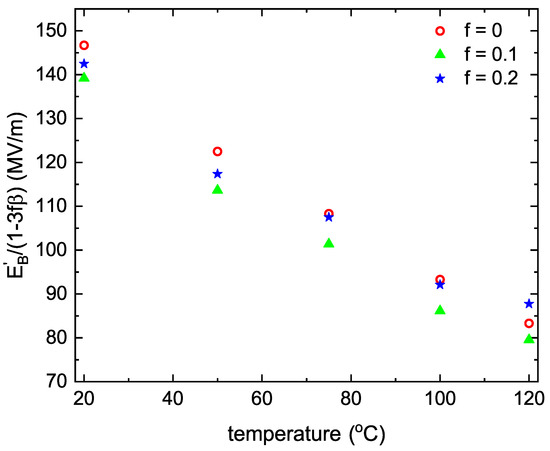
Figure 3.
The dependence of the quantity on the temperature for different volume fractions of BaTiO NPs embedded in PVDF matrix indicated in the inset. The experimental data are taken from Figure 5b in Ref. [6]. The experimental error bars are not available.
In another set of experiments, BaTiO NPs of 30–50 nm in diameter were surface modified using a pentafluorobenzyl phosphonic acid (PFBPA) and incorporated into a poly(vinylidene fluoride-cohexafluoropropylene) (P(VDF-HFP)) matrix [7]. Again, for relatively small volume fractions of NPs (), the breakdown field strength linearly decreases with f (see Figure 4). The value of deduced from the slope of this dependence is about , and taking [7], one obtains . For comparison, the calculated value of obtained with is about 0.83.
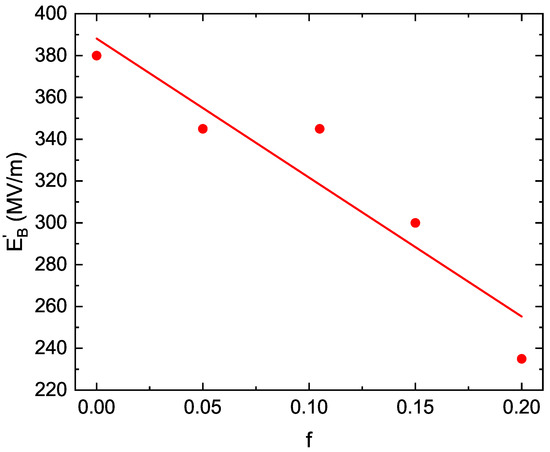
Figure 4.
The dependence of the breakdown field strength on the volume fraction of BaTiO NPs embedded in P(VDF-HFP) matrix. The straight line is the best linear fit to the experimental data shown by circles and taken from Figure 8b in Ref. [7]. The experimental error bars are not available.
Finally, a decrease in the breakdown field strength was also observed for BaTiO NPs of 7 nm in diameter dispersed in polystyrene (PS) [8]. A linear fit of this dependence (Figure 5) gives which, together with the value for the PS [8], provides . The calculated value with is .
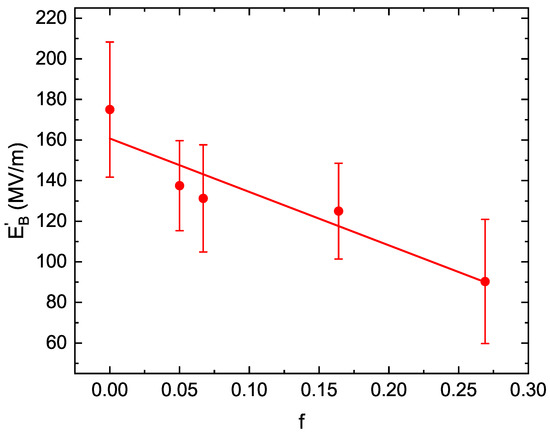
Figure 5.
The dependence of the breakdown field strength on the volume fraction of BaTiO NPs embedded in PS matrix. The straight line is the best linear fit to the experimental data shown by circles and taken from Figure 5 in Ref. [8].
As one can see from the above consideration, the values of the effective dielectric permittivity of BaTiO NPs derived from different measurements differ from each other significantly which points at a dominant role of the interface polarization at the boundary between an NP and a polymer matrix. The obtained values of are in the range between 10 and 70 which is much less than the values typical for thin BaTiO films [30]. This discrepancy can be attributed to the existence of a nonferroelectric surface layer in the NPs which has a low dielectric permittivity, its relative contribution being that it is increasing with a decrease in the NP size [32,33].
5. Conclusions
In the present paper, we have developed a first-principles approach which allows one to calculate the local electric field in a nanocomposite capacitor and the parameters which characterize the electrical breakdown in it. It is found that for relatively low volume fractions of NPs (, the breakdown voltage linearly decreases with f. The slope of this dependence is determined by the parameter which is related to the NP polarizability.
A comparison with the available experimental data on the breakdown strength in polymer films doped with BaTiO NPs has revealed that the effective dielectric permittivity of NPs differs remarkably for different host polymers and is significantly lower than the values typical for ferroelectrics. These findings point at a dominant role of the interface polarization at the NP-polymer interface and an existence of a nonferroelectric surface layer.
Author Contributions
Conceptualization, V.B. and T.E.; funding acquisition, T.E.; investigation, V.B.; methodology, V.B.; project administration, T.E.; writing—original draft, V.B.; writing—review and editing, T.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research is kindly supported by the IE Industrial Elektronik project (SFD-17-0036), which has received EU co-financing from the European Social Fund.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, H.; Liu, F.; Fan, B.; Ai, D.; Peng, Z.; Wang, Q. Nanostructured ferroelectric-polymer composites for capacitive energy storage. Small Methods 2018, 2, 1700399. [Google Scholar] [CrossRef]
- Cao, Y.; Irwin, P.C.; Younsi, K. The future of nanodielectrics in the electrical power industry. IEEE Trans. Dielectr. Electr. Insul. 2004, 11, 797–807. [Google Scholar]
- Dang, Z.-M.; Yuan, J.-K.; Zha, J.-W.; Zhou, T.; Li, S.-T.; Hu, G.-H. Fundamentals, processes and applications of high-permittivity polymer-matrix composites. Prog. Mater. Sci. 2012, 57, 660–723. [Google Scholar] [CrossRef]
- Dang, Z.-M.; Yuan, J.-K.; Yao, S.-H.; Liao, R.-J. Flexible nanodielectric materials with high permittivity for power energy storage. Adv. Mater. 2013, 25, 6334–6365. [Google Scholar] [CrossRef]
- Prateek Thakur, V.K.; Gupta, R.K. Recent progress on ferroelectric polymer-based nanocomposites for high energy density capacitors: Synthesis, dielectric properties, and future aspects. Chem. Rev. 2016, 116, 4260–4317. [Google Scholar] [CrossRef]
- Rajib, M.; Shuvo, M.A.I.; Karim, H.; Delfin, D.; Afrin, S.; Lin, Y. Temperature influence on dielectric energy storage of nanocomposites. Ceram. Int. 2015, 41, 1807–1813. [Google Scholar] [CrossRef]
- Kim, P.; Doss, N.M.; Tillotson, J.P.; Hotchkiss, P.J.; Pan, M.-J.; Marder, S.R.; Li, J.; Calame, J.P.; Perry, J.W. High energy density nanocomposites based on surface-modified BaTiO3 and a ferroelectric polymer. ACS Nano 2009, 3, 2581–2592. [Google Scholar] [CrossRef]
- Grabowski, C.A.; Fillery, S.P.; Koerner, H.; Tchoul, M.; Drummy, L.; Beier, C.W.; Brutchey, R.L.; Durstock, M.F.; Vaia, R.A. Dielectric performance of high permitivity nanocomposites: Impact of polystyrene grafting on BaTiO3 and TiO2. Nanocomposites 2016, 2, 117–124. [Google Scholar] [CrossRef] [Green Version]
- Smith, R.C.; Liang, C.; Landry, M.; Nelson, J.K.; Schadler, L.S. The mechanisms leading to the useful electrical properties of polymer nanodielectrics. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 187–196. [Google Scholar] [CrossRef]
- Dou, X.; Liu, X.; Zhang, Y.; Feng, H.; Chen, J.-F.; Du, S. Improved dielectric strength of barium titanate-polyvinylidene fluoride nanocomposite. Appl. Phys. Lett. 2009, 95, 132904. [Google Scholar] [CrossRef]
- Bi, K.; Bi, M.; Hao, Y.; Luo, W.; Cai, Z.; Wang, X.; Huang, Y. Ultrafine core-shell BaTiO3@SiO2 structures for nanocomposite capacitors with high energy density. Nano Energy 2018, 51, 513–523. [Google Scholar] [CrossRef]
- Zhou, Y.; Yuan, C.; Wang, S.; Zhu, Y.; Cheng, S.; Yang, X.; Yang, Y.; Hu, J.; He, J.; Li, Q. Interface-modulated nanocomposites based on polypropylene for high-temperature energy storage. Energy Storage Mater. 2020, 28, 255–263. [Google Scholar] [CrossRef]
- Cheng, L.; Liu, W.; Zhang, Z.; Zhou, Y.; Li, S. Enhanced breakdown strength and restrained dielectric loss of polypropylene/maleic anhydride grafted polypropylene/core-shell ZrO2@SiO2 nanocomposites. Polym. Compos. 2022, 43, 2175–2183. [Google Scholar] [CrossRef]
- Maxwell Garnett, J.C. Colours in metal glasses and in metallic films. Phil. Trans. R. Soc. A 1904, 203, 385–420. [Google Scholar]
- Markel, V.A. Introduction to the Maxwell Garnett approximation: Tutorial. J. Opt. Soc. Am. A 2016, 33, 1244–1256. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bordo, V.; Ebel, T. How to determine the capacitance of a nanocomposite capacitor. AIP Adv. 2022, 12, 045107. [Google Scholar] [CrossRef]
- Forlani, F.; Minnaja, N. Thickness influence in breakdown phenomena of thin dielectric films. Phys. Stat. Sol. 1964, 4, 311–324. [Google Scholar] [CrossRef]
- Nordheim, L. Zur Theorie der thermischen Emission und der Reflexion von Elektronen an Metallen. Z. Phys. 1928, 46, 833–855. [Google Scholar] [CrossRef]
- Fowler, R.H.; Nordheim, L. Electron emission in intense electric fields. Proc. R. Soc. A 1928, 119, 173–181. [Google Scholar]
- Schmidlin, F.W. Enhanced tunneling through dielectric films due to ionic defects. J. Appl. Phys. 1966, 37, 2823–2832. [Google Scholar] [CrossRef]
- Nha, H.; Jhe, W. Cavity quantum electrodynamics between parallel dielectric surfaces. Phys. Rev. A 1996, 54, 3505–3513. [Google Scholar] [CrossRef] [PubMed]
- Stratton, J.A. Electromagnetic Theory; McGraw-Hill: New York, NY, USA, 1941; p. 206. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics, 6th ed.; Pergamon Press: Oxford, UK, 1980; p. 100. [Google Scholar]
- Bordo, V.G. Local field in finite-size metamaterials: Application to composites of dielectrics and metal nanoparticles. Phys. Rev. B 2018, 97, 115410. [Google Scholar] [CrossRef] [Green Version]
- Wylie, J.M.; Sipe, J.E. Quantum electrodynamics near an interface. Phys. Rev. A 1984, 30, 1185–1193. [Google Scholar] [CrossRef]
- Bordo, V.G. Self-excitation of surface plasmon polaritons. Phys. Rev. B 2016, 93, 155421. [Google Scholar] [CrossRef] [Green Version]
- Sipe, J.E. The ATR spectra of multipole surface plasmons. Surf. Sci. 1979, 84, 75–105. [Google Scholar] [CrossRef]
- Sipe, J.E. The dipole antenna problem in surface physics: A new approach. Surf. Sci. 1981, 105, 489–504. [Google Scholar] [CrossRef]
- Bordo, V.G. Dicke superradiance from a plasmonic nanocomposite slab. J. Opt. Soc. Am. B 2021, 38, 2104–2111. [Google Scholar] [CrossRef]
- Bajac, B.; Vukmirović, J.; Tripković, D.; Djurdjić, E.; Stanojev, J.; Cvejić, Ž.; Škorić, B.; Srdić, V.V. Structural characterization and dielectric properties of BaTiO3 thin films obtained by spin coating. Process. Appl. Ceram. 2014, 8, 219–224. [Google Scholar] [CrossRef]
- Wang, S.; Liu, L.; Zeng, Y.; Zhou, B.; Teng, K.; Ma, M.; Chen, L.; Xu, Z.J. Improving dielectric properties of poly(vinylidene fluoride) composites: Effects of surface functionalization of exfoliated graphene. Adhes. Sci. Technol. 2015, 29, 678–690. [Google Scholar] [CrossRef]
- Goswami, A.K. Dielectric properties of unsintered barium titanate. J. Appl. Phys. 1969, 40, 619–624. [Google Scholar] [CrossRef]
- Hoshina, T. Size effect of barium titanate: Fine particles and ceramics. J. Ceram. Soc. Jpn. 2013, 121, 156–161. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).