Research Status of and Trends in 3D Geological Property Modeling Methods: A Review
Abstract
:1. Introduction
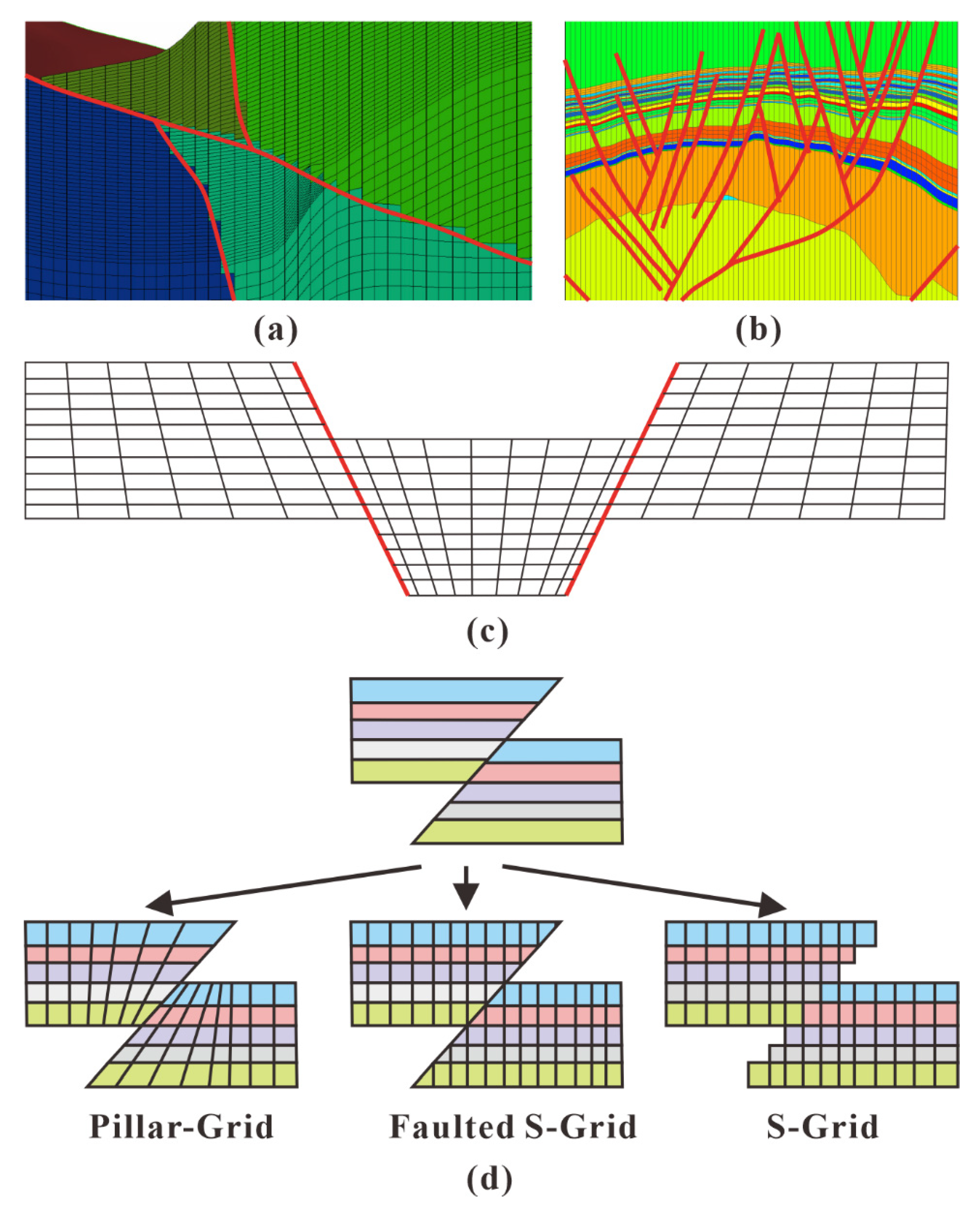
2. Research on Reservoir Grid Generation Method
3. Interpolation Methods for 3D Property Modeling
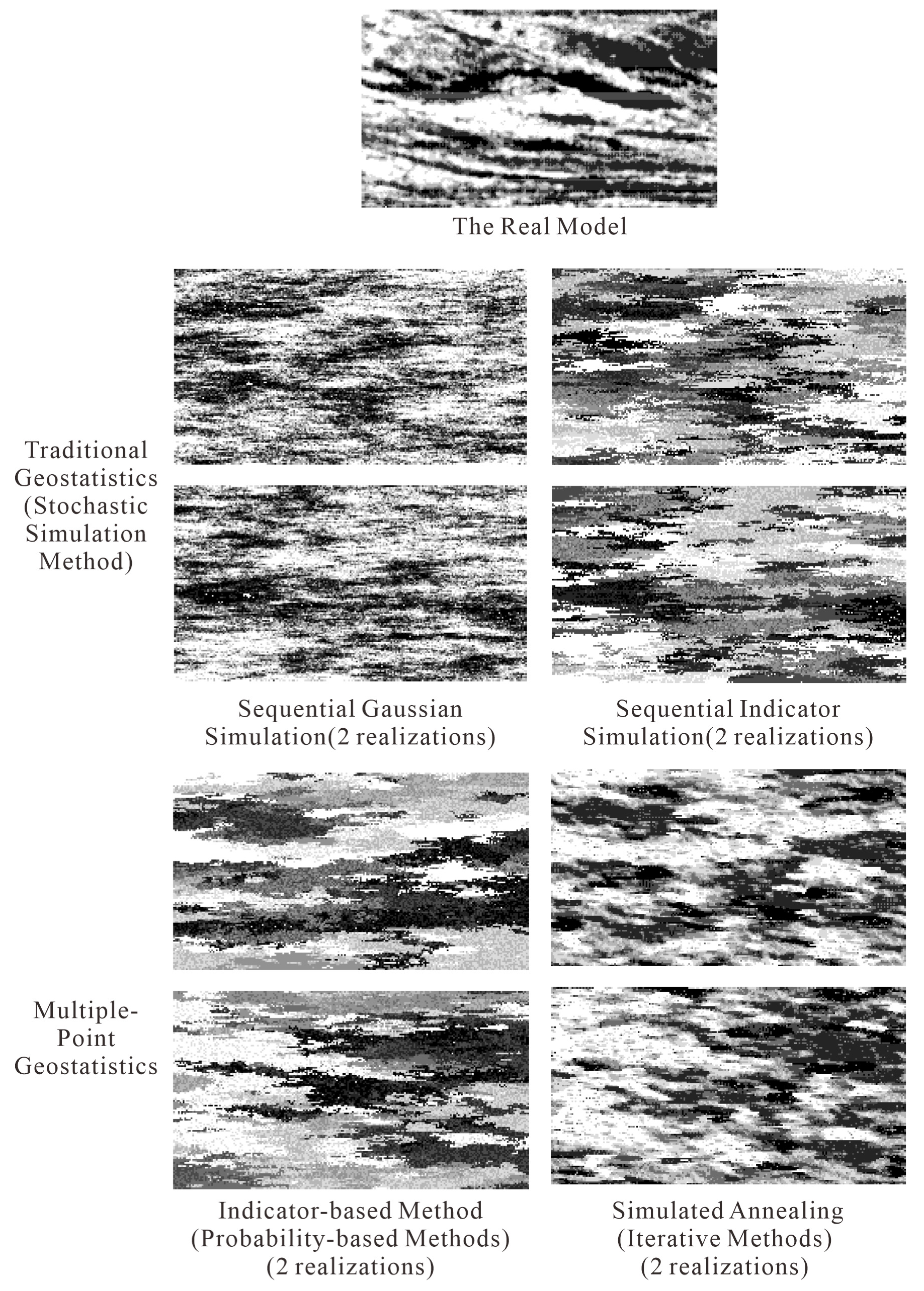
3.1. Traditional Geostatistical Methods
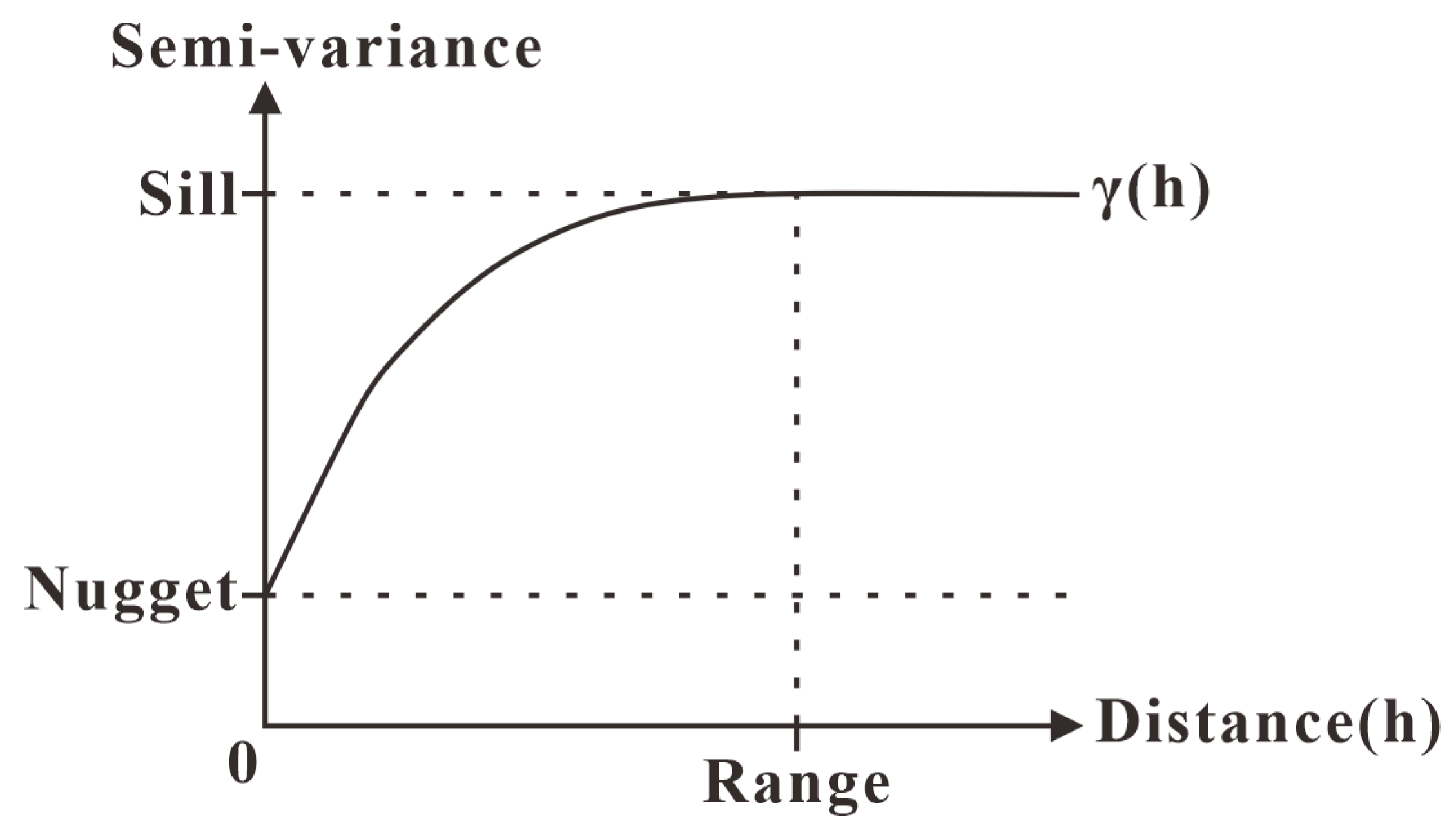
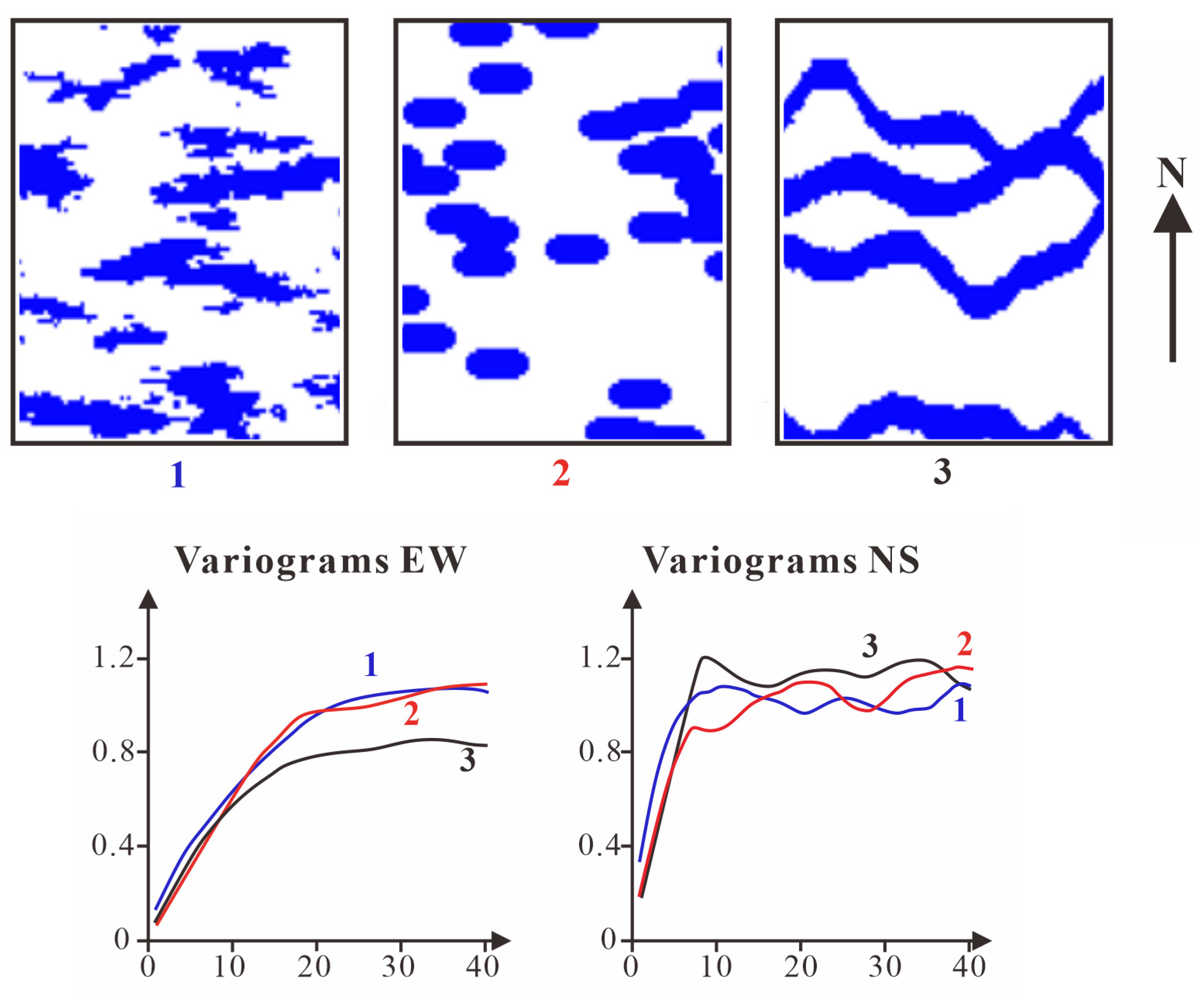
3.1.1. Kriging Method
3.1.2. Stochastic Simulation Method
Sequential Gaussian Simulation
Sequential Indicator Simulation
3.1.3. Object-Based Method
3.2. Multiple-Point Geostatistics Methods
3.2.1. Probability-Based Methods
Single Normal Extended Simulation (SNESIM)
Indicator-Based Method
Impala
3.2.2. Iterative Methods
Simulated Annealing (SA)
Neural Networks
Markov Model
Gibbs Sampling Method
3.2.3. Pattern-Based Methods
Simpat
Direct Sampling Method
Filtersim
Wavelet Analysis-Based Method
3.3. Deep-Learning Based Modeling Methods
4. Discussions
5. Conclusions
- (1)
- Although there are various studies on the grid forms for the numerical simulation of reservoirs, orthogonal hexahedral grids are still the most suitable for simulation and computation in the current application field.
- (2)
- Most geological phenomena are nonstationary, to simulate various types of reservoirs; how to improve geostatistics by adding geological constraints and reducing the limitation of stationarity is the main development trend.
- (3)
- Multiple-point geostatistics is a developing trend in 3D properties modeling and is more accurate than traditional geostatistics; some limitations still exist for different approaches.
- (4)
- The multiscale problem of multiple-point geostatistical results has always been a research hotspot in this field.
- (5)
- As a new method, deep learning algorithms and application verification are still in the stage of rapid development, and new research results continue to appear.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, S.; Xiao, K.; Wang, X. Three-dimensional geological property model and its visualization. Geol. Bull. China 2010, 29, 1554–1557. [Google Scholar]
- Yao, L. Research on Three-Dimensional Property Modeling Method Based on Geostatistics; Peking University: Beijing, China, 2008. [Google Scholar]
- Wu, S. Reservoir Characterization and Modeling; Petroleum Industry Press: Beijing, China, 2010. [Google Scholar]
- Journel, A.G. Geostatistics for conditional simulation of ore bodies. Econ. Geol. 1974, 69, 673–687. [Google Scholar] [CrossRef]
- Journel, A.G.; Huijbregts, C. Mining Geostatistics; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Dowd, P.A. A Review of Recent Developments in Geostatistics. Comput. Geosci. 1991, 17, 1481–1500. [Google Scholar] [CrossRef]
- Qiu, Y. A proposed flow-diagram for reservoir sedimentological study. Pet. Explor. Dev. 1990, 1, 85–90. [Google Scholar]
- Zhang, T.; Wang, J. The principle of stochastic modelling and stochastic simulation of reservoir. Well Logging Technol. 1995, 6, 391–397. [Google Scholar]
- Yu, X.; Li, J. Geological Modeling and Computer Simulation of Clastic Reservoirs; Geological Publishing House: Beijing, China, 1996. [Google Scholar]
- Zhang, Y.; Xiong, Q.; Wang, Z.; Wu, S. Description of Terrestrial Reservoirs; Petroleum Industry Press: Beijing, China, 1997. [Google Scholar]
- Pan, M.; Fang, Y.; Qu, H. Discussion on Several Foundational Issues in Three-Dimensional Geological Modeling. Geogr. Geo-Inf. Sci. 2007, 23, 1–5. [Google Scholar]
- Ming, J. A Study on Three-Dimensional Geological Modeling. Geogr. Geo-Inf. Sci. 2011, 27, 14–18. [Google Scholar]
- Cui, Y.; Xia, B.; Chen, G.; Luo, Z. Gridding and its geological meaning in reservoir modeling. Acta Pet. Sin. 2012, 33, 854–858. [Google Scholar]
- Hoffman, K.S.; Neave, J.W.; Nilsen, E.H. Application of the fused fault block method in structural modeling and reservoir gridding of complex structures. In Proceedings of the 2006 SEG Annual Meeting, New Orleans, LA, USA, 1–6 October 2006; Society of Exploration Geophysicists: New Orleans, LA, USA, 2006. [Google Scholar]
- Wu, X.H.; Parashkevov, R.R. Effect of grid deviation on flow solutions. SPE J. 2009, 14, 67–77. [Google Scholar] [CrossRef]
- Zakrevsky, K.E. Geological 3D Modelling; EAGE Publications: Houten, The Netherlands, 2011. [Google Scholar]
- Thom, J.; Höcker, C. 3-D grid types in geomodeling and simulation–how the choice of the model container determines modeling results. In Proceedings of the AAPG Annual Convention and Exhibition, Denver, CO, USA, 7–10 June 2009; AAPG: Tulsa, AK, USA, 2009. [Google Scholar]
- Gringarten, E.J.; Arpat, G.B.; Haouesse, M.A.; Dutranois, A.; Deny, L.; Jayr, S.; Tertois, A.L.; Mallet, J.L.; Bernal, A.; Nghiem, L.X. New grids for robust reservoir modeling. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 21–24 September 2008; Society of Petroleum Engineers: The Woodlands, TX, USA, 2008. [Google Scholar] [CrossRef]
- Mallet, J.L.; Arpat, B.; Cognot, R.; Deny, L.; Dulac, J.C.; Gringarten, E.; Jayr, S.; Levy, B. Beyond Stratigraphic Grids: Changing the Paradigm in International Forum on Reservoir Simulation; Abu-Dhabi, A.K., Heinemann, Z., Eds.; EAGE Publications: Utrecht, The Netherlands, 2007; p. 49. [Google Scholar]
- Fremming, N.P. 3D geological model construction using a 3D grid. In Proceedings of the ECMOR VIII-8th European Conference on the Mathematics of Oil Recovery, Freiberg, Germany, 3–6 September 2002; European Association of Geoscientists & Engineers (EAGE): Utrecht, The Netherlands, 2002. [Google Scholar] [CrossRef] [Green Version]
- Ponting, D.K. Corner point geometry in reservoir simulation. In Proceedings of the 1st European Conference on Mathematics of Oil Recovery, Cambridge, UK, 14–16 July 1989; Clarendon Press: Oxford, UK, 1989; pp. 45–65. [Google Scholar]
- Ye, J.; Wu, X.; Zhu, Y.; Liu, H.; Luo, K. A study of computer-aided reservoir simulation history fitting method for large-scale angular point network ibex. Acta Pet. Sin. 2007, 28, 83–86. [Google Scholar]
- Han, J.; Shi, F.; Wu, S.; Fan, Z. Generation algorithm of corner-point grids based on skeleton model. Comput. Eng. 2008, 34, 90–95. [Google Scholar]
- Ruiu, J.; Caumon, G.; Merland, R.; Cherpeau, N.; Slotte, P.A. Consideration and algorithm for the construction of XY orthogonal truncated grids. In Proceedings of the 31st Gocad Meeting, Nancy, France, 7–10 June 2011; AspenTech Subsurface Science & Engineering: Bedford, MA, USA, 2011. [Google Scholar]
- Gringarten, E.J.; Haouesse, M.A.; Arpat, G.B.; Nghiem, L.X. Advantages of using vertical stair step faults in reservoir grids for flow simulation. In Proceedings of the SPE Reservoir Simulation Symposium, The Woodlands, TX, USA, 2–4 February 2009; Society of Petroleum Engineers: The Woodlands, TX, USA, 2009. [Google Scholar] [CrossRef]
- Heinemann, Z.E.; Brand, C.W. Gridding techniques in reservoir simulation. In Proceedings of the First and Second International Forum on Reservoir Simulation, Alpbach, Austria, 12–16 September 1988 and 3–8 September 1989; Society of Petroleum Engineers: The Woodlands, TX, USA, 1988; pp. 404–415. [Google Scholar]
- Heinemann, Z.E.; Brand, C.; Munka, M.; Chen, Y.M. Modeling reservoir geometry with irregular grids. In Proceedings of the SPE Symposium on Reservoir Simulation, Houston, TX, USA, 6 February 1989; Society of Petroleum Engineers: The Woodlands, TX, USA, 1989; pp. 6–8. [Google Scholar] [CrossRef]
- Heinemann, Z.E.; Brand, C.W.; Munka, M.; Chen, Y.M. Modeling reservoir geometry with irregular grids. SPE Reserv. Eng. 1991, 6, 225–232. [Google Scholar] [CrossRef]
- Deimbacher, F.X.; Heinemann, Z.E. Time-dependent incorporation of locally irregular grids in large reservoir simulation models. In Proceedings of the SPE Symposium on Reservoir Simulation, New Orleans, LA, USA, 6 February 1993; Society of Petroleum Engineers: The Woodlands, TX, USA, 1993; pp. 35–40. [Google Scholar] [CrossRef]
- Nacul, E.C.; Aziz, K. Use of irregular grid in reservoir simulation. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 6–9 October 1991; Society of Petroleum Engineers: The Woodlands, TX, USA, 1991; pp. 6–9. [Google Scholar] [CrossRef]
- Palagi, C.L.; Aziz, K. The modeling of vertical and horizontal wells with voronoi grid. In Proceedings of the Western Regional Meeting, Richardson, TX, USA, 30 March–1 April 1992; Society of Petroleum Engineers: The Woodlands, TX, USA, 1992; pp. 2–8. [Google Scholar]
- Palagi, C.L.; Aziz, K. Modeling vertical and horizontal wells with voronoi grid. SPE Reserv. Eng. 1994, 9, 15–21. [Google Scholar] [CrossRef]
- Evazi, M.; Mahani, H.; Hejranfar, K.; Masihi, M. Vorticity-based PEBI grids for improved upscaling of two phase flow. In Europec/EAGE Conference and Exhibition; Society of Petroleum Engineers: The Woodlands, TX, USA, 2008. [Google Scholar]
- Mlacnik, M.J.; Durlofsky, L.J.; Heinemann, Z.E. Sequentially adapted flow-based PEBI grids for reservoir simulation. SPE J. 2006, 11, 317–327. [Google Scholar] [CrossRef]
- Herbert, M.; Reingruber, A.J.; Shotts, D.R.; Dobbs, W.C. Use of PEBI grids for a heavily faulted reservoir in the Gulf of Mexico. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 5–8 October 2003; Paper SPE 84373. SPE: The Woodlands, TX, USA, 2003; pp. 5–8. [Google Scholar]
- Prévost, M.; Lepage, F.; Durlofsky, L.J.; Mallet, J.L. Unstructured 3D gridding and upscaling for coarse modelling of geometrically complex reservoirs. Pet. Geosci. 2005, 11, 339–345. [Google Scholar] [CrossRef]
- Xie, H.; Ma, Y.; Huan, G.; Guo, S. Study of unstructured grids in reservoir numerical simulation. Acta Pet. Sin. 2001, 22, 63–66. [Google Scholar]
- Lin, C. Research, Development, and Application of Reservoir Numerical Simulator Based on PEBI Grid; University of Science and Technology of China: Hefei, China, 2010. [Google Scholar]
- Song, H. Research on Numerical Simulation of Reservoirs Based on PEBI Grid; China University of Petroleum: Beijing, China, 2011. [Google Scholar]
- Song, H. Research on PEBI Grid Technology in Numerical Simulation of Reservoirs; China University of Petroleum: Beijing, China, 2012. [Google Scholar]
- Liu, L.; Liao, X.; Chen, Q. Usage of hybrid PEBI grid in fine reservoir simulation. Acta Pet. Sin. 2003, 24, 64–67. [Google Scholar]
- An, Y.; Wu, X.; Han, G. Application of numerical simulation of complex well based on hybrid PEBI grid. J. China Univ. Pet. 2007, 31, 60–63. [Google Scholar]
- Xiang, Z.; Zhang, L.; Chen, Z.; Chen, P.; Su, L.; Ma, L. Algorithm for constructing PEBI mesh of arbitrarily shaped and constrained planar domains in oil reservoir. J. Southwest Pet. Univ. 2006, 28, 32–35. [Google Scholar]
- Zha, W.; Li, D.; Lu, D.; Kong, X. PEBI grid division in inter-well interference area. Acta Pet. Sin. 2008, 29, 742–746. [Google Scholar]
- Zha, W.; Li, D.; Zhang, L.; Lu, D. The method of PEBI grid meshing. Well Test. 2013, 22, 23–26. [Google Scholar]
- Zha, W. Numerical Computation of Reservoirs Based on PEBI Grid and its Implementation; University of Science and Technology of China: Hefei, China, 2009. [Google Scholar]
- Matheron, G. Principles of geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Matheron, G. The Theory of Regionalized Variables and Its Application; Les Cahiers du Centre de morphologie mathématique de Fontainebleau, EÌ cole national supeÌ rieure des mines: Paris, French, 1971. [Google Scholar]
- Krige, D.G. A statistical approach to some basic mine valuation problems on the witwatersrand. J. Chem. Metall. Min. Soc. S. Afr. 1951, 94, 95–111. [Google Scholar]
- Deutsch, C.V.; Journel, A.G. GSLIB. Geostatistical Software Library and User’s Guide, 2nd ed.; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Goovaerts, P. Geostatistics for Natural Resource Evaluation; Oxford University Press: Oxford, Oxfordshire, England, 1997. [Google Scholar]
- Journel, A.G. Nonparametric estimation of spatial distributions. J. Int. Assoc. Math. Geol. 1983, 15, 445–468. [Google Scholar] [CrossRef]
- Doyen, P.M.; de Buyl, M.H.; Guidish, T.M. Porosity from seismic data, a geostatistical approach. Explor. Geophys. 1989, 20, 245. [Google Scholar] [CrossRef]
- Xu, W.; Tran, T.T.; Srivastava, R.M.; Journel, A.G. Integrating seismic data in reservoir modeling: The collocated cokriging alternative. In Proceedings of the 67th Annual Technical Conference and Exhibition, Washington, DC, USA, 4–7 October 1992; Society of Petroleum Engineers: Washington, DC, USA, 1992; pp. 833–842. [Google Scholar]
- Matheron, G. The intrinsic random functions and their applications. Adv. Appl. Probab. 1973, 5, 439–468. [Google Scholar] [CrossRef] [Green Version]
- Journel, A.B.; Alabert, F.G. Focusing on spatial connectivity of extreme-valued attributes: Stochastic indicator models of reservoir heterogeneities. AAPG Bull. 1989, 73, 3. [Google Scholar] [CrossRef]
- Journel, A.G.; Deutsch, C.V. Entropy and spatial disorder. Math. Geosci. 1993, 25, 329–355. [Google Scholar] [CrossRef]
- Alabert, F.G.; Massonnat, G.J. Heterogeneity in a complex turbiditic reservoir: Stochastic modelling of facies and petrophysical variability. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 23–26 September 1990; SPE: New Orleans, LA, USA, 1990. [Google Scholar]
- Zhu, H.; Journel, A.G. Formatting and integrating soft data: Stochastic imaging via the markov-bayes algorithm. In Geostatistics Tróia ’92. Quantitative Geology and Geostatistics; Soares, A., Ed.; Springer: Dordrecht, The Netherlands, 1993; pp. 1–12. [Google Scholar]
- Isaaks, E.H.; Isaaks, E.H. The Application of Monte Carlo Methods to the Analysis of Spatially Correlated Data; Stanford University: Stanford, CA, USA, 1990. [Google Scholar]
- Srivastava, R.M. Reservoir characterization with probability field simulation. SEG Tech. Program Expand. Abstr. 1999, 12, 1396. [Google Scholar]
- Chilès, J.P.; Delfiner, P. Geostatistics: Modeling Spatial Uncertainty; John Wiley & Sons, Inc.: New York, NY, USA, 2012. [Google Scholar]
- Maksimov, M.M.; Galushko, V.V.; Kutcherov, A.B.; Surguchev, L.M. Parallel nested factorization algorithms. Sports Illus. Com 1993, 16, 54–58. [Google Scholar] [CrossRef]
- Ravenne, C.; Beucher, H.; Ravenne, C. Recent Development in Description of Sedimentary Bodies in a Fluvio Deltaic Reservoir and Their 3D Conditional Simulations; Society of Petroleum Engineers: The Woodlands, TX, USA, 1988. [Google Scholar]
- Rudkiewicz, J.L.; Guérillot, D.; Galli, A. An integrated software for stochastic modelling of reservoir lithology and property with an example from the yorkshire middle jurassic. In North Sea Oil and Gas Reservoirs—II; Buller, A.T., Berg, E., Hjelmeland, O., Kleppe, J., Torsæter, O., Aasen, J.O., Eds.; Springer: Dordrecht, The Netherlands, 1990; pp. 399–406. [Google Scholar]
- Deutsch, C.V.; Gringarten, E. Accounting for multiple-point continuity in geostatistical modeling. In Proceedings of the 6th International Geostatistics Congress, Cape Town, Southern Africa, 10–14 April 2000; pp. 156–165. [Google Scholar]
- Haldorsen, H.H.; Lake, L.W. A new approach to shale management in field-scale models. Soc. Pet. Eng. J. 1984, 24, 447–457. [Google Scholar] [CrossRef]
- Stoyan, D.; Kendall, W.S.; Mecke, T. Stochastic Geometry and its Application; Wiley & Sons/Akademie-Verlag: Berlin, Germany, 1987. [Google Scholar]
- Haldorsen, H.H.; Damsleth, E. Stochastic modeling. J. Pet. Technol. 1990, 42, 404–412. [Google Scholar] [CrossRef]
- Deutsch, C.V.; Wang, L. Hierarchical object-based stochastic modeling of fluvial reservoirs. Math. Geosci. 1996, 28, 857–880. [Google Scholar] [CrossRef]
- Holden, L.; Hauge, R.; Skare, Ø.; Skorstad, A. Modeling of fluvial reservoirs with object models. Math. Geosci. 1998, 30, 473–496. [Google Scholar] [CrossRef]
- Guardiano, F.B.; Srivastava, R.M. Multivariate geostatistics: Beyond bivariate moments. In Geostatistics Troia ‘92; Soares, A., Ed.; Springer: Dordrecht, The Netherlands, 1993; pp. 133–144. [Google Scholar]
- Strebelle, S. Sequential Simulation Drawing Structures from Training Images; Stanford University: Stanford, CA, USA, 2000. [Google Scholar]
- Strebelle, S.B.; Journel, A.G. Reservoir modeling using multiple-point statistics. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 30 September 2001; SPE: New Orleans, LA, USA, 2001. [Google Scholar]
- Ortiz, J.M.; Deutsch, C.V. Indicator simulation accounting for multiple-point statistics. Math. Geosci. 2004, 36, 545–565. [Google Scholar] [CrossRef]
- Ortiz, J.M.; Emery, X. Integrating multiple-point statistics into sequential simulation algorithms. In Geostatistics Banff 2004; Leuangthong, O., Deutsch, C.V., Eds.; Springer: Dordrecht, The Netherlands, 2005; pp. 969–978. [Google Scholar]
- Straubhaar, J.; Renard, P.; Mariethoz, G.; Froidevaux, R.; Besson, O. An improved parallel multiple-point algorithm using a list approach. Math. Geosci. 2011, 43, 305–328. [Google Scholar] [CrossRef]
- Deutsch, C.V. Annealing Techniques Applied to Reservoir Modeling and the Integration of Geological and Engineering (Well Test) Data. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1992. [Google Scholar]
- Goovaerts, P. Stochastic simulation of categorical variables using a classification algorithm and simulated annealing. Math. Geosci. 1996, 28, 909–921. [Google Scholar] [CrossRef]
- Fang, J.H.; Wang, P.P. Random field generation using simulated annealing vs. fractal-based stochastic interpolation. Math. Geosci. 1997, 29, 849–858. [Google Scholar] [CrossRef]
- Norrena, K.P.; Deutsch, C.V. Automatic determination of well placement subject to geostatistical and economic constraints. In Proceedings of the SPE International Thermal Operations and Heavy Oil Symposium and International Horizontal Well Technology Conference, Calgary, AB, Canada, 4–7 November 2002; Society of Petroleum Engineers: The Woodlands, TX, USA, 2002. [Google Scholar] [CrossRef]
- Deutsch, C.V.; Wen, X.H. Integrating large-scale soft data by simulated annealing and probability constraints. Math. Geosci. 2000, 32, 49–67. [Google Scholar] [CrossRef]
- Peredo, O.; Ortiz, J.M. Parallel implementation of simulated annealing to reproduce multiple-point statistics. Comput. Geosci. 2011, 37, 1110–1121. [Google Scholar] [CrossRef]
- Caers, J.; Journel, A.G. Stochastic reservoir simulation using neural networks trained on outcrop data. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 27–30 September 1998; SPE: New Orleans, LA, USA, 1998. [Google Scholar]
- Caers, J.; Ma, X. Modeling conditional distributions of facies from seismic using neural nets. Math. Geosci. 2002, 34, 143–167. [Google Scholar] [CrossRef]
- Besag, J. Spatial interaction and the statistical analysis of lattice systems. J. R. Stat. Soc. B 1974, 36, 192–225. [Google Scholar] [CrossRef]
- Tjelmeland, H. Stochastic Models in Reservoir Characterization and Markov Random Fields for Compact Objects. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 1996. [Google Scholar]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef] [Green Version]
- Daly, C. Higher order models using entropy, markov random fields and sequential simulation. In Geostatistics Banff 2004; Leuangthong, O., Deutsch, C.V., Eds.; Springer: Dordrecht, The Netherlands, 2005; pp. 215–224. [Google Scholar]
- Tjelmeland, H.; Eidsvik, J. Directional metropolis: Hastings updates for posteriors with nonlinear likelihoods. In Geostatistics Banff 2004; Leuangthong, O., Deutsch, C.V., Eds.; Springer: Dordrecht, The Netherlands, 2005; pp. 95–104. [Google Scholar]
- Geman, S.; Geman, D. Stochastic relaxation, gibbs distributions, and the bayesian restoration of images. In Neurocomputing: Foundations of Research; Anderson, J.A., Rosenfeld, E., Eds.; MIT Press: Cambridge, MA, USA, 1987; pp. 611–634. [Google Scholar]
- Lyster, S.; Deutsch, C.V. Mps simulation in a gibbs sampler algorithm. In Proceedings of the Eighth International Geostatistics Congress, Santiago, Chile, 1–5 December 2008; pp. 79–88. [Google Scholar]
- Lyster, S.; Deutsch, C. Artifacts near conditioning data in mps gibbs sampling. In Centre for Computational Geostatistics; Alberta University: Edmonton, AB, Canada, 2007; pp. 505–518. [Google Scholar]
- Arpat, G.B. Sequential Simulation with Patterns; Stanford University: Stanford, CA, USA, 2005. [Google Scholar]
- Arpat, G.B.; Caers, J. Conditional simulation with patterns. Math. Geosci. 2007, 39, 177–203. [Google Scholar] [CrossRef]
- Mariethoz, G.; Renard, P. Reconstruction of incomplete data sets or images using direct sampling. Math. Geosci. 2010, 42, 245–268. [Google Scholar] [CrossRef] [Green Version]
- Mariethoz, G.; Renard, P.; Straubhaar, J. The direct sampling method to perform multiple-point geostatistical simulations. Water Resour. Res. 2010, 46, W11536. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T. Filter-Based Training Pattern Classification for Spatial Pattern Simulation. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2006. [Google Scholar]
- Wu, J. 4D Seismic and Multiple-Point Pattern Data Integration Using Geostatistics. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2007. [Google Scholar]
- Chatterjee, S.; Dimitrakopoulos, R.; Mustapha, H. Dimensional reduction of pattern-based simulation using wavelet analysis. Math. Geosci. 2012, 44, 343–374. [Google Scholar] [CrossRef] [Green Version]
- Mallat, S. A Wavelet Tour of Signal Processing; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Liu, Y.-Y.; Ma, X.-H.; Zhang, X.-W.; Guo, W.; Kang, L.-X.; Yu, R.-Z.; Sun, Y.-P. A deep-learning-based prediction method of the estimated ultimate recovery (EUR) of shale gas wells. Pet. Sci. 2021, 18, 1450–1464. [Google Scholar] [CrossRef]
- Yin, X.; Yang, F.; Wu, G. Application of neural network to predicting reservoir and calculating thickness in cb oilfield. J. China Univ. Pet. 1998, 22, 17–20. [Google Scholar]
- Zheng, Q.; Han, D. Estimation of reservoir distribution parameters using higher-order neural network spproach. Prog. Geophys. 2007, 22, 552–555. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. Adv. Neural Inf. Process. Syst. 2014, 27, 2672–2680. [Google Scholar] [CrossRef]
- Chan, S.; Elsheikh, A.H. Parametrization and Generation of Geological Models with Generative Adversarial Networks. arXiv 2017, arXiv:1708.01810. [Google Scholar]
- Laloy, E.; Hérault, R.; Jacques, D.; Linde, N. Training-image based geostatistical inversion using a spatial generative adversarial neural network. arXiv 2017, arXiv:1708.04975. [Google Scholar] [CrossRef] [Green Version]
- Dupont, E.; Zhang, T.; Tilke, P.; Liang, L.; Bailey, W. Generating Realistic Geology Conditioned on Physical Measurements with Generative Adversarial Networks. arXiv 2018, arXiv:1802.03065. [Google Scholar]
- Zhang, T.; Tilke, P.; Dupont, E. Generating Geologically Realistic 3D Reservoir Facies Models Using Deep Learning of Sedimentary Architecture with Generative Adversarial Networks. In Proceedings of the International Petroleum Technology Conference, Beijing, China, 26–28 March 2019. [Google Scholar]
- Mosser, L.; Dubrule, O.; Blunt, M.J. Conditioning of three-dimensional generative adversarial networks for pore and reservoir-scale models. arXiv 2018, arXiv:1802.05622. [Google Scholar]
- Exterkoetter, R.; Bordignon, F.; de Figueiredo, L.P.; Roisenberg, M.; Rodrigues, B.B. Petroleum Reservoir Connectivity Patterns Reconstruction Using Deep Convolutional Generative Adversarial Networks. In Proceedings of the 2018 7th Brazilian Conference on Intelligent Systems, Sao Paulo, Brazil, 22–25 October 2018. [Google Scholar]
- Yuyang, L.; Xinhua, M.; Xiaowei, Z.; Wei, G.; Lixia, K.; Rongze, Y.; Yuping, S. Shale gas well flowback rate prediction for Weiyuan field based on a deep learning algorithm. J. Pet. Sci. Eng. 2021, 203, 108637. [Google Scholar] [CrossRef]
- Deng, H.; Zheng, Y.; Chen, J.; Yu, S.; Xiao, K.; Mao, X. Learning 3D Mineral Prospectivity from 3D Geological Models Using Convolutional Neural Networks: Application to a Structure-controlled Hydrothermal Gold Deposit. Comput. Geosci. 2022, 161, 105074. [Google Scholar] [CrossRef]
- Liu, Y.; Durlofsky, L.J. 3D CNN-PCA: A Deep-Learning-Based Parameterization for Complex Geomodels. Comput. Geosci. 2021, 148, 104676. [Google Scholar] [CrossRef]
- Erten, O.; Deutsch, C.V. Assessment of variogram reproduction in the simulation of decorrelated factors. Stoch. Environ. Res. Risk Assess. 2021, 35, 2583–2604. [Google Scholar] [CrossRef]

| Kriging Method | Applicability | Advantages | Disadvantages | |
|---|---|---|---|---|
| Simple Kriging | Satisfy the second-order stationary condition; It is suitable for the situation with small spatial variability; The expectation of the random function at each position point is a known constant | The algorithm is simple, fast and widely used | The second-order stationary condition cannot be satisfied in practice; Cannot be used in situations with any trend; Need to know the expectation of variables | |
| Ordinary Kriging | Satisfy the second-order stationary condition; It is suitable for the situation with large spatial variability; The random function of each position point should have expectation; The expectation of random function at each position can be different; The data distribution shall not have obvious trend | There is no need to predict expectations; The algorithm is simple, fast and widely used | The second-order stationary condition cannot be satisfied in practice; It cannot be used in situations with obvious trends | |
| Universal Kriging | Satisfy the second-order stationary condition; It is suitable for the situation with large spatial variability; The random function of each position point should have expectation; The expectation of random function at each position can be different; The data distribution shall not have obvious trend The attribute does not satisfy the general stationary assumption; Showing a trend in a certain direction; After filtering out the drift of the original data, ensure that the residual is stable | The algorithm is simple and fast; For geological conditions with obvious trend, the interpolation result is better than simple and ordinary Kriging | The selection of mathematical function form representing drift has a certain error; The residual interpolation variogram needs to be estimated; For complex data distribution, the drift part is difficult to obtain | |
| External Drift Kriging | External variables need to reflect the spatial distribution trend of main variables; The distribution of external variables in space is known and changes smoothly | Compared with the interpolation method based on logging data, the result obtained by external information participating in interpolation is more accurate | When the external variables are not smooth, the stability of the algorithm is poor | |
| Collocated Co-kriging | At the position of the estimation point, the secondary variable must be known | The parameters shall meet the second-order stability; It is applicable to the case where there are few observed data of the estimated variable | Only the secondary variables with the same position as the estimated variables need to be retained, and the secondary variables of all data points are not required; Collaborative simulation, interpolation results are more accurate; Secondary variables have little effect on the accuracy of estimation | When the study area is large and there are few reliable data, the reliability of the interpolation results is not good |
| Intrinsic Collocated Co-kriging | The secondary data are retained at location being estimated and at the primary data locations | |||
| Kriging Method | Applicability | Advantages | Disadvantages |
|---|---|---|---|
| Sequential Gaussian Simulation | Random variables conform to Gaussian distribution, or conform to Gaussian distribution after data transformation; For continuous variables | With different random paths each time, different simulation effects are obtained. According to geological experience, the most suitable simulation results are selected | It is not suitable for continuous variables with strong anisotropy; The accuracy of simulation results is closely related to the variation function |
| Sequential Gaussian collocated collaborative simulation | Random variables conform to Gaussian distribution, or conform to Gaussian distribution after data transformation; Applicable to continuous variables; At the position of the estimation point, the spatial distribution of external variables is known; The main variable and external variable satisfy the second-order stationary | Using external parameter collaborative simulation, the interpolation result is more accurate | It is not suitable for continuous variables with strong anisotropy; The accuracy of simulation results is closely related to the variation function |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zhang, X.; Guo, W.; Kang, L.; Gao, J.; Yu, R.; Sun, Y.; Pan, M. Research Status of and Trends in 3D Geological Property Modeling Methods: A Review. Appl. Sci. 2022, 12, 5648. https://doi.org/10.3390/app12115648
Liu Y, Zhang X, Guo W, Kang L, Gao J, Yu R, Sun Y, Pan M. Research Status of and Trends in 3D Geological Property Modeling Methods: A Review. Applied Sciences. 2022; 12(11):5648. https://doi.org/10.3390/app12115648
Chicago/Turabian StyleLiu, Yuyang, Xiaowei Zhang, Wei Guo, Lixia Kang, Jinliang Gao, Rongze Yu, Yuping Sun, and Mao Pan. 2022. "Research Status of and Trends in 3D Geological Property Modeling Methods: A Review" Applied Sciences 12, no. 11: 5648. https://doi.org/10.3390/app12115648
APA StyleLiu, Y., Zhang, X., Guo, W., Kang, L., Gao, J., Yu, R., Sun, Y., & Pan, M. (2022). Research Status of and Trends in 3D Geological Property Modeling Methods: A Review. Applied Sciences, 12(11), 5648. https://doi.org/10.3390/app12115648