Mixed-Integer-Based Path and Morphing Planning for a Tensegrity Drone
Abstract
:1. Introduction
2. State of the Art
2.1. Protective Cage Design for Drones
2.2. Mechanical Design of Tensegrity Structures
2.3. Deformation-Enabled Path Planning
2.4. Motion Planning for Rigid Drones
2.5. Convex and Mixed Integer Optimization in Motion Planning
3. Problem Statement
3.1. Static Equilibrium of Tensegrity Structures
3.2. Obstacle-Free Space Description
3.3. Path Planning as a Mixed-Integer Convex Program
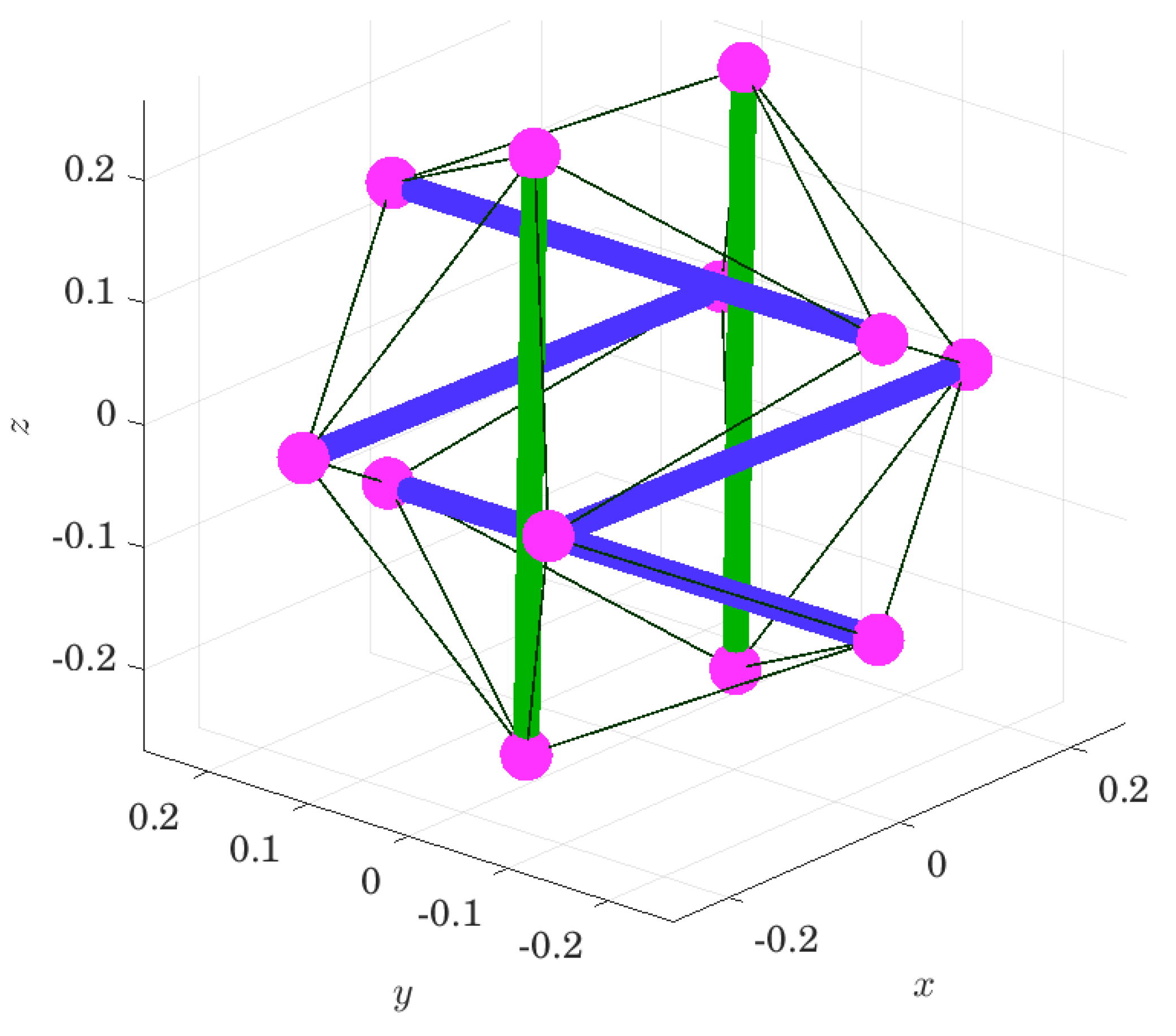
4. Configurations Dataset
4.1. Configuration Vector
4.2. Dataset Generation
| Algorithm 1 Configurations dataset generation algorithm |
Input: , , Output: Dataset whiledo end while |
5. Mixed-Integer Convex Path and Morphing Planner
6. Numerical Studies, Results
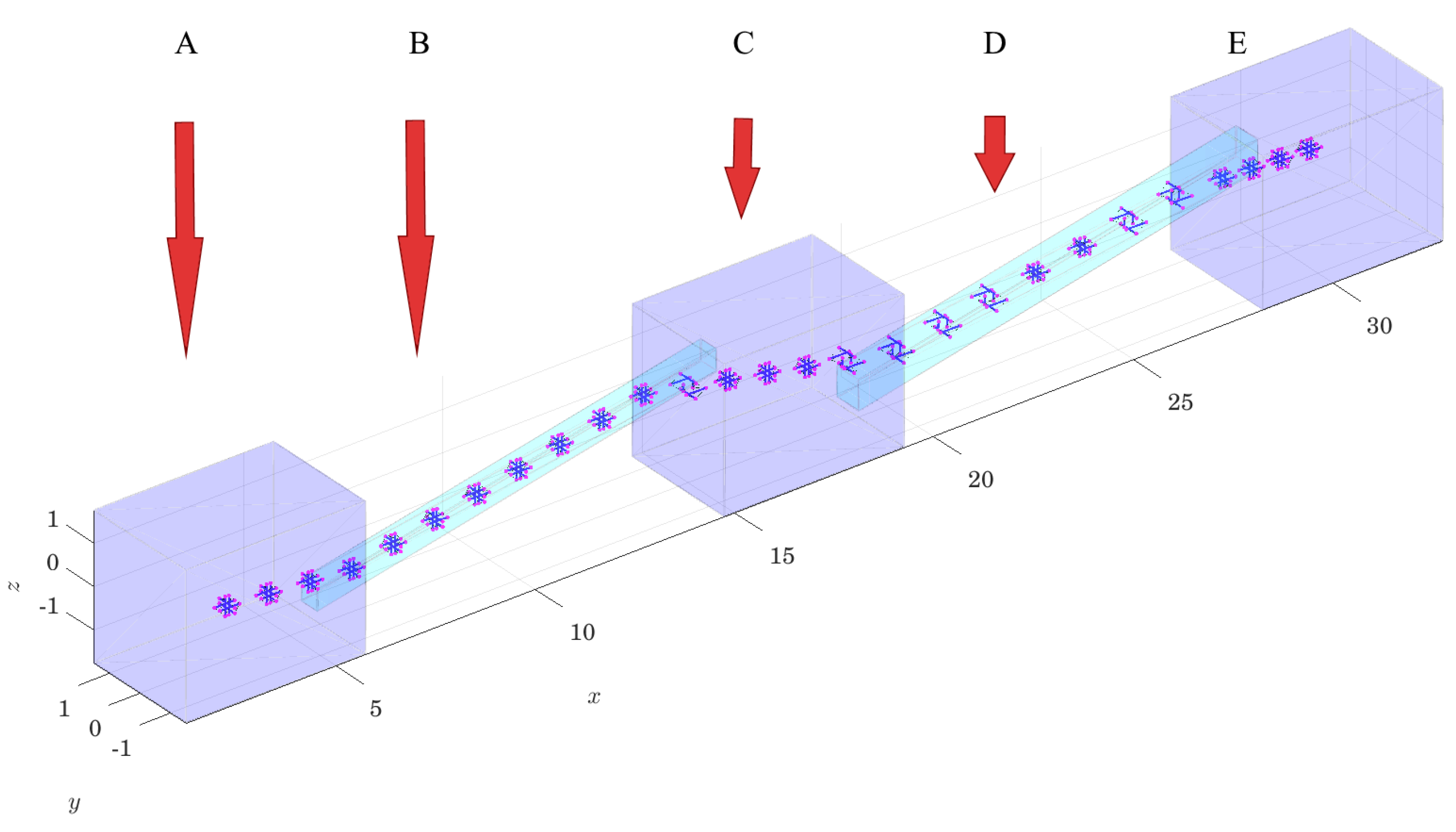
6.1. Planning Drone Path and Deformation through a Series of Rooms
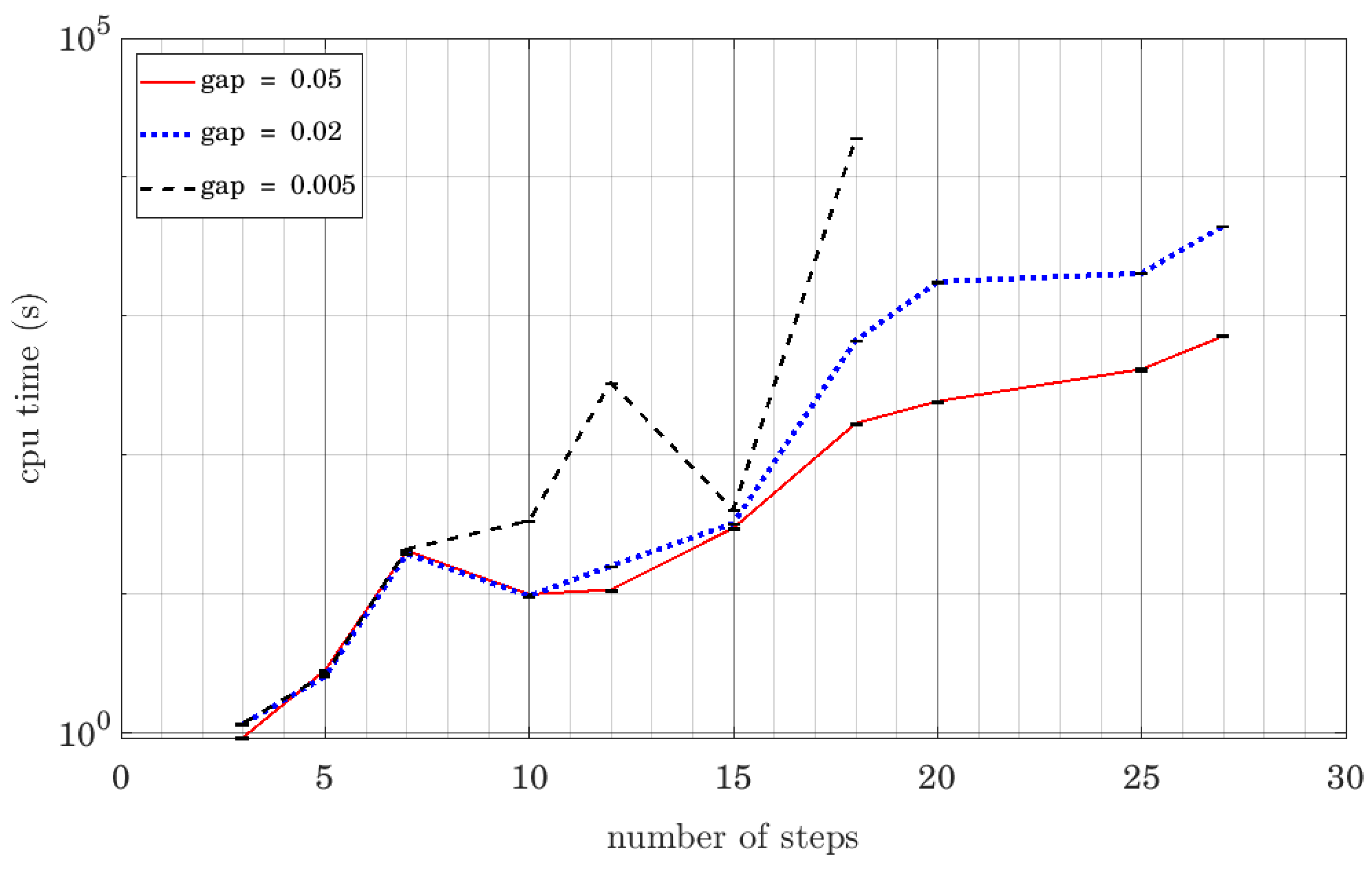
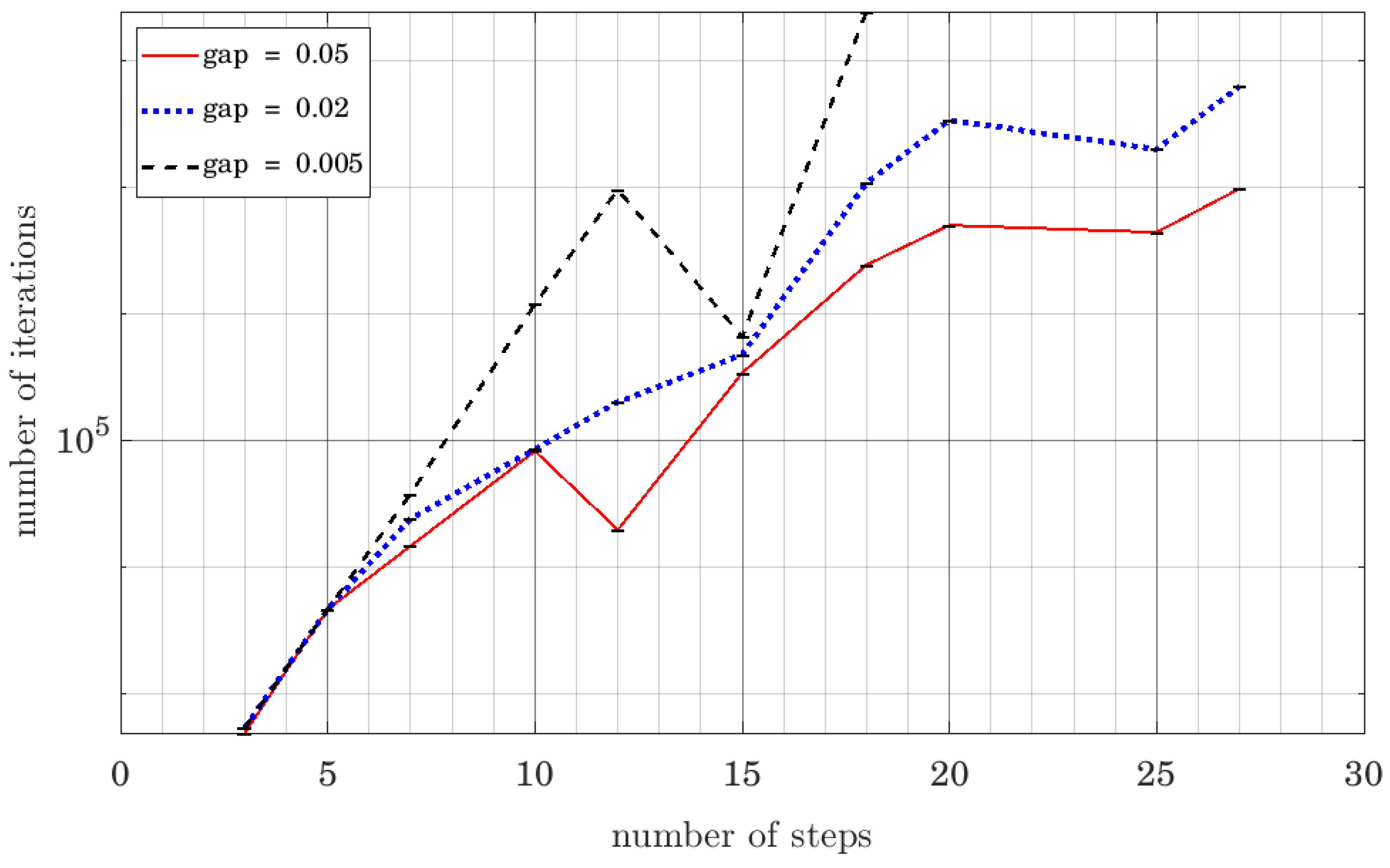
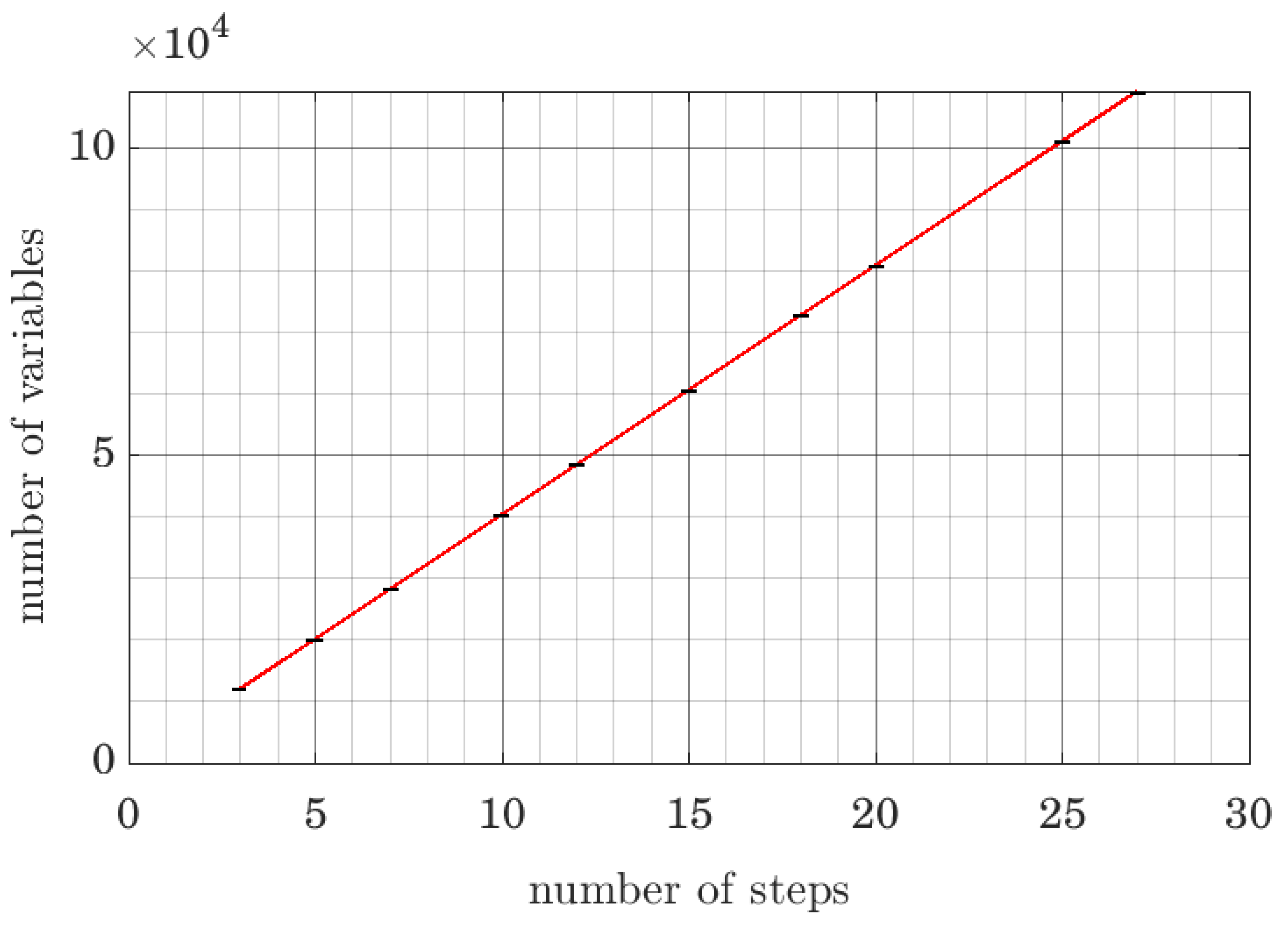
6.2. Study of the Computational Cost of the Algorithm
7. Experimental Study
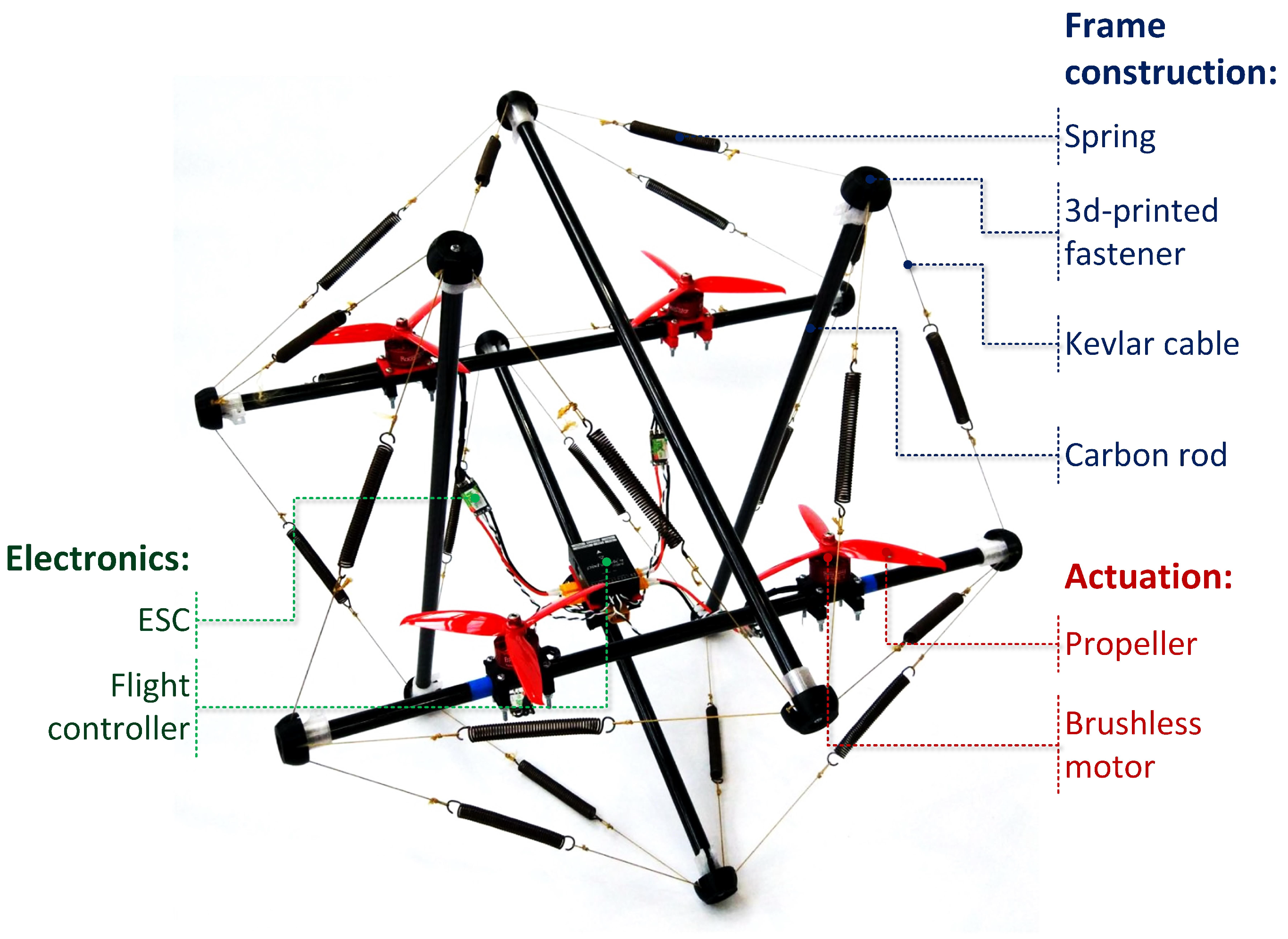
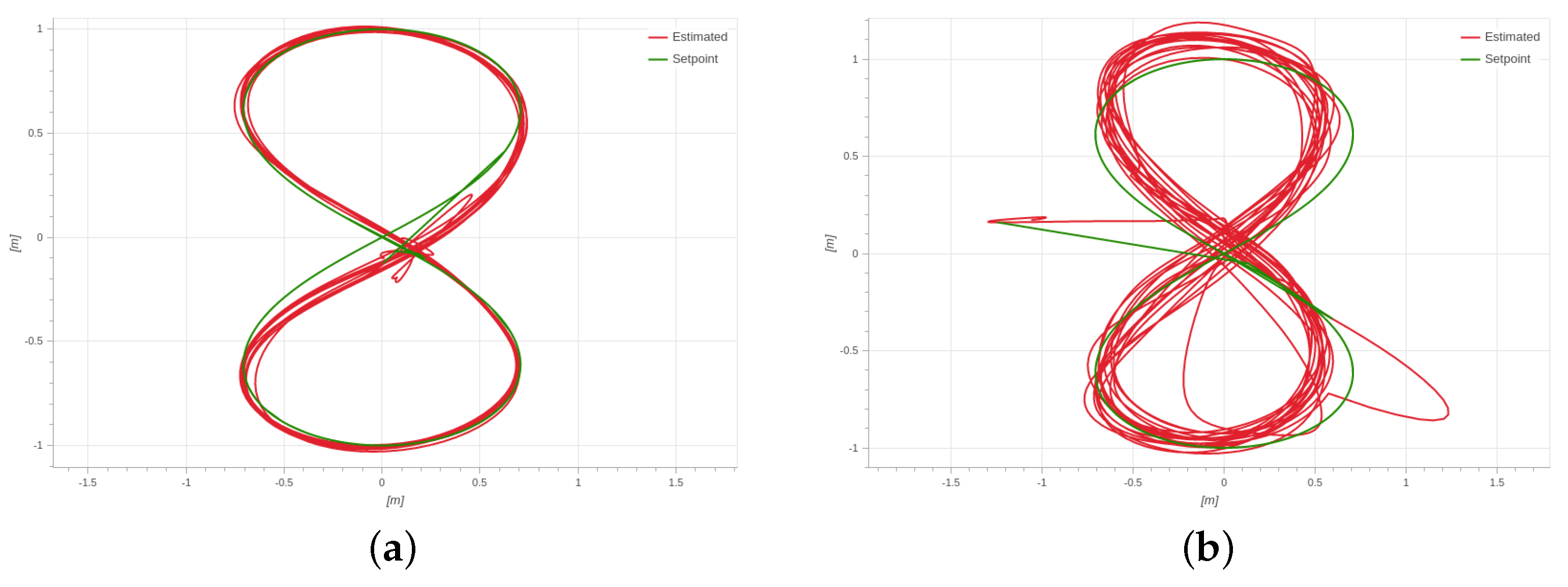
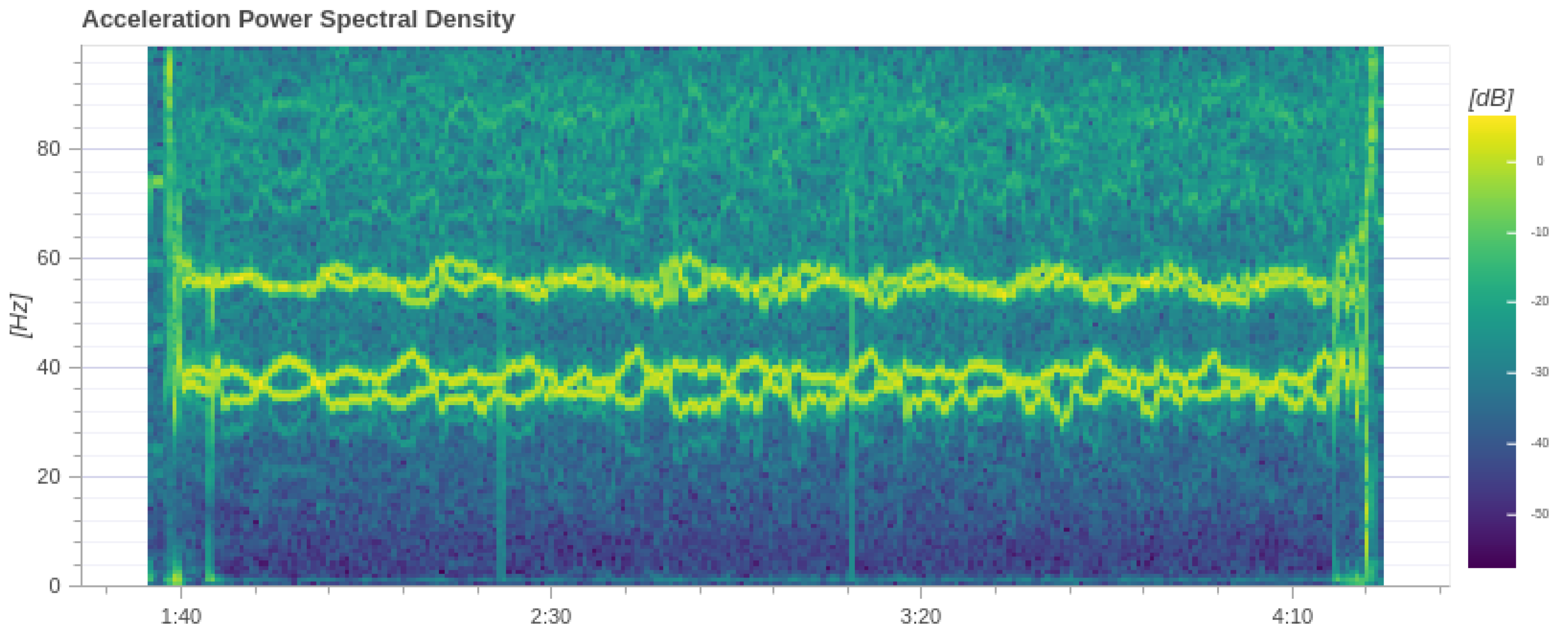
7.1. Pure Tensegrity Drone
7.2. Tensegrity Drone with Strut Contact
8. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MICP | Mixed-Integer Convex Programming |
| IRIS | Iterative Regional Inflation by Semi-definite programming |
| SDPs | Semidefinite Programs |
| MIQP | Mixed-Integer Quadratic Program |
| UAV | Unmanned Aerial Vehicle |
| HVAC | Heating, Ventilation, and Air-Conditioning |
| RRT | Rapidly Exploring Random Tree |
| QCQP | Quadratically Constrained Quadratic Programming |
| MIP | Mixed-Integer Programming |
References
- Kardasz, P.; Doskocz, J.; Hejduk, M.; Wiejkut, P.; Zarzycki, H. Drones and possibilities of their using. J. Civ. Environ. Eng. 2016, 6, 1–7. [Google Scholar] [CrossRef]
- Edgerton, K.; Throneberry, G.; Takeshita, A.; Hocut, C.; Shu, F.; Abdelkefi, A. Numerical and experimental comparative performance analysis of emerging spherical-caged drones. Aerosp. Sci. Technol. 2019, 95, 105512. [Google Scholar] [CrossRef]
- Kornatowski, P.M.; Mintchev, S.; Floreano, D. An origami-inspired cargo drone. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 6855–6862. [Google Scholar]
- Chen, C.S.; Ingber, D.E. Tensegrity and mechanoregulation: From skeleton to cytoskeleton. Osteoarthr. Cartil. 1999, 7, 81–94. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Motro, R. Tensegrity: Structural Systems for the Future; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Skelton, R.E.; Adhikari, R.; Pinaud, J.P.; Chan, W.; Helton, J. An introduction to the mechanics of tensegrity structures. In Proceedings of the 40th IEEE Conference on Decision and Control (Cat. No. 01CH37228), Orlando, FL, USA, 4–7 December 2001; Volume 5, pp. 4254–4259. [Google Scholar]
- Moored, K.; Kemp, T.; Houle, N.E.; Bart-Smith, H. Analytical predictions, optimization, and design of a tensegrity-based artificial pectoral fin. Int. J. Solids Struct. 2011, 48, 3142–3159. [Google Scholar] [CrossRef] [Green Version]
- Jáuregui, V.G. Tensegrity Structures and Their Application to Architecture; Universidad de Cantabria: Santander, Spain, 2020; Volume 2. [Google Scholar]
- Bouderbala, M.; Motro, R. Folding tensegrity systems. In Proceedings of the IUTAM-IASS Symposium on Deployable Structures: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2000; pp. 27–36. [Google Scholar]
- Vespignani, M.; Friesen, J.M.; SunSpiral, V.; Bruce, J. Design of superball v2, a compliant tensegrity robot for absorbing large impacts. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 2865–2871. [Google Scholar]
- Caluwaerts, K.; Despraz, J.; Işçen, A.; Sabelhaus, A.P.; Bruce, J.; Schrauwen, B.; SunSpiral, V. Design and control of compliant tensegrity robots through simulation and hardware validation. J. R. Soc. Interface 2014, 11, 20140520. [Google Scholar] [CrossRef] [Green Version]
- Savin, S.; Klimchik, A. Morphing-Enabled Path Planning for Flying Tensegrity Robots as a Semidefinite Program. Front. Robot. AI 2022, 9. [Google Scholar] [CrossRef]
- Abtahi, P.; Zhao, D.Y.; E, J.L.; Landay, J.A. Drone near me: Exploring touch-based human-drone interaction. Proc. ACM Interact. Mobile Wearable Ubiquitous Technol. 2017, 1, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Kornatowski, P.M.; Feroskhan, M.; Stewart, W.J.; Floreano, D. A morphing cargo drone for safe flight in proximity of humans. IEEE Robot. Autom. Lett. 2020, 5, 4233–4240. [Google Scholar] [CrossRef]
- Klaptocz, A.; Briod, A.; Daler, L.; Zufferey, J.C.; Floreano, D. Euler spring collision protection for flying robots. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 1886–1892. [Google Scholar]
- Borik, A.; Kallangodan, A.; Farhat, W.; Abougharib, A.; Jaradat, M.A.; Mukhopadhyay, S.; Abdel-Hafez, M. Caged Quadrotor Drone for Inspection of Central HVAC Ducts. In Proceedings of the 2019 Advances in Science and Engineering Technology International Conferences (ASET), Dubai, United Arab Emirates, 26 March–10 April 2019; pp. 1–7. [Google Scholar]
- Zha, J.; Wu, X.; Kroeger, J.; Perez, N.; Mueller, M.W. A collision-resilient aerial vehicle with icosahedron tensegrity structure. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 1407–1412. [Google Scholar]
- Sultan, C. Tensegrity: 60 years of art, science, and engineering. Adv. Appl. Mech. 2009, 43, 69–145. [Google Scholar]
- Furuya, H. Concept of deployable tensegrity structures in space application. Int. J. Space Struct. 1992, 7, 143–151. [Google Scholar] [CrossRef]
- de Jager, B.; Skelton, R.E. Stiffness of planar tensegrity truss topologies. Int. J. Solids Struct. 2006, 43, 1308–1330. [Google Scholar] [CrossRef] [Green Version]
- Sabelhaus, A.P.; Bruce, J.; Caluwaerts, K.; Manovi, P.; Firoozi, R.F.; Dobi, S.; Agogino, A.M.; SunSpiral, V. System design and locomotion of SUPERball, an untethered tensegrity robot. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2867–2873. [Google Scholar]
- Bruce, J.; Sabelhaus, A.P.; Chen, Y.; Lu, D.; Morse, K.; Milam, S.; Caluwaerts, K.; Agogino, A.M.; SunSpiral, V. SUPERball: Exploring Tensegrities for Planetary Probes. 2014. Available online: https://ntrs.nasa.gov/api/citations/20190001649/downloads/20190001649.pdf (accessed on 30 April 2022).
- Sabelhaus, A.P.; Bruce, J.; Caluwaerts, K.; Chen, Y.; Lu, D.; Liu, Y.; Agogino, A.K.; SunSpiral, V.; Agogino, A.M. Hardware Design and Testing of SUPERball, a Modular Tensegrity Robot. 2014. Available online: https://ntrs.nasa.gov/api/citations/20140011157/downloads/20140011157.pdf, (accessed on 30 April 2022).
- Lee, S.; Lee, J. A novel method for topology design of tensegrity structures. Compos. Struct. 2016, 152, 11–19. [Google Scholar] [CrossRef]
- Khafizov, R.; Savin, S. Length-Constrained Mixed-Integer Convex Programming-based Generation of Tensegrity Structures. In Proceedings of the 2021 6th IEEE International Conference on Advanced Robotics and Mechatronics (ICARM), Chongqing, China, 3–5 July 2021; pp. 125–131. [Google Scholar]
- Murakami, H. Static and dynamic analyses of tensegrity structures. Part II. Quasi-static analysis. Int. J. Solids Struct. 2001, 38, 3615–3629. [Google Scholar] [CrossRef]
- Xu, X.; Wang, Y.; Luo, Y. Finding member connectivities and nodal positions of tensegrity structures based on force density method and mixed integer nonlinear programming. Eng. Struct. 2018, 166, 240–250. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Zhu, S.X.; Li, S.X.; Xu, G.K. Analytical form-finding of tensegrities using determinant of force-density matrix. Compos. Struct. 2018, 189, 87–98. [Google Scholar] [CrossRef]
- Savin, S.; Balakhnov, O.; Klimchik, A. Energy-based local forward and inverse kinematics methods for tensegrity robots. In Proceedings of the 2020 Fourth IEEE International Conference on Robotic Computing (IRC), Taichung, Taiwan, 9–11 November 2020; pp. 280–284. [Google Scholar]
- Park, J.K.; Chung, T.M. Boundary-RRT* algorithm for drone collision avoidance and interleaved path re-planning. J. Inf. Process. Syst. 2020, 16, 1324–1342. [Google Scholar]
- Han, T.; Wu, W.; Huang, C.; Xuan, Y. Path planning of UAV based on Voronoi diagram and DPSO. Procedia Eng. 2012, 29, 4198–4203. [Google Scholar] [CrossRef] [Green Version]
- Pehlivanoglu, Y.V. A new vibrational genetic algorithm enhanced with a Voronoi diagram for path planning of autonomous UAV. Aerosp. Sci. Technol. 2012, 16, 47–55. [Google Scholar] [CrossRef]
- Fu, Z.; Yu, J.; Xie, G.; Chen, Y.; Mao, Y. A heuristic evolutionary algorithm of UAV path planning. Wirel. Commun. Mob. Comput. 2018, 2018, 2851964. [Google Scholar] [CrossRef] [Green Version]
- Niu, X.; Yuan, X.; Zhou, Y.; Fan, H. UAV track planning based on evolution algorithm in embedded system. Microprocess. Microsystems 2020, 75, 103068. [Google Scholar] [CrossRef]
- Lopez, B.T.; How, J.P. Aggressive 3-D collision avoidance for high-speed navigation. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5759–5765. [Google Scholar]
- LaValle, S.M.; Kuffner, J.J., Jr. Randomized kinodynamic planning. Int. J. Robot. Res. 2001, 20, 378–400. [Google Scholar] [CrossRef]
- Pivtoraiko, M.; Mellinger, D.; Kumar, V. Incremental micro-UAV motion replanning for exploring unknown environments. In Proceedings of the 2013 IEEE international conference on robotics and automation, Karlsruhe, Germany, 6–10 May 2013; pp. 2452–2458. [Google Scholar]
- Chen, J.; Liu, T.; Shen, S. Online generation of collision-free trajectories for quadrotor flight in unknown cluttered environments. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1476–1483. [Google Scholar]
- Oleynikova, H.; Taylor, Z.; Siegwart, R.; Nieto, J. Safe local exploration for replanning in cluttered unknown environments for microaerial vehicles. IEEE Robot. Autom. Lett. 2018, 3, 1474–1481. [Google Scholar] [CrossRef] [Green Version]
- Tordesillas, J.; Lopez, B.T.; Carter, J.; Ware, J.; How, J.P. Real-time planning with multi-fidelity models for agile flights in unknown environments. In Proceedings of the 2019 international conference on robotics and automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 725–731. [Google Scholar]
- Gao, F.; Wu, W.; Lin, Y.; Shen, S. Online safe trajectory generation for quadrotors using fast marching method and bernstein basis polynomial. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 344–351. [Google Scholar]
- Yang, L.; Qi, J.; Song, D.; Xiao, J.; Han, J.; Xia, Y. Survey of robot 3D path planning algorithms. J. Control. Sci. Eng. 2016, 2016, 7426913. [Google Scholar] [CrossRef] [Green Version]
- Deits, R.; Tedrake, R. Footstep planning on uneven terrain with mixed-integer convex optimization. In Proceedings of the 2014 IEEE-RAS International Conference on Humanoid Robots, Madrid, Spain, 18–20 November 2014; pp. 279–286. [Google Scholar]
- Deits, R.; Tedrake, R. Computing Large Convex Regions of Obstacle-Free Space Through Semidefinite Programming. In Proceedings of the Eleventh International Workshop on the Algorithmic Foundations of Robotics, Istanbul, Turkey, 3–5 August 2014; pp. 109–124. [Google Scholar]
- Zhong, X.; Wu, Y.; Wang, D.; Wang, Q.; Xu, C.; Gao, F. Generating large convex polytopes directly on point clouds. arXiv 2020, arXiv:2010.08744. [Google Scholar]
- Savin, S. An algorithm for generating convex obstacle-free regions based on stereographic projection. In Proceedings of the 2017 International Siberian Conference on Control and Communications (SIBCON), Astana, Kazakhstan, 29–30 June 2017; pp. 1–6. [Google Scholar]
- Grossmann, I.E. Review of nonlinear mixed-integer and disjunctive programming techniques. Optim. Eng. 2002, 3, 227–252. [Google Scholar] [CrossRef]
- Anand, R.; Aggarwal, D.; Kumar, V. A comparative analysis of optimization solvers. J. Stat. Manag. Syst. 2017, 20, 623–635. [Google Scholar] [CrossRef]
- Nedelchev, S.; Gaponov, I.; Ryu, J.H. Accurate dynamic modeling of twisted string actuators accounting for string compliance and friction. IEEE Robot. Autom. Lett. 2020, 5, 3438–3443. [Google Scholar] [CrossRef]


| Parameters | Number of Steps, K | |
|---|---|---|
| Number of binary variables | 65 | 351 |
| Number of linear inequalities | 14,400 | 77,760 |
| Solution time | 2.8 s | 733 s |
| Parameters | Value |
|---|---|
| Strut length | 0.5 m |
| Strut mass | 0.01 kg |
| Cable rest length | 0.305 m |
| Cable stiffness | 0.58 N/mm |
| Total mass | 0.836 kg |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Savin, S.; Al Badr, A.; Devitt, D.; Fedorenko, R.; Klimchik, A. Mixed-Integer-Based Path and Morphing Planning for a Tensegrity Drone. Appl. Sci. 2022, 12, 5588. https://doi.org/10.3390/app12115588
Savin S, Al Badr A, Devitt D, Fedorenko R, Klimchik A. Mixed-Integer-Based Path and Morphing Planning for a Tensegrity Drone. Applied Sciences. 2022; 12(11):5588. https://doi.org/10.3390/app12115588
Chicago/Turabian StyleSavin, Sergei, Amer Al Badr, Dmitry Devitt, Roman Fedorenko, and Alexandr Klimchik. 2022. "Mixed-Integer-Based Path and Morphing Planning for a Tensegrity Drone" Applied Sciences 12, no. 11: 5588. https://doi.org/10.3390/app12115588
APA StyleSavin, S., Al Badr, A., Devitt, D., Fedorenko, R., & Klimchik, A. (2022). Mixed-Integer-Based Path and Morphing Planning for a Tensegrity Drone. Applied Sciences, 12(11), 5588. https://doi.org/10.3390/app12115588










