Abstract
Fused Deposition Modeling (FDM) is a type of Additive Manufacturing (AM) technology that is becoming increasingly common in numerous applications thanks to its versatility and reduced material waste. However, the complex physical phenomena occurring during extrusion, including the dynamics of non-Newtonian fluids, viscoelastic behaviors and rheology, make the use of heuristic observations preferable to that of analytical approaches. Consequently, engineers have focused on optimizing materials and hardware rather than control algorithms. The limited knowledge about extrusion and deposition dynamics usually confines the control action to the motion of the printing head while keeping a constant flow rate. Existing attempts to synchronize motion and extrusion consists of open loop compensations, which, however, require identified transfer functions or need to be tuned manually. This article aims to compactly review FDM technologies from a control perspective by presenting (i) the models of extrusion and deposition and (ii) the control strategies currently adopted in industry.
1. Introduction
Additive Manufacturing is a process that, unlike conventional machining, fabricates an object by continuously stacking material in the form of layers rather than removing it from a block [1]. Initially born for rapid prototyping purposes, AM quickly shifted towards mass production thanks to its elevated versatility, reduction in material waste and ability to manufacture geometries that are otherwise impossible to obtain. However, the advantages above come with some limitations, such as low throughput, high uncertainties and sensitivity to defects.
Different AM technologies have emerged to process different materials, including polymers [2], metals [3], ceramics [4] and concrete [5]. Amongst them, the most mature ones are known as (i) Fused Deposition Modeling (FDM), (ii) Powder Bed Fusion (PBF), Stereolithography (SLA), (iii) Direct Energy Deposition (DED) and (iv) Laminated Object Manufacturing (LOM). In this work, the focus is on FDM, which is specialized in plastic materials and composites, making this technology extremely pervasive in a wide range of sectors. In general, the FDM process comprises the following subroutines [6].
- Offline:
- →
- slicing;
- →
- path planning;
- Online:
- →
- motion control;
- →
- extrusion control.
The offline phase is a preliminary step that takes place during simulation, in which dedicated software elaborates on the digital model (e.g., CAD) of the part with the aim of planning the optimal building trajectory based on specific factors, such as accuracy or build time. Given the nature of AM, some of these variables are inversely proportional to each other, which makes finding the optimal trajectory a multi-variable optimization problem with several trade-offs. In practice, this problem is dealt with by solving the sub-routines known as slicing and path planning. The reader is referred to [7] for a dedicated review of slicing and path planning strategies, which are briefly summarized in the following.
The slicing operation consists of determining the layer-wise partition of the part to be fabricated. Based on the application and on the machinery available, the layers can be planar or non-planar, and their height can be constant or adaptive. Planar layers allow the end-effector (EE) to keep a fixed orientation, hence enabling the implementation of simple configurations, such as gantries. Conversely, non-planar layers require the use of an EE with additional degrees of freedom.
Path planning consists of defining the ideal sequence of poses the EE needs to follow (usually represented as B-splines or Beziér curves) in order to build the part. There exist numerous path planning algorithms depending on the feature they aim to optimize, e.g., accuracy, build time or surface roughness.
The online phase represents the realization of the trajectory planned and is responsible for the correct execution of motion and extrusion. Current industrial robots can achieve accuracy and repeatability tolerances that exceed the requirements for most FDM applications. Therefore, the motion system is not discussed in this work since it is a negligible source of error with respect to the extrusion one
Extrusion is defined as the process of enforcing the flow of a semi-solid material through pressure and heat. In FDM, the raw material, which is usually powder, pellet or filament of solid polymers, is compressed and heated until reaching the melting temperature; then, it melts inside the extruder and is extruded through the nozzle as a viscous fluid. The block constituted by the extruder and the nozzle is also called the printing head, and it coincides with the EE of the printer. Outside the nozzle, the geometrical arrangement of the extrudate and the ability to maintain the shape obtained until solidification are the final and most important aspects of extrusion and are both determined primarily by the composition of the material [8].
The complex extrusion dynamics makes model-based approaches inconvenient, causing engineers to resort to experience and qualitative observations. For this reason, statistical methods are commonly used to determine optimal process parameters [9,10]. Numerous studies have dealt with rheological effects in FDM [11,12,13]; however, although providing engineers with insight and knowledge, their approach requires extensive simulation or experimentation that needs to be tailored to each application before being implementable into the production line. Hence, flow models tend to be very specific, and their correctness is highly sensitive to changes in materials and printing systems. The common approach consists of setting a constant rate of extrusion and then adapting the path to it. Although some efforts have been made towards motion-extrusion synchronization in recent years, they mostly focus on open-loop controllers to improve the consistency of deposition but have limited knowledge of the system or real-time measurements. The difficulties of monitoring online quantities such as outlet pressure or strand width do not make it possible to close the loop on flow deposition since sensors can interfere with the printing operation.
Some contributions [14,15,16] have addressed the automation of monitoring strategies, which can lead to the collection of a high-volume of data to be used both offline for analysis purposes or online for control purposes. Such a promising direction suggests that adding a control on the flow deposition through proper inline monitoring represents the next step towards tighter tolerances in AM. To this end, this study presents a selective literature review focusing on (i) analytical models of the extrusion process and flow deposition together with a set of qualitative considerations that have been observed in practice or simulations, and, in the second part of the paper, on (ii) control strategies adopted to date in industry, highlighting their strength and limitations.
2. Systems
This section describes the most viable models of extrusion in FDM, which can be divided into two phases. The first phase regards the dynamics within the extruder, while the second one focuses on the behavior of the material as it exits the nozzle.
2.1. Extrusion
Extrusion in FD consists of ejecting semi-molten material through an orifice by applying pressure. It occurs in the extruder, which processes solid material into a glass-like fluid by applying heat and pressure simultaneously, leading to an outward stream with controlled throughput and shape. This review focuses on two of the most diffused material in FDM: filament (also called Fused Filament Fabrication or FFF) and pellet, each of which requires a tailored extruder, as it is described hereafter.
2.1.1. Single-Screw
The technologies used to extrude powder or pellet involve a screw mechanism. Several different screw configurations have been developed [17], including single, twin or multiple screws. This article focuses on the single screw version since it is the most studied and widespread.
Figure 1 depicts a scheme of a single screw extruder and highlights its components: hopper, endless screw, barrel, heaters and nozzle. The pellet or powder is introduced through the hopper into the first section of the screw. The rotation presses the material toward the tip. Along the way, friction and heat melt the material. In the final section of the screw, the nozzle directs the flow outwards. The phase shift from solid to liquid occurs gradually from hopper to nozzle, forming four sections based on the percentage of melted material: solid conveying zone [18,19,20,21], pre-melting zone, melting zone [22,23,24,25] and melt conveying zone [26,27,28,29]. Continuously modeling the interaction between solid granulate and fluid-like melt is not trivial, and to date, there exists no global model that describes the complete screw extrusion process. The authors refer to this article [30] for a comprehensive review of the mathematical models of both single-screw and twin-screw extrusion configurations, grouped by melting section.

Figure 1.
Scheme of the single-screw extruder: 1—solid polymer; 2—hopper; 3—barrel; 4—screw; 5—heaters; 6—die; 7—extrudate; A—solid conveying zone; B—pre-melting zone; C—melting zone; D—melt conveying zone; E—melt flow zone. Image from reference [30].
Two operating conditions of the screw can be identified: (i) flood fed and (ii) starve fed. The former is achieved at a filling factor (FF) of 1, defined as [31]
where is the volume of the screw channel occupied with material, while V is the volume of the screw channel. A filling factor lower than one leads to starvation. Starvation occurs when the screw rotation is so high that the output flow rate exceeds the input flow rate provided by the hopper. When air bubbles form during a flood fed extrusion, these can cause discontinuities in the flow that lead to defects of the part. A controlled starve fed extrusion, however, shows several advantages, such as a decrease in the chances of clogging and an acceleration of the melting process [31].
The key variable for control purposes is the volumetric flow rate q exiting from the nozzle. As a first approximation, the flow rate q of single-screw extrusion can be written as [31]:
where is the volumetric drag flow and the volumetric pressure flow, which can be defined as
where is the pressure increase in the screw channel, the viscosity of the material, the fully filled length of the screw channel and and represent geometrical constants.
Equation (3) represents a static model that is valid at steady-state, whereas it does not describe the dynamics of the flow rate during transient states. The dynamical behavior of the extruder is usually studied through demanding software simulations based on discrete element methods, often under strong assumptions, e.g., the fluid being isothermal or Newtonian. Moreover, the coupling between the flow rate and temperature is often neglected in practice, and the model of the extruder is usually considered only as a function of the rotation speed of the screw. The common approach consists of parametrizing the transfer function between the rotation speed and flow rate as a first-order transfer function with delay and then selecting the parameter values that best fit the data, which are collected as step responses of the rotation speed at a constant temperature.
2.1.2. Filament Extruder
In FFF, extrusion occurs by pushing the filament into a heated chamber called liquefier, in which the material is melted and directed to the nozzle (see Figure 2) [32]. The motion of the filament is induced by a couple of electrical motors that drive a roller each. A roller is a dented gear fixed to the end-effector whose ideal rotation impresses motion on the filament through friction in the form:
where is the linear speed of the filament, the rotation speed of the rollers and r the radius of the rollers at the gear teeth.
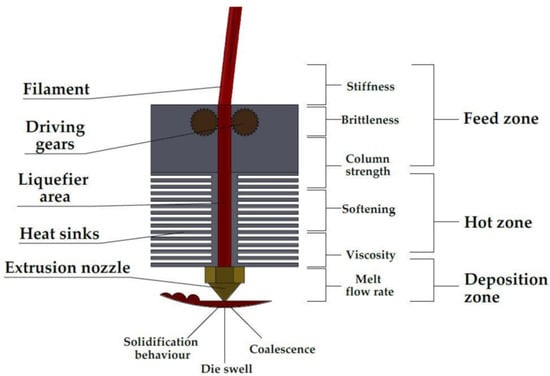
Figure 2.
Scheme of the extruder in FFF applications. Image from reference [33].
Loss of ideality can arise in terms of slippage or deformation phenomena.
- Slippage causes loss of speed given byand can be induced by roundness deviation, wear or insufficient torque;
- Deformation occurs in the filament indentation as a result of the compression exerted by the roller teeth, which can cut into the filament.
Slippage and deformation can lead to under-extrusion, and extreme slippage causes filament shredding that can clog the extruder [34]; it is therefore important that these phenomena are avoided.
The rollers push the filament into the liquefier, where the phase shift occurs. The pressure exerted by the descending filament pushes the molten material through the nozzle. Based on the connection between the driving motors and the liquiefier, two types of extruder can be identified:
- Direct: the motors are mounted directly on top of the liquefier. The load on the end-effector is higher, but the movement of the filament is more constrained and hence more controlled;
- Bowden: only the liquefier is mounted on the printing head, while the motors are placed in a fixed position of the machine, diminishing the load on the end-effector. However, the filament needs to cover some distance from the rollers to the liquefier, which may lead to bending and buckling.
The liquefier has been modeled analytically [35] both in the time and the frequency domains and the models obtained have been validated experimentally, reaching satisfactory prediction accuracy. The compression force to be applied to the filament to extrude the melt is derived as
where is the total pressure drop along the liquefier, and A is the cross-section of the filament (which is equal to the cross section of the liquefier). By imposing that the two drive rollers apply a total force F on the filament that equals the required one
the corresponding torque T exerted by each of the two drive rollers under ideal conditions can be written as
A first-order transfer function (where s is the complex frequency) between the Laplace transform of the reference flow rate and the transformed measured flow rate with time delay that approximates the liquefier dynamics at lower frequencies has also been developed
where is the time constant of the system, the static gain, R models the slippage between rollers and filament and L represents the properties of the material and the heat flux. The main assumptions of this derivation are that (i) the material behaves as a generalized Newton fluid; (ii) the flow is isothermal at steady-state but not during transient states, in which the viscosity is corrected based on temperature; (iii) slippage is present; and (iv) the torque is upper bounded.
Nevertheless, the flow rate is computed by approximating the extruder to a pipe, thus equaling the relationship between input and output flow
according to the mass conservation principle. This relation is simple and well approximates the static behavior.
Thanks to advancements in numerical simulation tools, nowadays, Computational Fluid Dynamics (CFD) software is commonly used in the industry to study a system under different conditions. Go et al. [36] have identified the main limitations to build rate in FFF and illustrated its trend as a function of resolution, under the constraints of extruder force, liquefier length and printing speed. Simulation and experimental results have shown that the trade-off between build rate and resolution is mostly influenced by printing speed, exhibiting a clear non-linear behavior.
Serdeczny et al. [37] have studied the melt dynamics in the liquefier through numerical simulations and have identified two different flow regimes, a stable and an unstable one, which derive from the interaction of two opposite phenomena, described herein:
- Filament advancement: when the feeding speed increases, the filament takes less time to cover the channel of the liquefier. At constant heat flow, the point along the liquefier in which the phase shift of the filament occurs (called transition point ) moves further towards the nozzle. In the extreme case, the filament does not melt completely and reaches the nozzle in the solid state.
- Backflow: at the transition point, the liquid portion of the material partially fills the thin air layer that separates the solid filament from the channel wall (see Figure 3). This creates a region where a portion of the liquid flows in the opposite direction of the feeding speed and recirculates, reducing the shear stress in the liquefier and leading to a drop in the feeding force.
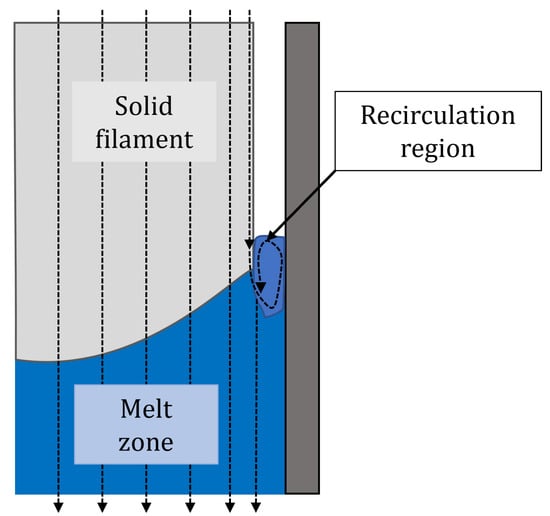 Figure 3. Example of the backflow phenomenon that occurs in the recirculating region.
Figure 3. Example of the backflow phenomenon that occurs in the recirculating region.
These two opposite phenomena are stable up to a certain value of filament speed, which when exceeded leads to oscillations in the feeding force. Therefore, the maximum printing speed is constrained by the length of the liquefier and the heat flux provided by the heaters so as to keep the melt zone sufficiently upstream of the nozzle. The temperature of the liquefier has the effect of reducing the feeding force necessary to achieve the same feed rate, while the feeding force raises when the nozzle diameter decreases due to higher shear rates.
2.2. Deposition
This section presents some of the analytical models found in the literature that relates the process parameters to the most important features of the part, e.g., strand geometry, surface roughness and global structure. Other key properties such as strength and hardness are mostly material-related and have not been treated in detail in this work.
2.2.1. Strand Geometry
Jin et al. [38] presented a geometrical model of the filament’s trajectory during deposition. After the extrudate reaches the substrate, it is possible to identify two different deposition conditions based on the ratio between nozzle-to-substrate distance z and nozzle diameter d, defined as the normalized gap
In the case : the exiting flow is free to deposit without any interference, reaching a free-standing height
which is only a function of the material’s properties at the given temperature ( is the surface energy, g the standard gravity, the density).
In the case : the printing head prevents the melt from expanding upwards and constrains it to spread horizontally. The strand height h is often approximated to be equal to the nozzle-to-substrate distance z. A simple model of strand geometry at steady-state can be computed using the mass conservation principle while assuming the shape of the cross-section to be oblong (see Figure 4), which results in a strand width given by [39,40]
where is the extrusion speed, the printing speed, d the nozzle diameter and z the distance between nozzle and substrate.
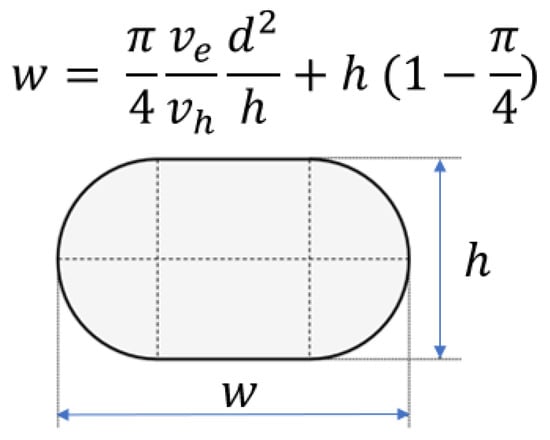
Figure 4.
Scheme of the assumed cross-section of the deposited strand. is the extrusion speed (i.e., the exiting velocity of the extrudate from the nozzle), the printing speed (i.e., the linear velocity of the EE), d the diameter of the nozzle, and h the high of the deposited strand, which is often assumed to be equal to the distance between the nozzle and the substrate z.
Alternatively, a different analytical model of width and height of the deposited strand has been obtained in the case of nozzle equipped with a spreading head [41], as depicted in Figure 5. The analytical model has been compared with the simulation results under the assumptions that the fluid is isothermal and Newtonian.

Figure 5.
Bottom view of an extruder with a spreading head. The extrudate flows from the nozzle with radius , while is the radius of the spreading head. L denotes how much the extrudate expands on the y axis during the printing with respect to the internal die, and w is the total width of the extrudate.
The strand geometry obtained is given by
where w and h are the strand width and height, respectively, , the external and internal radii, respectively, and q is the output flow rate. Moreover, the average temperature of the deposited strand is solved as
where Br is the Brinkman number, Ca the Cameron number, K the material consistency and k the thermal conductivity. The authors concluded that the hypothesis of isothermality holds at a substrate temperature higher than 100 °C and high printing speeds.
CFD software makes it possible to derive qualitative considerations by simulating the situation of interest. For example, Comminal et al. [39] performed simulations with the intent of studying the morphology of the strand under different printing conditions as a function of two factors: the normalized gap G and the velocity ratio
which is defined as the ratio between linear velocity of the printing head and extrusion speed . As presented in their work, variations of the above factors strongly impact the geometry of the strand cross-section but not the cross-sectional area (Figure 4). In general, both a reduction in the gap or the printing speed strengthen the side flow, thus increasing the width of the strand. The strand height, on the other hand, has been shown to shrink or swell depending on the velocity ratio. When this quantity is too low, the pressure that the exiting flow generates on the substrate can force the material to go upwards and achieve a concave section around the nozzle. In this case, the strand height is higher than the gap.
2.2.2. Surface Roughness
The surface finish of the printed part is primarily affected by the slicing strategy, which is responsible for setting the height of each layer. Intuitively, this operation can be seen as a discretization of the otherwise continuous ideal object, leading to an unavoidable loss of geometric fidelity. Smaller resolutions lead to smoother surfaces but at the expense of the deposition rate since (i) a lower diameter of the nozzle d and (ii) a higher number of layers are required to build the part. Specifically, the deposition rate decreases with the square of the increase in resolution [42].
The surface quality of the part is also determined by the roughness of each individual layer. Several models of surface roughness in FDM have been derived in the literatures [43,44]. In general, it has been shown that the surface roughness mostly depends on the layer height h and build orientation angle , as defined by [45]
where are constants that were identified from data. Other parameters such as feed rate, temperature, road width and air gap do not have much influence on the surface finish of the part since they are mostly responsible for filling the layers rather than defining the external contour.
2.2.3. Global Structure
The properties of the complete part depend on the interaction among the different layers and are often a function of the material only [8]. However, the process parameters that control the print locally have a strong effect on the global outcome. For instance, each layer must be able to sustain the stress induced by the extruded flow of the successive layer without deforming it excessively. This constraint translates into a limitation of the elastic strain of the substrate as [8]
where is the compression term provided by the weight of the next layer, and represents the compression term given by the flow motion.
Similarly, the lowest layers must bear the weight of all the successive deposits; hence [8]
The distortion ratio between structure deformation and layer height h is given by
and represents the deviation of the layer from the ideal plane of deposition, as shown in Figure 6. Such error is mainly induced by the shrinkage of the extrudate that occurs upon cooling down from glass temperature to room temperature.

Figure 6.
Scheme of the deformation phenomenon, quantified as .
The maximum acceptable distortion ratio can be written as
where . The condition becomes to avoid interference between printing head and substrate.
A crucial element for the mechanical properties of the printed part is the interlayer strength. It is defined as the ability to resist longitudinal stress (parallel to the deposition plane), and it is mainly affected by poor diffusion, which in turn depends on the temperature of both the substrate and new layer. A model of interlayer strength for plastic materials, validated through online measurements, has been presented [46] as
where is the predicted bond width between layers, w the nominal road width, the strength of the fully healed polymer, the interlayer penetration distance of diffusion between layers, and the diffusion distance at which full strength is achieved and the healing process is complete.
The interaction among layers and the resulting global part, including the effects of layer height h and strand-to-strand distance s, has been studied through numerical simulations [47]. The results can be summarized as follows:
- can cause considerable distortions in new the layers;
- Smaller h and s lead to smaller porosity and better surface roughness.
3. Control
With a slight abuse of terminology, the trajectory planning phase in FDM is included in this section, and the most widespread strategies are reviewed in the Offline subsection. The Online paragraph describes the most known techniques of real-time extrusion control divided by type of extruder.
3.1. Offline
Zhao et al. [7] reviewed both the slicing and path-planning operations for a variety of AM applications. For example, Thrimurthulu et al. [48] proposed an algorithm to determine an adaptive layer height for the whole part based on the minimization of a cost function that balances the trade-off between surface finishing and build time. The trajectory generation problem was surveyed in detail in [49], which categorized each contribution based on the goal their algorithm was designed to achieve, e.g., build time minimization or geometrical accuracy. One of the issues that planning algorithms must consider is the uneven material distribution occurring along corners. To this end, Han et al. [50] proposed to group each trajectory vector based on their similarity and to assign the appropriate flow rate to each group in order to minimize filling errors. Alternatively, a parametrization of the acceleration profile was proposed [51] in order to compensate for the uneven deposition at curves by maintaining a constant ratio between the printing head speed and extrusion speed.
3.2. Online
The simplest strategy for extrusion is to follow a constant reference throughout the complete process, irrespective of the trajectory. In this case, the online motion and extrusion controls are independent, and their joint effect needs to be considered during planning. The output flow rate is achieved indirectly by tracking a constant reference of the input actuators, e.g., the roller speed for the filament extruder or the screw rotation velocity for the single-screw extruder.
More advanced methods involve the synchronization between printing velocity and extrusion speed, which has been shown to improve the deposition evenness, especially at corners [51]. Although addressed in some cases [14], the improvement in the online control techniques is constrained by the difficulties in measuring the real flow rate without interfering with it, thus making it preferable to resort to the acquisition of the feeding speed instead.
3.2.1. Single-Screw
Abeykoon et al. [52] reviewed multiple contributions regarding the control of single-screw extruders. The earliest ones involved the tracking of heat temperature and pressure drop along the screw to control the viscosity and the flow rate, respectively. The extruder system was identified from plant data as a first-order transfer function or a time series, separately controlled via PI or PID algorithms [53,54,55,56]. Similarly, joint heat and extrusion control has been studied [57]. Other contributions employed viscosity control thanks to the implementation of an online viscometer or estimator through PID or Constrained Minimum Variance (CMV) methods [58]. Lastly, the suggested direction of improvement supported by the authors is Fuzzy Logic control [59] since its linguistic rules permit exploiting the high-level qualitative knowledge that engineers acquire through experience.
An alternative technique called Dynamic Disturbance Decoupling Control (DDDC) was presented [60]. Based on the Active Disturbance Rejection Control (ADRC) paradigm, this method has the advantages of (i) requiring little knowledge about the system and (ii) well rejecting disturbances and uncertainties. This makes it possible to control each heater independently but with limited overshoots, leading to remarkable energy savings.
3.2.2. Filament Extruder
In FFF, the control effort mainly regards the actuation of the rollers. Greeff et al. [34] introduced a slippage control by integrating a Computer Vision technique to estimate the head speed and the die width based on a stream of images. As shown in their article, the mismatch between roller speed and filament speed is often neglected by assuming zero slippage and no deformation, but this assumption becomes less valid as the roller speed increases and the temperature decreases.
A more robust approach regards the real-time synchronization or coordination between motion and extrusion, which leads to a more uniform strand deposition. Although the geometry of the extrudate is the principal concern, its control is usually performed in open-loop due to the practical difficulties of measuring die width or height in real-time. Han et al. [61] proposed a detailed block scheme of the overall FFF process, which includes the liquefier, extrusion and road forming dynamics. The approach involves the modeling of the relation between roller speed and flow rate and then the design of an open-loop compensation that controls the roller speed based on the reference head velocity, accounting for the die dynamics. However, each transfer function is assumed to be known, whereas generally, this is not the case in practice.
Ertay et al. [62] presented an adaptive controller to maintain the liquefier temperature at a constant value, while the extrusion speed was kept proportional to the head speed, showing improvements in the geometrical accuracy of the part.
A different feed-forward approach to control the flow rate of the single-screw extruder was studied [42] by identifying the system from plant data as a first-order transfer function with delay. Then, a first-order proper filter was manually tuned to fasten the plant’s response, leading to a better geometrical accuracy at corners.
4. Conclusions
Fused Deposition Modeling (FDM) is an appealing process for numerous applications thanks to its versatility and promptness, which makes it possible to fabricate arbitrary geometries in one single operation. However, extrusion dynamics is a complex physical phenomenon that is not trivial to model. In this review, (i) some formal models of the process and some qualitative considerations have been presented, and (ii) the most widespread strategies adopted in the industry have been reviewed. The goal is to ease the study of FDM from the control viewpoint, which is usually less prioritized with respect to material and hardware.
Some interesting open challenges have been highlighted, which involve the dynamic modeling of the extrusion and deposition processes. Analytical models exist, but they are focused on static relationships. Differential equations are used solely in Computational Fluid Dynamics (CFD) software, which iteratively solves momentum and energy balances to propagate the solution among each node according to Discrete Element Methods. Despite the usefulness of such tools, their computational requirements make them inapplicable for online prediction.
The most viable solutions revolve around black or gray box identification from experimental data. In this case, the extruder is usually parametrized as a first-order transfer function with delay, whose poles, gain and delay are selected as the ones that best fit the data. Nevertheless, the accuracy of this type of approximation is acceptable only locally and cannot be generalized to different printing conditions. A different and effective identification approach involves Deep Learning (DL) methods. For instance, in different applications, Recurrent Neural Networks (RNNs) or Long-Short Term Memory (LSTM) networks are able to well approximate the system dynamics, enabling the use of model-based control strategies, such as Model Predictive Control [63] or Internal Model Control [64]. However, DL is extremely data-hungry and thus properly automated acquisition systems are necessary for this approach. Nowadays, inline monitoring has been dealt with in several ways, from the installing of a rheometer on the printing head to geometry estimation via Computer Vision.
The lack of formal knowledge about the dynamics of the extrudate severely affects the choice of control strategy. The simplest one consists of keeping the extrusion rate constant throughout the print and adapting the path plan to it. Some of the contributions examined have designed synchronization between motion and extrusion along corners by decreasing the extrusion rate proportionally to the linear acceleration of the extruder. Alternatively, an open loop compensation can be tuned to fasten the extrusion response to accelerations of the printing head. A promising approach involves the use of fuzzy controllers, which are designed to translate high-level linguistic rules into suitable control laws.
Author Contributions
Conceptualization, M.M.; methodology, M.M.; formal analysis, M.M.; investigation, M.M.; resources, F.C.; data curation, M.M.; writing—original draft preparation, M.M.; writing—review and editing, M.D., G.M. and H.A.; visualization, M.M.; supervision, M.D., G.M. and H.A.; project administration, M.S. and F.C.; funding acquisition, F.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work is co-funded by POR FESR 2014-2020—Call HUB Research and Innovation of Regione Lombardia’s project IRCRAM 4.0 (International Research Center for Robot and Additive Manufacturing 4.0—Project ID 1175193).
Acknowledgments
Special thanks to the Camozzi Group for their help and support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bikas, H.; Stavropoulos, P.; Chryssolouris, G. Additive manufacturing methods and modelling approaches: A critical review. Int. J. Adv. Manuf. Technol. 2016, 83, 389–405. [Google Scholar] [CrossRef] [Green Version]
- Ligon, S.C.; Liska, R.; Stampfl, J.; Gurr, M.; Mulhaupt, R. Polymers for 3D printing and customized additive manufacturing. Chem. Rev. 2017, 117, 10212–10290. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Herzog, D.; Seyda, V.; Wycisk, E.; Emmelmann, C. Additive manufacturing of metals. Acta Mater. 2016, 117, 371–392. [Google Scholar] [CrossRef]
- Zocca, A.; Colombo, P.; Gomes, C.M.; Günster, J. Additive manufacturing of ceramics: Issues, potentialities, and opportunities. J. Am. Ceram. Soc. 2015, 98, 1983–2001. [Google Scholar] [CrossRef]
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Sathies, T.; Senthil, P.; Anoop, M. A review on advancements in applications of fused deposition modelling process. Rapid Prototyp. J. 2020, 26, 669–687. [Google Scholar]
- Zhao, D.; Guo, W. Shape and performance controlled advanced design for additive manufacturing: A review of slicing and path planning. J. Manuf. Sci. Eng. 2020, 142, 010801. [Google Scholar] [CrossRef]
- Duty, C.; Ajinjeru, C.; Kishore, V.; Compton, B.; Hmeidat, N.; Chen, X.; Liu, P.; Hassen, A.A.; Lindahl, J.; Kunc, V. What makes a material printable? A viscoelastic model for extrusion-based 3D printing of polymers. J. Manuf. Process. 2018, 35, 526–537. [Google Scholar] [CrossRef]
- Mohamed, O.A.; Masood, S.H.; Bhowmik, J.L. Optimization of fused deposition modeling process parameters: A review of current research and future prospects. Adv. Manuf. 2015, 3, 42–53. [Google Scholar] [CrossRef]
- Mohamed, O.A.; Masood, S.H.; Bhowmik, J.L. Optimization of fused deposition modeling process parameters for dimensional accuracy using I-optimality criterion. Measurement 2016, 81, 174–196. [Google Scholar] [CrossRef]
- Kamani, K.; Donley, G.J.; Rogers, S.A. Unification of the Rheological Physics of Yield Stress Fluids. Phys. Rev. Lett. 2021, 126, 218002. [Google Scholar] [CrossRef]
- Phan, D.D.; Swain, Z.R.; Mackay, M.E. Rheological and heat transfer effects in fused filament fabrication. J. Rheol. 2018, 62, 1097–1107. [Google Scholar] [CrossRef]
- Wang, Z.; Smith, D.E. Rheology effects on predicted fiber orientation and elastic properties in large scale polymer composite additive manufacturing. J. Compos. Sci. 2018, 2, 10. [Google Scholar] [CrossRef] [Green Version]
- Coogan, T.J.; Kazmer, D.O. In-line rheological monitoring of fused deposition modeling. J. Rheol. 2019, 63, 141–155. [Google Scholar] [CrossRef]
- Faes, M.; Abbeloos, W.; Vogeler, F.; Valkenaers, H.; Coppens, K.; Goedeme, T.; Ferraris, E. Process monitoring of extrusion based 3D printing via laser scanning. arXiv 2016, arXiv:1612.02219. [Google Scholar]
- Ceruti, A.; Liverani, A.; Bombardi, T. Augmented vision and interactive monitoring in 3D printing process. Int. J. Interact. Des. Manuf. 2017, 11, 385–395. [Google Scholar] [CrossRef]
- Mikulionok, I.; Radchenko, L. Screw extrusion of thermoplastics: I. General model of the screw extrusion. Russ. J. Appl. Chem. 2012, 85, 489–504. [Google Scholar] [CrossRef]
- Tadmor, Z.; Broyer, E. Solids conveying in screw extruders Part II: Non isothermal model. Polym. Eng. Sci. 1972, 12, 378–386. [Google Scholar] [CrossRef]
- Broyer, E.; Tadmor, Z. Solids conveying in screw extruders Part I: A modified isothermal model. Polym. Eng. Sci. 1972, 12, 12–24. [Google Scholar] [CrossRef]
- Moysey, P.; Thompson, M. Investigation of solids transport in a single-screw extruder using a 3-D discrete particle simulation. Polym. Eng. Sci. 2004, 44, 2203–2215. [Google Scholar] [CrossRef]
- Moysey, P.; Thompson, M. Modelling the solids inflow and solids conveying of single-screw extruders using the discrete element method. Powder Technol. 2005, 153, 95–107. [Google Scholar] [CrossRef]
- Edmondson, I.; Fenner, R. Melting of thermoplastics in single screw extruders. Polymer 1975, 16, 49–56. [Google Scholar] [CrossRef]
- Lindt, J. A dynamic melting model for a single-screw extruder. Polym. Eng. Sci. 1976, 16, 284–291. [Google Scholar] [CrossRef]
- Cox, A.; Fenner, R. Melting performance in the single screw extrusion of thermoplastics. Polym. Eng. Sci. 1980, 20, 562–571. [Google Scholar] [CrossRef]
- Elbirli, B.; Lindt, J.; Gottgetreu, S.; Baba, S. Mathematical modeling of melting of polymers in a single-screw extruder. Polym. Eng. Sci. 1984, 24, 988–999. [Google Scholar] [CrossRef]
- Marschik, C.; Roland, W.; Miethlinger, J. A network-theory-based comparative study of melt-conveying models in single-screw extrusion: A. isothermal flow. Polymers 2018, 10, 929. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pachner, S.; Loew-Baselli, B.; Affenzeller, M.; Miethlinger, J. A Generalized 2D output model of polymer melt flow in single-screw extrusion. Int. Polym. Process. 2017, 32, 209–216. [Google Scholar] [CrossRef]
- Marschik, C.; Roland, W.; Löw-Baselli, B.; Miethlinger, J. A heuristic method for modeling three-dimensional non-Newtonian flows of polymer melts in single-screw extruders. J. Non-Newton. Fluid Mech. 2017, 248, 27–39. [Google Scholar] [CrossRef]
- Polychronopoulos, N.; Vlachopoulos, J. Computer flow simulation of moffatt eddies in single screw extrusion. Int. Polym. Process. 2018, 33, 662–668. [Google Scholar] [CrossRef]
- Wilczynski, K.; Nastaj, A.; Lewandowski, A.; Wilczynski, K.J.; Buziak, K. Fundamentals of global modeling for polymer extrusion. Polymers 2019, 11, 2106. [Google Scholar] [CrossRef] [Green Version]
- Wilczynski, K.; Lewandowski, A.; Wilczynski, K.J. Experimental study for starve-fed single screw extrusion of thermoplastics. Polym. Eng. Sci. 2012, 52, 1258–1270. [Google Scholar] [CrossRef]
- Dey, A.; Roan Eagle, I.N.; Yodo, N. A review on filament materials for fused filament fabrication. J. Manuf. Mater. Process. 2021, 5, 69. [Google Scholar] [CrossRef]
- Fuenmayor, E.; Forde, M.; Healy, A.V.; Devine, D.M.; Lyons, J.G.; McConville, C.; Major, I. Material considerations for fused-filament fabrication of solid dosage forms. Pharmaceutics 2018, 10, 44. [Google Scholar] [CrossRef] [Green Version]
- Greeff, G.P.; Schilling, M. Closed loop control of slippage during filament transport in molten material extrusion. Addit. Manuf. 2017, 14, 31–38. [Google Scholar] [CrossRef]
- Bellini, A.; Guçeri, S.; Bertoldi, M. Liquefier dynamics in fused deposition. J. Manuf. Sci. Eng. 2004, 126, 237–246. [Google Scholar] [CrossRef]
- Go, J.; Schiffres, S.N.; Stevens, A.G.; Hart, A.J. Rate limits of additive manufacturing by fused filament fabrication and guidelines for high-throughput system design. Addit. Manuf. 2017, 16, 1–11. [Google Scholar] [CrossRef]
- Serdeczny, M.P.; Comminal, R.; Mollah, M.T.; Pedersen, D.B.; Spangenberg, J. Numerical modeling of the polymer flow through the hot-end in filament-based material extrusion additive manufacturing. Addit. Manuf. 2020, 36, 101454. [Google Scholar] [CrossRef]
- Jin, Y.z.; Zhang, J.f.; Wang, Y.; Zhu, Z.c. Filament geometrical model and nozzle trajectory analysis in the fused deposition modeling process. J. Zhejiang Univ.-Sci. A 2009, 10, 370–376. [Google Scholar] [CrossRef]
- Comminal, R.; Serdeczny, M.P.; Pedersen, D.B.; Spangenberg, J. Numerical modeling of the strand deposition flow in extrusion-based additive manufacturing. Addit. Manuf. 2018, 20, 68–76. [Google Scholar] [CrossRef] [Green Version]
- Serdeczny, M.P.; Comminal, R.; Pedersen, D.B.; Spangenberg, J. Experimental validation of a numerical model for the strand shape in material extrusion additive manufacturing. Addit. Manuf. 2018, 24, 145–153. [Google Scholar] [CrossRef]
- Agassant, J.F.; Pigeonneau, F.; Sardo, L.; Vincent, M. Flow analysis of the polymer spreading during extrusion additive manufacturing. Addit. Manuf. 2019, 29, 100794. [Google Scholar] [CrossRef] [Green Version]
- Chesser, P.; Post, B.; Roschli, A.; Carnal, C.; Lind, R.; Borish, M.; Love, L. Extrusion control for high quality printing on Big Area Additive Manufacturing (BAAM) systems. Addit. Manuf. 2019, 28, 445–455. [Google Scholar] [CrossRef]
- Ahn, D.; Kweon, J.H.; Kwon, S.; Song, J.; Lee, S. Representation of surface roughness in fused deposition modeling. J. Mater. Process. Technol. 2009, 209, 5593–5600. [Google Scholar] [CrossRef]
- Rahmati, S.; Vahabli, E. Evaluation of analytical modeling for improvement of surface roughness of FDM test part using measurement results. Int. J. Adv. Manuf. Technol. 2015, 79, 823–829. [Google Scholar] [CrossRef]
- Taufik, M.; Jain, P.K. A study of build edge profile for prediction of surface roughness in fused deposition modeling. J. Manuf. Sci. Eng. 2016, 138, 061002. [Google Scholar] [CrossRef]
- Coogan, T.J.; Kazmer, D.O. Prediction of interlayer strength in material extrusion additive manufacturing. Addit. Manuf. 2020, 35, 101368. [Google Scholar] [CrossRef]
- Serdeczny, M.P.; Comminal, R.; Pedersen, D.B.; Spangenberg, J. Numerical simulations of the mesostructure formation in material extrusion additive manufacturing. Addit. Manuf. 2019, 28, 419–429. [Google Scholar] [CrossRef]
- Thrimurthulu, K.; Pandey, P.M.; Reddy, N.V. Optimum part deposition orientation in fused deposition modeling. Int. J. Mach. Tools Manuf. 2004, 44, 585–594. [Google Scholar] [CrossRef]
- Jiang, J.; Ma, Y. Path planning strategies to optimize accuracy, quality, build time and material use in additive manufacturing: A review. Micromachines 2020, 11, 633. [Google Scholar] [CrossRef]
- Han, W.; Jafari, M.A.; Danforth, S.C.; Safari, A. Tool path-based deposition planning in fused deposition processes. J. Manuf. Sci. Eng. 2002, 124, 462–472. [Google Scholar] [CrossRef]
- Comminal, R.; Serdeczny, M.P.; Pedersen, D.B.; Spangenberg, J. Motion planning and numerical simulation of material deposition at corners in extrusion additive manufacturing. Addit. Manuf. 2019, 29, 100753. [Google Scholar] [CrossRef]
- Abeykoon, C. Single screw extrusion control: A comprehensive review and directions for improvements. Control. Eng. Pract. 2016, 51, 69–80. [Google Scholar] [CrossRef] [Green Version]
- Fingerle, D. Autogenic melt temperature control system for plastic extrusion. J. Elastomers Plast. 1978, 10, 293–310. [Google Scholar] [CrossRef]
- Parnaby, J.; Kochhar, A.K.; Wood, B. Development of computer control strategies for plastic extruders. Polym. Eng. Sci. 1975, 15, 594–605. [Google Scholar] [CrossRef]
- Kochhar, A.; Parnaby, J. Dynamical modelling and control of plastics extrusion processes. Automatica 1977, 13, 177–183. [Google Scholar] [CrossRef]
- Costin, M.; Taylor, P.; Wright, J. On the dynamics and control of a plasticating extruder. Polym. Eng. Sci. 1982, 22, 1095–1106. [Google Scholar] [CrossRef]
- Previdi, F.; Savaresi, S.M.; Panarotto, A. Design of a feedback control system for real-time control of flow in a single-screw extruder. Control Eng. Pract. 2006, 14, 1111–1121. [Google Scholar] [CrossRef]
- Chiu, S.H.; Lin, C.C. Applying the constrained minimum variance control theory on in-line viscosity control in the extrusion molding process. J. Polym. Res. 1998, 5, 171–175. [Google Scholar] [CrossRef]
- Jang, J.S.R.; Sun, C.T.; Mizutani, E. Neuro-fuzzy and soft computing-a computational approach to learning and machine intelligence [Book Review]. IEEE Trans. Autom. Control 1997, 42, 1482–1484. [Google Scholar] [CrossRef]
- Zheng, Q.; Gao, Z. An energy saving, factory-validated disturbance decoupling control design for extrusion processes. In Proceedings of the 10th World Congress on Intelligent Control and Automation, Beijing, China, 6–8 July 2012; pp. 2891–2896. [Google Scholar]
- Han, W.; Jafari, M.A. Coordination control of positioning and deposition in layered manufacturing. IEEE Trans. Ind. Electron. 2007, 54, 651–659. [Google Scholar] [CrossRef]
- Ertay, D.S.; Yuen, A.; Altintas, Y. Synchronized material deposition rate control with path velocity on fused filament fabrication machines. Addit. Manuf. 2018, 19, 205–213. [Google Scholar] [CrossRef] [Green Version]
- Terzi, E.; Bonassi, F.; Farina, M.; Scattolini, R. Learning model predictive control with long short-term memory networks. Int. J. Robust Nonlinear Control 2021, 18, 8877–8896. [Google Scholar] [CrossRef]
- Bonassi, F.; Scattolini, R. Recurrent neural network-based Internal Model Control of unknown nonlinear stable systems. arXiv 2021, arXiv:2108.04585. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).