Analysis and Modeling of Mechanical Ventilation Operation Behaviors of Occupants in Cold Regions of North China
Abstract
:1. Introduction
2. Methods and Data
2.1. Monitored Households and Mechanical Ventilation System
2.2. Long-Term Field Data Collection and Preprocessing
2.3. Model
2.3.1. K-Means
2.3.2. Logistic Regression
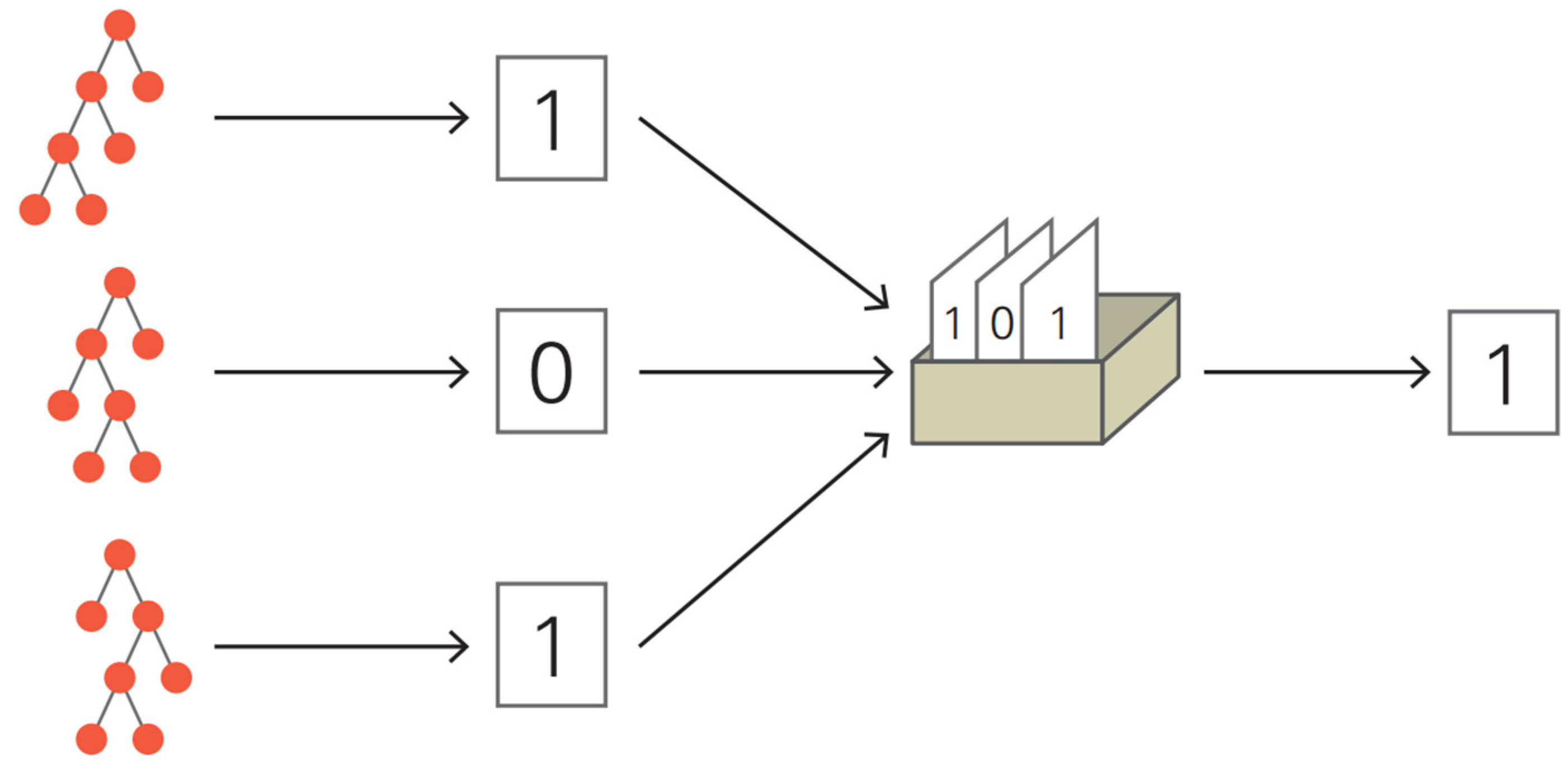
2.3.3. Random Forest
2.4. Model Evaluation Criteria
3. Result and Discussion
3.1. Statistics of Behavior in Mechanical Ventilation Operation
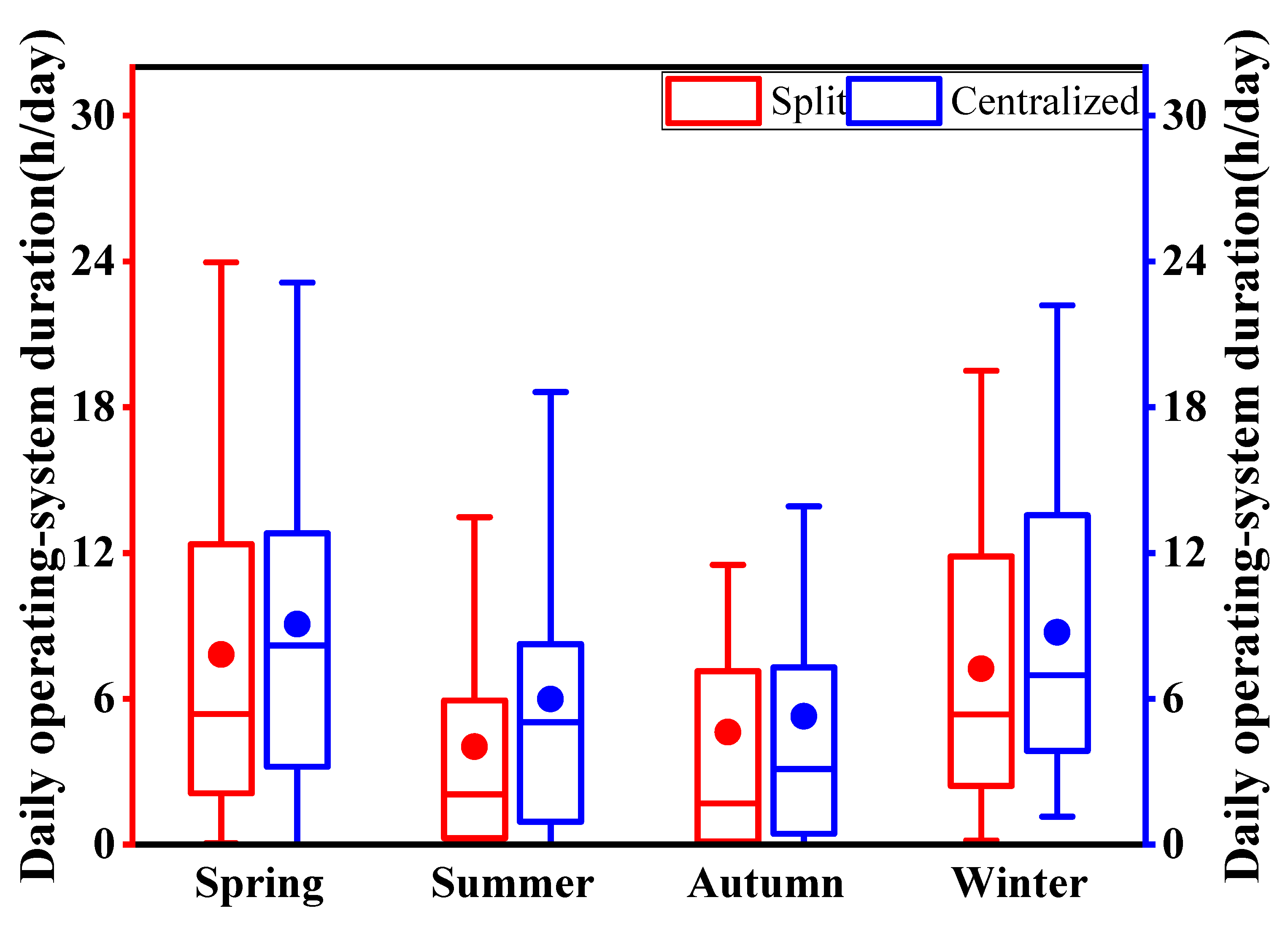
3.1.1. Operation Duration of the Mechanical Ventilation System
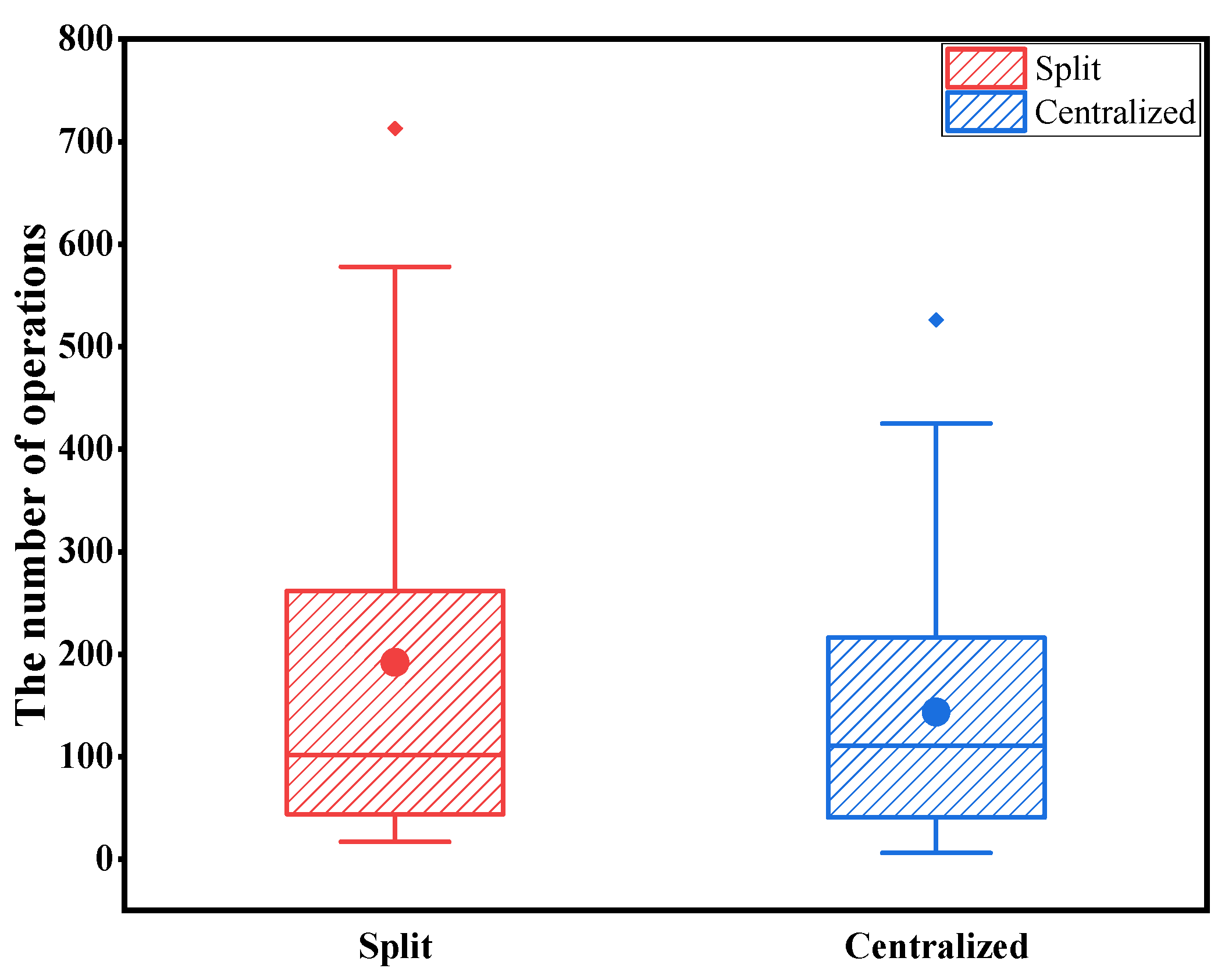
3.1.2. Operation Behavior in the Split and Centralized Mechanical Ventilation Systems
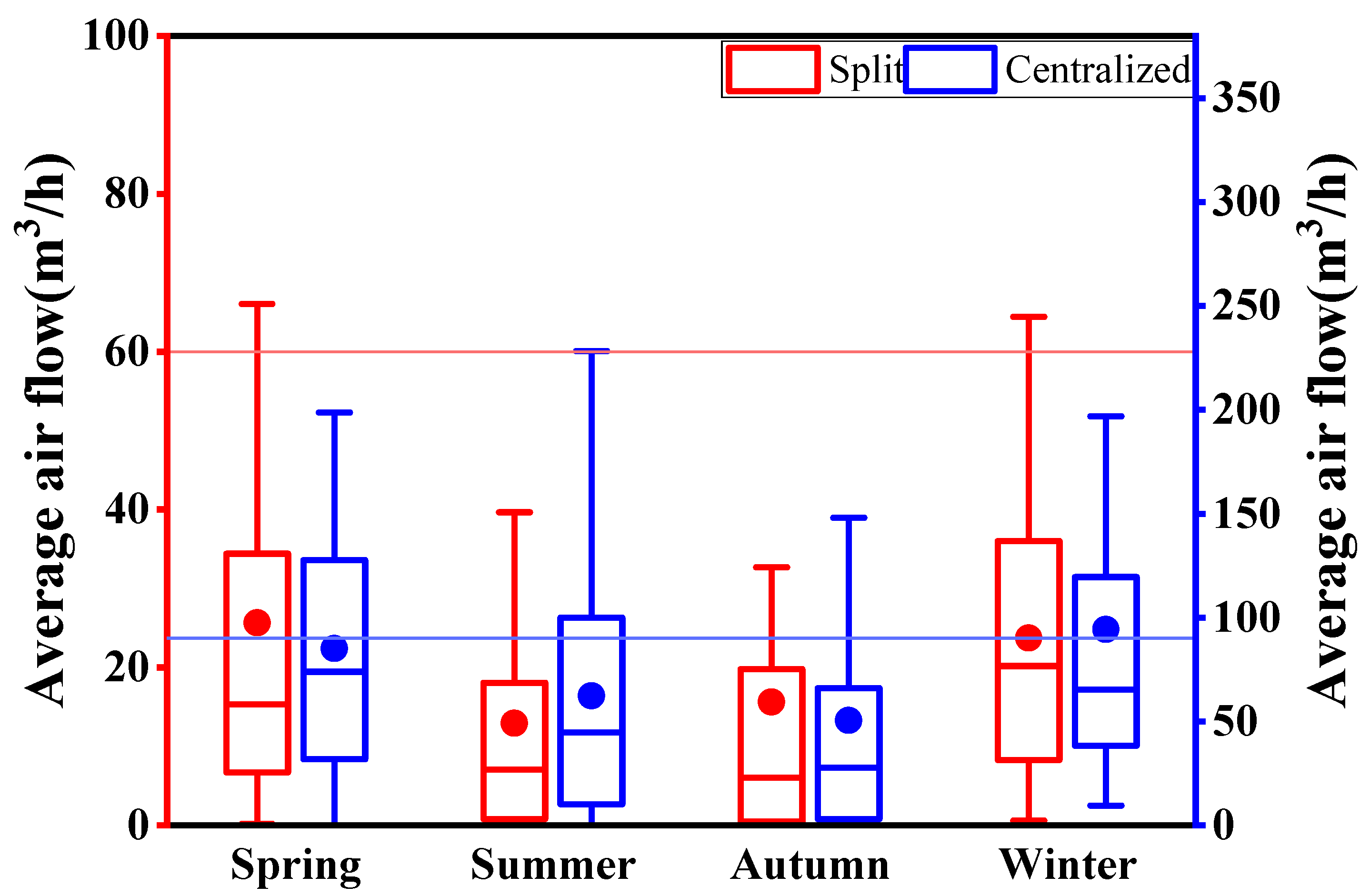
3.1.3. Operation Ventilation Flow Rate of Split and Centralized Mechanical Ventilation Systems
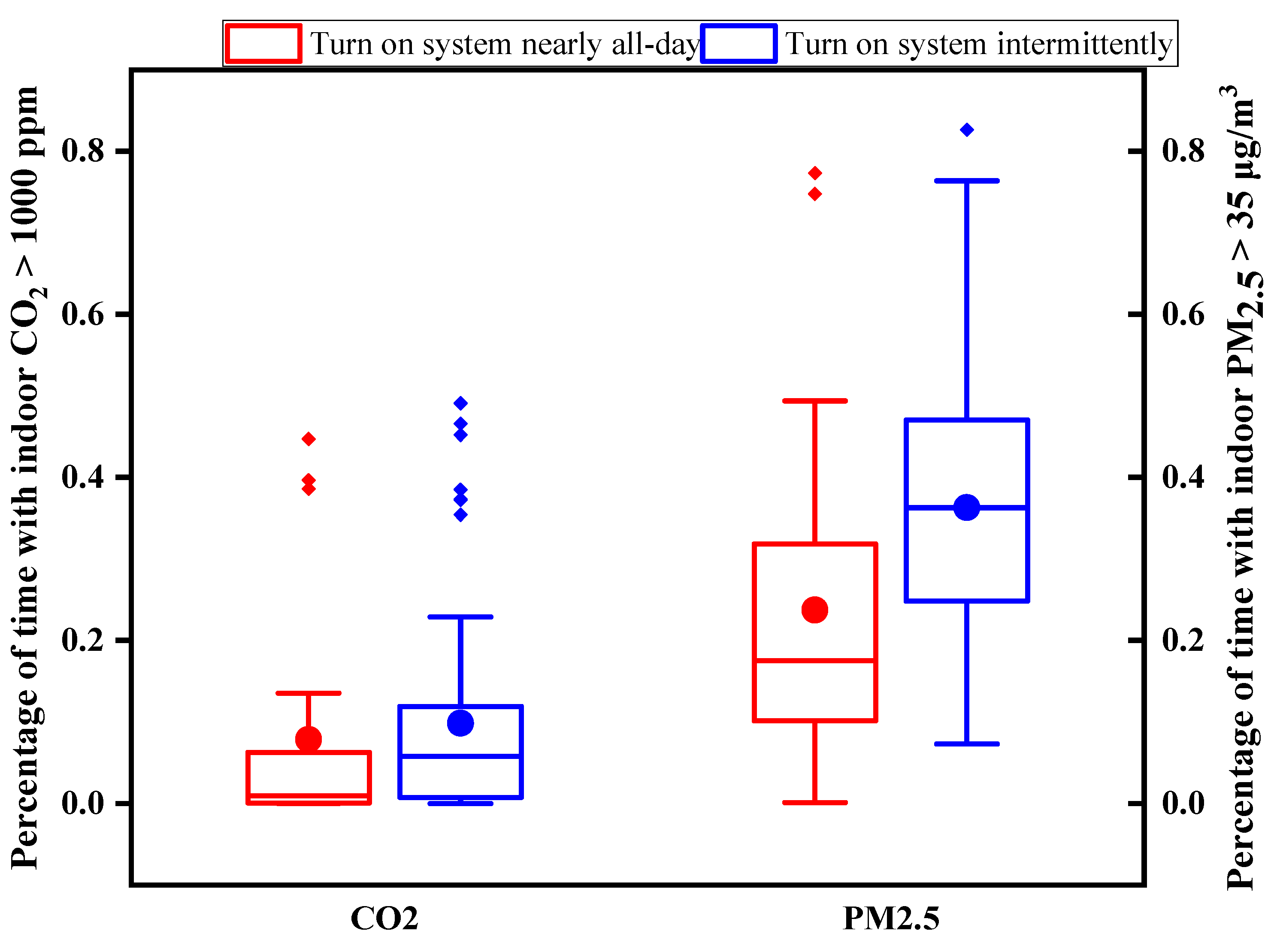
3.1.4. The Long-Term IAQ of Households with Mechanical Ventilation Systems
3.2. Modeling of Behavior in Mechanical Ventilation Operation
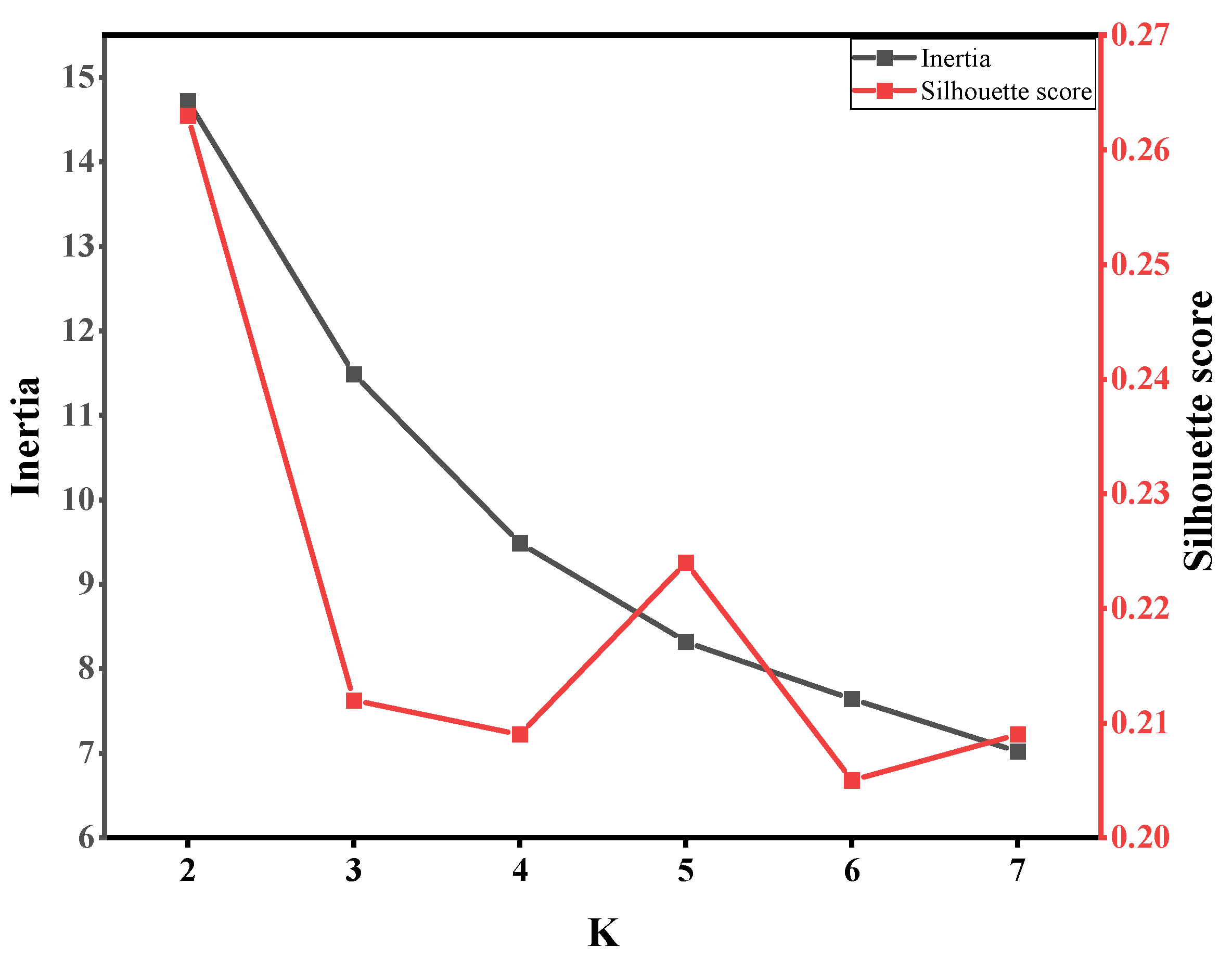
3.2.1. K-Means Clustering
- (1)
- Outdoor air PM2.5 concentration-driven (Cluster 1): In this cluster, the Pearson’s correlation coefficient between the outdoor PM2.5 concentration and the state of the mechanical ventilation system is significantly higher than the other factors (with p-value being 0.00). This indicated that households of this cluster might have been sensitive to the outdoor air quality when they chose to switch on the ventilation system.
- (2)
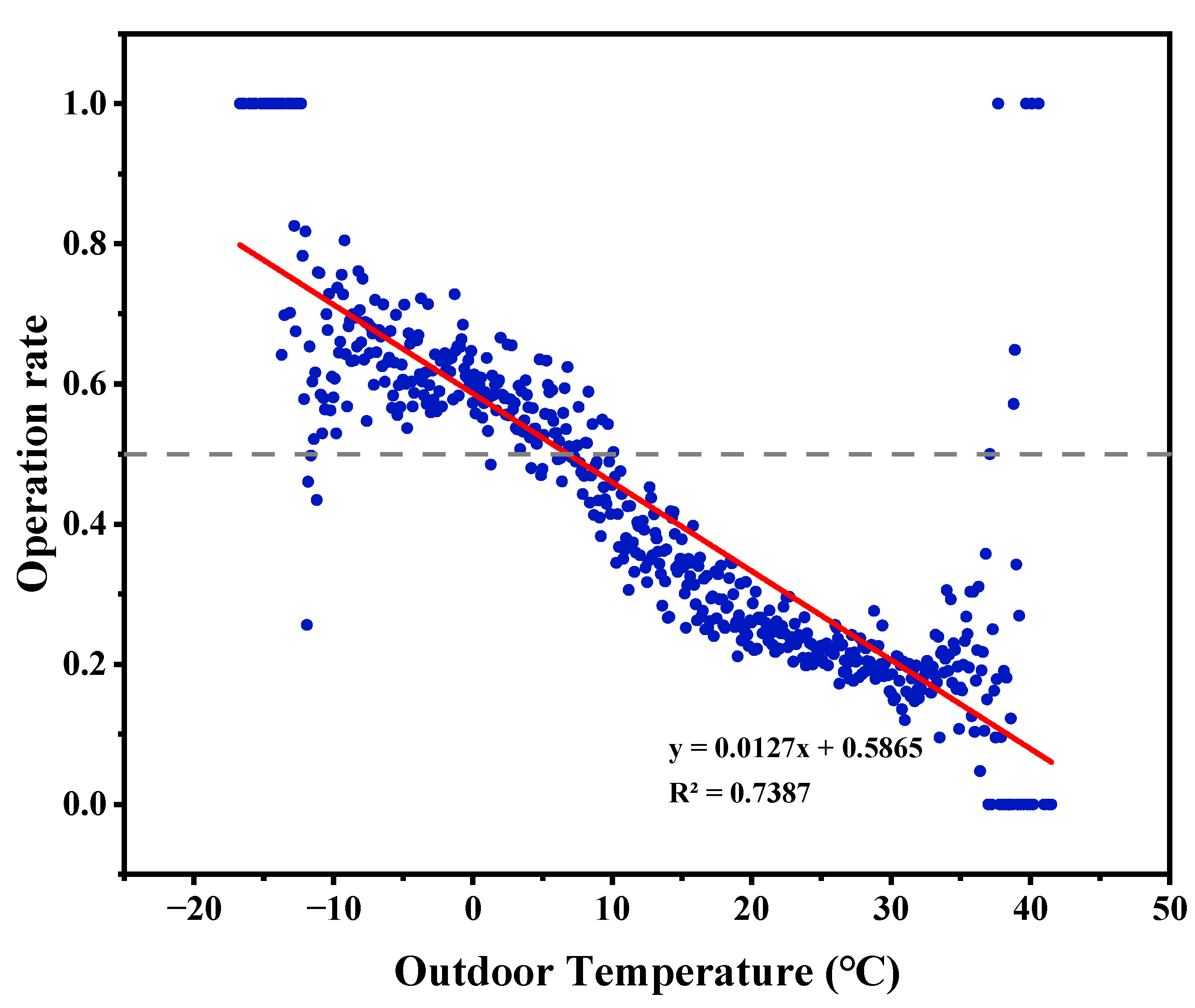
- Outdoor temperature-driven (Cluster 2): In this cluster, only the Pearson’s correlation coefficient between outdoor temperature and the state of system is significant as −0.32 (absolute value greater than 0.2). Figure 10 shows the relationship between mechanical ventilation system operation rate and outdoor temperature. The 50% operation rate point and the value of the outdoor temperature at this point are marked. Thus, households of this cluster may be susceptible to outdoor temperature and tend to close the window and switch on mechanical ventilation system when outdoor temperatures drops to 6.8 °C.
- (3)
- Temperature and time-driven (Cluster 3): In this cluster, the Pearson’s correlation coefficients of indoor and outdoor temperature (with the status of the system) are both greater than 0.3, while that related to the month is −0.51. This indicated that these households were more inclined to switch on the system in spring and summer seasons. When the temperature increased, the air conditioner would be switched on and the windows would be closed in summer, while they were more willing to keep the system operating for ventilation.
- (4)
- Mixed factors-driven (Cluster 4): In this cluster, the correlation coefficient of indoor and outdoor temperature, outdoor PM2.5 concentration and month (with the status of the system) are all significant. This suggests that the system operation behavior of this cluster could be affected by a combination of these factors.
- (5)
- Random behavior (Cluster 5): In this cluster, the correlation coefficients of all these factors (with the status of the system) are not significant. It could be that households in this cluster were not easily affected by these objective factors, but possibly by subjective factors, where behavior was more likely to be random.
3.2.2. Feature Selection
3.2.3. Predictive Modeling
4. Conclusions
- (1)
- About 24% households operated mechanical ventilation system nearly all day. The average daily operating system duration of the centralized system was 7.3 h/day, which was longer than that of the split system. The split system was operated more frequently. The IAQ of the households using the system almost all-day is better than that of intermittent operation.
- (2)
- Using K-means clustering, five patterns were discovered for the behavior of mechanical ventilation operation, including outdoor air PM2.5 concentration-driven, outdoor temperature-driven, temperature and time-driven, mixed factors-driven and random behavior pattern.
- (3)
- Based on the five clusters of households, the models established by the random forest algorithm showed a better performance than that of logistic regression, and guaranteed high accuracy even when the imbalance rate of dataset was high. Therefore, the random forest algorithm can well predict the behavior in mechanical ventilation operation in residential buildings, and it can be applied in building simulation to improve the performance in future studies.
Author Contributions
Funding
Institutional Review Board Statement
Acknowledgments
Conflicts of Interest
References
- Brasche, S.; Bischof, W. Daily time spent indoors in German homes–baseline data for the assessment of indoor exposure of German occupants. Int. J. Hyg. Environ. Health 2005, 208, 247–253. [Google Scholar] [CrossRef] [PubMed]
- Massey, D.; Masih, J.; Kulshrestha, A.; Habil, M.; Taneja, A. Indoor/outdoor relationship of fine particles less than 2.5 μm (PM2.5) in residential homes locations in central Indian region. Build. Environ. 2009, 44, 2037–2045. [Google Scholar] [CrossRef]
- Sundell, J. On the history of indoor air quality and health. Indoor Air 2004, 14, 51–58. [Google Scholar] [CrossRef] [PubMed]
- Abbey, D.E.; Ostro, B.E.; Petersen, F.; Burchette, R.J. Chronic respiratory symptoms associated with estimated long-term ambient concentrations of fine particulates less than 2.5 microns in aerodynamic diameter (PM2.5) and other air pollutants. J. Expo. Anal. Environ. Epidemiol. 1995, 5, 137–159. [Google Scholar] [PubMed]
- Hu, W.; Downward, G.S.; Reiss, B.; Xu, J.; Bassig, B.A.; Hosgood III, H.D.; Zhang, L.; Seow, W.J.; Wu, G.; Chapman, R.S. Personal and indoor PM2. 5 exposure from burning solid fuels in vented and unvented stoves in a rural region of China with a high incidence of lung cancer. Environ. Sci. Technol. 2014, 48, 8456–8464. [Google Scholar] [CrossRef] [Green Version]
- Dockery, D.W.; Pope, C.A.; Xu, X.; Spengler, J.D.; Ware, J.H.; Fay, M.E.; Ferris, B.G., Jr.; Speizer, F.E. An association between air pollution and mortality in six US cities. N. Engl. J. Med. 1993, 329, 1753–1759. [Google Scholar] [CrossRef] [Green Version]
- Brunekreef, B.; Holgate, S.T. Air pollution and health. Lancet 2002, 360, 1233–1242. [Google Scholar] [CrossRef]
- De Kok, T.M.; Driece, H.A.; Hogervorst, J.G.; Briedé, J.J. Toxicological assessment of ambient and traffic-related particulate matter: A review of recent studies. Mutat. Res. Rev. Mutat. Res. 2006, 613, 103–122. [Google Scholar] [CrossRef]
- Lai, D.; Qi, Y.; Liu, J.; Dai, X.; Zhao, L.; Wei, S. Ventilation behavior in residential buildings with mechanical ventilation systems across different climate zones in China. Build. Environ. 2018, 143, 679–690. [Google Scholar] [CrossRef] [Green Version]
- Zhao, L.; Liu, J. Operating behavior and corresponding performance of mechanical ventilation systems in Chinese residential buildings. Build. Environ. 2020, 170, 106600. [Google Scholar] [CrossRef]
- Zhao, Y.; Sun, H.; Tu, D. Effect of mechanical ventilation and natural ventilation on indoor climates in Urumqi residential buildings. Build. Environ. 2018, 144, 108–118. [Google Scholar] [CrossRef]
- Stabile, L.; Buonanno, G.; Frattolillo, A.; Dell’Isola, M. The effect of the ventilation retrofit in a school on CO2, airborne particles, and energy consumptions. Build. Environ. 2019, 156, 1–11. [Google Scholar] [CrossRef]
- Zhao, L.; Liu, J.; Ren, J. Impact of various ventilation modes on IAQ and energy consumption in Chinese dwellings: First long-term monitoring study in Tianjin, China. Build. Environ. 2018, 143, 99–106. [Google Scholar] [CrossRef]
- Liu, J.; Dai, X.; Li, X.; Jia, S.; Pei, J.; Sun, Y.; Lai, D.; Shen, X.; Sun, H.; Yin, H.; et al. Indoor air quality and occupants’ ventilation habits in China: Seasonal measurement and long-term monitoring. Build. Environ. 2018, 142, 119–129. [Google Scholar] [CrossRef]
- Liu, S.; Song, R.; Zhang, T. Residential building ventilation in situations with outdoor PM2.5 pollution. Build. Environ. 2021, 202, 108040. [Google Scholar] [CrossRef]
- Park, J.S.; Kim, H.J. A field study of occupant behavior and energy consumption in apartments with mechanical ventilation. Energy Build. 2012, 50, 19–25. [Google Scholar] [CrossRef]
- Kim, H.; Hong, T.; Kim, J. Automatic ventilation control algorithm considering the indoor environmental quality factors and occupant ventilation behavior using a logistic regression model. Build. Environ. 2019, 153, 46–59. [Google Scholar] [CrossRef]
- Balvedi, B.F.; Ghisi, E.; Lamberts, R. A review of occupant behaviour in residential buildings. Energy Build. 2018, 174, 495–505. [Google Scholar] [CrossRef]
- Zhang, T.; Su, Z.; Wang, J.; Wang, S. Ventilation, indoor particle filtration, and energy consumption of an apartment in northern China. Build. Environ. 2018, 143, 280–292. [Google Scholar] [CrossRef]
- Ben-David, T.; Waring, M.S. Impact of natural versus mechanical ventilation on simulated indoor air quality and energy consumption in offices in fourteen U.S. cities. Build. Environ. 2016, 104, 320–336. [Google Scholar] [CrossRef] [Green Version]
- Heydarian, A.; McIlvennie, C.; Arpan, L.; Yousefi, S.; Syndicus, M.; Schweiker, M.; Jazizadeh, F.; Rissetto, R.; Pisello, A.L.; Piselli, C.; et al. What drives our behaviors in buildings? A review on occupant interactions with building systems from the lens of behavioral theories. Build. Environ. 2020, 179, 106928. [Google Scholar] [CrossRef]
- Ren, X.; Zhang, C.; Zhao, Y.; Boxem, G.; Zeiler, W.; Li, T. A data mining-based method for revealing occupant behavior patterns in using mechanical ventilation systems of Dutch dwellings. Energy Build. 2019, 193, 99–110. [Google Scholar] [CrossRef]
- Liu, H.; Sun, H.; Mo, H.; Liu, J. Analysis and modeling of air conditioner usage behavior in residential buildings using monitoring data during hot and humid season. Energy Build. 2021, 250, 111297. [Google Scholar] [CrossRef]
- Cho, H.; Cabrera, D.; Sardy, S.; Kilchherr, R.; Yilmaz, S.; Patel, M.K. Evaluation of performance of energy efficient hybrid ventilation system and analysis of occupants’ behavior to control windows. Build. Environ. 2021, 188, 107434. [Google Scholar] [CrossRef]
- Markovic, R.; Grintal, E.; Wölki, D.; Frisch, J.; van Treeck, C. Window opening model using deep learning methods. Build. Environ. 2018, 145, 319–329. [Google Scholar] [CrossRef] [Green Version]
- Mo, H.; Sun, H.; Liu, J.; Wei, S. Developing window behavior models for residential buildings using XGBoost algorithm. Energy Build. 2019, 205, 109564. [Google Scholar] [CrossRef]
- Zhao, W.-L.; Deng, C.-H.; Ngo, C.-W. k-means: A revisit. Neurocomputing 2018, 291, 195–206. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef] [Green Version]
- Hosmer, D.W., Jr.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 398. [Google Scholar]
- Andersen, R.; Fabi, V.; Toftum, J.; Corgnati, S.P.; Olesen, B.W. Window opening behaviour modelled from measurements in Danish dwellings. Build. Environ. 2013, 69, 101–113. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, A.; Korres, N.E.; Ploennigs, J.; Elhadi, H.; Menzel, K. Mining building performance data for energy-efficient operation. Adv. Eng. Inform. 2011, 25, 341–354. [Google Scholar] [CrossRef]
- Hanley, J.A.; McNeil, B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, R.; Nie, F.; Li, X.; Wei, X. Feature Selection with Multi-View Data: A Survey. Inf. Fusion 2019, 50, 158–167. [Google Scholar] [CrossRef]
- Olson, R.S.; Moore, J.H. TPOT: A tree-based pipeline optimization tool for automating machine learning. In Automatic Machine Learning; PMLR: Cambridge, MA, USA, 2016; pp. 66–74. [Google Scholar]
- Stazi, F.; Naspi, F.; D’Orazio, M. Modelling window status in school classrooms. Results from a case study in Italy. Build. Environ. 2017, 111, 24–32. [Google Scholar] [CrossRef]
- Yao, M.; Zhao, B. Window opening behavior of occupants in residential buildings in Beijing. Build. Environ. 2017, 124, 441–449. [Google Scholar] [CrossRef]
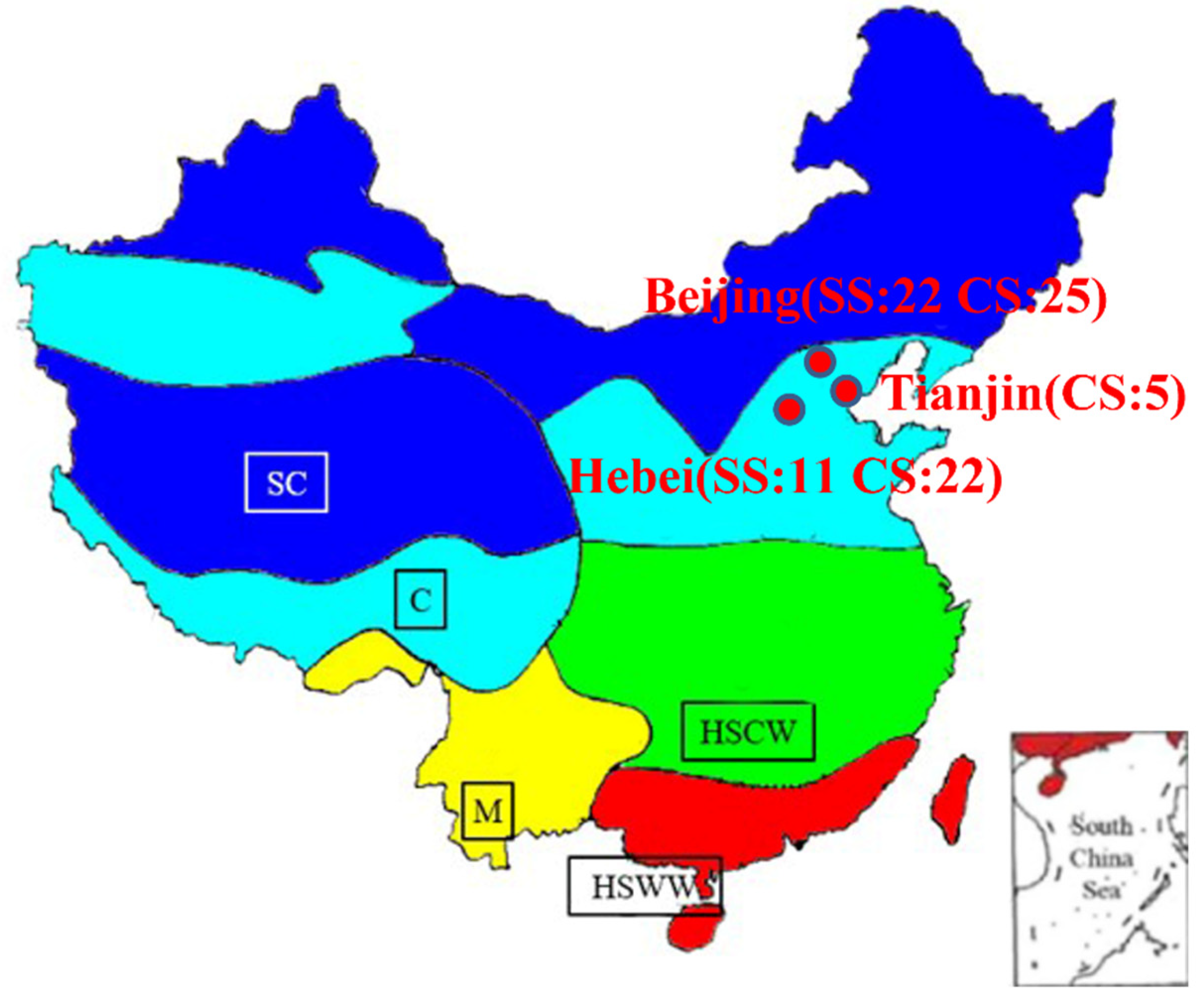
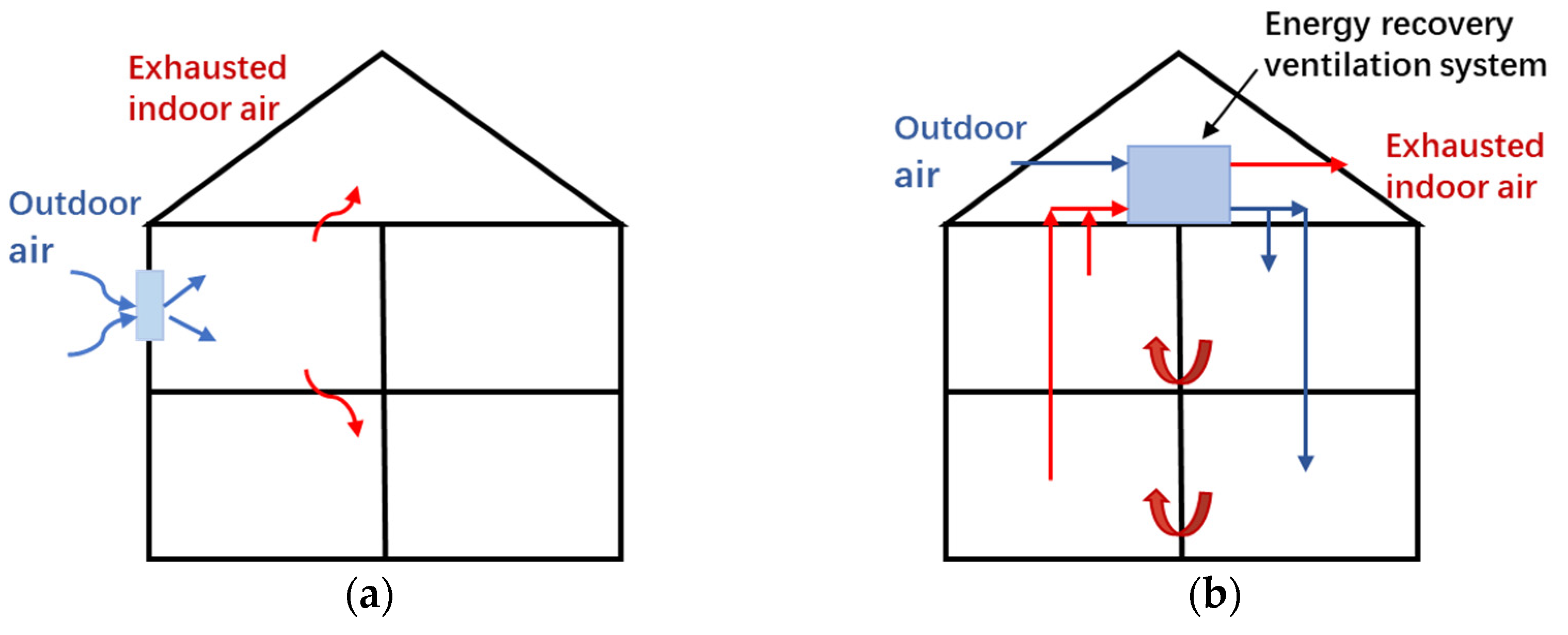
| Parameter | Split | Centralized |
|---|---|---|
| Air flow (m3/h) | 60–130 | 100–500 |
| Usage area (m2) | 30 | 120–180 |
| Rated power (W) | 22 | 165 |
| Noise (dB) | 32–49 | 29–56 |
| Product size (mm) | 840 × 300 × 185 | 1541 × 600 × 405 |
| Net weight (kg) | 13.8 | 65 |
| Actual Data | Prediction | |
|---|---|---|
| 0 | 1 | |
| 0 | TP | FN |
| 1 | FP | TN |
| CO2_In | PM2.5_In | T_In | PM2.5_Out | T_Out | RH_Out | |
|---|---|---|---|---|---|---|
| mean | 678.46 | 53.45 | 24.69 | 56.92 | 13.52 | 49.58 |
| std | 398.55 | 157.47 | 3.77 | 55.08 | 12.50 | 24.13 |
| min | 400.00 | 0.00 | 5.00 | 0.00 | −20.20 | 0.00 |
| 50% | 646.00 | 20.00 | 25.00 | 41.00 | 14.80 | 48.00 |
| max | 5000.00 | 1000.00 | 38.00 | 500.00 | 41.5 | 100.00 |
| Cluster | CO2_In | PM2.5_In | T_In | PM2.5_Out | T_Out | RH_Out | H | M | Spring | Summer | Autumn | Winter |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.1 | −0.03 | −0.13 | 0.4 | −0.06 | 0.07 | −0.01 | −0.09 | 0.18 | −0.18 | −0.06 | 0.08 |
| 2 | 0.02 | −0.13 | −0.2 | 0.14 | −0.32 | −0.07 | −0.04 | −0.05 | −0.09 | −0.23 | −0.07 | 0.34 |
| 3 | 0.12 | −0.1 | 0.31 | 0.03 | 0.35 | 0.13 | 0.03 | −0.51 | 0.24 | 0.36 | −0.33 | −0.27 |
| 4 | 0.05 | −0.12 | −0.28 | 0.26 | −0.36 | −0.12 | −0.03 | −0.37 | 0.23 | −0.4 | −0.19 | 0.34 |
| 5 | 0.08 | −0.06 | −0.02 | 0.04 | 0.07 | −0.01 | 0.04 | 0.16 | −0.01 | −0.01 | 0.1 | −0.04 |
| Cluster | Selected Features |
|---|---|
| 1 | PM2.5_Out, T_In, T_Out, RH_Out, H, M, spring, summer, autumn, winter |
| 2 | PM2.5_Out, T_Out, M, summer, autumn, winter |
| 3 | PM2.5_In, PM2.5_Out, T_Out, RH_Out, spring, summer, autumn, winter |
| 4 | PM2.5_ Out, T_In, T_Out, RH_Out, H, M, summer, autumn, winter |
| 5 | PM2.5_In, PM2.5_Out, spring, summer |
| Cluster 1 | Cluster 2 | Cluster 3 | Cluster 4 | Cluster 5 | Non-Clustered | |
|---|---|---|---|---|---|---|
| Turned off ‘0’ | 313,539 | 650,844 | 727,724 | 189,814 | 1,464,552 | 3,346,473 |
| Turned on ‘1’ | 198,744 | 400,476 | 466,301 | 164,897 | 259,305 | 1,489,723 |
| Imbalance rate | 22.4% | 23.8% | 21.9% | 7.0% | 69.9% | 38.4% |
| Baseline accuracy | 0.612 | 0.619 | 0.609 | 0.535 | 0.85 | 0.692 |
| Cluster | CO2_In | PM2.5_In | T_In | PM2.5_Out | T_Out | RH_Out | H | M | Spring | Summer | Autumn | Winter |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | - | - | 0.0081 | 0.1323 | −0.0489 | 0.0046 | −0.0046 | −0.2086 | −0.9559 | −3.0263 | −2.6139 | −1.6464 |
| 2 | - | - | - | −0.0563 | 0.0409 | - | - | 0.132 | - | −0.3494 | 0.5361 | 0.4178 |
| 3 | - | −0.0091 | - | 0.0694 | −0.0457 | 0.0071 | - | - | −1.9499 | −2.5650 | −2.5533 | −1.4521 |
| 4 | - | - | 0.0015 | 0.2067 | 0.0135 | 0.0093 | 0.0162 | −0.2557 | - | −4.2519 | −5.1079 | −4.4742 |
| 5 | - | −0.0234 | - | 0.0554 | - | - | - | - | −3.4051 | −5.7716 | - | - |
| Cluster 1 | Cluster 2 | Cluster 3 | Cluster 4 | Cluster 5 | ||
|---|---|---|---|---|---|---|
| LR | ACC | 0.784 | 0.665 | 0.717 | 0.785 | 0.874 |
| AUC | 0.773 | 0.649 | 0.703 | 0.792 | 0.806 | |
| RF | ACC | 0.999 | 0.994 | 0.994 | 0.999 | 0.998 |
| AUC | 0.999 | 0.994 | 0.994 | 0.999 | 0.998 | |
| Cluster 1 | Cluster 2 | Cluster 3 | Cluster 4 | Cluster 5 | Non-Classified | |
|---|---|---|---|---|---|---|
| ACC | 0.785 | 0.664 | 0.718 | 0.784 | 0.875 | 0.698 |
| AUC | 0.774 | 0.650 | 0.700 | 0.790 | 0.807 | 0.647 |
| Cluster 1 | Cluster 2 | Cluster 3 | Cluster 4 | Cluster 5 | |
|---|---|---|---|---|---|
| ACC | 0.999 | 0.985 | 0.989 | 0.992 | 0.994 |
| AUC | 0.999 | 0.985 | 0.989 | 0.992 | 0.990 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Sun, H. Analysis and Modeling of Mechanical Ventilation Operation Behaviors of Occupants in Cold Regions of North China. Appl. Sci. 2022, 12, 5143. https://doi.org/10.3390/app12105143
Zhang C, Sun H. Analysis and Modeling of Mechanical Ventilation Operation Behaviors of Occupants in Cold Regions of North China. Applied Sciences. 2022; 12(10):5143. https://doi.org/10.3390/app12105143
Chicago/Turabian StyleZhang, Chenchen, and Hejiang Sun. 2022. "Analysis and Modeling of Mechanical Ventilation Operation Behaviors of Occupants in Cold Regions of North China" Applied Sciences 12, no. 10: 5143. https://doi.org/10.3390/app12105143
APA StyleZhang, C., & Sun, H. (2022). Analysis and Modeling of Mechanical Ventilation Operation Behaviors of Occupants in Cold Regions of North China. Applied Sciences, 12(10), 5143. https://doi.org/10.3390/app12105143





