New Product Short-Term Demands Forecasting with Boxplot-Based Fractional Grey Prediction Model
Abstract
:1. Introduction
2. Literature Review
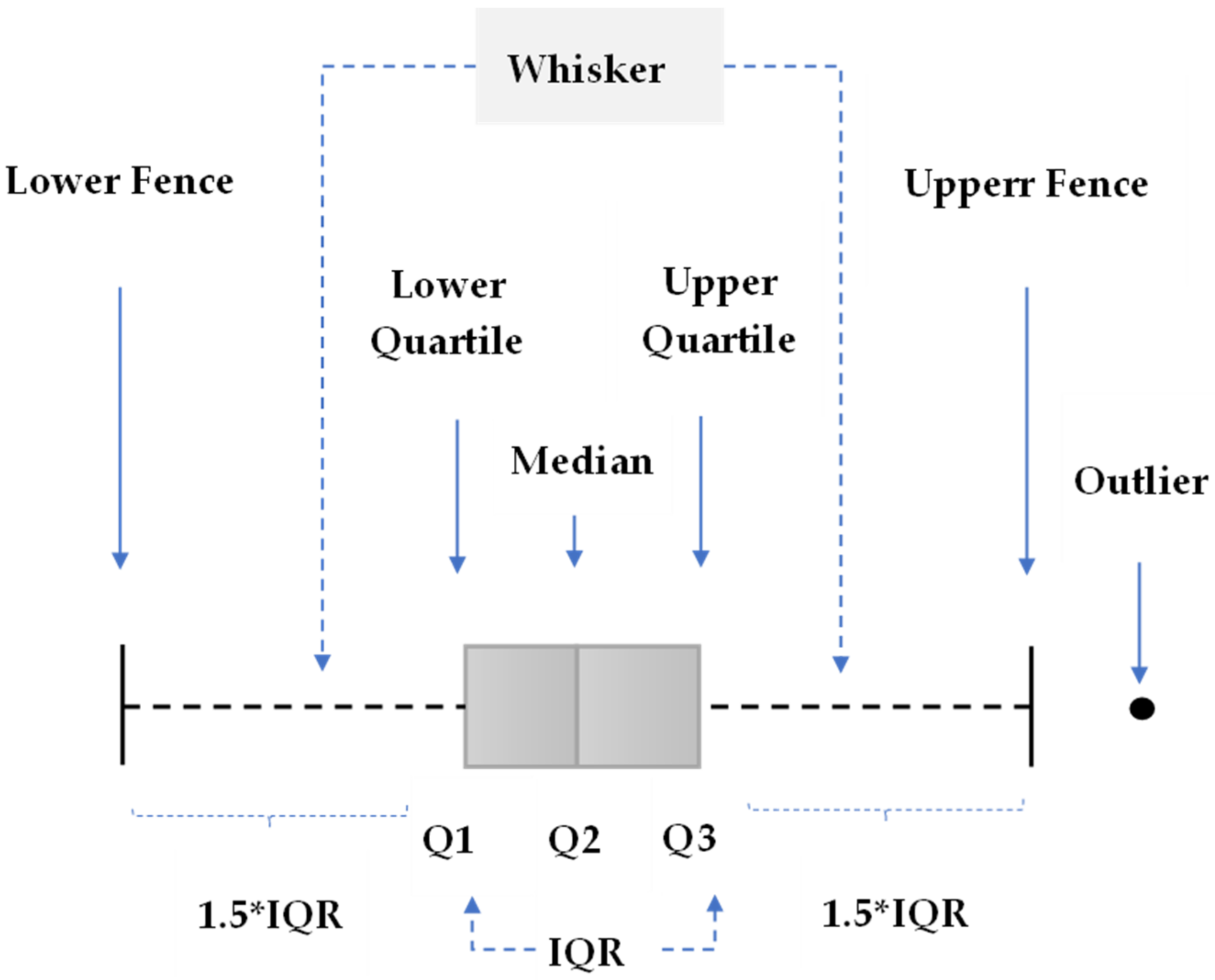
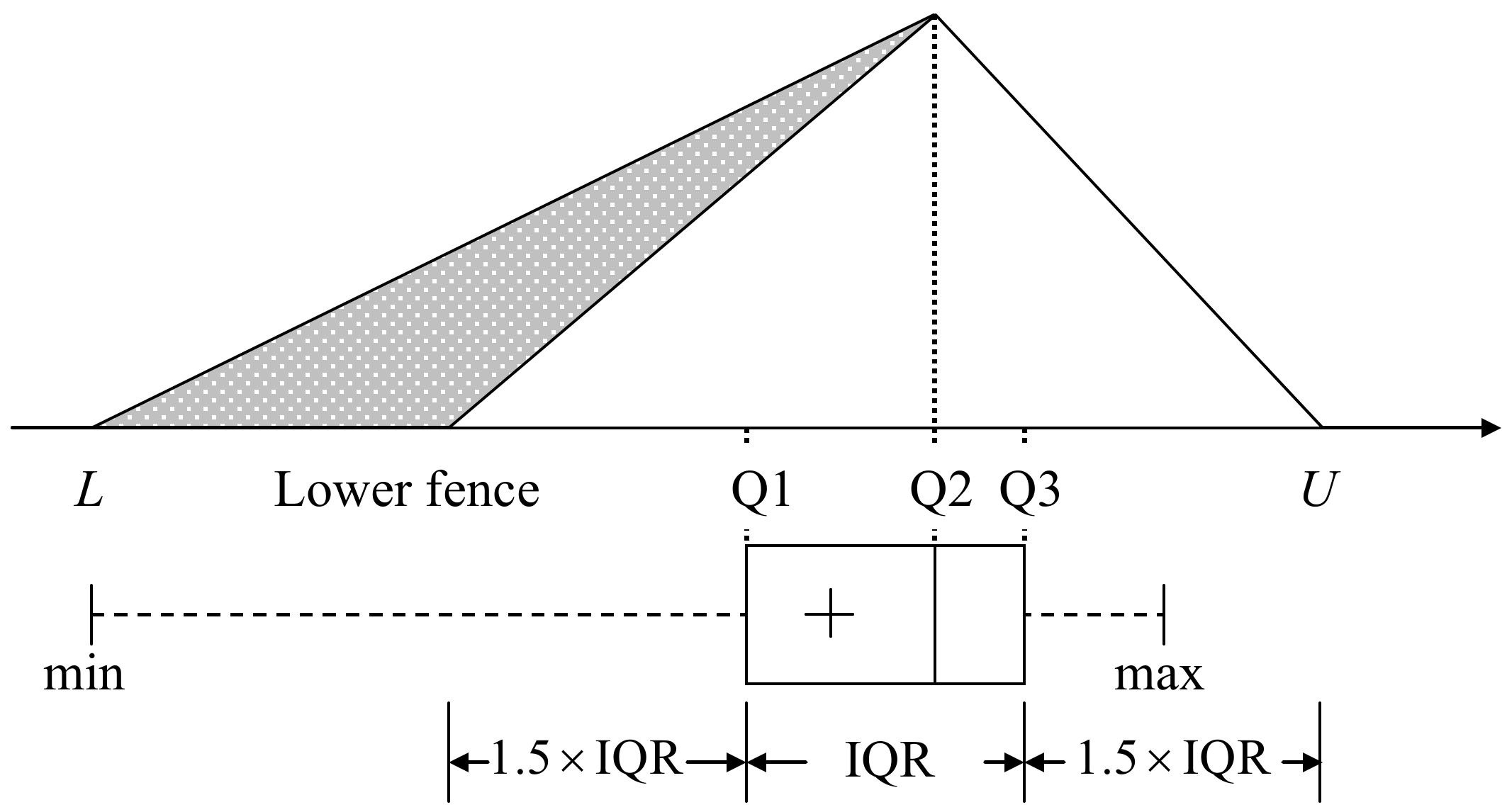
2.1. Box-And-Whisker Plot
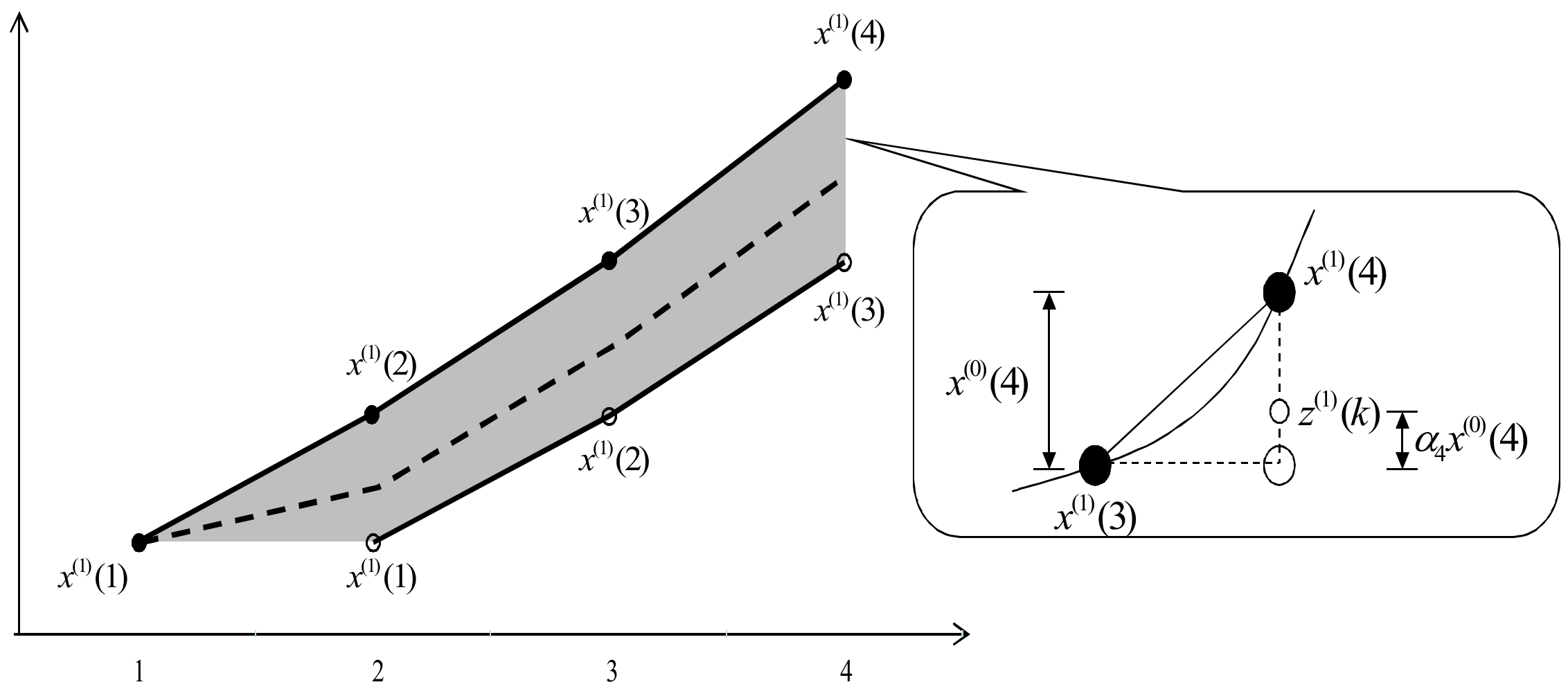
2.2. Grey System Model
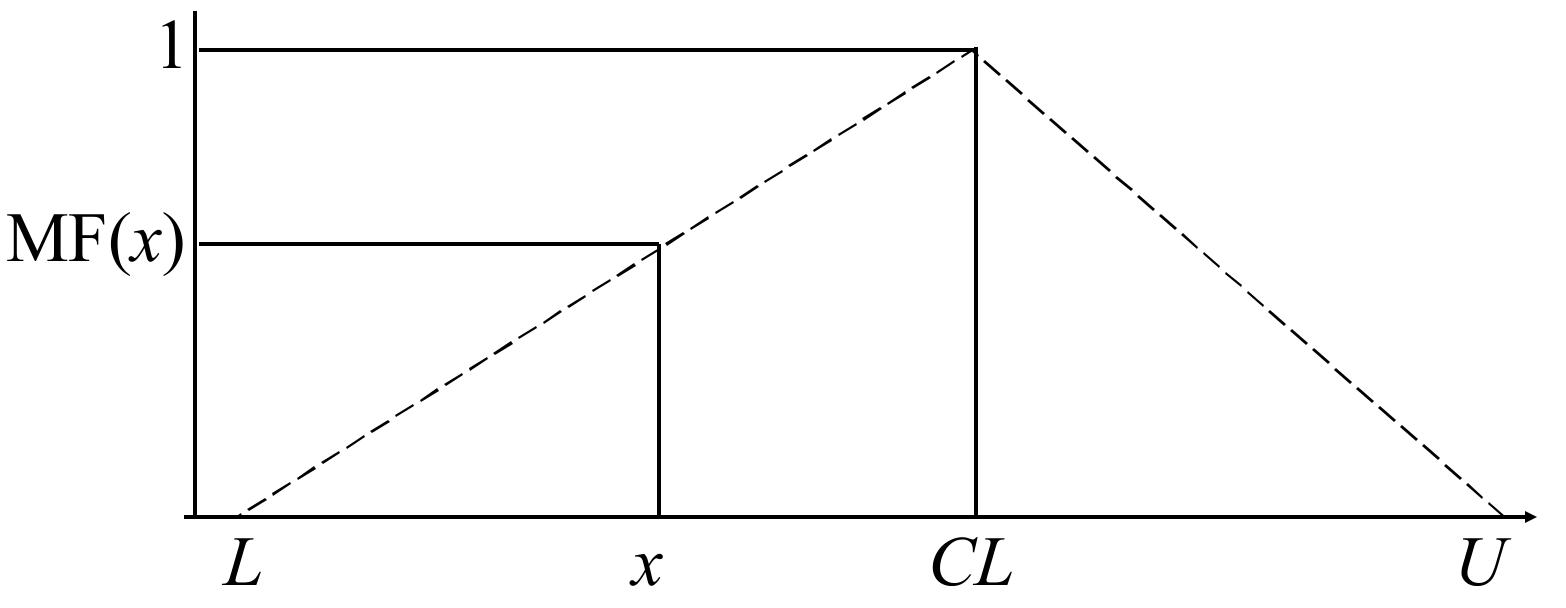
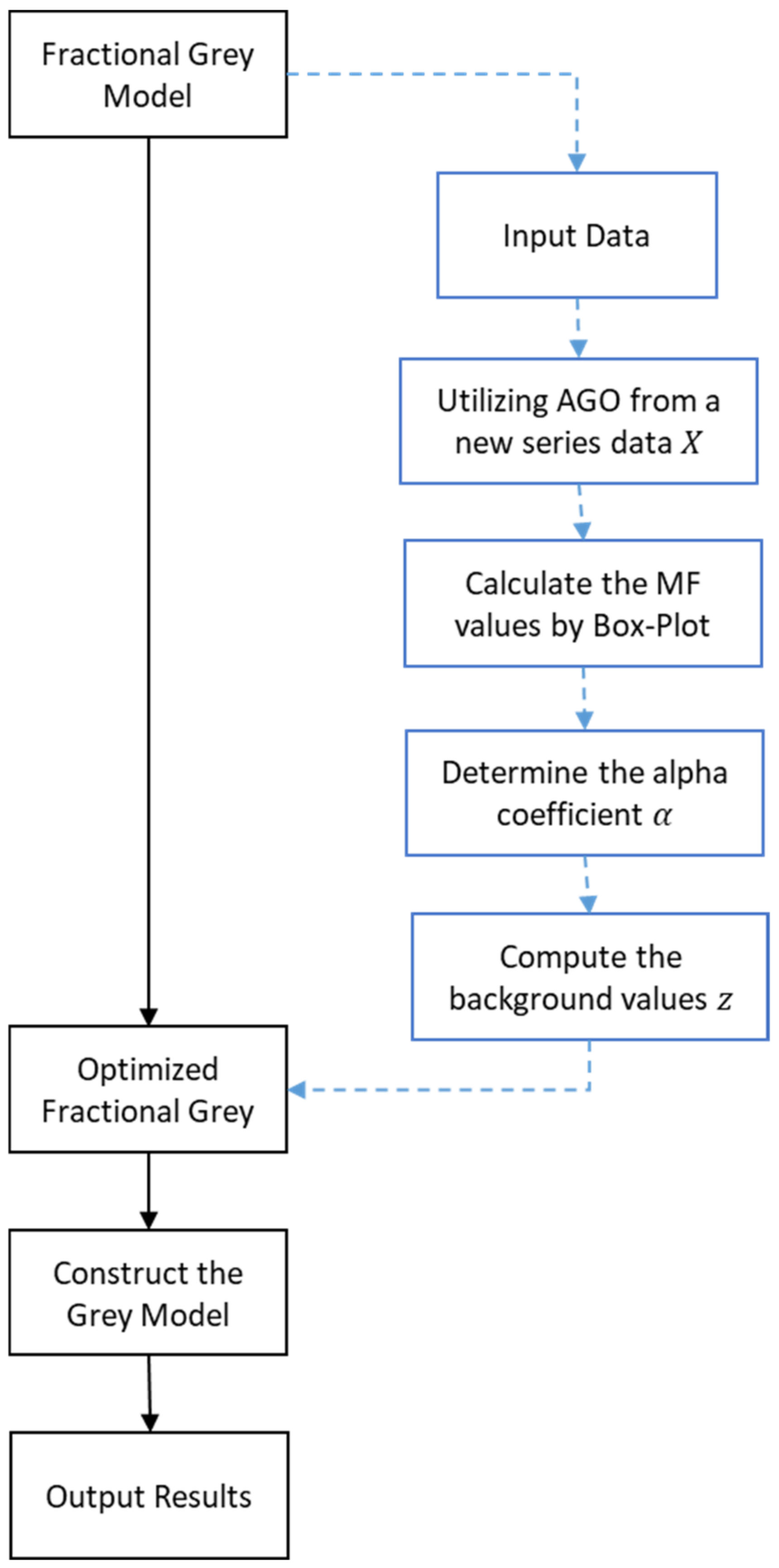
3. The Proposed Method
4. Experimental Results and Discussion
4.1. Data from This Case Study
4.2. MOEA Data
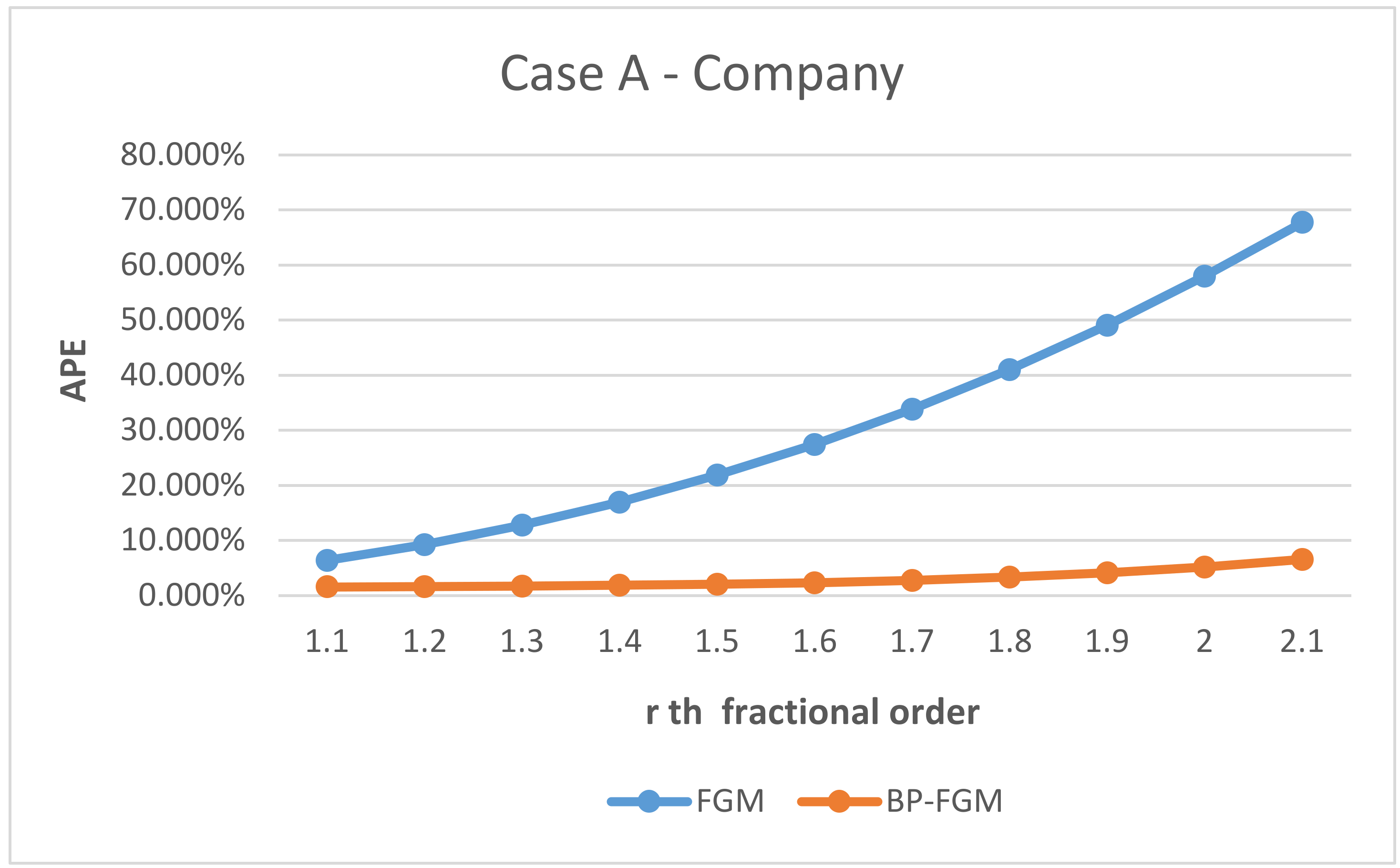
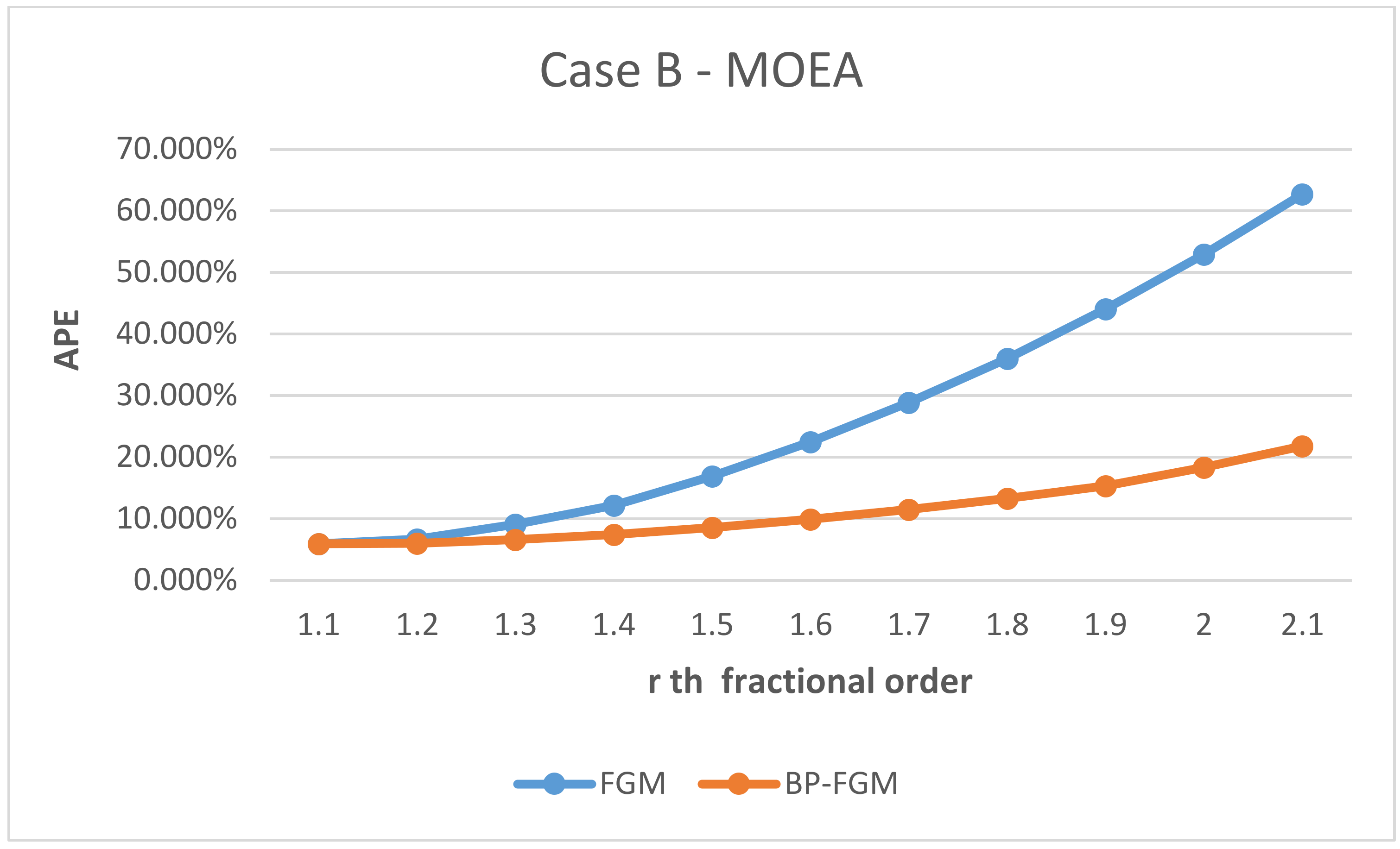
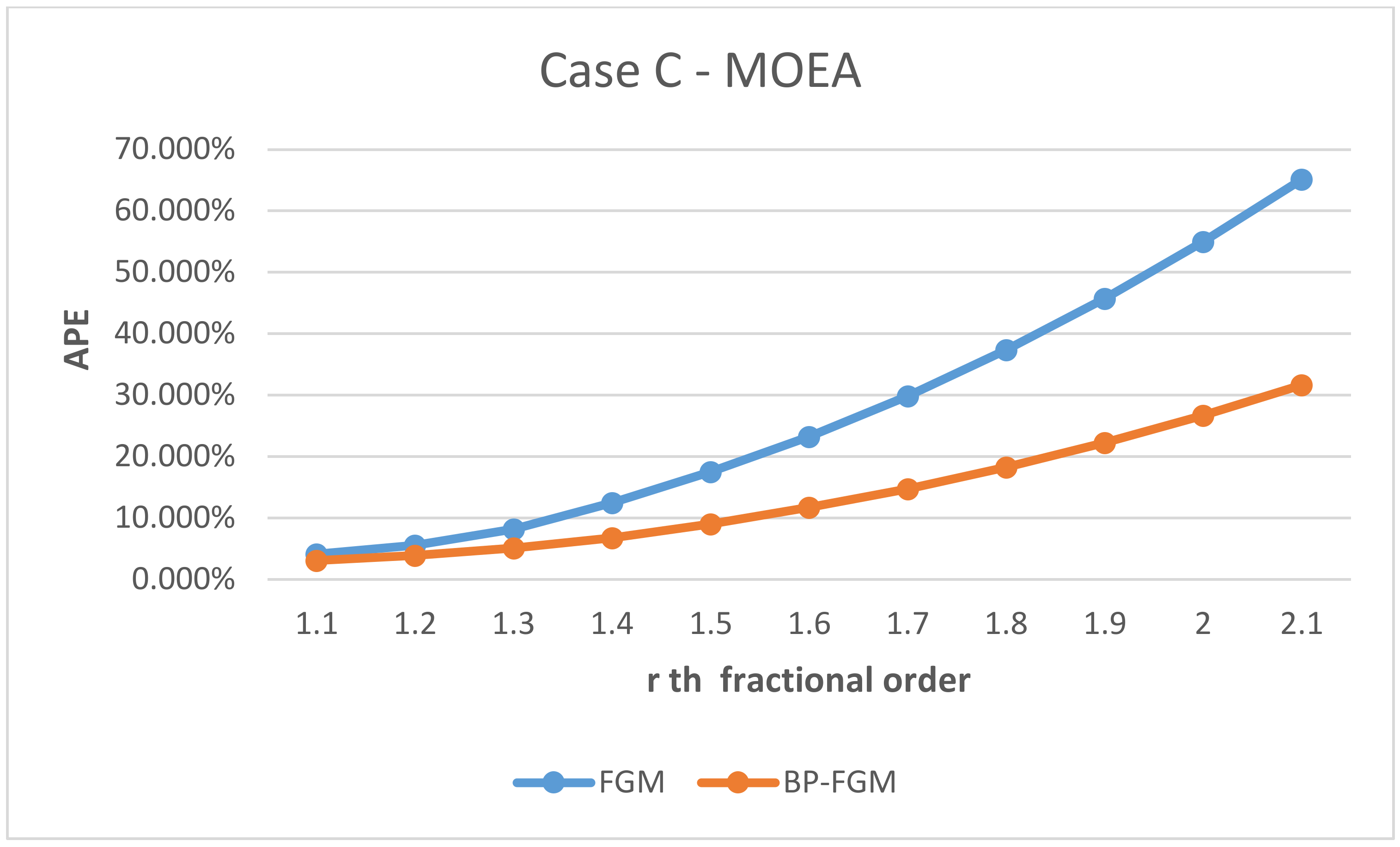
4.3. Analysis of the Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mas-Machuca, M.; Sainz, M.; Martinez-Costa, C. A review of forecasting models for new products. Intang. Cap. 2014, 10, 1–25. [Google Scholar] [CrossRef] [Green Version]
- Li, D.-C.; Chen, W.-C.; Chang, C.-J.; Chen, C.-C.; Wen, I.-H. Practical information diffusion techniques to accelerate new product pilot runs. Int. J. Prod. Res. 2015, 53, 5310–5319. [Google Scholar] [CrossRef]
- Chien, C.-F.; Chen, Y.-J.; Peng, J.-T. Manufacturing intelligence for semiconductor demand forecast based on technology diffusion and product life cycle. Int. J. Prod. Econ. 2010, 128, 496–509. [Google Scholar] [CrossRef]
- Deng, J.L. Control problems of grey systems. SCL Syst. Control Lett. 1982, 1, 288–294. [Google Scholar]
- Mao, S.; Gao, M.; Xiao, X.; Zhu, M. A novel fractional grey system model and its application. Appl. Math. Model. 2016, 40, 5063–5076. [Google Scholar] [CrossRef]
- Deng, J.L. Introduction to Grey system theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
- Wu, L.; Liu, S.; Fang, Z.; Xu, H. Properties of the GM(1,1) with fractional order accumulation. Appl. Math. Comput. 2015, 252, 287–293. [Google Scholar] [CrossRef]
- Wu, L.; Liu, S.; Yao, L.; Yan, S.; Liu, D. Grey system model with the fractional order accumulation. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 1775–1785. [Google Scholar] [CrossRef]
- Xie, W.; Wu, W.-Z.; Liu, C.; Goh, M. Generalized fractional grey system models: The memory effects perspective. ISA Trans. 2021. [Google Scholar] [CrossRef] [PubMed]
- Yuxiao, K.; Shuhua, M.; Yonghong, Z. Variable order fractional grey model and its application. Appl. Math. Model. 2021, 97, 619–635. [Google Scholar] [CrossRef]
- Hu, Y.-C.; Jiang, P.; Tsai, J.-F.; Yu, C.-Y. An Optimized Fractional Grey Prediction Model for Carbon Dioxide Emissions Forecasting. Int. J. Environ. Res. Public Health 2021, 18, 587. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Tao, Z.; Liu, J.; Cheng, J.; Chen, H. Exploiting fractional accumulation and background value optimization in multivariate interval grey prediction model and its application. Eng. Appl. Artif. Intell. 2021, 104, 104360. [Google Scholar] [CrossRef]
- Zhao, L.; Zhou, X. Forecasting Electricity Demand Using a New Grey Prediction Model with Smoothness Operator. Symmetry 2018, 10, 693. [Google Scholar] [CrossRef] [Green Version]
- Li, D.-C.; Chang, C.-J.; Chen, C.-C.; Chen, W.-C. Forecasting short-term electricity consumption using the adaptive grey-based approach—An Asian case. Omega 2012, 40, 767–773. [Google Scholar] [CrossRef]
- Tukey, J.W. Exploratory Data Analysis; Reading, Mass.; Addison-Wesley: Menlo Park, CA, USA; London, UK; Amsterdam, The Netherlands, 1977. [Google Scholar]
- Salkind, N.J. Encyclopedia of Research Design; SAGE: Newbury Park, CA, USA, 2010. [Google Scholar] [CrossRef]
- Shah, I.; Bibi, H.; Ali, S.; Wang, L.; Yue, Z. Forecasting One-Day-Ahead Electricity Prices for Italian Electricity Market Using Parametric and Nonparametric Approaches. IEEE Access 2020, 8, 123104–123113. [Google Scholar] [CrossRef]
- Shah, I.; Akbar, S.; Saba, T.; Ali, S.; Rehman, A. Short-Term Forecasting for the Electricity Spot Prices with Extreme Values Treatment. IEEE Access 2021, 9, 105451–105462. [Google Scholar] [CrossRef]

| Month of 2021 | Company A |
|---|---|
| August | 39 |
| September | 37 |
| October | 42 |
| November | 40 |
| December | 41 |
| Month of 2021 | Company B | Company C |
|---|---|---|
| January | 1072 | 1051 |
| February | 1011 | 1006 |
| March | 1262 | 1190 |
| April | 1051 | 1067 |
| May | 1121 | 1085 |
| June | 1151 | 1103 |
| July | 1111 | 1111 |
| August | 1162 | 1143 |
| September | 1212 | 1143 |
| October | 1191 | 1124 |
| November | 1234 | 1120 |
| Dec | 1279 | 1175 |
| Case/MAPE (%) | FGM (1,1) | BP-FGM (1,1) |
|---|---|---|
| Company A | 31.303% | 17.152% |
| Company B | 27.062% | 19.195% |
| Company C | 27.641% | 20.775% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.-C.; Huang, W.-K.; Lin, Y.-S. New Product Short-Term Demands Forecasting with Boxplot-Based Fractional Grey Prediction Model. Appl. Sci. 2022, 12, 5131. https://doi.org/10.3390/app12105131
Li D-C, Huang W-K, Lin Y-S. New Product Short-Term Demands Forecasting with Boxplot-Based Fractional Grey Prediction Model. Applied Sciences. 2022; 12(10):5131. https://doi.org/10.3390/app12105131
Chicago/Turabian StyleLi, Der-Chiang, Wen-Kuei Huang, and Yao-San Lin. 2022. "New Product Short-Term Demands Forecasting with Boxplot-Based Fractional Grey Prediction Model" Applied Sciences 12, no. 10: 5131. https://doi.org/10.3390/app12105131
APA StyleLi, D.-C., Huang, W.-K., & Lin, Y.-S. (2022). New Product Short-Term Demands Forecasting with Boxplot-Based Fractional Grey Prediction Model. Applied Sciences, 12(10), 5131. https://doi.org/10.3390/app12105131






