One-Shot Distributed Generalized Eigenvalue Problem (DGEP): Concept, Algorithm and Experiments ^†

Abstract

This paper focuses on the design of a distributed algorithm for generalized eigenvalue problems (GEPs) in one-shot communication. Since existing distributed methods for eigenvalue decomposition cannot be applied to GEP, a general one-shot distributed GEP framework is proposed. The theoretical analysis of the approximation error reveals its relation to the divergence of the data covariance, the eigenvalues of the empirical data covariance, and the number of local servers. If the symmetric data covariance has repeated eigenvalues in GEP, e.g., in canonical component analysis, we further modify the method for better convergence and prove the necessity experimentally. Numerical experiments validate the effectiveness of the proposed algorithms both on synthetic and real-world datasets.

1. Introduction

Nowadays, as the data dimension and quantity increases, distributed local servers are essential in storing large-scale data. The distributed framework enables many equivalent local servers to seek the solution to the same class of problems, where specific servers may provide insight for other servers. This process is usually achieved by iteratively exchanging information between local servers, namely, in multi-round communication, to partially improve the way they accomplish their tasks. As increasing scenarios, such as financial [1], medical [2], and biomedical [3] tasks, come into view, where they usually hold the sensitive and limited scale of datasets in a distributed manner, the distributed systems shall offer a relatively safe and efficient way to obtain a satisfying result.

There have been many works on distributed systems in the past decades, especially in classification [4,5] and regression [6,7,8,9]. However, the discussion about distributed generalized eigenvalue problem (GEP) is rare. GEP is known as another important type of learning task that involves (generalized) eigenvalue decomposition (GED), including Singular Value Decomposition (SVD) [10], Principal Component Analysis (PCA) [11], Canonical Correlation Analysis (CCA) [12], etc. In optimization, such problems can be formulated in the following way:

$$\underset{w\in {\mathbf{R}}^d}{max}{w}^{*}Aw\mathrm{s}.\mathrm{t}.w^{*}Bw=1,$$

(1)

where $A\in {\mathbf{R}}^{d\times d}$ is a symmetric matrix, $B\in {\mathbf{R}}^{d\times d}$ is a positive definite matrix, and $w^{*}$ denotes the conjugate transpose matrix of w. The optimization problem has an equivalent solution to ${\lambda }_{max}\left(B^{-\frac{1}{2}}A{B}^{-\frac{1}{2}}\right)$ [13], which pursues the maximum eigenvalue $\lambda$ of the symmetric data covariance $B^{-\frac{1}{2}}A{B}^{-\frac{1}{2}}$ with an invertible matrix B. In short, (1) finds the generalized eigenvector w corresponding to the largest eigenvalue of the data covariance. Then, we can build the relationship between GEP and GED. The Lagrangian for (1) is given by:

$$L(w;\lambda )=w^{*}Aw-\lambda (w^{*}Bw-1),$$

where $\lambda \in \mathbf{R}$ is the Lagrange multiplier. By equating the derivation of Lagrangian to zero, we obtain the generalized eigenvalue decomposition as below:

$$Aw=\lambda Bw,$$

(2)

where $w\in {\mathbf{R}}^d$ denotes the generalized eigenvector of GEP with respect to the generalized eigenvalue $\lambda$.

Since GEP plays a vital role in a large family of high-dimensional statistical models, distributed algorithms for GEP are desired. However, only some variant cases are discussed in the distributed manner. There are two common variants of GEP whose distributed algorithms are well studied. On the one hand, when the constraint of (1) is linear, distributed linearly constrained minimum variance (LCMV) is widely used in signal processing [14,15] with the same objective function in beamforming. However, its algorithms cannot deal with quadratic constraints in GEP obviously. On the other hand, when B in (1) is an identity matrix, GEP turns to the ordinary eigenvalue problem (EP). Moreover, distributed algorithms for EP are numerous due to its good characteristics. Further in detail, when A is symmetric, it is PCA, and it is SVD otherwise. For one-shot communication with efficiency, distributed PCA algorithms are given in [16,17,18]. In addition, distributed SVD [19] conducts distributed averaging over measurement vectors in one-shot communication. For iterative communication, a distributed sparse PCA [20] is proposed based on the power method, which is numerically efficient for the large-scale data. In addition, distributed SVD methods in [21,22] utilize the distributed power method in both the centralized and decentralized way. However, the distributed algorithms mentioned above cannot be used in distributed GEP because, in distributed systems, the sum of the local covariance matrices of GEP does not equal to the global centered covariance matrix while it equals in EP. We call this phenomenon the divergence of data covariance, which has been neglected in the previous work. Thus, although these distributed algorithms above perform well in theory and practice, they cannot be directly applied to distributed GEP. Due to the distributed data storage method, some techniques, e.g., partial differential equations, used in non-linear systems [23,24] cannot be used in distributed GEP. In brief, there is not a general distributed algorithm for GEP formulated as in  (1).

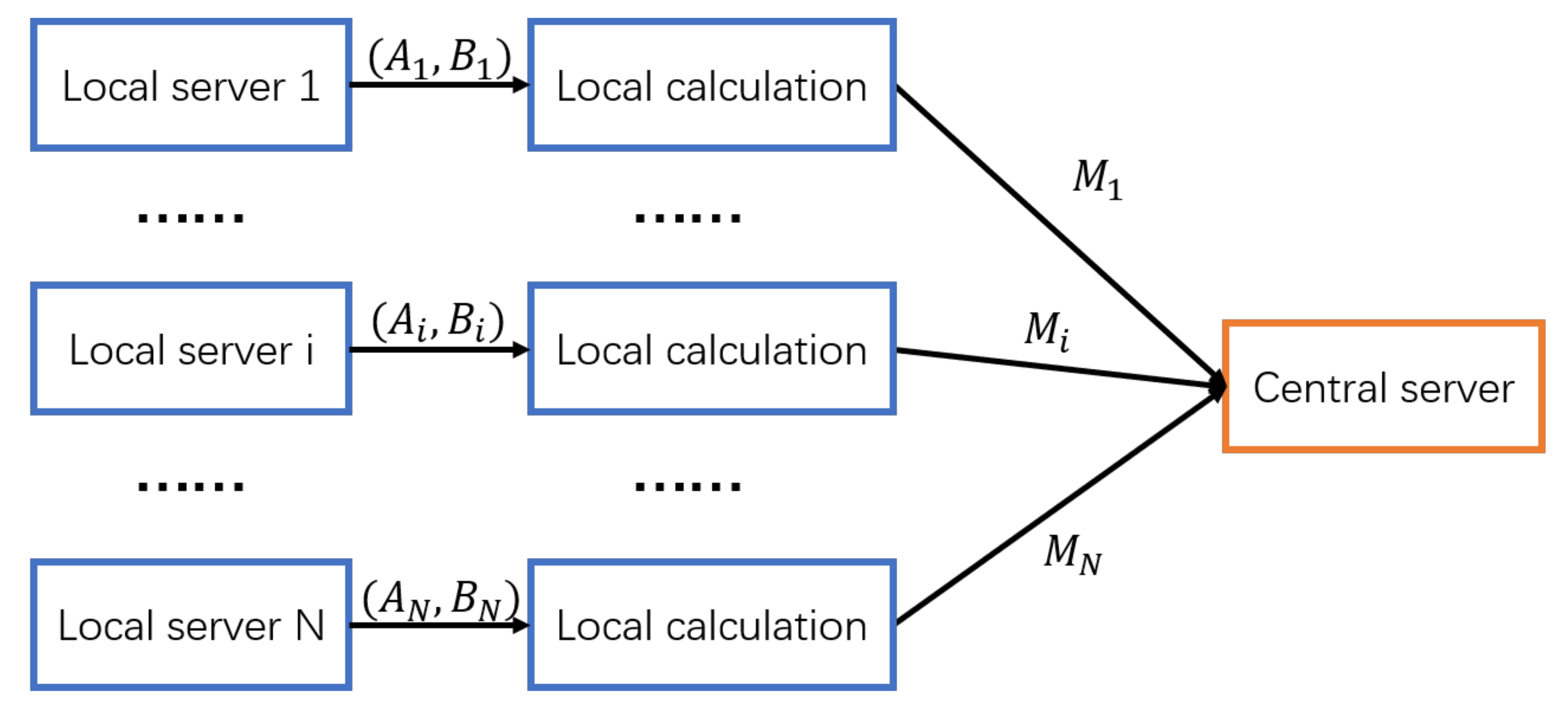
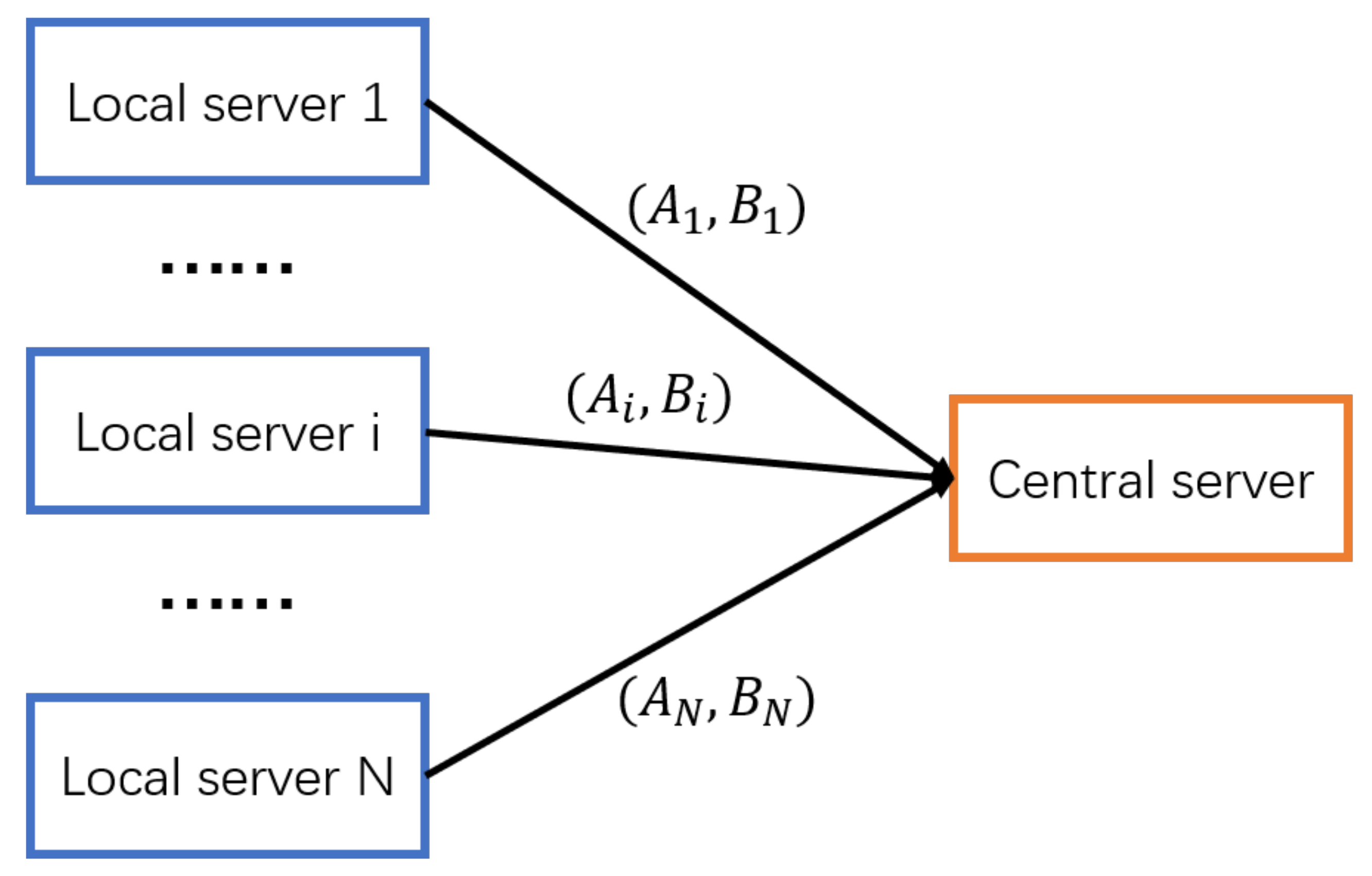
To solve GEP in a distributed manner, in this paper, we propose a one-shot algorithm with high communication efficiency and bounded approximation error. To our best knowledge, it is the first sample-distributed algorithm for GEP. The key is to estimate the centered global covariance from local empirical data covariances. Generally, there are two types of distributed algorithms: multi-round communication and one-shot. Algorithms with multi-round communication are usually more accurate but suffer from the high communication cost and the privacy risk. One-shot algorithms overcome these shortcomings but require better design and approximation analysis. Thus, for the proposed algorithm, we investigate the upper bound of the approximation error, and show it is concerned with the eigenvalues of the empirical data covariance and the number of local servers.

To demonstrate the effectiveness of the proposed distributed algorithm in practice, we consider Fisher’s Discriminant Analysis (FDA) [25] and CCA as specific applications of GEP. Among them, distributed FDA achieves remarkable performance in the learning task of binary classification. However, CCA is more special for its symmetric self-adjoint dilation [26] of the empirical covariance matrix in the GEP form. When using the power method (PM), which is commonly used to solve GEP for computation efficiency, the iterations become inefficient due to the repeated non-zero generalized eigenvalues of the covariance matrix, namely, no eigengap (see Corollary 1 in [27]). Note that such a problem only exists in sample-distributed CCA while not in feature-distributed ones [28,29]. To solve this problem in the sample-distributed setting, we reformulate the objective function of CCA and further propose the distributed multiple CCA algorithm for better convergence in the experiments.

The main contributions of the paper are summarized as follows:

• The first one-shot distributed algorithm is specially designed for the Generalized Eigenvalue Problem (GEP) with communication efficiency.
• The efficient reformulated distributed multiple CCA algorithm is established for better convergence under the distributed GEP framework and proven necessary in some cases.
• The approximation error is bounded theoretically in relation to the eigenvalues of the empirical data covariance and the number of local servers.

The remainder of the paper is organized as follows. Section 2 gives a general framework of the distributed GEP algorithm in one-shot communication and its extensional applications. In Section 3, we analyze the approximation error of the proposed algorithm. Section 4 puts forward the distributed multiple CCA algorithm with the power method as one detailed application. The performance of  numerical experiments is shown in Section 5. The conclusion is presented in Section 6. Based on our former conference paper, we provide thoughtful discussion about our formulation, the whole process, and extensional applications of distributed GEP in Section 2. We also complement the experiments both on synthetic and real-word datasets to illustrate the effectiveness of our proposed methods in Section 5.

2. Distributed GEP Algorithm and Its Extensional Applications

In this section, the GEP is represented as a trace optimization subjecting to fixed quadratic constraints. Then, a one-shot distributed GEP algorithm (DGEP) is proposed. We are seeking the generalized eigenvectors of the symmetric empirical data covariance in distributed settings with one-shot communication.

2.1. Problem Formulation

We consider a kind of distributed generalized eigenvalue problem, where the data of the same d observations are provided from N local servers to their shared believable central server. That is, the centered data are established as $X=[X_1,X_2,\cdots ,X_N]\in {\mathbf{R}}^{d\times nu{m}_1}$ and $Y=[Y_1,Y_2,\cdots ,Y_N]\in {\mathbf{R}}^{d\times nu{m}_2}$, where d is the feature dimension and $nu{m}_1$ and $nu{m}_2$ are the number of data X and Y. $X_i$ and $Y_i$ are i.i.d, respectively, for $i\in \{1,2,\cdots ,N\}$. Each local server prepares data matrices $A_i\in {\mathbf{R}}^{d\times d}$ and $B_i\in {\mathbf{R}}^{d\times d}$ according to the different tasks of GEP from X and Y. The centered GEP is formulated as a maximum optimization as below:

$$\underset{w\in {\mathbf{R}}^d}{max}{w}^{*}\left({\sum }_{i=1}^N{A}_i\right)w\mathrm{s}.\mathrm{t}.w^{*}\left({\sum }_{i=1}^N{B}_i\right)w=1.$$

(3)

It is equivalent to:

$$\underset{w\in {\mathbf{R}}^d}{max}{w}^{*}{M}_{0}w\mathrm{s}.\mathrm{t}.w^{*}w=1,$$

(4)

where the covariance matrix $M_0={\left({\sum }_{i=1}^N{B}_i\right)}^{-\frac{1}{2}}{\sum }_{i=1}^N{A}_i{\left({\sum }_{i=1}^N{B}_i\right)}^{-\frac{1}{2}}$ and $A_i,B_i,M_0\in {\mathbf{R}}^{d\times d}$ are all symmetric. The solution to (4) is the ground truth of the centered GEP.

In our distributed setting of GEP, the difficulty lies in estimating the centered covariance $M_0$ with local data. Hence, based on the trace maximization method, we formulate the central optimization problem in the central server as follows:

$$\underset{w\in {\mathbf{R}}^d}{max}{w}^{*}\left({\sum }_{i=1}^N{M}_i\right)w\mathrm{s}.\mathrm{t}.w^{*}w=1,$$

(5)

where $M_i={\left(B_i\right)}^{-\frac{1}{2}}{A}_i{\left(B_i\right)}^{-\frac{1}{2}}$ is the local covariance, calculated and stored locally.

2.2. Distributed GEP in One-Shot Communication

Then, the general one-shot distributed GEP algorithm (DGEP in Algorithm 1) is shown as below.

Algorithm 1 One-shot Distributed GEP algorithm (DGEP).

1:  In the local servers, calculate local covariance matrix $M_i$ in i-th local server and broadcast it to the central server. 2:  In the central server, calculate $\widehat{M}={\sum }_{i=1}^N{M}_i$ as the approximation of $M_0$. 3:  Computing the leading k eigenvectors $\widehat{W}$ of the approximate matrix $\widehat{M}$. 4:  Return $\widehat{W}$.

We focus on the  distributed optimization of GEP in  (5) with symmetric $M_i\in {\mathbf{R}}^{d\times d}$ for $i\in \{1,2,\cdots ,N\}$. N local servers broadcast the data covariance $M_i$ to the central server in one-shot communication for efficiency. Learning the generalized eigenvector $\widehat{w}\in {\mathbf{R}}^d$ occurs in the central server. To be more specific, the whole process is depicted in Figure 1, among which ’Local calculation’ denotes calculating the local covariance matrix, which is different from the traditional one-shot method in Figure 2. When solving (5) in the central server, SVD and the power method [30] can be carried out, among which the power method is to find a dominant eigenvalue and a corresponding eigenvector and is summarized in Algorithm 2.

Algorithm 2 The power method (PM) in the central server.

Input:  Given the covariance matrix $M\in {\mathbf{R}}^{d\times d}$ and the value of $max\_iter$. 1:  Initialize $w_0\in {\mathbf{R}}^d$. 2:  for t = 1 to $max\_iter$ do 3:    Calculate $w_t=M{w}_{t-1}$. 4:    Calculate $w_t=w_t/\parallel w_t\parallel$. 5:  end for Output:  $\widehat{w}=w_{max\_iter}$.

2.3. Discussion

In some cases, e.g., [21], they consider that the centered data covariance $M_0$ is divided into local agents as $M_0=[M_1,M_2,\cdots ,M_N]$ such that the distributed GEPs are reduced to distributed SVDs. However, in our distributed setting, which is more concrete, we can communicate the data covariance $A_i$ and $B_i$ and obtain the exact solution of the centered GEP as depicted in Figure 2.

Furthermore, from a data privacy perspective, since data covariance pair ($A_i$, $B_i$) may lose privacy for its simple symmetry, sending local covariance $M_i={\left(B_i\right)}^{-\frac{1}{2}}{A}_i{\left(B_i\right)}^{-\frac{1}{2}}$ to the central server is much safer and more efficient than sending $A_i$ and $B_i$ directly.

In addition, a dense $M_i$ is regarded as compromising a mix of multi-view data, which are hard to recover. However, there is a divergence between ${\sum }_i{M}_i$ and $M_0$, and it is decided by the data structure.

In this paper, we will further analyze the approximation error in this one-shot communication method in a distributed GEP.

Note that in the one-shot distributed system, it is assumed that node failure and asynchronization are ignored. All the local servers have a similar scale of data to ensure that synchronous communication will not result in a long delay in the whole system.

2.4. Extensional Applications of Distributed GEP

Many statistical tools in machine learning fields can be formulated as special instances of GEP in  (1) with the symmetric-definite matrix pair (A,B). We briefly give three instances below. They all fit for the proposed Algorithm 1 when in the distributed framework:

• PCA (Principal Component Analysis): It is the most widely used statistical technique for data analysis and dimensionality reduction. It involves the eigenvalue problem, which is reduced from GEP with a symmetric A and $B=I$.
• FDA (Fisher’s Discriminant Analysis [31]): It is desired to maximize the between-class variance $S_B$ and minimize the within-class variance $S_W$. Therefore, the instances of every class become close to one another, and the classes become far away from each other. It is a direct instace of GEP with $A=S_B$ and $B=S_W$.
• CCA (Canonical Correlation Analysis ): Given two random vectors X and Y, let ${\sum }_{XX}$ and ${\sum }_{YY}$ be the covariance matrices of X and Y, respectively. ${\sum }_{XY}$ is the cross-covariance matrix between X and Y. The canonical vectors $w_X$ and $w_Y$ can be obtained by solving GEP with $A=\left(\begin{array}{cc}0& {\sum }_{XY}\\ {\sum }_{XY}& 0\end{array}\right)$, $B=\left(\begin{array}{cc}{\sum }_{XX}& 0\\ 0& {\sum }_{YY}\end{array}\right)$, $w=\left(\begin{array}{cc}{w}_X& 0\\ 0& w_Y\end{array}\right)$.
• PLS (Partial Least Squares [32]): It is a common method for dimension reduction. Derived from CCA with X and Y, it is also an instance of GEP with $A=\left(\begin{array}{cc}0& {\sum }_{XY}\\ {\sum }_{XY}& 0\end{array}\right)$, $B=I$, $w=\left(\begin{array}{cc}{w}_X& 0\\ 0& w_Y\end{array}\right)$.

3. Approximation Error Analysis of Distributed GEP

In this section, we analyze the approximation error of DGEP in Algorithm 1, which is defined as the distance $\mathbf{D}$ between the centered ground truth $W_c$ and the estimator $\widehat{W}$. Without loss of generality, the top k subspace distance, measured by the sine of the angle ${\theta }_k$, is analyzed. Thus,

$$\parallel {\mathbf{D}}_k(W_c,\widehat{W})\parallel =sin\left({\theta }_k(W_c,\widehat{W})\right),$$

where $W_c,\widehat{W}\in {\mathcal{R}}^{d\times k}$, norm $\parallel ·\parallel$ denotes ${\ell }_2$ norm as default, and $\parallel {\mathbf{D}}_k(·,·)\parallel$ denotes the top k subspace distance. Our analysis is based on $sin\theta$ theorem in [33], which reveals how much the invariant subspace will be affected if the covariance matrix is slightly perturbed. We first define that the centered covariance before one-shot communication ${\sum }_1=M_0$ and the approximation covariance in the center server ${\sum }_2={\sum }_{i=1}^N{M}_i$ are represented by the detailed data matrix multiplication of $A_i$ and $B_i$, respectively. The goal of Algorithm 1 is to learn a central orthonormal matrix $\widehat{W}\in {\mathbf{R}}^{d\times k}$ to estimate $W_c$, which is the top k eigenspace of ${\sum }_1$ and also the ground truth. Our main result is in the following.

Theorem 1.

Given matrices ${\sum }_1\in {\mathbf{R}}^{d\times d}$ with eigenvalues ${\sigma }_1\ge \cdots \ge {\sigma }_d$ and ${\sum }_2\in {\mathbf{R}}^{d\times d}$ in the central server with eigenvalues ${\tilde{\sigma }}_1\ge \cdots \ge {\tilde{\sigma }}_d$. For a given dimension k, where $k\le d$, let $W_c=(w_1,\cdots ,w_k)\in {\mathbf{R}}^{d\times k}$ and $\widehat{W}=({\tilde{w}}_1,\cdots ,{\tilde{w}}_k)\in {\mathbf{R}}^{d\times k}$ have orthogonal columns satisfying ${\sum }_1{w}_j={\sigma }_j{w}_j$ and ${\sum }_2{\tilde{w}}_j={\tilde{\sigma }}_j{\tilde{w}}_j$ for $j=1,\cdots ,k$. Assume ${\Delta }_k=inf\{\parallel \widehat{\sigma }-\sigma |:\sigma \in [{\sigma }_k,{\sigma }_1],\widehat{\sigma }\in [-\infty ,{\widehat{\sigma }}_{k+1}]\cup [{\widehat{\sigma }}_0,\infty ]\}$, where ${\widehat{\sigma }}_0=-\infty$ and ${\widehat{\sigma }}_{k+1}=\infty$ and ${\Delta }_k>0$. The approximation error is upper-bounded by:

$$\begin{array}{c}\hfill ∥{\mathit{D}}_{\mathbf{k}}\left(W_c,\widehat{W}\right)∥\le \frac{{max}_i{a}_i}{N^3{\Delta }_k{max}_j{b}_j}+\frac{N}{{\Delta }_k}\underset{k}{max}\frac{a_k}{b_k},\end{array}$$

(6)

where $a_i,b_i$ are the maximum spectral radii of $A_i,B_i$, respectively.

Proof of Theorem 1. 

From the $sin\theta$ theorem in [33], a direct conclusion is obtained as:

$$∥{\mathit{D}}_k\left(W_c,\widehat{W}\right)∥=∥sin{\theta }_k\left(W_c,\widehat{W}\right)∥\le \frac{∥{\sum }_1-{\sum }_2∥}{{\Delta }_k}.$$

Considering Jensen’s Inequality for $\parallel B_i\parallel$, we have:

$${\left(\frac{{\sum }_{\mathrm{i}=1}^{\mathrm{N}}∥{\mathrm{B}}_{\mathrm{i}}∥}{\mathrm{N}}\right)}^{-\frac{1}{2}}\le \frac{1}{\mathrm{N}}\sum _{\mathrm{i}=1}^{\mathrm{N}}{∥{\mathrm{B}}_{\mathrm{i}}∥}^{-\frac{1}{2}},$$

and only if $∥B_1∥=∥B_2∥=\cdots =∥B_N∥$, the equality holds. That is, ${\left({\sum }_{\mathrm{i}=1}^{\mathrm{N}}∥{\mathrm{B}}_{\mathrm{i}}∥\right)}^{-\frac{1}{2}}\le {\mathrm{N}}^{-\frac{3}{2}}{\sum }_{\mathrm{i}=1}^{\mathrm{N}}{∥{\mathrm{B}}_{\mathrm{i}}∥}^{-\frac{1}{2}}$. Then:

$$\begin{array}{cc}\hfill ∥{\sum }_1-{\sum }_2∥& =∥{\mathrm{M}}_0-\sum _{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{M}}_{\mathrm{i}}∥=∥{\left(\sum _{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{B}}_{\mathrm{i}}\right)}^{-\frac{1}{2}}\sum _{i=1}^N{A}_i{\left(\sum _{i=1}^N{B}_i\right)}^{-\frac{1}{2}}-\sum _{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{B}}_{\mathrm{i}}^{-\frac{1}{2}}{\mathrm{A}}_{\mathrm{i}}{\mathrm{B}}_{\mathrm{i}}^{-\frac{1}{2}}∥\hfill \\ \hfill & \le ∥{\left(\sum _{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{B}}_{\mathrm{i}}\right)}^{-\frac{1}{2}}\sum _{i=1}^N{A}_i{\left(\sum _{i=1}^N{B}_i\right)}^{-\frac{1}{2}}∥+∥\sum _{i=1}^N{B}_i^{-\frac{1}{2}}{A}_i{B}_i^{-\frac{1}{2}}∥\hfill \\ \hfill & \le {\mathrm{N}}^{-3}\sum _{i=1}^N{∥B_i∥}^{-1}\sum _{i=1}^N∥A_i∥+\sum _{i=1}^N\left({\left.∥B_i∥\right|}^{-1}∥A_i∥\right)\hfill \\ \hfill & \le \frac{{max}_i{a}_i}{N^3{max}_j{b}_j}+N\underset{k}{max}\frac{a_k}{b_k},\hfill \end{array}$$

where $a_i,b_i$ are the maximum spectral radii of $A_i$, $B_i$, respectively, for $i=1,\dots ,N$. Hence, Theorem 1 is obtained.    □

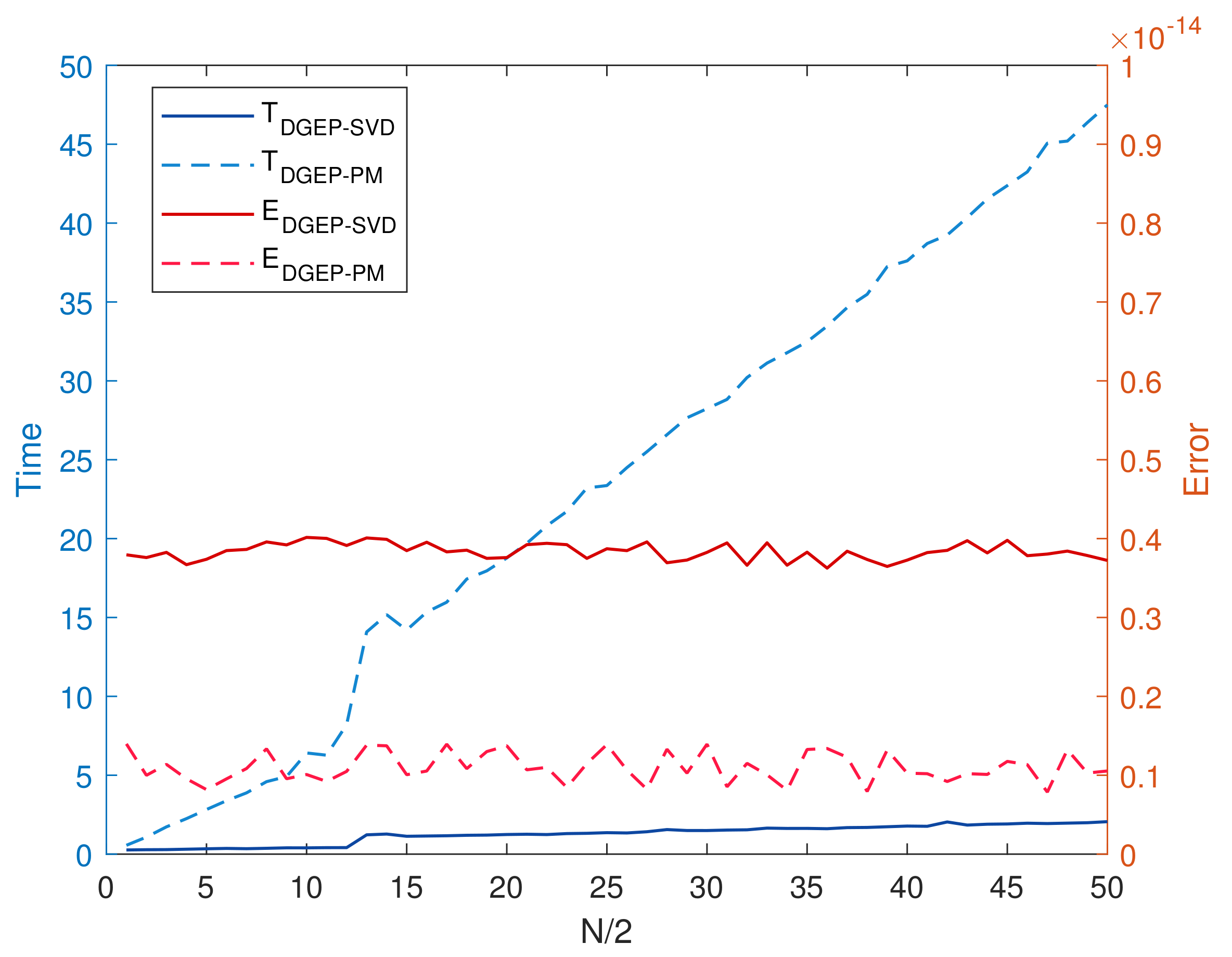
The upper bound of the approximation error of Algorithm 1 is concerned with the eigenvalues of the empirical data covariance, and the number of local servers. This accounts for the divergence of data covariance in one-shot communication. For the special case, such as distributed EP, $B_i=I$ for any local server, $b_j=1$ for any eigenvalue, and ${\sum }_1={\sum }_2$. When the number of local servers $N\to \infty$ and the eigengap is $\Delta \to \infty$, the right side of (6) approaches zero, satisfying the known conclusion.

4. Distributed Canonical Correlation Analysis and Its Multiple Formulation

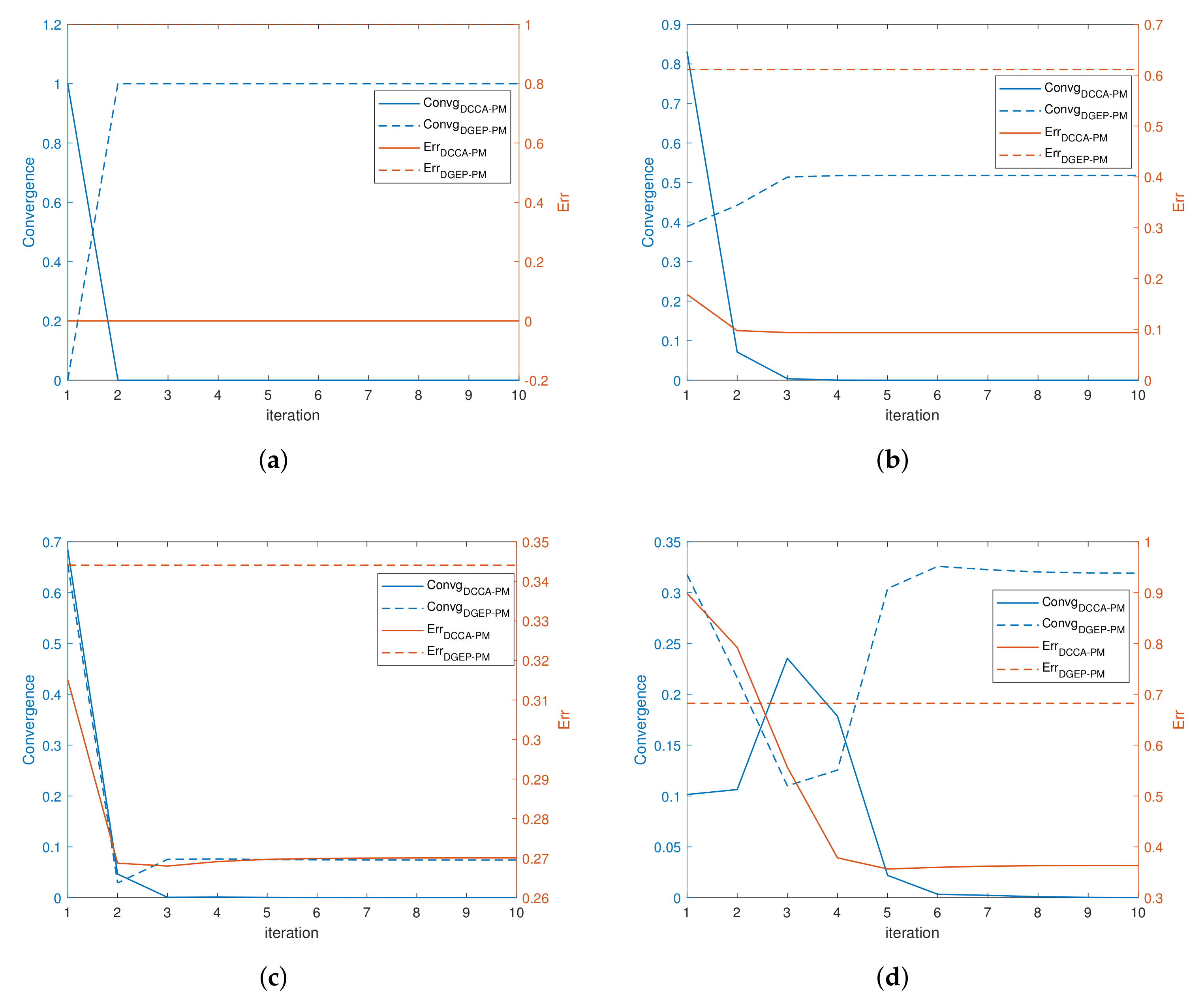
In this section, we investigate distributed CCA, which is a special instance of distributed GEP. In the classical setting, the CCA finds the linear combinations of two sets of random variables with maximal correlation. Furthermore, multiple CCA [34] is the cornerstone of multi-view learning. However, if considering the original data from each view, Algorithm 1 encounters the theoretical barrier of convergence in solving the distributed CCA with the tool of the power method. So, we put forward a new algorithm based on Algorithm 1 when using the power method in this section.

We first provide the mathematical formulation of CCA. Given d observations, denote $X=(x_1,\cdots ,x_d)\in {\mathbf{R}}^{n_1\times d}$, $Y=(y_1,\cdots ,y_d)\in {\mathbf{R}}^{n_2\times d}$. The covariances ${\sum }_{XY}=\mathbf{E}\left(X{Y}^{*}\right)=X{Y}^{*}$, ${\sum }_{XX}=\mathbf{E}\left(X{X}^{*}\right)=X{X}^{*}$ and ${\sum }_{YY}=\mathbf{E}\left(Y{Y}^{*}\right)=Y{Y}^{*}$. Without loss of generality, its multiple version is formulated as below:

$$\begin{array}{cc}\hfill & \underset{U,V}{max}\mathrm{Trace}\left(U^{*}X{Y}^{*}V\right)\hfill \\ \hfill & \begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& \hfill U^{*}X{X}^{*}U=I_k,U\in {\mathbf{R}}^{n_1\times k},\\ \hfill & \hfill V^{*}Y{Y}^{*}V=I_k,V\in {\mathbf{R}}^{n_2\times k},\end{array}\hfill \end{array}$$

(7)

where $I_k$ stands for identity matrix, and its number of columns is k, denoting the number of canonical components and normally $k\le min\{n_1,n_2\}$. When $k=1$, it degrades to the standard CCA. Recall from the formulation of CCA, we obtain:

$$\underset{W\in {\mathbf{R}}^{d\times k}}{max}\mathrm{Trace}\left(W^{*}AW\right)\mathrm{s}.\mathrm{t}.W^{*}BW=I_k,$$

(8)

where $A=\left(\begin{array}{cc}0& X{Y}^{*}\\ Y{X}^{*}& 0\end{array}\right)$, $B=\left(\begin{array}{cc}X{X}^{*}& 0\\ 0& Y{Y}^{*}\end{array}\right)$, $W=\left(\begin{array}{cc}U& 0\\ 0& V\end{array}\right)$. This kind of self-adjoint structure keeps the symmetry of A and B. 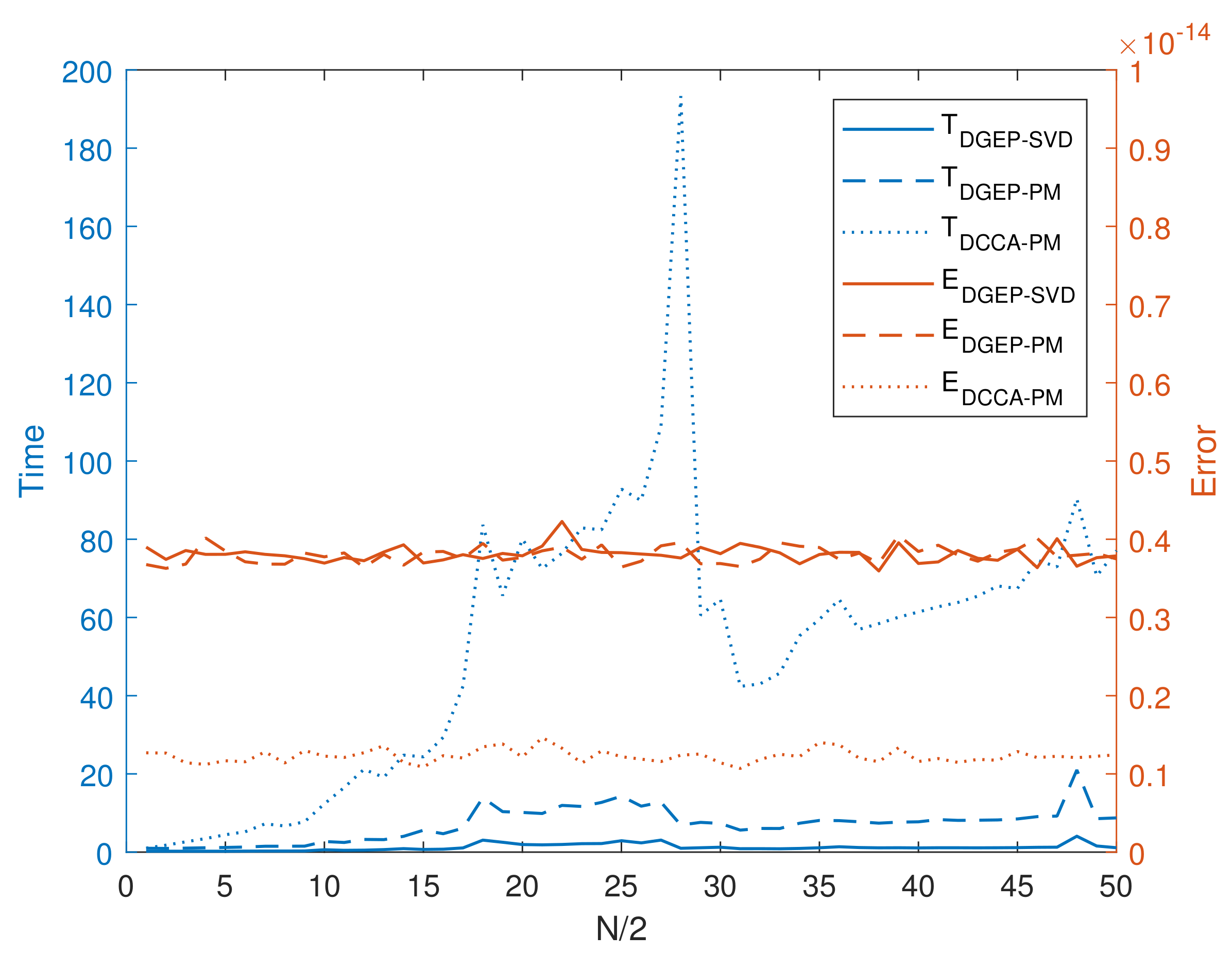However, according to Theorem 2 in [21], there must be an eigengap of $M=B^{-\frac{1}{2}}A{B}^{-\frac{1}{2}}\in {\mathbf{R}}^{d\times d}$ when using the power method. Hence, using Algorithm 1 in distributed CCA may not only increase the approximation error during communication but also result in a convergence barrier for no eigengap. We will also illustrate this barrier in further numerical experiments.

So, in this section, we reformulate CCA and put forward a one-shot distributed multiple CCA algorithm with the power method, which solves the inherent structure defect efficiently. The reformulated centered problem is shown as below:

$$\begin{array}{cc}\hfill \underset{W_1,W_2}{max}& \mathrm{Trace}\left(W_1^{*}{\left(X{X}^{*}\right)}^{-\frac{1}{2}*}X{Y}^{*}{\left(Y{Y}^{*}\right)}^{-\frac{1}{2}}{W}_2\right)\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& W_1^{*}{W}_1=I_k,W_2^{*}{W}_2=I_k,\hfill \end{array}$$

(9)

where $X=[X_1,X_2,\cdots ,X_N]$ and $Y=[Y_1,Y_2,\cdots ,Y_N]$ are concatenations of original data from N local servers. $M_0={\left(X{X}^{*}\right)}^{-\frac{1}{2}*}X{Y}^{*}{\left(Y{Y}^{*}\right)}^{-\frac{1}{2}}$ is the asymmetric covariance of the centered problem. The distributed optimization problem is:

$$\begin{array}{cc}\hfill \underset{W_1,W_2}{max}& \mathrm{Trace}\left(W_1^{*}\left(\sum _{i=1}^N{M}_i\right)W_2\right)\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& W_1^{*}{W}_1=I_k,W_2^{*}{W}_2=I_k,\hfill \end{array}$$

(10)

where the covariance $M_i={\left(X_i{X}_i^{*}\right)}^{-\frac{1}{2}*}{X}_i{Y}_i^{*}{\left(Y_i{Y}_i^{*}\right)}^{-\frac{1}{2}}$ for CCA is also asymmetric, and $\widehat{M}={\sum }_{i=1}^N{M}_i$ is an approximation of $M_0$ in the distributed setting. Then, we derive the one-shot distributed algorithm for multiple CCA in the following.

Algorithm 3 shows the one-shot distributed multiple CCA algorithm which improves the performance by breaking the self-adjoint symmetric GEP structure. The power iterations in the central optimization are divided into two parts as computing the eigenspace of ${\widehat{M}}_1={\sum }_{i=1}^N{M}_i{M}_i^{*}$ and ${\widehat{M}}_2={\sum }_{i=1}^N{M}_i^{*}{M}_i$. The process can be viewed as seeking the left and right singular vector of the approximated covariance $\widehat{M}$ at the same time. QR factorization [30] is used to become the orthonormal approximated eigenspace. The analysis of the approximated error of Algorithm 3 is similar as that in Section 3. The convergence boils down to that of the power method in [30].

Algorithm 3 One-shot Distributed multiple CCA algorithm.

1:   In the local servers, calculate local covariance matrix $M_i$ in i-th local server and broadcast $M_i{M}_i^{*}$ and $M_i^{*}{M}_i$, respectively, to the central server. 2:  In the central server, calculate the leading k eigenvectors of ${\widehat{M}}_1$ and ${\widehat{M}}_2$ as ${\widehat{W}}_1$ and ${\widehat{W}}_2$, respectively, by the power method in parallel. 3:  Return ${\widehat{W}}_1$ and ${\widehat{W}}_2$.

5. Numerical Experiments

In this section, numerical experiments on synthetic and real data are carried out to illustrate the effectiveness and accuracy of the proposed algorithms. In the GEP, Algorithm 1, as the first distributed algorithm for the GEP, is compared with the centered result. In the pursuit of the eigenvectors of the DGEP in the central server, SVD and the power method (PM) are carried out. They are denoted as DGEP-SVD and DGEP-PM in the following. In CCA, Algorithm 3 (denoted as DCCA-PM) and DGEP-PM are compared with the centered results. We only pursue the generalized eigenvector corresponding to the largest generalized eigenvalue for convenience in the maximum optimization of distributed GEP and distributed CCA, which is $k=1$. All the experiments are performed on MATLAB R2019a on a computer with 6 Core 2.20 GHz CPUs and 8GB RAM. The codes are available in https://github.com/kelenlv/one-shot-DGEP (accessed on 1 May 2022).

5.1. DGEP on Synthetic Datasets

Considering the general settings of the GEP in (1), we generate a symmetric matrix $A_i\in R^{d\times d}$ and a positive definite matrix $B_i\in R^{d\times d}$ randomly and independently, which compromise data-mixed information in the i-th local server with $i=1,\cdots ,N$. Then, we first evaluate Algorithm 1 including DGEP-SVD and DGEP-PM in running time and error. The running time concludes communication time and optimization time for DGEP-PM and the maximum iteration step of PM is set to be 10. The error is calculated as

$$Error=sin\left(subspace(\widehat{W},W_c)\right)=\parallel \widehat{W}-W_c\left(W_c^{*}\widehat{W}\right)\parallel ,$$

where $W_c$ is the ground truth, and $\widehat{W}$ is obtained in the central server. The performance of DGEP in time and error is depicted in Figure 3 with $d=1000$ and N varying from 2 to 100 in intervals of 2. As the number of local servers (N) increases, the running time of DGEP goes up, and SVD as a solver in MATLAB is efficient if the complexity $\mathcal{O}\left(d^3\right)$ is acceptable. The errors of DGEP-PM and DGEP-SVD are similar and keep in a low level as N varies.

Then, we investigate Algorithm 3 (DCCA-PM) and compare it to Algorithm 1 (DGEP-PM). Considering the settings of mutiple CCA in (8), we generate the self-adjoint symmetric $A_i$ and $B_i$ randomly and independently with $i=1,\cdots ,N$. The other settings are in the same. The performance in running time and error is depicted in Figure 4, with $d=1000$ and N varying from 2 to 100 in intervals of 2. The errors of DGEP-PM and DCCA-PM stay at a low level as N varies, and DCCA-PM performs better. However, excluding the abnormal experiment, the running time that DCCA-PM costs is eight times of that DGEP-PM costs on average. That is, when using PM, DCCA-PM achieves higher accuracy but more running time than DGEP-PM, which is a trade-off in real-world scenarios. It needs to be evaluated by the performance on real-world data to validate whether it is worthwhile.

5.2. DGEP on Real Datasets

The technique of FDA [31], as an instance of a GEP, is used in the binary classification of the GSE2187 dataset (https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE2187 (accessed on 1 May 2005)), which is a large cRNA microarray dataset reflecting the drugs and toxicants response of rats. Only two categories (toxicants and fibrates, named as $C_1$ and $C_2$, respectively, for short) are used in classification, and the missing values are filled with mean values. The data are randomly divided into training data and testing data with a ratio of 1:1. The detailed information is displayed in

Table 1. GSE2187 data structures: number of data ($num$), data dimension (d).

Data	Toxicants $\left({\mathit{C}}_1\right)$	Fibrates $\left({\mathit{C}}_2\right)$
$num$	181	107
d	8656	8656

.

The number of local servers is set to be 5, and the maximum iteration steps of PM is set to be 10. The binary classification accuracy from distributed data depends on the classification threshold of centered data, which is:

$$thres=\frac{W_c\times (nu{m}_{C_1}\times m_{C_1}-nu{m}_{C_2}\times m_{C_2})}{nu{m}_{C_1}+nu{m}_{C_2}},$$

with the mean of $C_1$ and $C_2$ ($m_{C_1}$ and $m_{C_2}$). The classification accuracy is calculated with $data\in {\mathbf{R}}^{num\times d}$ as:

$$ac{c}_{C_1}=\frac{{\sum }_{i=1}^{nu{m}_{C_1}}{\delta }_1(\widehat{W}\times dat{a}^{\prime },thres)}{nu{m}_{C_1}},ac{c}_{C_2}=\frac{{\sum }_{i=1}^{nu{m}_{C_2}}{\delta }_2(\widehat{W}\times dat{a}^{\prime },thres)}{nu{m}_{C_2}},$$

where ${\delta }_1$ and ${\delta }_2$ are the indicator functions. When the projected value is less than the mean threshold value, ${\delta }_1$ equals 1 and 0 otherwise, and ${\delta }_2$ is exactly the opposite. The repeated experiments are carried out 10 times and the classification accuracy in GSE2187 data is reported in

Table 2. Classification accuracy of GSE2187 data in FDA: training accuracy of $C_i$ ($ac{c}_{C_i}tr$), testing accuracy of $C_i$ ($ac{c}_{C_i}ts$).

Method		Accuracy	Mean Accuracy
Centered by SVD	$ac{c}_{C_1}tr$	1.0000 + 0.0000	1.0000 for train
	$ac{c}_{C_2}tr$	1.0000 + 0.0000
	$ac{c}_{C_1}ts$	0.9835 + 0.0250	0.9706 for test
	$ac{c}_{C_2}ts$	0.9576 + 0.0654
DGEP-SVD	$ac{c}_{C_1}tr$	0.9600+0.0711	0.9271 for train
	$ac{c}_{C_2}tr$	0.8943 + 0.0895
	$ac{c}_{C_1}ts$	0.9407 + 0.0990	0.9000 for test
	$ac{c}_{C_2}ts$	0.8593 + 0.1052
DGEP-PM	$ac{c}_{C_1}tr$	0.9578+0.0477	0.9326 for train
	$ac{c}_{C_2}tr$	0.9075 + 0.0625
	$ac{c}_{C_1}ts$	0.9505 + 0.0526	0.9123 for test
	$ac{c}_{C_2}ts$	0.8741 + 0.0745

.

The centered accuracy is regarded as the benchmark. Clearly, no algorithm can beat the performance of the best centered estimator. However, the classification accuracy of the proposed algorithm does not decrease much, even though there is the covariance divergence in the one-shot communication. Generally, DGEP including DGEP-SVD and DGEP-PM in the one-shot communication performs well in the distributed FDA application.

5.3. Distributed CCA on Real Datasets

In this case, we apply Algorithm 3 to a multi-classification problem where the feature is denoted as a view X and the class as another view Y. Two real datasets from the gene expression database [35] are considered as data-sensitive and are dispersed evenly for convenience in local servers. Each dataset is locally divided into training data and testing data in terms of the same data dimension d. The details are explained below, and the statistics can be found in

Table 3. Genedata structures: data dimension (d), number of data ($num$), number of training data ($t{r}_{num}$), number of testing data ($t{s}_{num}$), number of classes (K).

Type	Data	K	d	$\mathit{num}$	${\mathit{tr}}_{\mathit{num}}$	${\mathit{ts}}_{\mathit{num}}$
Gene Data	Lymphoma	3	4026	62	48	14
	SRBCT	4	2308	63	48	15

:

• Lymphoma: 42 samples of diffuse large B-cell lymphoma, 9 observations of follicular lymphoma, and 11 cases of chronic;
• SRBCT: the filtered dataset of 2308 gene expression profiles for 4 types of small round blue cell tumors of childhood.

The classification accuracy is defined as

$$acc=\frac{{\sum }_{i=1}^{num}\delta (o{l}_i,p{l}_i)}{num},$$

where $\delta (o{l}_i,p{l}_i)$ is the indicator function. When the obtained label $o{l}_i$ is equal to the provided label $p{l}_i$, it equals 1 and 0 otherwise. Considering the limited number of Gene data, the maximum N is set to be 8. The experiments on two gene datasets are repeated 20 times each, and the detailed mean accuracy is reported in

Table 4. Classification accuracy of Gene data: number of local servers (N), training and testing accuracy of Algorithm 3 ($ac{c}_{tr}$, $ac{c}_{ts}$).

	N		1 (Centered)	2	4	8
Type
Lymphoma		$ac{c}_{tr}$	1.0000 ± 0.0000	0.9937 ± 0.0141	0.9875 ± 0.0224	0.9875±0.0224
		$ac{c}_{ts}$	0.8429 ± 0.1251	0.8143 ± 0.0369	0.8286 ± 0.0499	0.8214 ± 0.0607
SRBCT		$ac{c}_{tr}$	1.0000 ± 0.0000	0.9826 ± 0.0425	0.8715 ± 0.0784	0.6076 ± 0.1600
		$ac{c}_{ts}$	0.6733 ± 0.1195	0.6444 ± 0.1167	0.6000 ± 0.1333	0.4667 ± 0.2271

. It reveals that the accuracy decreases as the number of local servers N goes up. The divergence of covariance in the distributed way influences the classification accuracy of Gene data, especially in SRBCT. However, it is acceptable especially in multi-classification.

When $N=1$, without the communication error, the results reveal that DGEP-PM, the distributed CCA in GEP form without an eigengap, leads to a worse accuracy which is no higher than 72% for training and 68% for testing in Lymphomia and no higher than 41% for training and 36% for testing in SRBCT. The performance of Algorithm 3 in Table 4 is obviously higher. To illustrate the difference in detail, we further investigate the convergence and the error of the two algorithms and show the result in Figure 5. For Lymphoma data as an instance, we define $convergence$ as the successive difference of the objective function value, and $Err$ as the error between the objective function value of the proposed method and ground truth. The maximum iteration is set to be 10. Due to no eigengap in using DGEP-PM in self-adjoint CCA, the convergence performance is poor, even totally on the contrary in Figure 5. However, DCCA-PM converges fast, which accounts for its better performance. In addition, it is validated that there has been progress in effectiveness compared with DGEP-PM.

6. Conclusions

The paper proposes a general distributed algorithm for a generalized eigenvalue problem (GEP) in one-shot communication. For multi-view analysis in DGEPs such as distributed CCA, the algorithm meets hard convergence when there are no eigengaps in the approximated covariance matrix. The one-shot distributed multiple CCA algorithm produced solves this problem. The theoretical analysis of the approximation error reveals the divergence of data covariance in the distributed system and gives the upper bound concerned with the eigenvalues of the data covariance and the number of local servers. The quantities of numerical experiments demonstrate the effectiveness of proposed algorithms in different applications.

As a one-shot method, our proposed algorithms amplify the computation efficiency for communication efficiency. Furthermore, we are devoted to developing an advanced distributed algorithm to obtain a more precise solution. It is believed that deep learning has achieved great development in many applications, including in distributed learning fields. How to combine our works and deep learning networks is the goal of our future work.