Abstract
Soil shear strength is an important indicator of soil erosion sensitivity and the tillage performance of the cultivated layer. Measuring soil shear strength at a field scale is difficult, time-consuming, and costly. This study proposes a new method to predict soil shear strength parameters (cohesion and internal friction angle) by combining cone penetration test (CPT) data and soil properties. A portable CPT measuring device with two pressure sensors was designed to collect two CPT data in farmland, namely cone tip resistance, and cone side pressure. Direct shear tests were performed in the laboratory to determine the soil shear strength parameters for 83 CPT data collection points. Two easily available soil properties (water content and bulk density) were determined via the oven-drying method. Using the two CPT data and the two soil properties as predictors, three machine learning (ML) models were built for predicting soil cohesion and the internal friction angle, including backpropagation neural network (BPNN), partial least squares regression (PLSR), and support vector regression (SVR). The prediction performance of each model was evaluated using the coefficient of determination (R2), the root-mean-square error (RMSE), and the relative error (RE). The results suggested that among all the evaluated models, the BPNN model was the most suitable prediction model for soil cohesion, and the SVR model performed best in predicting soil internal friction angle. Thus, our findings provide a foundation for the convenient and low-cost measurement of soil shear strength parameters.
1. Introduction
Soil shear strength is a useful measure for evaluating soil erosion sensitivity and the tillage performance of the cultivated layer of soil [1,2]. Shear strength is determined by two important parameters: cohesion (c) and internal friction angle (φ) [1,3]. When the tillage machine components work on the soil, the deformation, resistance, and compaction of the soil all affect the shear strength [4,5,6]. Shear failure takes place when the shear stress exceeds soil shear strength generally in soil structure fragmentation caused by tillage [7]. Shear strength also affects the load support capacity, plant growth, and water movement [8,9]. Rapid measurement of soil shear strength is of great significance for farmland management.
At present, a number of methods have been used to determine soil shear strength parameters in the laboratory, such as direct shear, ring shear, and triaxial shear tests [10,11,12]. Although these methods are highly accurate, indoor measurements of soil shear strength are complicated, time-consuming, and difficult to use on a large scale [2]. Thus, new, fast, economical, and large-scale methods for the precise prediction of soil shear strength parameters in farmland are increasingly in demand. The cone penetration test (CPT) has been widely used in geotechnical engineering due to its ability to be executed rapidly and to record the soil profiles continuously [13]. For instance, Begemann proposed that shear strength in clay could be estimated by the sleeve friction of the soil cone penetrator [14]. Salari et al., proposed a pedotransfer function method for determining the internal friction angle of soil through the standard penetration test [15]. Motaghedi and Armaghani calculated soil cohesion and internal friction angle by using three CPT data, namely cone tip resistance, sleeve friction, and pore water pressure, which are determined based on bearing capacity theory and the shear stress relationship at the failure condition [16]. Although the technology and equipment of CPT are well developed, there is little research on the use of CPT for measuring shear strength in agricultural soils. The main reason is that agriculture is different from geotechnical engineering. Its research object is arable soil, and traditional CPT devices cannot measure the parameters at a soil surface with the required resolution. Developing a portable CPT device to collect the relevant information about shear strength in cultivated-layer soils as modeling predictors would be effective for improving the detection accuracy and shortening the measurement time required.
It is well known that the shear strength of arable soil is governed by a range of soil properties, especially bulk density and water content [2,17]. Bulk density reflects the compactness of the soil’s structure, and water content directly affects the Coulomb force, the van der Waals force between soil particles, as well as the connection mode and cementation between soil particles. García et al., studied the effect of different soil densities and water content gradients on soil shear strength, determining that the effect of water content on soil shear strength is greater than that of soil density [18]. Zheng et al., studied the variation characteristics of bulk density and water content on the shear strength of tillage soil. Their research showed that the shear strength had a linear functional relationship with water content and a very significant positive, linear correlation with bulk density [19]. Zhang et al., also pointed out that bulk density and water content had a significant effect on the shear strength on the soil’s surface [20]. These studies demonstrate that it is beneficial to apply the aforementioned two soil properties to the prediction of shear strength parameters.
Modeling is the key to predicting soil shear strength parameters. Although the traditional empirical formula can be used to build the correlation model, the adjustment coefficient of the formula is difficult to determine [15,21], which dramatically reduces its prediction accuracy. In recent years, owing to the universal application of artificial intelligence (AI) approaches [22,23,24,25], machine learning (ML) has attracted increasing interest among soil scientists, and as a method for predicting soil properties [26,27,28]. ML is an interdisciplinary subfield of AI that promotes low-cost computing through algorithmic learning [29]. ML methods do not rely on a long list of physics-based equations and the prediction accuracy depends on the size of the dataset and the type of algorithm. ML can be divided into the following categories based on the application requirements: regression, probability estimation, classification, and clustering [30]. Regression is mainly utilized for predicting material properties. Commonly used regression algorithms in ML include the backpropagation neural network (BPNN), partial least squares regression (PLSR), and support vector regression (SVR) [31]. The BPNN model is the most widely used form of neural network and has strong nonlinear mapping capabilities. The PLSR model is particularly useful for predicting a group of dependent variables from a large number of independent variables, especially when there is a linear correlation between variables. The SVR model is based on support vector machine (SVM) theory, which can effectively simplify the complexity of high-dimensional space. Because of their advantages, BPNN, PLSR, and SVR models are widely used to predict soil properties. For example, Wang et al., compared the prediction performance of PLSR and BPNN for heavy metal concentrations in soil, and the results showed that the prediction accuracy of the BPNN model was higher than that of the PLSR model [32]. Zhu et al., applied SVR to predict the soil organic matter content and achieved good prediction results [33]. Nguyen et al., used clay content, natural moisture content, liquid limit, plastic limit, specific gravity, and void ratio as input variables to predict soil internal friction angle using the BPNN model [34].
This paper proposes a new method that predicts the shear strength parameters of agricultural soils using a combination of CPT data and soil properties. A portable CPT data measuring device that can quickly measure cone tip resistance and cone side pressure through one penetration operation was designed. Given that water content and bulk density have a clear influence on soil shear strength [2,17] and that they are easily obtained using the oven-drying method [35], these two soil properties were combined with the CPT data points for constructing the prediction models. To our knowledge, there are no studies that have explored predicting the soil shear strength parameters by combining CPT data and soil properties. As mentioned above, ML allows for low-cost computing through algorithmic learning, and the BPNN, PLSR, and SVR models are the most commonly used regression algorithms. In this study, ML models based on the BPNN, PLSR and SVR algorithms have been used to predict the soil shear strength parameters. Generally, each model has its own limitations [36]. For the BPNN model, there is no exact calculation formula for the number of hidden layer neurons (h). Selecting the penalty factor (p) and kernel parameter (g) for SVR modeling is very difficult. The PLSR model is not effective for nonlinear data and its modeling accuracy is affected by the number of principal component factors (PCFs). To address these challenges, a trial-and-error method is usually used to determine the h of the BPNN model, the grid search method is used to determine the values of p and g in the SVR model, and a leave-one-out cross-validation method is used to determine the optimal number of PCFs used in the PLSR model [33,37,38,39]. The aims of this paper are to (1) discuss a portable CPT data measuring device integrated with two pressure sensors and its use for rapid measurement of CPT data; (2) optimize the modeling parameters of the three ML models (BPNN, PLSR, and SVR) and evaluate their ability to predict soil cohesion and soil internal friction angle.
2. Materials and Methods
2.1. Instruments
Cone tip resistance and sleeve friction are two important measurement parameters in a CPT test [13,16]; however, the friction measuring device is complex and consists of several sophisticated components [40]. In order to simplify the measuring device and quickly obtain the CPT data, cone side pressure rather than sleeve friction was measured in our study. To obtain soil cone tip resistance and cone side pressure at different depths, a portable measuring device was developed (Figure 1). The device was mainly composed of a tripod, a ball screw slide table, a stepper motor, and a conical rod. The stepper motor was installed onto the tripod to ensure measuring stability. Its output shaft was connected with the screw of the ball screw sliding table through a shaft coupling to ensure good force transmission capability. During the operation of the device, the sliding table was driven up and down by the stepping motor, thus allowing the conical rod connected with the sliding block to penetrate the soil at a constant speed. To better penetrate the soil and measure the side pressure of the cone, the American Society of Agricultural Engineers (ASABE, St. Joseph, MI, USA) standard cones were modified by using two semi-cones to form a new cone. A film sensor was placed at the contact surface between the two semi-cones to measure the cone side pressure as the new cone penetrates the soil. The other end of the conical rod was linked to a load cell to detect the vertical penetration resistance of the cone, i.e., cone tip resistance.
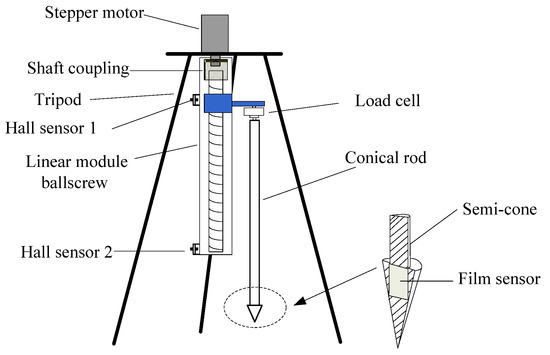
Figure 1.
Structural diagram of the portable CPT measuring device.
An automatic measuring and collection system was designed for real-time acquisition of sensor data and to control the movement of the conical rod (Figure 2). An STM32 single chip with type of STM32F103C8T6 provided by STMicroelectronics (Carrollton, Dallas, TX, USA) was used as the core processor for this system. A constant frequency control signal was given to the stepper motor driver by the output comparing mode of the timer inside the processor, which caused the stepper motor to rotate uniformly so that the cone-rod penetrated the soil at a consistent speed. Two Hall sensors with type of NJK-5002C provided by AOTORO (Yueqing, Zhejiang, China) were used as limit switches to ensure that the cone could reach the required penetration depth, and an SD card was used to store the output values of the sensors. The cone penetration depth (S) is calculated as follows [41]:
where S is the cone depth into the soil; M is the pitch of the thread screw rod; T is the number of rotary steps in the stepper motor; C is the number of steps needed by the motor to rotate one circle.
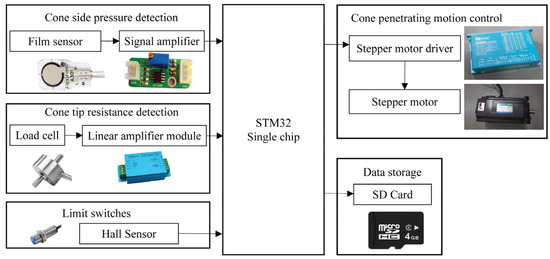
Figure 2.
Structural diagram of the system.
The load cell was selected based on the conical rod shape and the expected maximum resistance from the tested soil. A round stick was chosen and used to manufacture the cone, the apex angle of which accorded with the ASABE Standard (30-deg). After soil resistance tests in the research area and an investigation into the available commercial products, the DYZ-101 cylindrical pressure measuring sensor with a diameter of 25.4 mm from Da Yang Sensing System Engineering Co., Ltd. (Bengbu, China) was selected. This sensor has a measuring range of 0–2940 N and features high precision, large dynamic response, small volume, and strong anti-interference capability. Additionally, the film sensor was a Flexiforce A301 film pressure sensor purchased from Tekscan Inc. (Boston, MA, USA). This sensor is small in size, has a large measuring range (0–436 N), and can be easily integrated and installed into the sections of the semi-cones.
The sensor data were processed in parallel through a series of data processing units. The DYZ-101 sensor was powered by a 3 V power supply and can output 20 mV voltage signals under rated load (10 kN). The output signals from the sensor were linearly magnified by a magnifier and collected by the first interface of a built-in analog-to-digital converter (ADC) in the STM32 single-chip. Furthermore, the Flexiforce A301 sensor under action generated resistance-changing signals. For convenient data collection, these signals were processed by an MCP6004 power amplifier provided by Microchip Technology Inc. (Chandler, AZ, USA), and an operation amplifier LM324 was used to reverse the polarity of the signals (Figure 3). Hence, the output of the Flexiforce A301 sensor can be computed as follows:
where Vout is the output from the Flexiforce A301 sensor after signal processing; VREF is the reference voltage (=1.25 V); RF is reference resistance (=100 KΩ); Rs is the output resistance from the Flexiforce A301 sensor. Vout was collected by the second interface pass of the ADC. After the processed data from different sensors were collected by the ADC in the STM32 single chip, these data were stored on the SD card.
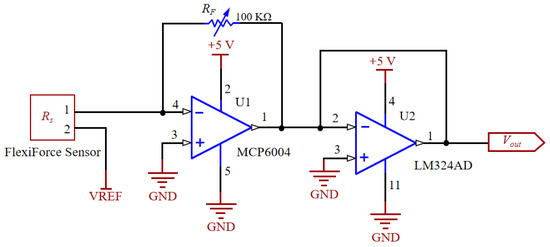
Figure 3.
Flexiforce sensing signal processing.
2.2. Sensors Calibration
To validate the performance of the designed system, a testing clamp that matched the cone that was manufactured. Based on the universal testing machine (Figure 4), the load cell and the film sensor were calibrated through vertical loading force and side loading force, respectively. Eight loading forces (50, 100, 150, 200, 250, 300, 350, and 400 N) were applied in the calibration experiments. The data output from the sensor and the film sensor was stored on the SD card during each gravity loading.
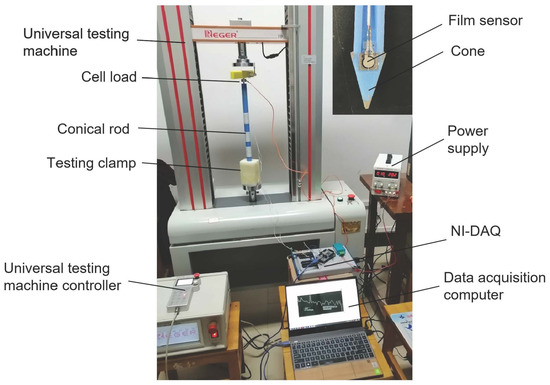
Figure 4.
Sensor calibration test.
Figure 5 shows the calibration results of the sensors. The calibration results were fitted by polynomials, which show the linear relationship between each sensor and the loading forces. Note that the fitting coefficient between loading force and the load cell is up to 0.9974 (Figure 5a), and the fitting coefficient between loading force and the output from the film sensor is 0.9867 (Figure 5b). The goodness-of-fit is close to 1 for both of the two sensors, suggesting that our calibrations are reasonable. Hence, the cone tip resistance and the side pressure can be determined as follows:
where Vlc is the output from the load cell; R is the cone tip resistance; Vfs is the output from the film sensor; P is the cone side pressure.
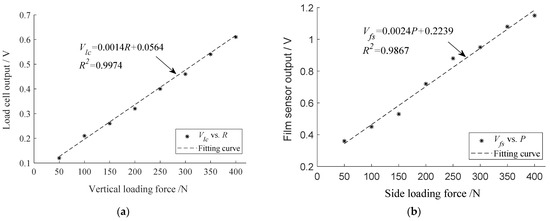
Figure 5.
Sensor’s calibration test. (a) Load cell; (b) film sensor.
2.3. Data Collection and Data Set Construction
2.3.1. Soil Sampling and Data Measurement
The cone penetration device designed in this study was used to randomly measure 83 soil sites in the test base at Huazhong Agricultural University (GPS: 30.4664° N, 114.3483° E), Wuhan of Hubei Province from the 16 to 30 March 2021. This test base was dominated by clayed soil, and the structural compositions of the soil samples are listed in Table 1.

Table 1.
The basic physical properties of soil in study area.
During penetration experiments, the cone vertically penetrated into soils at a penetrating speed of 20 mm/min with a penetration depth of 15 cm. The sensor data were collected by the automatic measuring and collection system in real time. In order to reduce the chance of operating errors, the measurements were repeated three times for each measuring point, and the average values were taken as the final result. Calculating the standard deviation of three repeated measurements, we found that the standard deviation of all 83 measuring sites was less than 5%, so the measurement results were considered reliable. Field measurements from the CPT device are shown in Figure 6a, and the typical output signals of the sensors are shown in Figure 6b.
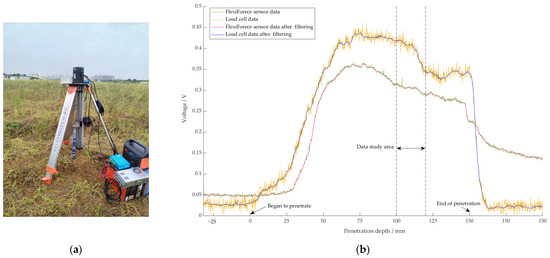
Figure 6.
CPT data acquisition. (a) CPT penetration test; (b) the output values of pressure sensors.
In Figure 6b, the sensors’ original data shows obvious ripples due to the vibration of the stepper motor and the difference in soil penetration resistance. The load cell signal ripple fluctuates more significantly than the film sensor ripple signal, which may be caused by the stepper motor transmitting the penetrating driving force in the vertical direction. To eliminate the ripple interference, we used the 20th-order median filtering method to process the sensors’ original data and obtain smooth curves; however, in this study, the calculation error may have come mainly from the filtering process. Because of the arithmetic rounding of the digital filter, some calculation error is inevitable [42]. By comparing the measured values with the filtered values, it was found that the average error between them is less than 3%, which is considered acceptable.
After the penetration test, soil sampling and laboratory measurement were carried out to obtain soil water content, bulk density, soil cohesion, and internal friction angle at the CPT measuring points. Within 20 cm of each PCT measuring point, the original soils at a depth of 10 cm from the ground were collected by carefully hammering metal cylinders (inner diameter 61.8 mm, height 20 mm) vertically into the soil. The reason for taking soil samples at this depth is that the depth of mechanized rotary tillage of primary crops such as rapeseed in the research area was 10 cm. From each measuring site, 8 soil samples were collected, of which 4 samples were used for direct shear tests [43] to determine soil shear strength τ, and the remaining samples were used for measuring soil water content and bulk density. Laboratory direct shear tests were conducted as per China standard GBT50123-2019, using the ZJ-D strain control direct shear tester produced by Nanjing Nantu Instrument Equipment Co., Ltd. (Nanjing, China). The normal stress applied in each measurement was 100, 200, 300, and 400 kPa, respectively, and the shear rate was maintained at 1.2 mm/min [3]. The shear strength parameters were computed using the Mohr–Coulomb failure criterion. Based on the Mohr–Coulomb failure envelope of shear strength and positive stress, soil cohesion (c) and internal friction angle (φ) were determined. Figure 7 shows the laboratory direct shear test.

Figure 7.
Laboratory direct shear test.
Soil water content (ω) and bulk density (d) were measured by the oven-drying method, and the calculation formula is as follows [35]:
where ω represents soil water content; d represents soil bulk density; mw represents the mass of wet soil; md represents the mass of dry soil; V represents the volume of the metal cylinders.
2.3.2. Dataset Construction
To make the sensors’ measured data consistent with the indoor test sampling depths, a penetration depth of 100~120 mm was taken as the data study area of the smooth curves in Figure 5. From the data in this study area, we extracted the maximum of the load cell and the maximum of the film sensor and converted them into the corresponding force values through Formulas (3) and (4), which are represented by R_max and P_max, respectively. By using R_max, P_max together with the soil water content (ω), soil bulk density (d), soil cohesion (c), and internal friction angle (φ) measured from indoor experiments, a 6-dimensional soil dataset was constructed. Since there were 83 soil sampling sites, the dimensions of the soil dataset are 83 × 6.
2.4. Proposed Machine Learning Models
In this study, ML models such as BPNN, PLSR, and SVR are used to predict the soil shear strength parameters. The ML modeling approach is depicted in Figure 8.
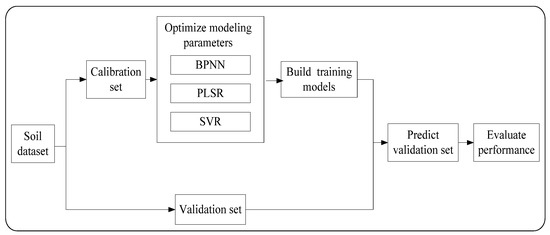
Figure 8.
ML modeling approach.
The modeling process contains 5 steps [44]:
- (1)
- The constructed dataset is divided into a calibration set and a validation set.
- (2)
- The key parameters of the ML models are determined using optimization methods.
- (3)
- Using the calibration set and determined modeling parameters, a prediction model is built by applying ML algorithms.
- (4)
- The trained ML models are used to predict the validation set.
- (5)
- The performance of each constructed model is evaluated based on the calculation of the predicted and the true value.
2.4.1. BPNN Model
A BPNN was used in this study because it is the most widely used and effective neural network learning algorithm [45]. The preliminary architecture of the BPNN was determined as 4-h-1, where 4 is the number of input layer neurons representing R_max, P_max, ω, and d. The number of hidden layer neurons is represented by h, and 1 represents the number of output layer neurons. To eliminate the effects of coupling among dependent variables on the modeling performances of the model, we built BPNN prediction models for c and φ separately.
However, the number of hidden layer neurons greatly affects the accuracy of BPNN [31]. So far, there is no exact formula to calculate the number of hidden layer neurons, but its range can be deduced using an empirical formula. A commonly used formula is as follows [33]:
where h is the number of neuron nodes in the hidden layer, n is the number of input nodes, and p is the number of output nodes, respectively; α is a coefficient from 1 to 10. Since n is 4 and p is 1, h can be assigned a value between 3 and 12.
In this paper, the coefficient of determination in the calibration set (Rc2) is taken as the evaluation index, and the trial-and-error method is adopted to select the appropriate number of hidden layer neurons within the above-calculated h range. The specific optimization steps are as follows:
- (1)
- For each h value within the range, a BPNN model is built, and the calibration set is tested 10 times by the BPNN.
- (2)
- The Rc2 corresponding to each test is calculated, and the average value of Rc2 corresponding to each h value is counted.
- (3)
- The optimal h value of modeling is determined according to the average value of Rc2. The larger the Rc2, the better the model.
In order to facilitate the construction of the BPNN model, it was created based on the newff function in the MATLAB toolbox in our study. The maximum number of iterations is set as 1000 times, the learning rate is 0.01, and the target error is 0.001. It is worth clarifying that in BPNN modeling, hidden layer neurons were an S-shaped transfer function tansig, while output layer neurons were a linear transfer function purelin.
2.4.2. PLSR Model
PLSR is very effective at predicting a group of dependent variables from a number of independent variables [46]. This new multivariable statistical data analytical method integrates principal component analysis and multivariable linear analysis. When the variables have a high linear correlation, a very effective PLSR model can be obtained. In this study, PLSR was used as one of the models to predict soil shear strength parameters.
Basically, PLSR can be divided into two processes [47]. The first involves identifying the principal component factors (PCFs) in the input variable space, and the second involves binding these PCFs to dependent variables; therefore, the number of principal component factors (PCFs) affects the performance of the model. In order to determine the appropriate PCF value, we used leave-one-out cross-validation and Akaike information criterion (AIC) to evaluate how the number of PCFs affected the performance of the PLSR model. AIC is calculated as follows [39]:
where N is the sample size; p is the number of PCFs; RSS is the sum of squared residuals for prediction with the PLSR model.
The PLSR method assumes that the variables from the input space X can be written as a linear combination of vectors t and e (namely scores) and that the variables from the output space Y can be written as a linear combination of q and u (namely loadings) [48]; therefore, these relationships are as follows [49]:
where X is the input variable space, X = {x1, x2, …, xm}; Y is the output variable space, Y = {y1, y2, …, ym}; m is the size of the sample; p is an arbitrary number of principal component factors; t and e are parameters of linear combinations for scores; q and u are parameters of linear combinations for loadings; T and Q are the block scoring matrix of m × p dimension; ET and UT are the block loading matrix of p × m dimension.
To build the PLSR models of soil cohesion and soil internal friction angle, using the NIPALS (nonlinear partial least squares) iterative algorithm [47], the decomposition of state vectors of the input and the dependent variables was obtained as assumed at the beginning. After that, the performance of the models was evaluated.
2.4.3. SVR Model
SVR is a support vector machine (SVM)-based regression technique and was proposed by Vapnik and Vladimir, who introduced an insensitive loss function into SVM to handle regression fitting [50]. Two types of regression methods, ε-SVR and ν-SVR, can be found in the LIBSVM toolbox [51]. Here, ε-SVR was selected, and the radial basis function (RBF) was used as the kernel function. The generalization ability of SVR is affected by two parameters, including the punishment factor p and the kernel parameter g. The p and g of the SVR model were determined using a grid searching method and 5-fold cross-validation [37]. Here, the two parameters optimized in 3 steps:
- (1)
- Give wide initial ranges so that p and g are both within 2−40 and 240.
- (2)
- Create grids with small step-by-step values based on the initial ranges.
- (3)
- Using the five-fold cross-validation, select the optimal values of p and g through the mean square error of cross-validation (MSECV). A smaller MSECV means a better combination of p and g.
Based on the optimal combination of SVR parameters, the prediction models of soil cohesion and soil internal friction angle were constructed by using LIBSVM toolbox in MATLAB, and their performance was evaluated.
2.5. Datasets Division
To build the cohesion and internal friction angle prediction models, we divided the soil dataset using the Kennard–Stone algorithm [52] into a calibration set and a validation set at the ratio of 7:3, so that the data volumes of the training set and the validation set are 58 and 25, respectively. Then prediction models of c and φ were established using the calibration set and predicted using the validation set.
2.6. Performance Evaluation
The coefficient of determination (R2) is often used to assess the prediction precision of the models, and an R2 value close to 1 indicates stronger prediction ability. The root-mean-square error (RMSE) can be used to further evaluate the prediction effect and precision of models. Determining the RMSE of the predicted values is a significant criterion since sometimes a relationship with a high R2 value may also exhibit a high RMSE value. Relative error (RE) can reflect the deviation between the predicted value and the actual value. In this study, R2 and RMSE were chosen to evaluate the predictive abilities of the models, and RE was used to comparatively assess the deviation between the predicted values of each model and the measured values. These evaluation indices were also used in Kayadelen’s research on the prediction of soil shear parameters [53]. The above three indices can be computed as follows [33,53]:
where R2 is the coefficient of deterministic; RMSE is root-mean-square error; RE is the relative error; fi is the predicted value; yi is the measured value; n is the number of samples in the calibration set (or the validation set).
The above three evaluation indicators are represented by RC2, RMSEc, and REC for the calibration set prediction, and RV2, RMSEV, and REV were used for the validation set prediction. The data preprocessing and modeling involved in this paper were all completed using MATLAB (MathWorks, Natick, MA, USA).
3. Results
3.1. Results of Measurements and Correlation Analysis
The basic descriptive statistics of CPT data, soil water content, soil bulk density, and shear strength parameters of the 83 soil measurement points are shown in Table 2. It can be seen from the table that the median and mean are closely distributed for all parameters, which indicates that the statistical distribution of these parameters for experimented samples is nearly normal. As shown in Table 2, the measured value of cone tip resistance ranges from a lower value of 138 N to a high value of 570 N. The average and median values of cone tip resistance are 317.36 N, and 317.42 N, respectively. The cone side pressure values range from 2.57 N to 261.51 N, with an average value of 106.58 N and a median value of 96.43 N. The cohesion value ranges from 1.74 to 38.95 kPa, with a mean of 20.77 kPa and a median of 20.91 kPa. The measured values of the internal friction angle ranged from 8.66° to 32.16°, with mean and median values of 18.73° and 17.70°, respectively. The measured water content values range from 11.88% to 25.84%, with a mean value of 17.68% and a median value of 17.25%, respectively. Among the measured parameters, the spatial variability of bulk density was the lowest ranging from 1.17 g/cm3 to 1.96 g/cm3, with mean and median values of 1.60 g/cm3 and 1.64 g/cm3, respectively.

Table 2.
Basic descriptive statistics for the original data set.
To determine the strength of the linear relationships between variables included in our study, the bivariate correlation technique was adopted to analyze the variables in the dataset, which is represented in a correlation matrix (Table 3). In the correlation analysis, the Pearson correlation coefficients (r values) with c and φ as dependent variables and the other selected soil properties as independent variables were investigated. Dual-variable correlation analysis shows that soil water content, cone tip resistance, and cone side pressure have significant influences on cohesion (r = −0.70, 0.75, and 0.77, respectively). Additionally, bulk density affects cohesion to a certain extent (r = 0.53). Cone side pressure significantly affects the internal friction angle (r = 0.84). These results indicate the potential to build high-performance prediction models by using these independent variables (ω, d, R, P) and two dependent variables (c, φ).

Table 3.
Correlation matrix of variables.
3.2. Results of Model Prediction
3.2.1. Results of BPNN Model Prediction
As shown in Figure 9, for predicting cohesion, the average Rc2 maximizes to 0.89 when the number of hidden layer neurons is 7. As for the internal friction angle, the average Rc2 is optimized to 0.87 when the number of hidden layer neurons is 5. Hence, the two BPNN network model structures shown in Figure 10 were used to predict c and φ, respectively.
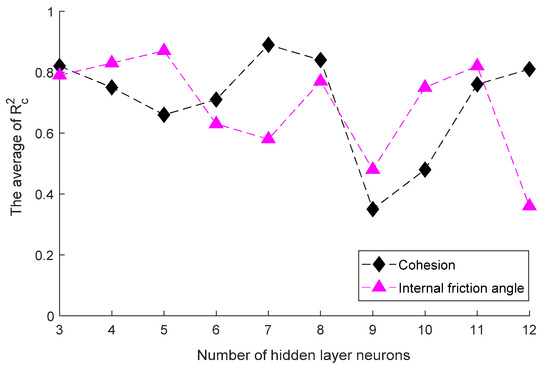
Figure 9.
Effects of the number of hidden layer neurons on correlation coefficient Rc2 in BPNN models.
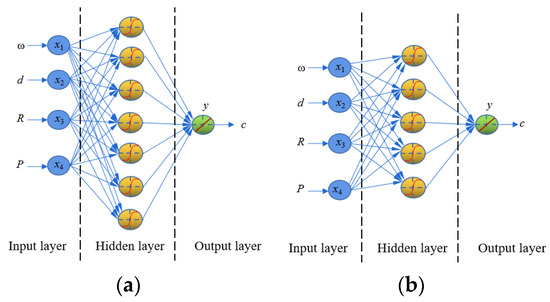
Figure 10.
Soil shearing parameters of BPNN models. (a) BPNN model for prediction of cohesion; (b) BPNN model for prediction of internal friction angle.
The predicted results for cohesion and the internal friction angle by BPNN models are illustrated in Figure 11. The results predicted with the calibration set are RC2 = 0.89, RMSEC = 3.39 (cohesion); RC2 = 0.79, RMSEC = 2.33 (internal friction angle). The prediction results of the validation set are RV2 = 0.87, RMSEV = 4.08 (cohesion); RV2 = 0.75, RMSEV = 3.28 (internal friction angle). Generally, if a proposed model gives R2 > 0.8, there is a strong correlation between the measured and predicted values for all the data available in the database; therefore, the results suggest that the BPNN model is well suited to predicting soil cohesion, but it is not suitable for predicting the internal friction angle.
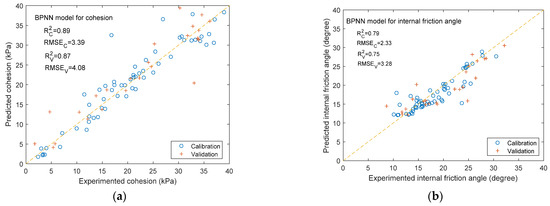
Figure 11.
Soil shearing parameters prediction of the BPNN models. (a) Cohesion; (b) internal friction angle.
3.2.2. Results of PLSR Model Prediction
Figure 12 shows the variation of AIC with the number of PCFs. The optimal number of PCFs can be selected when the AIC value is small. Thus, two PCFs were used in the PLSR prediction model for cohesion, and three PCFs were used for the PLSR model of the internal friction angle. The results of the cohesion and internal friction angle predicted by PLSR are illustrated in Figure 13.
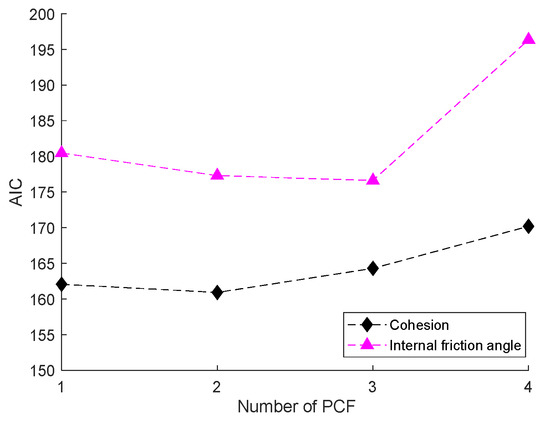
Figure 12.
Effects of number of hidden layer neurons on correlation coefficient RC2 in BPNN models.
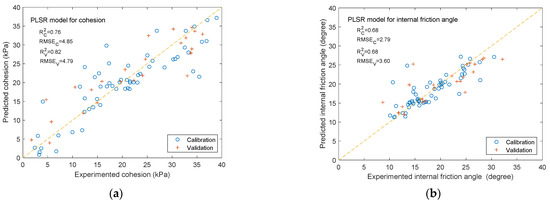
Figure 13.
Soil shear strength parameters prediction of PLSR models. (a) Soil cohesion; (b) soil internal friction angle.
For soil cohesion (Figure 13a), the performance of the PLSR model for the calibration set is RC2 = 0.76, RMSEC = 4.85, which is not satisfactory; however, its RV2 on the validation set is 0.82, greater than 0.8, showing good predictive ability. For the internal friction angle (Figure 13b), the PLSR model evaluation indexes RC2 and RV2 are both 0.68, far less than 0.80, indicating the predictive reliability of the model in both the calibration set and validation set is inadequate.
3.2.3. Results of SVR Model Prediction
To determine the modeling parameters of SVR, grid searching and five-fold cross-validation were used to select a suitable combination of p and g. Figure 14 shows the results of the SVR model parameters. Based on the minimum MSECV, we preferentially selected the values of p and g, which were 0.25 and 0.64, respectively, for cohesion, and 32.4 and 0.20, respectively, for internal friction angle.
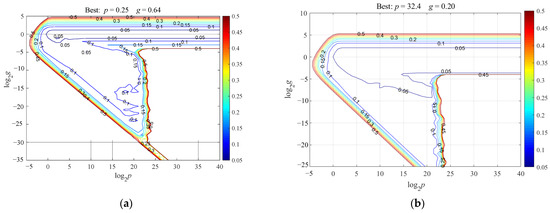
Figure 14.
Parameter optimization of SVR. (a) Cohesion; (b) internal friction angle.
The optimized p and g were used to construct the prediction models of cohesion and internal friction angle for the calibration set, and the validation set was used to test the models. The results are illustrated in Figure 15.
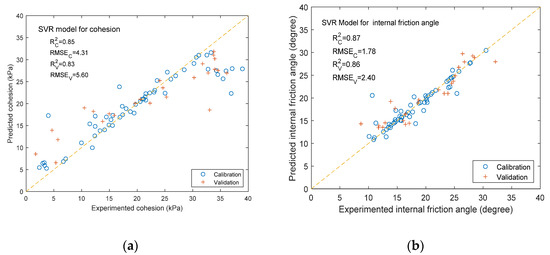
Figure 15.
Soil shearing parameters prediction of SVR models. (a) Soil cohesion; (b) soil internal friction angle.
As shown in Figure 15a, the predicted results of soil cohesion are RC2 = 0.85, RMSEC = 4.31, RV2 = 0.83, and RMSEV = 5.60. Both Rc2 and RV2 are greater than 0.80, indicating that the SVR model is successful in predicting cohesion. For the internal friction angle (Figure 15b), the predictive performance indicators in the SVR model for RC2, RMSEc, RV2, and RMSEV are 0.87, 1.78, 0.86, and 2.40, respectively. RC2 and RV2 are greater than 0.85, showing strong predictive performance.
3.3. Comparative Analysis of the Forecasting Performances of the Different Models
To evaluate the performances of the three ML models (BPNN, PLSR, and SVR) in predicting the soil cohesion and internal friction angle, we analytically assessed these models by using the evaluation indices RV2, RMSEV, and REV. Figure 16 shows a comparison of RV2 and RMSEV.
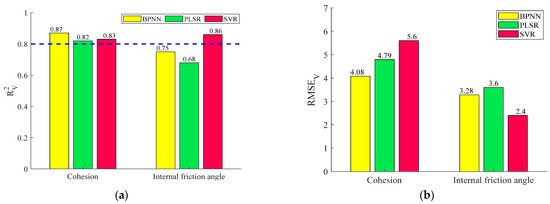
Figure 16.
Comparison of different indices. (a) Comparison of R2; (b) comparison of RPD.
As can be seen from Figure 16a, the RV2 of cohesion of the three ML models all reached above 0.8, showing good predictive ability, but BPNN exhibits the best prediction accuracy because its RV2 is the highest and its RMSEV is the smallest (Figure 16b). Although the RMSEV of the PLSR value is lower than that of SVR, its RV2 value is lower than that of SVR, and its RC2 is only 0.76 (Figure 13a), indicating that the correlation with the PLSR model is not good enough; therefore, we believe that SVR has a better ability to predict cohesion than PLSR. In conclusion, the predictive performance of the three ML models for cohesion is BPNN > SVR > PLSR.
For the internal friction angle, among the three ML models, only the SVR model had an RV2 value of greater than 0.8, and SVR has the lowest RMSEV with a value of 2.4, so the SVR model has the best performance. Both the RV2 and RMSEV values of BPNN are superior to those of PLSR, so its internal friction angle prediction performance is second only to that of SVR; therefore, the prediction ability of the internal friction angle by the three ML models is SVR > BPNN > PLSR.
Figure 17 illustrates the REV curves of different ML models, which compare the prediction deviations of the models.
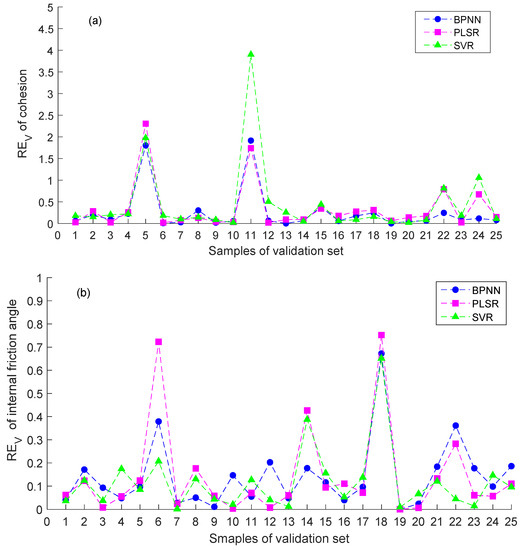
Figure 17.
REV change curves of different models. (a) Cohesion; (b) internal friction angle.
According to the results, for soil cohesion (Figure 17a), the REV of the BPNN, PLSR, and SVR models fluctuate within a range of 0~1.91, 0~2.31, and 0~3.90, respectively. The REV fluctuation range of the BPNN model is the narrowest, verifying that BPNN can more precisely predict soil cohesion than the other two models. As for internal friction angle (Figure 17b), the REV of the BPNN, PLSR, and SVR models varies from 0~0.67, 0~0.75, and 0~0.65, respectively. The fluctuation of the BPNN model is similar to that of the SVR model, but the SVR is slightly better than the BPNN model, and both of them are better than the PLSR model. Thus, we believe that the BPNN model is the best at predicting soil cohesion, and the SVR model is the most suitable for predicting the internal friction angle.
In addition, Figure 17a shows that samples 5 and 11 used for predicting soil cohesion have REV values that significantly deviate from those of the other samples in all three ML models. As can be seen from Figure 17b, samples 6 and 18, which were used to predict the angle of internal soil friction, show similar deviations. By checking the values of validation set samples, we found that the water content of sample 5 was the greatest of all samples, sample 11 showed the greatest cone tip resistance, sample 6 had the lowest cohesion, and the internal friction angle of sample 18 was the least of all the samples. This indicates that when the parameter value is the lowest or highest value, the prediction reliability of the model decreases.
4. Conclusions
In this study, a new method was proposed to predict soil shear strength parameters. The main intellectual merits of this work include the new attempt to combine CPT data with soil properties for modeling, the construction of a portable and low-cost CPT device, and the evaluation of the effectiveness of three ML models (BPNN, PLSR, and SVR) for predicting soil shear strength parameters using a combination of data. Compared with the laboratory direct shear test, this method is convenient to use, and the data are easy to obtain. The test results demonstrate that: (a) CPT data and soil properties can be combined to predict soil shear strength parameters, and (b) the BPNN model has an advantage in predicting soil cohesion, while the SVR model is optimal for predicting the soil’s internal friction angle. According to numerical and evaluation index tradeoffs, the BPNN model with a 4-7-1 neuron structure (RC2 = 0.89, RMSEC = 3.39, RV2 = 0.87, and RMSEV = 4.08) is the most suitable prediction model for soil cohesion, while the SVR model with punishment factor 32.4 and kernel parameter 0.20 (RC2 = 0.87, RMSEC = 1.78, RV2 = 0.86, and RMSEV = 2.40) is used to predict the soil’s internal friction angle.
This study effectively improves the determination efficiency of shear strength parameters for arable soil; however, in our work, soil water content and soil bulk density are measured using an oven-drying method, which is not conducive to real-time detection. In addition, it should be stressed that the models used can be reliably applied when the parameter values range between the minimum and maximum values of each parameter (as presented in Table 2); otherwise, the predicted value is unreliable; therefore, future research into a method that can quickly obtain soil water content and soil bulk density is necessary, and the number of soil samples should also be increased in order to increase the range of suitable models. Moreover, the model optimization algorithms should also be studied in order to reduce the computation complexity of the used models.
Author Contributions
Conceptualization, L.Z. and Q.Z.; methodology, Q.L.; software, Z.W., J.C. and Z.C.; validation, L.Z., Q.L. and Q.Z.; formal analysis, Q.B., J.C., and Z.W.; investigation, Q.Z. and Z.C.; resources, Q.L.; data curation, Z.W., Q.B. and J.C.; writing—original draft preparation, L.Z.; writing—review and editing, L.Z., Q.L. and Q.Z.; supervision, Q.Z.; project administration, Q.L.; funding acquisition, L.Z. and Q.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Nature Science Foundation of China (32001427), the China Postdoctoral Science Foundation (2021M701341), and the National Rape Crop Industry System Special Project Funding (CARS-12).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Moayedi, H.; Bui, D.T.; Dounis, A. Novel Nature-Inspired Hybrids of Neural Computing for Estimating Soil Shear Strength. Appl. Sci. 2019, 9, 4643. [Google Scholar] [CrossRef]
- Khaboushan, E.A.; Emami, H.; Mosaddeghi, M.R. Estimation of unsaturated shear strength parameters using easily-available soil properties. Soil Tillage Res. 2018, 184, 118–127. [Google Scholar] [CrossRef]
- Barbhuiya, G.H.; Hasan, S.D. Effect of nano-silica on physio-mechanical properties and microstructure of soil: A comprehensive review. Mater. Today Proc. 2021, 44, 217–221. [Google Scholar] [CrossRef]
- Imhoff, S.; Da Silva, A.P.; Fallow, D. Susceptibility to compaction, load support capacity, and soil compressibility of Hapludox. Soil Sci. Soc. 2004, 68, 17–24. [Google Scholar] [CrossRef]
- Schjønning, P.; Lamandé, M.; Keller, T. Subsoil shear strength—Measurements and prediction models based on readily available soil properties. Soil Till. Res. 2020, 200, 104638. [Google Scholar] [CrossRef]
- Blanco-Canqui, H.; Lal, R.; Owen, L.B.; Post, W.M.; Izaurralde, R.C. Strength properties and organic carbon of soils in the north appalachian region. Soil Sci. Soc. Am. J. 2005, 69, 663–673. [Google Scholar] [CrossRef]
- Stafford, J.V.; Tanner, D.W. Effect of rate on soil shear strength and soil-metal friction I. Shear strength. Soil Tillage Res. 1983, 3, 245–260. [Google Scholar] [CrossRef]
- Eudoxie, G.D.; Phillips, D.; Springer, R. Surface hardness as an indicator of soil strength of agricultural soils. Open J. Soil Sci. 2012, 2, 341–346. [Google Scholar] [CrossRef]
- Bradford, J.M.; Grossman, R.B. In-situ measurement of near-surface soil strength by the fall-cone device. Soil Sci. Soc. Am. J. 1982, 46, 685–688. [Google Scholar] [CrossRef]
- Wuddivira, M.N.; Stone, R.J.; Ekwue, E.I. Influence of cohesive and disruptive forces on strength and erodibility of tropical soils. Soil Tillage Res. 2013, 133, 40–48. [Google Scholar] [CrossRef]
- Khalili, N.; Geiser, F.; Blight, G.E. Effective stress in unsaturated soils: Review with new evidence. Int. J. Geomech. 2004, 4, 115–126. [Google Scholar] [CrossRef]
- Brzezinski, K.; Jozefiak, K.; Zbiciak, A. On the interpretation of shear parameters uncertainty with a linear regression approach. Measurement 2021, 174, 108949. [Google Scholar] [CrossRef]
- Bol, E.; Onalp, A.; Ozocak, A.; Sert, S. Estimation of the undrained shear strength of Adapazari fine grained soils by cone penetration test. Eng. Geol. 2019, 261, 105277. [Google Scholar] [CrossRef]
- Begemann, H.K. The friction jacket cone as an aide in determining the soil profile. In Proceedings of the 6th International Conference on Soil Mechanics and Foundation Engineering, Montreal, QC, Canada, 8–15 September 1965; Volume 1, pp. 17–20. [Google Scholar]
- Salari, P.; Lashkaripour, G.; Ghafoori, M. Presentation of empirical equations for estimating internal friction angle of SP and SC soils in Mashhad, Iran using standard penetration and direct shear tests and comparison with previous equations. Int. J. Geogr. Geol. 2015, 4, 89–95. [Google Scholar] [CrossRef][Green Version]
- Motaghedi, H.; Armaghani, D.J. New method for estimation of soil shear strength parameters using results of piezocone. Measurement 2016, 77, 132–142. [Google Scholar] [CrossRef]
- Satyanaga, A.; Bairakhmetov, N.; Kim, J.R.; Moon, S.W. Role of bimodal water retention curve on the unsaturated shear strength. Appl. Sci. 2022, 12, 1266. [Google Scholar] [CrossRef]
- García, A.J.H.; Jaime, Y.N.M. Savanna soil water content effect on its shear strength-compaction relationship. Rev. Cient. Agric. 2013, 12, 324–337. [Google Scholar]
- Zheng, Z.; Zhang, X.; Li, T.; Jin, W.; Lin, C. Change characteristics and influencing factors of soil shear strength during maize growing period. Trans. Chin. Soc. Agric. Mach. 2014, 45, 125–130. [Google Scholar] [CrossRef]
- Zhang, B.; Zhao, Q.G.; Horn, R.; Baumgartl, T. Shear strength of surface soil as affected by soil bulk density and soil water content. J. Soil Tillage Res. 2001, 34, 162–174. [Google Scholar] [CrossRef]
- Stefanow, D.; Dudziński, P.A. Soil shear strength determination methods–State of the art. Soil Till. Res. 2021, 208, 104881. [Google Scholar] [CrossRef]
- Baldi, P.; Brunak, S. Bioinformatics: The machine learning approach. Phys. Today 2002, 55, 57–58. [Google Scholar] [CrossRef]
- Li, G.; Li, Y.; Chen, H.; Deng, W. Fractional-order controller for course-keeping of underactuated surface vessels based on frequency domain specification and improved particle swarm optimization algorithm. Appl. Sci. 2022, 12, 3139. [Google Scholar] [CrossRef]
- Lee, M.; Jeon, I.; Jun, C. A deterministic methodology using smart card data for prediction of ridership on public transport. Appl. Sci. 2022, 12, 3867. [Google Scholar] [CrossRef]
- Cui, H.; Guan, Y.; Chen, H. Rolling element fault diagnosis based on VMD and sensitivity MCKD. IEEE Access 2021, 9, 120297–120308. [Google Scholar] [CrossRef]
- Özçoban, M.Ş.; Isenkul, M.E.; Sevgen, S.; Acarer, S.; Tüfekci, M. Modelling the effects of nanomaterial addition on the permeability of the compacted clay soil using machine learning-based flow resistance analysis. Appl. Sci. 2022, 12, 186. [Google Scholar] [CrossRef]
- Khalilmoghadam, B.; Afyuni, M.; Abbaspour, K.C.; Jalalian, A.; Schulin, R. Estimation of surface shear strength in Zagros region of Iran—A comparison of artificial neural networks and multiple-linear regression models. Geoderma 2009, 153, 29–36. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J. Using neural networks to predict soil water retention and soil hydraulic conductivity. Soil Tillage Res. 1998, 47, 37–42. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. Available online: https://www.science.org/doi/10.1126/science.aaa8415 (accessed on 21 March 2022). [CrossRef]
- Nasiri, S.; Khosravani, M.R. Machine learning in predicting mechanical behavior of additively manufactured parts. J. Mater. Res. Technol. 2021, 14, 1137–1153. [Google Scholar] [CrossRef]
- Huang, D.; Liu, H.; Zhu, L.; Li, M.; Xia, X.; Qi, J. Soil organic matter determination based on artificial olfactory system and PLSR-BPNN. Meas. Sci. Technol. 2021, 32, 035801. [Google Scholar] [CrossRef]
- Wang, X.; An, S.; Xu, Y.; Hou, H.; Chen, F.; Yang, Y.; Zhang, S.; Liu, R. A back propagation neural network model optimized by mind evolutionary algorithm for estimating Cd, Cr, and Pb concentrations in soils using Vis-NIR diffuse reflectance spectroscopy. Appl. Sci. 2020, 10, 51. [Google Scholar] [CrossRef]
- Zhu, L.; Jia, H.; Chen, Y.; Wang, Q.; Li, M.; Huang, D.; Bai, Y. A novel method for soil organic matter determination by using an artificial olfactory system. Sensors 2019, 19, 3417. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.; Ly, H.B.; Pham, B.T. Backpropagation neural network-based machine learning model for prediction of soil friction angle. Math. Probl. Eng. 2020, 2020, 8845768. [Google Scholar] [CrossRef]
- Yang, W.; Lan, H.; Li, M.; Meng, C. Predicting bulk density and porosity of soil using image processing and support vector regression. Trans. CSAE 2021, 37, 144–151. [Google Scholar] [CrossRef]
- Du, P.; Wang, J.; Yang, W.; Niu, T. A novel hybrid model for short-term wind power forecasting. Appl. Soft Comput. 2019, 80, 93–106. [Google Scholar] [CrossRef]
- Zhao, M.; Ren, J.; Ji, L.; Fu, C.; Li, J.; Zhou, M. Parameter selection of support vector machines and genetic algorithm based on change area search. Neural Comput. Appl. 2012, 21, 1–8. [Google Scholar] [CrossRef]
- Ji, W.; Shi, Z.; Huang, J.; Li, S. In situ measurement of some soil properties in paddy soil using visible and near-infrared spectroscopy. PLoS ONE 2014, 9, e105708. [Google Scholar] [CrossRef]
- Li, B.; Morris, J.; Martin, E.B. Model selection for partial least squares regression. Chemometr. Intell. Lab. 2002, 64, 79–89. [Google Scholar] [CrossRef]
- Zhou, W. Cone Penetrometer. In Encyclopedia of Engineering Geology; Bobrowsky, P., Marker, B., Eds.; Encyclopedia of Earth Sciences Series; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Spence, C.J.T.; Buchmann, N.A.; Jermy, M.C. Unsteady flow in the nasal cavity with high flow therapy measured by stereoscopic PIV. Exp. Fluids 2011, 52, 569–579. [Google Scholar] [CrossRef]
- Kambi, S.J.; Follett, R.F. Error analysis of filters implemented with floating point arithmetic. In Proceedings of the 26th Southeastern Symposium on System Theory, Athens, OH, USA, 20–22 March 1994; IEEE: Piscataway, NJ, USA, 1994; pp. 47–51. [Google Scholar] [CrossRef]
- Gan, J.k.M.; Fredlund, D.G.; Rahardjo, H. Determination of the shear strength parameters of an unsaturated soil using the direct shear test. Can. Geotech. J. 1988, 25, 500–510. [Google Scholar] [CrossRef]
- Li, W.; Jacobs, R.; Morgan, D. Predicting the thermodynamic stability of perovskite oxides using multiple machine learning techniques. Comput. Mater. Sci. 2018, 150, 454–463. [Google Scholar] [CrossRef]
- Chen, G.; Tang, W.; Chen, S.; Wang, S.; Cui, H. Prediction of self-healing of engineered cementitious composite using machine learning approaches. Appl. Sci. 2022, 12, 3605. [Google Scholar] [CrossRef]
- Rossel, V.; Walvoor, D.; Mcbratney, A.B.; Janik, L.J.; Skjemstad, J.O. Visible, near infrared, mid infrared or combined diffuse reflectance spectroscopy for simultaneous assessment of various soil properties. Geoderma 2003, 131, 59–75. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Jędrzejczyk, A.; Byrdy, A.; Firek, K.; Rusek, J. Partial least squares regression approach in the analysis of damage intensity changes to prefabricated RC buildings during the long term of mining activity. Appl. Sci. 2022, 12, 467. [Google Scholar] [CrossRef]
- Rosipal, R.; Krämer, N. Overview and Recent Advances in Partial Least Squares. In International Statistical and Optimization Perspectives Workshop “Subspace, Latent Structure and Feature Selection”, Bohinj, Slovenia, 23–25 February 2005; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3940, pp. 34–51. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory, 2nd ed.; Springer: New York, NY, USA, 2000; pp. 138–167. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Kennard, R.W.; Stone, L.A. Computer aided design of experiments. Technometrics 1969, 11, 137–148. [Google Scholar] [CrossRef]
- Kayadelen, C.; Gunaydın, O.; Fener, M.; Demir, A.; Ozvan, A. Modeling of the angle of shearing resistance of soils using soft computing systems. Expert Syst. Appl. 2009, 36, 11814–11826. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).