Suitability Evaluation of the Lining Form Based on Combination Weighting–Set Pair Analysis

Abstract

Aiming at the many uncertain factors in the suitability evaluation of reinforced concrete lining of high-pressure pipelines, the set pair analysis (SPA) theory is used to establish the suitability evaluation model. By summarizing the key influencing factors of typical lining design criteria, five suitability evaluation indices are determined from three criteria, i.e., the minimum overburden criterion, the minimum principal stress criterion, and the hydraulic fracturing criterion. In order to fully consider the subjective and objective factors, the combination ordered weighted averaging (C-OWA) operator and the criteria importance through intercriteria correlation (CRITIC)-entropy weighting model (EWM) were used to construct a combination weighting method, and the weight coefficients of each index were comprehensively determined. Based on the SPA theory and calculation rules, combined with the lining suitability grading criteria, the five-element connection degree of each index and the comprehensive connection degree of each working point were calculated. In this study, the model is applied to the suitability evaluation of reinforced concrete lining at each drilling point of the high-pressure pipeline of a pumped storage power station (PSPS) in Shanxi Province. The results show that the proposed model consisting of subjective weight and objective weight can effectively avoid the error caused by a single weight method, which improves the evaluation sensitivity and rationality.

1. Introduction

The pumped storage power station (PSPS) is a special power supply with many functions, such as peak shaving, valley filling, phase modulation, and emergency standby [1,2]. It not only has a flexible storage capacity which could support the deployment of wind and solar energy, but also helps to ensure the secure and stable operation of power grid [3,4]. In 2016, the signing of the “Paris Agreement” resulted in a quick development of green and low-carbon energy [5]. With rapid development of new energy, the construction of PSPS has once again entered the vision of decision makers in some major countries. The International Renewable Energy Agency (IRENA) proposed that by 2030, the global installed capacity of energy storage will increase by 42% to 68% by 2017, and the increase in installed capacity of pumped storage will be in a range from about 40% to 50%. With commitment from the Chinese government, the peak of carbon dioxide emission and carbon neutrality will be achieved before 2030 and 2060, respectively, and it is estimated that the installed capacity of PSPS will reach about 120 million kW by 2030, continuing to maintain the world’s leading level. The opportunity of rapid development for PSPS could be expected both globally and domestically. Therefore, it is very urgent to speed up the construction of PSPS [6].

The key part of PSPS is the water conveyance system that connects the upper and lower reservoirs, which is similar to the blood vessels of the human body. In the design scheme, the water level difference and internal water pressure of the pipeline are generally high. Therefore, the lining must be able to have the ability to deal with problems caused by high water level difference and internal water pressure [7]. At present, the common forms of high-pressure pipelines are steel plate lining and reinforced concrete lining. The former has high price and complicated construction; the latter is economical and simple in manufacturing processes [8]. When designing and selecting the lining forms, it is necessary to consider the influence of a variety of uncertain factors to prevent unpredictable losses. From an economic and reasonable point of view, it is very important to choose an appropriate high-pressure pipeline lining form.

In order to select the appropriate lining form and avoid hydraulic fracturing under the effect of high water head, some design guidelines are commonly used for high-pressure pipelines, such as the minimum overburden criterion, the minimum principal stresses criterion, and the hydraulic fracturing criterion [9,10,11]. Zhang [10] discussed the interrelationship between these three guidelines and the application conditions, and confirmed that the engineering design for high-pressure pipelines should be focused on the reconnaissance and utilization of the surrounding rock geotechnical conditions and crustal stress state as well as the permeability of rock mass under high water pressure, etc. Schleiss [12] discussed the influence of seepage pressure and stress distribution on lining cracking based on design criteria for reinforced concrete-lined tunnels. Kang Bian et al. [11] used the minimum overburden criterion and the minimum principal stress criterion to eliminate the possibility of cracking caused by improper lining design in the investigation of the causes of high-pressure pipe linings cracking in Huizhou PSPS. In addition, many scholars have used various mathematical models to simulate the hydraulics interactions in high-pressure pipelines in order to explore the key factors affecting the stability of reinforced concrete linings. Chen et al. [13] used a three-dimensional finite element method (3D-FEM) to effectively reflect the main influencing factors (such as the property of surrounding rocks, the internal water pressure, and the interaction and initial gap between surrounding rocks and lining) of the lining stress characteristics. Dadashi et al. [7] used the ABAQUS finite element program based on a direct-coupled method to analyze the hydraulic interaction of high-pressure pipelines and found that the reinforcement distribution and the lining thickness are the key factors affecting the lining stability. Zhou et al. [8] and Su [9] found that in situ stress, rock permeability, and the rock mass deformation modulus are all important parameters for the design of reinforced concrete linings by analyzing the hydraulics interactions in high-pressure hydraulic pipelines.

At present, the methods of selecting the lining form are mostly based on a quantitative perspective. In actual projects, there are also some cases in which the experts directly select the lining form qualitatively according to their engineering experiences. However, whether from a qualitative or quantitative point of view, few scholars have considered the interaction between deterministic and uncertain factors in the suitability evaluation of lining forms. The subjective and objective combination weighting–SPA can be well dealt with in this regard. In this study, a combination weighting–SPA evaluation model of a five-element connection degree was established based on the reinforced concrete lining form. In this model, C-OWA operator was used to calculate the subjective weights of evaluation indices, and the objective weight was determined by the CRITIC method and EWM. Based on the above model, the suitability evaluation indices of the lining form were discussed and selected.

2. The Suitability Level of Lining Form

The established suitability evaluation model in this study can not only utilize the results of current drilling exploration, reduce the workload, and improve the efficiency of design scheme, but also considers the decision of expert evaluation. The five evaluation indices are related to the minimum overburden thickness, the minimum in situ stress, the hydraulic fracturing pressure, the hydraulic gradient, and the surrounding rock classification, which can be recorded as A, B, C, D, and E, respectively. The suitability of the reinforced concrete lining form is divided into five evaluation levels: extremely suitable (I), more suitable (II), basically suitable (III), relatively unsuitable (IV), and extremely unsuitable (V). The relationship between indices and evaluation level of the lining is shown in

Table 1. Relationship between Indices and Evaluation Level of the Lining.

Evaluation Level	Extremely Suitable (I)	More Suitable (II)	Basically Suitable (III)	Relatively Unsuitable (IV)	Extremely Unsuitable (V)
A	>1.5	1.3~1.5	1.2~1.3	1.0~1.2	<1.0
B	>1.3	1.2~1.3	1.1~1.2	1.0~1.1	<1.0
C	>1.3	1.2~1.3	1.1~1.2	1.0~1.1	<1.0
D	<3	3~6	6~10	10~15	>15
E	100~50	50~30	30~10	10~3	<3

.

(a) Evaluation index A is selected with reference to the minimum overburden criterion. It is calculated by Equation (1). This index determines the suitability level of the safety degree of reinforced concrete linings by the ratio of the minimum overburden thickness of rock mass at the design location of high-pressure pipelines to the hydrostatic pressure. In the Norwegian criterion, the safety degree value is in the range of 1.05–1.1. However, the rock weathering in China is relatively deep. Professor Gu Zhaoqi’s suggestion is mostly adopted in the practical engineering applications and the evaluation level is more suitable when the index value is in the range of 1.3–1.5 [14].

$$A\ge \frac{r_{R}cos\alpha C_{RM}}{{\gamma }_w{h}_s}$$

(1)

where $C_{RM}$ is the minimum overburden thickness of rock mass (m); $h_s$ is the hydrostatic pressure head at the selected position of the high-pressure pipeline (m); ${\gamma }_w$ is the weight of water, which is taken as 10 kN/m³; ${\gamma }_R$ is the weight of rock mass (kN/m³); and α is the slope angle of the mountain body at the selected position of the high-pressure pipeline.

(b) Evaluation index B is selected according to the hydraulic fracturing criterion, which is used mainly to check the permeability of rock mass and fracture and determine whether they meet the requirements of permeability stability. The index is calculated by comparing the normal stress ${\sigma }_n$ on the joint or fracture surface with the hydrostatic pressure of high-pressure pipelines, which could help to determine the suitability level of the safety degree of reinforced concrete linings. When Equation (2) is satisfied, tensile stress does not occur on the joint or fracture surface of the surrounding rock under water pressure, and hydraulic fracturing does not occur on the surrounding rock. Generally, the index should have a certain safety margin. According to the engineering experience, it is more suitable for the value range of 1.2–1.3 [15].

$$B\ge \frac{{\sigma }_n}{{\gamma }_w{h}_s}$$

(2)

(c) Evaluation index C is selected according to the minimum principal stress criterion. This criterion is actually an engineering generalization of the hydraulic fracturing criterion. In engineering applications, the normal stress ${\sigma }_n$ is difficult to obtain on the joints or fracture surfaces of high-pressure pipelines, and therefore it is replaced by the minimum principal stress ${\sigma }_{min}$. The index uses the ratio of minimum principal stress ${\sigma }_{min}$ to the hydrostatic pressure in high-pressure pipelines to determine the suitability level of safety degree, taking the same range of values as the evaluation indicator B. It is obtained by Equation (3).

$$C\ge \frac{{\sigma }_{min}}{{\gamma }_w{h}_s}$$

(3)

(d) Evaluation index D is based on the hydraulic gradient of high-pressure pipelines to evaluate the suitability of reinforced concrete lining. The hydraulic gradient is closely related to the hydraulic fracturing criterion and is an important parameter for determining the permeability stability of the surrounding rock. According to the material and fracture development in the borehole fault fracture zone of high-pressure pipelines, there is a time-varying phenomenon along the fault fracture zone, and it is relatively strong. Combined with similar engineering experience, the high-pressure hydraulic gradient is generally not greater than 10~15 under I~III class hard surrounding rock conditions, and the hydraulic gradient in fault fracture zone and influence zone is recommended to be 3.0~6.0. Therefore, the hydraulic gradient value range is 6~10, which is basically suitable.

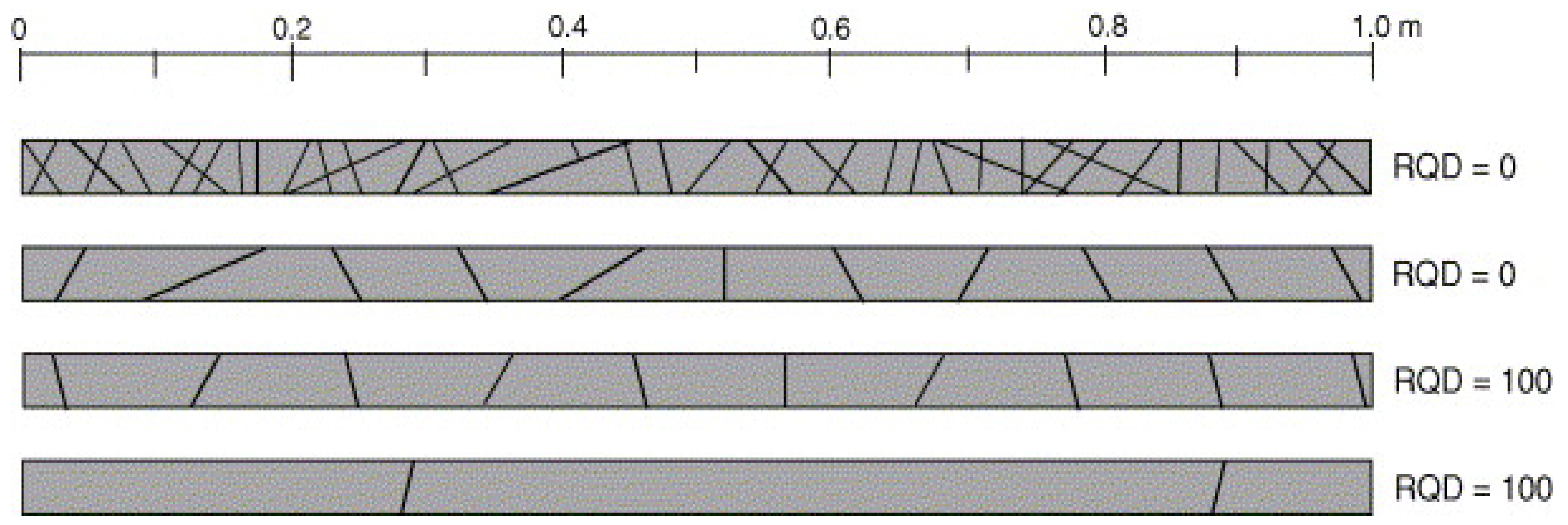
(e) Evaluation index E evaluates the suitability of reinforced concrete linings according to rock mass classification of high-pressure pipelines. This index is also an important impact parameter for the above criterions. In drilling exploration, the rock quality designation (RQD) is usually selected to determine the rock mass classification. However, many researchers pointed out that the RQD cannot directly reflect the rock structure type and rock block composition [16,17,18]. As shown in Figure 1, when the distance (intercept) between joints is 10 cm or less, the RQD is 0%, whereas when the distance is 11 cm or more, the RQD is 100%. Compared with RQD, the rock mass block index (RBI) is able to reflect the size of the rock mass [19]. For a rock mass with RQD equal to 90%, although its block composition varies among 10–30, >50, >100 cm, etc., the RBI values corresponding to each case are different. RBI is more accurate than RQD in reflecting the structural characteristics of the rock mass [20]. Therefore, RBI is an improvement and supplement to RQD, and the formula is shown in Equation (4).

$$\mathrm{RBI}=3C_{r3}+10C_{r10}+30C_{r30}+50C_{r50}+100C_{r100}$$

(4)

where, Cr₃, Cr₁₀, Cr₃₀, Cr_50, and Cr₁₀₀ are the core acquisition rates with lengths of 3~10, 10~30, 30~50, 50~100, and >100 cm, respectively. Furthermore, 3, 10, 30, 50, and 100 are all coefficients.

3. The Proposed Methodology

Figure 2 presents the flowchart of the proposed methodology for the suitable level of reinforced concrete lining. The main steps of the methodology are shown below.

3.1. C-OWA Operator

A commonly used aggregation operator is the ordered weighted averaging (OWA) operator [21]. The C-OWA operator is an improved weight calculation method based on OWA operator. It eliminates the subjectivity and extreme value of expert weight assigned by the orderly weighted average operation, making weight more objective and reasonable [22,23]. Steps are as follows:

(1)

Firstly, n experts were invited to score the importance of indices at the same level (using a 10-point system) to form the initial decision data A = (x_1j, x_2j, …, x_mj). Then, the initial decision data are arranged in descending order to acquire new decision data B = (y_0j, y_2j, …, y_(m−1)j).

(2)

The weighted vector $u_i$ of the decision data B is calculated by Equation (5).

$$u_i=\frac{C_{m-1}^i}{{\displaystyle \underset{k=0}{{{\displaystyle \sum }}^{}^{m-1}}}{C}_{m-1}^k}=\frac{C_{m-1}^i}{2^{m-1}}$$

(5)

where $C_{m-1}^i$ represents the combination number of i data selected from m−1 data, $i\in \left[0,m-1\right]$.

(3)

The absolute weight of the assessment index P_j is obtained by weighting the decision data B with the weighted vector $u_i$. The equation is as follows:

$$P_j={\displaystyle \underset{i=0}{{{\displaystyle \sum }}^{}^{m-1}}}{u}_i{y}_{ij}$$

(6)

where j represents the jth index.

(4)

According to the absolute weight, the relative weight of the assessment index λ_j is calculated by Equation (7).

$${\lambda }_j=\frac{P_j}{{\displaystyle \underset{j=1}{{{\displaystyle \sum }}^{}^n}}{P}_j}$$

(7)

3.2. CRITIC-EWM Method

3.2.1. CRITIC Method

The CRITIC method was proposed by Diakoulaki et al. in 1995, and the basic idea is to use two parameters (i.e., correlation coefficient and standard deviation) to determine the objective weight of the index [24]. The standard deviation indicates the contrast intensity of the index, and the larger the standard deviation is, the greater the value difference of each scheme [25]. Meanwhile, the correlation coefficient is a quantitative index of conflict, and the conflict decreases with the increase in the correlation coefficient [26]. It is mainly divided into five steps:

(1)

The initial indicator data matrix X is defined as follows:

$$X={\left(x_{ij}\right)}_{m\times n}$$

(8)

where $x_{ij}$ are the raw data of the jth index corresponding to the ith object.

(2)

Initial data normalization

In order to eliminate the impact of different dimensions on the evaluation results, it is necessary to standardize each index.

If the index value used is larger, the forward treatment is generally adopted by Equation (9).

$$y_{ij}=\frac{x_{ij}-\min (x_{ij})}{\max (x_{ij})-\min (x_{ij})}$$

(9)

If the index value is smaller, the reverse treatment is generally used by Equation (10).

$$y_{ij}=\frac{\max (x_{ij})-x_{ij}}{\max \left(x_{ij}\right)-\min (x_{ij})}$$

(10)

(3)

The standard deviation of each index is calculated by Equation (11).

$${\sigma }_j=\sqrt{\frac{1}{m-1}{\displaystyle \underset{i=1}{{{\displaystyle \sum }}^{}^m}}{\left(y_{ij}-{\overline{y}}_j\right)}^2}$$

(11)

where ${\sigma }_j$ is the standard deviation of the index x_j;${\overline{y}}_j$ is the average value of the jth index.

(4)

Correlation coefficient of the indices is calculated by Equation (12).

$$r_{ij}=\frac{{\displaystyle \underset{i=1}{{{\displaystyle \sum }}^{}^n}}\left(y_i-{\overline{y}}_i\right)\left(y_j-{\overline{y}}_j\right)}{\sqrt{{\displaystyle \underset{i=1}{{{\displaystyle \sum }}^{}^n}}{\left(y_i-{\overline{y}}_i\right)}^2{\displaystyle \underset{j=1}{{{\displaystyle \sum }}^{}^n}}{\left(y_j-{\overline{y}}_j\right)}^2}}$$

(12)

where $r_{ij}$ is the correlation coefficient between index x_i and x_j.

(5)

The objective weight of the indices is calculated by Equations (13) and (14).

$$B_j={\sigma }_j{\displaystyle \underset{i=1}{{{\displaystyle \sum }}^{}^n}}\left(1-r_{ij}\right)$$

(13)

$${\phi }_j=\frac{B_j}{{\displaystyle \underset{j=1}{{{\displaystyle \sum }}^{}^n}}{B}_j}$$

(14)

where $B_j$ is the composite information of the jth index.

3.2.2. Improved EWM

EWM is an objective weighting method for characterizing the dispersion of information on the indices [27,28]. In order to extend the scope of application of EWM and make it more convenient to use [29], the improved EWM to determine the objective weights of evaluation indices was adopted. Steps are as follows:

(1) Based on the CRITIC method, n indices and m samples are set in the evaluation, and the measured value of the jth index in the ith sample is recorded by Equation (15). The entropy value $R_j$ of the jth index is defined by Equation (16).

$$r_{ij}=\frac{y_{ij}+1}{{\displaystyle \underset{i=1}{{{\displaystyle \sum }}^{}^m}}(y_{ij}+1)}$$

(15)

$$R_j=\frac{-{\displaystyle \underset{i=1}{{{\displaystyle \sum }}^{}^m}}{r}_{ij}\ln r_{ij}}{\ln m}$$

(16)

(2) The improved entropy weight of the jth index is calculated by Equation (17).

$$e_j=\frac{1-R_j}{{\displaystyle \underset{j=1}{{{\displaystyle \sum }}^{}^n}}\left(1-R_j\right)}$$

(17)

3.2.3. Determining the Objective Weight

The CRITIC method can eliminate the influence of some indices with strong correlation and reduce the information overlap between indices. However, this method ignores the dispersion between data, and the improved EWM can effectively make up for this deficiency. The integration of these two methods can fully take into account the dispersion, correlation, and comparison intensity of the data, and more effectively reflect the differences and correlation of the objective data of the evaluation indices [30]. The specific formula of combined objective weight${\omega }_j$ is calculated by Equation (18).

$${\omega }_j=({\phi }_j+e_j)/2$$

(18)

3.3. Combination Weighting

The combination weighting method integrates expert experience and objective data. It makes the weighting of the evaluation indices reach the unity of subjective and objective, and improves the rationality of evaluation results. The multiplicative synthesis method [31] is used to determine the comprehensive weight. The calculation equation is:

$${\omega }_j^{\prime }=\frac{{\lambda }_j{\omega }_j}{{\displaystyle \underset{j=1}{{{\displaystyle \sum }}^{}^n}}{\lambda }_j{\omega }_j}$$

(19)

where ${\omega }_j^{\prime }$ represents the combination weight of the jth index and ${\lambda }_j$ and ${\omega }_j$ are the subjective and objective weights of the jth index, respectively.

3.4. SPA

The SPA method is an improved uncertainty theory which is an integrated certainty–uncertainty system [32,33,34]. It illustrates unsureness in three angles, namely “identity”, “discrepancy”, and “contrary”, and the connection degree is one of its main features [35,36]. These two objects are a system of interconnection, restriction, and interaction with each other, forming a pair of certainty and uncertainty sets H (A, B). The degree of connectedness of the two objects is determined as follows:

$$\mu =\frac{S}{K}+\frac{F}{K}i+\frac{P}{K}j=a+bi+cj$$

(20)

where μ is the connection degree between sets A and B, K stands for the total number of elements; S elements show identical properties, F elements demonstrate discrepant properties, and P elements display contrary properties; a, b, and c represent the degree of “identity”, “discrepancy”, and “contrary”, respectively, and a + b + c = 1; i is the uncertainty coefficient in [−1, 1]; and j is the contrary coefficient, j = −1.

The evaluation of a high-pressure pipe lining form is a complex work affected by a variety of uncertain factors. In order to accurately express the certain and uncertain relationships between the indices, the discrepancy in the ternary connection degree of its core elements was further subdivided to obtain a five-element connection degree expression in this study. The equation is as follows:

$$\{\begin{array}{c}u=a+b_1{i}_1+b_2{i}_2+b_3{i}_3+cj=a+bu+cv+dw+el\\ a+b+c+d+e=1\\ a,b,c,d,e\in 0,1\\ u,v,w\in -1,1,l=-1\end{array}$$

(21)

where, a, b, c, d, e are the connection degrees of the evaluation levels I, II, III, IV, and V, respectively, and u, v, w, and $l$ are connection component coefficients.

Combining the comprehensive weight of each index, the comprehensive five-element connection degree of the lining suitability level is calculated, and the calculation formula is obtained by Equation (22).

$$\mu =\underset{j=1}{{{\displaystyle \sum }}^{}^n}{a}_j{\omega }_j^{\prime }+\underset{j=1}{{{\displaystyle \sum }}^{}^n}{b}_j{\omega }_j^{\prime }u+\underset{j=1}{{{\displaystyle \sum }}^{}^n}{c}_j{\omega }_j^{\prime }v+\underset{j=1}{{{\displaystyle \sum }}^{}^n}{d}_j{\omega }_j^{\prime }w+\underset{j=1}{{{\displaystyle \sum }}^{}^n}{e}_j{\omega }_j^{\prime }l$$

(22)

4. Case Study

4.1. Project Overview

A PSPS in Shanxi Province has a proposed installed capacity of 1500 MW. The water conveyance system is arranged in the mountain beam between the upper and lower reservoirs, consisting of the diversion system and the tail water system, both of which adopt the arrangement of one pipe and two machines. Two high-pressure main pipes are arranged in parallel, with horizontal spacing of 28.04 m. The lengths of 1# and 2# high-pressure main pipes are 1338.93 m and 1370.11 m, respectively. The high-pressure main pipe is arranged by a buried three inclined shaft. The middle-up flat section and the middle-down flat section are set up with elevations of 1830 m and 1580 m, respectively.

The lithology of the project area is mainly biotite plagiogneiss and diopside-bearing biotite plagioclase amphibolite. The gneiss is a massive structure, and the primary gneissosity is mainly streamlined. It is affected by the late tectonic movement, and faults are more developed in the rock mass. The amphibolite is a massive structure and xenolith form. There is no obvious lithologic boundary between the two lithologies, but mainly in the form of a fracture and melting contact relationship.

Currently, it is in the peak period of new energy policy expansion and energy storage/storage power station construction demand. Due to the requirements of the construction period and design plan of the PSPS and the restriction of using hole-detecting explosives, there is no hole-detecting data for high-pressure pipelines. Therefore, the drilling data of the high-pressure pipeline (

Table 2. High-pressure pipeline section analysis data.

Drilling Number	A	B	C	D	E
1	2.43	4.79	7.07	5.89	33.93
2	2.04	2.93	4.96	8.20	69.12
3	1.82	2.79	3.67	8.20	86.40
4	1.80	2.44	4.52	9.38	15.98
5	1.66	0.76	1.71	13.09	46.77
6	1.59	0.37	2.99	17.19	74.11
7	1.60	1.34	1.76	25.32	6.82

) were used to establish a combination weighting–SPA evaluation model and to analyze the suitability range of reinforced concrete linings. The survey and drilling schematic of the hydropower station is shown in Figure 3.

${\gamma }_R$ = 26.5 kN/m³. The in situ stress of the borehole is measured by hydraulic fracturing method. ${\sigma }_{min}$is derived from the law of linear relationship between the evolution of the in situ stress of the borehole with depth [37,38].

4.2. Calculation of Index Weight

The C-OWA operator is used for group decision-making weighting and subjective weights are calculated for evaluation indices. Eight experts from the field of geological engineering and hydraulic engineering, as listed in

Table 3. Expert Information.

No.	Professional Field	Position	Educational Level
Expert 1	Geological Engineering	Senior Engineer	Master
Expert 2	Geological Engineering	Senior Engineer	Master
Expert 3	Geological Engineering	Professor	Doctor
Expert 4	Geological Engineering	Professor	Doctor
Expert 5	Hydraulic Engineering	Senior Engineer	Master
Expert 6	Hydraulic Engineering	Senior Engineer	Master
Expert 7	Hydraulic Engineering	Professor	Doctor
Expert 8	Hydraulic Engineering	Professor	Doctor

, were invited to score the importance of each evaluation index on a 10-point scale. The expert’s scores on the importance of each index were presented in

Table 4. Index importance scores.

Index	Expert 1	Expert 2	Expert 3	Expert 4	Expert 5	Expert 6	Expert 7	Expert 8
A	3	2.5	2	1	1.5	1	1.5	1.2
B	1	2	1.5	2	1.5	2	1	1.5
C	2	2.5	2.5	2.5	2.5	3	2.5	3
D	2.5	2.5	2	2.5	1.5	2	2.5	1.5
E	1.5	1	2	2	3	2.5	2.5	3

, in which the higher score means higher importance.

Firstly, the subjective weights of the indices λ_i are calculated by Equations (5)–(7):

${\lambda }_j$ = (0.1546, 0.1560, 0.2492, 0.2188, 0.2215);

Then, the combined objective weight of the indices ${\omega }_j$ is calculated by Equations (8)–(18):

${\omega }_j$ = (0.3343, 0.1612, 0.0924, 0.2471, 0.1650);

Finally, the combination weight of the indices ${\omega }_j^{\prime }$ is calculated by Equation (19):

${\omega }_j^{\prime }$ = (0.2714, 0.1320, 0.1209, 0.2838, 0.1918).

4.3. Level Determination

According to the equipartition principle, u = 0.5, v = 0, and w = −0.5 are taken to be located in the three quarter positions of the interval [−1, 1], and the value of the five-element connection degree of the comprehensive evaluation is calculated to determine the suitability level of the reinforced concrete lining form. The corresponding relationship between the five-element connection degree and the suitability level of the reinforced concrete lining form is shown in

Table 5. The Relationship between the Five-element Connection Degree and the Suitability Level.

Suitability Level	Extremely Suitable (I)	More Suitable (II)	Basically Suitable (III)	Relatively Unsuitable (IV)	Extremely Unsuitable (V)
$\mu$	[0.6, 1]	[0.2, 0.6)	[−0.2, 0.2)	[−0.6, −0.2)	[−1, −0.6)

.

4.4. Suitability Evaluation

According to Equation (22) and combined with Table 2 and Table 5, the suitability evaluation of seven groups of drilling samples for the reinforced concrete lining is carried out. The five-element connection degree of working points is shown in

Table 6. Five-element Connection Degree of Comprehensive Evaluation of Each Working Point.

Working Point	1	2	3	4	5	6	7
a	0.5243	0.7162	0.7162	0.5243	0.5222	0.5842	0.5243
b	0.3051	0.0000	0.0000	0.0000	0.0620	0.0000	0.0000
c	0.1706	0.2710	0.2710	0.3315	0.0000	0.0000	0.0045
d	0.0000	0.0129	0.0129	0.1442	0.2168	0.0000	0.1873
e	0.0000	0.0000	0.0000	0.0000	0.1990	0.4158	0.2838
$\mu$	0.6769	0.7097	0.7097	0.4522	0.2457	0.1683	0.1468

, and the results of each evaluation method are shown in

Table 7. Comparison of Evaluation Results.

Working Point	1	2	3	4	5	6	7
Expert subjective evaluation method	I	I	I	II	II	III	IV
Combined objective weighting–SPA	I	I	I	II	II	III	II
Combination weighting–SPA	I	I	I	II	II	III	III

. According to the evaluation results, all the high-pressure pipelines of the PSPS are basically suitable for reinforced concrete linings. From No. 1 to No. 7, with the increasing underground depth, the anisotropy of the high-pressure pipeline section gradually increases and the suitability of the reinforced concrete lining form gradually decreases, which is mainly due to the influence of in situ stress and surrounding rock classification.

By comparison, the results of the three methods are basically the same, except that the results of the three evaluation methods for No. 7 are slightly different (Table 7). The expert evaluation method shows that the rating level of the site is relatively unsuitable. The reason for this is that the experts believe that the surrounding rock classification has declined and the hydraulic gradient value is too large, which makes the use of reinforced concrete lining more unfavorable. However, the involved experts might have different knowledge backgrounds and insights, and consequently the determination of the weight coefficient varies from person to person. The evaluation level calculated by the objective combination weighting–SPA method is more suitable. Objective weight combination weighting is based on the measured data, using certain mathematical methods to objectively assign the weight of the evaluation index. The method lacks subjective control and is often prone to be inconsistent with the actual situation. In summary, for the evaluation process of the suitability of reinforced concrete lining form, using only one of the methods is not comprehensive enough, which might result in over- or under-estimation of the results. Therefore, the combination weighting method integrates the advantages of the subjective and objective weighting methods, combines expert knowledge while fully considering the objectivity of the sample data, minimizes the loss of information, and improves the evaluation reliability.

5. Discussion

(1) Based on the example of the lining form of high-pressure pipelines in PSPS and combining the C-OWA operator, CRITIC method, improved EWM theory, and SPA theory, a new suitability evaluation method is proposed. Compared with the traditional evaluation methods, the advantages of this method are summarized as follows: (1) The combination weighting method consisting of subjective weight and objective weight can effectively avoid the error caused by a single weight method and make the prediction result closer to the actual situation. (2) The case study shows that the multivariate connection degree model is reliable and can be accepted for evaluating the reinforced concrete lining forms suitability and conveniently for practical applications. In addition, the connection degree indicates the interconnection and mutual influence of each index, and can represent the certainty and uncertainty degree from a whole perspective view, and the identical–discrepancy–contrary relationships between the sample and the classification grade. (3) In the selection of evaluation indices, the RQD index, which conventionally characterizes the structural features of rock mass, is improved and supplemented. The RBI index is used to replace RQD, so that the results can more accurately reflect the size of the rock mass, which has obvious engineering practical significance for the quantitative analysis of the variation characteristics of physical and mechanical parameters of rock mass.

(2) The five evaluation indices were selected by the combination weighting–SPA model for the selection of lining forms of diversion tunnels, according to the three design criteria commonly used in hydraulic tunnels. Therefore, this model has certain representativeness and applicability. For the high-pressure pipelines to be evaluated, a similar suitability rating model for lining forms can be established by selecting evaluation indices with similar property characteristics. However, for different hydraulic tunnels, there may be different geological characteristics and risk environments. Therefore, the evaluation indices can be increased or decreased appropriately to meet the suitability evaluation of reinforced concrete lining forms for different high-pressure pipelines.

(3) There are still shortcomings in this study. The hydraulic tunnel design criterion in the proposed model is relatively conservative and basic. For complex cases, how to integrate weights into the evaluation model for the selection of lining forms and how to consider the effects of the index on lining stability remain to be clarified, and further efforts need to be made on accurately selecting an appropriate lining form to prevent accidents in the future. Therefore, a more scientific, rational, and universal classification standard needs to be realized through further research.

6. Conclusions

The relevant factors affecting the lining form were summarized by analyzing the three design criteria and constructs a relatively complete evaluation system for the suitability of reinforced concrete linings. The subjective–objective combination weighting–SPA model not only takes into account the influence of subjective judgment of experts, but also reflects the difference and relevance of objective data of evaluation indices, which improves the evaluation sensitivity and makes the evaluation results more in line with reality. The consistency of the evaluation results with those of other methods verifies the feasibility of the proposed method. This approach optimizes the evaluation process of the lining form and makes the results more comprehensive, objective, and rational. It has exceptional application value in the construction of hydraulic tunnels and can provide reference value and reference significance for the selection of lining forms of other PSPS.