Identification of Wiener Box-Jenkins Model for Anesthesia Using Particle Swarm Optimization
Abstract
:1. Introduction
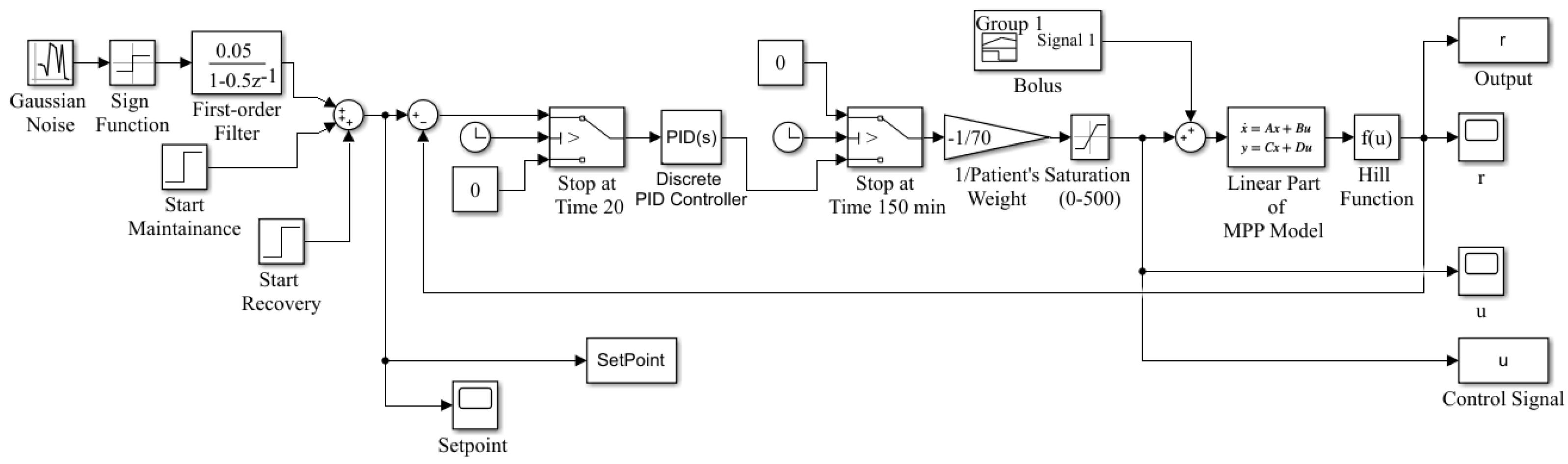
2. MPP Anesthesia Model Description
3. System Identification
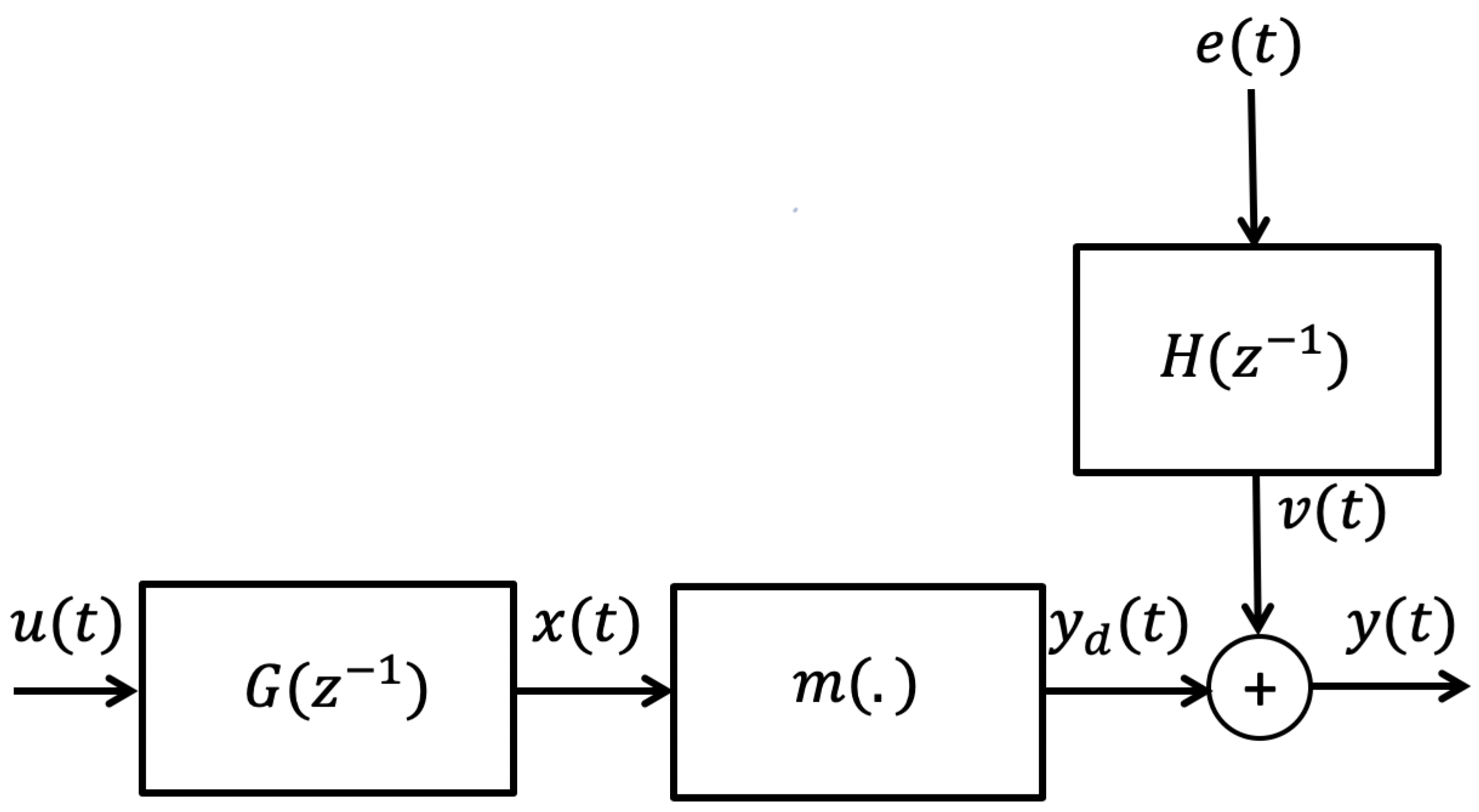
3.1. Wiener Box-Jenkins Model Structure
3.2. Prediction Error Method (PEM)
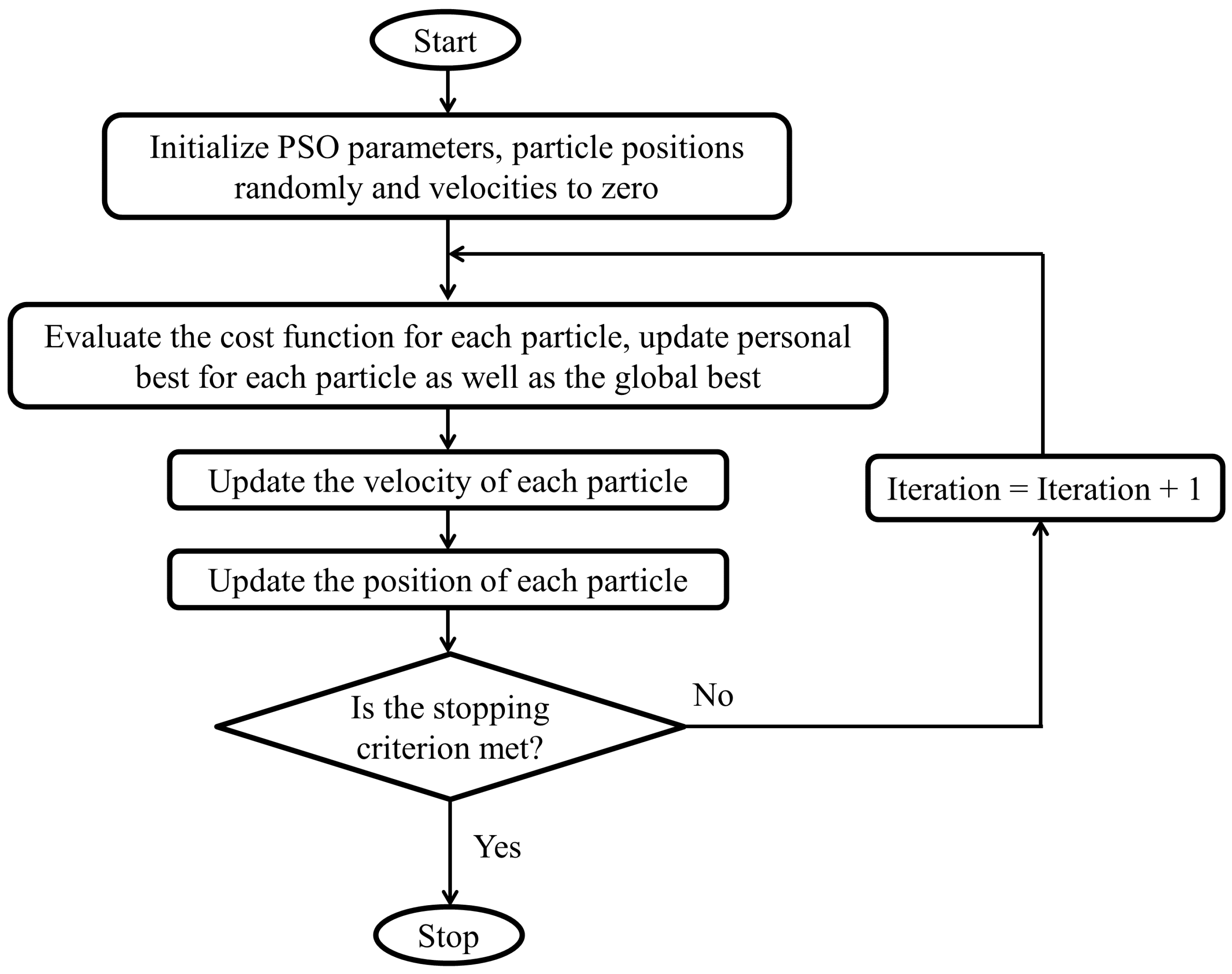
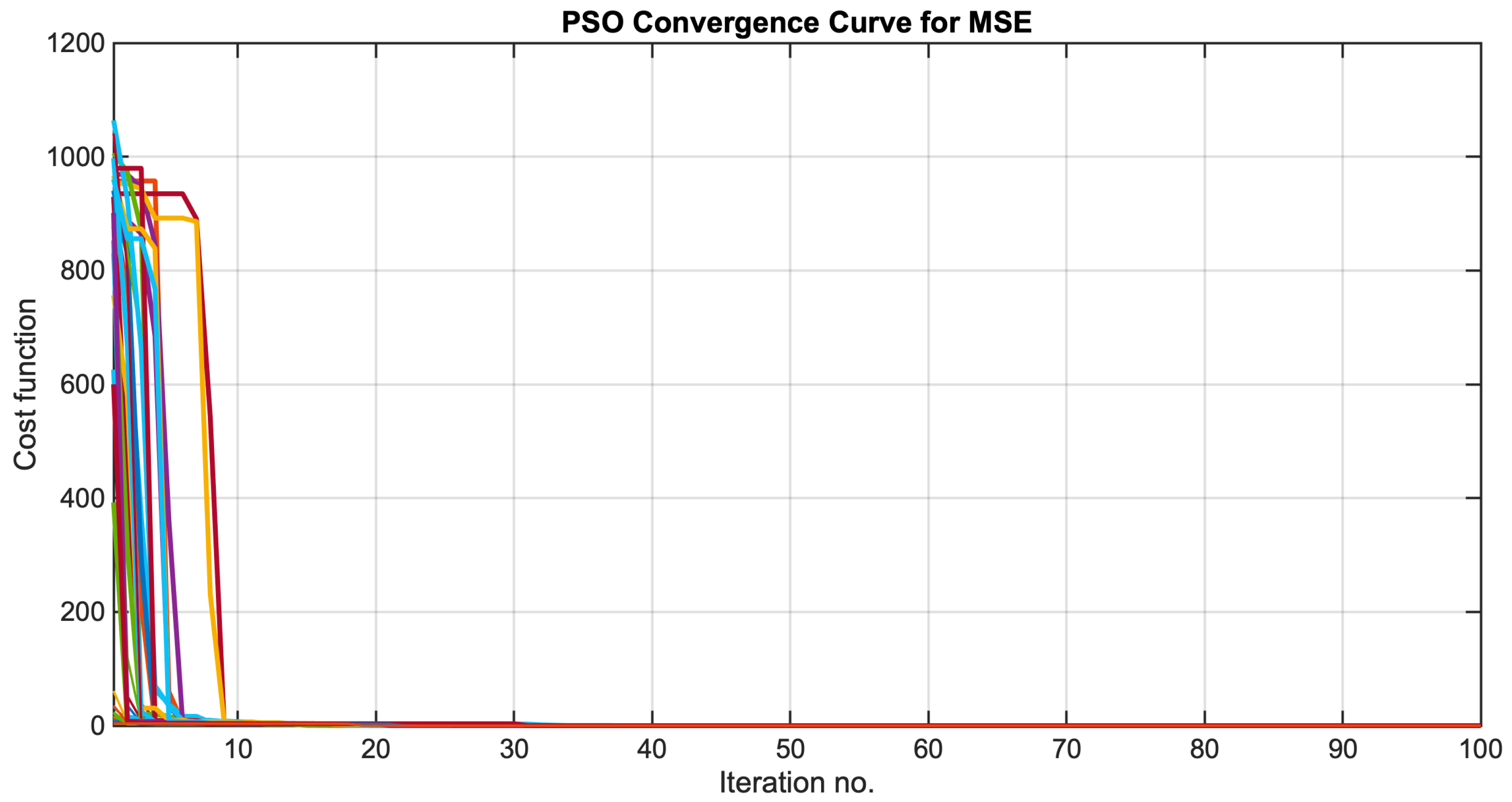
3.3. Iterative Optimization Using PSO
- Generate, randomly, a population of initial parameter vectors, solutions, or particles, , for , where is the population size. Each entry in the vector is initialized to a random number generated from a uniform distribution in the interval where and denote the lower and upper bounds, respectively, of the parameters. Additionally, initialize the velocity, , for each particle in the population, to zero.
- Evaluate the cost function given by (14) for each particle .
- Update the best value for each particle i by comparing the current cost of each particle with its previous best value.
- Update the population’s best value .
- Update the velocity of each particle using the following formula:where and denotes the velocity of particle i at iterations and t, respectively. The parameters , and are two random numbers, and and are two positive constants called the personal and global acceleration coefficients. The parameter w, called the inertia weight, controls the effect of the current particle solution on its next solution. The inertia weight is damped in each iteration using the following formula:where denotes the damping ratio of the inertia coefficient.
- Update each particle position using the following formula:
- If the change in is less than some given small tolerance or the maximum number of iterations is reached, the algorithm terminates; otherwise, go to step 2).
4. Simulation Results
4.1. Data Collection
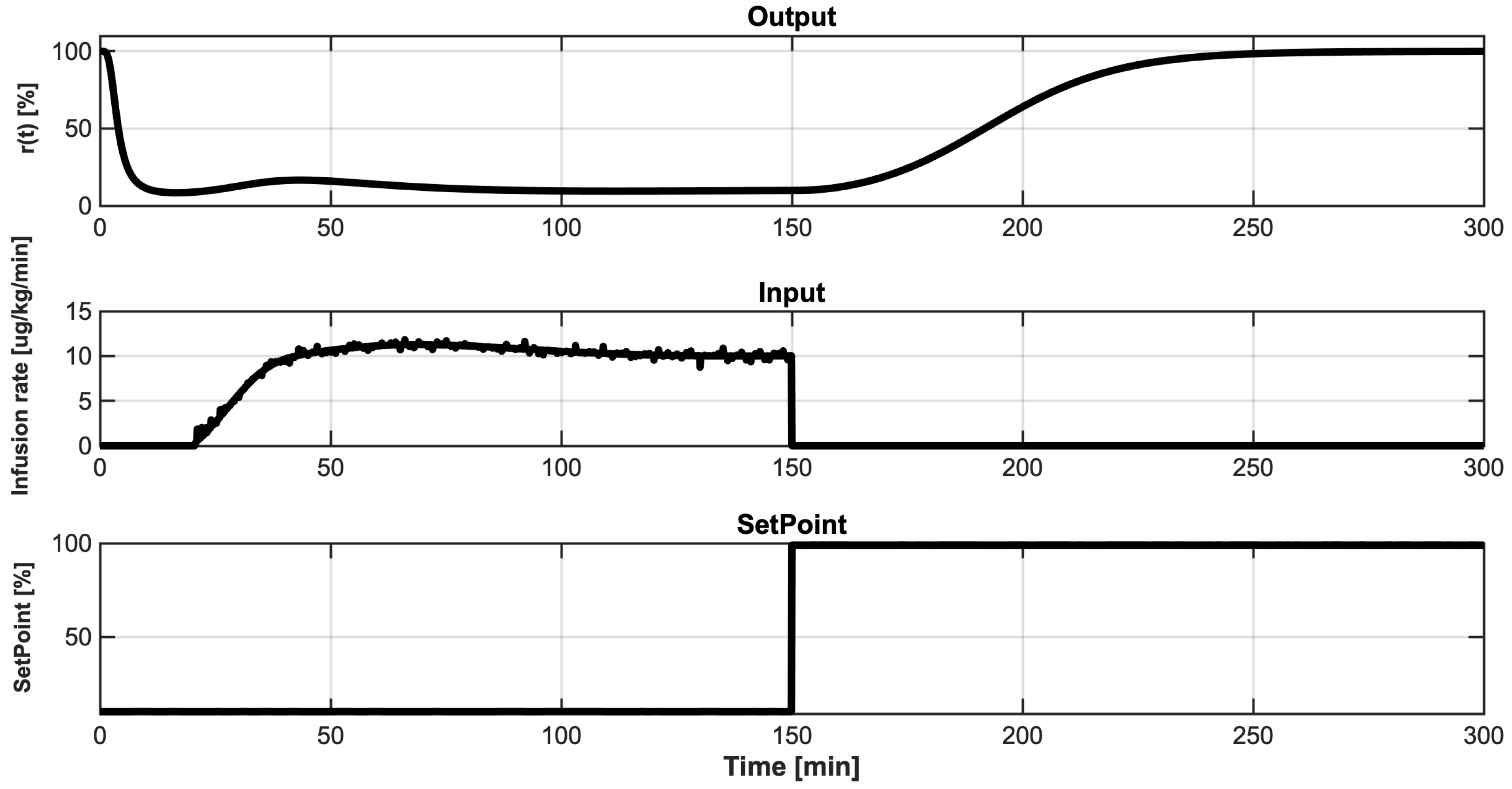
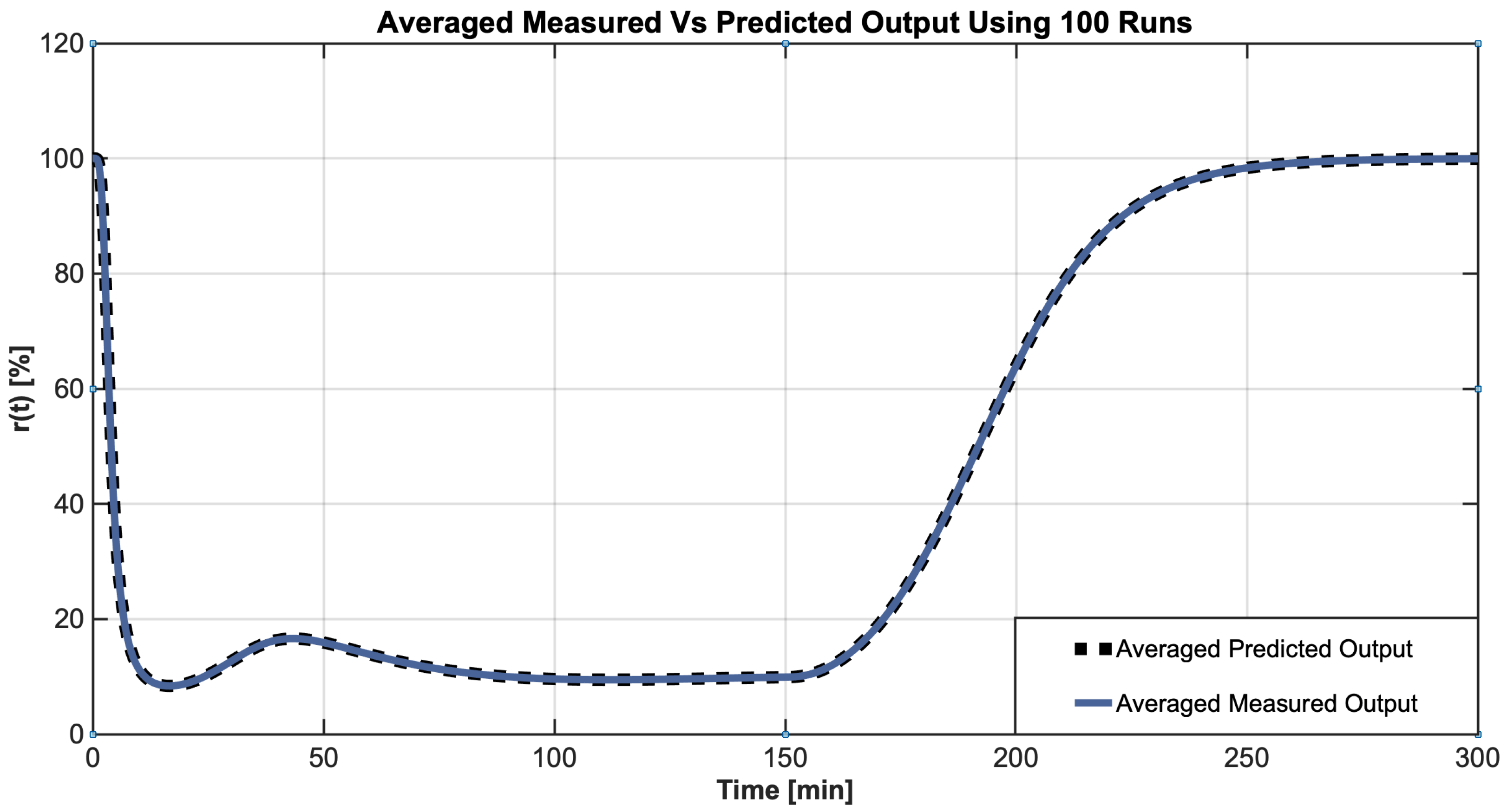
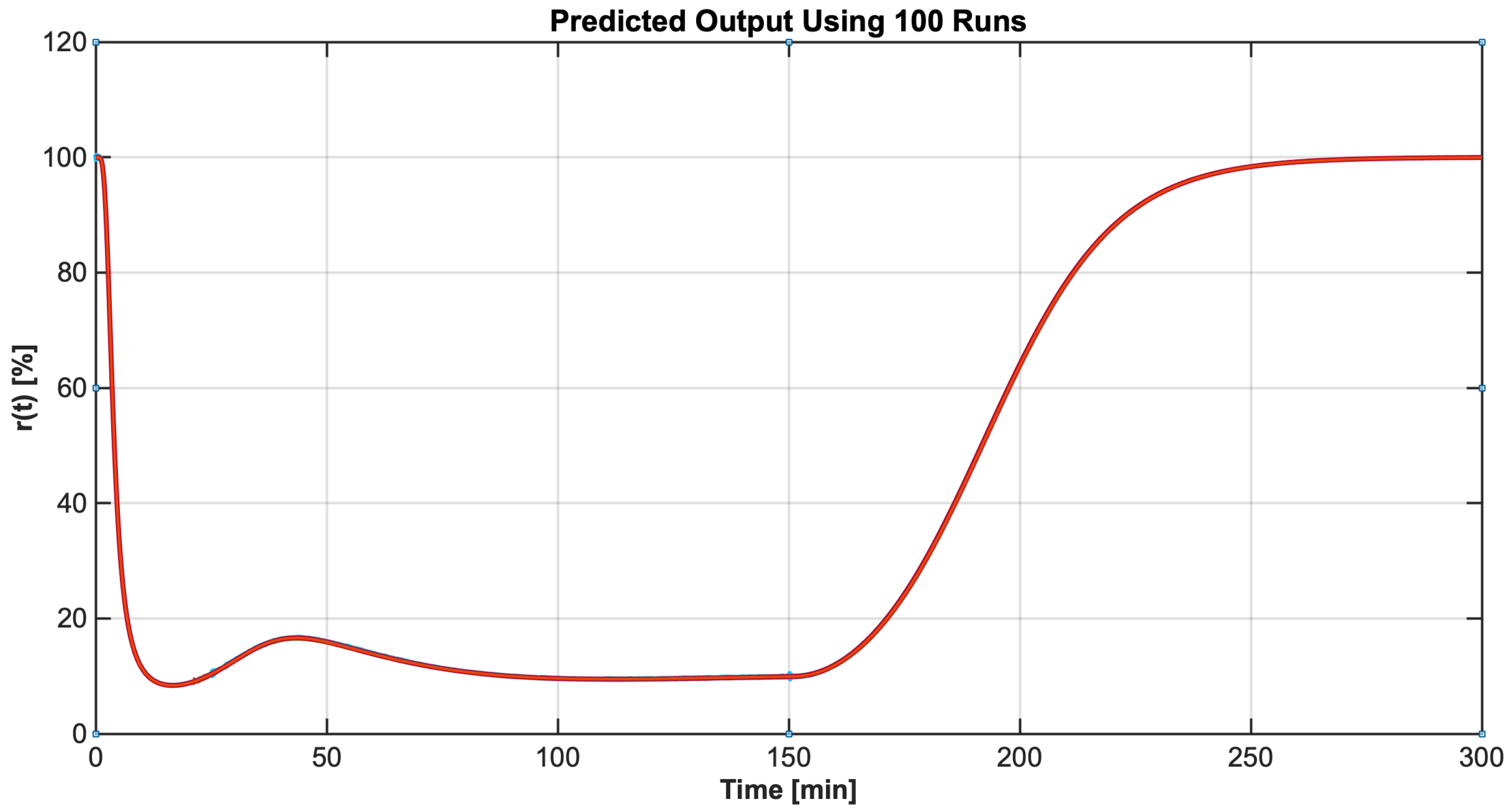
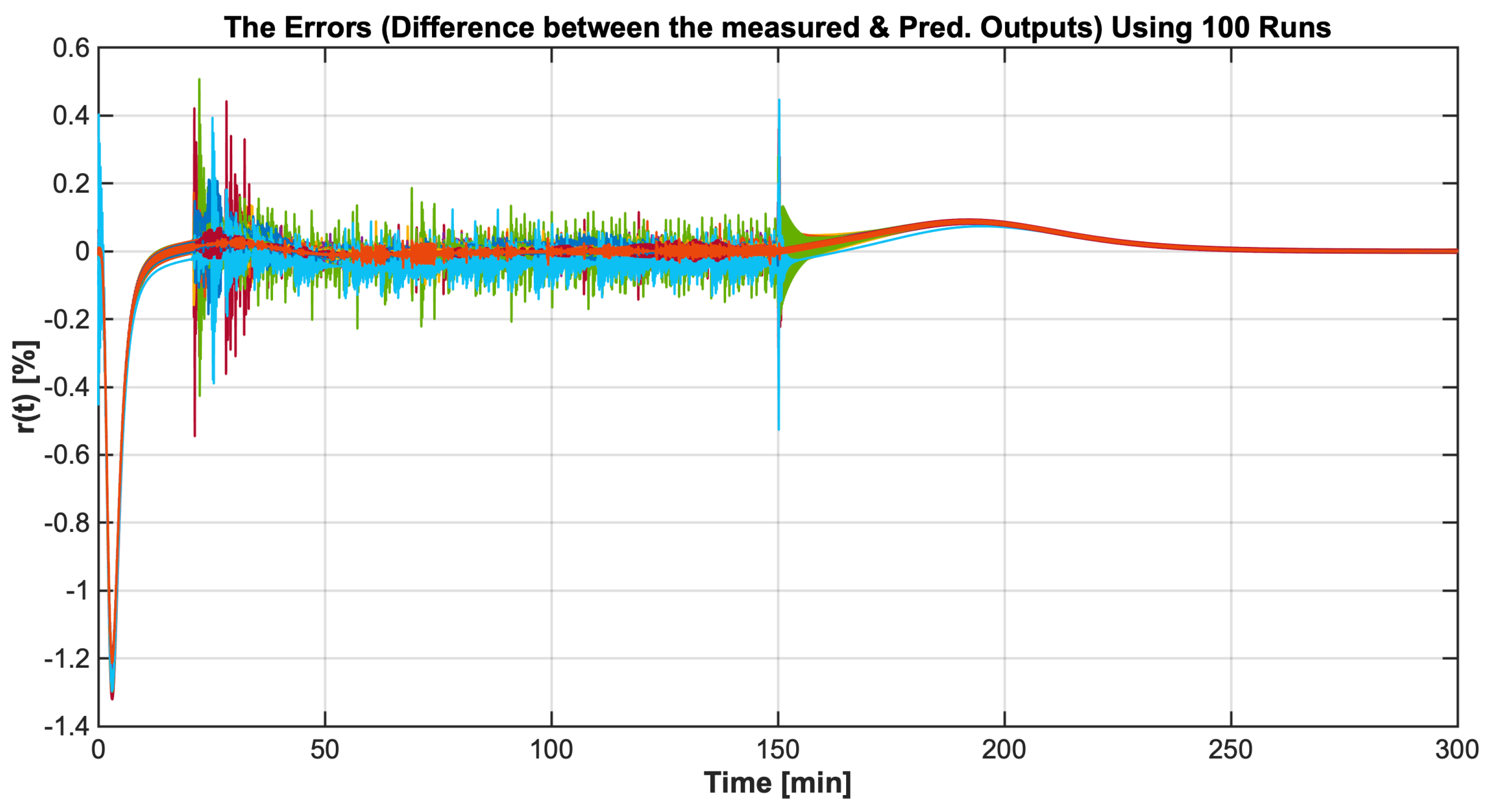
4.2. Identification Results
5. Summary and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Butterworth, J.; Mackey, D.; Wasnick, J. The Anesthesia Machine. In Morgan & Mikhail’s Clinical Anesthesiology, 5th ed.; McGraw-Hill Education: New York, NY, USA, 2013; pp. 43–86. [Google Scholar]
- Guo, Z.; Medvedev, M.; Merigo, L.; Latronico, N.; Paltengh, M.; Visioli, A. Synthetic patient database of drug effect in general anesthesia for evaluation of estimation and control algorithms. In Proceedings of the 18th IFAC Symposium System Identification, Stockholm, Sweden, 9–11 July 2018; pp. 323–328. [Google Scholar]
- Dumont, G. Closed-loop control of anesthesia—A review. In Proceedings of the 8th IFAC Symposium on Biological and Medical Systems, Budapest, Hungary, 29–31 August 2012; pp. 373–375. [Google Scholar]
- Da Silva, M. System Identification and Control for General Anesthesia Based on Parsimonious Wiener Models. Licentiate Thesis, Division of Systems and Control, Uppsala University, Uppsala, Sweden, 2012. [Google Scholar]
- Soltesz, K.; Hahn, J.; Dumont, G.; Ansermino, J. Individualized PID control of depth of anesthesia based on patient model identification during the induction phase of anesthesia. In Proceedings of the 50th IEEE Conference Decision and Control, Orlando, FL, USA, 12–15 December 2011; pp. 855–860. [Google Scholar]
- Medvedev, A.; Zhusubaliyev, Z.; Rosén, O.; Silva, M. Oscillations-free PID control of anesthetic drug delivery in neuromuscular blockade. Comput. Methods Programs Biomed. 2019, 171, 119–131. [Google Scholar] [CrossRef] [PubMed]
- Costa, B.; Mendonça, T. GALENO: Computer aided system for modeling, monitoring, and control in anesthesia. Adv. Control Appl. Eng. Ind. Syst. 2021, 3, e87. [Google Scholar] [CrossRef]
- Hegedus, E.; Birs, I.; Muresan, C. Fractional Order Control of the Combined Anaesthesia-Hemodynamic System: A Preliminary Study. IFAC-PapersOnLine 2021, 54, 19–24. [Google Scholar] [CrossRef]
- Ionescu, C.M.; De Keyser, R.; Torrico, B.C.; De Smet, T.; Struys, M.M.; Normey-Rico, J.E. Robust predictive control strategy applied for propofol dosing using BIS as a controlled variable during anesthesia. IEEE Trans. Biomed. Eng. 2008, 55, 2161–2170. [Google Scholar] [CrossRef] [PubMed]
- Araujo, H.; Xiao, B.; Liu, C.; Zhao, Y.; Lam, H. Design of type-1 and interval type-2 fuzzy PID control for anesthesia using genetic algorithms. J. Intell. Learn. Syst. Appl. 2014, 4, 70–93. [Google Scholar] [CrossRef] [Green Version]
- Jaklitsch, R.; Westenskow, D. A model-based self-adjusting two-phase controller for vecuronium-induced muscle relaxation during anesthesia. IEEE Trans. Biomed. Eng. 1987, 38, 583–594. [Google Scholar] [CrossRef] [PubMed]
- Kudva, H.; Warrier, J. Automated anesthesia delivery pump. IOSR J. Pharm. Biol. Sci. 2014, 9, 100–106. [Google Scholar] [CrossRef]
- Haddad, W.; Volyanskyy, K.; Bailey, J. Neuroadaptive output feedback control for automated anesthesia with noisy EEG measurements. IEEE Trans. Control Syst. Technol. 2011, 19, 311–326. [Google Scholar] [CrossRef]
- Soltesz, K.; Heusden, K.; Hast, M.; Ansermino, J.; Dumont, G. A synthesis method for automatic handling of inter-patient variability in closed-loop anesthesia. In Proceedings of the American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 4877–4882. [Google Scholar]
- Bibian, S.; Ries, C.; Huzmezan, M.; Dumont, G. Clinical anesthesia and control engineering: Terminology, concepts and issues. In Proceedings of the European Control Conference (ECC), Cambridge, UK, 1–4 September 2003; pp. 2430–2439. [Google Scholar] [CrossRef]
- Hahn, J.; Dumont, G.; Ansermino, J. A direct dynamic dose-response model of propofol for individualized anesthesia care. IEEE Trans. Biomed. Eng. 2012, 59, 571–578. [Google Scholar] [CrossRef] [PubMed]
- Brouse, C.; Karlen, W.; Dumont, G.; Myers, D.; Cooke, E.; Stinson, J.; Lim, J.; Ansermino, J. Real-time cardiorespiratory coherence detects antinociception during general anesthesia. In Proceedings of the 34th Annual International Conference IEEE EMBS, San Diego, CA, USA, 28 August–1 September 2012; pp. 3813–3816. [Google Scholar]
- Heusden, K.; Ansermino, J.; Dumont, G. Closed-loop instrumental variable identification of propofol anesthesia. In Proceedings of the IEEE Conference on Control Technology and Applications (CCTA), Mauna Lani Resort, HI, USA, 27–30 August 2017; pp. 1165–1170. [Google Scholar]
- Dumont, G.; Martinez, A.; Ansermino, J. Robust control of depth of anesthesia. Int. J. Adapt. Control Signal Process. 2008, 23, 435–454. [Google Scholar] [CrossRef]
- Ionescu, C.M.; Copot, D.; Neckebroek, M.; Muresan, C. Anesthesia regulation: Towards completing the picture. In Proceedings of the IEEE International Conference Automation, Quality and Testing, Robotics (AQTR), Cluj-Napoca, Romania, 24–26 May 2018; pp. 1–6. [Google Scholar]
- Da Silva, M.; Wigrn, T.; Mendonca, T. Nonlinear identification of a minimal neuromuscular blockade model in anesthesia. IEEE Trans. Control Syst. Technol. 2012, 20, 181–188. [Google Scholar] [CrossRef]
- Da Silva, M. Prediction error identification of minimally parameterized Wiener models in anesthesia. In Proceedings of the 18th IFAC World Congress, Milan, Italy, 28 August–2 September 2011; pp. 5615–5620. [Google Scholar]
- Heusden, K.; Dumont, G.; Soltesz, K.; Petersen, C.; Umedaly, A.; West, N.; Ansermino, J. Design and clinical evaluation of robust PID control of propofol anesthesia in children. IEEE Trans. Control Syst. Technol. 2014, 22, 491–501. [Google Scholar] [CrossRef] [Green Version]
- van Heusden, K.; Ansermino, J.; Soltesz, K.; Khosravi, S.; West, N.; Dumont, G. Quantification of the variability in response to propofol administration in children. IEEE Trans. Biomed. Eng. 2013, 60, 2521–2529. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Silva, M.; Mendonca, T.; Wigren, T. On-line nonlinear identification of the effect of drugs in anaesthesia using a minimal parameterization and BIS measurements. In Proceedings of the American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 4379–4384. [Google Scholar]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the 6th International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Pal, P.; Dasgupta, A.; Akhil, J.; Kar, R.; Mandal, D.; Ghosal, S. Identification of a Box-Jenkins structured two stage cascaded model using simplex particle swarm optimization algorithm. In Proceedings of the 2016 International Symposium on Intelligent Signal Processing and Communication Systems, Phuket, Thailand, 24–27 October 2016; pp. 1–4. [Google Scholar]
- Montain, M.; Blanco, A.; Bandoni, J. Optimal drug infusion profiles using a particle swarm optimization algorithm. Comput. Chem. Eng. 2015, 82, 13–24. [Google Scholar] [CrossRef]
- Alonso, H.; Mendonca, T.; Rocha, P. A hybrid method for parameter estimation and its application to biomedical systems. Comput. Methods Programs Biomed. 2008, 89, 112–122. [Google Scholar] [CrossRef] [PubMed]
- Ljung, L. System Identification: Theory for the User, 2nd ed.; Prentice Hall PTR: Hoboken, NJ, USA, 1999. [Google Scholar]
- Pintelon, R.; Schoukens, J. System Identification: A Frequency Domain Approach, 2nd ed.; Wiley-IEEE Press: New York, NY, USA, 2012. [Google Scholar]
- Aljamaan, I.; Westwick, D.; Foley, M. Non-iterative identification of IIR Wiener systems using orthogonal polynomial. In Proceedings of the 17th IFAC World Congress Conference, Cape Town, South Africa, 24–29 August 2014; Volume 47, pp. 487–492. [Google Scholar]
- Dempsey, E.; Westwick, D. Identification of Hammerstein models with cubic spline nonlinearities. IEEE Trans. Biomed. Eng. 2004, 51, 237–245. [Google Scholar] [CrossRef] [PubMed]
- Aljamaan, I.; Bshait, B.; Westwick, D. Separable least squares identification of Wiener Box-Jenkins models. In Proceedings of the 18th IFAC World Congress, Milan, Italy, 28 August–2 September 2011; Volume 18, pp. 4434–4439. [Google Scholar]
- Bonyadi, M.; Michalewicz, Z. Particle swarm optimization for single objective continuous space problems: A review. Evol. Comput. 2017, 25, 1–54. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Merigo, L.; Padula, F.; Latronico, N.; Mendonca, T.; Paltenghi, M.; Rocha, P.; Visioli, A. Optimized PID tuning for the automatic control of neuromuscular blockade. In Proceedings of the 3rd IFAC Conference on Advances in Control PID, Ghent, Belgium, 9–11 May 2018; Volume 51, pp. 66–71. [Google Scholar]
| Parameter | Value |
|---|---|
| Population size, | 50 |
| −2 | |
| +2 | |
| Inertia coefficient, w | |
| Damping ratio of inertia coefficient, | |
| Personal acceleration coefficient, | 2.0 |
| Social acceleration coefficient, | 2.0 |
| Maximum iterations | 00 |
| Parameter | Value | |
|---|---|---|
| PID controller | ||
| Patient | ||
| 1 | ||
| 2 | ||
| 10 |
| Parameter | Value |
|---|---|
| MSE | MAE | MAPE | ||
|---|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aljamaan, I.; Alenany, A. Identification of Wiener Box-Jenkins Model for Anesthesia Using Particle Swarm Optimization. Appl. Sci. 2022, 12, 4817. https://doi.org/10.3390/app12104817
Aljamaan I, Alenany A. Identification of Wiener Box-Jenkins Model for Anesthesia Using Particle Swarm Optimization. Applied Sciences. 2022; 12(10):4817. https://doi.org/10.3390/app12104817
Chicago/Turabian StyleAljamaan, Ibrahim, and Ahmed Alenany. 2022. "Identification of Wiener Box-Jenkins Model for Anesthesia Using Particle Swarm Optimization" Applied Sciences 12, no. 10: 4817. https://doi.org/10.3390/app12104817
APA StyleAljamaan, I., & Alenany, A. (2022). Identification of Wiener Box-Jenkins Model for Anesthesia Using Particle Swarm Optimization. Applied Sciences, 12(10), 4817. https://doi.org/10.3390/app12104817







