Initiation and Fracture Characteristics of Different Width Cracks of Concretes under Compressional Loading
Abstract
1. Introduction
2. Materials and Methods
2.1. Specimen Preparation
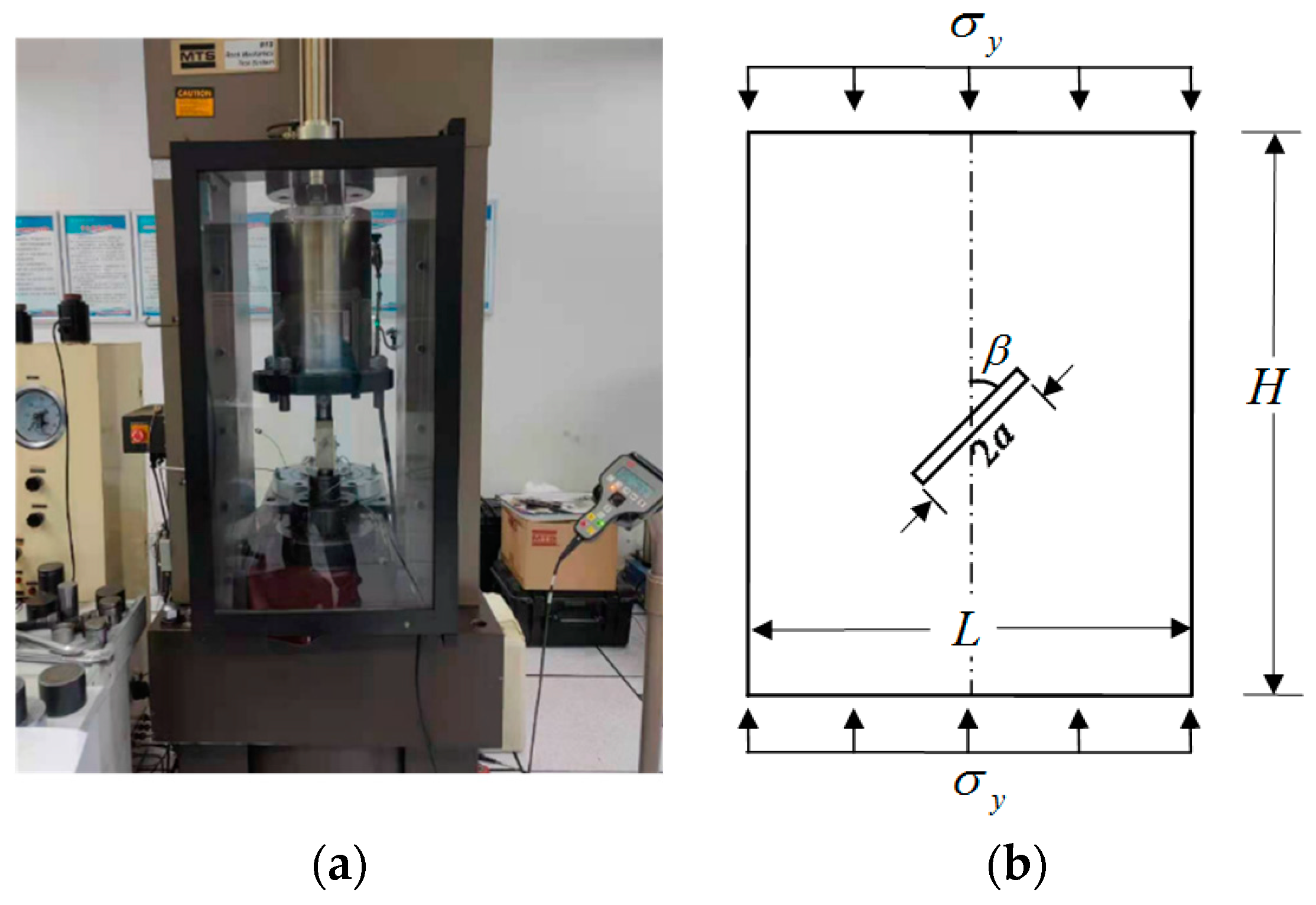
2.2. Compression Shear Fracture Test of Concrete Samples
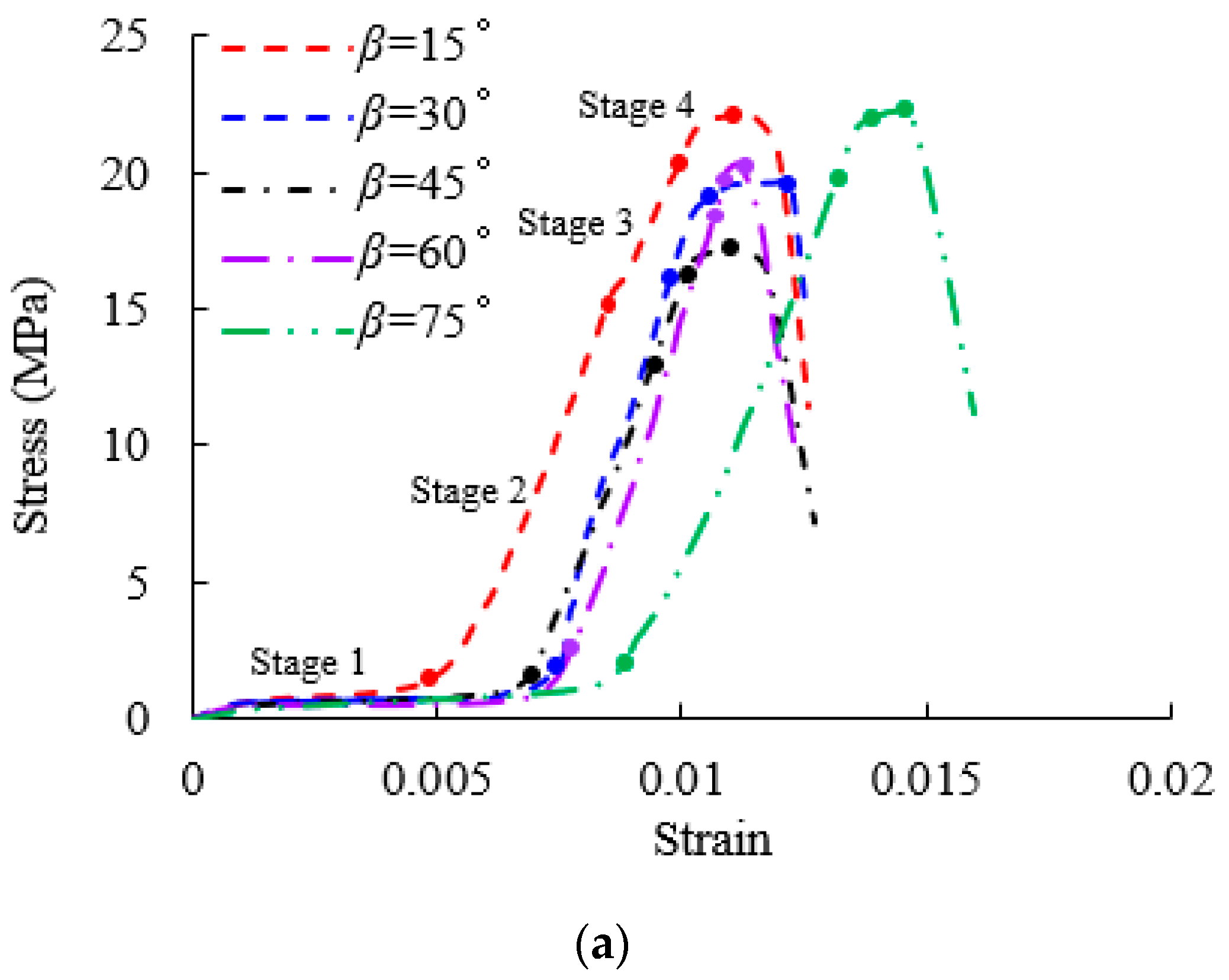
2.3. Analysis of the Experimental Results
3. Fracture Criterion of Brittle Material
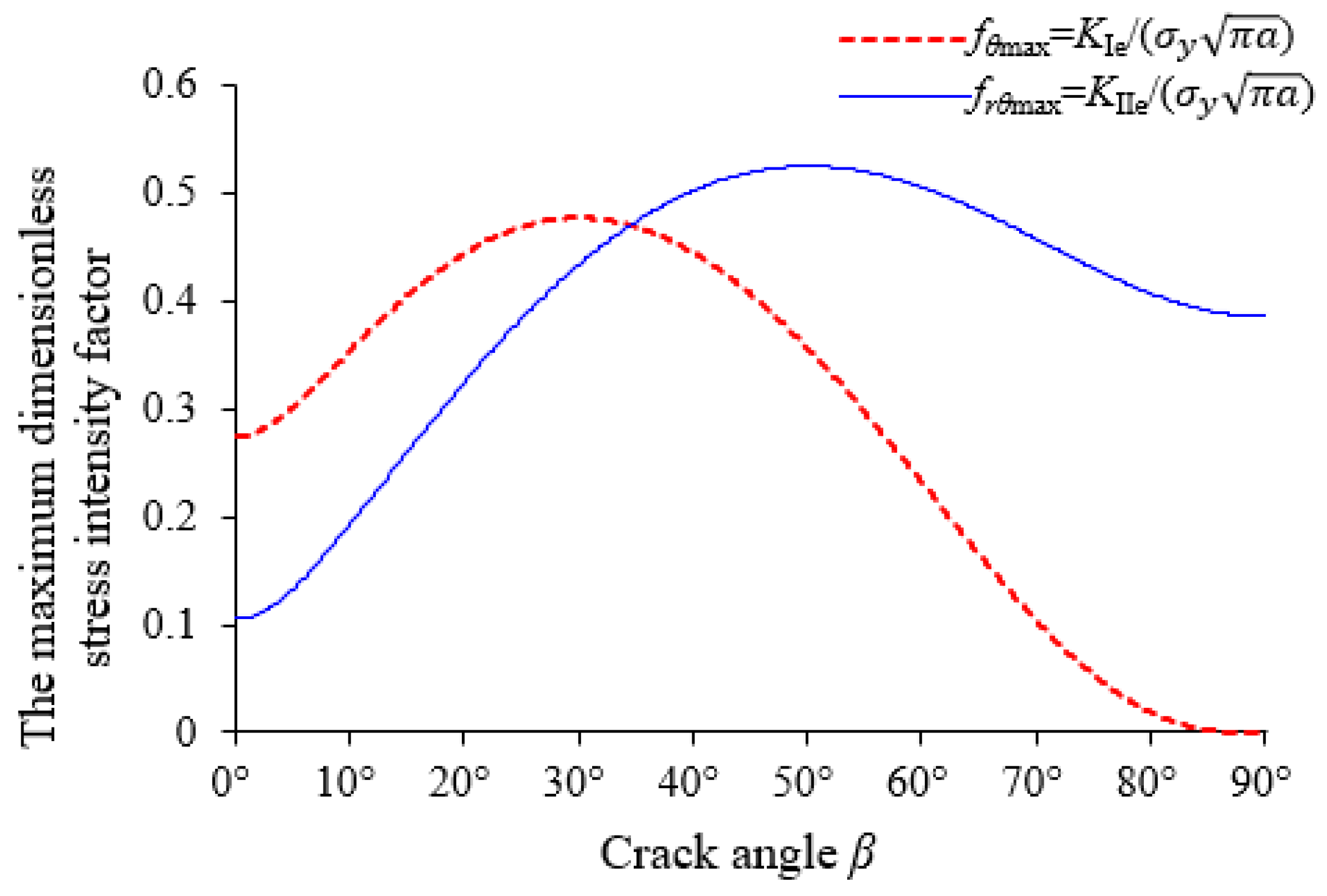
3.1. The Maximum Circumferential Stress Theory
3.2. The Radial Shear Stress Criterion
4. Numerical Analysis and Failure Mechanism of a Single-Crack Specimen
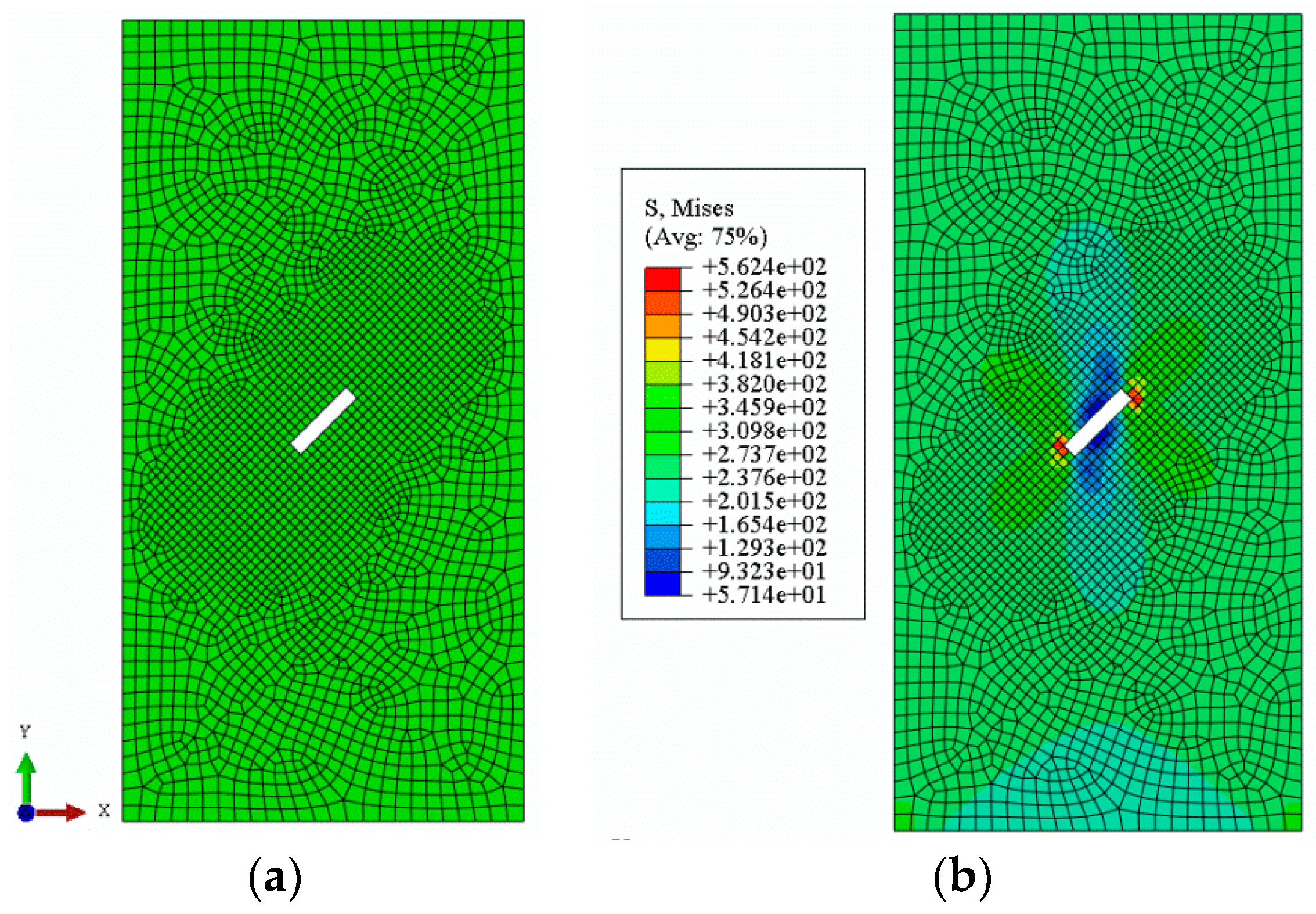
4.1. Numerical Model and Parameter Analysis
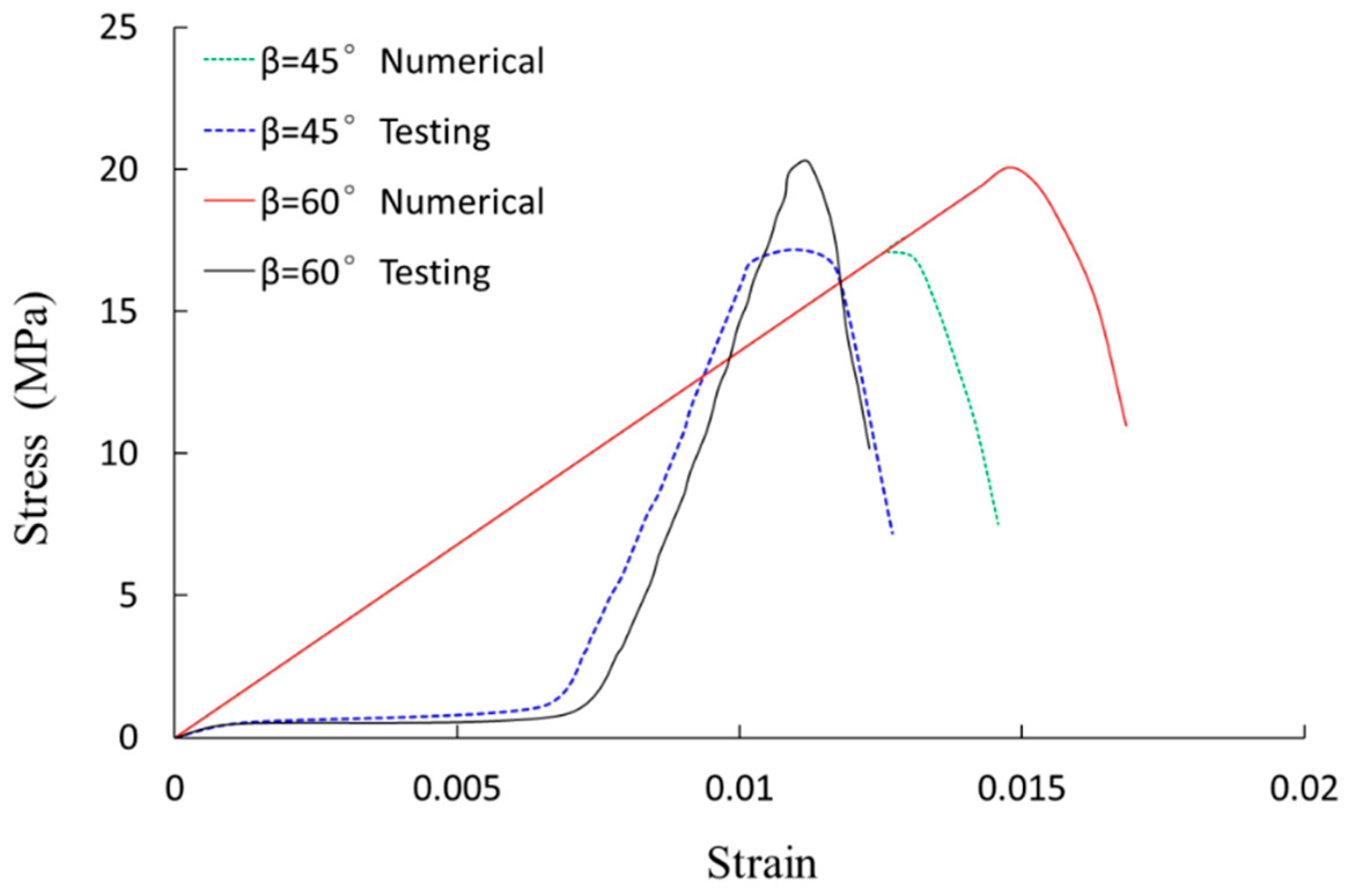
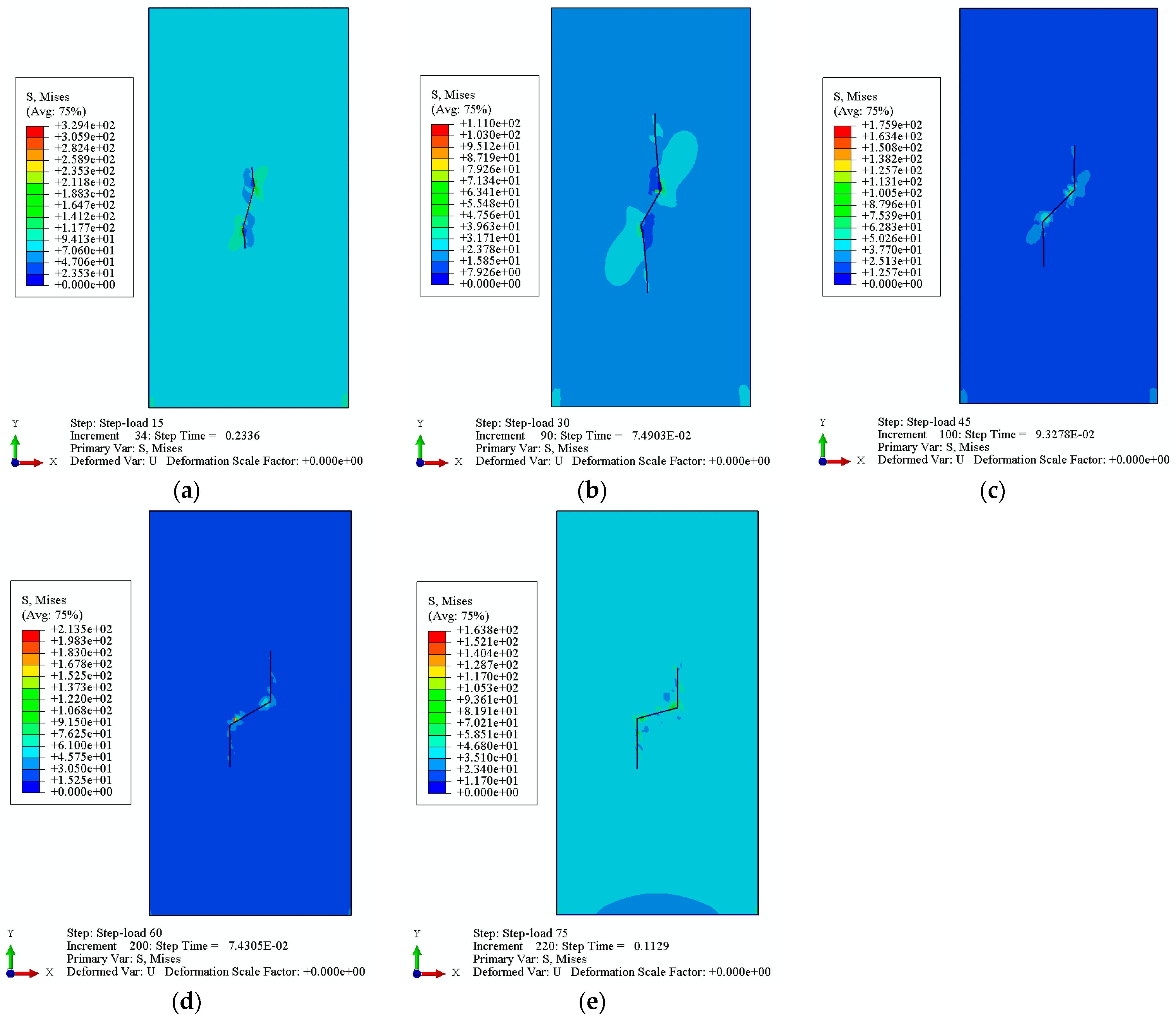
4.2. Failure Mechanism of a Closed Pre-Crack Concrete Sample
4.3. Failure Mechanism of a Non-Closed Single-Crack Concrete Sample
5. Conclusions
- (1)
- The strength of the concrete sample decreases initially and then increases with increasing crack angle. For the same crack angle, the greater the crack width, the higher the strength of the non-closed crack sample. The crack width has a significant effect on the initiation angle.
- (2)
- With the maximum circumferential stress theory, it is difficult to depict the fracture propagation of non-closed cracks under compression. When KI < 0, a non-closed crack under uniaxial compression will have a mode-I stress intensity factor. The circumferential compressive stress created by the mode-I stress intensity factor will restrain the circumferential tensile stress caused by the mode-II stress intensity factor. If and , the rupture angle will be close to the direction of the maximum radial shear stress for a non-closed crack.
Author Contributions
Funding
Conflicts of Interest
References
- Farzampour, A. Compressive Behavior of Concrete under Environmental Effects; IntechOpen: London, UK, 2019; pp. 92–104. [Google Scholar]
- Malhotra, V.M.; Carino, N.J. The maturity method. In Handbook on Nondestructive Testing of Concrete; CRC Press: Boca, LA, USA; Raton, FL, USA, 2003; pp. 102–148. [Google Scholar]
- Bobet, A.; Einstein, H.H. Fracture coalescence in rock-type materials under uniaxial and biaxial compression. Int. J. Rock Mech. Min. Sci. 1998, 35, 863–888. [Google Scholar] [CrossRef]
- Bobet, A. The initiation of secondary cracks in compression. Int. J. Rock Mech. Min. Sci. 2000, 66, 187–219. [Google Scholar] [CrossRef]
- Vasarhelyi, B.; Bobet, A. Modeling of crack initiation, propagation and coalescence in niaxial compression. Rock Mech. Rock Eng. 2000, 33, 119–139. [Google Scholar]
- Tang, C.A.; Lin, P.; Wong, R.H.C.; Chau, K.T. Analysis of crack coalescence in rock-like materials containing three flaws—Part II: Numerical approach. Int. J. Rock Mech. Min. Sci. 2001, 38, 925–939. [Google Scholar] [CrossRef]
- Sagong, M.; Bobet, A. Coalescence of multiple flaws in a rock-model material in uniaxial compression. Int. J. Rock Mech. Min. Sci. 2002, 39, 229–241. [Google Scholar] [CrossRef]
- Park, C.H.; Bobet, A. Crack coalescence in specimens with open and closed flaws: A comparison. Int. J. Rock Mech. Min. Sci. 2009, 46, 819–829. [Google Scholar] [CrossRef]
- Tang, S.B.; Huang, R.Q.; Tang, C.A.; Lianga, Z.Z.; Heap, M.J. The failure processes analysis of rock slope using numerical modelling techniques. Eng. Fail. Anal. 2017, 79, 999–1016. [Google Scholar] [CrossRef]
- Wu, L.Z.; Li, B.; Huang, R.Q.; Sun, P. Experimental study and modeling of shear rheology in sandstone with non-persistent joints. Eng. Geol. 2017, 222, 201–211. [Google Scholar] [CrossRef]
- Peng, J.; Wong, L.N.Y.; Liu, G.; Teh, C.I. Influence of initial micro-crack damage on strength and micro-cracking behavior of an intrusive crystalline rock. Bull. Eng. Geol. Environ. 2019, 78, 2957–2971. [Google Scholar] [CrossRef]
- Lu, Y.N.; Qi, Y.; Tenardi, M.; Long, R. Mixed-mode fracture in a soft elastomer. Extrem. Mech. Lett. 2021, 48, 101380. [Google Scholar] [CrossRef]
- Wu, L.Z.; Zhou, J.T.; Luo, L.; Yang, L.P. Rock dynamic fracture of a novel semi-circular-disk specimen. Int. J. Rock Mech. Min. Sci. 2022, 152, 105047. [Google Scholar] [CrossRef]
- Xin, J.; Jiang, Y.; Zhou, J.; Zhou, J.; Peng, L.; Liu, S.; Tang, T. Bridge deformation prediction based on SHM data using improved VMD and conditional KDE. Eng. Struct. 2022, 261, 114285. [Google Scholar] [CrossRef]
- Wang, Q.Z.; Jia, X.M.; Wu, L.Z. Wide-range stress intensity factors for the ISRM suggested method using CCNBD specimens for rock fracture toughness tests. Int. J. Rock Mech. Min. Sci. 2004, 41, 709–716. [Google Scholar] [CrossRef]
- Al-Mukhtar, A.M.; Merkel, B. Simulation of the crack propagation in rocks using fracture mechanics approach. J. Fail. Anal. Prev. 2015, 15, 90–100. [Google Scholar] [CrossRef]
- Huang, R.Q.; Wu, L.Z.; He, Q.; Li, J.H. Stress intensity factor analysis and the stability of overhanging rock. Rock Mech. Rock Eng. 2017, 50, 2135–2142. [Google Scholar] [CrossRef]
- Huang, R.Q.; Wu, L.Z.; Li, B. Crack initiation criteria and fracture simulation for pre-cracked sandstones. Adv. Mater. Sci. Eng. 2019, 2019, 9359410. [Google Scholar] [CrossRef]
- Wu, L.Z.; Shao, G.Q.; Huang, R.Q.; He, Q. Overhanging Rock: Theoretical, Physical and Numerical Modeling. Rock Mech. Rock Eng. 2018, 51, 3585–3597. [Google Scholar] [CrossRef]
- Erdogan, F.; Sih, G.C. On the crack extension in plates under plane loading and transverse shear. J. Basic Eng. 1963, 85, 519–525. [Google Scholar] [CrossRef]
- Hussian, M.A.; Pu, E.L.; Underwood, J.H. Strain energy release rate for a crack under combined mode I and mode II. In Fracture Analysis; ASTM STP 560; ASTM International: West Conshohocken, PA, USA, 1974; pp. 2–28. [Google Scholar]
- Sih, G.C. Energy-density concept in fracture mechanics. Eng. Fract. Mech. 1973, 5, 1037–1040. [Google Scholar] [CrossRef]
- Nuismer, R.J. An energy release rate criterion for mixed mode fracture. Int. J. Rock Mech. Min. 1975, 11, 245–250. [Google Scholar] [CrossRef]
- Zhu, S.R.; Wu, L.Z.; Huang, J. Application of an improved P(m)-SOR iteration method for flow in partially saturated soils. Comput. Geosci. 2022, 26, 131–145. [Google Scholar] [CrossRef]
- Marji, M.F.; Dehghani, I. Kinked crack analysis by a hybridized boundary element/boundary collocation method. Int. J. Solids Struct. 2010, 47, 922–933. [Google Scholar] [CrossRef][Green Version]
- Marji, M.F. On the use of power series solution method in the crack analysis of brittle materials by indirect boundary element method. Eng. Fract. Mech. 2013, 98, 365–382. [Google Scholar] [CrossRef]
- Sun, Z.Q. Is crack branching under shear loading caused by shear fracture—A critical review on maximum circumferential stress theory. Trans. Nonferrous Met. Soc. China 2001, 11, 287–292. [Google Scholar]
- Horii, H.; Nemat-Nasser, S. Compression-induced microcrack growth in brittle solids: Axial splitting and shear failure. J. Geophys. Res. 1985, 90, 3105–3125. [Google Scholar] [CrossRef]
- Huang, J.F.; Chen, G.L.; Zhao, Y.H.; Wang, R. An experimental study of the strain field development prior to failure of a marble plate under compression. Tectonophysics 1990, 175, 269–284. [Google Scholar]
- Shen, B.; Stephansson, O.; Einstein, H.H.; Ghahreman, B. Coalescence of fractures under shear stress experiments. J. Geophys. Res. 1995, 100, 5975–5990. [Google Scholar] [CrossRef]
- Wong, R.H.C.; Chau, K.T. Crack coalescence in a rock-like material containing two cracks. Int. J. Rock Mech. Min. Sci. 1998, 35, 147–164. [Google Scholar] [CrossRef]
- Sahouryeh, E.; Dyskin, A.V.; Germanovich, L.N. Crack growth under biaxial compression. Eng. Fract. Mech. 2002, 69, 2187–2198. [Google Scholar] [CrossRef]
- Li, Y.P.; Chen, L.Z.; Wang, Y.H. Experimental research on pre-cracked marble under compression. Int. J. Solids Struct. 2005, 42, 2505–2516. [Google Scholar] [CrossRef]
- Park, C.H.; Bobet, A. Crack initiation and propagation from frictional fractures. In Proceedings of the 1st Canada–US Rock Mechanics Symposium, Vancouver, BC, Canada, 27–31 May 2007; pp. 557–564. [Google Scholar]
- Park, C.H. Coalescence of Frictional Fractures in Rock Materials. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2008. [Google Scholar]
- Yang, S.Q.; Dai, Y.H.; Han, L.J.; Jin, Z.Q. Experimental study on mechanical behavior of brittle marble specimens containing different flaws under uniaxial compression. Eng. Fract. Mech. 2009, 76, 1833–1845. [Google Scholar] [CrossRef]
- Yang, S.Q. Crack coalescence behavior of brittle sandstone specimens containing two coplanar fissures in the process of deformation failure. Eng. Fract. Mech. 2011, 78, 3059–3081. [Google Scholar] [CrossRef]
- Park, C.H.; Bobet, A. Crack initiation, propagation and coalescence from frictional flaws in uniaxial compression. Eng. Fract. Mech. 2010, 77, 2727–2748. [Google Scholar] [CrossRef]
- Janeiro, R.P.; Einstein, H.H. Experimental study of the cracking behavior of specimens containing inclusions (under uniaxial compression). Int. J. Fract. 2010, 164, 83–102. [Google Scholar] [CrossRef]
- Lee, H.; Jeon, S. An experimental and numerical study of fracture coalescence in pre-cracked specimens under uniaxial compression. Int. J. Solids Struct. 2011, 48, 979–999. [Google Scholar] [CrossRef]
- Jia, L.C.; Chen, M.; Zhang, W.; Xu, T.; Zhou, Y.; Hou, B.; Jin, Y. Experimental study and numerical modeling of brittle fracture of carbonate rock under uniaxial compression. Mech. Res. Commun. 2013, 50, 58–62. [Google Scholar] [CrossRef]
- Zhao, Y.H. Crack pattern evolution and a fractal damage constitutive model for rock. Int. J. Rock Mech. Min. 1998, 35, 349–366. [Google Scholar] [CrossRef]
- Fujii, Y.; Ishijima, Y. Consideration of fracture growth from an inclined slit and inclined initial fracture at the surface of rock and mortar in compression. Int. J. Rock Mech. Min. Sci. 2004, 41, 1035–1041. [Google Scholar] [CrossRef]
- Awaji, H.; Sato, S. Combined mode fracture toughness measurement by the disk test. J. Eng. Mater. Technol. 1978, 100, 175–182. [Google Scholar] [CrossRef]
- Atkinson, C.; Smelser, R.E.; Sanchez, J. Combined mode fracture via the cracked Brazilian disk. Int. J. Fract. 1982, 18, 279–291. [Google Scholar] [CrossRef]
- Shetty, D.K.; Rosenfield, A.R.; Duckworth, W.H. Mixed mode fracture of ceramic in diametrical compression. J. Am. Ceram. Soc. 1986, 69, 437–443. [Google Scholar] [CrossRef]
- Fowell, R.J.; Xu, C. The use of the cracked Brazilian disk geometry for rock fracture investigations. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1994, 31, 571–579. [Google Scholar] [CrossRef]
- Krishnan, G.R.; Zhao, X.L.; Zaman, M.; Rogiers, J.C. Fracture toughness of a soft sandstone. Int. J. Rock Mech. Min. Sci. 1998, 35, 195–218. [Google Scholar] [CrossRef]
- Khan, K.; Al-Shayea, N.A. Effects of specimen geometry and testing method on mixed-mode I–II fracture toughness of a limestone rock from Saudi Arabia. Rock Mech. Rock Eng. 2000, 33, 179–206. [Google Scholar] [CrossRef]
- Al-Shayea, N.A.; Khan, K.; Abduljauwad, S.N. Effects of confining pressure and temperature on mixed-mode (I–II) fracture toughness of a limestone rock formation. Int. J. Rock Mech. Rock Sci. 2000, 37, 629–643. [Google Scholar] [CrossRef]
- Al-Shayea, N.A. Crack propagation trajectories for rocks under mixed mode I–II fracture. Eng. Geol. 2005, 81, 84–97. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Aliha, M.R.M. On the use of Brazilian disc specimen for calculating mixed mode I–II fracture toughness of rock materials. Eng. Fract. Mech. 2008, 75, 4631–4641. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Sistaninia, M. Mode II fracture study of rocks using Brazilian disk specimens. Int. J. Rock Mech. Min. Sci. 2011, 48, 819–826. [Google Scholar] [CrossRef]
- Dai, F.; Xia, K.; Zheng, H.; Wang, Y.X. Determination of dynamic rock mode-I fracture parameters using cracked chevron notched semi-circular bend specimen. Eng. Fract. Mech. 2011, 78, 2633–2644. [Google Scholar] [CrossRef]
- Wu, L.Z.; Li, B.; Huang, R.Q.; Wang, Q.Z. Study on Mode I-II hybrid fracture criteria for the stability analysis of sliding overhanging rock. Eng. Geol. 2016, 209, 187–195. [Google Scholar] [CrossRef]
- Lawn, B.R.; Wilshaw, T.R. Fracture of Brittle Solids; Cambridge University Press: London, UK, 1975. [Google Scholar]






| Cement | Gypsum | Quartz Sand | Water | Water-Reducing Agent | Water-Proofing Agent | |||
|---|---|---|---|---|---|---|---|---|
| 0.60 mm | 0.30 mm | 0.15 mm | ≤0.075 mm | |||||
| 33.60% | 8.06% | 12.33% | 13.41% | 13.60% | 0.96% | 16.89% | 0.86% | 0.29% |
| Cases | Crack Width d (mm) | Crack Length a (mm) | Crack Angle β (°) |
|---|---|---|---|
| 1 | 0.5 | 10 | 15 |
| 2 | 0.5 | 10 | 30 |
| 3 | 0.5 | 10 | 45 |
| 4 | 0.5 | 10 | 60 |
| 5 | 0.5 | 10 | 75 |
| 6 | 3 | 10 | 15 |
| 7 | 3 | 10 | 30 |
| 8 | 3 | 10 | 45 |
| 9 | 3 | 10 | 60 |
| 10 | 3 | 10 | 75 |
| Cases | Crack Width d (mm) | Crack Angle β (°) | Peak Strength (MPa) | Initiation Angle (°) |
|---|---|---|---|---|
| 1 | 0.5 | 15 | 22.03 | 10 |
| 2 | 0.5 | 30 | 19.60 | 54 |
| 3 | 0.5 | 45 | 17.18 | 55 |
| 4 | 0.5 | 60 | 20.30 | - |
| 5 | 0.5 | 75 | 21.97 | 67 |
| 7 | 3.0 | 15 | 14.80 | 11 |
| 8 | 3.0 | 30 | 14.45 | 39 |
| 9 | 3.0 | 45 | 16.17 | 41 |
| 10 | 3.0 | 60 | 16.40 | - |
| 11 | 3.0 | 75 | 18.36 | - |
| Material | Elastic Modulus E (GPa) | Friction Coefficient u | Poisson’s Ratio v |
|---|---|---|---|
| Concrete | 1.354 | 0.12 | 0.21 |
| Cases | Crack Width (mm) | Crack Angle β (°) | Maximum Circumferential Stress at Crack Tip (MPa) | The Direction of the Maximum Circumferential Stress (°) | Maximum Radial Shear Stress at Crack Tip (MPa) | The Direction of the Maximum Radial Shear Stress (°) |
|---|---|---|---|---|---|---|
| 1 | 0.5 | 15 | 10.25 | 13.5 | 8.12 | 0 |
| 2 | 30 | 13.0 | 46.5 | 10.44 | 0 | |
| 3 | 45 | 14.97 | 61 | 11.98 | 0 | |
| 4 | 60 | 12.74 | 66 | 9.44 | 0 | |
| 5 | 75 | 11.73 | 72 | 9.44 | 0 | |
| 6 | 3.0 | 15 | 13.13 | 14 | 8.53 | −10 |
| 7 | 30 | 15.42 | 46 | 14.67 | 2.5 | |
| 8 | 45 | 12.33 | 81 | 17.75 | 7.5 | |
| 9 | 60 | 7.74 | 102 | 17.07 | 12 | |
| 10 | 75 | 1.55 | 124 | 14.68 | 41 |
| Cases | Crack Angle β (°) | The Initiation Angles of Experimental Work (°) | The Initiation Angles by Numerical Simulation (°) | The Direction of the Maximum Circumferential Stress (°) | The Direction of the Maximum Radial Shear Stress (°) |
|---|---|---|---|---|---|
| 1 | 15 | 11 | 13 | 13 | 0 |
| 2 | 30 | 47 | 47 | 47 | 0 |
| 3 | 45 | 68 | 63 | 63 | 0 |
| 4 | 60 | 73 | 66 | 65 | 0 |
| 5 | 75 | 69 | 70 | 73 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.; Zhou, J.; Yang, J.; Xin, J.; Zhang, H.; Li, B. Initiation and Fracture Characteristics of Different Width Cracks of Concretes under Compressional Loading. Appl. Sci. 2022, 12, 4803. https://doi.org/10.3390/app12104803
Wu L, Zhou J, Yang J, Xin J, Zhang H, Li B. Initiation and Fracture Characteristics of Different Width Cracks of Concretes under Compressional Loading. Applied Sciences. 2022; 12(10):4803. https://doi.org/10.3390/app12104803
Chicago/Turabian StyleWu, Lizhou, Jianting Zhou, Jun Yang, Jingzhou Xin, Hong Zhang, and Bu Li. 2022. "Initiation and Fracture Characteristics of Different Width Cracks of Concretes under Compressional Loading" Applied Sciences 12, no. 10: 4803. https://doi.org/10.3390/app12104803
APA StyleWu, L., Zhou, J., Yang, J., Xin, J., Zhang, H., & Li, B. (2022). Initiation and Fracture Characteristics of Different Width Cracks of Concretes under Compressional Loading. Applied Sciences, 12(10), 4803. https://doi.org/10.3390/app12104803








