Using the Hurst Exponent and Entropy Measures to Predict Effective Transmissibility in Empirical Series of Malaria Incidence
Abstract
1. Introduction
2. Data, Modelling Methods and Analysis Tools
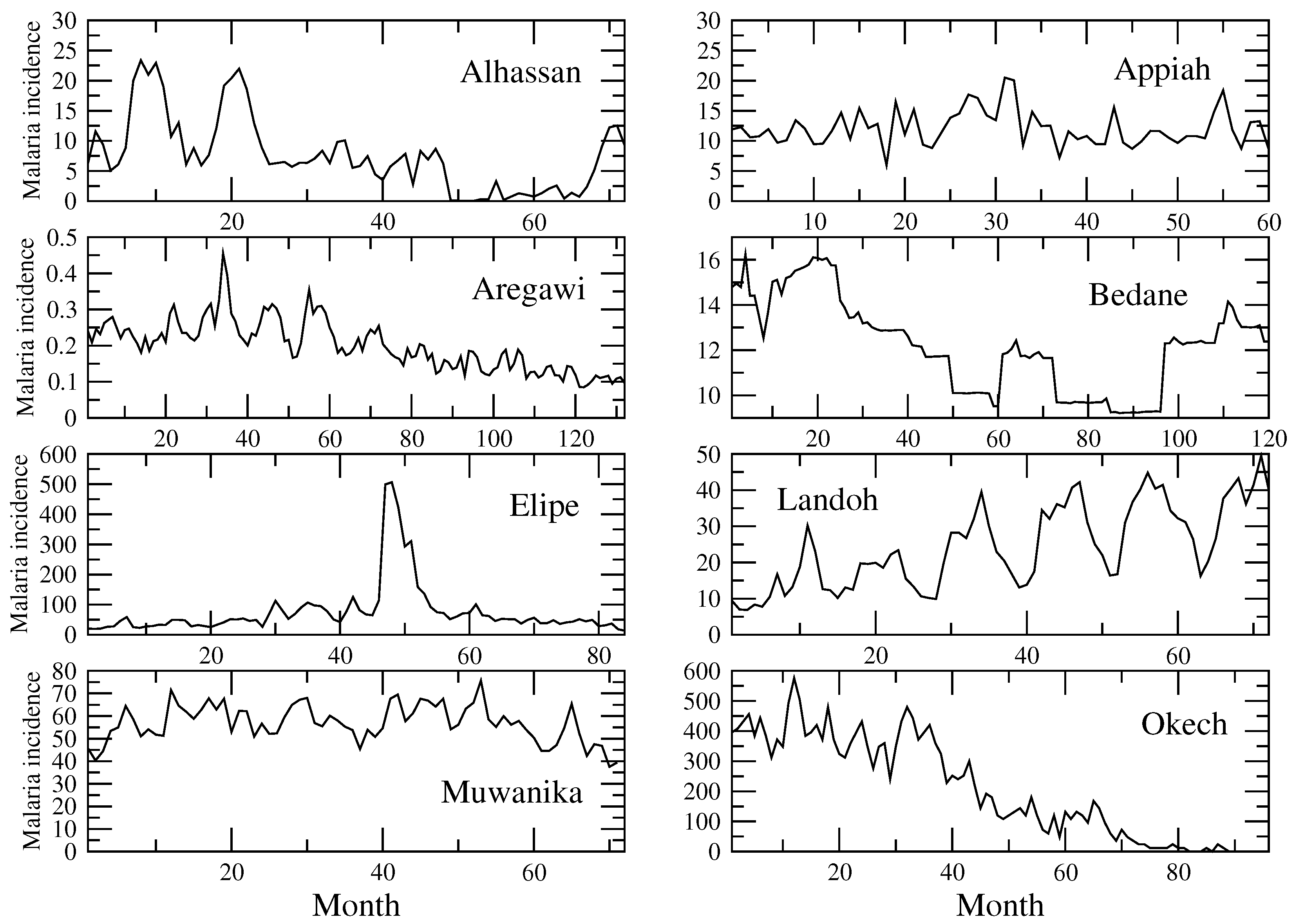
2.1. Empirical Series of Malaria Incidence
2.2. Agent Model for Malarial Spreading
2.3. Hurst Exponent and Entropy to Assess Memory Effects in Stochastic Series
2.4. Estimating the Hurst Exponent and Entropy in Series of Malaria Incidence
3. Qualitative Analysis and Robustness Assessment of the Hurst Exponent and Entropy in Empirical Time Series Behavior
4. Autocorrelation Function and Stochastic Memory in Malaria Empirical Series
5. Towards a More Quantitative Malaria Model for Predicting Effective Gametocytemia
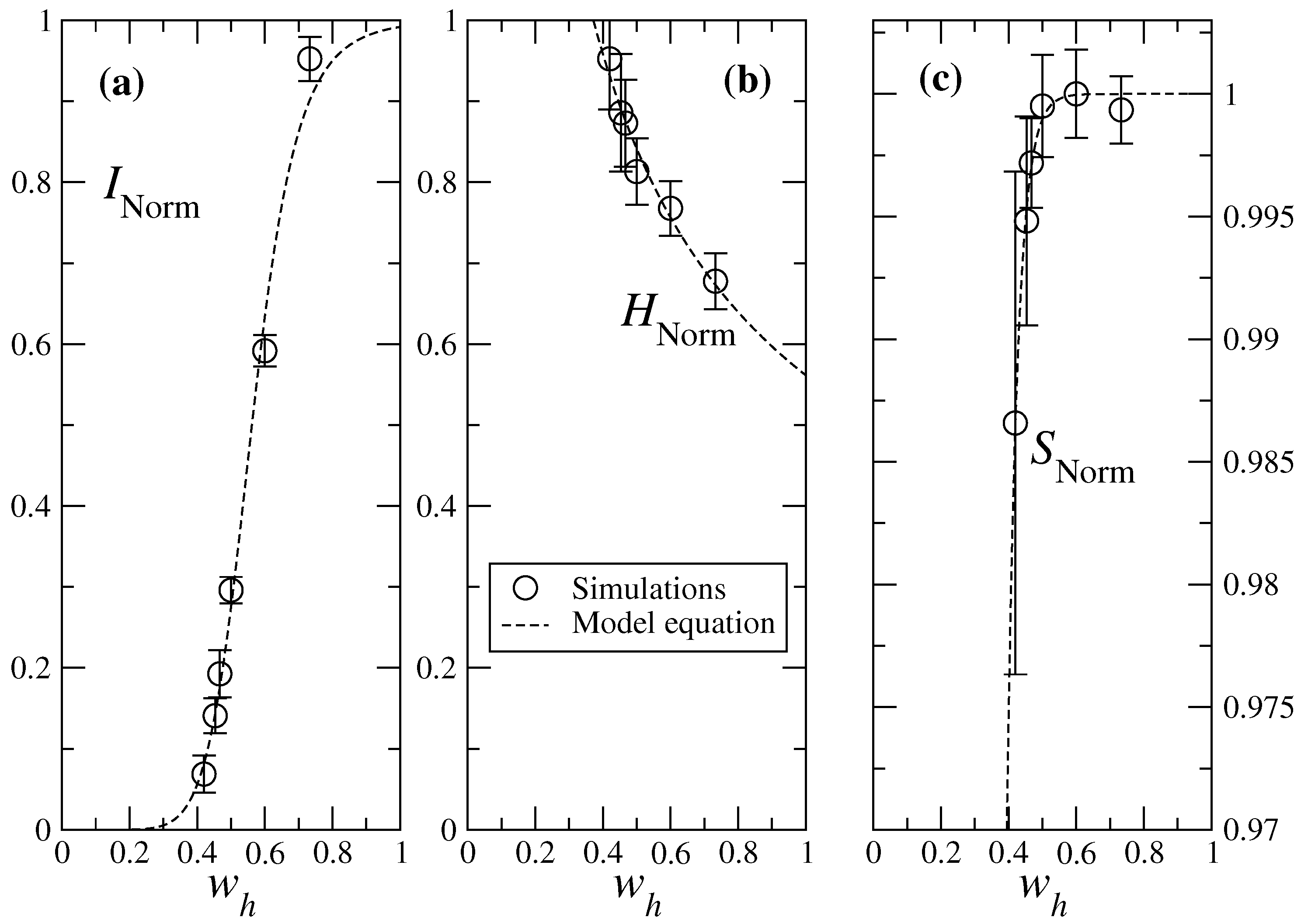
5.1. Models for the Three Observables as Function of Parameter Gametocytemia
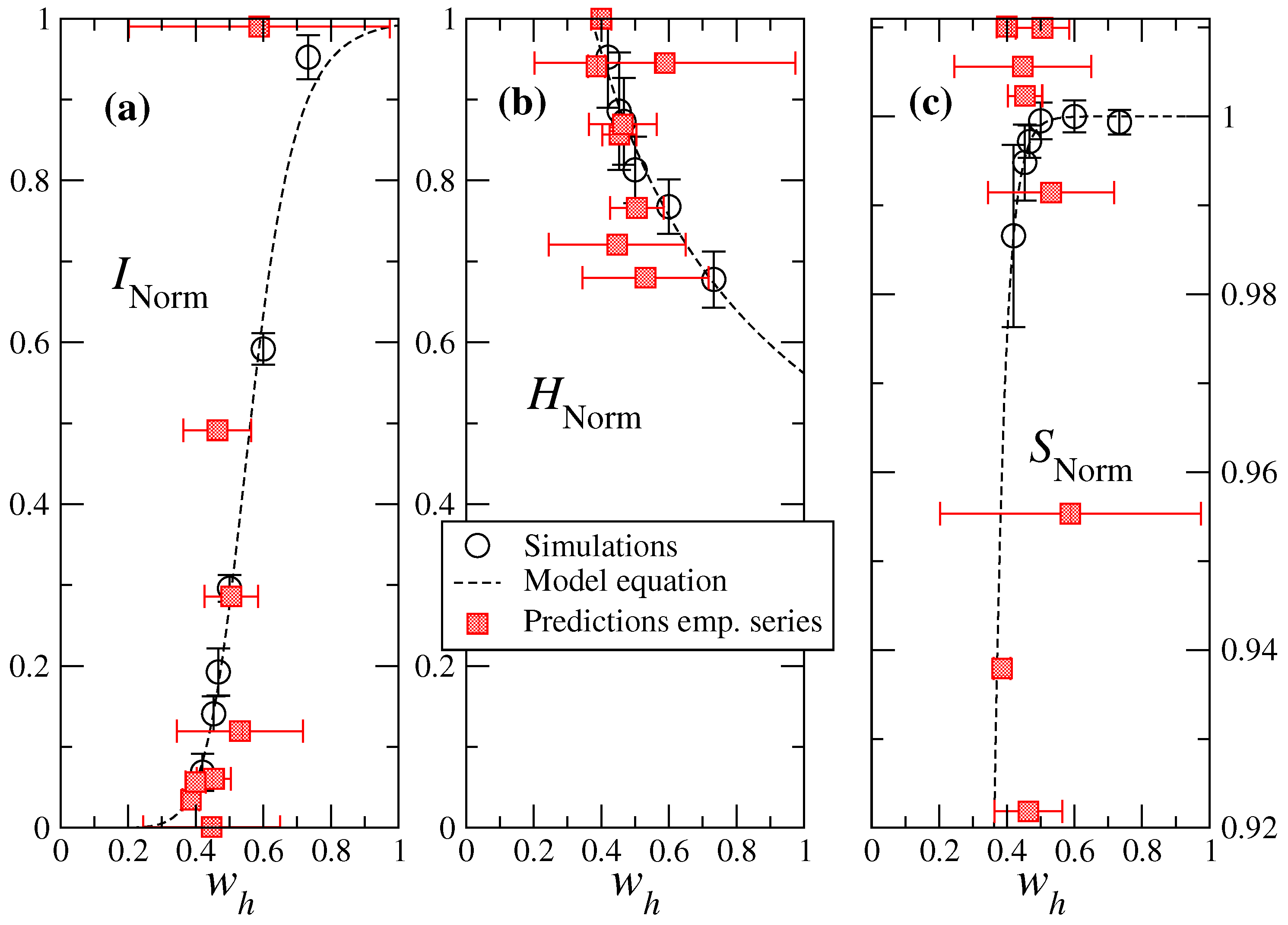
5.2. Prediction of Effective Gametocytemia for Empirical Cases
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Qualitative Analysis of Hurst Exponent and Entropy: Case-by-Case Description
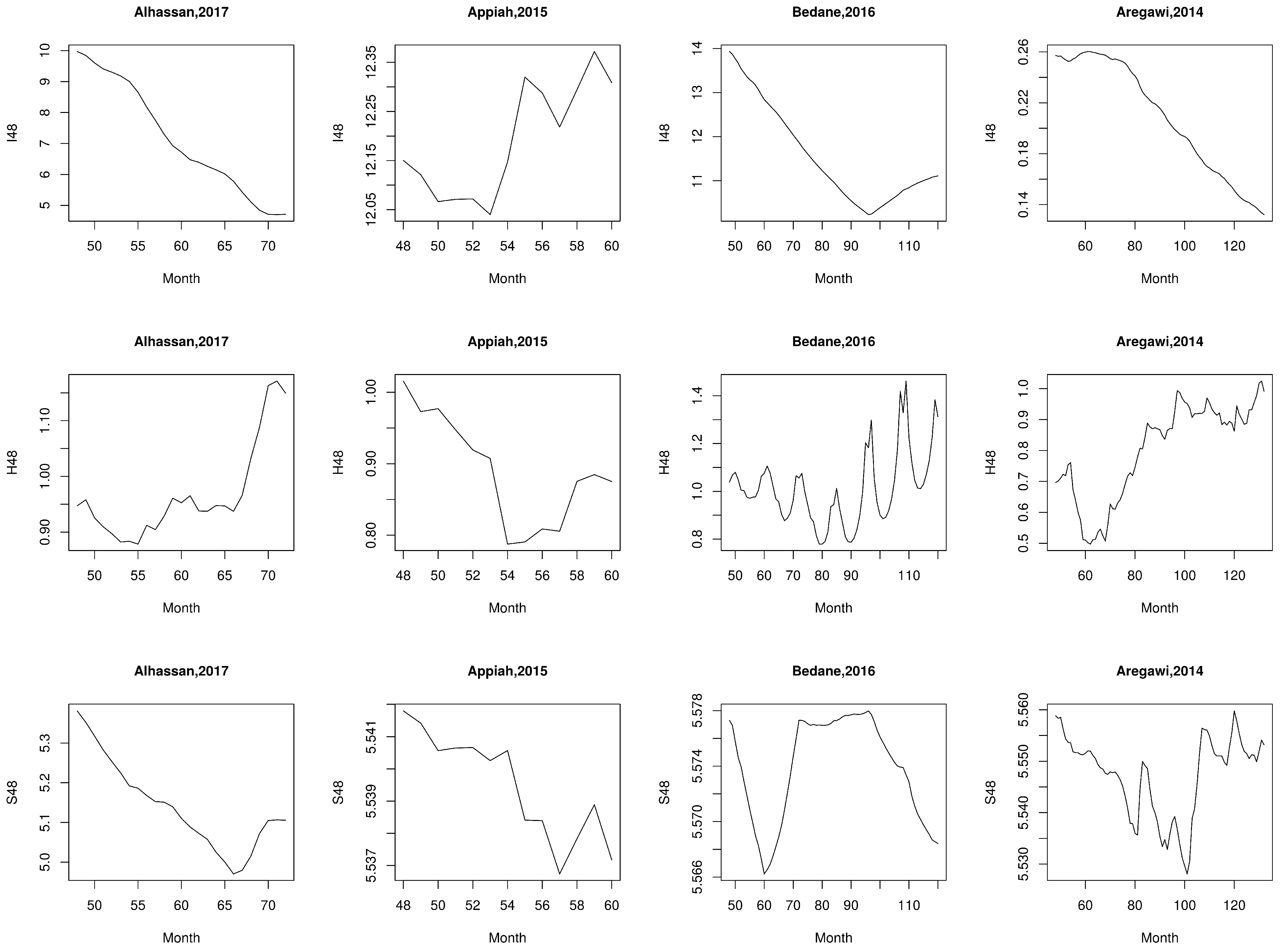
Appendix A.1. Alhassan (2017)
Appendix A.2. Appiah (2015)
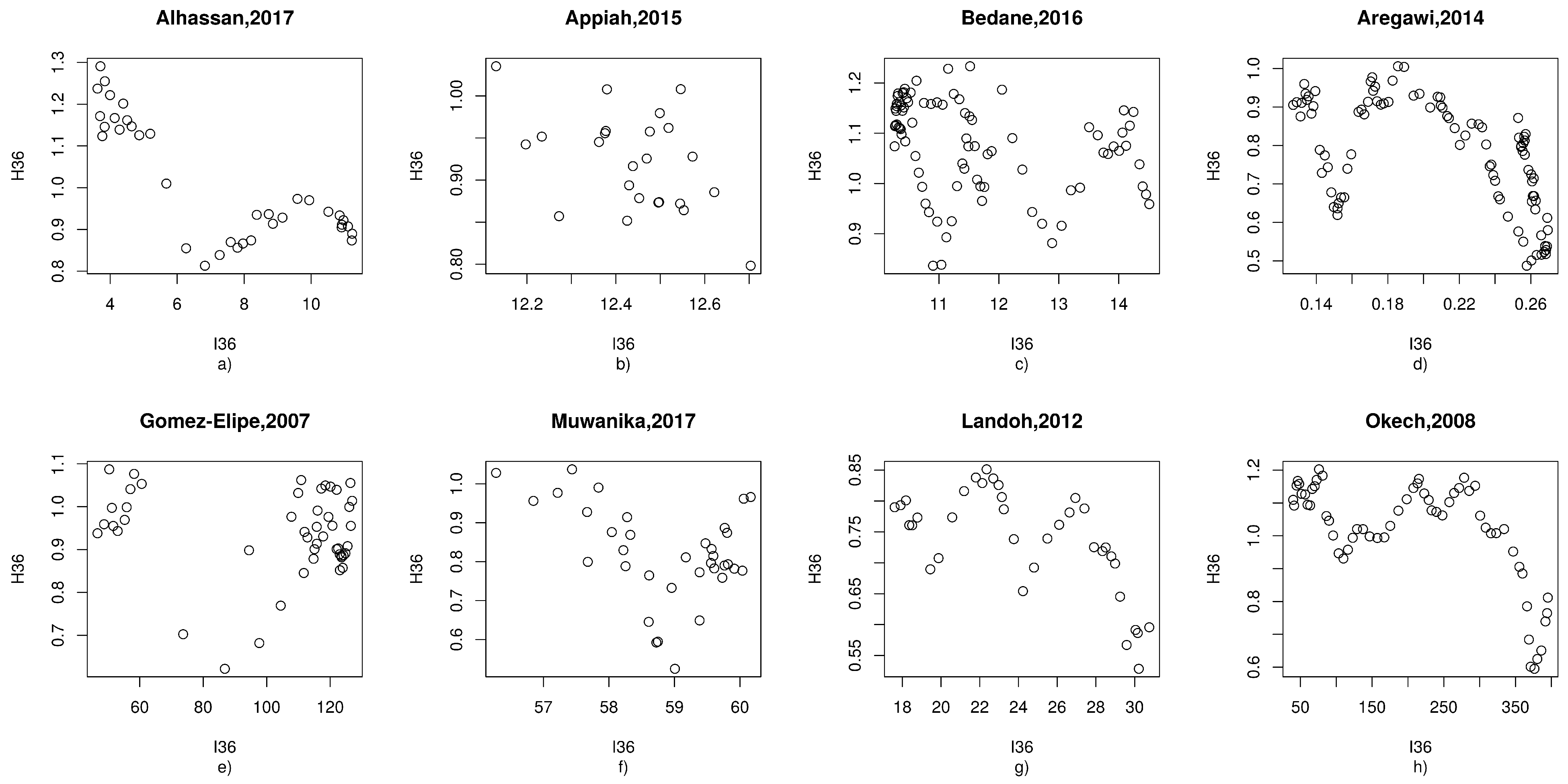
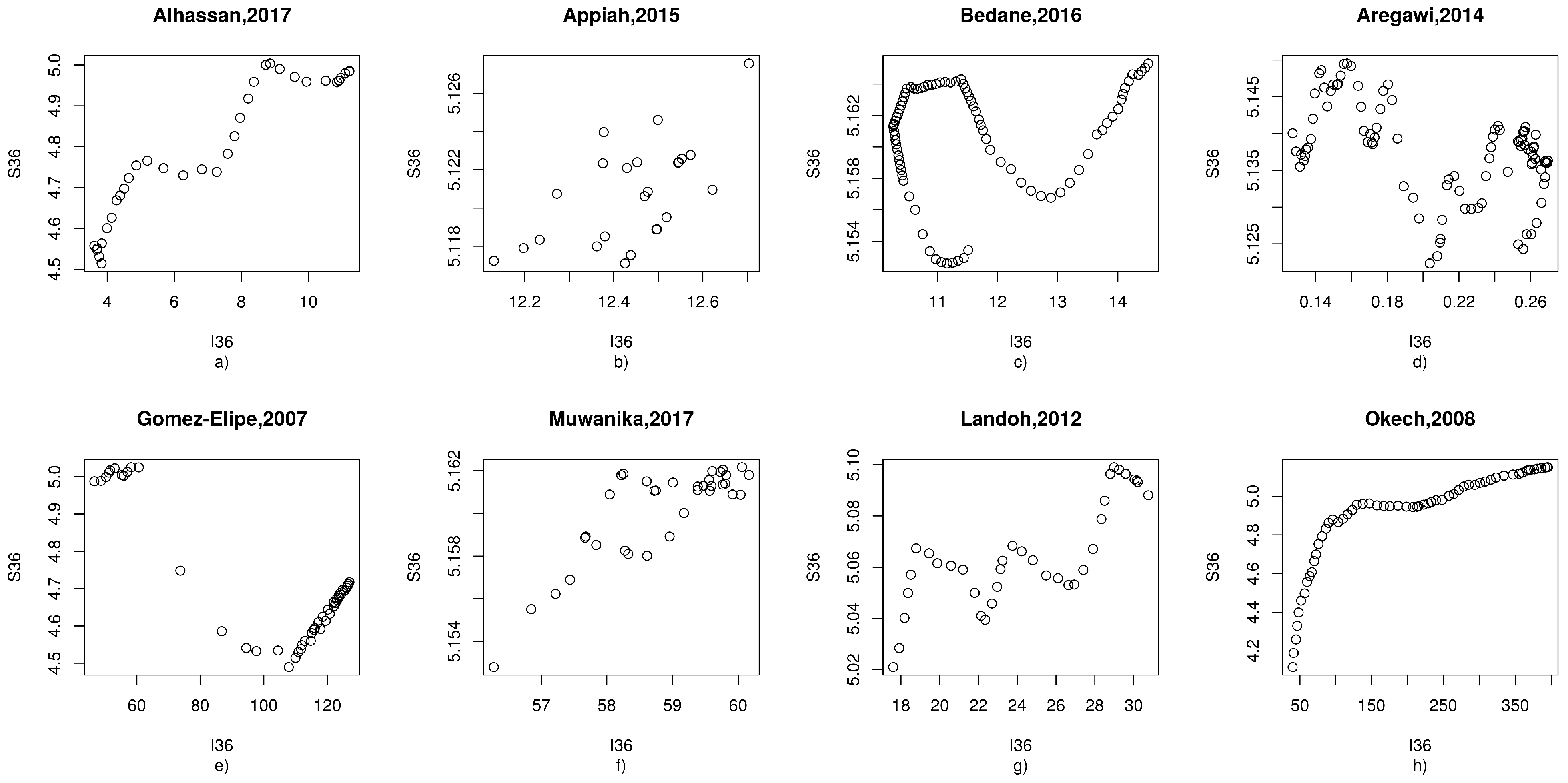

Appendix A.3. Bedane (2016)
Appendix A.4. Aregawi (2014)
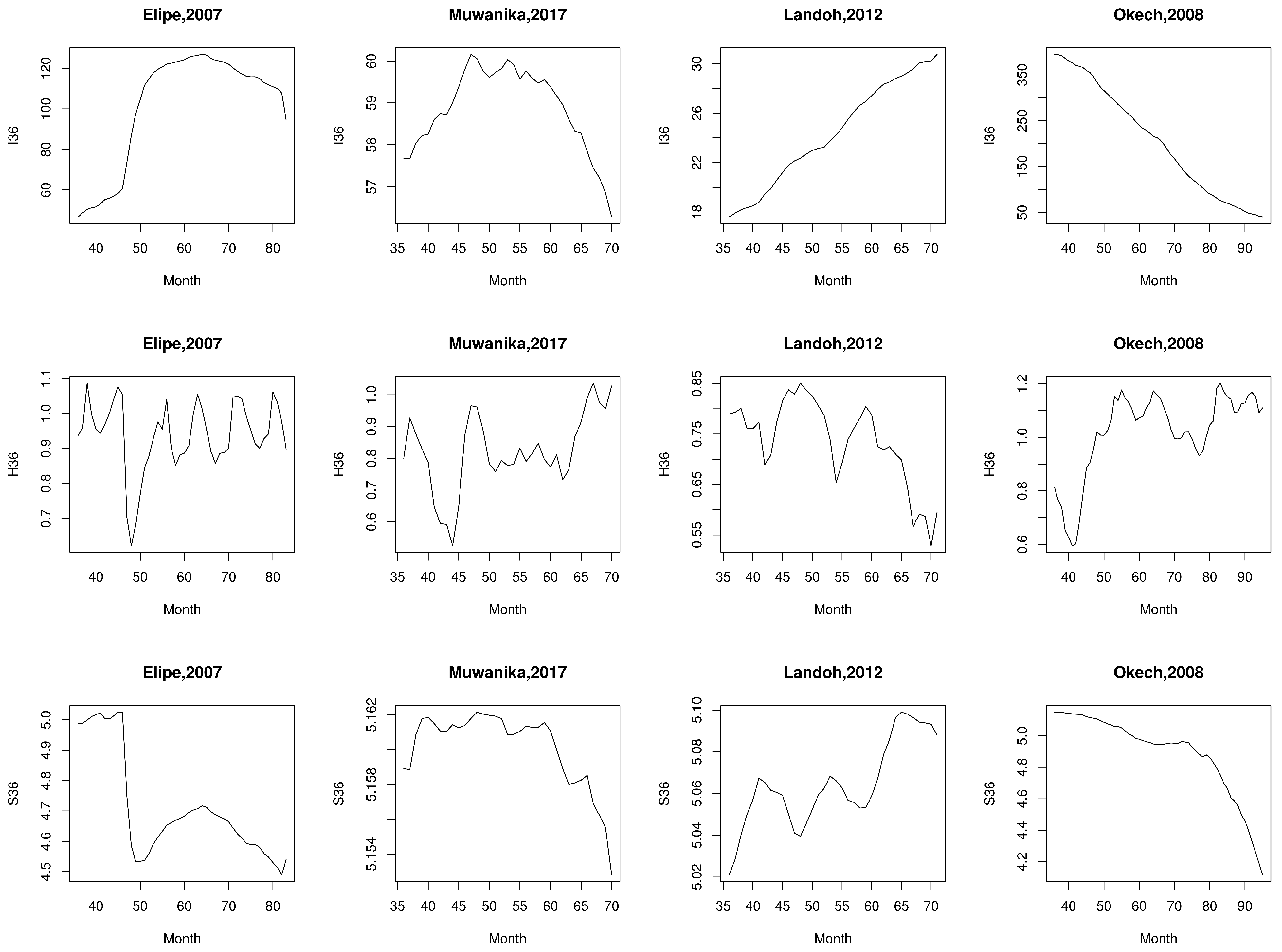
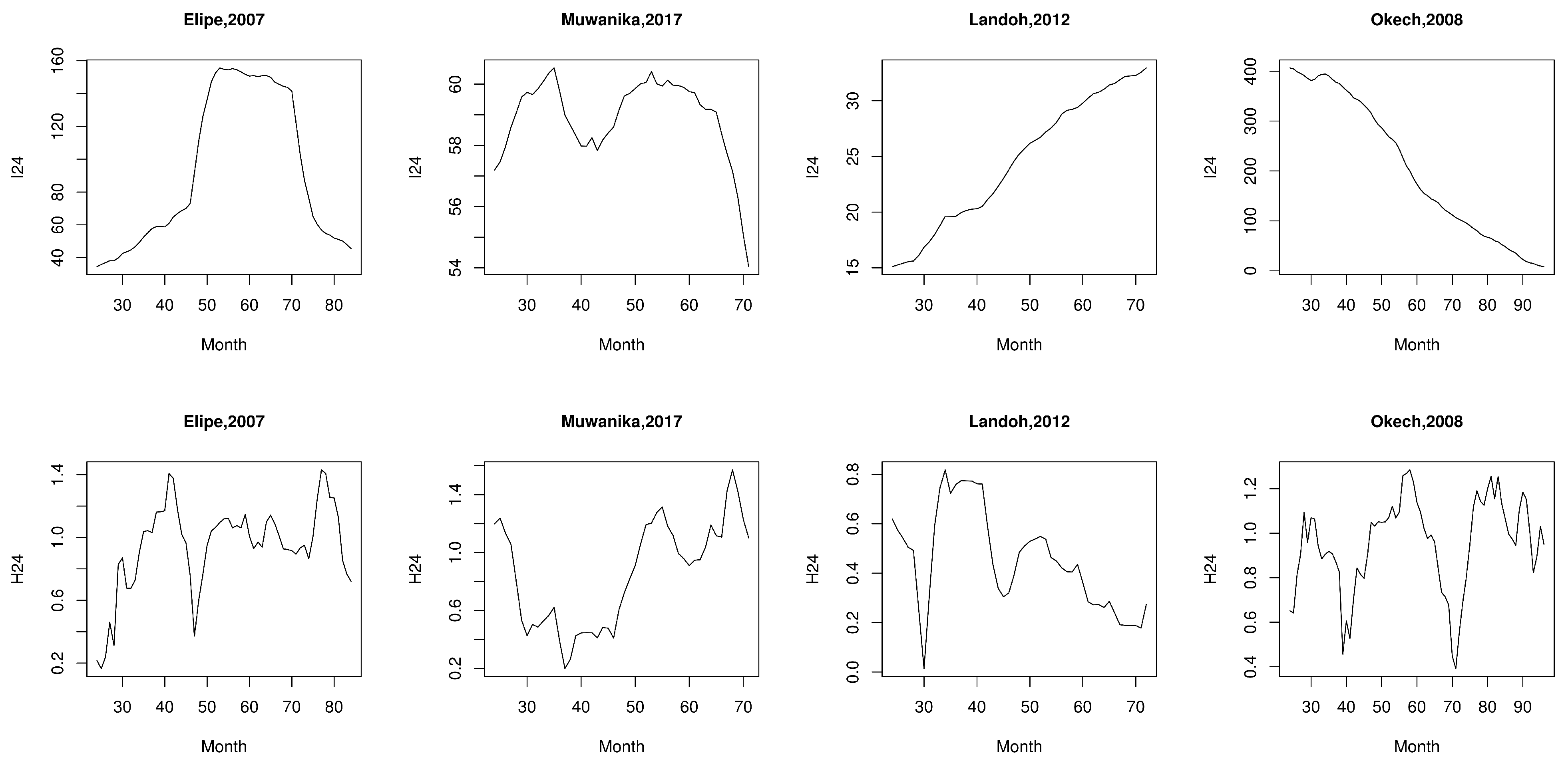
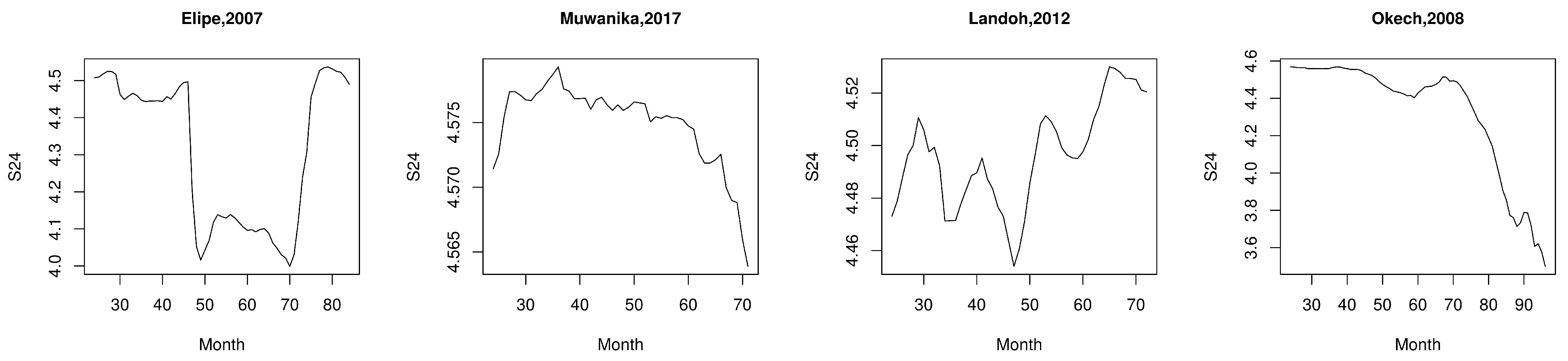
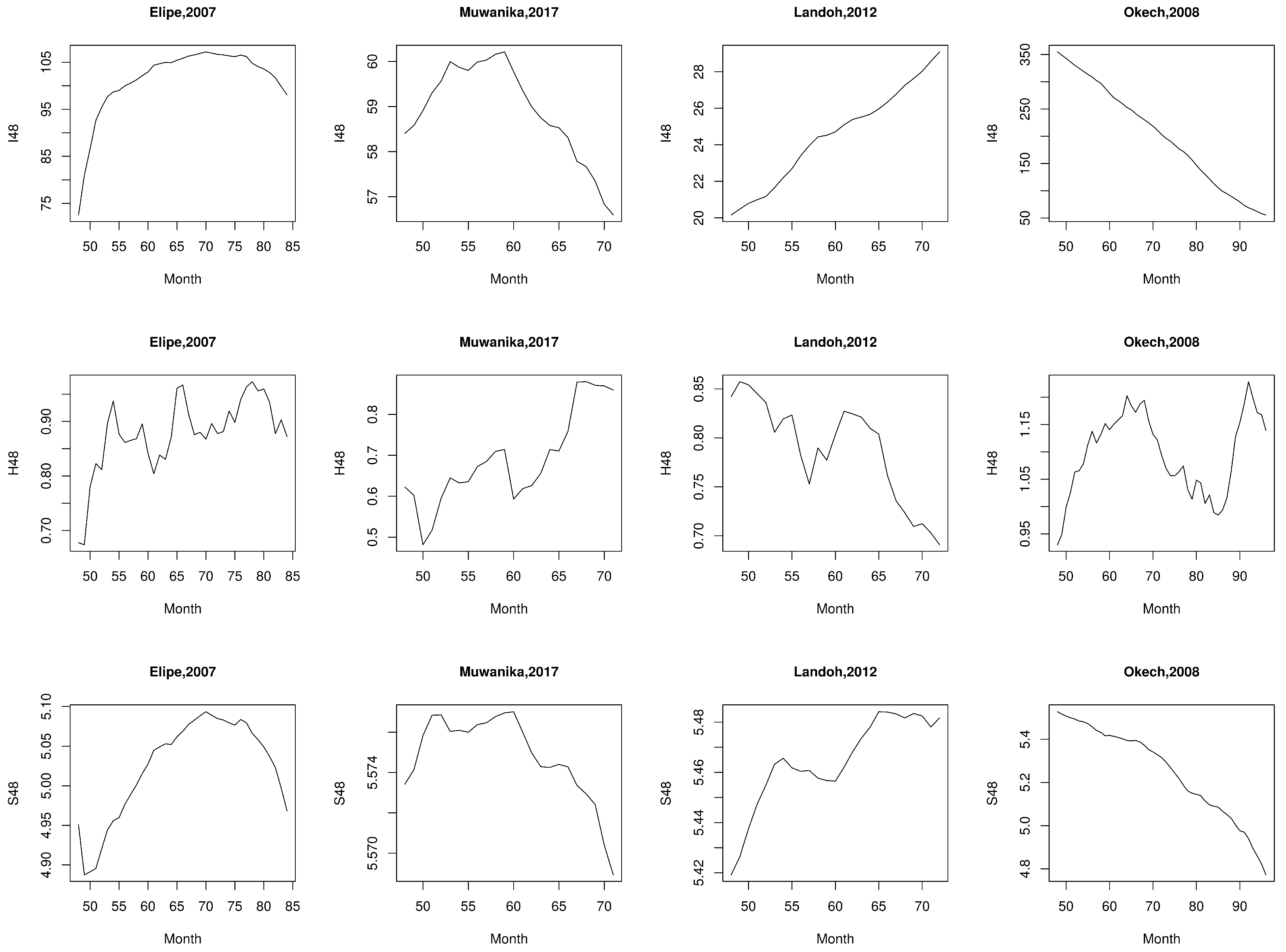
Appendix A.5. Gomez-Elipe (2007)
Appendix A.6. Muwanika (2017)
Appendix A.7. Landoh (2012)
Appendix A.8. Okech (2008)
Appendix B. Inspecting the Robustness of 36-Month Averages

| Empirical Series | GHE for | GHE for |
|---|---|---|
| Aregawi [22] | 0.48 | 0.49 |
| Alhassan [21] | 0.48 | 0.56 |
| Bedane [23] | 0.73 | 0.48 |
| Appiah [16] | 0.21 | 0.09 |
| Landoh [25] | 0.65 | 0.62 |
| Muwanika [26] | 0.41 | 0.37 |
| Elipe [24] | 0.73 | 0.60 |
| Okech [27] | 0.26 | 0.42 |
Appendix C. Arima Models of the Incidence of Malaria
| Level | Malaria Transmission Intensity | Malaria Incidence (±SE) | ||
|---|---|---|---|---|
| Low | 0.420 | Phase transition | 7.7 (±0.89) | |
| High | 0.733 | Epidemic stability | 169.7 (±0.64) | |
| Series | Follow-Up (months) | Region | Trend | Malaria incidence (±SD) |
| Okech, 2008 | 96 | Kenya | decreasing | 205.1 (±169.8) |
| Landoh, 2012 | 72 | Togo | increasing | 24.4 (±11.5) |
| SARIMA | Model | |
|---|---|---|
| 0.420 | ||
| 0.733 | ||
| 0.420 | 0.733 | |
| −0.3635 | −0.3495 | |
| 0.3415 | −0.2344 | |
| −0.3455 | −0.2997 | |
| −0.5422 | −0.2221 | |
| 0.6564 | −0.2273 | |
| −0.1574 | −0.7408 | |
| −1.4685 | – | |
| 0.7626 | – | |
| (drift) | – | – |
| 10.89 | 1037 | |
| AICc | 1849.32 | 3426.29 |
| Empirical Series | SARIMA | |
|---|---|---|
| Okech, 2008 | ||
| Landoh, 2012 | ||
| Okech, 2008 | Landoh, 2012 | |
| 0.6357 | 0.5306 | |
| −0.8778 | −1.000 | |
| – | −0.4894 | |
| −0.6522 | – | |
| 2518 | 17.49 | |
| AICc | 900.8 | 351.15 |
References
- Retief, F.; Cilliers, L. The death of Alexander the Great. Acta Theol. Suppl. 2005, 7, 14–28. [Google Scholar] [CrossRef]
- World Health Organization. World Malaria Report; World Health Organization: Geneva, Switzerland, 2020; Available online: https://www.who.int (accessed on 16 October 2021).
- Sequeira, J.; Louçã, J.; Mendes, A.M.; Lind, P.G. Transition from endemic behavior to eradication of malaria due to combined drug therapies: An agent-model approach. J. Theor. Biol. 2020, 484, 110030. [Google Scholar] [CrossRef] [PubMed]
- Sequeira, J.; Louçã, J.; Mendes, A.M.; Lind, P.G. A Model for Assessing the Quantitative Effects of Heterogeneous Affinity in Malaria Transmission along with Ivermectin Mass Administration. Appl. Sci. 2020, 10, 8696. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; Holden Day: San Francisco, CA, USA, 1970. [Google Scholar]
- Hurst, H.E. The Long-Term Storage Capacity of Reservoir. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Carbone, A.; Castelli, G.; Stanley, H.E. Time-dependent Hurst exponent in financial time series. Physica A 2004, 344, 267–271. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Van Ness, J.W. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Wallis, J.R. Noah, Joseph and operational hydrology. Water Resour. Res. 1968, 4, 909–918. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman Editors: San Francisco, CA, USA, 1982. [Google Scholar]
- Allard, R. Use of time-series analysis in infectious disease surveillance. Bull. World Health Organ. 1998, 76, 327–333. [Google Scholar]
- Permanasari, A.E.; Hidayah, I.; Bustoni, I.A. SARIMA (Seasonal ARIMA) implementation on time series to forecast the number of Malaria incidence. In Proceedings of the International Conference on Information Technology and Electrical Engineering (ICITEE), Yogyakarta, Indonesia, 7–8 October 2013; Volume 2, pp. 203–207. [Google Scholar]
- Golestani, A.; Gras, R. Can we predict the unpredictable? Sci. Rep. 2014, 4, 6834. [Google Scholar] [CrossRef]
- Kumar, V.; Mangal, A.; Panesar, S.; Yadav, G.; Talwar, R.; Raut, D.; Singh, S. Forecasting malaria cases using climatic factors in delhi, India: A time series analysis. Malar. Res. Treat. 2014, 2014, 482851. [Google Scholar] [CrossRef]
- Musa, M.I. Malaria Disease Distribution in Sudan Using Time Series ARIMA Model. Int. J. Public Health Sci. 2015, 4, 7–16. [Google Scholar]
- Appiah, S.T.; Otoo, H.; Nabubie, I.B. Times Series Analysis Of Malaria Cases In Ejisu- Juaben Municipality. Int. J. Sci. Technol. Res. 2015, 4, 220–226. [Google Scholar]
- Sarkar, R.R.; Chatterjee, C. Application of Different Time Series Models on Epidemiological Data—Comparison and Predictions for Malaria Prevalence. SM J. Biom. Biostat. 2017, 2, 1022. [Google Scholar] [CrossRef]
- Ferrão, J.L.; Mendes, J.M.; Painho, M. Modelling the influence of climate on malaria occurrence in Chimoio Municipality, Mozambique. Parasites Vectors 2017, 10, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Chatfield, C. The Analysis of Time Series; Chapman & Hall/CRC: Boca Raton, FL, USA, 2006. [Google Scholar]
- Shumway, R.H.; Stoffer, D.S. Time Series Analysis and Its Applications; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Alhassan, E.A.; Isaac, A.M.; Emmanuel, A. Time Series Analysis of Malaria Cases in Kasena Nankana Municipality. Int. J. Stat. Appl. 2017, 7, 43–56. [Google Scholar]
- Aregawi, M.; Lynch, M.; Bekele, W.; Kebede, H.; Jima, D.; Taffese, H.S.; Yenehun, M.A.; Lilay, A.; Williams, R.; Thomson, M.; et al. Time series analysis of trends in malaria cases and deaths at hospitals and the effect of antimalarial interventions, 2001–2011, Ethiopia. PLoS ONE 2014, 9, e106359. [Google Scholar] [CrossRef]
- Bedane, A.S.; Tanto, T.K.; Asena, T.F. Malaria Distribution in Kucha District of Gamo Gofa Zone, Ethiopia: A Time Series Approach. Am. J. Theor. Appl. Stat. 2016, 5, 70–79. [Google Scholar] [CrossRef][Green Version]
- Gomez-Elipe, A.; Otero, A.; van Herp, M.; Aguirre-Jaime, A. Forecasting malaria incidence based on monthly case reports and environmental factors in Karuzi, Burundi, 1997–2003. Malar. J. 2007, 6, 129. [Google Scholar] [CrossRef]
- Landoh, E.D.; Tchamdja, P.; Saka, B.; Tint, K.S.; Gitta, S.N.; Wasswa, P.; Christiaan, J. Morbidity and mortality due to malaria in Est Mono district, Togo, from 2005 to 2010: A times series analysis. Malar. J. 2012, 11, 389. [Google Scholar] [CrossRef]
- Muwanika, F.R.; Atuhaire, L.K.; Ocaya, B. Prediction of Monthly Malaria Incidence in Uganda and its Implications for Preventive Interventions. J. Med. Diagn. Meth. 2017, 6, 2. [Google Scholar]
- Okech, B.A.; Mwobobia, I.K.; Kamau, A.; Muiruri, S.; Mutiso, N.; Nyambura, J.; Mwatele, C.; Amano, T.; Mwandawiro, C.S. Use of integrated malaria management reduces malaria in Kenya. PLoS ONE 2008, 3, e4050. [Google Scholar] [CrossRef]
- Ferrão, J.L.; Mendes, J.M.; Painho, M.; Zacarias, S. Malaria mortality characterization and the relationship between malaria mortality and climate in Chimoio, Mozambique. Malar. J. 2017, 16, 212. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Santamaria-Bonfil, G.; Gershenson, C.; Fernéz, N. A Package for Measuring emergence, Self-organization, and Complexity Based on Shannon entropy. Front. Robot. AI 2017, 4, 1–12. [Google Scholar] [CrossRef]
- Anis, A.; Lloyd, E.H. The expected value of the adjusted rescaled Hurst range of independent normal summands. Biometrica 1976, 63, 283–298. [Google Scholar] [CrossRef]
- Sánchez-Granero, M.A.; Trinidad-Segovia, J.E.; García-Pérez, J. Some comments on Hurst exponent and the long memory processes on capital markets. Physica A 2008, 387, 5543–5551. [Google Scholar] [CrossRef]
- Barunik, J.; Kristoufek, L. On Hurst exponent estimation under heavy tailed distributions. Physica A 2010, 389, 3844–3855. [Google Scholar] [CrossRef]
- Franzke, C.L.E.; Osprey, S.M.; Davini, P.; Watkins, N.W. A Dynamical Systems Explanation of the Hurst Effect and Atmospheric Low-Frequency Variability. Sci. Rep. 2015, 5, 9068. [Google Scholar] [CrossRef]
- Abeku, T.A.; De Vlas, S.J.; Borsboom, G.; Teklehaimanot, A.; Kebede, A.; Olana, D.; Van Oortmarssen, G.J.; Habbema, J.D.F. Forecasting malaria incidence from historical morbidity patterns in epidemic-prone areas of Ethiopia: A simple seasonal adjustment method performs best. Trop. Med. Int. Health 2002, 7, 851–857. [Google Scholar] [CrossRef] [PubMed]
- Lima, M.V.M.; Laporta, G.Z. Evaluation of prediction models for the occurrence of malaria in the state of Amapá, Brazil, 1997–2016: An ecological study. Epidemiol. Serv. Saúde Brasília 2021, 30, e2020080. [Google Scholar] [CrossRef]
- Graves, T.; Gramacy, R.; Watkins, N.; Franzke, C. A brief history of long memory: Hurst, Mandelbrot and the road to ARFIMA, 1951–1980. Entropy 2017, 19, 437. [Google Scholar] [CrossRef]
- Gao, J.B.; Hu, J.; Tung, W.W. Tung, Facilitating joint chaos and fractal analysis of biosignals through nonlinear adaptive filtering. PLoS ONE 2011, 6, e24331. [Google Scholar] [CrossRef]
- Gao, J.B.; Hu, J.; Mao, X.; Perc, M. Culturomics meets random fractal theory: Insights into long-range correlations of social and natural phenomena over the past two centuries. J. R. Soc. Interface 2012, 9, 1956–1964. [Google Scholar] [CrossRef] [PubMed]
- Flynn, M.N.; Pereira, W.L.R.S. Ecological diagnosis from biotic data by Hurst exponent and the R/S analysis adaptation to short time series. Biomatemática 2013, 23, 1–14. [Google Scholar]
- Corrêa, C.S.; Schuch, D.A.; Queiroz, A.P.; Fisch, G.; Corrêa, F.N.; Coutinho, M.M. The Long-Range Memory and the Fractal Dimension: A Case Study for Alcântara. J. Aerosp. Technol. Manag. 2017, 9, 461–468. [Google Scholar] [CrossRef]
- Garcia, M.N.L.; Requena, J.P.R. Different methodologies and uses of the Hurst exponent in econophysics. Estud. Econ. Appl. 2019, 37, 96–108. [Google Scholar] [CrossRef]
- Kirichenko, L.; Radivilova, T.; Bulakh, V. Generalized approach to Hurst exponent estimating by time series. Inf. Control Meas. Econ. Environ. Prot. 2018, 8, 28–31. [Google Scholar] [CrossRef]
- Sensoy, A. Generalized Hurst exponent approach to efficiency in MENA markets. Physica A 2013, 392, 5019–5026. [Google Scholar] [CrossRef]
- Julián, M.; Alcaraz, R.; Rieta, J.J. Generalized Hurst Exponents as a Tool to Estimate Atrial Fibrillation Organization from the Surface ECG. Comput. Cardiol. 2013, 40, 1199–1202. [Google Scholar]
- Ganguly, K.S.; Modak, S.; Chattopadhyay, A.K.; Ganguly, K.S.; Mukherjee, T.K.; Dutta, A.; Biswas, D. Forecasting Based On a SARIMA Model of Urban Malaria for Kolkata. Am. J. Epidemiol. Infect. Dis. 2016, 4, 22–33. [Google Scholar]
- Ostovar, A.; Haghdoost, A.A.; Rahimiforoushani, A.; Raeisi, A.; Majdzadeh, R. Time series analysis of meteorological factors influencing Malaria in south eastern Iran. J. Arthropod. Borne Dis. 2016, 10, 222–237. [Google Scholar]
- Getnet, B.; Ayalew, S. Developing Stochastic Model For Forecasting Malaria Cases In Addis Zemen, South Gondar, Ethiopia: A Time Series Analysis. Nat. Sci. 2017, 15, 64–77. [Google Scholar]
- Anokye, R.; Acheampong, E.; Owusu, I.; Obeng, E.I. Time series analysis of malaria in kumasi: Using arima models to forecast Time series analysis of malaria in kumasi: Using arima models to forecast. Cogent Soc. Sci. 2018, 3, 1–13. [Google Scholar]
- Helfenstein, U. The use of transfer function models, intervention analysis and related time series methods in epidemiology. Int. J. Epidemiol. 1991, 20, 808–815. [Google Scholar] [CrossRef] [PubMed]
- Briët, O.J.T.; Vounatsou, P.; Gunawardena, D.M.; Galappaththy, G.N.L.; Amerasinghe, P.H. Models for short term malaria prediction in Sri Lanka. Malar. J. 2008, 7, 76. [Google Scholar] [CrossRef]
- Wangdi, K.; Singhasivanon, P.; Silawan, T.; Lawpoolsri, S.; White, N.J.; Kaewkungwal, J. Development of temporal modelling for forecasting and prediction of malaria infections using time-series and ARIMAX analyses: A case study in endemic districts of Bhutan. Malar. J. 2010, 9, 251. [Google Scholar] [CrossRef] [PubMed]
- Hay, S.I.; Rogers, D.J.; Shanks, G.D.; Snow, R.W. Malaria early warning in Kenya Simon. Trends Parasitol. 2001, 17, 95–99. [Google Scholar] [CrossRef]

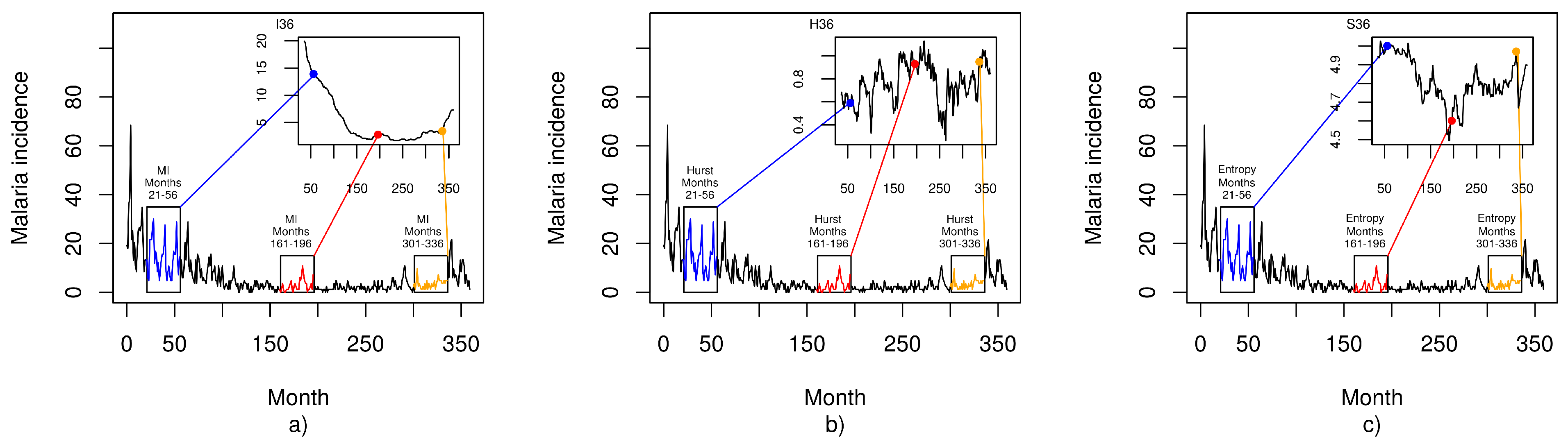
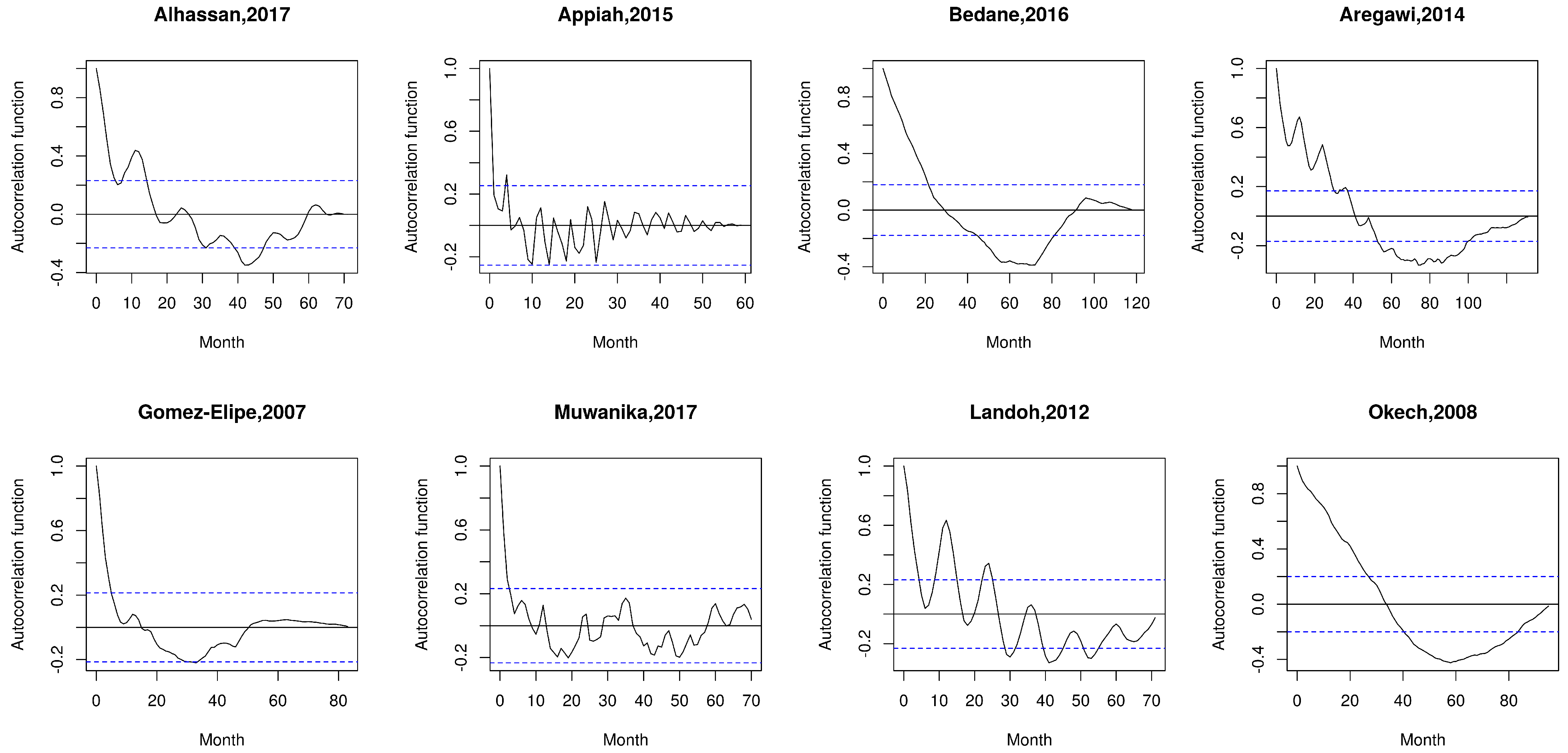
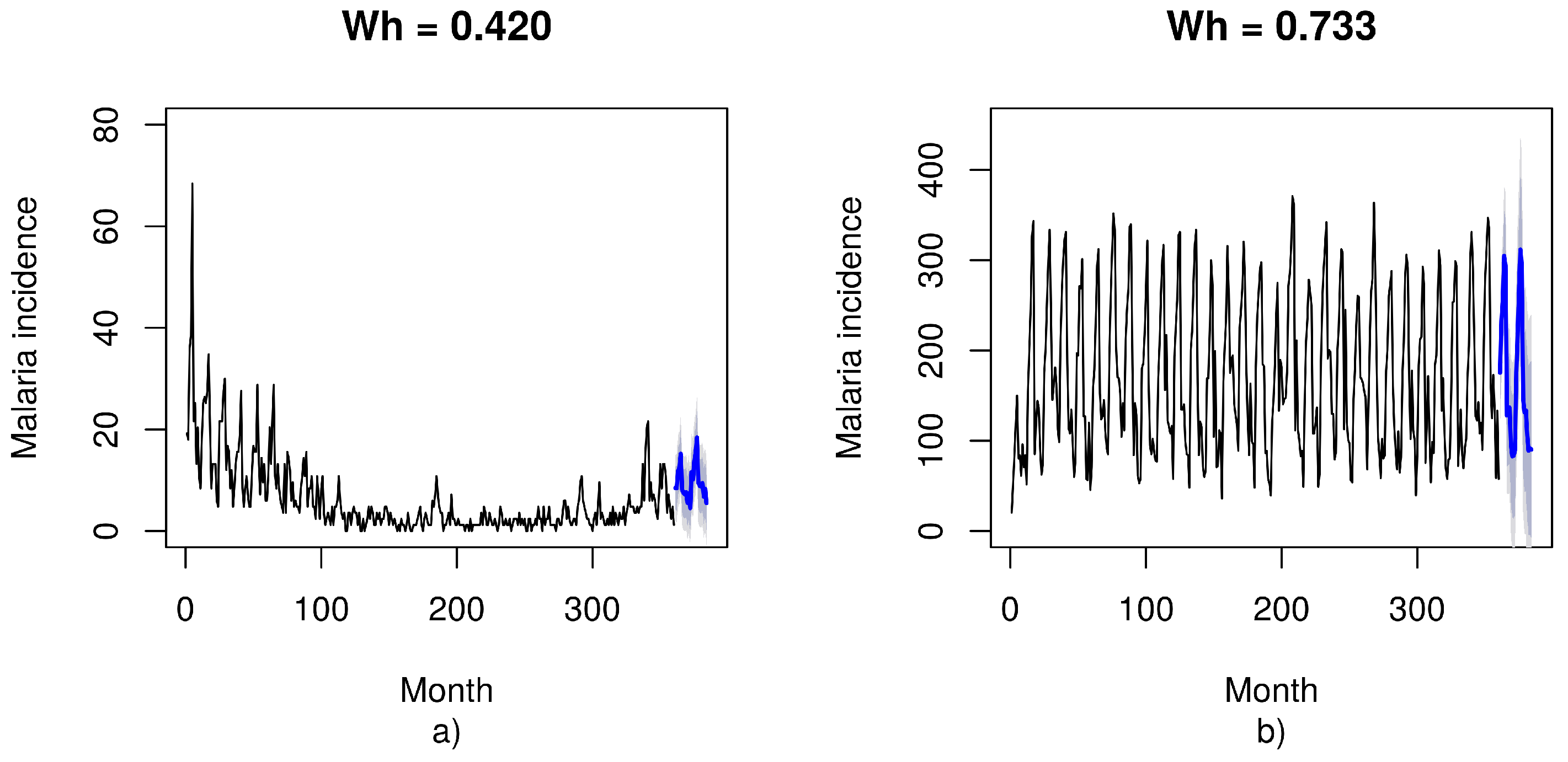

| Empirical Series | Year | I 36 Months () | H 36 Months () | S 36 Months () | Duration Months |
|---|---|---|---|---|---|
| Aregawi [22] | 2014 | 0.208 ± 0.0495 | 0.7766 ± 0.1428 | 5.138 ± 0.0064 | 132 |
| Alhassan [21] | 2017 | 7.091 ± 2.808 | 1.014 ± 0.1425 | 4.792 ± 0.1717 | 72 |
| Bedane [23] | 2016 | 11.63 ± 1.355 | 1.077 ± 0.0925 | 5.161 ± 0.0036 | 120 |
| Appiah [16] | 2015 | 12.44 ± 0.1318 | 0.9229 ± 0.0570 | 5.121 ± 0.0026 | 60 |
| Landoh [25] | 2012 | 24.54 ± 4.312 | 0.7326 ± 0.0850 | 5.065 ± 0.0206 | 72 |
| Muwanika [26] | 2017 | 58.76 ± 1.112 | 0.8254 ± 0.1236 | 5.160 ± 0.0027 | 71 |
| Elipe [24] | 2007 | 101.0 ± 28.20 | 0.9367 ± 0.0993 | 4.710 ± 0.1733 | 84 |
| Okech [27] | 2008 | 203.4 ± 120.2 | 1.018 ± 0.1568 | 4.881 ± 0.2774 | 96 |
| Empirical Series | () Median | () | () | () Median | () | () | () Median | () | () |
|---|---|---|---|---|---|---|---|---|---|
| Aregawi, 2014 | 0.22 | 0.16 | 0.26 | 0.80 | 0.66 | 0.90 | 5.14 | 5.13 | 5.14 |
| Alhassan, 2017 | 7.43 | 4.36 | 9.68 | 0.94 | 0.90 | 1.15 | 4.77 | 4.68 | 4.96 |
| Bedane, 2016 | 11.2 | 10.4 | 12.4 | 1.10 | 1.00 | 1.15 | 5.16 | 5.16 | 5.16 |
| Appiah, 2015 | 12.5 | 12.4 | 12.5 | 0.93 | 0.87 | 0.96 | 5.12 | 5.12 | 5.12 |
| Landoh, 2012 | 24.0 | 21.0 | 28.4 | 0.76 | 0.70 | 0.80 | 5.06 | 5.05 | 5.08 |
| Muwanika, 2017 | 59.0 | 58.2 | 59.7 | 0.81 | 0.77 | 0.90 | 5.16 | 5.16 | 5.16 |
| Elipe, 2007 | 115 | 83.5 | 122 | 0.95 | 0.89 | 1.00 | 4.67 | 4.59 | 4.72 |
| Okech, 2008 | 211 | 89.1 | 310 | 1.06 | 0.98 | 1.13 | 4.96 | 4.85 | 5.08 |
| Average | 24 Months | 36 Months | 48 Months | |||
|---|---|---|---|---|---|---|
| Pearson coeff. | ||||||
| Aregawi, 2014 [22] | 0.048 | 0.216 | 0.323 | 0.223 | 0.727 | 0.012 |
| Alhassan, 2017 [21] | 0.528 | 0.657 | 0.638 | 0.879 | 0.530 | 0.746 |
| Bedane, 2016 [23] | 0.006 | 0.107 | 0.094 | 0.027 | 0.000 | 0.181 |
| Appiah, 2015 [16] | 0.336 | 0.620 | 0.222 | 0.353 | 0.299 | 0.534 |
| Landoh, 2012 [25] | 0.310 | 0.339 | 0.436 | 0.633 | 0.722 | 0.743 |
| Muwanika, 2017 [26] | 0.043 | 0.547 | 0.175 | 0.748 | 0.449 | 0.903 |
| Elipe, 2007 [24] | 0.074 | 0.886 | 0.012 | 0.655 | 0.590 | 0.683 |
| Okech, 2008 [27] | 0.068 | 0.603 | 0.414 | 0.069 | 0.013 | 0.949 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sequeira, J.; Louçã, J.; Mendes, A.M.; Lind, P.G. Using the Hurst Exponent and Entropy Measures to Predict Effective Transmissibility in Empirical Series of Malaria Incidence. Appl. Sci. 2022, 12, 496. https://doi.org/10.3390/app12010496
Sequeira J, Louçã J, Mendes AM, Lind PG. Using the Hurst Exponent and Entropy Measures to Predict Effective Transmissibility in Empirical Series of Malaria Incidence. Applied Sciences. 2022; 12(1):496. https://doi.org/10.3390/app12010496
Chicago/Turabian StyleSequeira, João, Jorge Louçã, António M. Mendes, and Pedro G. Lind. 2022. "Using the Hurst Exponent and Entropy Measures to Predict Effective Transmissibility in Empirical Series of Malaria Incidence" Applied Sciences 12, no. 1: 496. https://doi.org/10.3390/app12010496
APA StyleSequeira, J., Louçã, J., Mendes, A. M., & Lind, P. G. (2022). Using the Hurst Exponent and Entropy Measures to Predict Effective Transmissibility in Empirical Series of Malaria Incidence. Applied Sciences, 12(1), 496. https://doi.org/10.3390/app12010496