Axial Compression Performance and Residual Strength Calculation of Concrete-Encased CFST Composite Columns Exposure to High Temperature

Abstract

Concrete-encased concrete-filled steel tube (CFST) composite columns provide high bearing capacity, good seismic performance and an easier connection with arbitrary angle beams, which are widely used in high-rise buildings. Considering the high frequency of building fires, experimental research investigated the axial compressive behavior of the composite columns’ exposure to high temperature in this paper. Fourteen specimens after exposure to high temperatures with different parameters, including the heating temperature, steel tube diameter and concrete cover thickness, were fabricated to test under axial compressive loading. The failure pattern, load-displacement curve, bearing capacity, initial stiffness, deformation performance and damage rule of the specimens were discussed. The test results showed obvious differences in damage of specimens subjected to various high temperatures. The failure of the specimens began with the spalling and crushing of the concrete at the edge and ends in a lantern shape. The load-displacement curves of the specimens were significantly affected by high temperature, while the influence the of steel tube diameter and concrete cover thickness was relatively weak. A method of calculating axially loaded capacity for the composite column exposure to high temperature is proposed considering the effects of the main parameters of heating temperature and steel tube position, and the calculated results are in good agreement with the experimental results.

1. Introduction

With the rapid development of high-rise buildings, concrete-filled steel tube (CFST) columns have received extensive attention and investigation due to their high strength and performance. Concrete-filled steel tube (CFST) columns have higher bearing capacity and ductility than normal steel reinforced concrete (RC) columns [1,2]. However, their bearing capacity degrades rapidly after fire exposure, so a series of research studies have been performed on the fire performance of CFST column structures [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. Tao et al. [5] analyzed the post-fire bond between the steel tube and concrete in 37 CFST columns. Moliner et al. [6] carried out 16 fire tests of high strength CFST columns. Hu et al. [7] reported a numerical study on the temperature distribution of high-strength concrete-filled steel tube subjected to a fire. Generally, it was found that the outer steel tube is easily damaged, especially when subjected to high temperature without protection [4,8]. Espinos et al. [9,10,11] investigated the post-fire performance of concrete-filled circular hollow section columns and concrete-filled elliptical hollow section columns. It was found that the post-fire performance of circular columns was better than that of square columns, while the eccentricity of columns had a significant effect on their fire performance. Lu et al. [12] investigated the fire performance of high strength self-consolidating concrete-filled steel tubular stub columns. Song et al. [13] and Huo et al. [15] revealed the behavior of CFST joints subjected to standard fire loading. Ding and Wang [17] and Han et al. [18] observed the fire resistance of CFST frames. A number of research studies have been performed on the fire resistance of columns under non-uniform fire [19]. To sum up, previous studies revealed that the residual strength of CFST columns after fire exposure is less than that of columns at ambient temperature because the outer concrete is brittle and easily damaged.

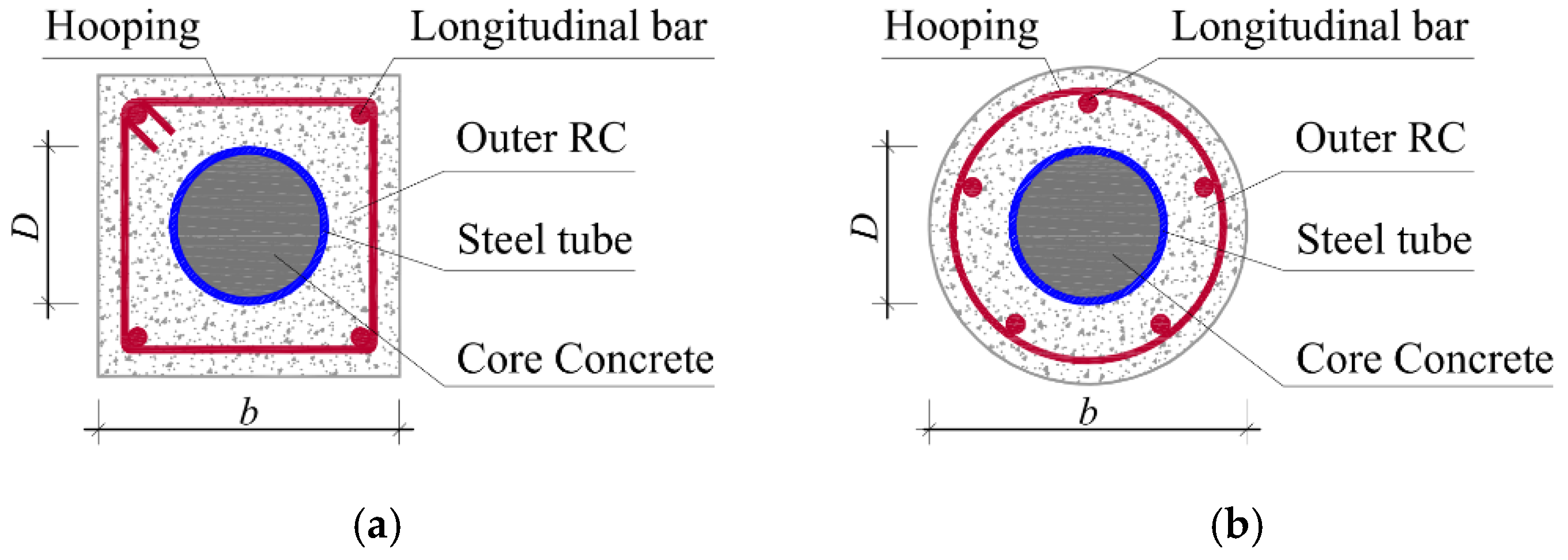
To improve the mechanical properties of CFST columns, a new type of composite of CFST columns wrapped in reinforced concrete (RC) was proposed, which are also called concrete-encased CFST composite columns or steel tube-reinforced concrete composite columns [14,16], as shown in Figure 1. The outer RC wraps the inner CFST column, so its fire resistance is better than that of conventional CFST columns. The outer RC component improves the durability of concrete-encased CFST columns. Additionally, the outward buckling of the inner steel tube can be limited due to the existence of outer RC. Generally, it was found that concrete-encased CFST composite columns have a higher bearing capacity and ductility than conventional CFST columns at ambient temperature [20,21,22,23,24,25,26,27].

Due to their excellent mechanical properties, concrete-encased CFST composite columns have been widely used in high-rise and super high-rise buildings. However, research studies on the fire and post-fire mechanical performance of concrete-encased CFST composite column structures are relatively few. Xu et al. [28] carried out experimental research on the fire resistance of concrete-encased CFST composite columns subjected to ISO-834 standard fire, which mainly evaluated the temperature distribution, fire resistance, displacement versus time relationship, and failure mechanism of the composite columns. Xu et al. and Bao et al. [29,30] conducted numerical analysis investigations on concrete-encased CFST composite columns subjected to 3-side fire and ISO-834 standard fire, respectively. The influences of important parameters, such as fire duration time, sectional dimension, slenderness ratio, and sectional core area ratio, on the temperature field of the composite columns were investigated. The previous research on concrete-encased CFST composite column exposure to high temperature focused on the fire-resistance performance and lack of research on residual performance and residual bearing capacity. It is urgent that the mechanical properties and damage rules of concrete-encased CFST composite column structures after fire exposure be studied; in particular, the residual bearing capacity of these structures should be further studied for evaluation and repair after fire damage.

In this paper, 14 concrete-encased CFST composite columns subjected to high temperatures were designed for an axial compression loading test. The influence of different heating parameters, steel tube diameters, and concrete cover thicknesses on the axial compressive performance and damage rules were investigated, and a calculation method for the residual bearing capacity of the composite columns after fire exposure was proposed.

2. Experimental Programs

2.1. Specimen Preparation

A total of 14 concrete-encased CFST composite columns were designed and manufactured, and successively subjected to high temperature and axial compression tests. The section size of each column specimen was 200 mm × 200 mm, and the column length was 600 mm. The concrete design strength was C60. The specimen test parameters included the heating temperature (ambient temperature (20 °C), 200 °C, 300 °C, 400 °C, 500 °C, 600 °C, 700 °C, 800 °C), the external diameter of the steel tube (89 mm, 114 mm, 138 mm), and the thickness of concrete cover (10 mm, 20 mm, 30 mm). The design details of all specimens are summarized in

Table 1. Design details of each column specimen.

Number	Parameter	b/mm	h/mm	H/mm	Vertical Rebar	Stirrups	d × δ/mm	κ	a/mm	T/°C	t/min
ZA-1	T	200	200	600	4Φ12	Φ6@80	114 × 3.5	0.570	20	20	/
ZA-1A	T and κ	200	200	600	4Φ12	Φ6@80	89 × 3.8	0.445	20	20	/
ZA-1B	T and κ	200	200	600	4Φ12	Φ6@80	138 × 3.0	0.690	20	20	/
ZA-2	T	200	200	600	4Φ12	Φ6@80	114 × 3.5	0.570	20	200	60
ZA-3	T	200	200	600	4Φ12	Φ6@80	114 × 3.5	0.570	20	300	60
ZA-4	T	200	200	600	4Φ12	Φ6@80	114 × 3.5	0.570	20	400	60
ZA-5	T	200	200	600	4Φ12	Φ6@80	114 × 3.5	0.570	20	500	60
ZA-6	T	200	200	600	4Φ12	Φ6@80	114 × 3.5	0.570	20	600	60
ZA-6A	T and κ	200	200	600	4Φ12	Φ6@80	89 × 3.8	0.445	20	600	60
ZA-6B	T and κ	200	200	600	4Φ12	Φ6@80	138 × 3.0	0.690	20	600	60
ZA-6-10	T and a	200	200	600	4Φ12	Φ6@80	114 × 3.5	0.570	10	600	60
ZA-6-30	T and a	200	200	600	4Φ12	Φ6@80	114 × 3.5	0.570	30	600	60
ZA-7	T	200	200	600	4Φ12	Φ6@80	114 × 3.5	0.570	20	700	60
ZA-8	T	200	200	600	4Φ12	Φ6@80	114 × 3.5	0.570	20	800	60

Note: b, h and H are the section width, section height, and length of each column specimen respectively; d and δ are the external diameter and thickness of the inner steel tube, respectively; κ (κ = d/b) represents the position coefficient of the steel tube; a denotes the thickness of concrete cover; T represents the highest temperature of fire endurance; t denotes the constant temperature time; Φ has been used to describe the diameter of the steel bar.

.

Two types of steel were used in the test: rebar and steel tube. The stirrup was Φ6 HRB400 steel reinforcement bar. The stirrup spacing in the unencrypted area located within 400 mm in the middle of the column was 80 mm, and the other area was 30 mm. Longitudinal rebars were 4Φ12 HRB400 steel reinforcements located at four corners. The steel tubes were strength grade Q235B straight-welded circular steel tubes. There were 5 types of reinforcement for all specimen sections, as shown in Figure 2.

The steel tube and the outer steel cage were welded at both ends to fix their positions. After the steel frame was welded successfully, it was put into a mold, then concrete was poured in layers and compacted with a vibrator. After pouring, the two ends of the specimens were polished smooth with a grinder to ensure the whole section was under uniform force, that is, the steel tube and RC component could work effectively during the whole loading process. All specimens were adopted with natural curing until tested.

2.2. Material Properties

Twenty-four steel standard samples, which were divided into eight groups corresponding to different heating temperatures, were tested for each batch of reinforced and steel tubes. The designed cube compressive strength of commercial concrete produced by China Resources Concrete (Nanning) Co. LTD was 60 MPa. The specific materials were as follows: cement: P·O 42.5 ordinary Portland cement; water; sand: natural river sand; coarse aggregate: crushed stones (5–10 mm); active admixtures: silica fume, slag powder, superplasticizer. Additional details on the materials are given in

Table 2. Concrete mix proportion (kg/m³).

Cement	Water	Sand	Coarse Aggregate	Slag Powder	Silica Fume	Superplasticizer
380	163	687	1000	120	40	10.8

.

According to the standard test method (Chinese code GB/T 50081-2002 [31]), 24,150 mm × 300 mm cylinder concrete blocks were reserved and divided into eight groups. At the same time, the concrete standard samples and the column specimens were standing indoors and cured under identical conditions for 28 days.

After curing, all specimens (the concrete standard samples, the steel standard samples, and the column specimens) were exposed to high temperature using an RX3-45-9 industrial box resistance furnace at the State Key Laboratory of Engineering Disaster Prevention and Structural Safety, Guangxi University (China). The heating device and measured temperature rise curves are shown in Figure 3. First, all specimens were heated to the design temperature, which was kept constant for 60 min. Then, the test specimens were taken out and cooled naturally to ambient temperature (20 °C).

The residual strengths of cylinder concrete and steel were respectively tested using Chinese code GB/T 50081-2002 [31] and GB/T 228.1-2010 [32]; the compression strength of cylinder concrete f_c’ (T) and yield strength of steel f_y(T) are shown in

Table 3. Residual compressive strength of concrete cylinder blocks.

T/°C	20 °C	200 °C	300 °C	400 °C	500 °C	600 °C	700 °C	800 °C
fc’ (T) /MPa	54.56	43.11	32.74	26.68	19.9	15.76	10.84	5.89

Note: f_c^’ (T) represents the compressive strength of the 28-day concrete cylinder blocks after fire exposure. When the temperature was 500 °C or above, some test blocks burst. The compressive strength value is the average value of the measured strength of the remaining test blocks.

and

Table 4. Residual yield strength of steel.

Steel Type	d/mm	20 °C	200 °C	300 °C	400 °C	500 °C	600 °C	700 °C	800 °C
Rebar	6	473.26	487.02	486.5	468.51	475.82	467.19	368.63	375.63
	12	432.04	431.38	431.18	433.96	435.46	416.87	367.66	380.05
Steel tube	89	412.83	426.22	/	433.60	/	396.32	/	342.65
	114	409.55	426.22	434.25	444.6	417.1	401.36	369.51	327.64
	138	361.27	380.01	/	382.95	/	343.21	/	296.24

, respectively.

2.3. Test Procedure for Axial Compression Loading

The column specimens, which were subjected to high temperature under identical conditions for the standard samples and then naturally cooled to ambient temperature, were subjected to axial force loading using a 500 T Electro-hydraulic Servo Testing Machine at the State Key Laboratory of Engineering Disaster Prevention and Structural Safety, Guangxi University. The loading device is shown in Figure 4. FRP was wrapped around both ends of the specimen and fitted with a unique 100 mm wide steel hoop to prevent the specimen from being crushed locally. Firstly, the preloading rate was 10 kN/min, and the target axial load was 10% of the estimated ultimate bearing capacity. Then, displacement control was used for loading, and the loading rate was 0.5 mm/min. When the bearing capacity of specimens fell to 70% of the peak load, the loading was stopped. Loading and displacement gauges connected to the IMP data acquisition system recorded the experimental results automatically.

3. Test Results and Discussion

3.1. Failure Patterns of the Composite Columns under Compression Loading

The axial compression failure patterns of the concrete-encased CFST composite columns subjected to high temperature were similar to those at ambient temperature, but the influence of the heating temperature, steel tube diameter, and concrete cover thickness was obvious, as shown in Figure 5.

When the heating temperature T < 500 °C, the concrete cover did not completely peel off until failure, the vertical and oblique cracks staggered to form the main cracks, and the edge concrete collapsed and failed without longitudinal reinforcement bulking or stirrup deformation. When T ≥ 500 °C, the concrete cover was badly damaged and could not contribute to the ultimate bearing capacity of the specimen. At the same time, the damage to the outer concrete was serious, and the loading was mostly borne by the CFST with excellent deformation capacity, resulting in a large ultimate displacement until failure. The outer concrete was seriously peeled off, some stirrup bars were exposed and deformed, and the longitudinal reinforcements buckled.

At the same heating temperature, the larger the diameter of the steel tube, the more pronounced the peeling of the concrete cover, and the more serious the apparent damage to the specimen. The damage degree of the outer concrete increased as the thickness of the concrete cover increased.

3.2. Load-Displacement Curve

The axial load-displacement curves of specimens are shown in Figure 6.

(1) Figure 6a shows that the failure process can be divided into four stages. (a) Elastic stage (OA): At the initial stage of loading, no cracks were found on the surface of the concrete, and the load and displacement presented a linear relationship. (b) Elastic-plastic stage (AB): With the increase in displacement, when the longitudinal strain reached about 3.3‰, cracks appeared and continued to extend, and the curve gradually showed a nonlinear change. (c) Descending stage (BC): After reaching the peak load, the bearing capacity decreased, and the rate of decline was steep. (d) Residual stage (CD): As the displacement continued to increase, the bearing capacity of the specimen decreased significantly, the curve became flat, and the specimen was in the residual stage when the longitudinal strain reached about 10.0‰.

(2) Figure 6b shows that the influence of heating temperature on the load-displacement curves was obvious. With the increase in heating temperature, the slope of the curve in the elastic stage gradually became smaller, that is, the initial stiffness decreased. The residual stage of the curves at T < 600 °C was not obvious, whereas it was the opposite at T ≥ 600 °C. The main reason is the outer RC subjected to high temperature was seriously damaged, and the load was mainly transferred by the core CFST columns.

(3) Figure 6c,d indicate the influence of the steel tube diameter and concrete cover thickness on the load-displacement curves. There was no significant difference in the slope of the descending section of the curve with different steel tube diameters at ambient temperature as the diameter of the steel tube increased. However, when exposed to high temperature (T = 600 °C), the descending section of the curve gradually flattened. The curves of specimens with different concrete cover thicknesses basically coincided at the initial stage but decreased slowly as the concrete cover thickness increased.

4. Analysis of Influential Factors

According to the load-displacement curves of each column specimen, the characteristic point parameters of the cracking load (N_cr(T)), peak load (N_u(T)), initial stiffness (EA₀(T)), and displacement ductility coefficient (μ(T)) can be obtained, as shown in

Table 5. Measured characteristic point parameters of specimens.

Number	Parameter	d × δ/mm	a/mm	T/°C	Ncr(T)/kN	Nu(T)/kN	Ncr(T)/Nu(T)	EA0(T)/MN	μ(T)
ZA-1	T	114 × 3.5	20	20	2010.0	2451.0	0.820	720.65	2.21
ZA-1A	T and κ	89 × 3.8	20	20	1920.5	2341.5	0.820	692.52	2.08
ZA-1B	T and κ	138 × 3.0	20	20	2077.0	2524.5	0.823	739.82	2.34
ZA-2	T	114 × 3.5	20	200	1522.0	2056.5	0.740	675.85	2.12
ZA-3	T	114 × 3.5	20	300	1454.5	2049.0	0.710	632.22	1.84
ZA-4	T	114 × 3.5	20	400	1385.5	2027.5	0.683	570.47	1.55
ZA-5	T	114 × 3.5	20	500	1136.0	1775.5	0.640	515.94	1.92
ZA-6	T	114 × 3.5	20	600	876.0	1653.0	0.530	439.56	2.13
ZA-6A	T and κ	89 × 3.8	20	600	855.0	1628.0	0.525	421.38	1.73
ZA-6B	T and κ	138 × 3.0	20	600	958.5	1682.0	0.570	453.29	2.21
ZA-6-10	T and a	114 × 3.5	10	600	841.0	1790.0	0.470	414.00	1.58
ZA-6-30	T and a	114 × 3.5	30	600	946.5	1578.5	0.600	442.81	2.98
ZA-7	T	114 × 3.5	20	700	534.0	1403.5	0.380	345.91	2.49
ZA-8	T	114 × 3.5	20	800	415.5	1256.0	0.331	298.35	2.61

, in which the initial stiffness is the secant stiffness at 0.4 N_u(T) in the ascending section of the curves. The displacement ductility coefficient refers to the ratio of the ultimate displacement corresponding to 85% N_u(T) at the post-peak stage to the yield displacement determined by the general yield moment method.

4.1. Crack Load

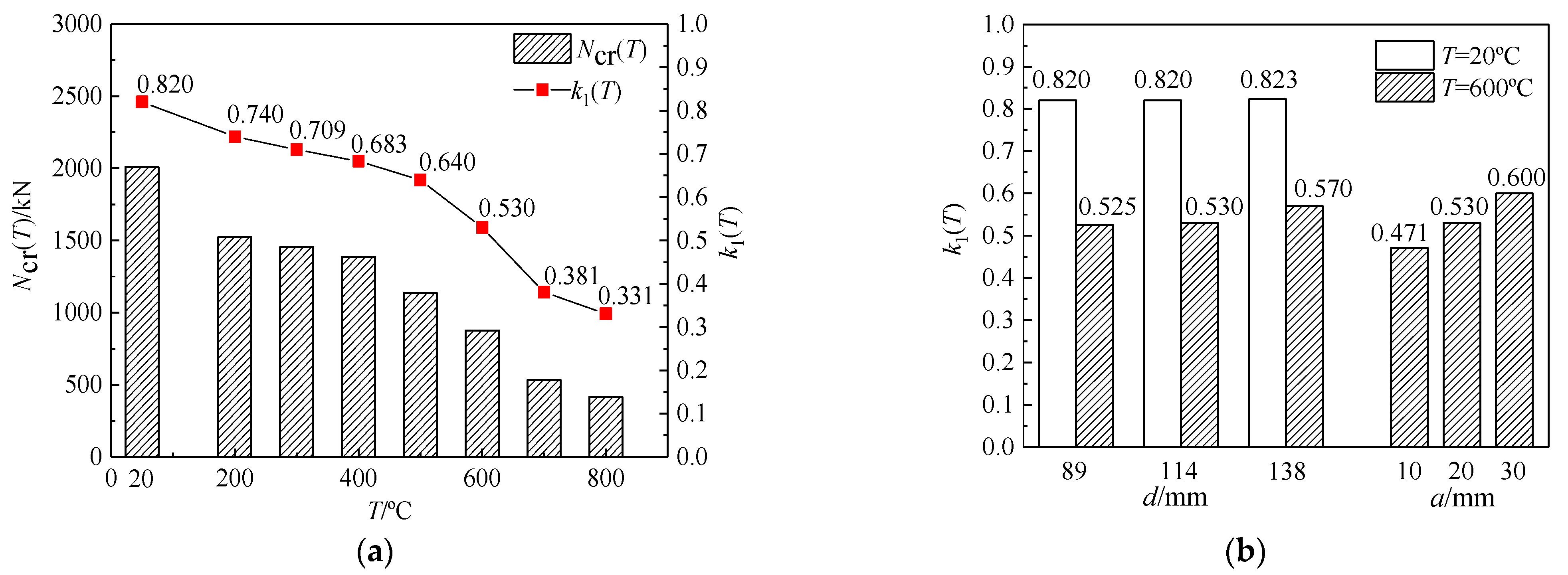
The variations in the ratio (k₁(T)) of the crack load to the peak load of the composite columns subjected to different fire exposure are shown in Figure 7.

It can be seen from Figure 7a that the crack load of specimens decreased with the increase in the heating temperature, which declined more slowly within the range of 200 °C ≤ T ≤ 400 °C and then fell rapidly. Compared with the ambient temperature, the crack loads of the specimens at T = 700 °C and 800 °C decreased by 73.43% and 79.33%, respectively. The k₁(T)-value of the specimen at ambient temperature was 82%, while that of the specimen at T = 800 °C was only 33%. It can be seen that the k₁(T)-value was more reduced by the increase in heating temperature, indicating that the higher the heating temperature was, the earlier the surface crack of the specimen appeared.

Figure 7b reflects that the diameter of the steel tube had no significant influence on the k₁(T)-value at ambient temperature, which was stable at about 82%. At high temperature (T = 600 °C), the k₁(T)-value uniformly increased with increases in steel tube diameter and concrete cover thickness, but the increase was small with the increase in steel tube diameter.

4.2. Residual Ultimate Bearing Capacity

To analyze the influence of the heating temperature on the residual bearing capacity of specimens, the heating temperature influence coefficient k₂(T) of bearing capacity was introduced:

$$k_2(T)=\frac{N_{\mathrm{u}}(T)}{N_{\mathrm{u}}}$$

(1)

where N_u(T) and N_u are the ultimate bearing capacity of the specimens subjected to high temperature and ambient temperature, respectively. Figure 8 shows the variation in the heating temperature influence coefficient of bearing capacity.

As shown in Figure 8a, the influence of the heating temperature on the ultimate bearing capacity of the specimens was very obvious. As the heating temperature increased, the ultimate bearing capacity of specimens decreased continuously. Compared with the specimen under ambient temperature, the k₂(T) curve decreased slowly and not significantly (about 16.1~17.3%) within the range of 200 °C ≤ T ≤ 400 °C. Thereafter, the k₂(T) curve dropped sharply and its decline varied from 27.6% to 48.8%. If the reduction in residual bearing capacity is regarded as the approximately linear variation with the heating temperature, the average rate of decrease was 6.256%·100 °C⁻¹.

Figure 8b reflects the influence of steel tube diameter (d) on the ultimate bearing capacity of the specimens. It can be seen that under both ambient temperature and high temperature (T = 600 °C), the ultimate bearing capacity increased with the increase in steel tube diameter. Compared with specimens with d = 89 mm, the ultimate bearing capacity of the specimens with d = 114 mm and 138 mm increased by 4.68% and 7.82%, respectively at ambient temperature, while it rose by 1.54% and 3.32%, respectively, under exposure to high temperature (T = 600 °C).

Figure 8b indicates that the residual bearing capacity of the specimens after high temperature (T = 600 °C) exposure decreased with the increase in concrete cover thickness (a). The residual bearing capacity of specimens with a = 20 mm and 30 mm decreased by 7.65% and 11.82% compared with that of specimens with a = 10 mm. The main reason is that the concrete cover thickness basically failed at high temperature. When the concrete cover thickness was larger, the stirrup inner confining concrete was smaller, which reduced the bearing capacity of the outer RC and led to a reduction in overall bearing capacity of the specimens.

4.3. Initial Stiffness Degradation

To analyze the axial compressive initial stiffness degradation of the specimens after fire exposure, the heating temperature influence coefficient η(T) of initial stiffness was introduced:

$$\eta (T)=\frac{E{A}_0(T)}{E{A}_0}$$

(2)

where EA₀(T) and EA₀ are the axial compression initial stiffness of the specimens subjected to high temperature and ambient temperature, respectively. The initial stiffness of the specimen can be expressed by the secant line stiffness corresponding to 0.4 N_u(T) at the ascending section of the load-displacement curve.

Figure 9 shows the variation in the heating temperature influence coefficient of initial stiffness. It can be seen that the initial stiffness decreased continuously, with a reduction between 6% and 59%, with the increase in heating temperature, which was approximately linear, as shown in Figure 9a. Compared with specimens with d = 89 mm, the initial stiffness of the specimens with d = 114 mm and 138 mm increased by 4.07% and 6.83%, respectively, at ambient temperature, while it increased by 4.32% and 7.57%, respectively, under exposure to high temperature (T = 600 °C). The increase in initial stiffness under the two different temperatures was similar, indicating that the steel tube diameter had little influence on the strengthening of the initial stiffness of the specimen. If the reduction in initial stiffness is regarded as an approximately linear variation with the heating temperature, the average rate of decrease is 7.513%·100 °C⁻¹, as depicted in Figure 9b. It can be observed that the degradation rate for initial stiffness is faster and more severe than that for residual bearing capacity. Figure 9b illustrates that under exposure to high temperature (T = 600 °C), the initial stiffness of the specimens with concrete cover thickness a = 20 mm and 30 mm was increased by 6.18% and 6.96%, respectively, compared to that of specimens with concrete cover thickness a = 10 mm.

4.4. Deformation Performance

The deformation performance of the concrete-encased CFST composite columns changed under exposure to high temperature, and could usually be evaluated with the deformation coefficient μ, which is the ratio of the ultimate displacement corresponding to failure load to yield displacement of the specimens. For the convenience of analysis, the heating temperature influence coefficient ζ(T) of deformation was introduced:

$$\zeta (T)=\frac{\mu (T)}{{\mu }_0}$$

(3)

where μ(T) and μ₀ are the axial compression deformation coefficient of the specimens subjected to high temperature and ambient temperature, respectively.

Figure 10 shows the variation of the heating temperature influence coefficient of deformation. It can be seen from Figure 10a that with the increase in heating temperature, the deformation coefficient of the specimens takes T = 400 °C as the inflexion point, showing a trend of decreasing first and increasing later. When T = 400 °C, the deformation coefficient reached a valley value of 1.55, a decrease of 29.9% compared with specimens at ambient temperature. The main reason is that when the heating temperature was low (T ≤ 400 °C), the initial damage to the outer RC was small, and its load proportion borne in the late loading period was large. However, due to the limited deformation capacity of the outer RC after the damage, the core CFST could not give full play to the deformation capacity of the specimen as a whole. When the heating temperature was high (T > 400 °C), the damage to the outer RC was large, and it worsened with the increase in the heating temperature. As a result, the load borne by the outer RC was small at the later stage of loading. The overall deformation of the specimen increased with the increase in heating temperature due to the CFST with excellent deformation performance bearing most of the load.

It can be seen from Figure 10b that at both ambient temperature and high temperature (T = 600 °C), the deformation coefficient increased with the increase in steel tube diameter. The deformation capacity of the specimens with d = 114 mm and 138 mm increased by 6.25% and 12.5%, respectively, at the ambient temperature, while increasing by 23.12% and 27.74%, respectively, under exposure to high temperature (T = 600 °C) when compared to specimens with d = 89 mm. This shows that the diameter of the steel tube contributed to the slight increase in deformation capacity of specimens exposed to high temperature.

Figure 10b reflects that the deformation capacities of the specimens with a = 20 mm and 30 mm were increased by 34.81% and 55.61%, respectively, under exposure to high temperature (T = 600 °C) when compared to specimens with concrete cover thickness a = 10 mm. The main reason is that the greater the concrete cover thickness was, which basically failed after exposure to high temperature, the stronger the deformation performance of the specimens was, due to the good ductility of the core CFST columns.

4.5. Damage Analysis

To quantitatively evaluate the damage evolution rule for the composite columns exposed to high temperature, the damage variable parameter D is introduced. When D = 0, the specimen is in the non-destructive state. When D = 1, the specimen is completely destroyed. The damage variable parameter can be calculated according to the following formula:

$$D_{}=1-\frac{EA(T)}{E{A}_0(T)}$$

(4)

where EA₀(T) represents the initial stiffness of the specimen under the non-destructive state, that is, the secant stiffness corresponding to 0.4 N_u(T) at various high temperatures; EA(T) denotes the effective stiffness of the specimen after damage, that is, the secant stiffness at any time under different high temperatures.

In the whole loading process, the damage value of the specimen can be intuitively reflected by the damage evolution curve, as shown in Figure 11. Figure 11 indicates that the damage evolution curves can be divided into four stages:

(1) The horizontal line segment: the damage value at the initial stage of loading is an approximately horizontal line, and the specimen is in the elastic stage.

(2) The rapidly ascending segment: the damage value has increased rapidly, as manifested in the rapid development of cracks and the continuous peeling of concrete cover. The corresponding load-displacement curve is between the elastic-plastic stage and the descending section.

(3) The slowly ascending segment: the growth rate of the damage value has slowed, the concrete cover of the specimens has completely lost its function, and the corresponding load-displacement curve is between the descending section and residual section.

(4) The stable segment: the damage value shows almost no further increase, the outer RC of the specimen has basically lost its function, that is, the load is mainly borne by the core CFST column, and the corresponding load-displacement curve is in the residual section.

It can also be seen from Figure 11 that the damage evolution curves of the specimens were not significantly affected by the diameter of the steel tube or the thickness of the concrete cover, and far less so than by the heating temperature. The higher the heating temperature was, the more serious the initial damage to the specimen was. Before the average longitudinal strain reached 3.3‰, the damage evolution curve of the specimen was in the horizontal and linear segment, and the damage accumulation was very small. Subsequently, the rapidly ascending section of the curve became shorter with increased heating temperature. The failure strain corresponding to 85% N_u(T) of the specimens at T ≤ 500 °C varied between 13.3‰ and 16.7‰, while it was between 10.0‰ and 13.3‰ when T ≥ 600 °C. Finally, only the curves of specimens at T ≥ 600 °C could enter the stationary segment, and the deformation at the end of loading was relatively larger.

5. Calculation Method for Residual Bearing Capacity

Based on the Chinese “Technical specification for concrete-filled steel tube composite column structures” (CECS188:2005) [33], the axial bearing capacity of the concrete-encased CFST composite columns (N_u) is regarded as the sum of the bearing capacity of the outer RC and the core CFST column. The formula for calculation of the axial bearing capacity of the concrete-encased CFST short column is as follows:

$$N_{\mathrm{u}}=0.9(f_{\mathrm{co}}{A}_{\mathrm{co}}+f_{\mathrm{y}}{A}_{\mathrm{ss}})+f_{\mathrm{cc}}{A}_{\mathrm{cc}}(1+1.8\theta )$$

(5)

$$\theta =f_{\mathrm{a}}{A}_{\mathrm{a}}/(f_{\mathrm{cc}}{A}_{\mathrm{cc}})$$

(6)

$$f_{\mathrm{cc}}=f_{\mathrm{co}}=0.88{\alpha }_{\mathrm{c}1}{\alpha }_{\mathrm{c}2}{f}_{\mathrm{cu}}$$

(7)

where θ denotes the confinement index of the core CFST; f_cc and f_co are the compressive strength of concrete inner and outer steel tubes, respectively, which have the same strength value in this test; α_c1 and α_c2, which are determined according to Chinese code GB 50010-2010, represent the ratio of prismatic strength to cube strength (f_cu) and the brittleness coefficient of concrete, respectively; f_y and f_a are the yield strength of longitudinal reinforcement and steel tube, respectively; A_cc and A_co are the sectional area of concrete inside and outside steel tube, respectively; and A_ss and A_a are the sectional area of longitudinal reinforcement and the steel tube, respectively.

Considering only the damage from heating temperature to the residual bearing capacity of the overall specimen, the residual bearing capacity (N_u(T)) of the concrete-encased CFST composite columns subjected to high temperature can be calculated by Equation (8).

$$N_{\mathrm{u}}(T)=k_{\mathrm{T}}{N}_{\mathrm{u}}$$

(8)

where k_T denotes the high temperature influence coefficient of the residual bearing capacity after fire exposure, which is usually related to the heating temperature, section size, and other parameters. It is mainly regarded as the influence function of the heating temperature (T) and the position coefficient κ (κ = d/b, where d, b are the tube diameter and the section width, respectively) of the steel tube in this paper. Regression analysis of the test results can obtain the expression k_T, as follows:

$$k_{\mathrm{T}}=\frac{1}{1+{\kappa }^{{}_{0.8}}{(T-20)}^{1.8}\times {10}^{-5}}$$

(9)

Table 6. Test results and calculated results for specimens.

Number	Parameter	T/°C	d × δ/mm	κ	Nu (T)/kN	Nu-0/kN	kT	Nu-c (T)/kN	Nu-c (T)/Nu (T)
ZA-1	T	20	114 × 3.5	0.570	2451.0	2490.1	1.000	2490.1	1.016
ZA-1A	T and κ	20	89 × 3.8	0.445	2341.5	2336.1	1.000	2336.1	0.998
ZA-1B	T and κ	20	138 × 3.0	0.690	2524.5	2435.0	1.000	2435.0	0.965
ZA-2	T	200	114 × 3.5	0.570	2056.5	2490.1	0.932	2320.8	1.129
ZA-3	T	300	114 × 3.5	0.570	2049.0	2490.1	0.861	2144.0	1.046
ZA-4	T	400	114 × 3.5	0.570	2027.5	2490.1	0.781	1944.8	0.959
ZA-5	T	500	114 × 3.5	0.570	1775.5	2490.1	0.701	1745.6	0.983
ZA-6	T	600	114 × 3.5	0.570	1653.0	2490.1	0.625	1556.3	0.942
ZA-6A	T and κ	600	89 × 3.8	0.445	1628.0	2336.1	0.670	1565.2	0.961
ZA-6B	T and κ	600	138 × 3.0	0.690	1682.0	2435.0	0.588	1431.8	0.851
ZA-6-10	T and a	600	114 × 3.5	0.570	1790.0	2490.1	0.625	1556.3	0.869
ZA-6-30	T and a	600	114 × 3.5	0.570	1578.5	2490.1	0.625	1556.3	0.986
ZA-7	T	700	114 × 3.5	0.570	1403.5	2490.1	0.555	1382.0	0.985
ZA-8	T	800	114 × 3.5	0.570	1256.0	2490.1	0.494	1230.1	0.979

Note: N_u-0 and N_u-c(T) correspond to the calculated results of Equations (5) and (8), respectively. In the test, the concrete compressive strength (f_c’) was measured by the cylinder blocks, so it must convert into the cube compressive strength (f_cu). According to Chinese code GB 50010-2010 [34] and CEB-FIP [35], the ratio value of f_c’/f_cu varies from 0.80 to 0.89, and it can be taken as 0.86 because of the concrete strength grade C60 used in this test.

shows the theoretically calculated values for N_u-c(T) of the residual bearing capacity. As can be seen from Table 6, the average ratio of the calculated values to the test values was 0.976, and the coefficient of variation was 0.067, which shows that the calculated results using the above method are in good agreement with the test results.

6. Conclusions

(1) Compared with the concrete cylinder blocks, the composite columns had no obvious cracks, and the explosion phenomenon occurred due to the action of steel reinforcement bars.

(2) The failure patterns in the column specimens were greatly affected by the heating temperature, the diameter of the steel tube, and the thickness of the concrete cover. The higher the heating temperature was, the earlier the vertical cracks appeared and the concrete cover fell off. The greater the steel tube diameter and the concrete cover thickness were, the more serious the damage to the outer RC was.

(3) The load-displacement curve of the specimen displayed an elastic stage, elastic-plastic stage, descending stage, and residual stage, which were not greatly affected by the diameter of the steel tube or the thickness of the concrete cover, but very significantly affected by the heating temperature.

(4) With the increase in the heating temperature, the bearing capacity and initial stiffness of the specimen decreased continuously, and the latter displayed a faster rate of decline due to the increased damage after fire exposure, while the deformation capacity first decreased and then increased. With the increase in steel tube diameter, the bearing capacity and deformation capacity increased, and the initial stiffness had no obvious effect. With the increase in concrete cover thickness, the bearing capacity decreased, and the initial stiffness and deformation capacity increased.

(5) Considering the influence of the heating temperature and the steel tube position, a method of calculating the axial compression bearing capacity of the concrete-encased CFST composite columns after high temperature exposure was put forward on the basis of the Chinese technical specification CECS 188:2005.