Abstract
During the operation period, the deformation of an ultra-high arch dam is affected by the large fluctuation of the reservoir water level. Under the dual coupling of the ultra-high dam and the complex water level conditions, the traditional variational analysis method cannot be sufficiently applied to its deformation analysis. The deformation analysis of the ultra-high arch dam, however, is very important in order to judge the dam safety state. To analyze the deformation law of different parts of an ultra-high arch dam, the panel data clustering theory is used to construct a Spatio-temporal characteristic model of dam deformation. In order to solve the difficult problem of the fluctuating displacement of dam deformation with water level effect, three displacement component indexes (absolute quantity, growing, and fluctuation) are proposed to characterize dam deformation. To further optimize the panel clustering deformation model, the objective weight coefficient of clustering comprehensive distance is calculated based on the CRITIC (CRiteria Importance Through Inter-criteria Correlation) method. The zoning rules of the ultra-high arch dam are established by using the idea of the CSP (Constraint Satisfaction Problem) index, and the complex water level of the reservoir is simulated in the whole process. Finally, the dynamic cluster analysis of dam deformation is realized. Through a case study, three typical working conditions including the rapid rise and fall of water level and the normal operation are calculated, and the deformation laws of different deformation zones are analyzed. The results show that the model can reasonably describe the deformation law of an ultra-high arch dam under different water levels, conveniently and intuitively select representative measuring points and key monitoring parts, effectively reducing the analysis workload of lots of measuring points, and improve the reliability of arch dam deformation analysis.
1. Introduction
With the improvement of dam building technology, the ultra-high arch dam has reached the level of 300 m, e.g., the maximum dam height of Xiaowan in China is 294.5 m, the maximum dam height of Baihetan in China (under construction) is 289 m, the maximum dam height of Xiluodu arch dam in China is 285.5 m, and the maximum dam height of Enguri arch dam in the Republic of Georgia is 271.5 m [1,2]. Due to the large volume, height, fluctuation range of water level, and complex deformation distribution under load, the ultra-high arch dam is an extremely complex nonlinear statically indeterminate structure. A large number of monitoring facilities are often required to monitor its operational state [3,4]. The displacement of the dam is a direct indicator of the safety situation. During the rapid rise and fall of the reservoir water level, the influence of water pressure on dam deformation is especially prominent. Currently, determining the deformation law of an ultra-high arch dam is difficult and research is still needed [5,6,7]. Therefore, it is of great value to study the deformation law of ultra-high arch dams from both a safety and a theoretical point of view.
Due to the high reading frequency of the instrument for monitoring the state of the dam, an automatic monitoring instrument achieves one to two measurements a day, so it is possible to accumulate a large amount of data. If all data are modeled and analyzed point by point, it is not only time- and labor-consuming, but also not conducive to mastering the operational behavior of the dam in time. Therefore, a reasonable method is needed to distinguish a wide range of the same type of measuring points, so as to select various representative measuring points for analysis which will ensure the time- and effectiveness of safety monitoring.
At present, the prediction analysis method is usually a deformation time series of dam single or multiple measuring points combined with an intelligent algorithm [8,9,10,11]. Rankovic V. et al. developed a support vector regression identification model to predict the structural behavior of the dam [12], Su et al. proposed a wavelet support vector machine-based prediction model of dam deformation [13], Chen et al. presented a prediction model of arch dam deformation via correlated multi-target stacking [14], and Zheng D. et al. analyzed the deformation and stress behavior of a high concrete dam under the effect of reservoir basin deformation [15]. The described methods can obtain highly reliable analysis results and prediction accuracy for the local range of general structures. In addition, the effects and monitoring of water levels on the dynamic properties of concrete arch dams have also been deeply studied [16,17].
However, when using these methods for the monitoring analysis of an ultra-high arch dam the following problems often occur: (a) Due to the huge volume span, the water level fluctuates in both the amplitude and temperature gradient of an ultra-high arch dam. Given the comprehensive influence of various factors such as constraints and material properties, the deformation of different parts often varies greatly. If analyzed from a single time series, it cannot reflect the overall correlation state of the dam body. If a section of spatial measurement points is considered, the dynamic change trend of different measurement points is ignored. (b) When the monitoring data of a measuring point is wrong, or the data loss is serious due to instrument damage, the deformation analysis within a local range of measuring points can easily report a large error or wrong result. Feedback of this result to the dam operation state can easily lead to biased judgment, which cannot truly describe the deformation characteristics of an ultra-high arch dam. (c) When the monitoring time series is short, the linear correlation degree of deformation of measuring points at different parts of the dam is high. If the modeling analysis is carried out directly, the reliability of the results is often low due to the low degree of freedom of the data.
In view of the above problems, the panel data clustering theory [18] is applied and transforms the dam single point measurement point analysis method into an area analysis method. This method comprehensively considers the deformation characteristics of the dam space-time measurement points and can fully mine the deformation monitoring information in the two dimensions of time and section. Previous papers have researched the deformation application of clustering algorithms and the application of panel data theory. Bashari et al. used a fuzzy clustering-based model to estimate of deformation modulus of rock masses [19], Chen et al. built a DP-GMM clustering-based ensemble learning prediction methodology to study dam deformation [20], Li Y. G. et al. proposed a clustering method for panel data based on adaptive weighting [21], Zhang et al. studied quantile-regression-based clustering for panel data [22], Liu et al. applied panel data to achieve a three ways decisions based grey incidence analysis clustering approach on the regional high-tech industrialization [23], and Wang et al. proposed a mixed-coefficient panel model for evaluating the overall deformation behavior of dams [24]. It can be seen from the above research that the clustering algorithm has strong applicability and accuracy in analyzing structural engineering deformation. Panel clustering analysis has been well applied in environment, agriculture, and engineering fields, and needs further development in the application of dam deformation. Because the distance of panel clustering analysis is the core index to determine the clustering, the displacement is often divided into “absolute” and “increment”, ignoring the fluctuating displacement of dam deformation with the accompanying effect of water level. Therefore, the calculation method of fluctuation distance in arch dam displacement is proposed to adapt to the complex water level condition of the dam.
Due to the large variation of the comprehensive distance in the process of dynamic clustering, the CRITIC method is used to calculate the objective weight coefficient of the comprehensive distance of clustering [25]. This is done to balance the local and global optimization. This method not only considers the amount of information of evaluation indexes but also considers the discrimination and conflict between evaluation indexes. In a large number of research applications, the CRITIC method has high result accuracy and strong sensitivity to evaluation indicators. The CRITIC method has a high ability to optimize and integrate the evaluation information, especially when the database is large and there are many influencing factors [26]. The CRITIC method has been well applied and studied in many fields involving statistics, such as process improvement in aluminum alloys [27], software selection problems [28], and intelligent healthcare management evaluations [29]. In the cluster analysis of dam deformation, the number of cluster partitions is one of the key indexes to evaluate the results [30,31]. Generally, the clustering algorithm automatically calculates the number of clusters according to the characteristics of the database and its algorithm, which makes the number of clusters difficult to control and consistent in different databases [32]. Under different water level conditions, the number of partitions of the clustering algorithm is based on panel data and the CRITIC method is sensitive to the database. If the number of clusters is very small, the deformation partition has no discrimination. If the number is very large, the significance of cluster analysis will be lost. If the number of clusters is inconsistent, the results cannot be compared and analyzed. For these three cases, it is difficult to further analyze the deformation characteristics of the dam. In order to avoid the above three situations, the number of clusters needs to be constrained and optimized. Because panel data clustering is a concentrated hierarchical clustering algorithm, the CSP index is particularly suitable for single link concentrated hierarchical clustering algorithms [33,34]. The advantage of the CSP index is to solve and optimize the multi-weight factor problem [35,36], especially the clustering problem. The zoning rules of the ultra-high arch dam are established through the idea of the CSP index, which can simulate the water level in different stages of the reservoir in the whole process and realize the dynamic cluster analysis of dam deformation.
In order to improve the effectiveness of deformation clustering method analysis under the dynamic and complex water level, the clustering fluctuation distance is applied. This is done in accordance with the deformation characteristics under different working conditions, i.e., during the rapid rise period of the reservoir water level upstream of the ultra-high arch dam and the operation period of normal water level. Furthermore, the clustering method of panel data is optimized to construct the dam deformation zoning model based on PCCM (Panel data-CRITIC- CSP model). The dam deformation is partitioned, and the complex water level of the reservoir is simulated in the whole process. Next, the dynamic cluster analysis of dam deformation is realized. A better classification of samples, considering the Spatio-temporal correlation characteristics of dam deformation measurement points, is obtained. Finally, the representative measurement points are selected from each subclass for subsequent analysis. This method can out-perform traditional single-point analysis and reflect the overall Spatio-temporal change state of an ultra-high arch dam under large-scale water level fluctuation.
2. Deformation Zoning Model of Ultra-High Arch Dam
2.1. Panel Data Theory
Panel data is a data form integrating time series and section information [37]. The panel data of the dam deformation attribute can be constructed by assigning the measured point attribute to the dam deformation. Through continuous monitoring of a large number of monitoring points of an ultra-high arch dam, a series of deformation values () of monitoring points (i) in different periods (t) can be obtained, which can be expressed as follows:
where i is the number of monitoring points; t is the monitoring time; and is the deformation value, which contains the information of two dimensions of time and space and can reflect the deformation correlation and dynamic changes of different parts of the dam at the same time. It has obvious rationality and superiority compared with a simple time series or section series.
2.2. Matrix Expression of Spatiotemporal Characteristic Level of Panel Data
Panel data is the direct embodiment of the dynamic clustering of dam deformation, and its Spatio-temporal characteristic attributes are mainly described from three aspects [35]: (a) absolute index, which is the original value of panel data, (b) growing index, which is the embodiment of the growth rate of sample objects, and (c) fluctuation index, which is the embodiment of the growth rate and change rate of the sample.
When analyzing the dam deformation monitoring value, the similarity of the deformation sequence is reflected by effectively integrating the three indexes of “absolute quantity”, “growing”, and “fluctuation” of the dam deformation value [23]. The third index is very important to describe the deformation of an ultra-high arch dam under complex water levels, but many studies have not been carried out. For the deformation data set , the following definitions are given [38]:
Definition 1.
The mean functionand variance functionof dam deformation measuring point i in period T are
where all symbols are the same as Equation (1).
Definition 2.
The “absolute” distancebetween the measuring pointand the measuring pointas
where and are the deformation values of measuring points and in period t respectively.
Definition 3.
The “growing” distance between measuring point i and measuring point j as:
where ; ; and are the difference of absolute quantity between two adjacent periods of deformation respectively.
Definition 4.
The “fluctuation” distance between measuring point i and measuring point j as:
where all symbols are the same as Equation (2).
In addition, to prevent large differences in the order of magnitude between the three distances, the above distances can also be standardized, so as to ensure that each distance plays a role. For example, the standardized transformation formula of absolute distance is:
where is the standardized treatment of absolute distance and and are the maximum and minimum values of absolute distance, respectively. The standardized formula of other distances is the same. During a specific calculation, whether to standardize or not can be selected according to the order of magnitude difference of the three distances. Generally, when the order of magnitude difference is greater than or equal to , it is recommended to standardize.
With the above basic definitions, in order to accurately describe the temporal and spatial deformation characteristics of each measuring point of the dam, the “comprehensive” distance between the measuring point and the
measuring point is applied as a
comprehensive criterion for deformation similarity:
Or
where is the weight of distance and is the standardized representation of distance. The comprehensive distance is the weighted combination of , , and , and Equation (8) is the standardized form of comprehensive distance.
2.3. Calculating the Objective Weight Coefficient of Comprehensive Distance
To improve the stability and reliability of the single panel data clustering method, according to the characteristics of the comprehensive distance index evaluation system of dam deformation measuring points, the objective weight coefficient of the comprehensive distance is calculated by the CRITIC (CRiteria Importance Through Inter-criteria Correlation) method. This method realizes the purpose of optimizing clustering through quantitative analysis within evaluation indexes and quantitative calculation between evaluation indexes [25,39].
Since all distance indicators of the comprehensive distance are positive, the evaluation matrix can be directly dimensionless processed. Assuming that there are m evaluation objects and n evaluation indicators at each measuring point, the dimensionless characteristic evaluation value and matrix of the no. i evaluation index for the no. j evaluation object is and respectively. From this, the standard deviation of each index data and the correlation coefficient between the indexes are as follows:
where is the mean value of the no. index, that is, the mean value of the elements in the no. row of the matrix ; is the covariance between the no. row and the no. row of the evaluation matrix .
The CRITIC method uses the standard deviation of the index to represent the discrimination of the index, that is, the difference of the value of the same index for different objects. The index correlation coefficient is used to measure the size and direction of conflict between indexes, so as to give the information content of each index as follows:
where is the quantitative value of the conflict between the no. index and other indexes.
The larger the , the greater the amount of information contained in the no. index, the more important the index is and the greater the weight should be. Then the objective weight given by CRITIC is:
After the weight coefficient of the no. index is obtained, it is substituted into Equations (7) and (8) to obtain the comprehensive distance between different measuring points of the dam, so as to generate the incidence matrix of the comprehensive distance, which is used as the similarity criterion of dam deformation.
2.4. Optimizing Cluster Number
After the weight coefficient of the comprehensive distance of dam deformation is calculated by the critical method, the number of zonings of dam deformation needs to be determined. The CSP index is used to evaluate the best value of the single link condensed hierarchical clustering algorithm [40,41] (panel data clustering is a single link condensed hierarchical clustering algorithm). The implementation steps are as follows:
Firstly, it is assumed that measuring points of the dam have been divided into regions on the layer , which is recorded as . is the number of measuring points in the region . Let the comprehensive distance matrix of measuring points obtained above be, and define, the compact density within the class of the region , and the separation between classes are and respectively:
where represents the weight of the minimum spanning tree composed of all measuring points in the region , and its value is the sum of the weights of all edges in the minimum spanning tree with the comprehensive distance between measuring points as the weight.
Then, the cluster dispersion degree and cluster coincidence degree of the measuring points in the area are given respectively by subtracting and summing the indicators and , and the indicator can be defined as:
Finally, the CSP index positively reflects the clustering effectiveness of different regions of the dam body. By calculating the average value of the CSP index of all regions to evaluate the clustering effect of the layer , the best number of clustering regions can be further obtained as follows:
3. Deformation Zoning Model of the Ultra-High Arch Dam
After the arch dam deformation zoning is obtained according to the above clustering method, representative measuring points can be selected in different areas for modeling and fitting analysis, and the dynamic change law of dam zoning in different operation stages can be analyzed. There are many functions to realize the modeling of dam displacements, such as hydrostatic-seasonal-time (HST), hydrostatic-thermal-time (HTT), multiple linear regression (MLR), and recent ones based on principal components analysis or machine learning [42]. Arch dam displacement is mainly affected by water pressure, temperature, aging, and other factors, so the dam displacement statistical model is composed of a water pressure component, temperature component, and an aging component [43,44]. The specific fitting function of dam displacement is as follows:
where is the constant term and is the water pressure component coefficient; is the upstream water head on the monitoring date and is the upstream water head on starting date; is the cumulative number of days from the monitoring date to the starting date; is the cumulative number of days from the first day of the monitoring period to the starting date, and and are the regression coefficient of temperature factors. is the cumulative number of days from the monitoring date to the starting date divided by 100; is the cumulative number of days from the first day of the monitoring period to the starting date divided by 100, and and are the aging component coefficients.
Based on the above clustering zoning and statistical model theory, the dynamic deformation zoning model of an ultra-high arch dam operating at complex water level is constructed and the analysis steps of the model are as follows:
Step 1: According to the water level change law of ultra-high arch dam, the operating water level is classified according to stages, and the water level of a certain stage is selected for analysis.
Step 2: The monitoring data in this period is input according to the panel data format, and three “distances” are calculated according to Equations (2) to (6).
Step 3: Using the CRITIC method, the weights of three distances are calculated according to Equations (9) to (12) and substituted into Equations (7) and (8) to generate the space-time characteristic matrix of all measuring points.
Step 4: Assuming that all measuring points at the initial time form a zone, the sum of squares of deviations of all measuring points are calculated at the initial time. Let , calculate the clustering deviation and clustering coincidence degree of each time iteratively and obtain according to Equations (13) to (15), until all measuring points are divided into one area.
Step 5: The better zoning threshold is determined according to Equation (16) and output the dam deformation zoning map.
Step 6: According to the deformation zoning results of the ultra-high arch dam, the time-space characteristics of ultra-high arch dam deformation are analyzed.
Step 7: The representative observation points of each characteristic zone are selected for deformation prediction and monitoring, and modeling analysis is conducted according to Equation (17).
The deformation zoning and monitoring model of an ultra-high arch dam operating at a complex water level is shown in Figure 1.
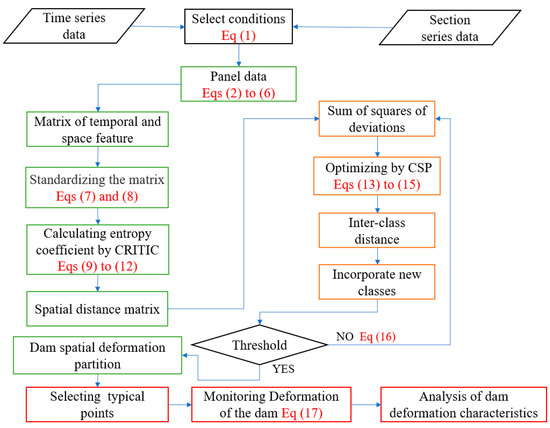
Figure 1.
Flow chart of the deformation zoning and monitoring model of an ultra-high arch dam operating at a complex water level.
4. Case Study
4.1. Project Profile
The ultra-high arch dam is a concrete double curvature arch dam, which is in southwest China. The dam crest elevation is 1885 m, the lowest elevation of the foundation surface is 1580 m, the normal pool level of the reservoir is 1880 m, and the maximum dam height is 305 m. The concrete arch dam is shown in Figure 2. The reservoir has been impounded since December 2012. From the beginning of 2014, the reservoir has been impounded, lifted, and operated in three stages, and dropped slightly at the end of the second stage. The third stage of water storage reached the normal pool level from June 2014 to the end of 2014, and then the reservoir operated normally. The change in water level is shown in Figure 3. The starting surface of the water level altitude of the dam is the mean sea level of the Yellow Sea (Qingdao tidal station) in China.

Figure 2.
The concrete arch dam.
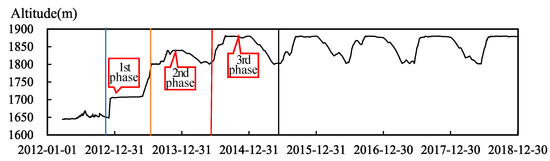
Figure 3.
Process diagram of upstream reservoir water level.
According to water level variation characteristics, three phases of water level conditions are selected for comprehensive cluster analysis.
The first phase: from December 2012 to June 2013, that is, the water storage stage with the rapid rise of the reservoir water level.
The second phase: from July 2013 to June 2014, that is, the reservoir water level rises to the normal pool level and falls back.
The third phase: from July 2014 to June 2015, that is, the first annual cycle of reservoir water level operation, which can represent the variation law of subsequent normal operation of the reservoir.
The research object is the observation data of deformation along the river flow direction of 32 groups of displacement monitoring points of the dam. The layout of displacement monitoring points is shown in Figure 4. The displacement monitoring system of the inverse plumb line is automatic. The sampling frequency is taken, and the actual monitoring frequency is once a day. The layout of the inverse plumb line and the displacement monitoring points are shown in Figure 5. Since the floating ball can move freely, the displacement of the dam can be measured by the moving distance of the inverse plumb line.
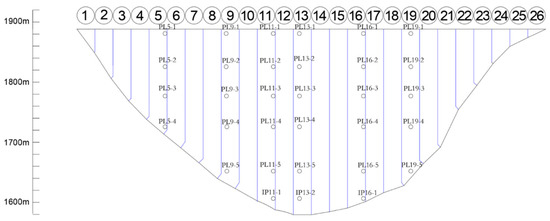
Figure 4.
Distribution of deformation measurement points of the arch dam.
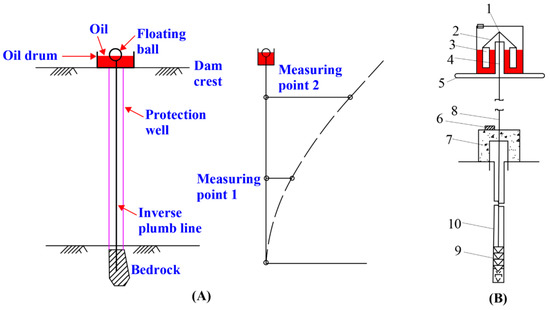
Figure 5.
The layout of the inverse plumb line and the displacement monitoring points. (A). The layout of the inverse plumb line (B). Detail drawing of inverse plumb line measuring point (1-oil drum, 2-connecting support, 3-floating ball, 4-connecting rod, 5-floating barrel frame, 6-coordinate instrument base, 7-concrete observation pier, 8-inverse plumb line (stainless steel wire), 9-anchor block, and 10- protection well).
4.2. Characteristics Analysis of the Dam Deformation Zoning
The 32 groups of deformation measuring points of the ultra-high arch dam were input according to the panel data format and the dam displacement zoning under three water level stages was calculated according to the process of the above dam deformation clustering zoning model. Three standardized distances were weighted by the CRITIC method. Based on the CSP index classification idea, after iterative calculation, the clustering threshold k = 6 was determined. The deformed partition model outputs the average value of zone number k from 2 to 32. The results are shown in Figure 6. When k is equal to 6, its value is the largest. Currently, the inter-class distance and intraclass distance reach optimal harmony. To compare and analyze the dam deformation state under different water levels during operation, the clustering threshold is locked in the whole process.
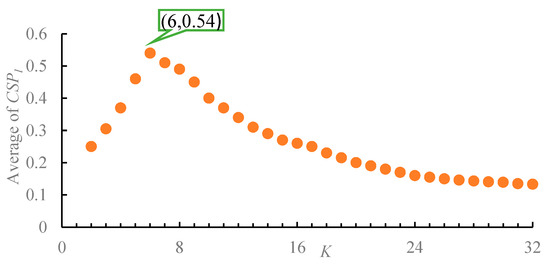
Figure 6.
The average value of with the different number of zones.
4.2.1. Temporal and Spatial Characteristics Analysis of the Dam Deformation
- (1)
- Deformation characteristics analysis of the first phase
In the first phase, from December 2012 to June 2013, under the storage condition of the rapid rise of reservoir water level, the following zoning results are calculated. The zoning of dam deformation monitoring points is shown in Table 1 and the zoning of dam deformation is shown in Figure 7. It can be seen from the table and figure that the distance between I, II, III, and IV is small and can be approximately equidistant, indicating that the deformation level of the dam body in the early stage is generally a linear distribution. The area with large dam deformation is mainly in the middle and lower parts of the dam. The area of Zone VI is the largest, and the deformation of the dam edge is less obvious than that of the central area. The gradient of distance variation in the part of the dam’s bottom is greater than that at the top of the dam.

Table 1.
Zoning results of deformation measuring points of the ultra-high arch dam during the first phase.
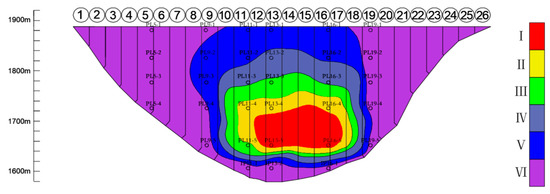
Figure 7.
Deformation partition diagram of the ultra-high arch dam during the first phase.
- (2)
- Deformation characteristics analysis of the second phase
In the second phase, from July 2013 to June 2014, the reservoir water level rose to the design water level and fell back. The zoning results of dam deformation measurement points are shown in Table 2 and Figure 8. Compared with the first phase, the boundary of each deformation zone is smoother after the dam body coordinates and adapts to the water pressure for a certain time. Due to the continuous rise of water level, zones I, II, III, and IV expand upward in varying degrees, in which area I changes significantly and its area expands rapidly. The change and extension of area V to the left and right bank is obvious. At this phase, the dam deformation is mainly reflected in the direct feedback to the water pressure.

Table 2.
Zoning results of deformation measuring points of the ultra-high arch dam during the second phase.
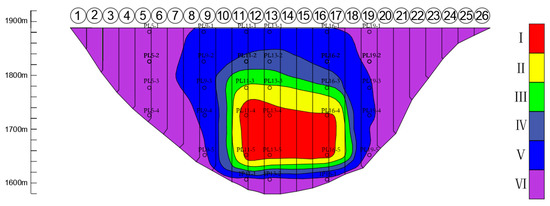
Figure 8.
Deformation partition diagram of the ultra-high arch dam during the second phase.
- (3)
- Deformation characteristics analysis of the third phase
In the third phase, from July 2014 to June 2015, the reservoir water level is in normal operation for a cycle year. The zoning results of dam deformation measurement points are shown in Table 3, and the zoning of dam deformation is shown in Figure 9. Compared with the second phase, with the loading of continuous high-water pressure, the area of zone I is further expanded, and the dam deformation gradually extends from the middle-lower part to the middle-upper part. The change in Zone IV is obvious, which is mainly caused by the aging of water pressure. Zone V shows a trend of development to the left and right banks of the dam. All zones except zone Ⅵ have the trend of upward expansion to varying degrees, but the area changes little.

Table 3.
Zoning results of deformation measuring points of the ultra-high arch dam during the third phase.
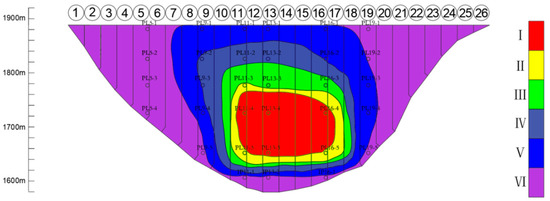
Figure 9.
Deformation partition diagram of the ultra-high arch dam during the third phase.
- (4)
- Deformation characteristics analysis of the different operation phases
For different operation phases, the zones corresponding to the monitoring points are different. By comparing and analyzing their changes, the deformation law of the ultra-high arch dam under the complex change of water level in the early stage of operation can be obtained. In particular, the monitoring points with more changes in zoning can be analyzed, so that the dam managers can be more targeted when analyzing the operation state of the dam. The zoning of deformation measuring points at different operation phases of the ultra-high arch dam is shown in Figure 10.
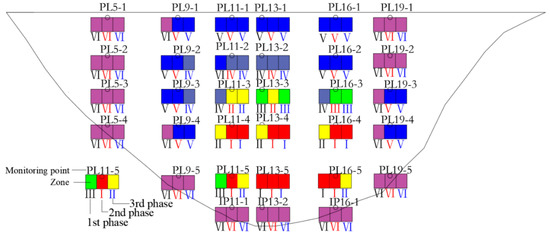
Figure 10.
Deformation zoning of the ultra-high arch dam in different operation phases.
It can be seen from Figure 8 that in the early stage of the operation when the water level of the dam changes greatly, the measuring points sensitive to the water level is concentrated in the middle of the dam body, and the zoning at the edge of the dam body changes little, among which the measuring points distributed in zones I, II, and III change the most. With the advance of the dam operation, the deformation zoning gradually extends to the outside, and the level of the zoning is gradually improved. The sensitive deformation measuring points with more changes of the dam mainly include PL11-3, PL11-4, PL11-5, PL13-3, PL13-4, PL16-3, PL16-4, and PL16-5. Dam managers need to focus on the monitoring status of measuring points in the middle of the dam body and study and judge the safety status of dam operation in real-time. In addition, since the overall displacement of the areas on both sides of the dam (Zone VI) is small, managers need to pay attention to the measuring points in Zone VI with fast displacement change rate to evaluate the behavior of the dam, especially the measuring points with abnormal data in Zone VI. Managers need to comprehensively evaluate the performance of the dam according to the state of each zone of the dam.
4.2.2. Water Level Characteristics Analysis of the Dam Deformation
According to the above clustering and zoning results, the time series from the beginning of 2013 to the middle of 2015 is taken as the time series, and one representative measuring point is selected from each of the six types of deformation zones (in which two representative measuring points are selected in Zone VI, i.e., one at the dam crest and one at the dam foundation) to form the panel data time series, as shown in Figure 11. In the figure, the deformation along the river is positive and the deformation against the river is negative. The seven measuring points selected are PL13-5, PL16-4, PL13-3, PL13-2, PL16-2, PL5-1, and IP13-2, which can directly and efficiently reflect the corresponding relationship between water level, dam height, and dam deformation. Meantime, the correlation between water level and displacement is calculated by the maximum information coefficient (MIC) algorithm. The results are shown in Table 4. Where MIC = 1 indicates complete correlation and MIC = 0 means completely irrelevant.
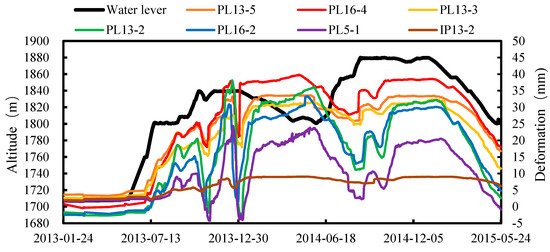
Figure 11.
Relationship between the deformation of representative monitoring points and variation of reservoir water level.

Table 4.
Zoning results of deformation measuring points of the ultra-high arch dam during the third phase.
From the above dam deformation clustering results and the time series of representative measuring points, it can be concluded that:
- Dam deformation is greatly affected by water levels. With the rise of the water level, the deformation of the dam changes obviously, which also proves the rationality of the water pressure component in the statistical model.
- There is an obvious positive correlation between water level and deformation, and the influence of water level on dam deformation is hysteretic. In addition, with the rise of the water level, the cluster center area also rises, indicating that the trend of the expansion and upward movement of the maximum deformation area of the dam body is consistent with the engineering practice.
- The maximum deformation of the dam is the dam section of the middle riverbed. Because the absolute height of the dam body is large and the bearing water pressure is correspondingly larger, the deformation is more obvious. Similarly, due to low water pressure, the deformation of dam sections on both banks is not as significant as that of dam sections in the middle of the riverbed.
- In different elevations of the same dam section, because the water pressure is linearly distributed with the water depth from top to bottom, the water depth pressure in the middle and lower part is large, and the corresponding deformation is more obvious. Although the water depth near the dam bottom is the largest, the dam bottom is equivalent to the constraint of the fixed end due to the existence of the foundation cementation surface, so the deformation is the smallest. For example, the deformation of measuring point IP13-2 is basically unchanged due to its proximity to the dam foundation. However, it can also be seen from the clustering zoning that the gradient of dam bottom zoning changes greatly, and the deformation increases rapidly at the part far away from the dam bottom constraint area.
In general, the dam deformation shows an obvious positive correlation with the change of water level. The maximum deformation occurs in the middle of the dam, that is, between the elevation of 1660 m and 1740 m, which should be regarded as the key observation part. In addition, with the rapid rise of the water level, the maximum deformation part of the dam rises and expands, and the fluctuation expansion range is between 10 m and 20 m.
4.3. Deformation Safety Monitoring of Important Monitoring Points of Dam
According to the clustering results of dam deformation zoning, the monitoring points PL11-4, PL11-5, PL13-4, PL13-5, PL16-4, and PL16-5 in the deformation sensitive area in the middle of the dam are selected as key monitoring points. The key monitoring parts of dam deformation are modeled and analyzed, in which the water pressure component is taken as the fourth power, and the temperature component is replaced by two groups of harmonic factors [40], so as to obtain the monitoring model of representative measuring points. The fitting value, predicted value, and the residual value of deformation at monitoring points are shown in Figure 12. And the calculation accuracy of monitoring points at key monitoring positions is shown in Table 5.
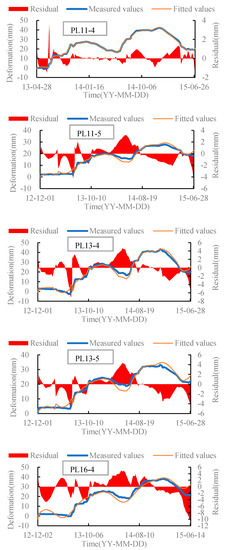
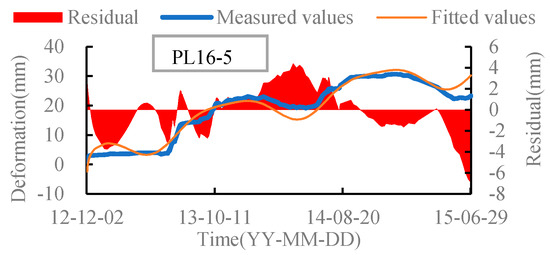
Figure 12.
Measurement points fitting and residual diagram.

Table 5.
Model accuracy of representative key monitoring positions.
It can be seen from Figure 10 and Table 4 that the multi-correlation coefficient of the deformation fitting values of important monitoring points is between 0.96 and 1.0, and the root mean squared error is between 0 and 3, indicating high fitting accuracy. The mean relative error of the predicted value of deformation is less than 5%, which shows that the model is reasonable, the accuracy can meet the requirements of engineering practice, and can be used to monitor the deformation of the dam.
5. Conclusions
Under the condition of complex reservoir water level at the initial stage of operation, the deformation of an ultra-high arch dam varies greatly between different parts. Because the traditional deformation analysis method is difficult to apply to the deformation law analysis of an ultra-high arch dam, the clustering and zoning model based on the panel data theory improved by the CRITIC method and CSP index is constructed in this paper. Additionally, the temporal and spatial characteristics of the deformation measurement points of an ultra-high arch dam are comprehensively considered in this model. It not only reflects the spatial correlation characteristics of different measuring points but also characterizes the dynamic change characteristics of deformation measuring points.
The distance indexes of the three-panel data defined can represent the space-time matrix of dam body deformation of the ultra-high arch dam. The dam deformation-sensitive area is in the middle and lower part of the dam at the initial stage and gradually moves to the middle with the increase of operation time. Therefore, the middle area is an important object of dam displacement monitoring. Meanwhile, the monitoring points with more changes in dam deformation zoning are also concentrated in the middle of the dam. The analysis of the deformation characteristics of the dam body conforms to the deformation law of the ultra-high arch dam. The clustering results can make the temporal and spatial characteristics and water level characteristics of dam deformation more efficiently analyzed.
The case study shows that good dynamic clustering and zoning results under different water level conditions of an ultra-high arch dam are obtained by this model and it has strong adaptability and reliability. On this basis, the interference and biased judgment caused by different measuring points can be eliminated when monitoring, predicting, and analyzing the representative measuring points of the same type. Moreover, the workload of analysis is greatly reduced, and it could make the management personnel more efficient at mastering the operation behavior of the dam in time. The model can solve the problem of analyzing the deformation field of a statically indeterminate arch dam and can also be extended to the study of temperature field, stress field, and gravity of a dam.
With the increase of dam operation time, the law of dam deformation under normal operating conditions will also change. Because only the normal water level operation condition of the ultra-high arch dam in the early service stage is considered in this paper, the research of the long operation time can be carried out according to the operation characteristics in the actual project. It would be also advisable that comparative analyses such as observational methods, numerical back-analyses, and centrifuge modeling techniques be used and discussed to demonstrate reliability and facilitate cross-verification of the work [45,46].
Author Contributions
Formal analysis, Y.L. and D.Z.; Methodology, D.Z. and Y.L.; Writing-original draft, Y.L. and X.W.; Writing-review & editing, Y.L., C.G. and T.K.; Supervision, D.Z. and C.G., Data curation, E.C. and J.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China (2018YFC1508603, 2018YFC0407104, 2018YFC0407101, 2016YFC0401601), National Natural Science Foundation of China (Grant Nos. 51379068, 51579083, 51579085, 51579086, 51609074, 51739003, 51779086), the program of China Scholarship Council (No.202006710021).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, R. Key technologies in the design and construction of 300 m ultra-high arch dams. Engineering 2016, 3, 350–359. [Google Scholar] [CrossRef]
- Yin, T.; Li, Q.; Hu, Y.; Yu, S.; Liang, G. Coupled Thermo-Hydro-Mechanical Analysis of Valley Narrowing Deformation of High Arch Dam: A Case Study of the Xiluodu Project in China. Appl. Sci. 2020, 10, 524. [Google Scholar] [CrossRef]
- Zhao, E.; Wu, C. Unified egg ellipse critical threshold estimation for the deformation behavior of ultrahigh arch dams. Eng. Struct. 2020, 214, 110598. [Google Scholar] [CrossRef]
- Wang, R.K.; Chen, L.; Zhang, C. Seismic design of Xiluodu ultra-high arch dam. Water Sci. Eng. 2018, 11, 28–41. [Google Scholar] [CrossRef]
- Tao, Z.; Liu, Y.; Yang, Q.; Wang, S. Study on the nonlinear deformation and failure mechanism of a high arch dam and foundation based on geomechanical model test. Eng. Struct. 2020, 207, 110287. [Google Scholar] [CrossRef]
- Fu, X.; Gu, C.; Qin, D. Deformation features of a super-high arch dam structural system. Optik 2017, 130, 681–695. [Google Scholar] [CrossRef]
- He, M.-J.; Li, H.; Xu, J.-R.; Wang, H.-L.; Xu, W.-Y.; Chen, S.-Z. Estimation of unloading relaxation depth of Baihetan Arch Dam foundation using long-short term memory network. Water. Sci. Eng. 2021, 14, 149–158. [Google Scholar] [CrossRef]
- Cao, E.; Bao, T.; Gu, C.; Li, H.; Liu, Y.; Hu, S. A Novel Hybrid Decomposition—Ensemble Prediction Model for Dam Deformation. Appl. Sci. 2020, 10, 5700. [Google Scholar] [CrossRef]
- Zheng, D.; Cheng, L.; Bao, T.; Lv, B. Integrated parameter inversion analysis method of a CFRD based on multi-output support vector machines and the clonal selection algorithm. Comput. Geotech. 2013, 47, 68–77. [Google Scholar] [CrossRef]
- Zhao, E.; Wu, C. Centroid deformation-based nonlinear safety monitoring model for arch dam performance evaluation. Eng. Struct. 2021, 243, 112652. [Google Scholar] [CrossRef]
- Wang, Y.-Q.; Zhao, R.-H.; Liu, Y.; Chen, Y.-Z.; Ma, X.-Y. Shape Optimization of Single-Curvature Arch Dam Based on Sequential Kriging-Genetic Algorithm. Appl. Sci. 2019, 9, 4366. [Google Scholar] [CrossRef]
- Rankovic, V.; Grujović, N.; Divac, D.; Milivojević, N. Development of support vector regression identification model for prediction of dam structural behaviour. Struct. Saf. 2014, 48, 33–39. [Google Scholar] [CrossRef]
- Su, H.; Li, X.; Yang, B.; Wen, Z. Wavelet support vector machine-based prediction model of dam deformation. Mech. Syst. Signal. Pract. 2018, 110, 412–427. [Google Scholar] [CrossRef]
- Chen, S.; Gu, C.; Lin, C.; Hariri-Ardebili, M.A. Prediction of Arch Dam Deformation via Correlated Multi-Target Stacking. Appl. Math. Model. 2021, 91, 1175–1193. [Google Scholar] [CrossRef]
- Zheng, D.; Xu, Y.; Yang, M.; Gu, H.; Zhao, E. Deformation and stress behavior analysis of high concrete dam under the effect of reservoir basin deformation. Comput. Concrete 2016, 18, 1153–1173. [Google Scholar] [CrossRef]
- Guo, S.; Liang, H.; Wu, S.; Xiong, K.; Li, D.; Chen, H.; Zhang, A. Seismic damage investigation of arch dams under different water levels based on massively parallel computation. Soil. Dyn. Earthq. Eng. 2020, 129, 105917. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Kazemiyan, M.S.; Sani, A.A. A Literature Review on Dynamic Analysis of Concrete Gravity and Arch Dams. Arch. Comput. Method E 2021, 28, 4357–4372. [Google Scholar] [CrossRef]
- Feng, G.; Gao, J.; Peng, B.; Zhang, X. A varying-coefficient panel data model with fixed effects: Theory and an application to US commercial banks. J. Econom. 2017, 196, 68–82. [Google Scholar] [CrossRef]
- Bashari, A.; Beiki, M.; Talebinejad, A. Estimation of deformation modulus of rock masses by using fuzzy clustering-based modeling. Int. J. Rock Mech. Min. 2011, 48, 1224–1234. [Google Scholar] [CrossRef]
- Chen, W.; Wang, X.; Cai, Z.; Liu, C.X.; Zhu, Y.S.; Lin, W. DP-GMM clustering-based ensemble learning prediction methodology for dam deformation considering spatiotemporal differentiation—ScienceDirect. Knowl.-Based Syst. 2021, 222, 106964. [Google Scholar] [CrossRef]
- Li, Y.G.; Dai, Y.; He, X.Q. Clustering method for panel data based on adaptive weighting. Syst. Eng. Theor. Pract. 2013, 33, 388–395. [Google Scholar]
- Zhang, Y.; Wang, H.J.; Zhu, Z. Quantile-regression-based clustering for panel data. J. Econom. 2019, 213, 54–67. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, R.S.; Forrest, Y.L. Three way decisions based grey incidence analysis clustering approach for panel data and its application. Kybernetes 2019, 48, 2117–2137. [Google Scholar] [CrossRef]
- Wang, S.; Xu, C.; Liu, Y.; Wu, B. Mixed-coefficient panel model for evaluating the overall deformation behavior of high arch dams using the spatial clustering. Struct. Control Health Monit. 2021, 28, e2809. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The critic method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Mrabah, N.; Khan, N.M.; Ksantini, R.; Lachiri, Z. Deep clustering with a Dynamic Autoencoder: From reconstruction towards centroids construction. Neural. Netw. 2020, 130, 206–228. [Google Scholar] [CrossRef]
- Sudhagar, S.; Sakthivel, M.; Mathew, P.J.; Daniel, S.A.A. A multi criteria decision making approach for process improvement in friction stir welding of aluminium alloy. Measurement 2017, 108, 1–8. [Google Scholar] [CrossRef]
- Tus, A.; Adali, E.A. The new combination with CRITIC and WASPAS methods for the time and attendance software selection problem. Opsearch 2019, 56, 528–538. [Google Scholar] [CrossRef]
- Peng, X.; Krishankumar, R.; Ravichandran, K.S. A novel interval-valued fuzzy soft decision-making method based on CoCoSo and CRITIC for intelligent healthcare management evaluation. Soft Comput. 2021, 25, 4213–4241. [Google Scholar] [CrossRef]
- Zhou, W.; Zhao, W.-Z.; Zhang, Y.-N.; Ding, Z.-J. Cluster analysis of acoustic emission signals and deformation measurement for delaminated glass fiber epoxy composites. Compos. Struct. 2018, 195, 349–358. [Google Scholar] [CrossRef]
- Ordóñez, C.; Argüelles, R.; Sanz-Ablanedo, E.; Roca-Pardiñas, J. Deformation analysis in tunnels through curve clustering. Appl. Math. Model. 2016, 40, 1325–1332. [Google Scholar] [CrossRef]
- Larrosa, J.; Meseguer, P.; Schiex, T. Maintaining reversible DAC for max-CSP. Artif. Intell. 1999, 107, 149–163. [Google Scholar] [CrossRef][Green Version]
- Givry, S.D.; Heras, F.; Zytnicki, M.; Larrosa, J. Existential arc consistency: Getting closer to full arc consistency in weighted CSPS. IJCAI 2005, 1, 84–89. [Google Scholar] [CrossRef]
- Prosser, P. Hybrid algorithms for constraint satisfaction problems. Comput. Intell. 1993, 9, 268–299. [Google Scholar] [CrossRef]
- Xu, W.; Gong, F.; Zhou, G. Clustering phase of a general constraint satisfaction problem model d-k-CSP. Phys. A. 2019, 537, 122708. [Google Scholar] [CrossRef]
- Galanis, A.; Goldberg, L.A.; Yang, K. Approximating partition functions of bounded-degree Boolean counting Constraint Satisfaction Problems. J. Comput. Syst. Sci. 2021, 115, 187–213. [Google Scholar] [CrossRef]
- Jiang, B.; Yang, Y.; Gao, J.; Hsiao, C. Recursive estimation in large panel data models: Theory and Practice. J. Econom. 2021, 224, 439–465. [Google Scholar] [CrossRef]
- Shi, Z.; Gu, C.; Qin, D. Variable-intercept panel model for deformation zoning of a super-high arch dam. Springerplus 2016, 5, 898. [Google Scholar] [CrossRef]
- Kumari, M.; Kulkarni, M.S. Single-measure and Multi-measure Approach of Predictive Manufacturing Control: A Comparative Study. Comput. Ind. Eng. 2018, 127, 182–195. [Google Scholar] [CrossRef]
- Shah, I. A hybrid algorithm for finding minimal unsatisfiable subsets in over-constrained CSPs. Int. J. Intell. Syst. 2011, 26. [Google Scholar] [CrossRef]
- Liu, N.; Xu, Z.; Zeng, X.-J.; Ren, P. An agglomerative Hierarchical clustering algorithm for linear ordinal rankings. Inform. Sci. 2021, 557, 170–193. [Google Scholar] [CrossRef]
- Salazar, F.; Morán, R.; Toledo, M.Á.; Oñate, E. Data-Based Models for the Prediction of Dam Behaviour: A Review and Some Methodological Considerations. Arch. Comput. Method E 2017, 24, 1–21. [Google Scholar] [CrossRef]
- Dai, B.; Gu, C.; Zhao, E.; Qin, X. Statistical model optimized random forest regression model for concrete dam deformation monitoring. Struct. Control Health Monit. 2018, 25, e2170. [Google Scholar] [CrossRef]
- Zhao, E.; Wu, C. Risk probabilistic assessment of ultrahigh arch dams through regression panel modeling on deformation behavior. Struct. Control Health Monit. 2021, 28, e2716. [Google Scholar] [CrossRef]
- Ong, D.E.L.; Sim, Y.S.; Leung, C.F. Performance of Field and Numerical Back-Analysis of Floating Stone Columns in Soft Clay Considering the Influence of Dilatancy. Int. J. Geomech. 2018, 18, 1–16. [Google Scholar] [CrossRef]
- Ong, D.E.L.; Leung, C.F.; Chow, Y.K. Piles subject to excavation-induced soil movement in clay. In Proceedings of the 13th European Conference on Soil Mechanics and Geotechnical Engineering, Prague, Czech Republic, 25–28 August 2003; Volume 2, pp. 777–782. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).