Fuzzy Regulator for Two-Phase Gas–Liquid Pipe Flows Control
Abstract
1. Introduction
2. The Two-Phase Gas–Liquid Mixtures Flow
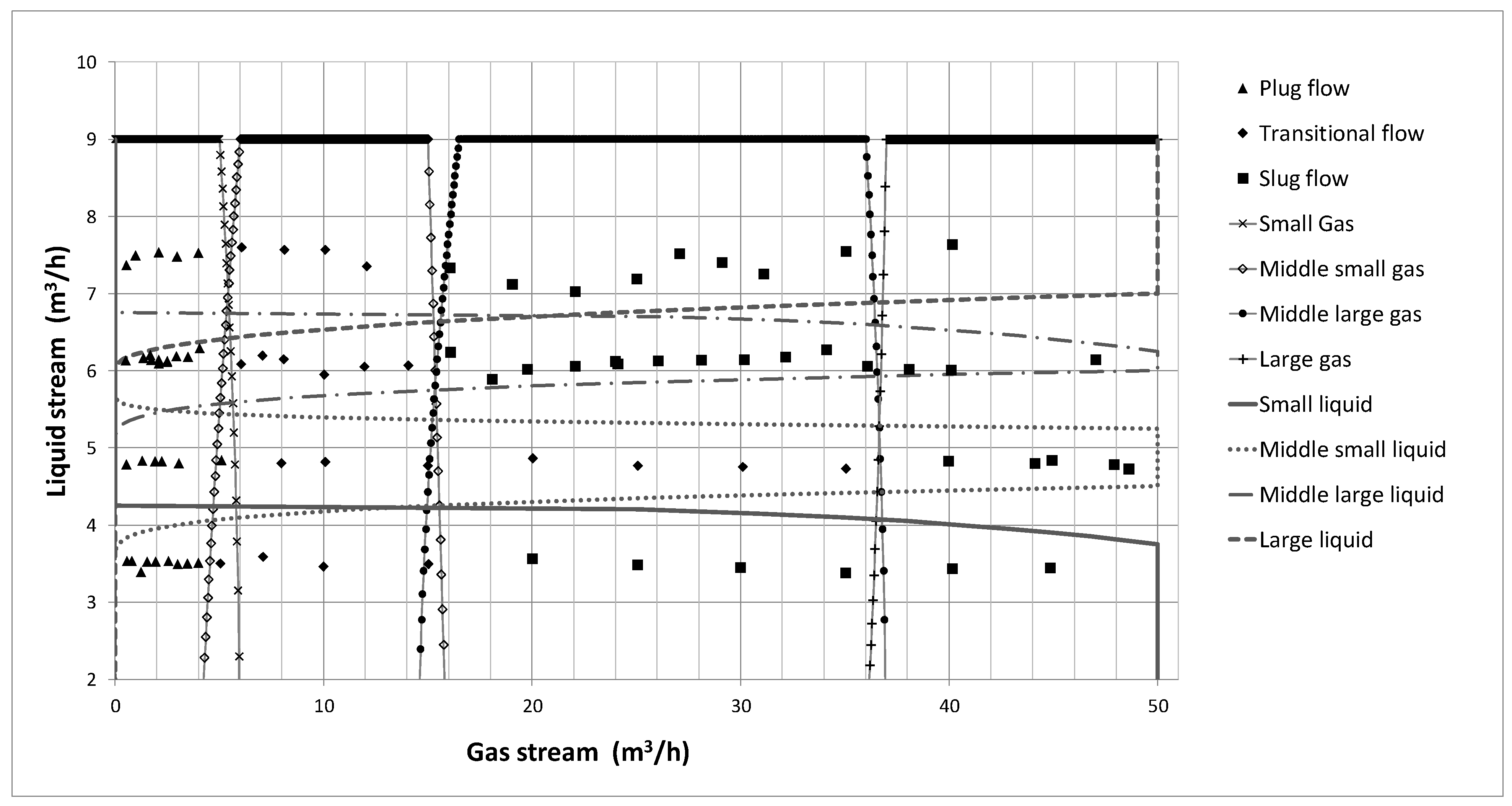
2.1. Characteristics of the Flow Types
2.2. Flow Type Recognition
2.3. Control Techniques for Flow Processes
3. Two-Phase Flow Experimental Rig: Facility and Control Methodology
4. Fuzzy Regulator Principles
if (SG = t1SG) or (SG = t2SG) and (SL = t1SL) then (Fc = t3Fc)
- V—variable name, e.g., gas stream,
- T—set of variable terms, e.g., small, medium, or big
- D—crisp domain of a linguistic variable, e.g., ,
- G—the syntactic rule, whose grammar generates the derivative terms—the T labels, e.g., T(gas stream) = {…, “medium small”, “medium”, …}
- M—the semantic rule that sets the meaning M(l) to each linguistic value l.
- d—is the domain of the measurement,
- —is the mean measurement value for the measurement data collected in time t,
- —is the standard abbreviation for the measurement data collected in time t,
- —is the i-th term of input signal S.
then (NSG = t2SG) and (NSL = t2SL),
- SC, SL—the signals of the first class: the fuzzified value of the gas stream and the fuzzified values of the liquid stream,
- fC, fG—the signals of the second class: the current flow type and the required (given) flow type,
- tij—the i-th value (term) of the j-th input signal.
- —the membership functions describing the first class linguistic variables (fuzzy sets—µSG(x), µSC(x)),
- —the membership functions describing the second class linguistic variables (fuzzy relations—µfC(x,y), µfG(x,y)).
5. Implementation
- The module for input signal fuzzification (1) that contains the first class (measurement data) (2) and second class (flow type) (3) signals fuzzification modules,
- The diagnostic signals (Z1, Z2, Z3) retrieved from the measurement instruments,
- The flow type reference signal set by the user (Z4),
- The inference rules module (4),
- The inference module based on the modified fuzzified Mamdani implication,
- The defuzzification module that implements the center of sums defuzzification method (5) and which processes the fuzzified control signals (Z′1 and Z′2),
- The module of the crisp sets (n1 and n2) (6).
- For the linguistic variable—fuzzified gas stream:
- For the linguistic variable—fuzzified liquid stream:
- x—is the gas stream value,
- y—is the liquid stream value,
- —is the membership level of the flow type achieved for the gas stream x and liquid stream y,
- —is the membership level determined for i-th term of the fuzzified gas stream for the measured value x of the gas stream,
- —is the membership level determined for i-th term of the fuzzified liquid stream for the measured value y of the liquid stream.
andflow type is plugandrequired flow type is slug
thenfuzzy gas stream is largeandfuzzy liquid stream is large
- Area #2 represents the current flow type,
- Area #3 represents the required flow type,
- Area #2 corresponds with the fuzzified values of gas and liquid streams that determine for current flow type.
6. Results
- Establishing the initial state,
- Selecting the required flow type by the expert,
- Validation of the stabilized flow type by the expert and the feedback from the diagnostic module [30].
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Clark, J.H.; Ashby, W.R. An Introduction to Cybernetics. OR 1965, 16, 492. [Google Scholar] [CrossRef][Green Version]
- Anderson, J.D. Computational Fluid Dynamics: The Basics with Applications; McGraw-Hill Science/Engineering/Math: New York, NY, USA, 1995; ISBN 9780070016859. [Google Scholar]
- Bellman, R.E.; Zadeh, L.A. Decision-Making in a Fuzzy Environment. Manage. Sci. 1970, 17, B-141–B-164. [Google Scholar] [CrossRef]
- Chhabra, R.P.; Richardson, J.F. Encyclopedia of Fluid Mechanics; Cheremisinoff, N.P., Ed.; Gulf: Houston, TX, USA, 1986. [Google Scholar]
- Pląskowski, A.; Beck, M.S.; Thorn, R.; Dyakowski, T. Imaging Industrial Flows—Applications of Electrical Process Tomography; IOP Publishing: Bristol, UK, 1995; ISBN 0750302968. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Popinet, S. An accurate adaptive solver for surface-tension-driven interfacial flows. J. Comput. Phys. 2009, 228, 5838–5866. [Google Scholar] [CrossRef]
- Della Pia, A.; Chiatto, M.; De Luca, L. Global eigenmodes of thin liquid sheets by means of Volume-of-Fluid simulations. Phys. Fluids 2020, 32, 082112. [Google Scholar] [CrossRef]
- Della Pia, A.; Chiatto, M.; De Luca, L. Receptivity to forcing disturbances in subcritical liquid sheet flows. Phys. Fluids 2021, 33, 032113. [Google Scholar] [CrossRef]
- Schmidt, S.; Oberleithner, K. Instability of forced planar liquid jets: Mean field analysis and nonlinear simulation. J. Fluid Mech. 2020, 883, A7. [Google Scholar] [CrossRef]
- Hewitt, G.F.; Roberts, D.N. Studies of Two-Phase Flow Patterns by Simultaneous X-ray and Flash Photography; Atomic Energy Research Establishment, Harwell: Berkshire, UK, 1969. [Google Scholar]
- Dziubinski, M.; Fidos, H.; Sosno, M. The flow pattern map of a two-phase non-Newtonian liquid–gas flow in the vertical pipe. Int. J. Multiph. Flow 2004, 30, 551–563. [Google Scholar] [CrossRef]
- Oshinowo, T.; Charles, M.E. Vertical two-phase flow part I. Flow pattern correlations. Can. J. Chem. Eng. 1974, 52, 25–35. [Google Scholar] [CrossRef]
- Taitel, Y.; Bornea, D.; Dukler, A.E. Modelling flow pattern transitions for steady upward gas-liquid flow in vertical tubes. AIChE J. 1980, 26, 345–354. [Google Scholar] [CrossRef]
- Grudzień, K.; Niedostatkiewicz, M.; Adrien, J.; Tejchman, J.; Maire, E. Quantitative estimation of volume changes of granular materials during silo flow using X-ray tomography. Chem. Eng. Process. Process Intensif. 2011, 50, 59–67. [Google Scholar] [CrossRef]
- Romanowski, A.; Grudzien, K.; Williams, R.A. Analysis and Interpretation of Hopper Flow Behaviour Using Electrical Capacitance Tomography. Part. Part. Syst. Charact. 2006, 23, 297–305. [Google Scholar] [CrossRef]
- Soleimani, M. Three-dimensional electrical capacitance tomography imaging. Insight-Non-Destructive Test. Cond. Monit. 2006, 48, 613–617. [Google Scholar] [CrossRef]
- Faia, P.; Silva, R.; Rasteiro, M.G.; Garcia, F. Electrical Tomography: A Review of Configurations, and Application to Fibre Flow Suspensions Characterisation. Appl. Sci. 2020, 10, 2355. [Google Scholar] [CrossRef]
- Wajman, R.; Banasiak, R.; Mazurkiewicz, L.; Dyakowski, T.; Sankowski, D. Spatial imaging with 3D capacitance measurements. Meas. Sci. Technol. 2006, 18, 3671. [Google Scholar] [CrossRef][Green Version]
- Wang, F.; Marashdeh, Q.; Fan, L.-S.; Warsito, W. Electrical Capacitance Volume Tomography: Design and Applications. Sensors 2010, 10, 1890–1917. [Google Scholar] [CrossRef] [PubMed]
- Rybak, G.; Chaniecki, Z.; Grudzień, K.; Romanowski, A.; Sankowski, D. Non–invasive methods of industrial processes control. Inform. Control Meas. Econ. Environ. Prot. 2014, 4, 41–45. [Google Scholar]
- Rymarczyk, T.; Tchorzewski, P.; Adamkiewicz, P.; Duda, K.; Szumowski, J.; Sikora, J. Practical Implementation of Electrical Tomography in a Distributed System to Examine the Condition of Objects. IEEE Sens. J. 2017, 17, 8166–8186. [Google Scholar] [CrossRef]
- Smolik, W.; Kryszyn, J.; Olszewski, T.; Szabatin, R. Methods of small capacitance measurement in Electrical Capacitance Tomography. Informatics Control Meas. Econ. Environ. Prot. 2017, 7, 105–110. [Google Scholar] [CrossRef]
- Kryszyn, J.; Wróblewski, P.; Stosio, M.; Wanta, D.; Olszewski, T.; Smolik, W.T. Architecture of EVT4 data acquisition system for electrical capacitance tomography. Measurement 2017, 101, 28–39. [Google Scholar] [CrossRef]
- Rymarczyk, T. Characterization of the shape of unknown objects by inverse numerical methods. Prz. Elektrotech. 2012, 88, 138–140. [Google Scholar]
- Rymarczyk, T.; Kozłowski, E.; Kłosowski, G. Electrical impedance tomography in 3D flood embankments testing—Elastic net approach. Trans. Inst. Meas. Control 2019, 42, 680–690. [Google Scholar] [CrossRef]
- Marashdeh, Q.; Wang, F.; Fan, L.S.; Warsito, W. Velocity measurement of multi-phase flows based on electrical capacitance volume tomography. In Proceedings of the IEEE Sensors, Atlanta, GA, USA, 28–31 October 2007; pp. 1017–1019. [Google Scholar]
- Liu, Z.; Babout, L.; Banasiak, R.; Sankowski, D. Effectiveness of rotatable sensor to improve image accuracy of ECT system. Flow Meas. Instrum. 2010, 21, 219–227. [Google Scholar] [CrossRef]
- Banasiak, R.; Wajman, R.; Jaworski, T.; Fiderek, P.; Fidos, H.; Nowakowski, J.; Sankowski, D. Study on two-phase flow regime visualization and identification using 3D electrical capacitance tomography and fuzzy-logic classification. Int. J. Multiph. Flow 2014, 58, 1–14. [Google Scholar] [CrossRef]
- Fiderek, P.; Kucharski, J.; Wajman, R. Fuzzy inference for two-phase gas-liquid flow type evaluation based on raw 3D ECT measurement data. Flow Meas. Instrum. 2017, 54, 88–96. [Google Scholar] [CrossRef]
- Banasiak, R.; Ye, Z.; Soleimani, M. Improving Three-Dimensional Electrical Capacitance Tomography Imaging Using Approximation Error Model Theory. J. Electromagn. Waves Appl. 2012, 26, 411–421. [Google Scholar] [CrossRef]
- Kapusta, P.; Majchrowicz, M.; Sankowski, D.; Jackowska-Strumiłło, L.; Banasiak, R. Distributed multi-node, multi-GPU, heterogeneous system for 3D image reconstruction in Electrical Capacitance Tomography—Network performance and application analysis. Przegląd Elektrotech. 2013, R. 89, 339–342. [Google Scholar]
- Taitel, Y. Stability of severe slugging. Int. J. Multiph. Flow 1986, 12, 203–217. [Google Scholar] [CrossRef]
- Abergel, F.; Temam, R. On some control problems in fluid mechanics. Theor. Comput. Fluid Dyn. 1990, 1, 303–325. [Google Scholar] [CrossRef]
- Bewley, T.R. Flow control: New challenges for a new Renaissance. Prog. Aerosp. Sci. 2001, 37, 21–58. [Google Scholar] [CrossRef]
- Brauner, N. Liquid-Liquid Two-Phase Flow Systems. In Modelling and Control of Two-Phase Phenomena; Bertola, V., Ed.; CISM Center: Udine, Italy, 2002. [Google Scholar]
- Havre, K.; Dalsmo, M. Active Feedback Control as a Solution to Severe Slugging. SPE Prod. Facil. 2002, 17, 138–148. [Google Scholar] [CrossRef]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control: Analysis and Design; John Wiley: Hoboken, NJ, USA, 2005; ISBN 9780470011676. [Google Scholar]
- Storkaas, E.; Skogestad, S. Controllability analysis of two-phase pipeline-riser systems at riser slugging conditions. Control Eng. Pract. 2007, 15, 567–581. [Google Scholar] [CrossRef]
- Godhavn, J.-M.; Fard, M.P.; Fuchs, P.H. New slug control strategies, tuning rules and experimental results. J. Process Control 2005, 15, 547–557. [Google Scholar] [CrossRef]
- Nygaard, G.; Naevdal, G. Modelling two-phase flow for control design in oil well drilling. In Proceedings of the 2005 IEEE Conference on Control Applications, CCA 2005, Toronto, ON, Canada, 23–25 July 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 675–680. [Google Scholar]
- Ogazi, A.I. Multiphase Severe Slug Flow Control. Ph.D. Thesis, Cranfield University, Cranfield, UK, 2011. [Google Scholar]
- Huang, S.-C.; Kim, J. Control and system identification of a separated flow. Phys. Fluids 2008, 20, 101509. [Google Scholar] [CrossRef]
- Jahanshahi, E.; Skogestad, S.; Grøtli, E.I. Nonlinear model-based control of two-phase flow in risers by feedback linearization. IFAC Proc. Vol. 2013, 9, 301–306. [Google Scholar] [CrossRef]
- Di Meglio, F.; Kaasa, G.-O.; Petit, N.; Alstad, V. Model-based control of slugging flow: An experimental case study. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 2995–3002. [Google Scholar]
- Kim, J.; Bewley, T.R. A Linear Systems Approach to Flow Control. Annu. Rev. Fluid Mech. 2007, 39, 383–417. [Google Scholar] [CrossRef]
- Ehinmowo, A.B.; Cao, Y. Stability analysis of slug flow control. Syst. Sci. Control Eng. 2016, 4, 183–191. [Google Scholar] [CrossRef]
- Pedersen, S.; Durdevic, P.; Yang, Z. Challenges in slug modeling and control for offshore oil and gas productions: A review study. Int. J. Multiph. Flow 2017, 88, 270–284. [Google Scholar] [CrossRef]
- Cheng, S.-T.; Chou, J.-H. Fuzzy Control to Improve Energy-Economizing in Cyber-Physical Systems. Appl. Artif. Intell. 2016, 30, 1–15. [Google Scholar] [CrossRef]
- Galichet, S.; Foulloy, L.; Chebre, M.; Beauchene, J.P. Fuzzy logic control of a floating level in a refinery tank. In Proceedings of the 1994 IEEE 3rd International Fuzzy Systems Conference, Orlando, FL, USA, 26–29 June 1994; IEEE: Piscataway, NJ, USA, 1994; pp. 1538–1542. [Google Scholar]
- Arakawa, A.; Sekimizu, K.; Sumida, S. Fuzzy Logic Control Application for BWR Recirculation Flow Control System. J. Nucl. Sci. Technol. 1988, 25, 263–273. [Google Scholar] [CrossRef][Green Version]
- Pistun, E.; Yakymchuk, N. Development of the automatic control system of pumping station for urban water supply. Informatics Control Meas. Econ. Environ. Prot. 2014, 4, 68–71. [Google Scholar] [CrossRef]
- Rezeka, S.F.; Attia, A.-H.; Saleh, A.M. Management of air-conditioning systems in residential buildings by using fuzzy logic. Alex. Eng. J. 2015, 54, 91–98. [Google Scholar] [CrossRef][Green Version]
- Tobi, T.; Hanafusa, T. A practical application of fuzzy control for an air-conditioning system. Int. J. Approx. Reason. 1991, 5, 331–348. [Google Scholar] [CrossRef]
- Attia, A.-H.; Rezeka, S.F.; Saleh, A.M. Fuzzy logic control of air-conditioning system in residential buildings. Alex. Eng. J. 2015, 54, 395–403. [Google Scholar] [CrossRef]
- Paris, B.; Eynard, J.; Grieu, S.; Polit, M. Hybrid PID-fuzzy control scheme for managing energy resources in buildings. Appl. Soft Comput. 2011, 11, 5068–5080. [Google Scholar] [CrossRef]
- Chandan, S.; Agnihotri, R. Fuzzy logic Controller for Flowing Fluids. Int. J. Adv. Res. Comput. Eng. Technol. 2012, 1, 98–101. [Google Scholar]
- Pruna, E.; Andaluz, V.H.; Proano, L.E.; Carvajal, C.P.; Escobar, I.; Pilatasig, M. Construction and analysis of PID, fuzzy and predictive controllers in flow system. In Proceedings of the 2016 IEEE International Conference on Automatica (ICA-ACCA), Curicó, Chile, 19–21 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–7. [Google Scholar]
- Poornapushpakala, S. Simulation of neuro—Fuzzy controller for a flow process using MATLAB. In Proceedings of the 2015 International Conference on Circuits, Power and Computing Technologies [ICCPCT-2015], Nagercoil, India, 19–20 March 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–4. [Google Scholar]
- AL-Qutami, T.A.H.; Ibrahim, R. Design of a Fuzzy Logic process Controller for flow applications and implementation in series tanks Pilot Plant. In Proceedings of the 2015 International Conference on Industrial Instrumentation and Control (ICIC), Pune, India, 28–30 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 450–455. [Google Scholar]
- Perfilieva, I. Fuzzy IF-THEN Rules from Logical Point of View. In Computational Intelligence, Theory and Applications SE—67; Reusch, B., Ed.; Springer: Berlin/Heidelberg, Germany, 2006; Volume 38, pp. 691–697. ISBN 978-3-540-34780-4. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Rondeau, L.; Ruelas, R.; Levrat, L.; Lamotte, M. A defuzzification method respecting the fuzzification. Fuzzy Sets Syst. 1997, 86, 311–320. [Google Scholar] [CrossRef]
- Taitel, Y.; Dukler, A.E. A model for predicting flow regime transitions in horizontal and near horizontal gas-liquid flow. AIChE J. 1976, 22, 47–55. [Google Scholar] [CrossRef]
- Mitsuishi, T. Continuity of approximate reasoning using center of sums defuzzification method. In Proceedings of the MIPRO, 2012 Proceedings of the 35th International Convention, Opatija, Croatia, 21–25 May 2012; pp. 991–994. [Google Scholar]





| Test Run | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Human expert evaluation | Plug → Transitional | Transitional → Plug | Plug → Slug | Slug → Plug | Plug → Transitional | Transitional → Slug | Slug → Transitional | Transitional → Slug | Slug → Plug | Plug → Slug | Slug → Transitional | Transitional → Stratified | Stratified → Slug | Slug → Dispersed | Dispersed → Stratified |
| Presented system evaluation | Plug → Transitional | Transitional → Plug | Plug → Slug | Slug → Plug | Plug → Transitional | Transitional → Slug | Slug → Transitional | Transitional → Slug | Slug → Plug | Plug → Slug | Slug → Transitional | Transitional → Stratified | Stratified → Slug | Slug → Dispersed | Dispersed → Stratified |
| Test Run | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| Human expert evaluation | Stratified → Waved | Waved → Stratified | Stratified → Slug | Slug → Dispersed | Dispersed → Transitional | Transitional → Dispersed | Dispersed → Plug | Plug → Waved | Waved → Plug | Plug → Dispersed | Dispersed → Stratified | Stratified → Dispersed | Dispersed → Waved | Waved → Dispersed | Dispersed → Slug |
| Presented system evaluation | Stratified → Waved | Waved → Stratified | Stratified → Slug | Slug → Dispersed | Dispersed → Transitional | Transitional → Dispersed | Dispersed → Plug | Plug → Waved | Waved → Plug | Plug → Dispersed | Dispersed → Stratified | Stratified → Dispersed | Dispersed → Waved | Waved → Dispersed | Dispersed → Slug |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fiderek, P.; Kucharski, J.; Wajman, R. Fuzzy Regulator for Two-Phase Gas–Liquid Pipe Flows Control. Appl. Sci. 2022, 12, 399. https://doi.org/10.3390/app12010399
Fiderek P, Kucharski J, Wajman R. Fuzzy Regulator for Two-Phase Gas–Liquid Pipe Flows Control. Applied Sciences. 2022; 12(1):399. https://doi.org/10.3390/app12010399
Chicago/Turabian StyleFiderek, Paweł, Jacek Kucharski, and Radosław Wajman. 2022. "Fuzzy Regulator for Two-Phase Gas–Liquid Pipe Flows Control" Applied Sciences 12, no. 1: 399. https://doi.org/10.3390/app12010399
APA StyleFiderek, P., Kucharski, J., & Wajman, R. (2022). Fuzzy Regulator for Two-Phase Gas–Liquid Pipe Flows Control. Applied Sciences, 12(1), 399. https://doi.org/10.3390/app12010399








