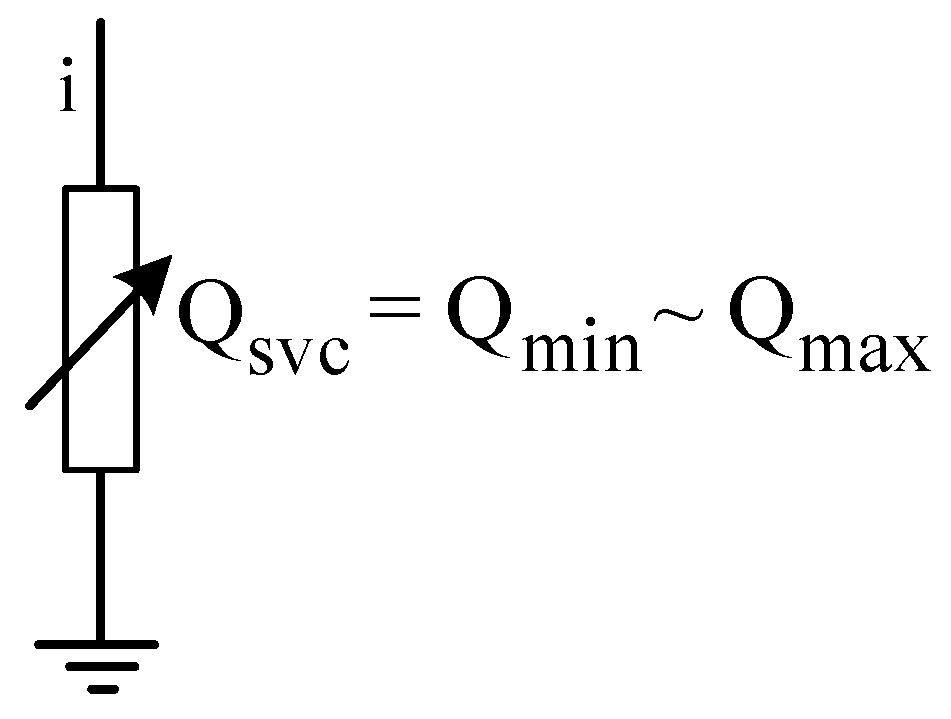Optimal Management of Reactive Power Considering Voltage and Location of Control Devices Using Artificial Bee Algorithm

Abstract

Reactive power compensation is one of the practical tools that can be used to improve power systems and reduce costs. These benefits are achieved when the compensators are installed in a suitable place with optimal capacity. This study solves the issues of optimal supply and the purchase of reactive power in the IEEE 30-bus power system, especially when considering voltage stability and reducing total generation and operational costs, including generation costs, reserves, and the installation of reactive power control devices. The modified version of the artificial bee colony (MABC) algorithm is proposed to solve optimization problems and its results are compared with the artificial bee colony (ABC) algorithm, the particle swarm optimization (PSO) algorithm and the genetic algorithm (GA). The simulation results showed that the minimum losses in the power system requires further costs for reactive power compensation. Also, optimization results proved that the proposed MABC algorithm has a lower active power loss, reactive power costs, a better voltage profile and greater stability than the other three algorithms.

1. Introduction

Reactive power compensation located near the place of consumption is one of the most effective ways to modify power system performances [1,2,3]. The use of reactive power compensators such as capacitor banks, flexible AC transmission system (FACTS) devices, as well as on-load tap changers (OLTC) adjustments are common methods used to control the reactive current flowing in the power system. Reactive power compensations generate required reactive power near the load instead of being supplied from a distant power plant [4]. As a result, the power factor is corrected, loss is reduced and line capacity is increased. But these benefits can only be achieved when reactive power compensators are optimally sized and properly controlled. Therefore, the supply and purchase of reactive power is an essential issue in novel grids. In recent studies, voltage stability and optimal reactive power flow are integrated.

Many algorithms have been proposed to solve the problem of optimal reactive power compensation. In [5], a new method based on the multi-objective genetic algorithm (NSGAII) was proposed for capacitor placement in a harmonic polluted system. The optimization results showed that the proposed method can converge to a set of optimal results in the search space. In [6], an innovative hybrid artificial bee colony and particle swarm optimization (ABC-PSO) algorithm was proposed for capacitor bank sizing in a radial distribution feeder. The optimization results indicated that the proposed ABC-PSO algorithm performed better than the PSO and ABC algorithms. In the proposed method in [7], an integrated approach of loss sensitivity factor (LSF) and voltage stability index (VSI) were used to determine the optimal placement of reactive power compensators. Also, the genetic algorithm (GA) was used to determine the optimal size of the compensators. In [8], optimal Static Var Compensator (SVC) placement was done by the ABC algorithm. The objective function was the reduction of ohmic losses and the improvement of the power quality. In [9], optimal thyristor-controlled series compensator (TCSC) placement in IEEE 57 and IEEE 118 Bus Systems was achieved. The ABC algorithm was used for optimization to reduce transmission loss. The results of optimization by the ABC algorithm and comparison with some other metaheuristic algorithms proved the superiority of ABC algorithm. In [10], the fuzzy based ABC algorithm was used to solve the optimization problem of voltage regulator and capacitor placement. The use of the fuzzy method allowed simultaneous minimization of losses in the radial distribution system and voltage deviation. In [11], a new modified version of the ABC algorithm for optimal location of shunt compensators was proposed. In order to validate the proposed ABC algorithm, a number of power systems of different sizes and complexities were used and also compared with meta-heuristic optimization algorithms. The results showed that the proposed method was able to provide better solutions.

Usually, a reactive power supply aims to minimize the active power loss or increase voltage stability. In general, it can be said that it aims to reduce the costs of reactive power. Reactive power resources have to supply and purchase reactive power in the grid [12]. The separate costs of grid-connected generators, line charging capacitors, capacitors installed on the buses and reactive power compensators are all worth mentioning, as each one presents an independent problem. It should be noted that the costs of reactive power generation resources depend on their operation conditions, while the cost of compensators depends on their capacity and installation location, which should be modeled accurately.

In this paper, a modified version of the artificial bee colony algorithm is proposed to solve the optimization problem. The percentage of the adjustable on-load tap changers (OLTC), capacity of the capacitor banks, and optimal location and capacity of the reactive power compensators are considered as control parameters. Changing these parameters affects the reactive power distribution, voltage profile and stability. Also, the effect of using different objective functions to determine the location and size of various reactive power compensators in the power system is evaluated.

The rest of this paper is organized as follows. Section 2 presents the reactive power supply problem. Section 3 discusses reactive power supply costs. Section 4 formulates the optimization problem. Section 5 introduces the MABC algorithm. Finally, Section 6 presents the numerical simulation and compares the results.

2. Reactive Power Supply

This paper aims to achieve an optimized voltage profile of the grid, reducing power system loss and minimizing reactive compensation costs by optimizing the reactive power supply. Due to the inherent relationship between reactive power and the voltage profile, optimizing the reactive power flow and reactive power supply improves the voltage profile. Thus, the reactive power supply should be determined using the best method. Maximizing the output reserve reactive power of the generators, maximizing the line charge and minimizing costs are the three main goals of reactive power compensation. Three different methods have been presented in which the costs corresponding to the best operation mode of the network are determined. The costs include the total cost of supplying reactive power by various resources, including generators, the line charging capacitance, installed capacitors and reactive power compensators, and the costs of active power loss. The three methods of the reactive power supply include:

(a)

Maximizing the output reserve reactive power of the generators: increasing the reactive reserve power or reducing the reactive output power that increases the dynamic voltage stability.

(b)

Maximizing the line charge: increasing the reactive output power of the inherent reactive power generation resources or the lines’ capacitance.

(c)

Minimizing the costs: the total cost of reactive power supply might be minimized by observing the system constraints.

Reducing voltage deviation, increasing voltage stability and reducing active power loss are three methods for improving the voltage profile [13].

3. Mathematical Formulation of the Reactive Power Supply

The total cost corresponding to active losses, which is supplied by the generators, can be determined only when the share of losses corresponding to each generator is known. Similarly, the costs of investing in reactive power demand and reactive power loss should be determined. The total cost is described as follows [14]:

$$Cost=Cos{t}_{QG}+Cos{t}_{QCap}+Cos{t}_{Qcharg}+Cos{t}_{QFact}$$

(1)

where $Cos{t}_{QG}$, $Cos{t}_{QCap}$,$Cos{t}_{Qcharg}$ and $Cos{t}_{QFact}$ are the reactive power generation costs of the generators, capacitors, line charge and compensators respectively. The total cost will be minimized when the cost of each reactive power compensation method is at its lowest value.

3.1. The Reactive Power Generation Cost of the Generators

In Equation (2), the coefficients a_i, b_i, c_i are the cost coefficients of the active power generation of the generators, N_g is the number of the generators and $\sin \theta$ are proportional to the power factor of each generator.

$$Cos{t}_{QG}={\displaystyle \sum }_{i=1}^{N_g}\left(C_i+b_i\sin \theta Q{G}_i+a_i\sin {\theta }^{2}Q{G}_i^2\right)$$

(2)

3.2. The Cost of Reactive Power Generation of the Capacitors Installed on Buses

The reactive power generation cost of the installed capacitors that is spent on the buses depends on the initial investment used to install the capacitance of interest on the bus. Also, to convert the costs to $/h, the lifetime of the capacitance per hour should be considered. Equation (3) can be used to calculate the capacitor bank cost.

$$Cos{t}_{QCap}={\displaystyle \sum }_{i=1}^{N_C}\frac{QCa{p}_I.c_C}{L.U}$$

(3)

where N_c is the number of the capacitor, c_c is the price per kVAr of the installed capacitor and Q_CapI is the capacitance of the i^th capacitor. In addition, the parameter U is the performance factor and describes a ratio of the capacitor lifetime that is spent on generating reactive power. Also, L is the life time factor.

3.3. The Cost of Generating Reactive Power from the Line Charge

The total cost of generating reactive power to the total capacitors of the line charge is equal to the total cost of each line capacitance, which is the product of reactive power generation and cost of each unit’s reactive power generation, as given in Equations (4) and (5). The parameter C is equal to the average cost of generating each unit’s reactive power of all grid resources. Figure 1 shows the π-model of the transmission lines with tap changer.

$$Q_{charg}={\displaystyle \sum }_{char{g}^{=1}}^{N_{charg}}{Q}_{charg{h}_{i-j}}={\displaystyle \sum }_{char{g}^{=1}}^{N_{charg}}\left(V_i^2\frac{y{c}_{ij}}{2}+V_j^2\frac{y{c}_{ij}}{2}\right)$$

(4)

$$Cos{t}_{Qcharg}=Q_{charg}\ast C_{ave}$$

(5)

In Equation (4), Q_charg is the reactive power generated by line capacitor charge, V_i and V_j are the voltage amplitude of buses i and j and the line admittance. In general, if a transformer exists at the beginning of a bus, the line charge admittance is calculated as follows:

$$I_i=V_i\left(y_s\left(t-1\right)t+0.5y_{c.ij}{t}^2\right)+y_{s}t\left(V_i-V_j\right)$$

(6)

$$I_j=V_j\left(y_s\left(1-t\right)+0.5y_{c.ij}\right)+y_{s}t\left(V_i-V_j\right)$$

(7)

where, V_i and V_j are ith and jth terminal voltage, y_s and y_c,ij are series admittance and susceptance, I_i and I_j are line current.

3.4. Cost of Reactive Power Generation of the Compensators

Reactive power compensators of interest are SVC and TCSC, which are connected in series and parallel. In this section, these two devices are modeled and then, similar to previous sections, the cost of generating each reactive power unit is calculated. It should be pointed out that the optimal location and capacity of these two devices in the network is not known, and their generation costs and the total cost of reactive power supply should be minimized by selecting the proper location and capacitance.

3.4.1. SVC

This device is connected in parallel with buses that might operate in capacitive or inductive modes. It can be modeled as a capacitor with variable capacitance ranging from positive to negative. In power flow equations, the bus with SVC is considered as a generator bus with zero active power generation [12]. Figure 2 shows the SVC model.

The total cost of SVC is a second-order function of its nominal capacity. The SVC cost can be calculated by Equation (8) [13].

$$C_{svc}=0.0003s^2-0.3051S+127.38\left(\frac{US\$}{K}var\right)$$

(8)

In the above equation, S is the rated capacity of the SVC in MVAr. Considering the 5-year lifetime, the cost is calculated in $/h.

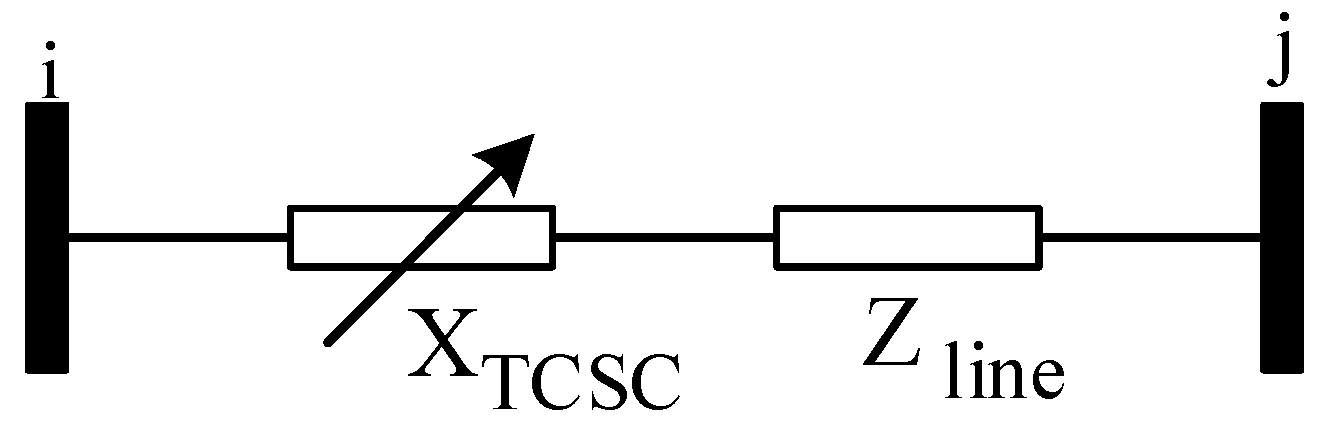
3.4.2. TCSC

This device is modeled as a reactance in series with the transmission line and can operate in both capacitive and inductive ranges. The capacity of the TCSC depends on the reactance of the transmission line on which it is installed [12]. As mentioned in Equation (9), the equivalent impedance is the sum of the line impedance and the TCSC impedance. In most cases, the TCSC is in capacitive mode and its reactance is negative. Therefore, the equivalent impedance is less than the transmission line impedance. Figure 3 shows the TCSC model.

$$X_{ij}=X_{line}+X_{TCSC}=\left(1+r_{TCSC}\right)X_{line}$$

(9)

In the above equation, X_line is the reactance of the transmission line and r_TCSC is the compensation factor. The compensation factor usually varies between 0.2 and −0.8. The cost of the TCSC, similar to the SVC, is a second-order function of its reactive power injection.

The cost function [13] is as follows:

$$C_{TCSC}=0.0015s^2-0.7130S+153.75\left(\frac{US\$}{K}var\right)$$

(10)

In this equation, S is the reactive power flowing through the transmission line before and after installing the TCSC.

4. Defining the Optimization Objectives

The mathematical definition of the reactive power supply is presented in this section. This section defines the problem presented in Section 2 mathematically. Four new objective functions with two classic objective functions are studied here. The constraints are considered as a penalty factor (P) in the objective functions:

$$P_{QG}={\displaystyle \sum }_{i=1}^{Ng}[-min\left(1-\frac{Q_G}{Q_G},0\right)+min\left(\frac{\left|Q_G\right|}{\left|Q_G^{min}\right|}-1,0\right)]$$

(11)

$$P_V={\displaystyle \sum }_{i=1}^{Nbus}[-min\left(1-\frac{V}{V^{max}},0\right)+min\left(\frac{V}{V^{min}}-1\right)]$$

(12)

$$P_{tap}={\displaystyle \sum }_{i=1}^{Ntap}[-min\left(1-\frac{t}{t^{max}},0\right)+min\left(\frac{t}{t^{min}}-1,0\right)]$$

(13)

$$P_{cap}={\displaystyle \sum }_{i=1}^{Ncap}[-min\left(1-\frac{Q_{cap}}{Q_{cap}},0\right)+min\left(\frac{\left|Q_{cap}\right|}{\left|Q_{cap}^{min}\right|}-1,0\right)]$$

(14)

4.1. The Proposed Objective Functions

The first objective function is reducing the output power of the synchronous generators of the network (increasing the reserve of the reactive power generated by the generators) that generate reactive power.

$$Q_G={\displaystyle \sum }_{i=1}^{NG}{Q}_{G_i} , \forall Q_{G_i}>0$$

(15)

$$min{f}_1=Q_G\times \left(1+\alpha P_{QG}+\beta P_V+\lambda P_{tap}+\delta P_{Cap}\right)$$

(16)

The second objective function is increasing the output power of the reactive power generation resources or the line charging capacitors. To achieve these conditions, the voltage of the buses should be increased, which improves the voltage profile.

$$max{f}_2=Q_{charg}\times \left(1+\alpha P_{QG}+\beta P_V+\lambda P_{tap}+\delta P_{Cap}\right)$$

(17)

The third objective function is minimizing the costs of supply and the purchase of the total reactive power

$$min{f}_3=Cos{t}_{QG}\times \left(1+\alpha P_{QG}+\beta P_V+\lambda P_{tap}+\delta P_{Cap}\right)$$

(18)

The fourth objective function is minimizing the supply and purchase costs of reactive power considering the reactive power generation costs of the compensators installed in the network. The total costs of this function should be lower than the cost calculated in the previous section so that installing new reactive power compensators is cost-effective. Thus, this objective function can be represented as follows:

$$P_{loss}={\displaystyle \sum }_{i=1}^{NG}{P}_{G_i},{\displaystyle \sum }_{j=1}^{Nbus}P{D}_j$$

(19)

$$min{f}_4=P_{loss}\times \left(1+\alpha P_{QG}+\beta P_V+\lambda P_{tap}+\delta P_{Cap}\right)$$

(20)

In which $P_{G_i}$ is the total power generation of the network generators, and $P{D}_j$ is the real load connected to each bus.

4.2. The Classic Objective Functions

4.2.1. Minimizing the L-Index

In the following equation, i is the index related to G generator buses and j is the index of the load buses. The matrix is calculated using the following equations [15].

$$L_{max}=max\left(L_j\right),L_j=\left|1-{\displaystyle \sum }_{i=1}^{NG}\left(\frac{V_i}{V_j}\right)\right|$$

(21)

$$min{f}_5=L_{max}\times \left(1+\alpha P_{QG}+\beta P_V+\lambda P_{tap}+\delta P_{Cap}\right)$$

(22)

$$\left[\begin{array}{c}{I}_G\\ I_L\end{array}\right]=\left[\begin{array}{cc}{Y}_{GG}& Y_{GL}\\ Y_{LG}& Y_{LL}\end{array}\right]\left[\begin{array}{c}{V}_G\\ V_L\end{array}\right]$$

(23)

In the above equations $V_G,I_G,V_L,I_L$ are the current and voltage vectors of the generator buses and the load. By sorting the above equations, Equation (22) is obtained:

$$\left[\begin{array}{c}{V}_L\\ I_G\end{array}\right]=\left[\begin{array}{cc}{Z}_{LL}& F_{LG}\\ K_{GL}& Y_{GG}\end{array}\right]\left[\begin{array}{c}{I}_L\\ V_G\end{array}\right]$$

(24)

Finally:

$$\left[F_{LG}\right]=-{\left[Y_{LL}\right]}^{-1}\left[Y_{LG}\right]$$

(25)

To improve voltage stability, the L-index for each load bus should not exceed its upper limit, which is one. In other words, the L-index describes the system stability and the maximum value among L_j load buses. This index is a numerical quantity that estimates the real distance of the system from its stability boundary.

4.2.2. Improving the Voltage Profile

Another aim of reactive power compensation is to minimize buses voltage deviation. The voltage deviation function is calculated as Equation (26).

$$\Delta V=\frac{1}{N_{bus}}{\displaystyle \sum }_{i=1}^{N_{bus}}\left|V_{Nom}-V_i\right|$$

(26)

where N_bus is the number of buses, V_i is the i^th bus voltage amplitude and V_nom is the nominal voltage equal to 1^pu. Voltage deviation is minimized when the voltage amplitude for all buses is close to the nominal value. The sixth objective function can be represented as Equation (27).

$$min{f}_6=\Delta V\times \left(1+\alpha P_{QG}+\beta P_V+\lambda P_{tap}+\delta P_{Cap}\right)$$

(27)

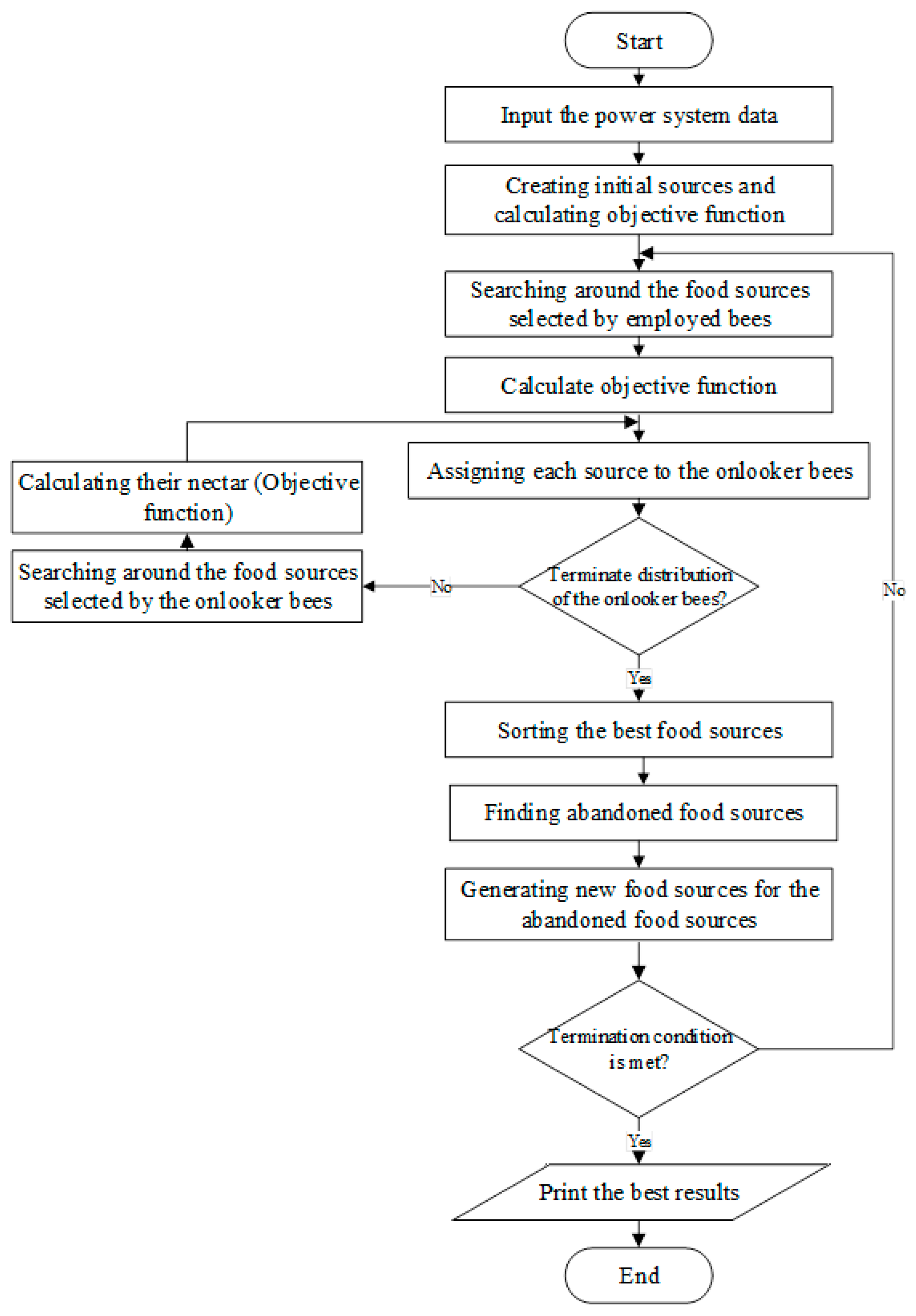
5. Modified Artificial Bee Colony (MABC) Algorithm

The algorithm used in this paper for solving the problem is the modified version of the artificial bee colony (MABC) algorithm. The ABC algorithm is an algorithm based on the random movement of bees, which provides higher quality and accuracy.

5.1. ABC

In this algorithm, the food sources solve the problem, and the extractable nectar represents the corresponding fitness. In this algorithm, the bees are divided into three groups: employed, onlooker and scout bees. The performance of this algorithm is as follows [16]:

(a)

Primary preparation: similar to any optimization algorithm, this algorithm starts with an initial population, and the problem evaluation requires determining the population based on the random selection of the upper and lower limit of the problem.

(b)

Repeat: the scout bees select each food source based on the probability obtained from Equation (28) and corresponding to the source.

$$p_i=\frac{f_i}{{{\displaystyle \sum }}_{n=1}^N{f}_n}$$

(28)

In the above equation, f_i is the fitness of each source, and N is the number of employed bees. In this step, to extract more nectar from each source, new sources are created by combining old food sources so that a source’s performance can be represented.

$$v_{ij}=x_{ij}+{\phi }_{ij}\left(x_{ij}-x_{kj}\right)$$

(29)

In which φ_ij is a random number between −1 and 1, and j is an integer random number between one and a variable decision-making dimension.

(c)

Replacing the bees: in this algorithm, if a food source cannot be improved (exceed the determined value), the food source is left and replaced by a new random population selected by the onlooker bees. After generating and evaluating each food source, its performance is compared with the previous food sources. If the value of the objective function for a new source is less than an old one, it will replace an old source. Otherwise, the old food source is used.

$$x_i^j=x_{min}^j+rand\left(0,1\right)\ast \left(x_{max}^j-x_{min}^j\right)$$

(30)

5.2. Improved ABC

Although the basic case of this algorithm is efficient for solving large problems with various modalities, if the problem is constrained, its convergence rate is decreased. Three modifications are therefore applied to improve this algorithm. Changing the repeat pattern: in this case, instead of changing only one cell of the population, all cells of a group might change considering the following rule:

$$v_{ij}=\{\begin{array}{c}{x}_{ij}+{\phi }_{ij}\left(x_{ij}-x_{kj}\right) R_{ij}<MR\\ x_{ij} otherwise\end{array}$$

(31)

MR is an arbitrary number between [0, 1] in the above equation and $R_{ij}$ is a random number in the same interval. According to Equation (31), ${\phi }_{ij}$ is a random number in the range of $\left[-1,1\right]$ indicating that the movement step from one source to another is constant, while larger or smaller steps might be required in some problems; thus, ${\phi }_{ij}$ is selected in the range of $\left[-a,a\right]$ considering the problem conditions before selection. Adaptive modification of the repeat steps, as mentioned above, requires more extractions for various food sources or exploring new sources, which can be implemented if the movement steps of each source change adaptively. To this end, the Rosenberg law is used. This law, known as the 0/2 law, operates in each m iteration of the main loop [9].

$$a\left(t+1\right)=\{\begin{array}{c}a\left(t\right)\times 0.85, if \Psi \left(m\right)<0.2\\ a\left(t\right)\times 0.85, if \Psi \left(m\right)>0.2\\ a\left(t\right) , if \Psi \left(m\right)=0.2\end{array}$$

(32)

In the above equation, t is the loop’s counter, $\Psi \left(m\right)$ is the number of successful repetitions to the total repetitions in iteration m. To better understand the presented definitions of the MABC algorithm in solving the optimization problems, its flowchart is shown in Figure 4.

6. Simulation Results

The decision-making variables in the above equations include the generator bus voltage, tap changers, reactive power generated by the capacitors, optimal location and capacity of the SVC and TCSC. The reactive power flow also changes; thus, ABC can be used to achieve the most optimal case. To evaluate the performance of this method, it is applied to the standard 30-bus network represented in the attachment. Information on the network is found in [17]. There are two capacitor banks that are also installed on buses 5 and 24 with a maximum value of 4.3 and 19 MVAr, respectively. The voltage magnitude in generator buses and load buses varies between 0.96 to 1.05 and 0.94 to 1.06, respectively. To determine the optimal location and capacity, one SVC and TCSC are installed, which are considered as a sequence with three cells for the optimization problem, where the first two cells represent the location (SVC bus number and line number for the TCSC) and the third cell represents capacity. According to the generator bus model for the SVC, its optimal reactive capacity is calculated using the power flow [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34]. The capacitance range of the SCV is between −50 to 50 MVAr. The simulation results of the 30-bus network that include the system’s decision-making variables and performance parameters for the proposed algorithm (MABC), the artificial bee colony (ABC) algorithm, the particle swarm optimization (PSO) algorithm and also the genetic algorithm (GA) are given in

Table 1. Optimization res.

		f1				f2				f3
		PSO	GA	ABC	MABC	PSO	GA	ABC	MABC	PSO	GA	ABC	MABC
Loss (MW)		12.83	12.94	12.85	12.36	12.92	12.98	12.88	12.39	13.07	13.13	12.94	12.72
Line charging reactive power (MVAr)		27.45	26.23	27.14	28.32	32.21	31.47	32.27	33.14	30.24	30.19	30.54	31.03
Generator reactive reserve (MVAr)		161.8	159.3	160.9	162.7	147.6	145.1	149.2	149.9	157.3	151.4	157.2	158.7
Reactive power supply cost ($/h)		394.5	397.2	387.2	381.6	437.7	430.8.7	435	426.7	357.6	359.6	353.2	350.1
Average voltage of the bus		0.964	0.953	0.972	0.991	1.014	1.016	1.012	1.011	0.984	1.003	0.992	1
Capacitors (MVar)	Bus.5	18.4	19.7	18.2	19.1	19.3	19.8	19.4	18.9	19.1	19.3	19.3	19.8
	Bus.24	4.3	4.23	4.11	3.91	4.3	3.86	4.11	4.05	4.3	4.3	4.09	4.3
SVC	Bus number	7	7	24	28	27	27	27	27	9	8	28	28
	(MVar) capacity	44.6	48.2	49.3	49.7	40.4	42.7	40.6	45.1	41.2	38.5	40.6	40.3
TCSC	Line number	35	28	36	41	34	27	32	16	11	32	12	8
	compensation percentage	−0.63	−0.52	−0.82	−0.51	−0.68	−0.83	−0.82	−0.86	−0.84	−0.23	−0.41	−0.32
		f4				f5				f6
		PSO	GA	ABC	MABC	PSO	GA	ABC	MABC	PSO	GA	ABC	MABC
Loss (MW)		12.77	12.32	11.89	11.52	13.21	13.18	13.09	13.02	12.88	12.65	12.23	12.1
Line charging reactive power (MVAr)		28.4	28.9	29.2	29.5	28.3	29.3	28.2	30.4	34.2	33.1	34.9	34.9
Generator reactive reserve (MVAr)		133.7	135.2	136.4	137.2	137.4	138.1	137.9	138.6	143.2	146.9	147.8	149
Reactive power supply cost ($/h)		463.2	465.1	460.1	457.8	493.1	490.4	487.3	481.6	568.2	569.4	561.5	553.2
Average voltage of the bus		0.996	0.996	0.997	0.998	0.993	0.992	0.996	0.997	1.04	1.02	1.01	1
Capacitors (MVAr)	Bus.5	19.2	18.4	19.6	17.2	3.45	3.67	3.88	2.79	19.2	18.4	18.7	15.7
	Bus.24	4.2	4.1	4.3	4.3	0	0	0	0	4.2	3.9	4.1	3.6
SVC	Bus number	23	23	25	24	23	23	25	21	13	12	27	28
	(MVar) capacity	16.5	14.23	15.61	13.58	50.9	51.1	50.8	48.4	41.4	36.8	45.2	37.7
TCSC	Line number	7	9	12	3	32	35	31	34	12	32	14	40
	compensation percentage	−0.64	−0.43	−0.23	−0.18	−0.83	−0.78	−0.65	−0.81	−0.81	−0.41	−0.78	−0.47

.

The optimal solutions of the six objective functions mentioned for the proposed modified artificial bee colony (MABC) algorithm are compared with the optimal solutions of the GA, PSO and ABC algorithms. In all cases, the MABC algorithm has a lower loss and costs and also a better voltage profile than three other algorithms. The power system total active power loss is 12.36 MW for the MABC algorithm when the f1 function is considered as an objective function. The total losses are 12.83 MW, 12.94 MW and 12.85 MW for the PSO, GA and ABC algorithms respectively. Also, the reactive power supply costs are 394.5 $/h for PSO, 397.2 $/h for GA, 387.2 $/h for ABC and 381.6 $/h for MABC. The average voltage of the buses for the second objective function, f₂, is maximum. However, the value of this parameter for the other functions is acceptable. The third objective function (f₃), which is the cost of supplying reactive power, is the minimum of 350.1 $/h, while it is 481 and 553 $/h for f₅ and f₆ for the proposed MABC algorithm. Also, in this case, the reactive power supply cost by using MABC is less than the PSO, GA and ABC algorithms. By using loss as the objective function (f₄), the loss is reduced to 11.52 MW for the MABC. The losses are 12.77 MW for PSO, 12.32 MW for GA and 11.89 MW for the ABC algorithm. In the objective function (f₄), the reactive output power of the generators is reduced, and the reactive output power of the capacitor banks and the SVC is increased to reduce the costs. As the power flowing through the lines is reduced, the loss is also reduced.

Using two 19.8 and 4.3 MVAr capacitor banks, one 40.3 MVAr SVC on bus 28 and a TCSC with 0.32% compensation on line 8, the cost of supplying the reactive power of the network is reduced and voltage deviation is at a minimum.

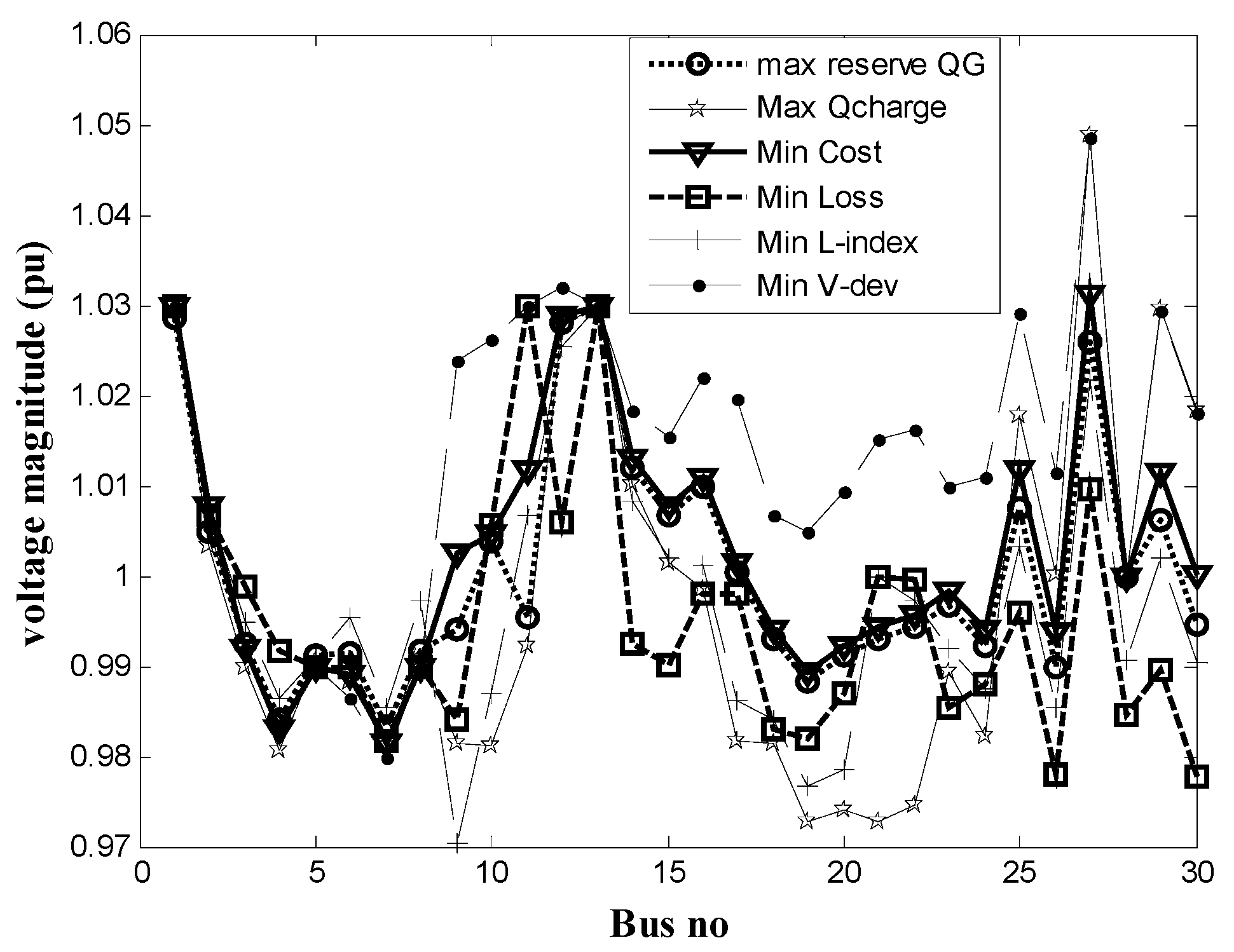
The voltage profile is shown in Figure 5 to evaluate the voltage stability and the voltage profile changes in the different objective functions.

As can be seen, the best voltage profile is obtained for the objective function that minimizes the voltage violation. The voltage profile that minimizes the total purchase cost of reactive power is also favorable.

7. Conclusions

This paper studies reactive power supply to supply the reactive power demand, aiming to improve the voltage profile and voltage stability. All parameters and variables that affect the reactive power distribution of the network, such as the voltage of the generators, tap changer of the transformers and capacity of the capacitor banks, are considered in the equations. Also, to increase the system’s flexibility and improve its efficiency in terms of optimal capacity, location, voltage, and SVC and TCSC devices are examined. By employing the modified artificial bee colony algorithm and the third objective function, the supply and purchase of reactive power is minimized. The simulation results indicate that the minimum active power losses in the power system require more payment to reactive power compensation. Minimum loss in the power system is about 11.52 MW, so 457.8$ should be spend for reactive power compensation. Also, optimization results prove that, in all the scenarios, the proposed MABC algorithm has a lower active power loss, reactive power cost and better voltage profile than the PSO, GA and ABC algorithms.