Experimental Evidence of Specimen-Size Effects on EN-AW6082 Aluminum Alloy in VHCF Regime
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Ultrasonic Fatigue Testing Machine
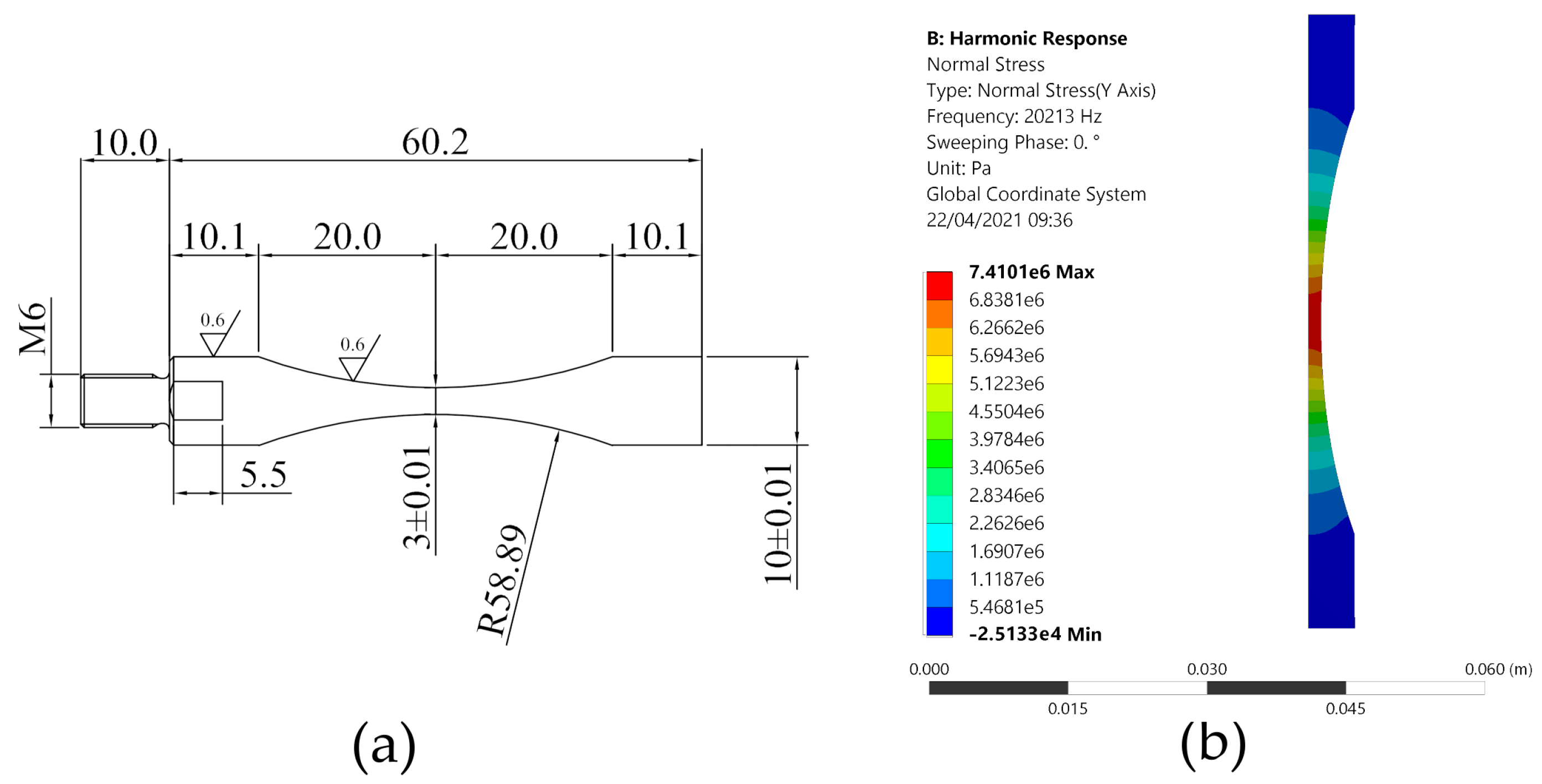
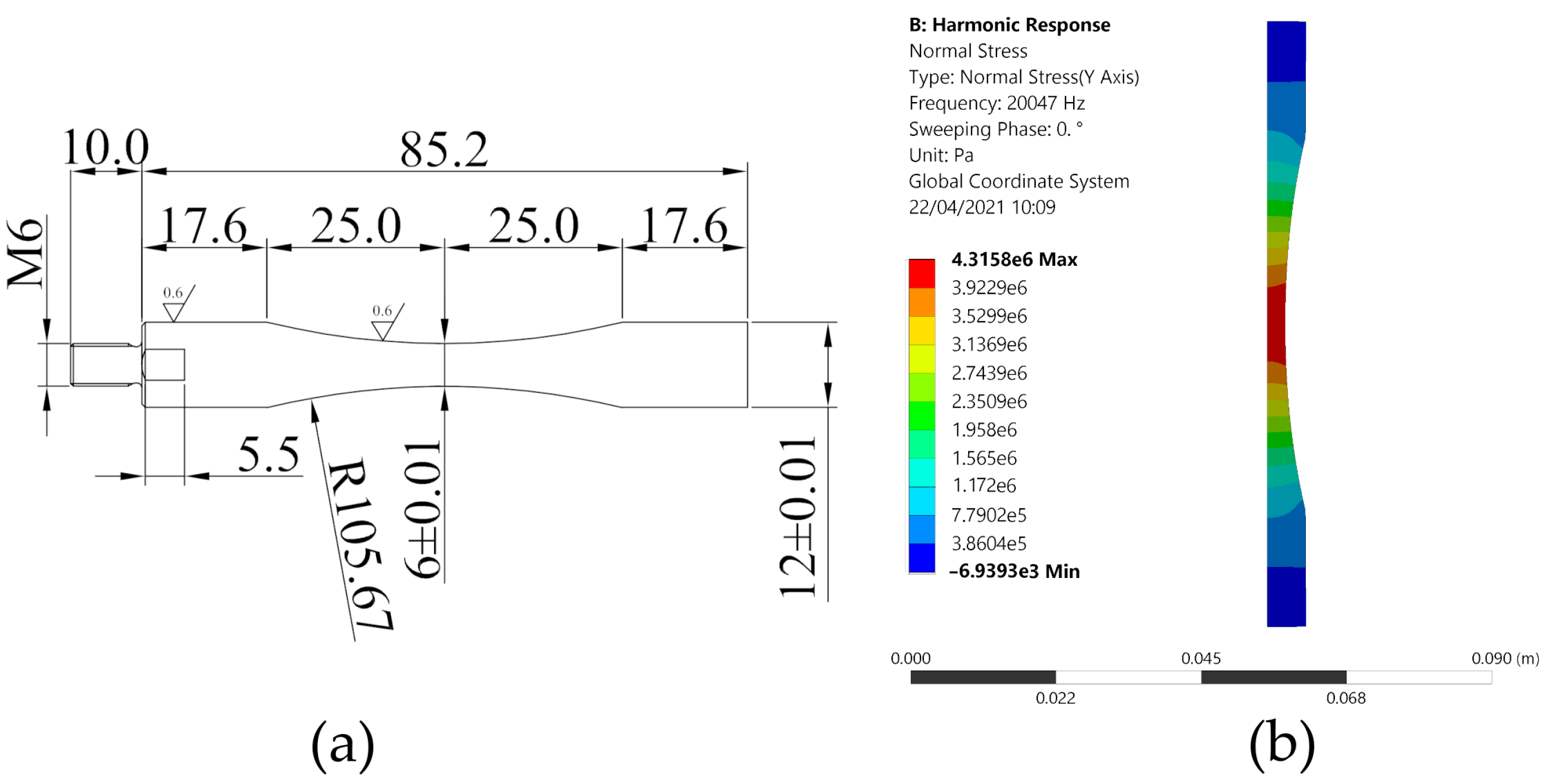
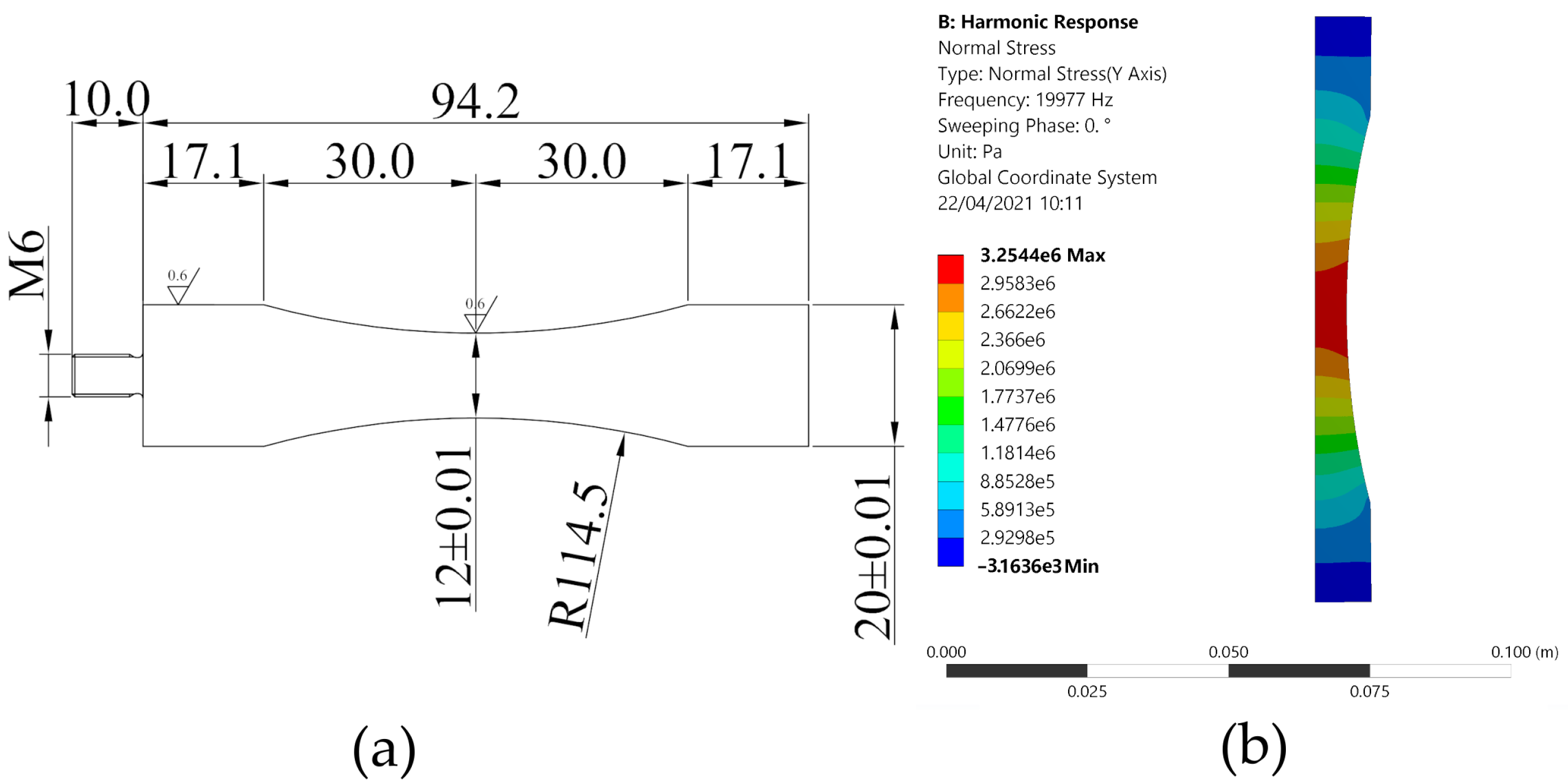
2.3. Specimens Design
3. Results
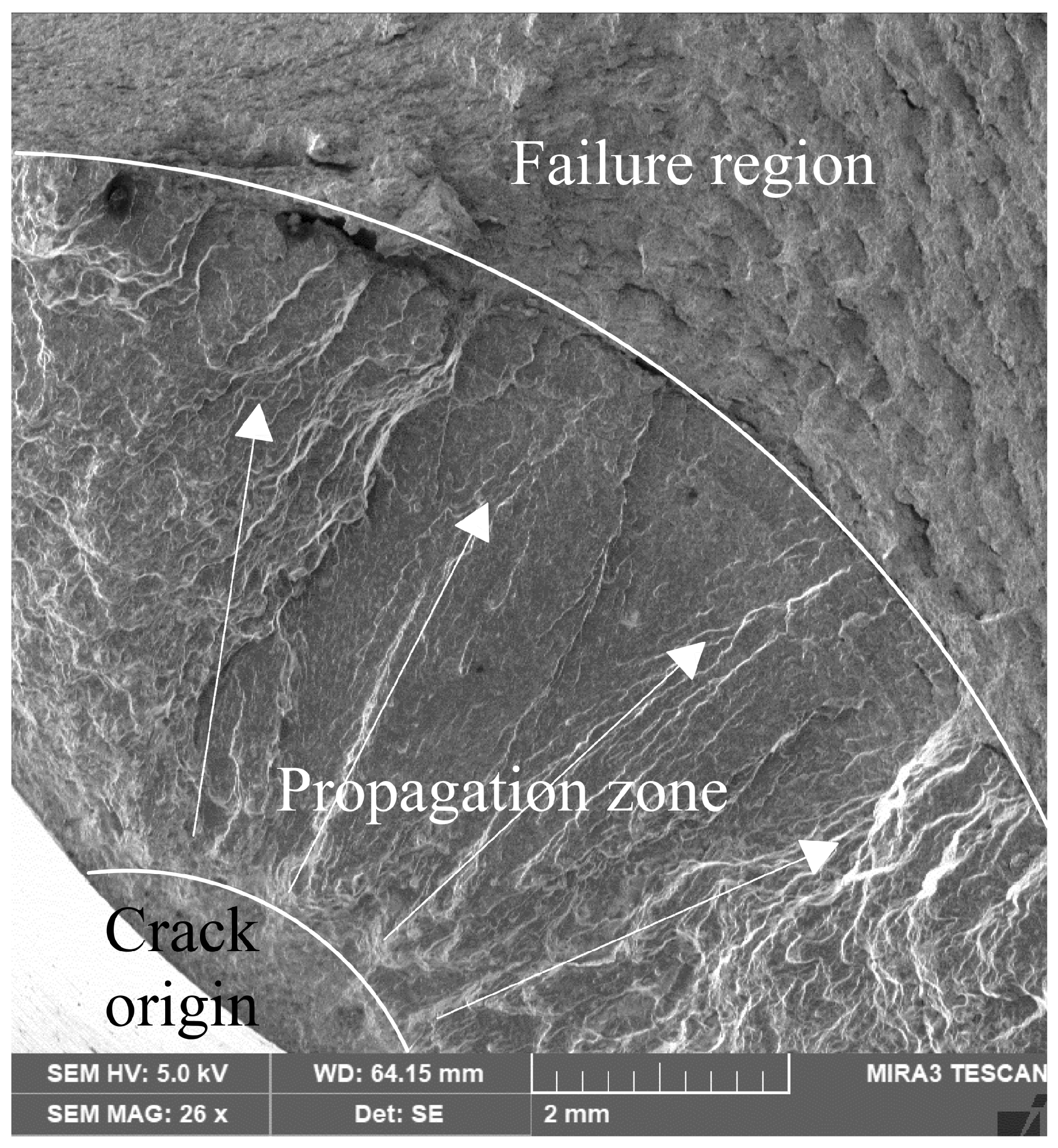
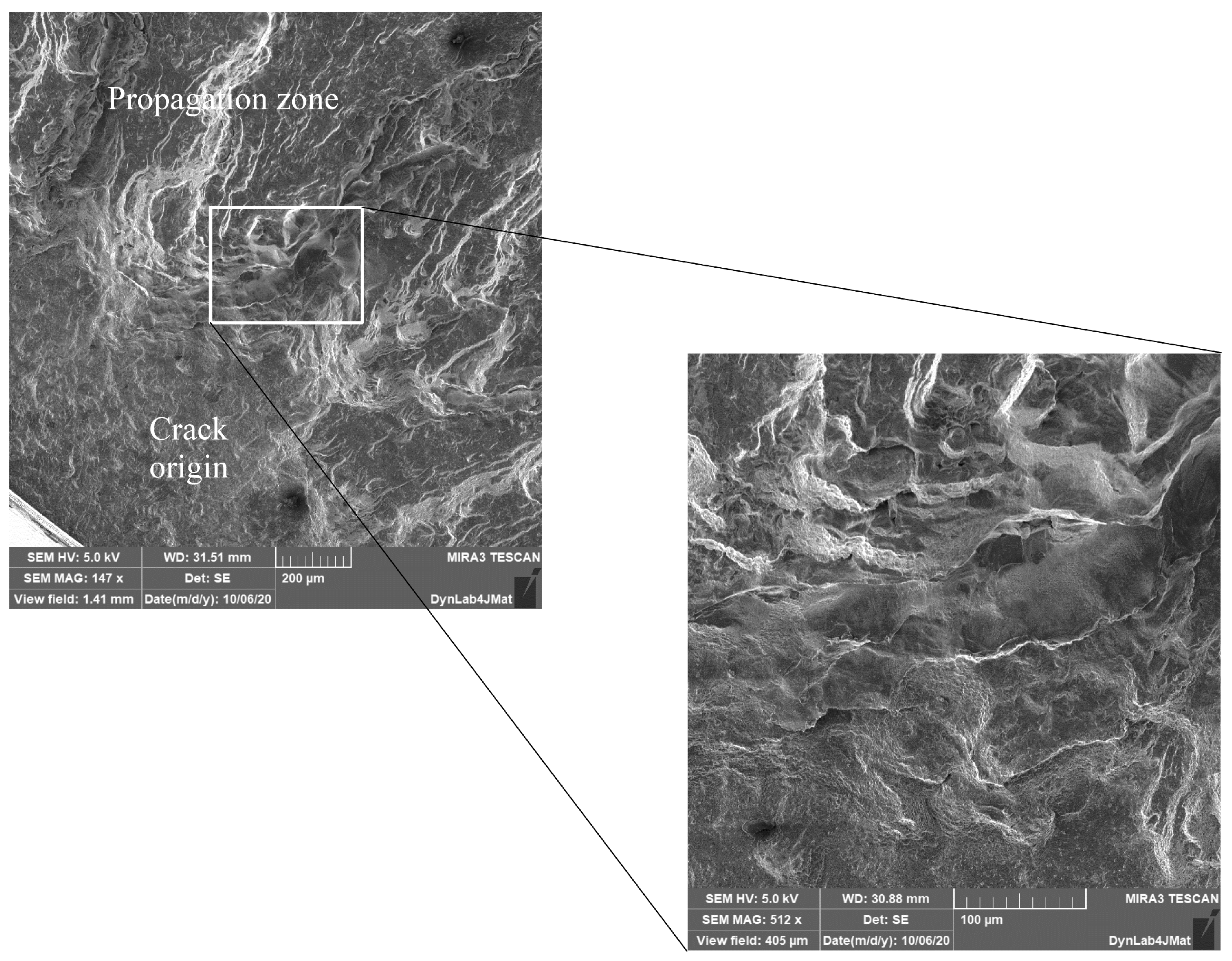
3.1. Experimental Results and Fracture Surface Analysis
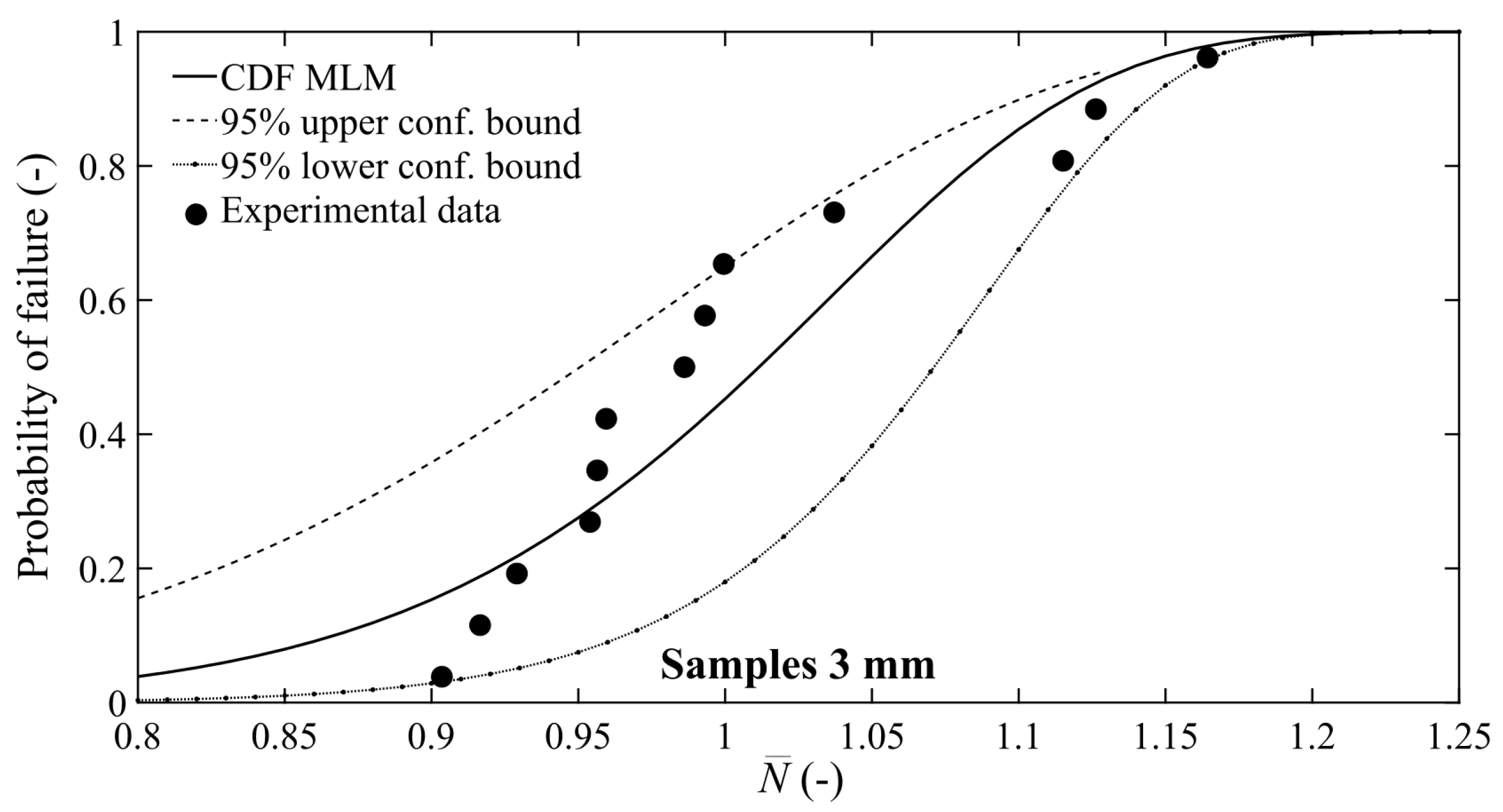
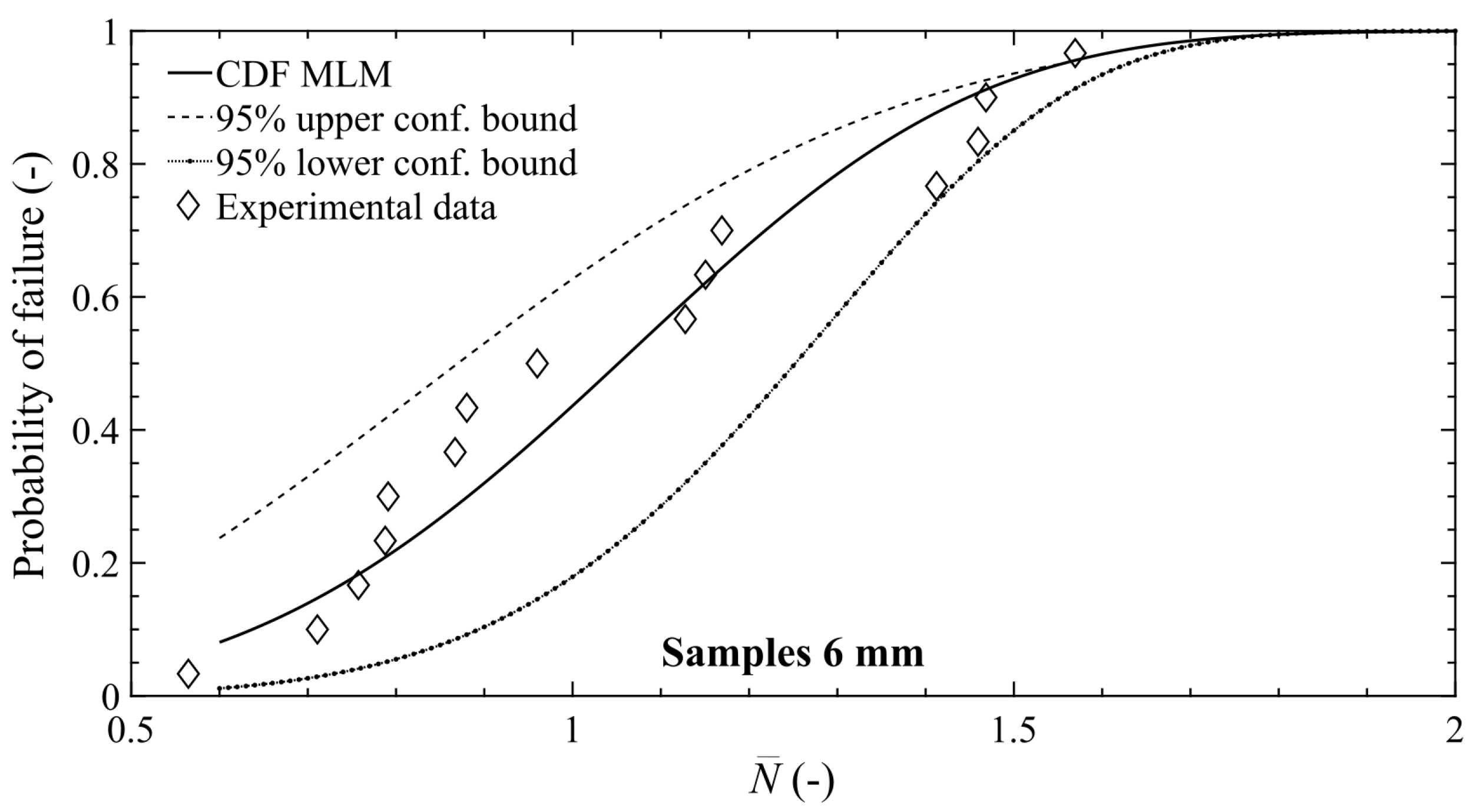
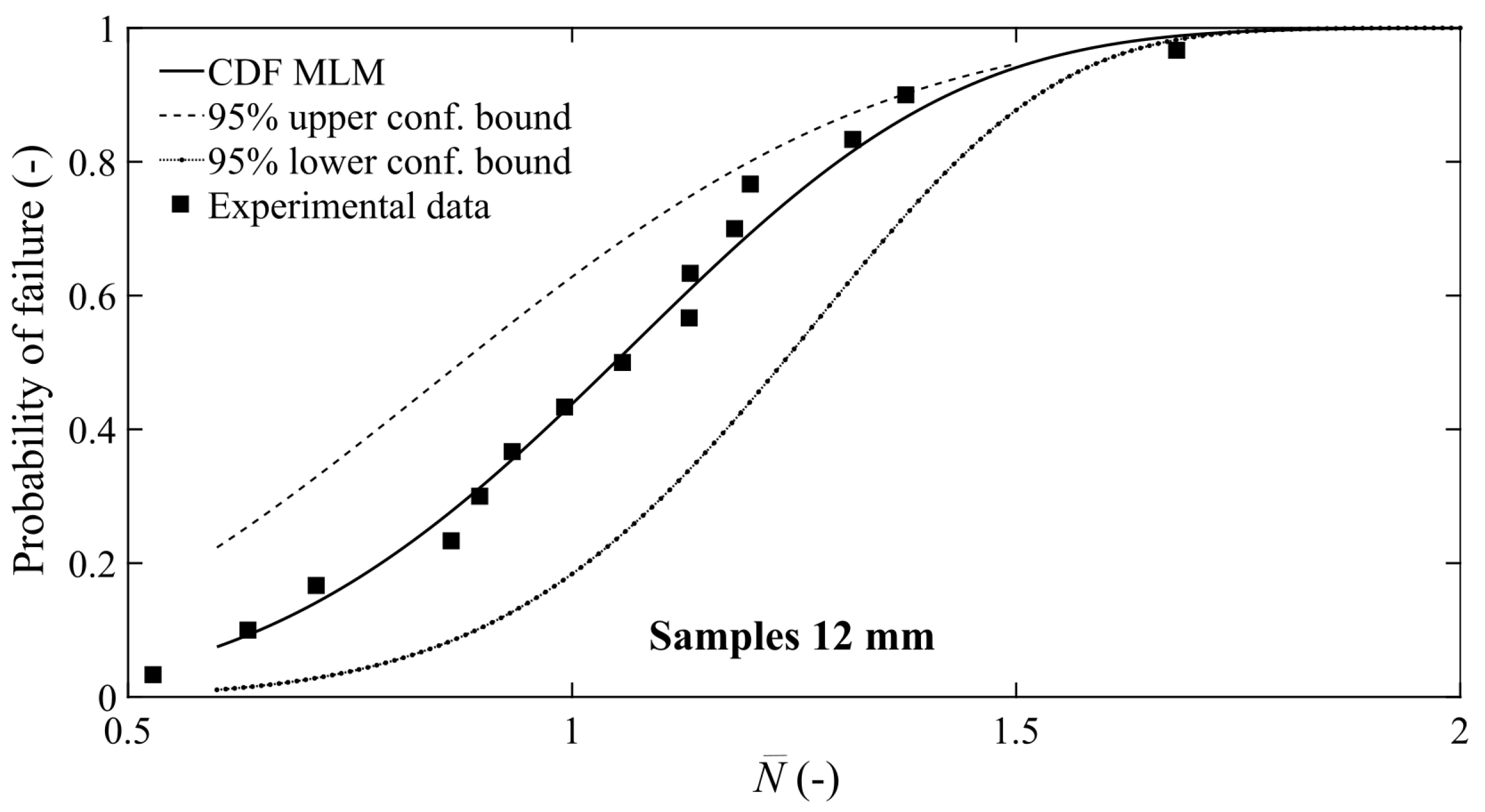
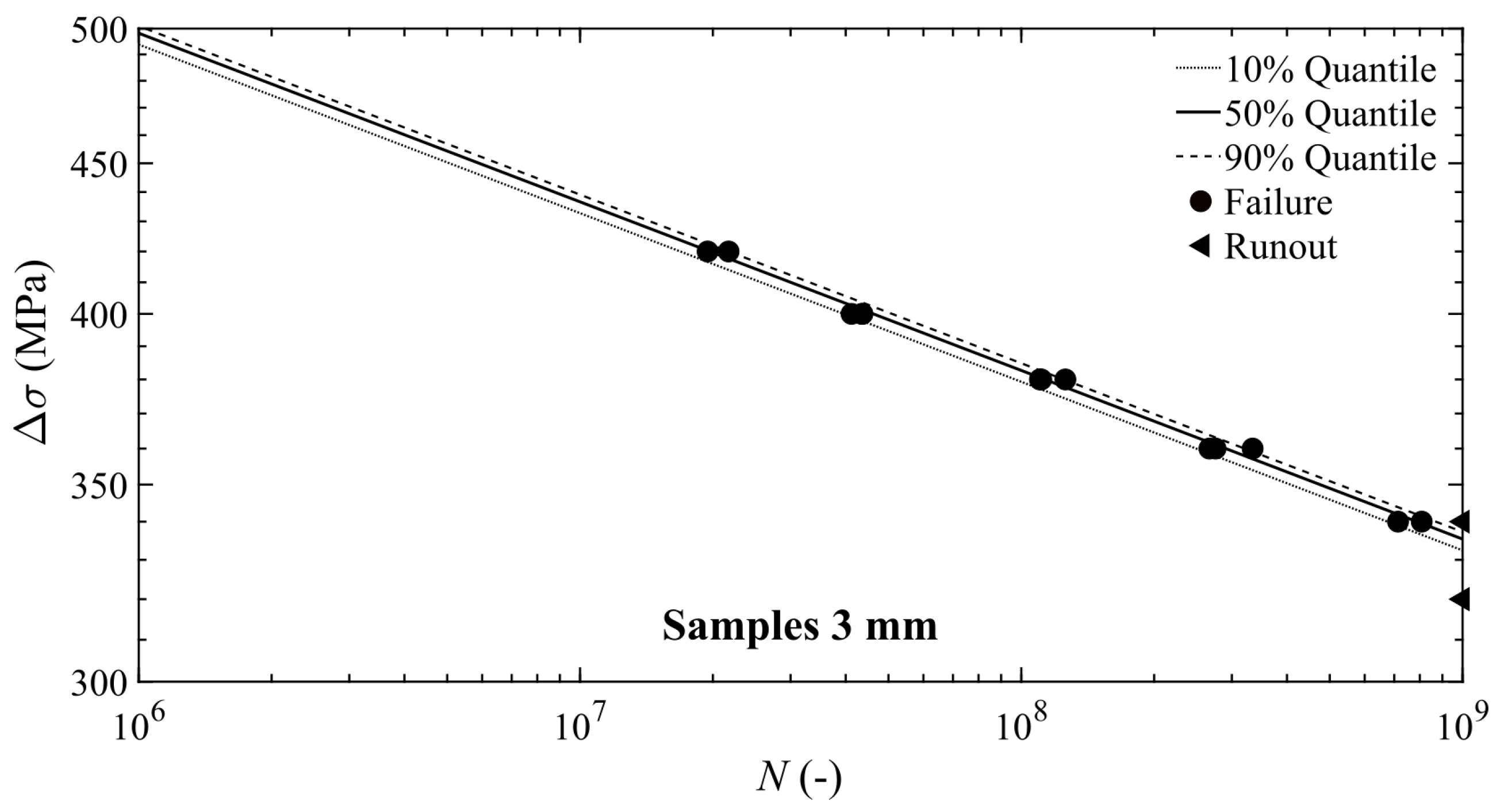
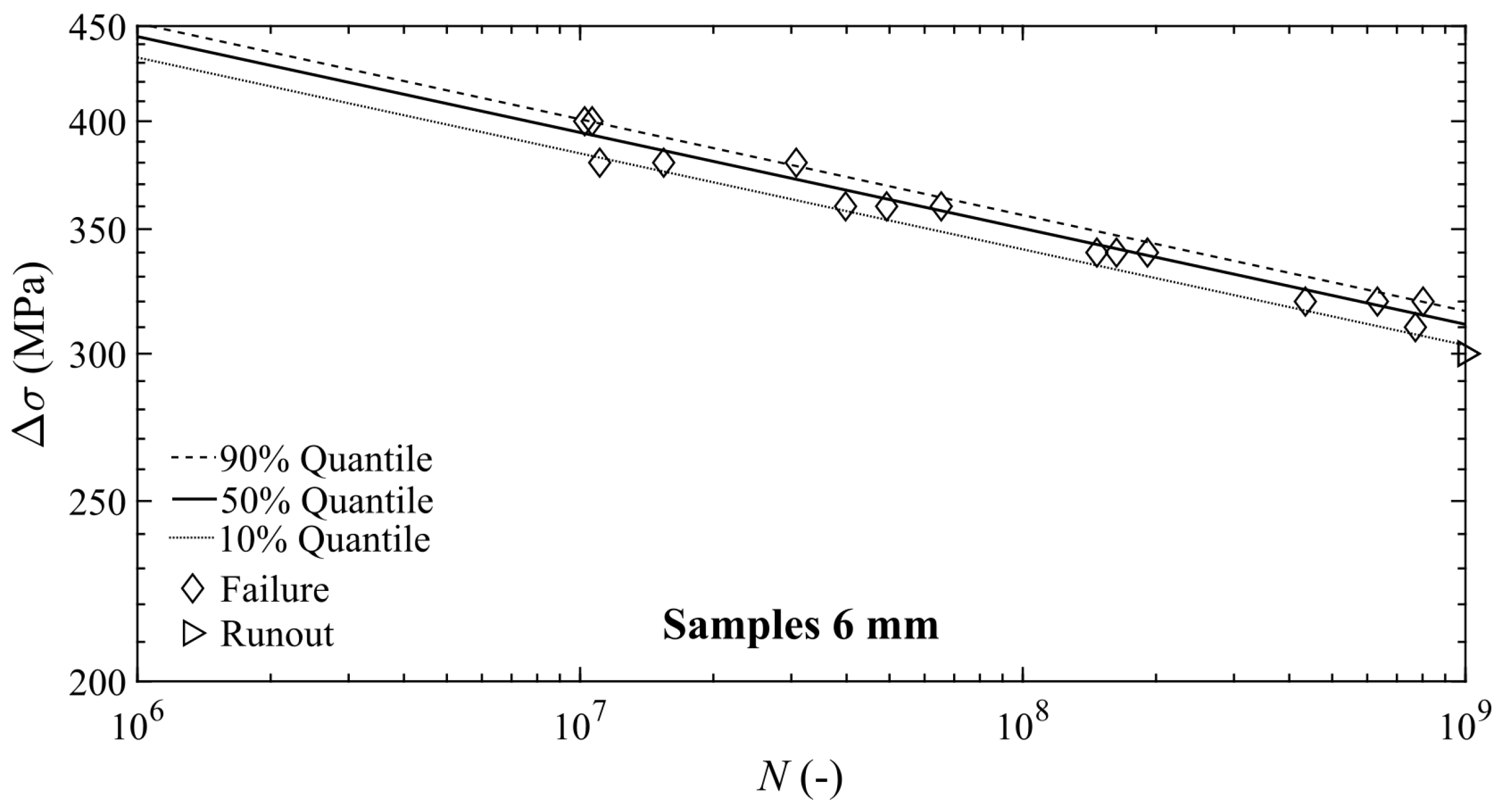
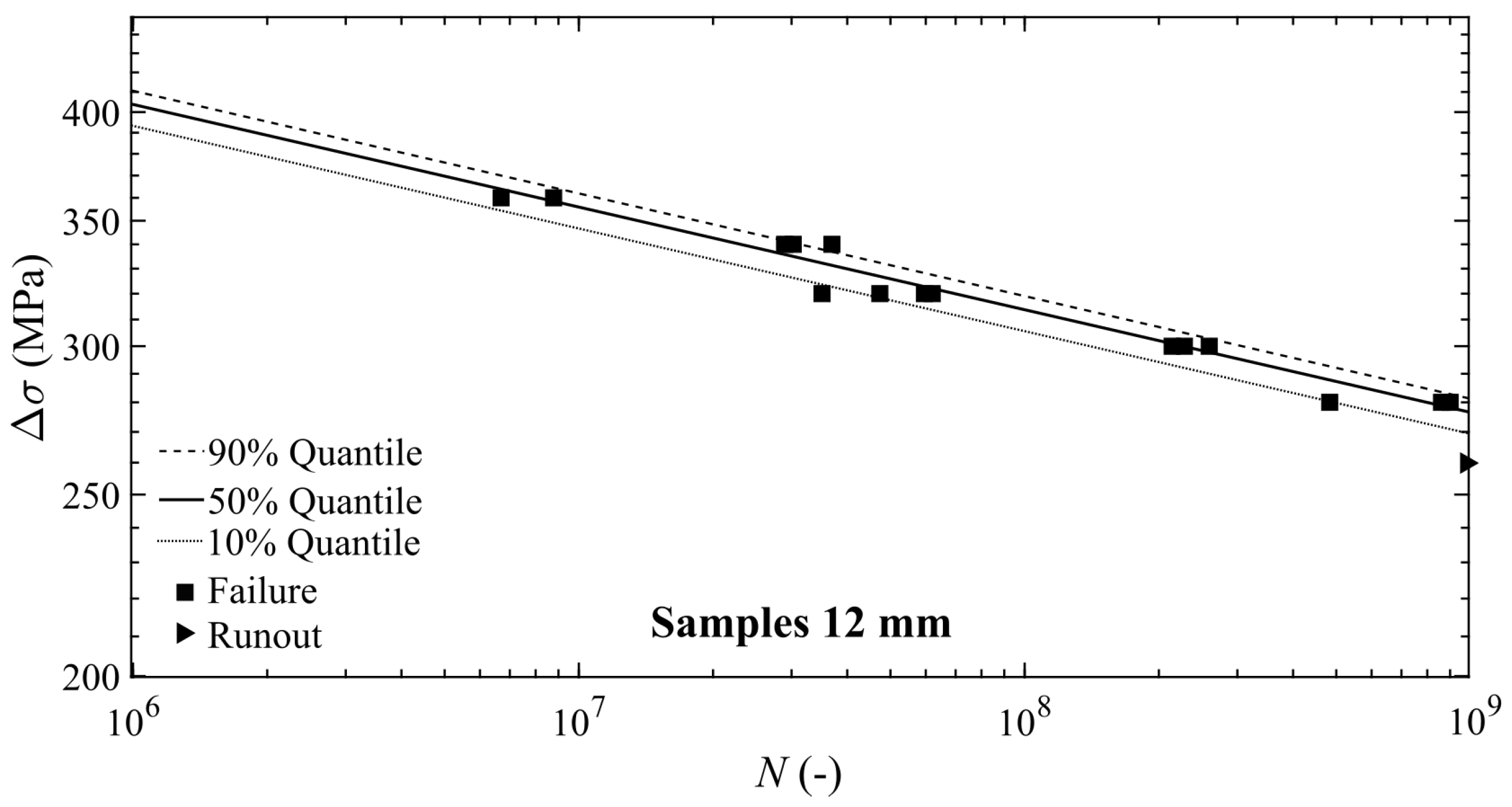
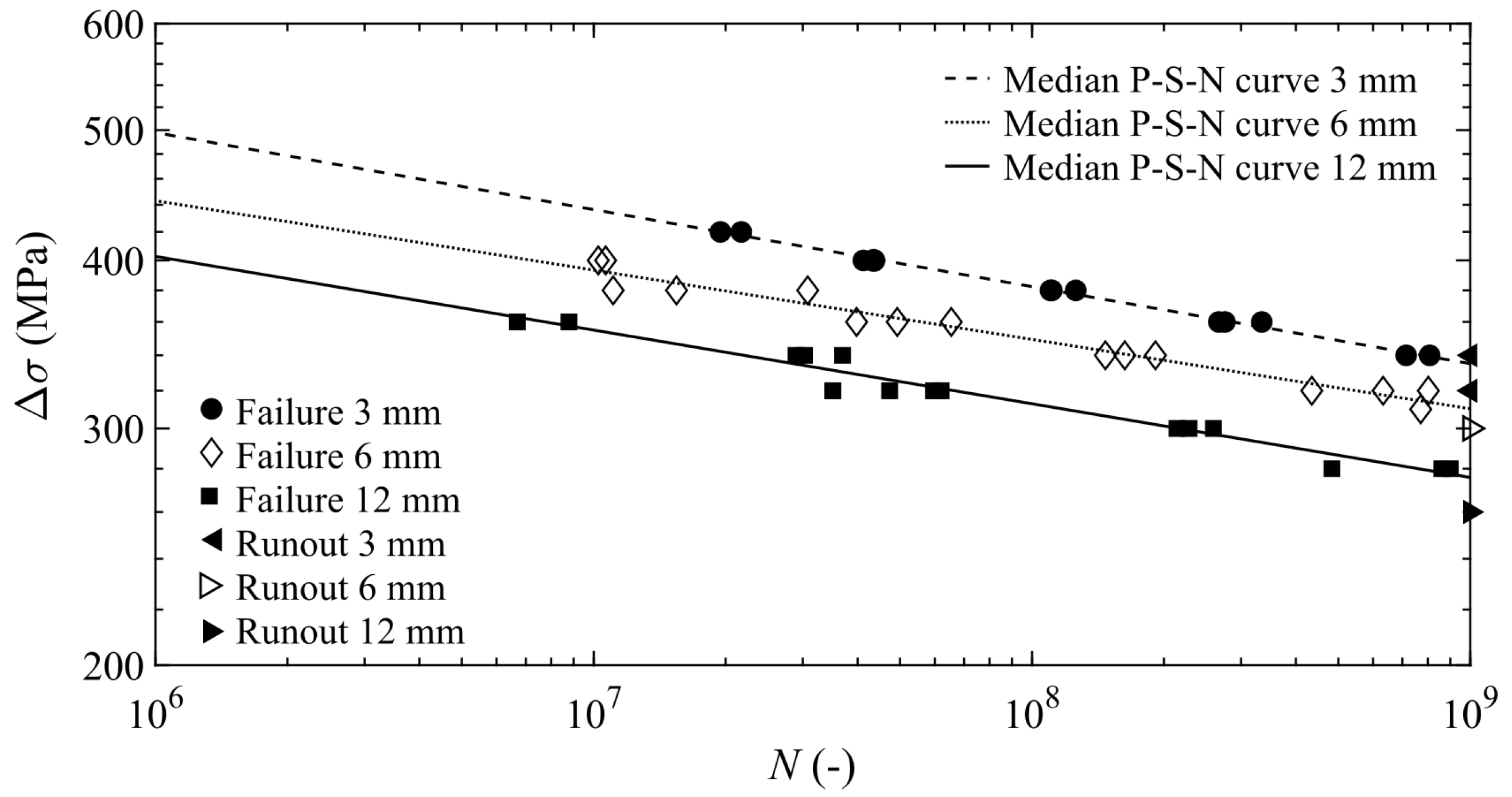
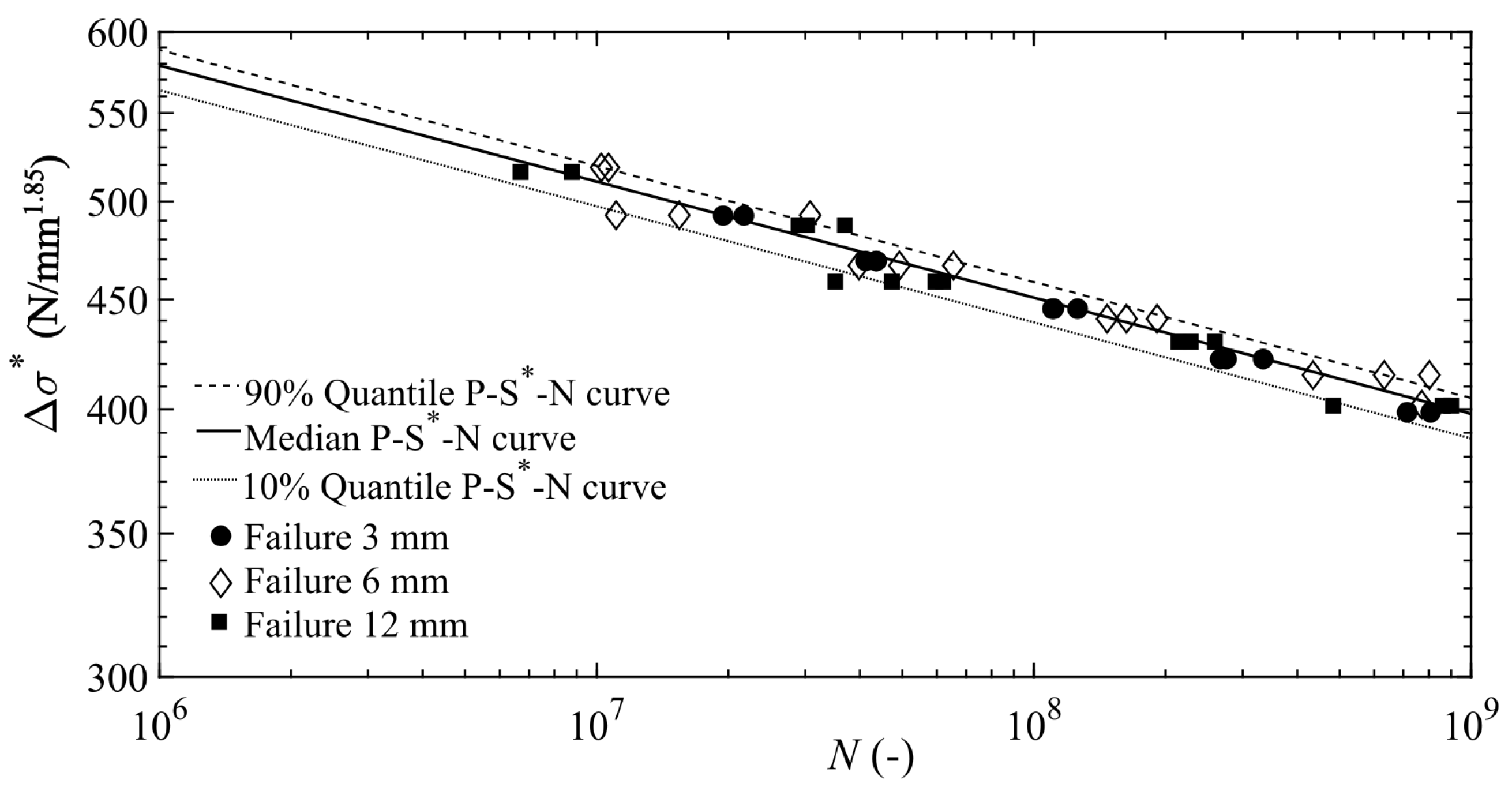
3.2. P-S-N Curves
3.3. Theoretical Interpretation of the Specimen-Size Effect on Fatigue Resistance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| VHCF | Very High Cycle Fatigue |
| SLM | Selective Laser Melting |
| AISI | American Iron and Steel Institute |
| P-S-N | Probabilistic Stress-Life |
| UFTM | Ultrasonic Fatigue Testing Machine |
| SEM | Scanning Electron Microscope |
| CDF | Cumulative Distribution Function |
| MLM | Maximum Likelihood Method |
References
- Stanzl-Tschegg, S.E.; Mayer, H. Fatigue and fatigue crack growth of aluminium alloys at very high numbers of cycles. Int. J. Fatigue 2001, 23, 231–237. [Google Scholar] [CrossRef]
- Sharma, A.; Oh, M.C.; Ahn, B. Recent Advances in Very High Cycle Fatigue Behavior of Metals and Alloys—A Review. Metals 2020, 10, 1200. [Google Scholar] [CrossRef]
- Bathias, C.; Paris, P.C. Gigacycle Fatigue in Mechanical Practice; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar] [CrossRef]
- Mayer, H. Recent Developments in Ultrasonic Fatigue. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 3–29. [Google Scholar] [CrossRef]
- Invernizzi, S.; Montagnoli, F.; Carpinteri, A. Fatigue Assessment of the Collapsed XXth Century Cable-Stayed Polcevera Bridge in Genoa. Procedia Struct. Integr. 2019, 18, 237–244. [Google Scholar] [CrossRef]
- Invernizzi, S.; Montagnoli, F.; Carpinteri, A. The collapse of the Morandi’s bridge: Remarks about fatigue and corrosion. In Proceedings of the IABSE Symposium, Wroclaw 2020: Synergy of Culture and Civil Engineering—History and Challenges, Wroclaw, Poland, 7–9 October 2020; pp. 1040–1047. [Google Scholar]
- Invernizzi, S.; Montagnoli, F.; Carpinteri, A. Corrosion Fatigue Investigation on the Possible Collapse Reasons of Polcevera Bridge in Genoa. Lect. Notes Mech. Eng. 2020, 151–159. [Google Scholar] [CrossRef]
- Stanzl-Tschegg, S. Very High Cycle Fatigue Measuring Techniques. Int. J. Fatigue 2014, 60, 2–17. [Google Scholar] [CrossRef]
- Furuya, Y. Specimen Size Effects on Gigacycle Fatigue Properties of High-Strength Steel under Ultrasonic Fatigue Testing. Scr. Mater. 2008, 58, 1014–1017. [Google Scholar] [CrossRef]
- Furuya, Y. Size Effects in Gigacycle Fatigue of High-Strength Steel under Ultrasonic Fatigue Testing. Procedia Eng. 2010, 2, 485–490. [Google Scholar] [CrossRef]
- Furuya, Y. Notable Size Effects on Very High Cycle Fatigue Properties of High-Strength Steel. Mater. Sci. Eng. A 2011, 528, 5234–5240. [Google Scholar] [CrossRef]
- Murakami, Y.; Kodama, S.; Konuma, S. Quantitative Evaluation of Effects of Non-Metallic Inclusions on Fatigue Strength of High Strength Steels. I: Basic Fatigue Mechanism and Evaluation of Correlation between the Fatigue Fracture Stress and the Size and Location of Non-Metallic Inclusions. Int. J. Fatigue 1989, 11, 291–298. [Google Scholar] [CrossRef]
- Murakami, Y.; Usuki, H. Quantitative Evaluation of Effects of Non-Metallic Inclusions on Fatigue Strength of High Strength Steels. II: Fatigue Limit Evaluation Based on Statistics for Extreme Values of Inclusion Size. Int. J. Fatigue 1989, 11, 299–307. [Google Scholar] [CrossRef]
- Tridello, A.; Paolino, D.S.; Chiandussi, G.; Rossetto, M. Comparison between Dog-Bone and Gaussian Specimens for Size Effect Evaluation in Gigacycle Fatigue. Frat. Integrità Strutt. 2013, 26, 49–56. [Google Scholar] [CrossRef]
- Tridello, A.; Paolino, D.S.; Chiandussi, G.; Rossetto, M. Gaussian Specimens for Gigacycle Fatigue Tests: Evaluation of Temperature Increment. Key Eng. Mater. 2015, 627, 85–88. [Google Scholar] [CrossRef]
- Tridello, A.; Paolino, D.S.; Chiandussi, G.; Rossetto, M. Gaussian Specimens for Gigacycle Fatigue Tests: Damping Effects. Procedia Eng. 2014, 74, 113–118. [Google Scholar] [CrossRef][Green Version]
- Tridello, A.; Paolino, D.S.; Chiandussi, G.; Rossetto, M. VHCF Strength Decrement in Large H13 Steel Specimens Subjected to ESR Process. Procedia Struct. Integr. 2016, 2, 1117–1124. [Google Scholar] [CrossRef]
- Tridello, A.; Paolino, D.S.; Chiandussi, G.; Rossetto, M. VHCF Response of AISI H13 Steel: Assessment of Size Effects through Gaussian Specimens. Procedia Eng. 2015, 109, 121–127. [Google Scholar] [CrossRef]
- Tridello, A.; Paolino, D.S.; Rossetto, M. Ultrasonic VHCF Tests on Very Large Specimens with Risk-Volume up to 5000 mm3. Appl. Sci. 2020, 10, 2210. [Google Scholar] [CrossRef]
- Tridello, A.; Biffi, C.A.; Fiocchi, J.; Bassani, P.; Chiandussi, G.; Rossetto, M.; Tuissi, A.; Paolino, D.S. VHCF Response of As-Built SLM AlSi10Mg Specimens with Large Loaded Volume. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 1918–1928. [Google Scholar] [CrossRef]
- Tridello, A.; Fiocchi, J.; Biffi, C.A.; Chiandussi, G.; Rossetto, M.; Tuissi, A.; Paolino, D.S. VHCF Response of Heat-Treated SLM Ti6Al4V Gaussian Specimens with Large Loaded Volume. Procedia Struct. Integr. 2019, 18, 314–321. [Google Scholar] [CrossRef]
- Xue, H.; Sun, Z.; Zhang, X.; Gao, T.; Li, Z. Very High Cycle Fatigue of a Cast Aluminum Alloy: Size Effect and Crack Initiation. J. Mater. Eng. Perform. 2018, 27, 5406–5416. [Google Scholar] [CrossRef]
- Carpinteri, A.; Montagnoli, F.; Invernizzi, S. Scaling and Fractality in Fatigue Resistance: Specimen-Size Effects on Wöhler’s Curve and Fatigue Limit. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 1869–1879. [Google Scholar] [CrossRef]
- ASTM E1876-15. Standard Test Method for Dynamic Young’s Modulus, Shear Modulus, and Poisson’s Ratio by Impulse Excitation of Vibration; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar] [CrossRef]
- ASTM B557M-15. Standard Test Methods for Tension Testing Wrought and Cast Aluminum- and Magnesium-Alloy Products (Metric); ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar] [CrossRef]
- ASTM E10-15. Standard Test Method for Brinell Hardness of Metallic Materials; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar] [CrossRef]
- Naoe, T.; Xiong, Z.; Futakawa, M. Temperature Measurement for In-Situ Crack Monitoring under High-Frequency Loading. J. Nucl. Mater. 2018, 506, 12–18. [Google Scholar] [CrossRef]
- Furuya, Y. Gigacycle Fatigue Properties of Double-Melted SCM440 Steel and Size Effects. ISIJ Int. 2014, 54, 1436–1442. [Google Scholar] [CrossRef]
- Tridello, A. VHCF Response of Gaussian Specimens Made of High-Strength Steels: Comparison between Unrefined and Refined AISI H13. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 1676–1689. [Google Scholar] [CrossRef]
- Krewerth, D.; Weidner, A.; Biermann, H. Application of in Situ Thermography for Evaluating the High-Cycle and Very High-Cycle Fatigue Behaviour of Cast Aluminium Alloy AlSi7Mg (T6). Ultrasonics 2013, 53, 1441–1449. [Google Scholar] [CrossRef] [PubMed]
- Goglio, L.; Rossetto, M. Comparison of Fatigue Data Using the Maximum Likelihood Method. Eng. Fract. Mech. 2004, 71, 725–736. [Google Scholar] [CrossRef]
- Barbosa, J.F.; Correia, J.A.F.O.; Freire Júnior, R.C.S.; Zhu, S.P.; De Jesus, A.M.P. Probabilistic S-N Fields Based on Statistical Distributions Applied to Metallic and Composite Materials: State of the Art. Adv. Mech. Eng. 2019, 11, 1–22. [Google Scholar] [CrossRef]
- Freire Júnior, R.C.S.; Belísio, A.S. Probabilistic S-N Curves Using Exponential and Power Laws Equations. Compos. Part B Eng. 2014, 56, 582–590. [Google Scholar] [CrossRef]
- Pedrosa, B.; Correia, J.A.F.O.; Rebelo, C.A.S.; Veljkovic, M. Reliability of Fatigue Strength Curves for Riveted Connections Using Normal and Weibull Distribution Functions. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2020, 6, 1–8. [Google Scholar] [CrossRef]
- Barbosa, J.F.; Carlos Silverio Freire Júnior, R.; Correia, J.A.F.O.; De Jesus, A.M.P.; Calçada, R.A.B. Analysis of the Fatigue Life Estimators of the Materials Using Small Samples. J. Strain Anal. Eng. Des. 2018, 53, 699–710. [Google Scholar] [CrossRef]
- Carpinteri, A. Scaling Laws and Renormalization Groups for Strength and Toughness of Disordered Materials. Int. J. Solids Struct. 1994, 31, 291–302. [Google Scholar] [CrossRef]
- Carpinteri, A. Fractal Nature of Material Microstructure and Size Effects on Apparent Mechanical Properties. Mech. Mater. 1994, 18, 89–101. [Google Scholar] [CrossRef]
- Carpinteri, A.; Chiaia, B.; Cornetti, P. A Scale-Invariant Cohesive Crack Model for Quasi-Brittle Materials. Eng. Fract. Mech. 2002, 69, 207–217. [Google Scholar] [CrossRef]
- Carpinteri, A.; Chiaia, B.; Cornetti, P. On the Mechanics of Quasi-Brittle Materials with a Fractal Microstructure. Eng. Fract. Mech. 2003, 70, 2321–2349. [Google Scholar] [CrossRef]
- Carpinteri, A.; Ferro, G.; Invernizzi, S. The Nominal Tensile Strength of Disordered Materials: A Statistical Fracture Mechanics Approach. Eng. Fract. Mech. 1997, 58, 421–435. [Google Scholar] [CrossRef]
- Carpinteri, A.; Chiaia, B.; Ferro, G. Size Effects on Nominal Tensile Strength of Concrete Structures: Multifractality of Material Ligaments and Dimensional Transition from Order to Disorder. Mater. Struct. 1995, 28, 311–317. [Google Scholar] [CrossRef]
- Carpinteri, A.; Chiaia, B. Power Scaling Laws and Dimensional Transitions in Solid Mechanics. Chaos Solitons Fractals 1996, 7, 1343–1364. [Google Scholar] [CrossRef]
- Carpinteri, A.; Montagnoli, F. Scaling and Fractality in Fatigue Crack Growth: Implications to Paris’ Law and Wöhler’s Curve. Procedia Struct. Integr. 2019, 14, 957–963. [Google Scholar] [CrossRef]
- Carpinteri, A.; Spagnoli, A.; Vantadori, S. Size Effect in S-N Curves: A Fractal Approach to Finite-Life Fatigue Strength. Int. J. Fatigue 2009, 31, 927–933. [Google Scholar] [CrossRef]
- Montagnoli, F.; Invernizzi, S.; Carpinteri, A. Fractality and Size Effect in Fatigue Damage Accumulation: Comparison between Paris and Wöhler Perspectives. Lect. Notes Mech. Eng. 2020, 188–196. [Google Scholar] [CrossRef]




| Element | Si | Mg | Mn | Cu | Fe | Cr | Zi | Ti |
|---|---|---|---|---|---|---|---|---|
| Min% | 0.70 | 0.60 | 0.40 | |||||
| Max% | 1.30 | 1.20 | 1.00 | 0.10 | 0.50 | 0.25 | 0.20 | 0.10 |
| Diameter of Bar | (kg/m) | (GPa) | (MPa) | (MPa) | (%) | Brinnel Hardness (HB) |
|---|---|---|---|---|---|---|
| 20 mm | 2713 | 72.3 | – | – | – | 91 |
| 30 mm | 2700 | 70.1 | 357 | 375 | 11 | 91 |
| Specimen | (MPa/m) | (Hz) | (–) | (mm) |
|---|---|---|---|---|
| 3 mm | 7.474 | 20,213 | 1.021 | 42 |
| 6 mm | 4.233 | 20,047 | 1.025 | 301 |
| 12 mm | 3.350 | 19,947 | 1.046 | 1731 |
| Diameter | ||
|---|---|---|
| 3 mm | 12.2091 | 1.0423 |
| 6 mm | 3.7579 | 1.1596 |
| 12 mm | 3.9214 | 1.1508 |
| GoF Statistics Tests | A-D | C-vM | K-S | |
|---|---|---|---|---|
| Actual values | 7.792 | 0.701 | 0.143 | 0.242 |
| Critical values | 7.815 | 0.728 | 0.214 | 0.316 |
| GoF Statistics Tests | A-D | C-vM | K-S | |
|---|---|---|---|---|
| Actual values | 7.000 | 0.475 | 0.077 | 0.168 |
| Critical values | 7.815 | 0.731 | 0.215 | 0.331 |
| GoF Statistics Tests | A-D | C-vM | K-S | |
|---|---|---|---|---|
| Actual values | 0.600 | 0.156 | 0.019 | 0.107 |
| Critical values | 7.815 | 0.731 | 0.215 | 0.338 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Invernizzi, S.; Montagnoli, F.; Carpinteri, A. Experimental Evidence of Specimen-Size Effects on EN-AW6082 Aluminum Alloy in VHCF Regime. Appl. Sci. 2021, 11, 4272. https://doi.org/10.3390/app11094272
Invernizzi S, Montagnoli F, Carpinteri A. Experimental Evidence of Specimen-Size Effects on EN-AW6082 Aluminum Alloy in VHCF Regime. Applied Sciences. 2021; 11(9):4272. https://doi.org/10.3390/app11094272
Chicago/Turabian StyleInvernizzi, Stefano, Francesco Montagnoli, and Alberto Carpinteri. 2021. "Experimental Evidence of Specimen-Size Effects on EN-AW6082 Aluminum Alloy in VHCF Regime" Applied Sciences 11, no. 9: 4272. https://doi.org/10.3390/app11094272
APA StyleInvernizzi, S., Montagnoli, F., & Carpinteri, A. (2021). Experimental Evidence of Specimen-Size Effects on EN-AW6082 Aluminum Alloy in VHCF Regime. Applied Sciences, 11(9), 4272. https://doi.org/10.3390/app11094272







