Machine Learning Model of Dimensionless Numbers to Predict Flow Patterns and Droplet Characteristics for Two-Phase Digital Flows
Abstract
1. Introduction
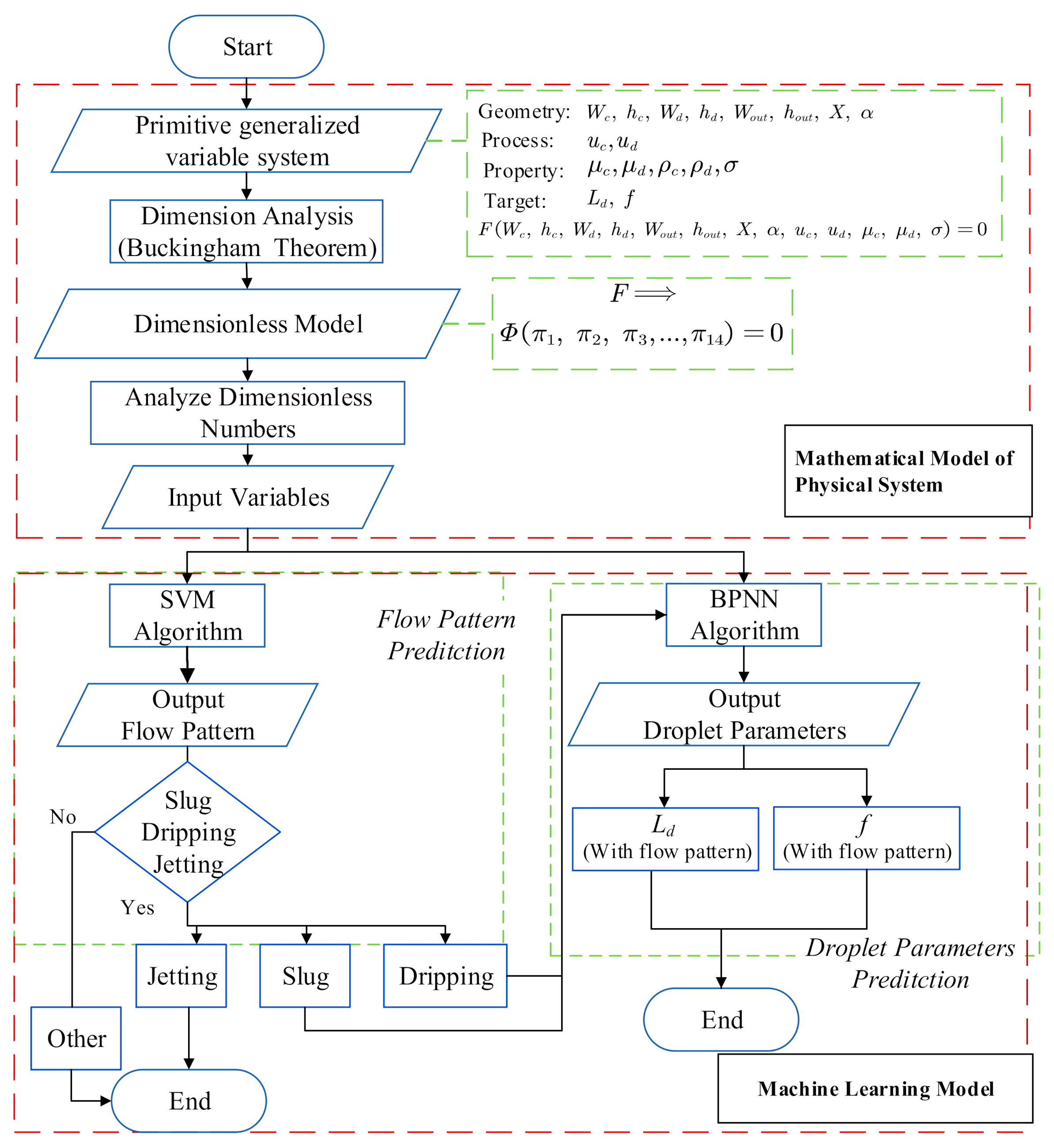
2. Methods and Data
2.1. Generalized Variable System to Diverse Geometry Configurations
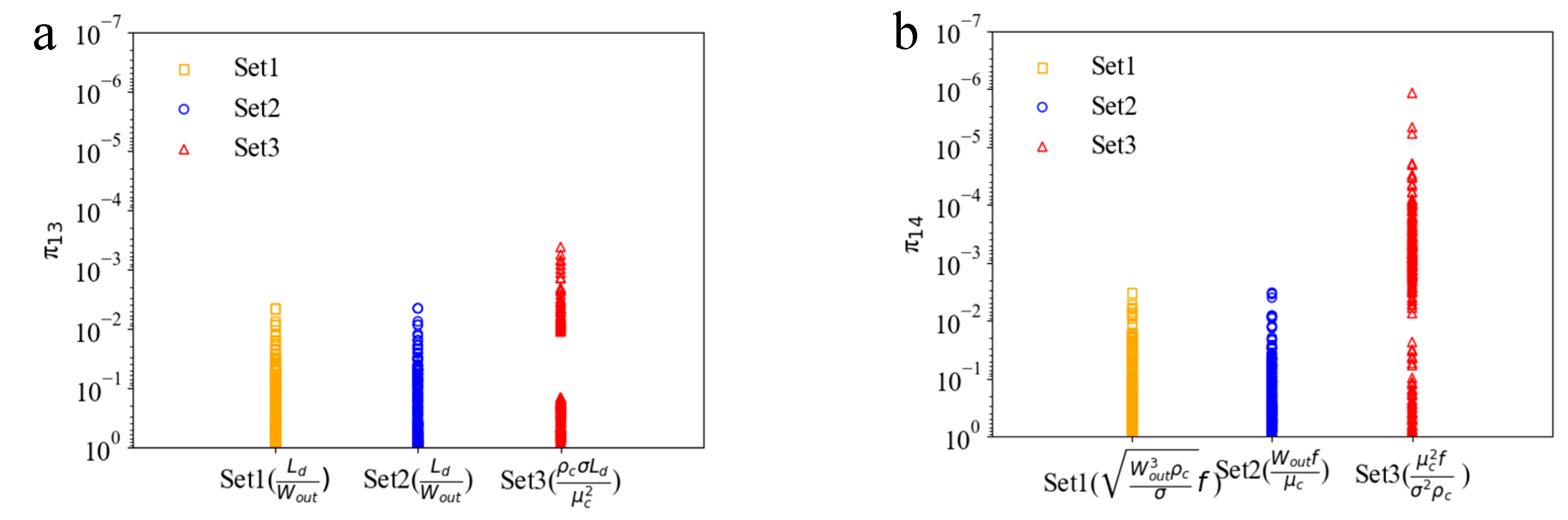
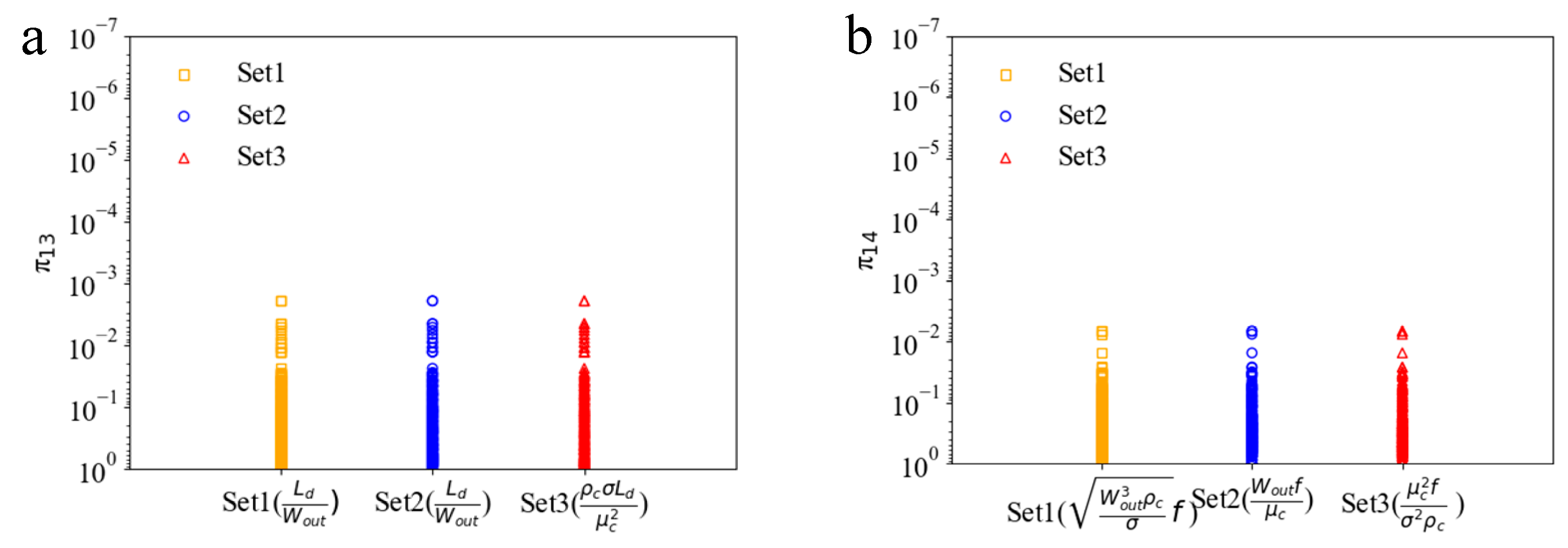
2.2. Input Variables Using Dimensionless Numbers or Primitive Parameters
3. Results and Discussion
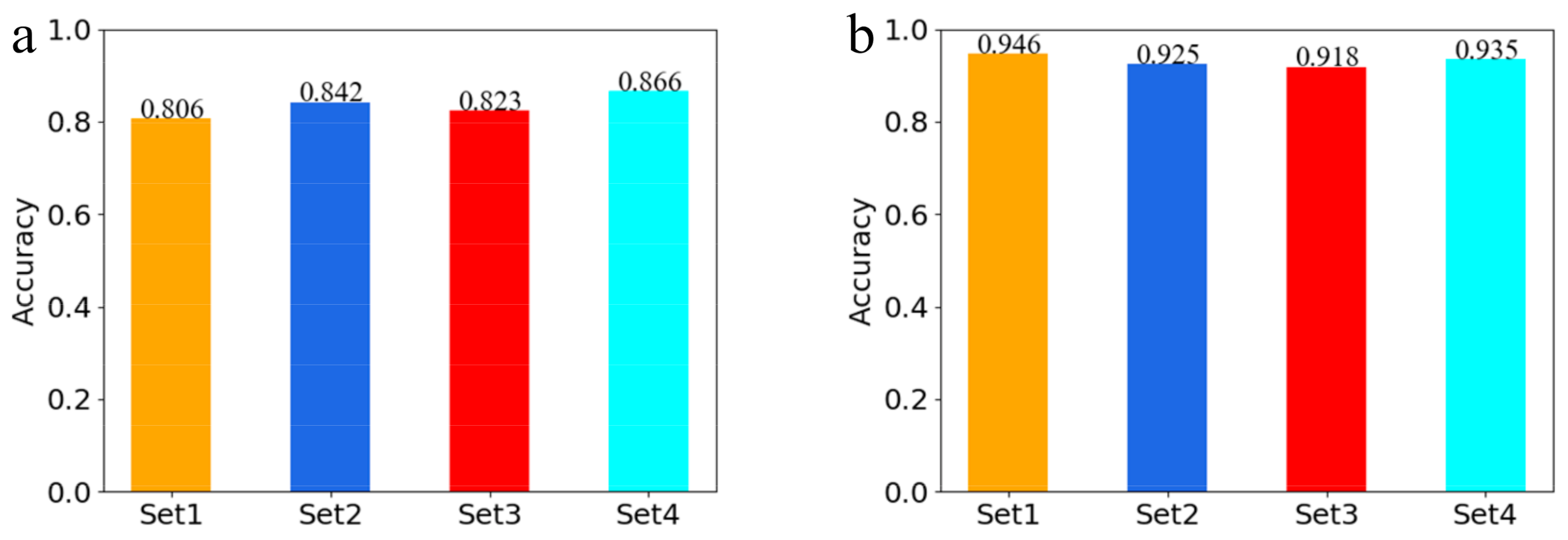
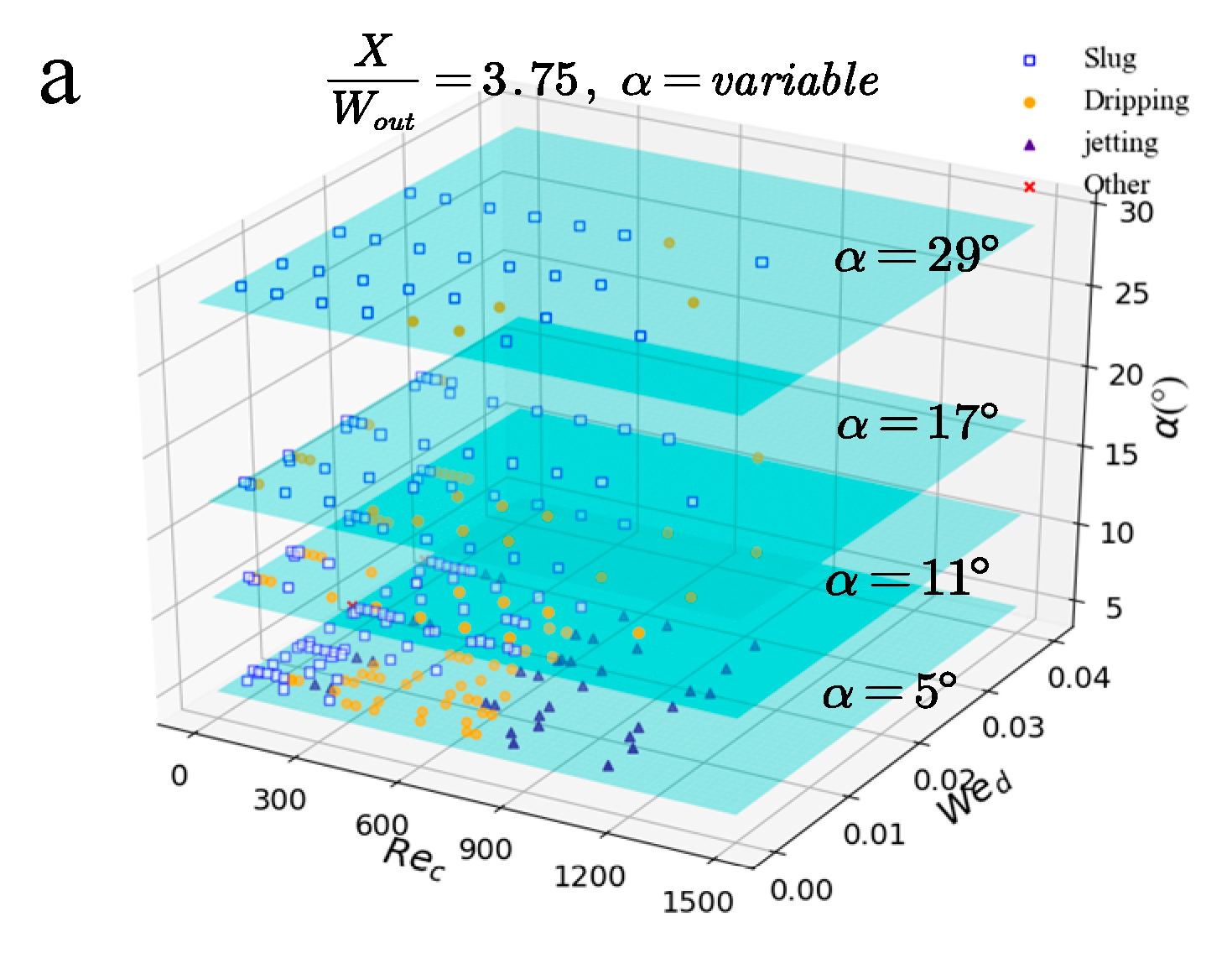
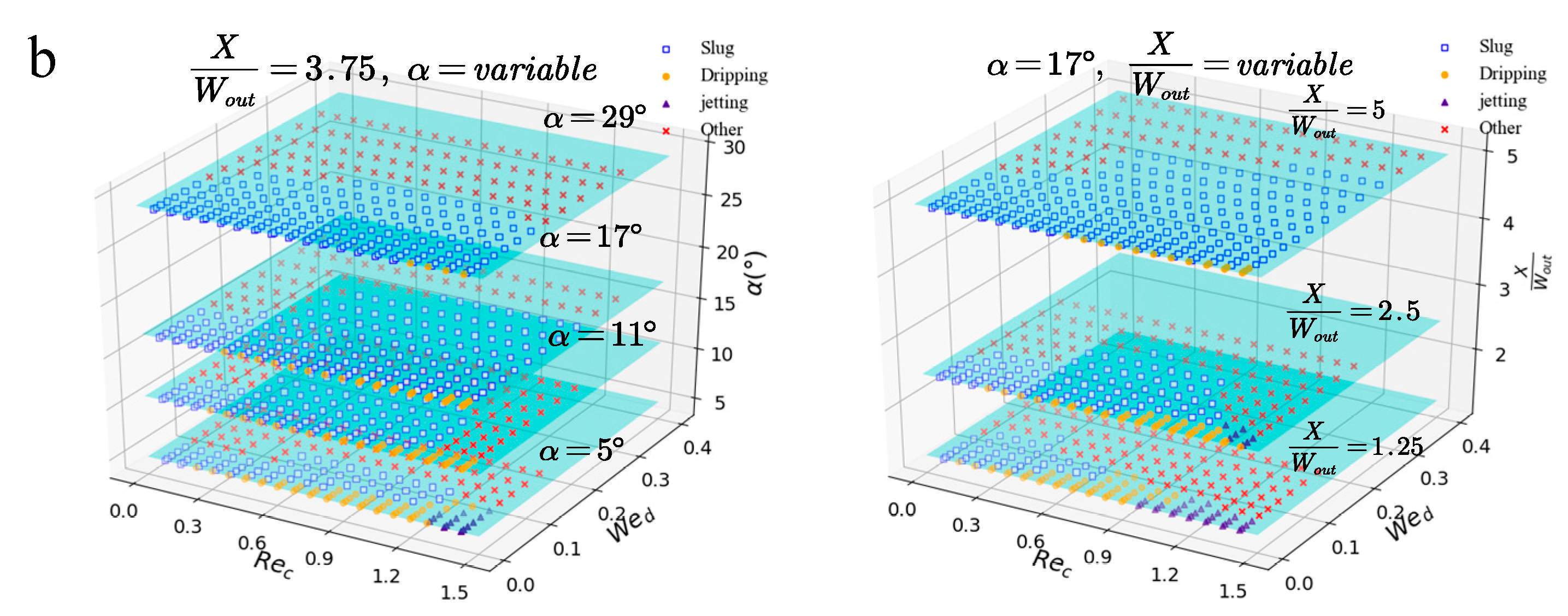
3.1. Recognition of Flow Patterns
3.2. Prediction of Droplet Characteristics
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Wc | the width of the continuous phase tube (μm) | u | the superficial velocity (m/s) |
| hc | the height of the continuous phase tube (μm) | Ld | the length of the droplet (μm) |
| dc | the diameter of the continuous phase tube (μm) | f | the frequency of the droplet (Hz) |
| Wd | the width of the dispersed phase tube (μm) | Greek characters | |
| hd | the height of the dispersed phase tube (μm) | σ | the surface tension (N/m) |
| dd | the diameter of the dispersed phase tube (μm) | ρ | the density (kg/m3) |
| Wout | the width of the outlet tube (μm) | μ | the dynamic viscosity (Pa•s) |
| hout | the height of the outlet tube (μm) | Subscripts | |
| dout | the diameter of the outlet tube (μm) | c | the continuous phase |
| X | the displacement of the injection nozzle (μm) | d | the dispersed phase |
| α | the tapered angle (rad) | out | the outlet tube |
References
- Sheidaei, Z.; Akbarzadeh, P.; Kashaninejad, N. Advances in numerical approaches for microfluidic cell analysis platforms. J. Sci. Adv. Mater. Dev. 2020, 5, 295–307. [Google Scholar] [CrossRef]
- Hongzhou, C.; Shuping, G.; Wenju, W.; Li, L.; Lulu, W.; Linjun, D.; Jingmin, L.; Xiaoli, R.; Li, B. Lab-on-a-chip technologies for genodermatoses: Recent progress and future perspectives. J. Dermatol. Sci. 2017, 85, 71–76. [Google Scholar] [CrossRef]
- Batool, S.; Nawaz, M. Investigation of thermal enhancement in non-Newtonian fluid with hybrid micro-structures in an enclosure. Int. Commun. Heat Mass Transf. 2020, 117. [Google Scholar] [CrossRef]
- Keniar, K.; El Fil, B.; Garimella, S. A critical review of analytical and numerical models of condensation in microchannels. Int. J. Refrig. 2020, 120, 314–330. [Google Scholar] [CrossRef]
- Roshani, M.; Sattari, M.A.; Muhammad Ali, P.J.; Roshani, G.H.; Nazemi, B.; Corniani, E.; Nazemi, E. Application of GMDH neural network technique to improve measuring precision of a simplified photon attenuation based two-phase flowmeter. Flow Measur. Instrum. 2020, 75, 101804. [Google Scholar] [CrossRef]
- Roshani, M.; Phan, G.; Hossein Roshani, G.; Hanus, R.; Nazemi, B.; Corniani, E.; Nazemi, E. Combination of X-ray tube and GMDH neural network as a nondestructive and potential technique for measuring characteristics of gas-oil–water three phase flows. Measurement 2021, 168, 108427. [Google Scholar] [CrossRef]
- Wu, Z.; Sundén, B. Liquid-liquid two-phase flow patterns in ultra-shallow straight and serpentine microchannels. Heat Mass Transf. 2018, 55, 1095–1108. [Google Scholar] [CrossRef]
- Erb, R.M.; Obrist, D.; Chen, P.W.; Studer, J.; Studart, A.R. Predicting sizes of droplets made by microfluidic flow-induced dripping. Soft Matter 2011, 7, 8757–8761. [Google Scholar] [CrossRef]
- Gu, Y.; Kojima, H.; Miki, N. Theoretical analysis of 3D emulsion droplet generation by a device using coaxial glass tubes. Sensors Actuators A Phys. 2011, 169, 326–332. [Google Scholar] [CrossRef]
- Lian, J.; Luo, X.; Huang, X.; Wang, Y.; Xu, Z.; Ruan, X. Investigation of microfluidic co-flow effects on step emulsification: Interfacial tension and flow velocities. Colloids Surfaces A Physicochem. Eng. Aspects 2019, 568, 381–390. [Google Scholar] [CrossRef]
- Du, J.; Ibaseta, N.; Guichardon, P. Generation of an O/W emulsion in a flow-focusing microchip: Importance of wetting conditions and of dynamic interfacial tension. Chem. Eng. Res. Des. 2020, 159, 615–627. [Google Scholar] [CrossRef]
- Rajiv, K.H.; Singh Sokhal, G. Effect of geometries and nanofluids on heat transfer and pressure drop in microchannels: A review. Mater. Today Proc. 2020, 28, 1841–1846. [Google Scholar] [CrossRef]
- Roshani, M.; Phan, G.T.T.; Jammal Muhammad Ali, P.; Hossein Roshani, G.; Hanus, R.; Duong, T.; Corniani, E.; Nazemi, E.; Mostafa Kalmoun, E. Evaluation of flow pattern recognition and void fraction measurement in two phase flow independent of oil pipeline’s scale layer thickness. Alex. Eng. J. 2021, 60, 1955–1966. [Google Scholar] [CrossRef]
- Timung, S.; Mandal, T.K. Prediction of flow pattern of gas–liquid flow through circular microchannel using probabilistic neural network. Appl. Soft Comput. 2013, 13, 1674–1685. [Google Scholar] [CrossRef]
- Nandagopal, M.S.G.; Abraham, E.; Selvaraju, N. Advanced neural network prediction and system identification of liquid-liquid flow patterns in circular microchannels with varying angle of confluence. Chem. Eng. J. 2017, 309, 850–865. [Google Scholar] [CrossRef]
- Al-Naser, M.; Elshafei, M.; Al-Sarkhi, A. Artificial neural network application for multiphase flow patterns detection: A new approach. J. Petrol. Sci. Eng. 2016, 145, 548–564. [Google Scholar] [CrossRef]
- Lin, Z.; Liu, X.; Lao, L.; Liu, H. Prediction of two-phase flow patterns in upward inclined pipes via deep learning. Energy 2020, 210, 118541. [Google Scholar] [CrossRef]
- Zhang, Y.; Azman, A.N.; Xu, K.-W.; Kang, C.; Kim, H.-B. Two-phase flow regime identification based on the liquid-phase velocity information and machine learning. Exp. Fluids 2020, 61, 62–72. [Google Scholar] [CrossRef]
- Buckingham, E. On physically similar systems; illustrations of the use of dimensional equations. Phys. Rev. 1914, 4, 345–376. [Google Scholar] [CrossRef]
- Kumbhar, S.G.; Sudhagar, P.E.; Desavale, R.G. Theoretical and experimental studies to predict vibration responses of defects in spherical roller bearings using dimension theory. Measurement 2020, 161, 107846. [Google Scholar] [CrossRef]
- Tang, R.C.O.; Jang, J.-H.; Lan, T.-H.; Wu, J.-C.; Yan, W.-M.; Sangeetha, T.; Wang, C.-T.; Ong, H.C.; Ong, Z.C. Review on design factors of microbial fuel cells using Buckingham’s Pi Theorem. Renew. Sustain. Energy Rev. 2020, 130. [Google Scholar] [CrossRef]
- Cramer, C.; Fischer, P.; Windhab, E.J. Drop formation in a co-flowing ambient fluid. Chem. Eng. Sci. 2004, 59, 3045–3058. [Google Scholar] [CrossRef]
- Hua, J.; Zhang, B.; Lou, J. Numerical simulation of microdroplet formation in coflowing immiscible liquids. AIChE J. 2007, 53, 2534–2548. [Google Scholar] [CrossRef]
- Chaves, I.L.; Duarte, L.C.; Coltro, W.K.T.; Santos, D.A. Droplet length and generation rate investigation inside microfluidic devices by means of CFD simulations and experiments. Chem. Eng. Res. Des. 2020, 161, 260–270. [Google Scholar] [CrossRef]
- Huang, D.; Wang, K.; Wang, Y.; Sun, H.; Liang, X.; Meng, T. Precise control for the size of droplet in T-junction microfluidic based on iterative learning method. J. Frankl. Inst. 2020, 357, 5302–5316. [Google Scholar] [CrossRef]
- Bai, L.; Zhao, S.; Fu, Y.; Cheng, Y. Experimental study of mass transfer in water/ionic liquid microdroplet systems using micro-LIF technique. Chem. Eng. J. 2016, 298, 281–290. [Google Scholar] [CrossRef]
- Wang, Z.L. Speed up bubbling in a tapered co-flow geometry. Chem. Eng. J. 2015, 263, 346–355. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, C.; Liu, X.; Yi, C.; Wang, Z.L. Experimental studies of microchannel tapering on droplet forming acceleration in liquid paraffin/ethanol coaxial flows. Materials 2020, 13, 944. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Binkhonain, M.; Zhao, L. A review of machine learning algorithms for identification and classification of non-functional requirements. Expert Syst. Appl. X 2019, 1, 100001. [Google Scholar]
- Vijayanand, M.; Varahamoorthi, R.; Kumaradhas, P.; Sivamani, S.; Kulkarni, M.V. Regression-BPNN modelling of surfactant concentration effects in electroless Ni B coating and optimization using genetic algorithm. Surface Coat. Technol. 2021, 409, 126878. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, W.; Luo, Z.; Sun, X.; Li, Z.; Lin, L. Ultrasonic characterization of thermal barrier coatings porosity through BP neural network optimizing Gaussian process regression algorithm. Ultrasonics 2020, 100, 105981. [Google Scholar] [CrossRef]
- Ni, Y.Q.; Li, M. Wind pressure data reconstruction using neural network techniques: A comparison between BPNN and GRNN. Measurement 2016, 88, 468–476. [Google Scholar] [CrossRef]
- Akbar, M.K.; Plummer, D.A.; Ghiaasiaan, S.M. On gas–liquid two-phase flow regimes in microchannels. Int. J. Multiphase Flow 2003, 29, 855–865. [Google Scholar] [CrossRef]
- Laborie, S.; Cabassud, C.; Durandbourlier, L.; Laine, J.M. Characterisation of gas-liquid two-phase flow inside capillaries. Chem. Eng. Sci. 1999, 54, 5723–5735. [Google Scholar] [CrossRef]
- Hernández-Cid, D.; Pérez-González, V.H.; Gallo-Villanueva, R.C.; González-Valdez, J.; Mata-Gómez, M.A. Modeling droplet formation in microfluidic flow-focusing devices using the two-phases level set method. Mater. Today Proc. 2020. [Google Scholar] [CrossRef]
- Chaichana, C.; Thiangchanta, S. The heat load modelling for an air-conditioned room using Buckingham-Pi theorem. Energy Rep. 2020, 6, 656–661. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, G.; Yuan, Q. Liquid-liquid two-phase flow patterns in a rectangular microchannel. AIChE J. 2006, 52, 4052–4060. [Google Scholar] [CrossRef]
- Liu, X.; Wu, L.; Zhao, Y.; Chen, Y. Study of compound drop formation in axisymmetric microfluidic devices with different geometries. Colloids Surfaces A Physicochem. Eng. Aspects 2017, 533, 87–98. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, Q.; Zhu, C.; Fu, T.; Ma, Y.; Li, H.Z. Formation of droplet and “string of sausages” for water-ionic liquid ([BMIM][PF6]) two-phase flow in a flow-focusing device. Chem. Eng. Process. Process Intensif. 2018, 125, 8–17. [Google Scholar] [CrossRef]

| Citation | Type | Geometry Structure | Inlet Parameters | Outlet Parameters | Cross-Section | Normalized Parameters | |
|---|---|---|---|---|---|---|---|
| a | Cramer et al. [22] Hua et al. [23] | co-flow |  | dc, dd | dout | circular | 3 |
| b | Chaves et al. [24] Huang et al. [25] | Y/T-junction | 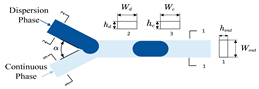 | Wc, hc, Wd, hd, α | Wout, hout | rectangle | 7 |
| c | Bai et al. [26] | cross-junction | 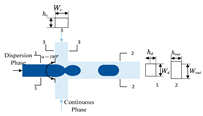 | Wd, hd, Wc, hc, α=180° | Wout, hout | rectangle | 7 |
| d | Our team [27,28] | tapered co-flow | 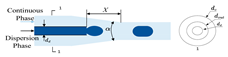 | X, α, dc, dd | dout | circular | 5 |
 | Wc, hc, Wd, hd, X, α | Wout, hout | rectangle | 8 |
| π | Set1 | Set2 | Set3 | |
|---|---|---|---|---|
| Independent Variables | π1 | |||
| π2 | ||||
| π3 | ||||
| π4 | ||||
| π5 | ||||
| π6 | ||||
| π7 | ||||
| π8 | ||||
| π9 | ||||
| π10 | ||||
| π11 | ||||
| π12 | ||||
| Target Variables | π13 | |||
| π14 |
| Dimensionless Numbers | Primitive Parameters | |||
|---|---|---|---|---|
| Equation | ||||
| Set | Set1 | Set2 | Set3 | Set4 |
| Input variables (Experiment 1) | π7, π9, π11, π12 (4 Dimensions) | π7, π10, π12 (3 Dimensions) | π3, π4, π5, π6 (4 Dimensions) | α, uc, ud, ρc, μc, σ (6 Dimensions) |
| Input variables (Experiment 2) | π6, π7, π11, π12 (4 Dimensions) | π6, π7, π10, π12 (4 Dimensions) | π3, π4, π5, π6 (4 Dimensions) | X, α, uc, ud (4 Dimensions) |
| Slug Pattern | Dripping Pattern | |
|---|---|---|
| Set1 |  |  |
| Set2 |  | 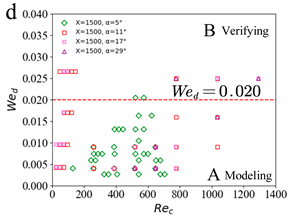 |
| Set3 | 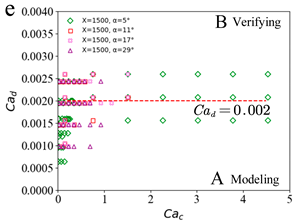 | 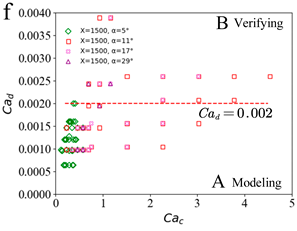 |
| Slug Pattern | Dripping Pattern | |
|---|---|---|
| Set1 | 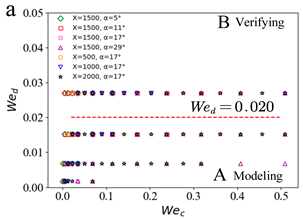 |  |
| Set2 | 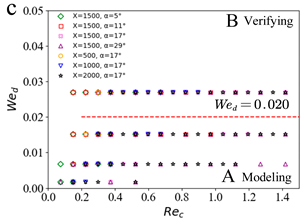 | 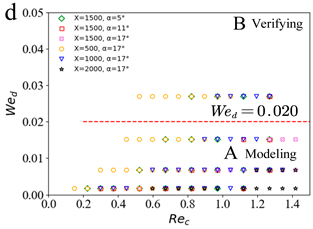 |
| Set3 | 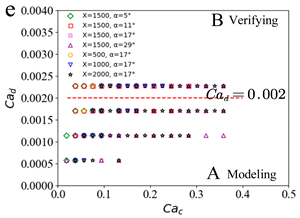 |  |
| Slug Pattern | Dripping Pattern | |
|---|---|---|
| Exp. 1 | 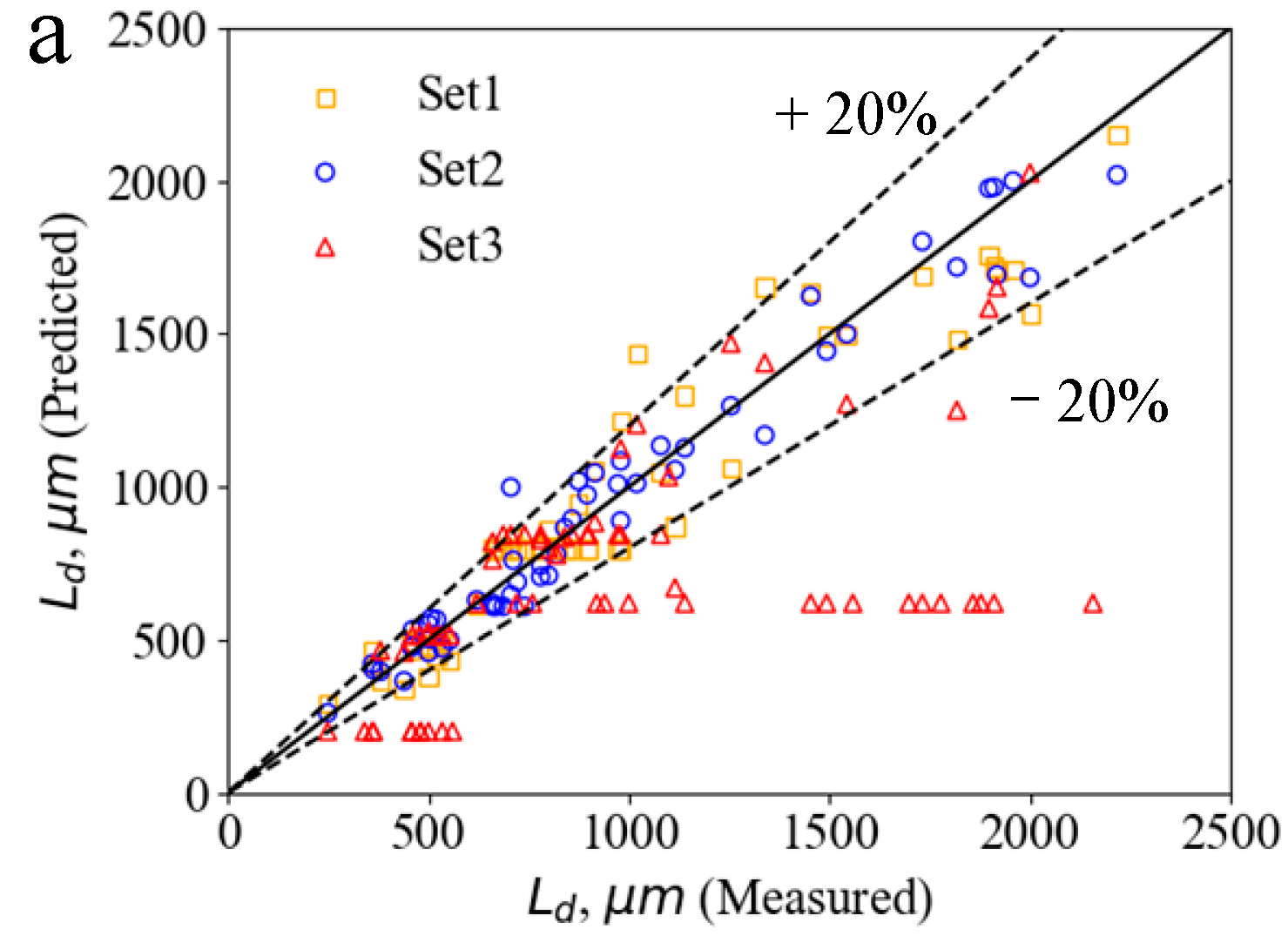 | 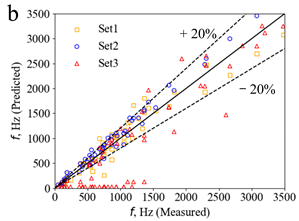 |
| Exp. 2 | 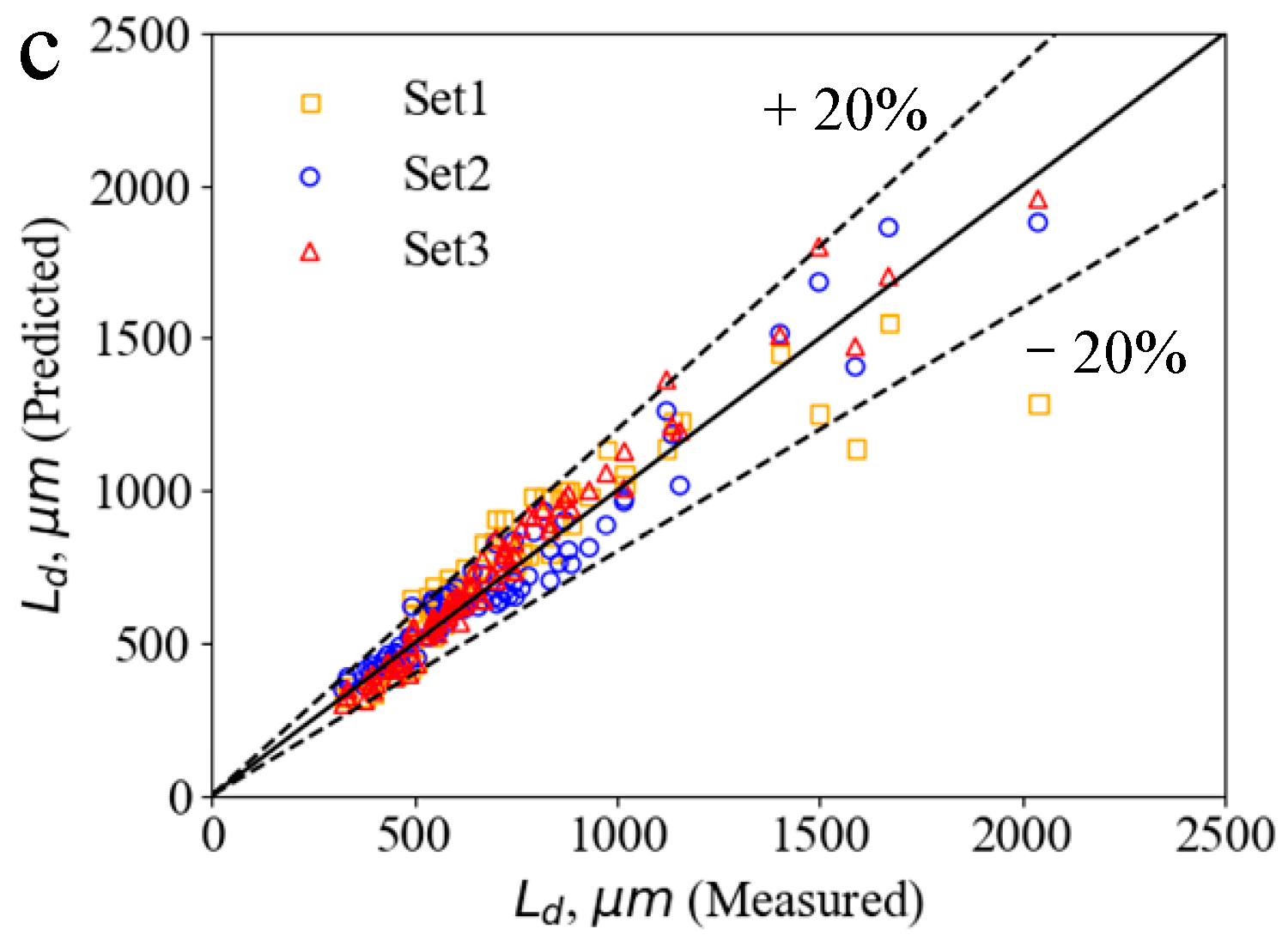 | 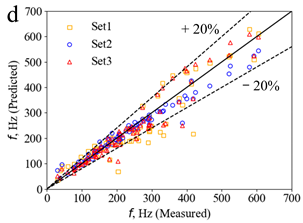 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Zhang, S.; Zhang, J.; Wang, Z. Machine Learning Model of Dimensionless Numbers to Predict Flow Patterns and Droplet Characteristics for Two-Phase Digital Flows. Appl. Sci. 2021, 11, 4251. https://doi.org/10.3390/app11094251
Zhang J, Zhang S, Zhang J, Wang Z. Machine Learning Model of Dimensionless Numbers to Predict Flow Patterns and Droplet Characteristics for Two-Phase Digital Flows. Applied Sciences. 2021; 11(9):4251. https://doi.org/10.3390/app11094251
Chicago/Turabian StyleZhang, Jinsong, Shuai Zhang, Jianhua Zhang, and Zhiliang Wang. 2021. "Machine Learning Model of Dimensionless Numbers to Predict Flow Patterns and Droplet Characteristics for Two-Phase Digital Flows" Applied Sciences 11, no. 9: 4251. https://doi.org/10.3390/app11094251
APA StyleZhang, J., Zhang, S., Zhang, J., & Wang, Z. (2021). Machine Learning Model of Dimensionless Numbers to Predict Flow Patterns and Droplet Characteristics for Two-Phase Digital Flows. Applied Sciences, 11(9), 4251. https://doi.org/10.3390/app11094251






