Mathematical Modelling of a Static Concentrating Photovoltaic: Simulation and Experimental Validation
Abstract
1. Introduction
2. Methodology
3. Mathematical Formulation of the CPV
3.1. RADTIRC as the Reference for the Model
3.2. Mathematical Model of a PV Cell
4. Simulation Process
5. Results and Discussions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Incident Angle (°) | Simulation | Experiment | Relative Error | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Voc (V) | Isc (A) | Pmax (W) | Voc (V) | Isc (A) | Pmax (W) | Voc (%) | Isc (%) | Pmax (%) | |
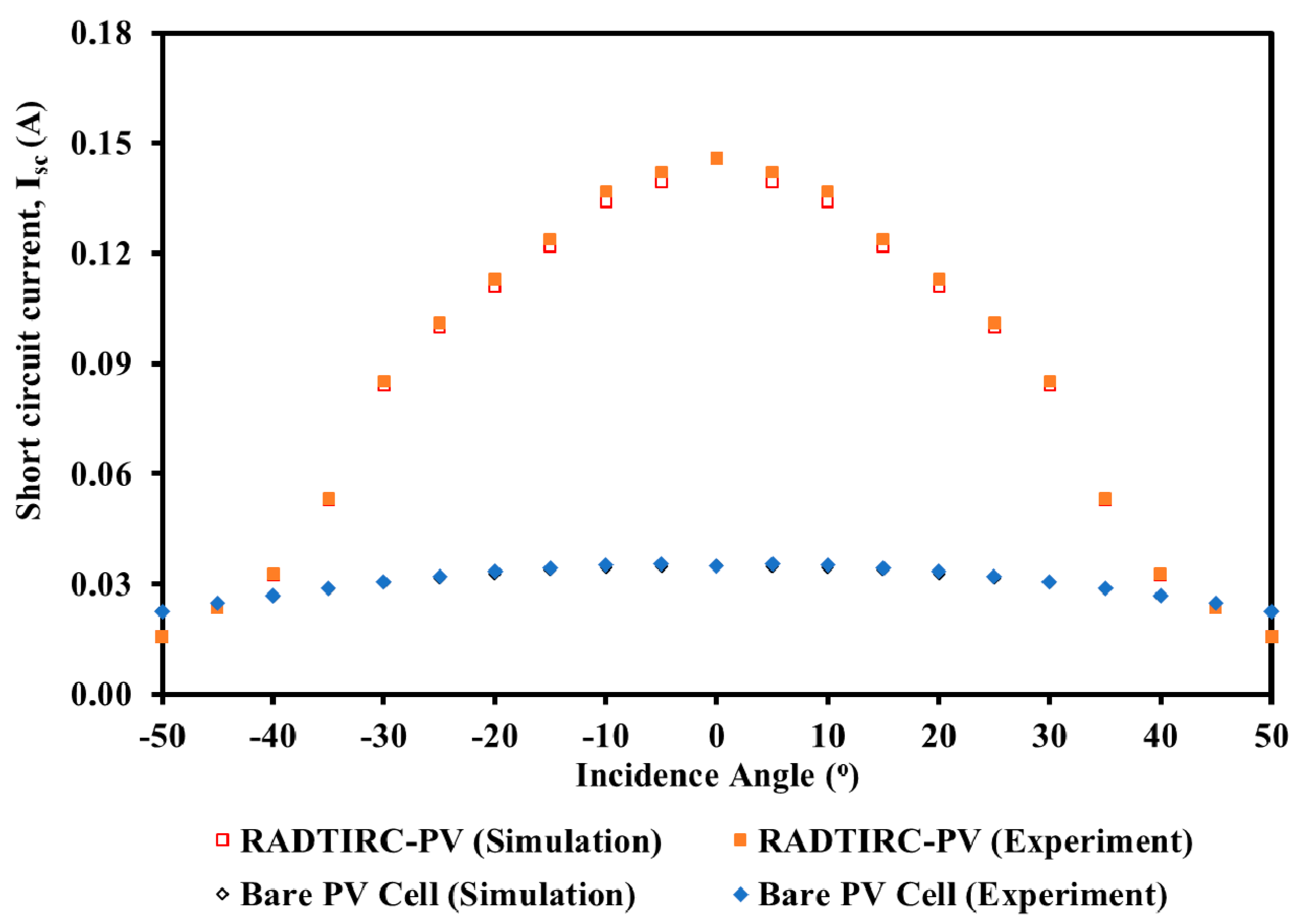
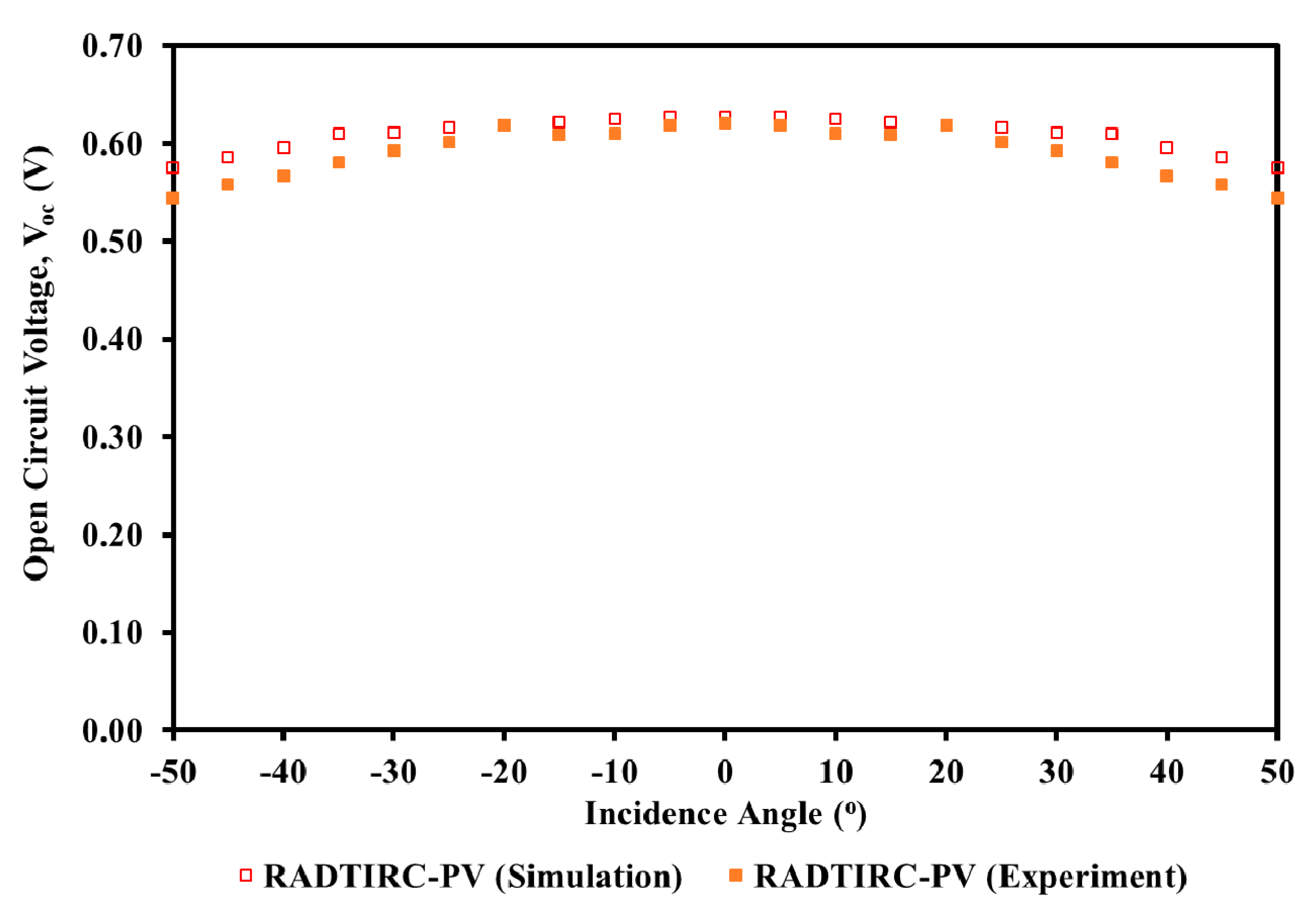
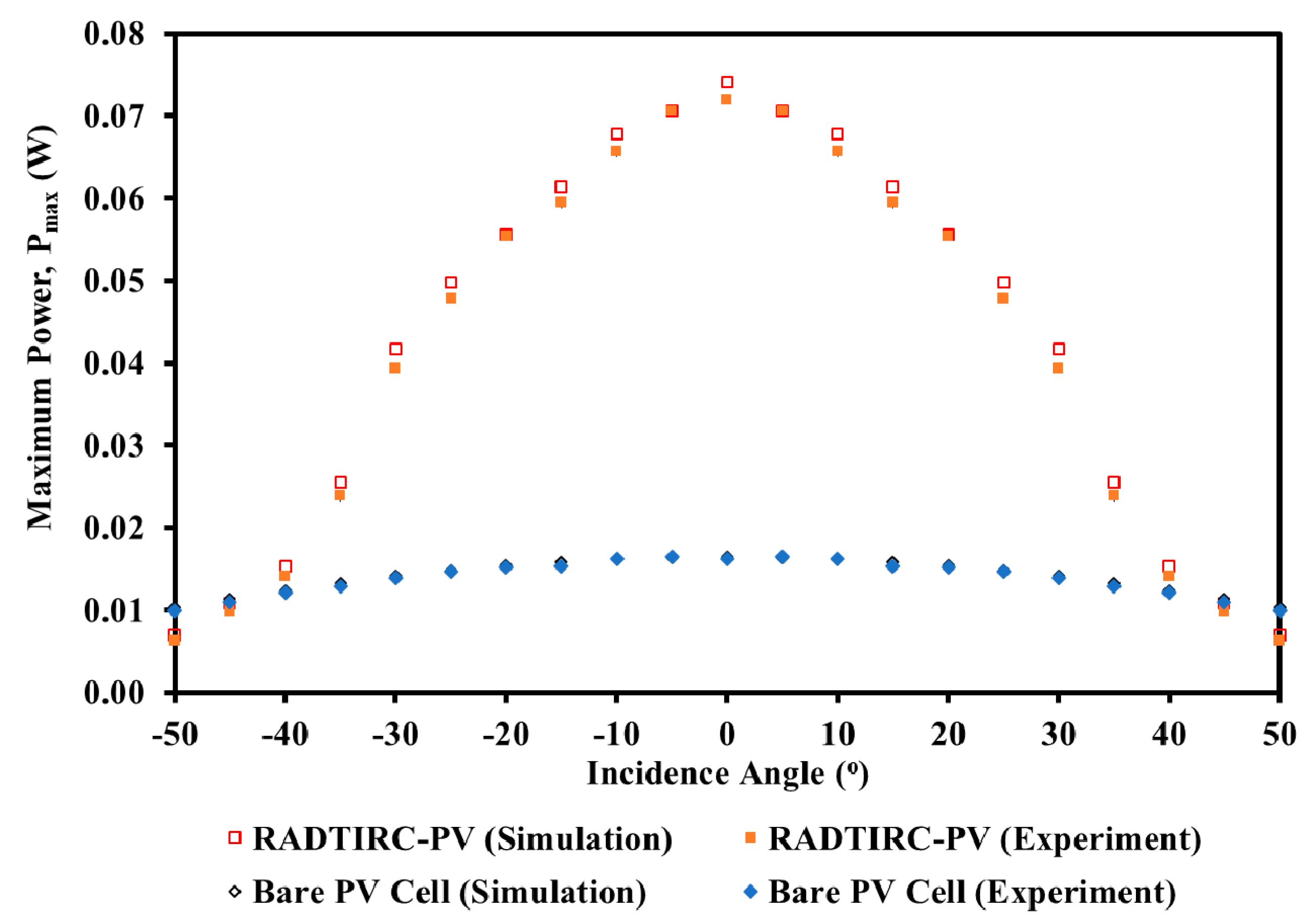
| 0 | 0.6270 | 0.1460 | 0.0740 | 0.6210 | 0.1460 | 0.0720 | 0.9569 | 0.0000 | 2.7074 |
| ±5 | 0.6270 | 0.1395 | 0.0706 | 0.6190 | 0.1420 | 0.0706 | 1.2759 | 1.8160 | 0.0168 |
| ±10 | 0.6250 | 0.1342 | 0.0678 | 0.6095 | 0.1370 | 0.0657 | 2.4800 | 2.1229 | 3.0815 |
| ±15 | 0.6220 | 0.1219 | 0.0613 | 0.6085 | 0.1240 | 0.0595 | 2.1704 | 1.7529 | 3.0085 |
| ±20 | 0.6190 | 0.1109 | 0.0556 | 0.6190 | 0.1130 | 0.0554 | 0.0000 | 1.8570 | 0.2555 |
| ±25 | 0.6160 | 0.0998 | 0.0497 | 0.6010 | 0.1010 | 0.0479 | 2.4351 | 1.1955 | 3.7888 |
| ±30 | 0.6110 | 0.0843 | 0.0417 | 0.5928 | 0.0851 | 0.0394 | 2.9787 | 0.9538 | 5.5375 |
| ±35 | 0.6100 | 0.0530 | 0.0255 | 0.5805 | 0.0532 | 0.0238 | 4.8361 | 0.4523 | 6.6623 |
| ±40 | 0.5960 | 0.0326 | 0.0153 | 0.5662 | 0.0327 | 0.0141 | 5.0000 | 0.3299 | 7.4529 |
| ±45 | 0.5860 | 0.0235 | 0.0108 | 0.5580 | 0.0235 | 0.0099 | 4.7782 | 0.1969 | 8.5441 |
| ±50 | 0.5750 | 0.0157 | 0.0070 | 0.5440 | 0.0156 | 0.0063 | 5.3913 | 0.4337 | 9.9681 |
| Incident Angle (°) | Simulation | Experiment | Relative Error | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Voc (V) | Isc (A) | Pmax (W) | Voc (V) | Isc (A) | Pmax (W) | Voc (%) | Isc (%) | Pmax (%) | |
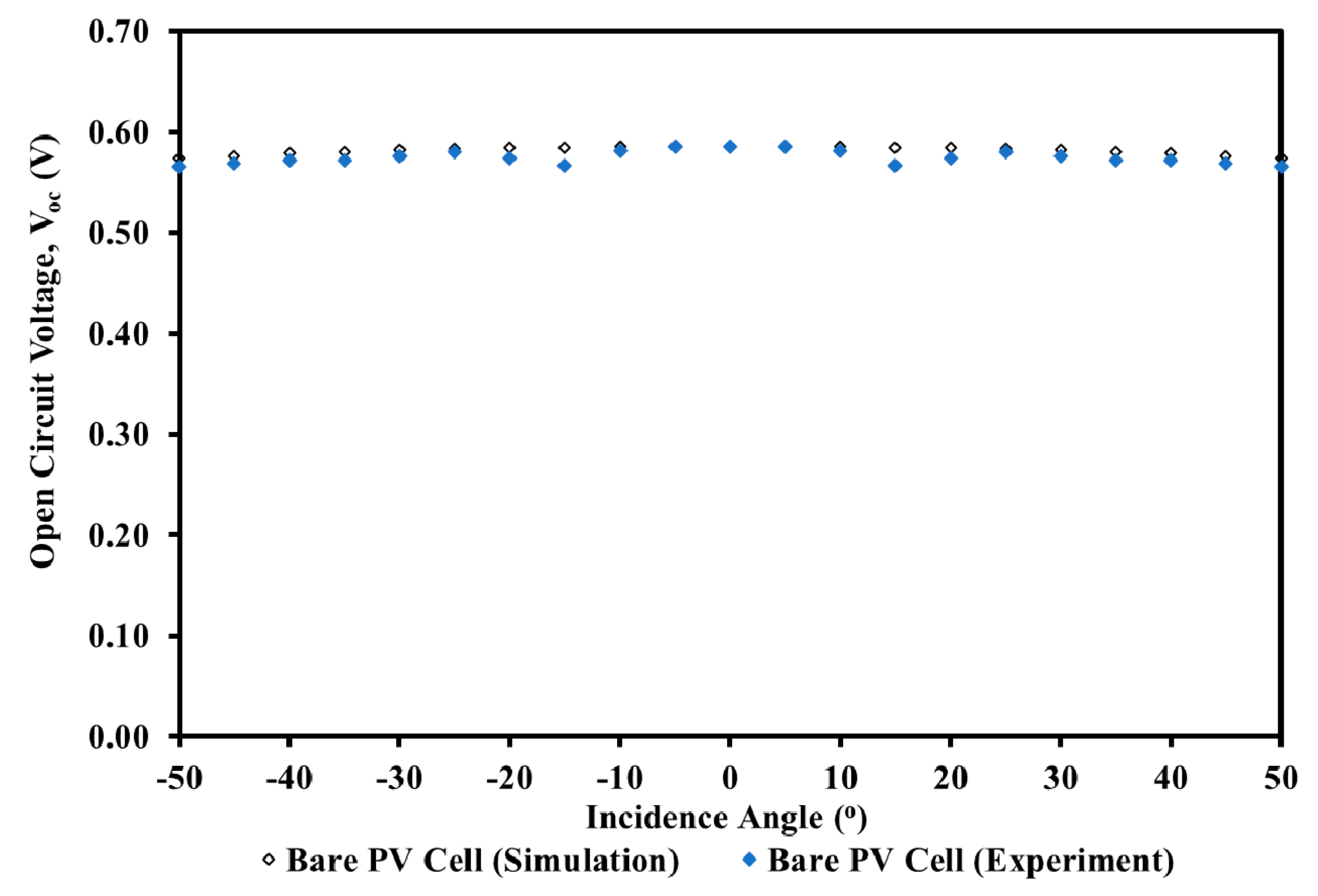
| 0 | 0.5860 | 0.0350 | 0.0165 | 0.5860 | 0.0350 | 0.0162 | 0.0000 | 0.0000 | 1.4684 |
| ±5 | 0.5860 | 0.0349 | 0.0164 | 0.5855 | 0.0355 | 0.0165 | 0.0853 | 1.8160 | 0.2868 |
| ±10 | 0.5860 | 0.0345 | 0.0162 | 0.5810 | 0.0352 | 0.0162 | 0.8532 | 2.1229 | 0.0304 |
| ±15 | 0.5850 | 0.0338 | 0.0159 | 0.5670 | 0.0344 | 0.0153 | 3.0769 | 1.7529 | 3.7463 |
| ±20 | 0.5840 | 0.0329 | 0.0154 | 0.5735 | 0.0335 | 0.0152 | 1.7979 | 1.8570 | 1.7812 |
| ±25 | 0.5830 | 0.0317 | 0.0148 | 0.5800 | 0.0321 | 0.0147 | 0.5146 | 1.1955 | 0.9565 |
| ±30 | 0.5820 | 0.0303 | 0.0141 | 0.5760 | 0.0306 | 0.0139 | 1.0309 | 0.9538 | 2.0716 |
| ±35 | 0.5800 | 0.0287 | 0.0133 | 0.5720 | 0.0288 | 0.0129 | 1.3793 | 0.4523 | 3.1050 |
| ±40 | 0.5790 | 0.0268 | 0.0124 | 0.5720 | 0.0269 | 0.0121 | 1.2090 | 0.3299 | 2.8453 |
| ±45 | 0.5760 | 0.0247 | 0.0114 | 0.5690 | 0.0247 | 0.0110 | 1.2153 | 0.1969 | 3.3874 |
| ±50 | 0.5740 | 0.0225 | 0.0103 | 0.5660 | 0.0224 | 0.0099 | 1.3937 | 0.4337 | 3.5023 |
| Incident Angle (°) | Simulation | Experiment | Relative Error | |||
|---|---|---|---|---|---|---|
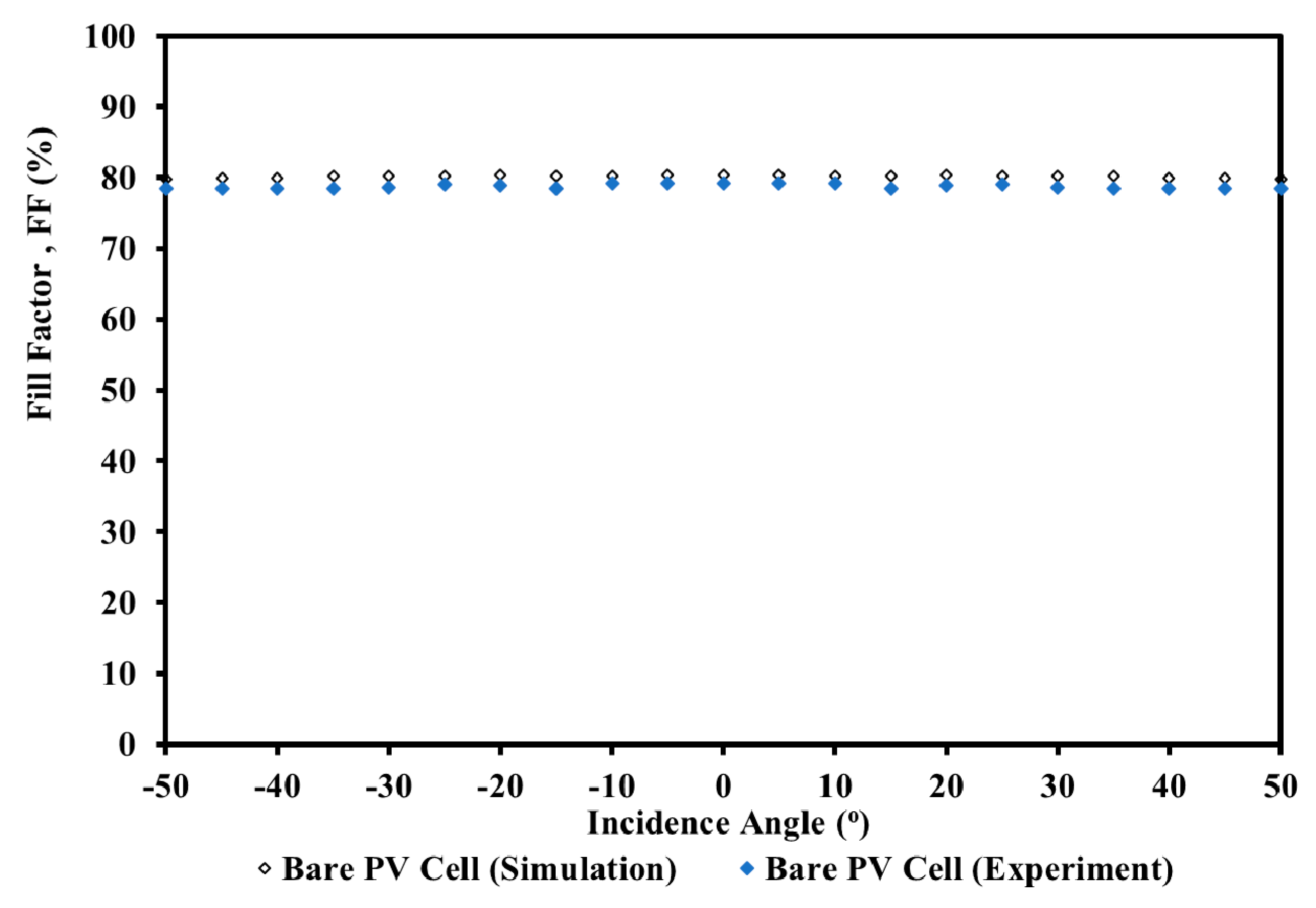
| Bare PV (FF) | RADTIRC-PV (FF) | Bare PV (FF) | RADTIRC-PV (FF) | Bare PV (%) | RADTIRC-PV (%) | |
| 0 | 80.3597 | 79.1796 | 80.8734 | 79.4441 | 1.4684 | 1.7673 |
| ±5 | 80.3411 | 79.2020 | 80.7149 | 80.3133 | 1.4179 | 0.4975 |
| ±10 | 80.2846 | 79.2681 | 80.8361 | 78.6674 | 1.2661 | 2.6828 |
| ±15 | 80.3282 | 78.3992 | 80.8798 | 78.8056 | 2.4014 | 2.5646 |
| ±20 | 80.3305 | 78.8794 | 80.9228 | 79.2444 | 1.8064 | 2.0740 |
| ±25 | 80.2897 | 78.9887 | 80.9121 | 78.8468 | 1.6204 | 2.5525 |
| ±30 | 80.2020 | 78.6089 | 80.9024 | 78.0245 | 1.9863 | 3.5572 |
| ±35 | 80.1988 | 78.4407 | 79.0707 | 77.2041 | 2.1922 | 2.3607 |
| ±40 | 79.9971 | 78.4134 | 78.6697 | 76.3865 | 1.9797 | 2.9023 |
| ±45 | 80.0004 | 78.3956 | 78.3793 | 75.4280 | 2.0059 | 3.7654 |
| ±50 | 79.7782 | 78.4123 | 77.6704 | 74.2350 | 1.7121 | 4.4231 |
| Incident Angle (°) | Simulation | Experiment | Relative Error (%) |
|---|---|---|---|
| 0 | 4.1714 | 4.1714 | 0.0000 |
| ±5 | 4.0000 | 4.0000 | 0.0000 |
| ±10 | 3.8920 | 3.8920 | 0.0000 |
| ±15 | 3.6047 | 3.6047 | 0.0000 |
| ±20 | 3.3731 | 3.3731 | 0.0000 |
| ±25 | 3.1464 | 3.1464 | 0.0000 |
| ±30 | 2.7810 | 2.7810 | 0.0000 |
| ±35 | 1.8472 | 1.8472 | 0.0000 |
| ±40 | 1.2156 | 1.2156 | 0.0000 |
| ±45 | 0.9514 | 0.9514 | 0.0000 |
| ±50 | 0.6964 | 0.6964 | 0.0000 |
References
- Qazi, S. Mobile photovoltaic systems for disaster relief and remote areas. In Standalone Photovoltaic (PV) Systems for Disaster Relief and Remote Areas; Reading, L., Ed.; Elsevier: Cambridge, MA, USA, 2017; pp. 83–112. [Google Scholar]
- Fadakar Masouleh, F.; Das, N.; Rozati, S. Nano-structured gratings for improved light absorption efficiency in solar cells. Energies 2016, 9, 756. [Google Scholar] [CrossRef]
- Das, N.; Wongsodihardjo, H.; Islam, S. Modeling of multi-junction photovoltaic cell using MATLAB/Simulink to improve the conversion efficiency. Renew. Energy 2015, 74, 917–924. [Google Scholar] [CrossRef]
- Jithin, M.; Saravanakumar, K.; Ganesan, V.; Reddy, V.R.; Razad, P.M.; Patidar, M.M.; Jeyadheepan, K.; Marimuthu, G.; Sreelakshmi, V.R.; Mahalakshmi, K. Growth, mechanism and properties of TiO2 nanorods embedded nanopillar: Evidence of lattice orientation effect. Superlattices Microstruct. 2017, 109, 145–153. [Google Scholar] [CrossRef]
- Zhang, K.N.; Jiang, Z.N.; Wang, T.; Qiao, J.W.; Feng, L.; Qin, C.C.; Yin, H.; So, S.K.; Hao, X.T. Exploring the mechanisms of exciton diffusion improvement in ternary polymer solar cells: From ultrafast to ultraslow temporal scale. Nano Energy 2021, 79, 105513. [Google Scholar] [CrossRef]
- Al Kurdi, K.; McCarthy, D.P.; McMeekin, D.P.; Furer, S.O.; Tremblay, M.H.; Barlow, S.; Bach, U.; Marder, S.R. A naphthalene diimide side-chain polymer as an electron-extraction layer for stable perovskite solar cells. Mater. Chem. Front. 2021, 5, 450–457. [Google Scholar] [CrossRef]
- Angmo, D.; DeLuca, G.; Scully, A.D.; Chesman, A.S.R.; Seeber, A.; Zuo, C.; Vak, D.; Bach, U.; Gao, M. A lab-to-fab study toward roll-to-roll fabrication of reproducible perovskite solar cells under ambient room conditions. Cell Rep. Phys. Sci. 2021, 2, 100293. [Google Scholar] [CrossRef]
- Masson, G.; Kaizuka, I. Trends in Photovoltaic Applications 2020; IEA PVPS: Paris, France, 2020. [Google Scholar]
- Martinez-Plaza, D.; Abdallah, A.; Figgis, B.W.; Mirza, T. Performance improvement techniques for photovoltaic systems in Qatar: Results of first year of outdoor exposure. Energy Procedia 2015, 77, 386–396. [Google Scholar] [CrossRef]
- Alamoudi, A.; Saaduddin, S.M.; Munir, A.B.; Muhammad-Sukki, F.; Abu-Bakar, S.H.; Mohd Yasin, S.H.; Karim, R.; Bani, N.A.; Mas’ud, A.A.; Ardila-Rey, J.A.; et al. Using static concentrator technology to achieve global energy goal. Sustainability 2019, 11, 3056. [Google Scholar] [CrossRef]
- Li, G.; Xuan, Q.; Akram, M.W.; Golizadeh Akhlaghi, Y.; Liu, H.; Shittu, S. Building integrated solar concentrating systems: A review. Appl. Energy 2020, 260, 114288. [Google Scholar] [CrossRef]
- Marín-Sáez, J.; Chemisana, D.; Atencia, J.; Collados, M.V. Outdoor performance evaluation of a holographic solar concentrator optimized for building integration. Appl. Energy 2019, 250, 1073–1084. [Google Scholar] [CrossRef]
- Day, J.; Senthilarasu, S.; Mallick, T.K. Enhanced efficiency for building integrated concentrator photovoltaic modules based on rare earth doped optics. Sol. Energy Mater. Sol. Cells 2019, 199, 83–90. [Google Scholar] [CrossRef]
- Xuan, Q.; Li, G.; Lu, Y.; Zhao, X.; Su, Y.; Ji, J.; Pei, G. A general optimization strategy for the annual performance enhancement of a solar concentrating system incorporated in the south-facing wall of a building. Indoor Built Environ. 2020, 29, 1386–1398. [Google Scholar] [CrossRef]
- Market Data Forecast. Concentrator Photovoltaic (CPV) Market. Segmentation by Product (Reflector and Refractor), by Application (Utility and Commercial), by Concentration Level (High. and Low) and Region. Industry Forecast. of 2021 to 2026; Telangana, India, 2021; Available online: https://www.marketdataforecast.com/market-reports/concentrator-photovoltaic-market (accessed on 1 April 2021).
- Wiesenfarth, M.; Philipps, S.P.; Bett, A.W.; Horowitz, K.; Kurtz, S. Current Status of Concentrator Photovoltaic (CPV) Technology; National Renewable Energy Lab: Denver, CO, USA, 2017.
- Welford, W.T.; Winston, R. High. Collection Nonimaging Optics; Academic Press: Cambridge, MA, USA, 1989; ISBN 9780127428857. [Google Scholar]
- Rönnelid, M.; Perers, B.; Karlsson, B. Construction and testing of a large-area CPC-collector and comparison with a flat plate collector. Sol. Energy 1996, 57, 177–184. [Google Scholar] [CrossRef]
- Pei, G.; Li, G.; Su, Y.; Ji, J.; Riffat, S.; Zheng, H. Preliminary ray tracing and experimental study on the effect of mirror coating on the optical efficiency of a solid dielectric compound parabolic concentrator. Energies 2012, 5, 3627–3639. [Google Scholar] [CrossRef]
- Goodman, N.B.; Ignatius, R.; Wharton, L.; Winston, R. Solid-dielectric compound parabolic concentrators: On their use with photovoltaic devices. Appl. Opt. 1976, 15, 2434–2436. [Google Scholar] [CrossRef] [PubMed]
- Mallick, T.K.; Eames, P.C.; Norton, B. Non-concentrating and asymmetric compound parabolic concentrating building façade integrated photovoltaics: An experimental comparison. Sol. Energy 2006, 80, 834–849. [Google Scholar] [CrossRef]
- Sarmah, N.; Richards, B.S.; Mallick, T.K. Design, development and indoor performance analysis of a low concentrating dielectric photovoltaic module. Sol. Energy 2014, 103, 390–401. [Google Scholar] [CrossRef]
- Mammo, E.D.; Sellami, N.; Mallick, T.K. Performance analysis of a reflective 3D crossed compound parabolic concentrating photovoltaic system for building façade integration. Prog. Photovolt. Res. Appl. 2013, 21, 1095–1103. [Google Scholar] [CrossRef]
- Uematsu, T.; Yazawa, Y.; Joge, T.; Kokunai, S. Fabrication and characterization of a flat-plate static-concentrator photovoltaic module. Sol. Energy Mater. Sol. Cells 2001, 67, 425–434. [Google Scholar] [CrossRef]
- Gajbert, H.; Hall, M.; Karlsson, B. Optimisation of reflector and module geometries for stationary, low-concentrating, façade-integrated photovoltaic systems. Sol. Energy Mater. Sol. Cells 2007, 91, 1788–1799. [Google Scholar] [CrossRef]
- Yoshioka, K.; Goma, S.; Hayakawa, S.; Saitoh, T. Preparation and properties of an experimental static concentrator with a new three-dimensional lens. Prog. Photovolt. Res. Appl. 1997, 5, 139–145. [Google Scholar] [CrossRef]
- Ning, X.; Winston, R.; O’Gallagher, J. Dielectric totally internally reflecting concentrators. Appl. Opt. 1987, 26, 300–305. [Google Scholar] [CrossRef] [PubMed]
- Freier, D.; Ramirez-Iniguez, R.; Gamio, C.; Jafry, T.; Muhammad-Sukki, F. Novel nonimaging solar concentrator for portable solar systems for developing countries. In Proceedings of the 2017 IEEE PES Power Africa, Accra, Ghana, 27–30 June 2017; pp. 307–310. [Google Scholar]
- Slooff, L.H.; Bende, E.E.; Burgers, A.R.; Budel, T.; Pravettoni, M.; Kenny, R.P.; Dunlop, E.D.; Büchtemann, A. A luminescent solar concentrator with 7.1% power conversion efficiency. Phys. Status Solidi Rapid Res. Lett. 2008, 2, 257–259. [Google Scholar] [CrossRef]
- Lin, Q.; Wang, Z.; Snaith, H.J.; Johnston, M.B.; Herz, L.M. Hybrid perovskites: Prospects for concentrator solar cells. Adv. Sci. 2018, 5, 1700792. [Google Scholar] [CrossRef]
- Wang, Z.; Lin, Q.; Wenger, B.; Christoforo, M.G.; Lin, Y.H.; Klug, M.T.; Johnston, M.B.; Herz, L.M.; Snaith, H.J. High irradiance performance of metal halide perovskites for concentrator photovoltaics. Nat. Energy 2018, 3, 855–861. [Google Scholar] [CrossRef]
- Hou, B.; Kim, B.; Lee, H.K.H.; Cho, Y.; Giraud, P.; Liu, M.; Zhang, J.; Davies, M.L.; Durrant, J.R.; Tsoi, W.C.; et al. Multiphoton absorption stimulated metal chalcogenide quantum dot solar cells under ambient and concentrated irradiance. Adv. Funct. Mater. 2020, 30, 2004563. [Google Scholar] [CrossRef]
- Neo, D.C.J.; Goh, W.P.; Lau, H.H.; Shanmugam, J.; Chen, Y.F. CuInS2 quantum dots with thick ZnSexS1-xShells for a luminescent solar concentrator. ACS Appl. Nano Mater. 2020, 3, 6489–6496. [Google Scholar] [CrossRef]
- Meinardi, F.; Ehrenberg, S.; Dhamo, L.; Carulli, F.; Mauri, M.; Bruni, F.; Simonutti, R.; Kortshagen, U.; Brovelli, S. Highly efficient luminescent solar concentrators based on earth-abundant indirect-bandgap silicon quantum dots. Nat. Photon. 2017, 11, 177–185. [Google Scholar] [CrossRef]
- Ma, J.; Man, K.L.; Ting, T.O.; Zhang, N.; Guan, S.U.; Wong, P.W.H. Approximate single-diode photovoltaic model for efficient I-V characteristics estimation. Sci. World J. 2013, 2013, 230471. [Google Scholar] [CrossRef]
- Mahmoud, Y.A.; Xiao, W.; Zeineldin, H.H. A parameterization approach for enhancing PV model accuracy. IEEE Trans. Ind. Electron. 2013, 60, 5708–5716. [Google Scholar] [CrossRef]
- Mehta, H.K.; Warke, H.; Kukadiya, K.; Panchal, A.K. Accurate expressions for single-diode-model solar cell parameterization. IEEE J. Photovolt. 2019, 9, 803–810. [Google Scholar] [CrossRef]
- Vinod; Kumar, R.; Singh, S.K. Solar photovoltaic modeling and simulation: As a renewable energy solution. Energy Rep. 2018, 4, 701–712. [Google Scholar] [CrossRef]
- Bader, S.; Ma, X.; Oelmann, B. One-diode photovoltaic model parameters at indoor illumination levels—A comparison. Sol. Energy 2019, 180, 707–716. [Google Scholar] [CrossRef]
- Kaddour, A.; Benyoucef, B. Simulation and modelization of parabolic solar concentrator. J. Earth Sci. Clim. Change 2012, 3, 1000113. [Google Scholar] [CrossRef]
- Benrhouma, I.; Victoria, M.; Hernandez, I.A.; Chaouachi, B. Modeling of a concentrating photovoltaic module. In Proceedings of the International Conference on Green Energy and Conversion Systems (GECS 2017), Hammamet, Tunisia, 23–25 March 2017; pp. 1–5. [Google Scholar]
- Fernández, E.F.; Almonacid, F.; Rodrigo, P.; Pérez-Higueras, P. Model for the prediction of the maximum power of a high concentrator photovoltaic module. Sol. Energy 2013, 97, 12–18. [Google Scholar] [CrossRef]
- Li, W.; Paul, M.C.; Baig, H.; Siviter, J.; Montecucco, A.; Mallick, T.K.; Knox, A.R. A three-point-based electrical model and its application in a photovoltaic thermal hybrid roof-top system with crossed compound parabolic concentrator. Renew. Energy 2019, 130, 400–415. [Google Scholar] [CrossRef]
- Ramirez-iniguez, R.; Muhammad-Sukki, F.; McMeekin, S.G.; Stewart, B.G. Optical Element. U.S. Patent 9,910,253, 2018. [Google Scholar]
- Muhammad-Sukki, F.; Abu-Bakar, S.H.; Ramirez-Iniguez, R.; McMeekin, S.G.; Stewart, B.G.; Sarmah, N.; Mallick, T.K.; Munir, A.B.; Mohd Yasin, S.H.; Abdul Rahim, R. Mirror symmetrical dielectric totally internally reflecting concentrator for building integrated photovoltaic systems. Appl. Energy 2014, 113, 32–40. [Google Scholar] [CrossRef]
- Abu-Bakar, S.H.; Muhammad-Sukki, F.; Freier, D.; Ramirez-Iniguez, R.; Mallick, T.K.; Munir, A.B.; Mohd Yasin, S.H.; Abubakar Mas’ud, A.; Md Yunus, N. Optimisation of the performance of a novel rotationally asymmetrical optical concentrator design for building integrated photovoltaic system. Energy 2015, 90, 1033–1045. [Google Scholar] [CrossRef]
- Abu-Bakar, S.H.; Muhammad-Sukki, F.; Freier, D.; Ramirez-Iniguez, R.; Mallick, T.K.; Munir, A.B.; Mohd Yasin, S.H.; Abubakar Mas’ud, A.; Bani, N.A. Performance analysis of a solar window incorporating a novel rotationally asymmetrical concentrator. Energy 2016, 99, 181–192. [Google Scholar] [CrossRef]
- Freier, D.; Muhammad-Sukki, F.; Abu-Bakar, S.; Ramirez-Iniguez, R.; Munir, A.B.; Mohd Yasin, S.H.; Bani, N.A.; Abubakar Mas’ud, A.; Ardila-Rey, J.A.; Karim, M.E. Annual prediction output of an RADTIRC-PV module. Energies 2018, 11, 544. [Google Scholar] [CrossRef]
- Sarmah, N.; Richards, B.S.; Mallick, T.K. Evaluation and optimization of the optical performance of low-concentrating dielectric compound parabolic concentrator using ray-tracing methods. Appl. Opt. 2011, 50, 3303–3310. [Google Scholar] [CrossRef]
- Mallick, T.K.; Eames, P.C. Design and fabrication of low concentrating second generation PRIDE concentrator. Sol. Energy Mater. Sol. Cells 2007, 91, 597–608. [Google Scholar] [CrossRef]
- Muhammad-Sukki, F.; Abu-Bakar, S.H.; Ramirez-Iniguez, R.; McMeekin, S.G.; Stewart, B.G.; Munir, A.B.; Mohd Yasin, S.H.; Abdul Rahim, R. Performance analysis of a mirror symmetrical dielectric totally internally reflecting concentrator for building integrated photovoltaic systems. Appl. Energy 2013, 111, 288–299. [Google Scholar] [CrossRef]
- Sellami, N.; Mallick, T.K. Optical efficiency study of PV crossed compound parabolic concentrator. Appl. Energy 2013, 102, 868–876. [Google Scholar] [CrossRef]
- Chaves, J. Introduction to Nonimaging Optics, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2015; ISBN 978-1420054293. [Google Scholar]
- Freier, D. Novel Nonimaging Concentrator Design for Portable Solar Photovoltaic Systems for Developing Countries; Glasgow Caledonian University: Glagow, UK, 2018. [Google Scholar]
- O’Gallagher, J.J. Nonimaging optics in solar energy. Synth. Lect. Energy Environ. Technol. Sci. Soc. 2008, 2, 1–120. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Taheri, H. Simple, fast and accurate two-diode model for photovoltaic modules. Sol. Energy Mater. Sol. Cells 2011, 95, 586–594. [Google Scholar] [CrossRef]
- Nishioka, K.; Sakitani, N.; Uraoka, Y.; Fuyuki, T. Analysis of multicrystalline silicon solar cells by modified 3-diode equivalent circuit model taking leakage current through periphery into consideration. Sol. Energy Mater. Sol. Cells 2007, 91, 1222–1227. [Google Scholar] [CrossRef]
- Kassis, A.; Saad, M. Analysis of multi-crystalline silicon solar cells at low illumination levels using a modified two-diode model. Sol. Energy Mater. Sol. Cells 2010, 94, 2108–2112. [Google Scholar] [CrossRef]
- Gow, J.A.; Manning, C.D. Development of a photovoltaic array model for use in power-electronics simulation studies. IEE Proc. Electr. Power Appl. 1999, 146, 193. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z. An improved modeling method to determine the model parameters of photovoltaic (PV) modules using differential evolution (DE). Sol. Energy 2011, 85, 2349–2359. [Google Scholar] [CrossRef]
- Bonkoungou, D.; Koalaga, Z.; Njomo, D. Modelling and simulation of photovoltaic module considering single-diode equivalent circuit model in MATLAB. Int. J. Emerg. Technol. Adv. Eng. 2013, 3, 493–502. [Google Scholar]
- Mayer, M.J.; Gróf, G. Extensive comparison of physical models for photovoltaic power forecasting. Appl. Energy 2020, 283, 116239. [Google Scholar] [CrossRef]
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Comprehensive approach to modeling and simulation of photovoltaic arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Dhass, A.D.; Prakash, Y.; Ramya, K.C. Effect of temperature on internal parameters of solar cell. Mater. Today Proc. 2020, 33, 732–735. [Google Scholar] [CrossRef]
- Baig, H.; Heasman, K.C.; Mallick, T.K. Non-uniform illumination in concentrating solar cells. Renew. Sustain. Energy Rev. 2012, 16, 5890–5909. [Google Scholar] [CrossRef]
- Abu-Bakar, S.H.; Muhammad-Sukki, F.; Freier, D.; Ramirez-Iniguez, R.; Mallick, T.K.; Munir, A.B.; Mohd Yasin, S.H.; Abubakar Mas’ud, A.; Md Yunus, N. Performance analysis of a novel rotationally asymmetrical compound parabolic concentrator. Appl. Energy 2015, 154, 221–231. [Google Scholar] [CrossRef]






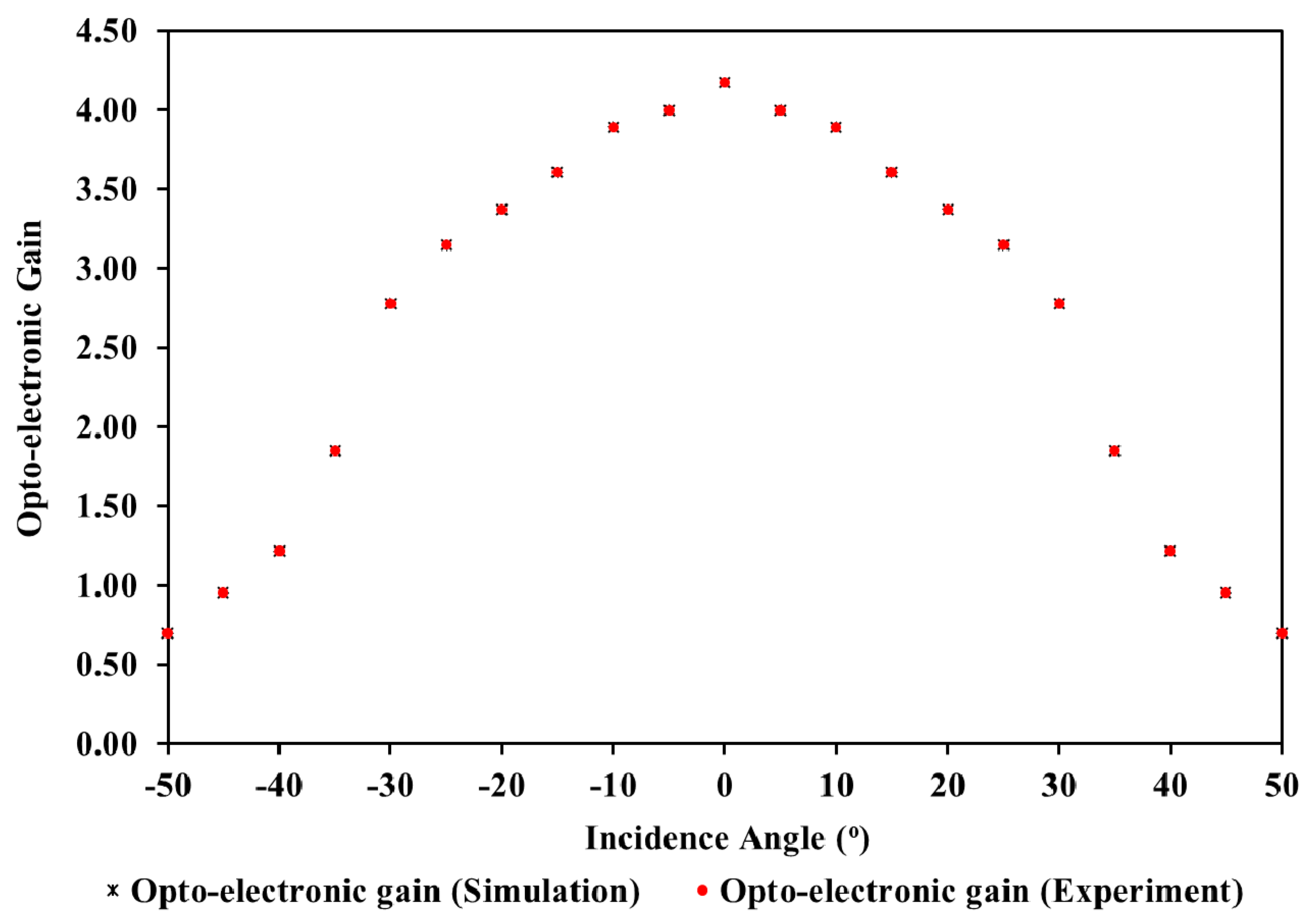
| Angle of Incidence (°) | Opto-Electronic Gain, Copto-e |
|---|---|
| 0 | 4.17143 |
| ±5 | 4.00000 |
| ±10 | 3.89205 |
| ±15 | 3.60465 |
| ±20 | 3.37313 |
| ±25 | 3.14642 |
| ±30 | 2.78105 |
| ±35 | 1.84722 |
| ±40 | 1.21561 |
| ±45 | 0.95142 |
| ±50 | 0.69643 |
| Component | Value |
|---|---|
| Solar radiation intensity, Gref | 1000 W/m2 |
| Reference Temperature, Tref | 25 °C |
| Square solar cell area, A | 1 cm2 |
| Short circuit current, Isc (at 0°) | 0.0350 A |
| Open-circuit voltage, Voc (at 0°) | 0.586 V |
| Ideality factor, n | 1.109 |
| Energy bandgap, Eg | 1.12 |
| Charge of an electron, q | 1.6 × 10−19 C |
| Boltzman constant, k | 1.38 × 10−23 m2 kg s−2 K−1 |
| Series resistance, Rs | 0.047994 Ω |
| Shunt resistance, Rsh | 2148.53 Ω |
| Short circuit current temperature coefficient, α | 0.00024 A/°C |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muhammad-Sukki, F.; Farooq, H.; Abu-Bakar, S.H.; Ardila-Rey, J.A.; Sellami, N.; Kilpatrick, C.; Muhtazaruddin, M.N.; Bani, N.A.; Zulkipli, M. Mathematical Modelling of a Static Concentrating Photovoltaic: Simulation and Experimental Validation. Appl. Sci. 2021, 11, 3894. https://doi.org/10.3390/app11093894
Muhammad-Sukki F, Farooq H, Abu-Bakar SH, Ardila-Rey JA, Sellami N, Kilpatrick C, Muhtazaruddin MN, Bani NA, Zulkipli M. Mathematical Modelling of a Static Concentrating Photovoltaic: Simulation and Experimental Validation. Applied Sciences. 2021; 11(9):3894. https://doi.org/10.3390/app11093894
Chicago/Turabian StyleMuhammad-Sukki, Firdaus, Haroon Farooq, Siti Hawa Abu-Bakar, Jorge Alfredo Ardila-Rey, Nazmi Sellami, Ciaran Kilpatrick, Mohd Nabil Muhtazaruddin, Nurul Aini Bani, and Muhammad Zulkipli. 2021. "Mathematical Modelling of a Static Concentrating Photovoltaic: Simulation and Experimental Validation" Applied Sciences 11, no. 9: 3894. https://doi.org/10.3390/app11093894
APA StyleMuhammad-Sukki, F., Farooq, H., Abu-Bakar, S. H., Ardila-Rey, J. A., Sellami, N., Kilpatrick, C., Muhtazaruddin, M. N., Bani, N. A., & Zulkipli, M. (2021). Mathematical Modelling of a Static Concentrating Photovoltaic: Simulation and Experimental Validation. Applied Sciences, 11(9), 3894. https://doi.org/10.3390/app11093894









