A Review of X-ray Microcalorimeters Based on Superconducting Transition Edge Sensors for Astrophysics and Particle Physics
Abstract
1. Introduction
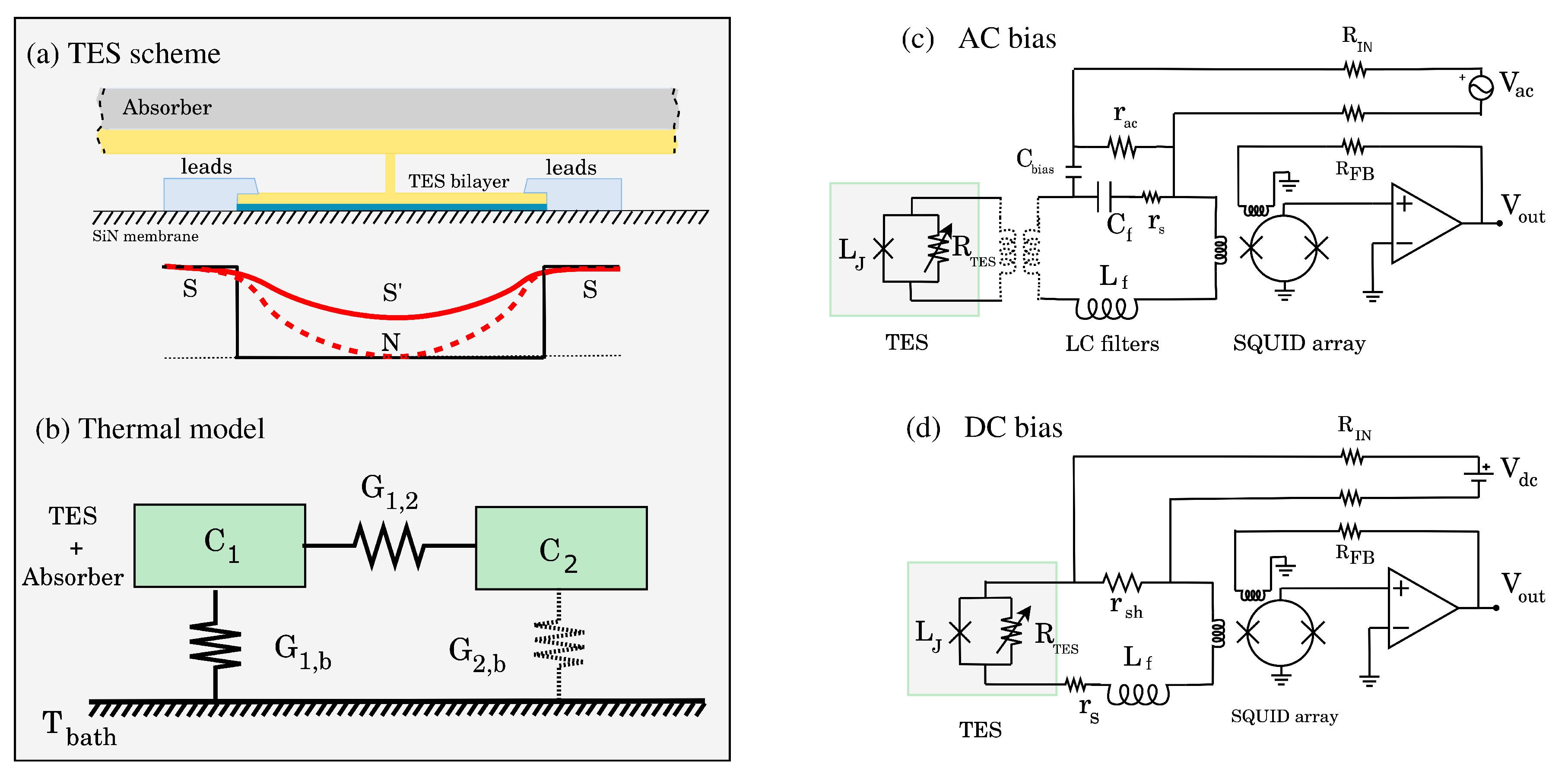
2. TES Physics and Models
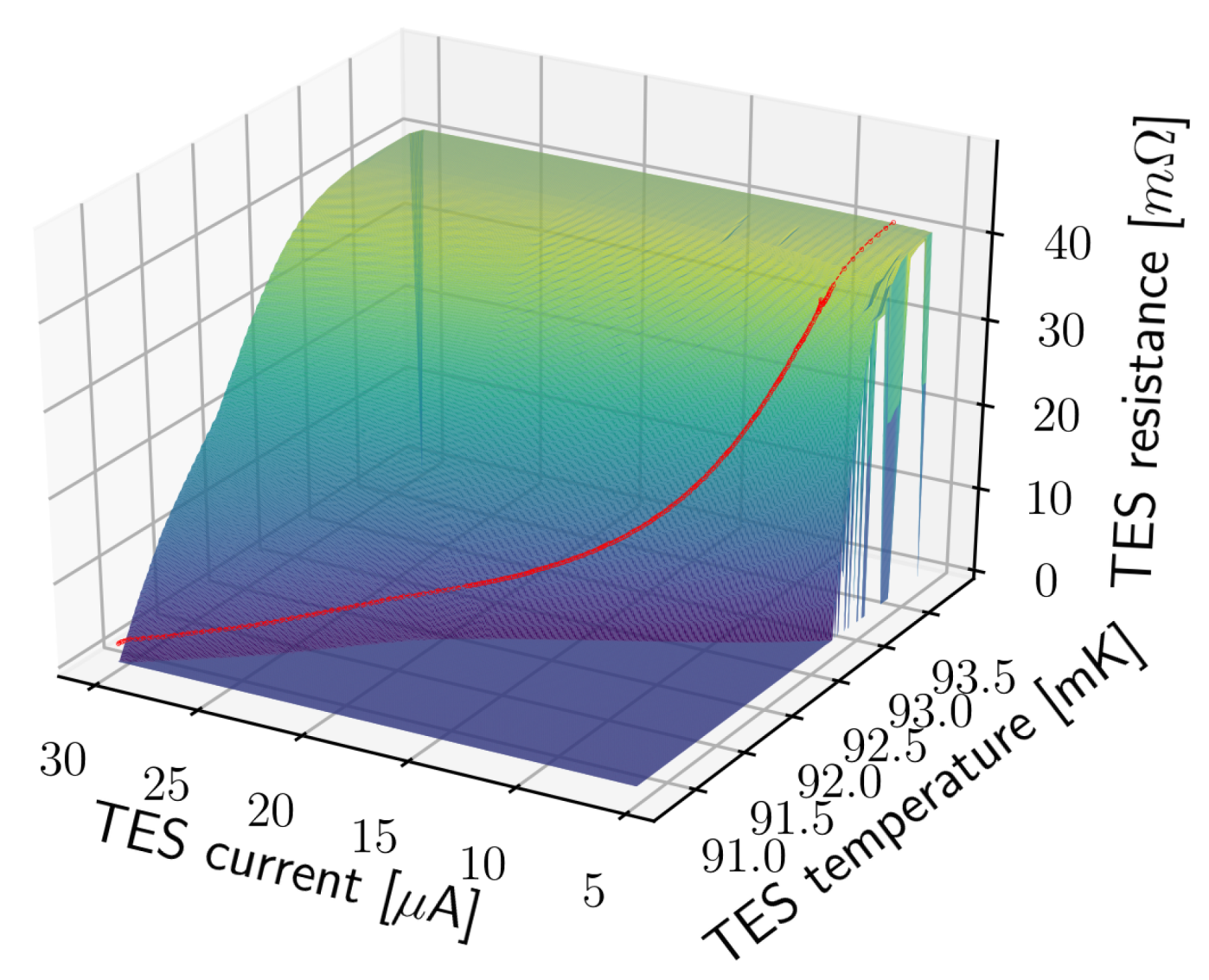
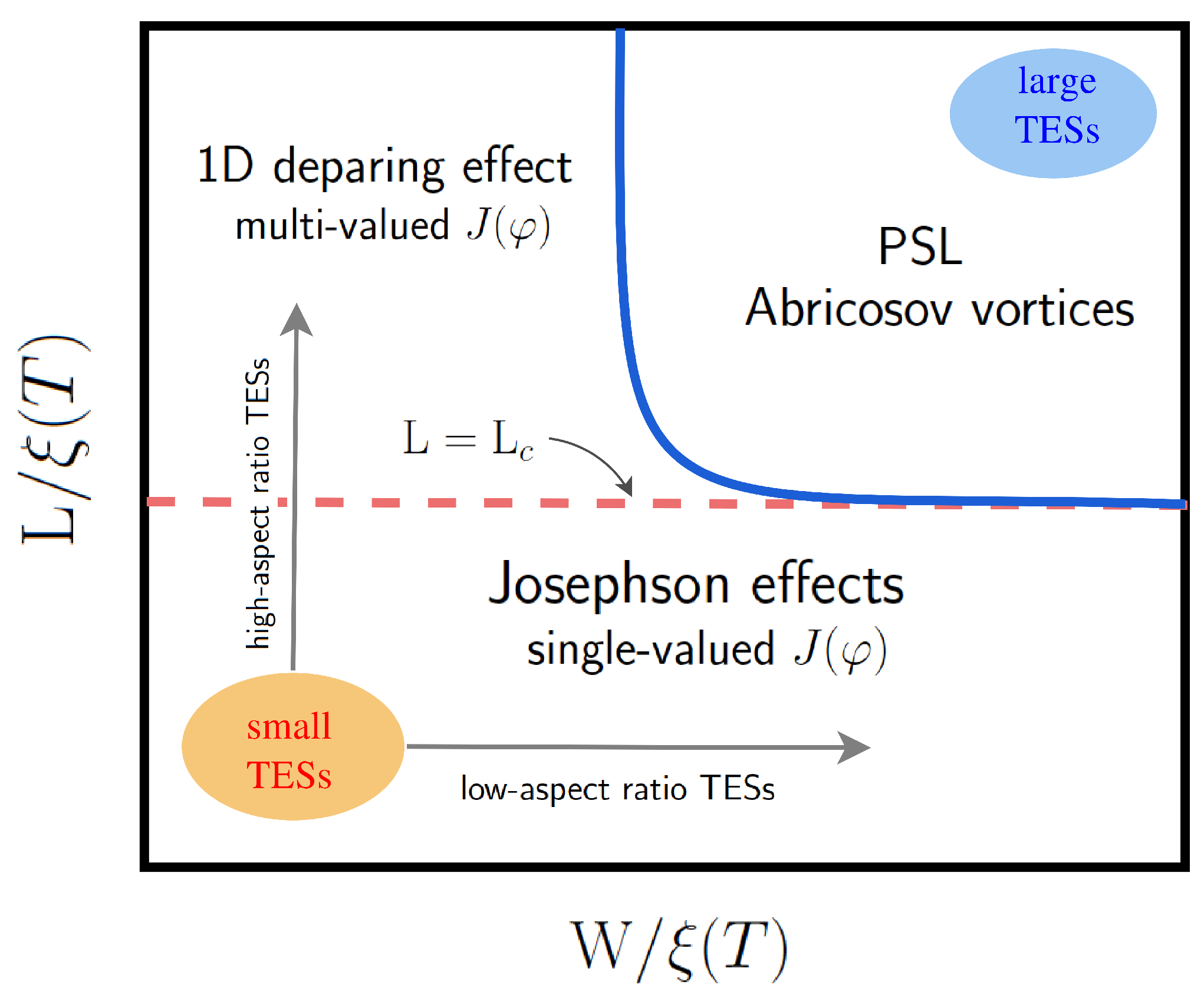
2.1. The Proximity Effects and the Resistive Transition
2.2. TES Electro-Thermal Equations
2.3. TES Noise
3. Large Arrays Fabrication
3.1. TES Bilayer
3.2. Thermal Coupling to the Bath
3.3. Absorbing Layer
4. Single Pixel Optimization
4.1. dc Bias
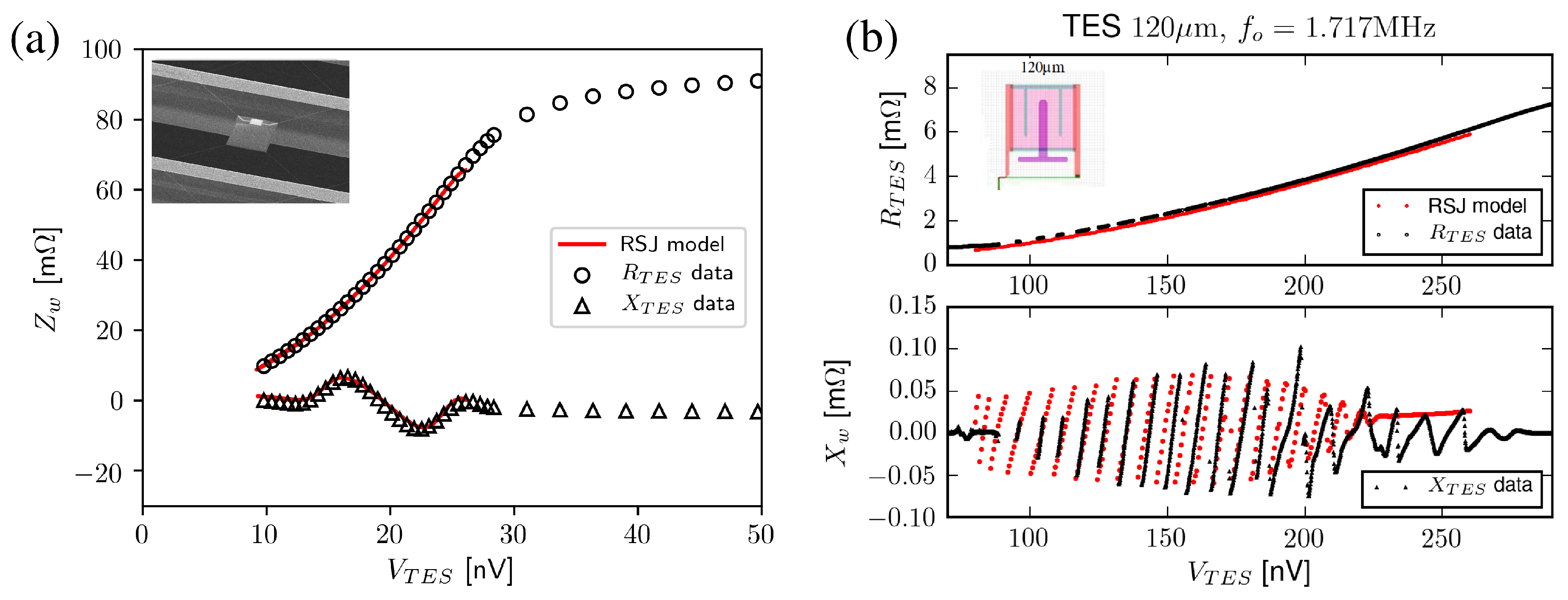
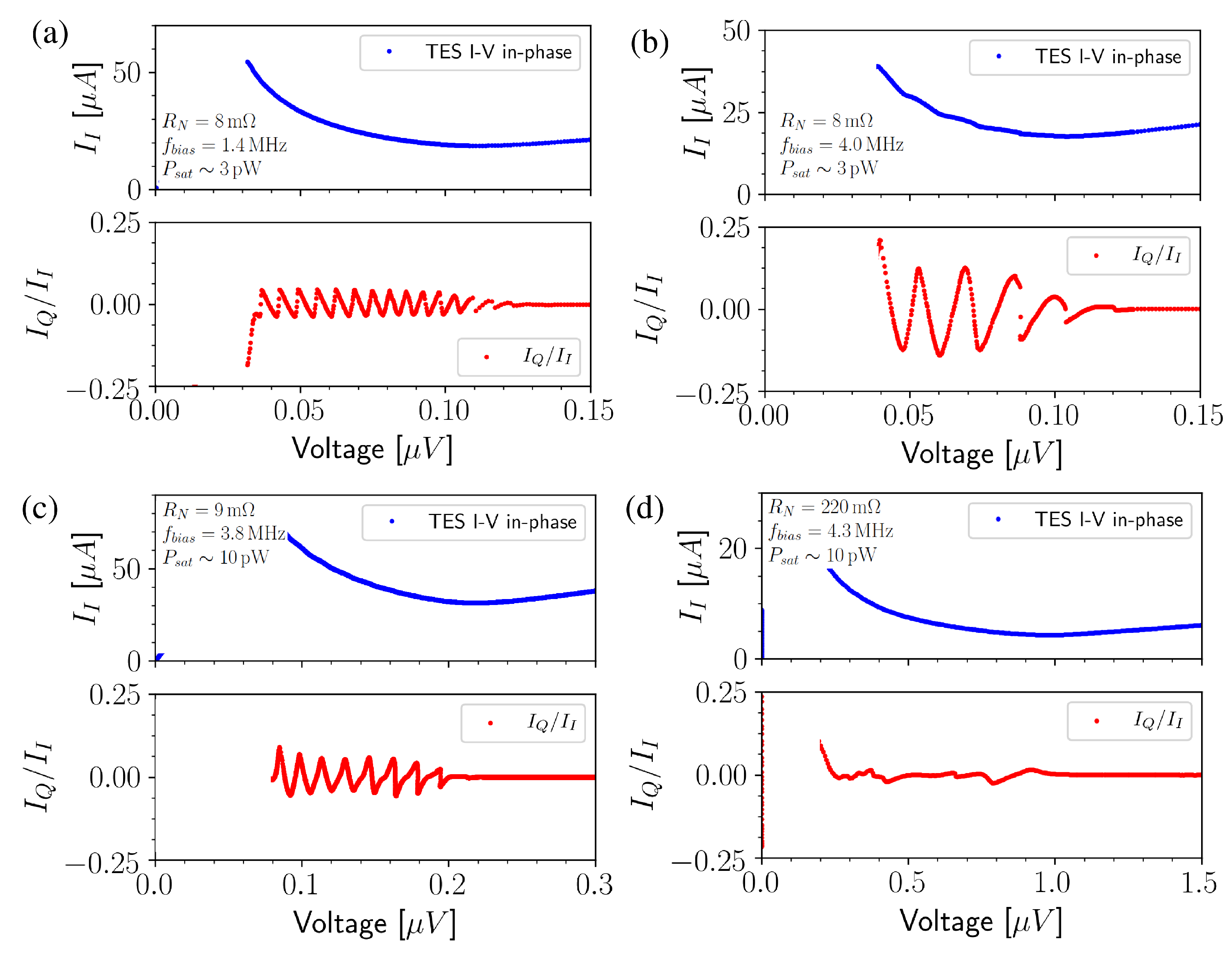
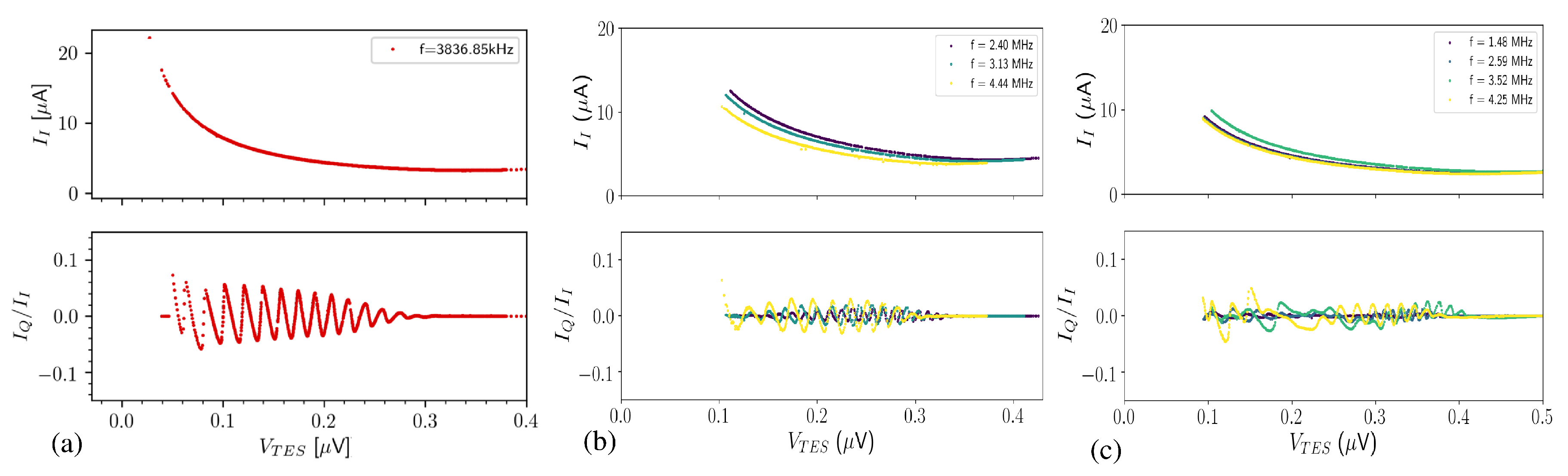
4.2. ac Bias
5. Multiplexing Readout
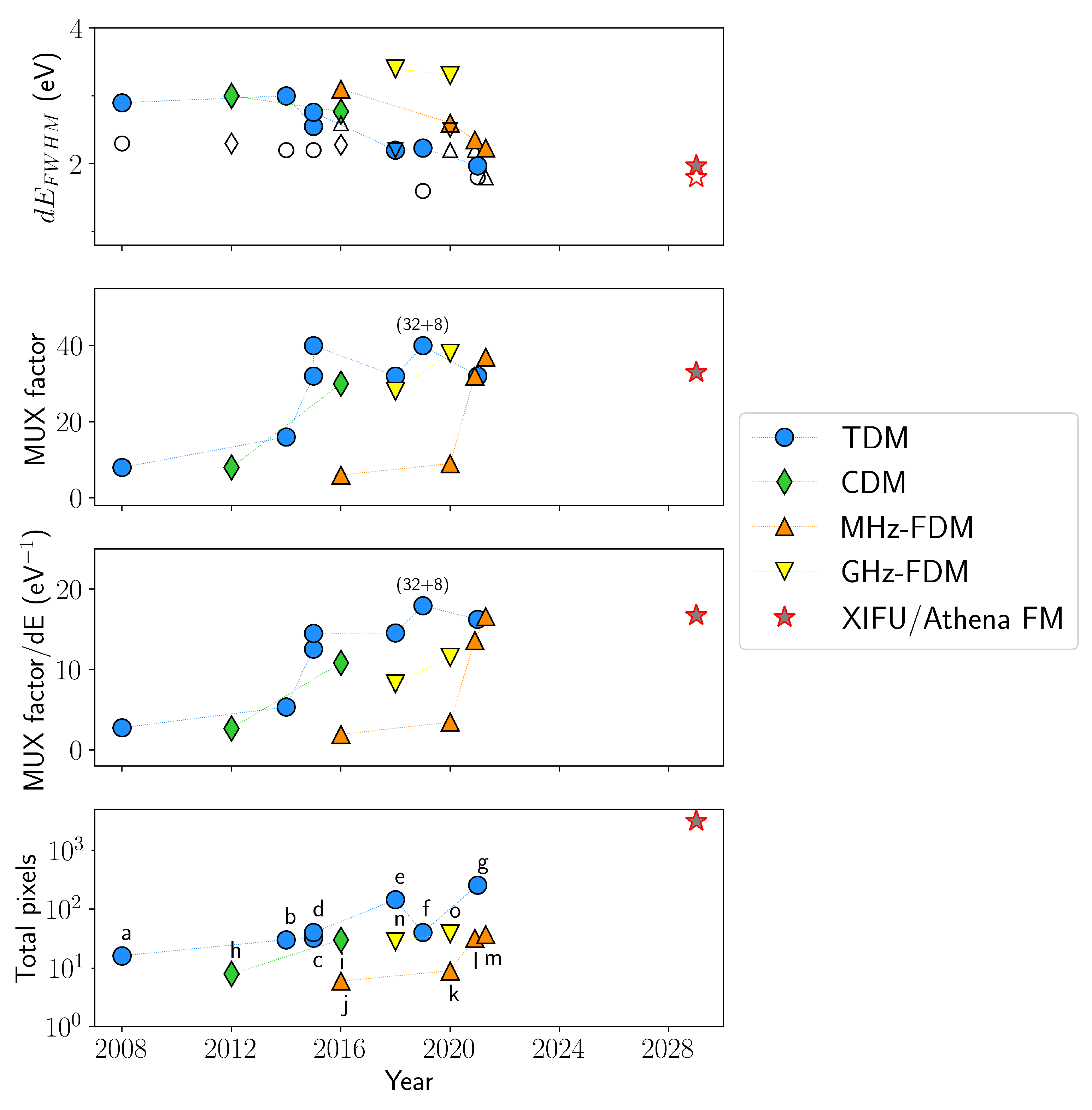
5.1. Time-Division and Code-Division Multiplexing
5.2. MHz-Frequency-Division Multiplexing
5.3. GHz-Frequency-Division Multiplexing
5.4. Thermal Multiplexing
6. Future Instruments for Astrophysics and Fundamental Physics Research
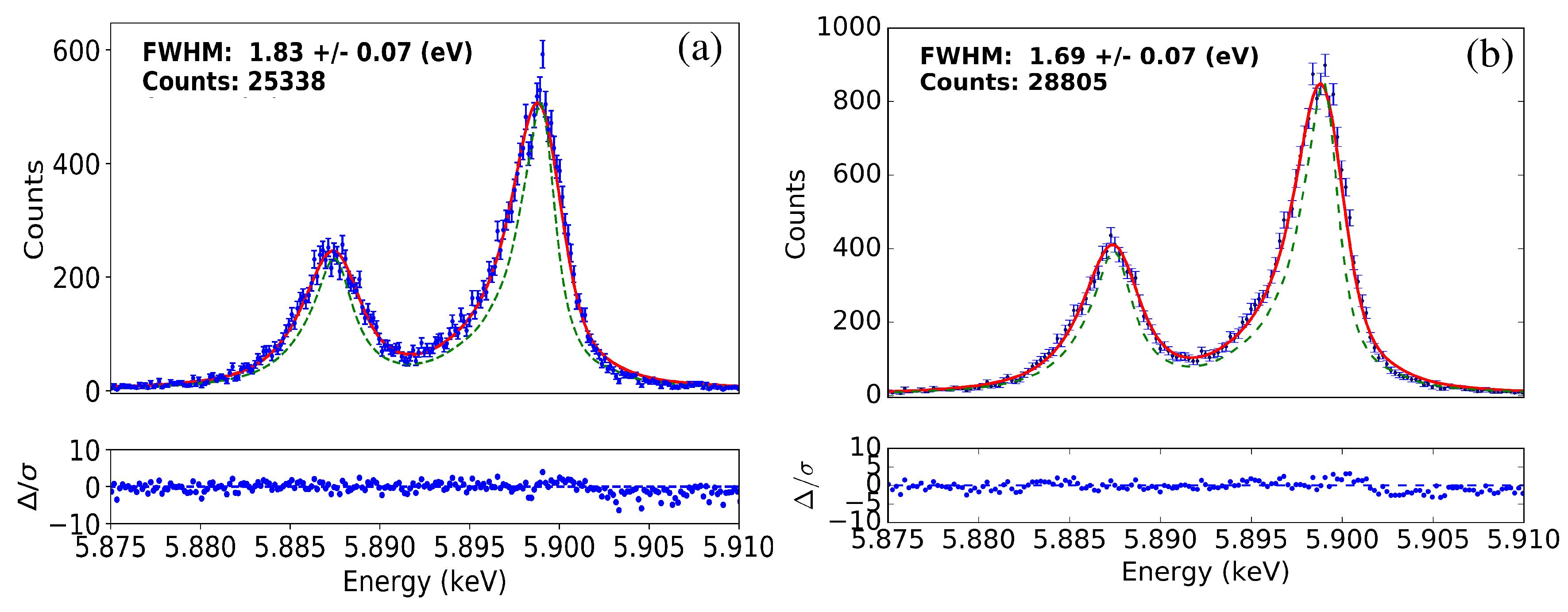
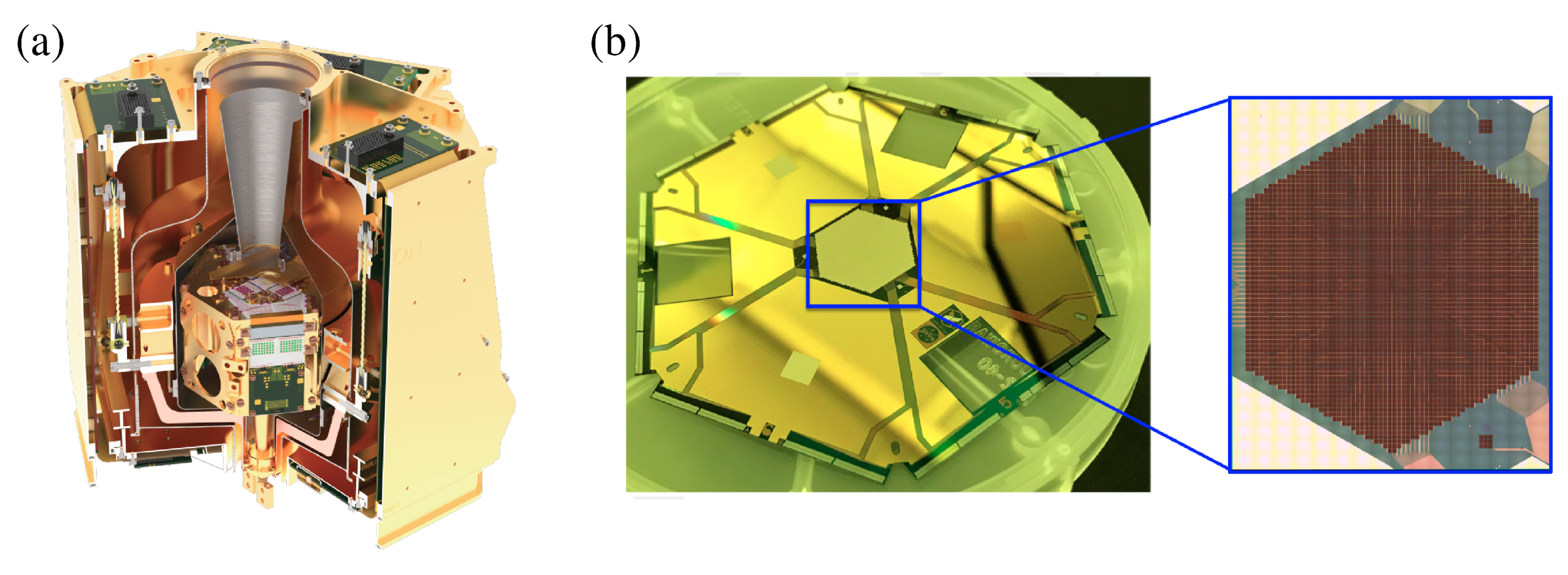
6.1. X-IFU Athena
6.2. Other Future X-ray Space Missions
6.3. Instruments for Particle-Physics And Cosmology
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adams, J.S.; Baker, R.; Bandler, S.R.; Bastidon, N.; Danowski, M.E.; Doriese, W.B.; Eckart, M.E.; Figueroa-Feliciano, E.; Fuhrman, J.; Goldfinger, D.C.; et al. First Operation of Transition-Edge Sensors in Space with the Micro-X Sounding Rocket; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; International Society for Optics and Photonics: Bellingham, WA, USA, 2021; Volume 11454, p. 1145414. [Google Scholar] [CrossRef]
- Barret, D.; Decourchelle, A.; Fabian, A.; Guainazzi, M.; Nandra, K.; Smith, R.; den Herder, J.W. The Athena space X-ray observatory and the astrophysics of hot plasma. Astron. Nachr. 2020, 341, 224–235. [Google Scholar] [CrossRef]
- Sugai, H.; Ade, P.A.R.; Akiba, Y.; Alonso, D.; Arnold, K.; Aumont, J.; Austermann, J.; Baccigalupi, C.; Banday, A.J.; Banerji, R.; et al. Updated Design of the CMB Polarization Experiment Satellite LiteBIRD. J. Low Temp. Phys. 2020, 199, 1107–1117. [Google Scholar] [CrossRef]
- A Ade, P.; Aguirre, J.; Ahmed, Z.; Aiola, S.; Ali, A.; Alonso, D.; Alvarez, M.A.; Arnold, K.; Ashton, P.; Austermann, J.; et al. The Simons Observatory: Science goals and forecasts. J. Cosmol. Astropart. Phys. 2019, 2019, 56. [Google Scholar] [CrossRef]
- Thornton, R.J. The Atacama Cosmology Telescope: The Polarization-sensitive ACTPol Instrument. Astrophys. J. Suppl. Ser. 2016, 227, 21. [Google Scholar] [CrossRef]
- Piat, M.; Stankowiak, G.; Battistelli, E.S.; de Bernardis, P.; Alessandro, G.D.; De Petris, M.; Grandsire, L.; Hamilton, J.C.; Hoang, T.D.; Marnieros, S.; et al. QUBIC IV: Performance of TES Bolometers and Readout Electronics. arXiv 2021, arXiv:2101.06787. [Google Scholar]
- Roelfsema, P.; Giard, M.; Najarro, F.; Wafelbakker, K.; Jellema, W.; Jackson, B.; Sibthorpe, B.; Audard, M.; Doi, Y.; di Giorgio, A.; et al. SAFARI new and improved: Extending the capabilities of SPICA’s imaging spectrometer. In Space Telescopes and Instrumentation 2014: Optical, Infrared, and Millimeter Wave; Clampin, M., Fazio, G.G., MacEwen, H.A., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2014; Volume 9143, pp. 419–429. [Google Scholar] [CrossRef]
- Nucciotti, A.; Alpert, B.; Balata, M.; Becker, D.; Bennett, D.; Bevilacqua, A.; Biasotti, M.; Ceriale, V.; Ceruti, G.; Corsini, D.; et al. Status of the HOLMES Experiment to Directly Measure the Neutrino Mass. J. Low Temp. Phys. 2018, 183, 1137–1145. [Google Scholar] [CrossRef]
- Doriese, W.B.; Morgan, K.M.; Bennett, D.A.; Denison, E.V.; Fitzgerald, C.P.; Fowler, J.W.; Gard, J.D.; Hays-Wehle, J.P.; Hilton, G.C.; Irwin, K.D.; et al. Developments in Time-Division Multiplexing of X-ray Transition-Edge Sensors. J. Low Temp. Phys. 2016, 184, 389–395. [Google Scholar] [CrossRef] [PubMed]
- Morgan, K.M.; Alpert, B.K.; Bennett, D.A.; Denison, E.V.; Doriese, W.B.; Fowler, J.W.; Gard, J.D.; Hilton, G.C.; Irwin, K.D.; Joe, Y.I.; et al. Code-division-multiplexed readout of large arrays of TES microcalorimeters. Appl. Phys. Lett. 2016, 109, 112604. [Google Scholar] [CrossRef]
- Mates, J.A.B.; Becker, D.T.; Bennett, D.A.; Dober, B.J.; Gard, J.D.; Hays-Wehle, J.P.; Fowler, J.W.; Hilton, G.C.; Reintsema, C.D.; Schmidt, D.R.; et al. Simultaneous readout of 128 X-ray and gamma-ray transition-edge microcalorimeters using microwave SQUID multiplexing. Appl. Phys. Lett. 2017, 111, 062601. [Google Scholar] [CrossRef]
- van der Kuur, J.; Gottardi, L.; Akamatsu, H.; van Leeuwen, B.J.; den Hartog, R.; Haas, D.; Kiviranta, M.; Jackson, B.J. Optimising the multiplex factor of the frequency domain multiplexed readout of the TES-based microcalorimeter imaging array for the X-IFU instrument on the Athena X-ray observatory. In Space Telescopes and Instrumentation 2016: Ultraviolet to Gamma Ray; den Herder, J.W.A., Takahashi, T., Bautz, M., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2016; Volume 9905, pp. 1666–1674. [Google Scholar] [CrossRef]
- McCammon, D. Thermal Equilibrium Calorimeters—An Introduction. In Cryogenic Particle Detection; Enss, C., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 1–34. [Google Scholar] [CrossRef]
- Irwin, K.; Hilton, G. Transition-Edge Sensors. In Cryogenic Particle Detection; Enss, C., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 63–150. [Google Scholar] [CrossRef]
- Ullom, J.N.; Bennett, D.A. Review of superconducting transition-edge sensors for X-ray and gamma-ray spectroscopy. Supercond. Sci. Technol. 2015, 28, 084003. [Google Scholar] [CrossRef]
- Barret, D.; Trong, T.L.; Den Herder, J.W.; Piro, L.; Barcons, X.; Huovelin, J.; Kelley, R.; Mas-Hesse, J.M.; Mitsuda, K.; Paltani, S.; et al. The ATHENA X-ray Integral Field Unit (X-IFU). In Space Telescopes and Instrumentation 2018: Ultraviolet to Gamma Ray; den Herder, J.W.A., Nikzad, S., Nakazawa, K., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2018; Volume 10699, pp. 324–338. [Google Scholar] [CrossRef]
- Lindeman, M.A.; Bandler, S.; Brekosky, R.P.; Chervenak, J.A.; Figueroa-Feliciano, E.; Finkbeiner, F.M.; Li, M.J.; Kilbourne, C.A. Impedance measurements and modeling of a transition-edge-sensor calorimeter. Rev. Sci. Instrum. 2004, 75, 1283–1289. [Google Scholar] [CrossRef]
- Irwin, K. Thermodynamics of nonlinear bolometers near equilibrium. Nucl. Instrum. Methods Phys. Res. Sect. A 2006, 559, 718–720. [Google Scholar] [CrossRef]
- Irwin, K.D. An application of electrothermal feedback for high resolution cryogenic particle detection. Appl. Phys. Lett. 1995, 66, 1998–2000. [Google Scholar] [CrossRef]
- Sadleir, J.E.; Smith, S.J.; Bandler, S.R.; Chervenak, J.A.; Clem, J.R. Longitudinal Proximity Effects in Superconducting Transition-Edge Sensors. Phys. Rev. Lett. 2010, 104, 047003. [Google Scholar] [CrossRef]
- Sadleir, J.E.; Smith, S.J.; Robinson, I.K.; Finkbeiner, F.M.; Chervenak, J.A.; Bandler, S.R.; Eckart, M.E.; Kilbourne, C.A. Proximity effects and nonequilibrium superconductivity in transition-edge sensors. Phys. Rev. B 2011, 84, 184502. [Google Scholar] [CrossRef]
- de Wit, M.; Gottardi, L.; Taralli, E.; Nagayoshi, K.; Ridder, M.L.; Akamatsu, H.; Bruijn, M.P.; D’Andrea, M.; van der Kuur, J.; Ravensberg, K.; et al. High aspect ratio transition edge sensors for X-ray spectrometry. J. Appl. Phys. 2020, 128, 224501. [Google Scholar] [CrossRef]
- Ridder, M.L.; Nagayoshi, K.; Bruijn, M.P.; Gottardi, L.; Taralli, E.; Khosropanah, P.; Akamatsu, H.; van der Kuur, J.; Ravensberg, K.; Visser, S.; et al. Study of TES Detector Transition Curve to Optimize the Pixel Design for Frequency-Division Multiplexing Readout. J. Low Temp. Phys. 2020, 199, 962–967. [Google Scholar] [CrossRef]
- Likharev, K.K. Superconducting weak links. Rev. Mod. Phys. 1979, 51, 101–159. [Google Scholar] [CrossRef]
- Golubov, A.A.; Kupriyanov, M.Y.; Il’ichev, E. The current-phase relation in Josephson junctions. Rev. Mod. Phys. 2004, 76, 411–469. [Google Scholar] [CrossRef]
- Kupriyanov, M.Y.; Likharev, K.K.; Lukichev, V.F. Influence of effective electron interaction on the critical current of Josephson weak links. Physica 1981, 108B, 1001–1002. [Google Scholar] [CrossRef]
- Kupriyanov, M.Y.; Lukichev, V.F. Influence of the proximity effect in the electrodes on the stationary properties of S–N–S Josephson structures. Sov. J. Low Temp. Phys. 1982, 8, 526–529. [Google Scholar]
- Kozorezov, A.G.; Golubov, A.A.; Martin, D.D.E.; de Korte, P.A.J.; Lindeman, M.A.; Hijmering, R.A.; Wigmore, J.K. Microscopic Model of a Transition Edge Sensor as a Weak Link. IEEE Trans. Appl. Supercond. 2011, 21, 250–253. [Google Scholar] [CrossRef]
- Harwin, R.C.; Goldie, D.J.; Withington, S. Modelling proximity effects in transition edge sensors to investigate the influence of lateral metal structures. Supercond. Sci. Technol. 2017, 30, 084001. [Google Scholar] [CrossRef]
- Harwin, R.C.; Goldie, D.J.; Withington, S.; Khosropanah, P.; Gottardi, L.; Gao, J.R. Proximity effect model for X-ray transition edge sensors. In High Energy, Optical, and Infrared Detectors for Astronomy VIII; Holland, A.D., Beletic, J., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2018; Volume 10709, pp. 350–361. [Google Scholar] [CrossRef]
- Kozorezov, A.; Golubov, A.A.; Martin, D.D.E.; de Korte, P.A.J.; Lindeman, M.A.; Hijmering, R.A.; van der Kuur, J.; Hoevers, H.F.C.; Gottardi, L.; Kupriyanov, M.Y.; et al. Modelling the resistive state in a transition edge sensor. Appl. Phys. Lett. 2011, 99, 063503. [Google Scholar] [CrossRef]
- Coffey, W.T.; Kalmykov, Y.P.; Titov, S.V.; Cleary, L. Smoluchowski equation approach for quantum Brownian motion in a tilted periodic potential. Phys. Rev. E 2008, 78, 031114. [Google Scholar] [CrossRef]
- Ambegaokar, V.; Halperin, B.I. Voltage Due to Thermal Noise in the dc Josephson Effect. Phys. Rev. Lett. 1969, 22, 1364–1366. [Google Scholar] [CrossRef]
- Smith, S.J.; Adams, J.S.; Bailey, C.N.; Bandler, S.R.; Busch, S.E.; Chervenak, J.A.; Eckart, M.E.; Finkbeiner, F.M.; Kilbourne, C.A.; Kelley, R.L.; et al. Implications of weak-link behavior on the performance of Mo/Au bilayer transition-edge sensors. J. Appl. Phys. 2013, 114, 074513–074524. [Google Scholar] [CrossRef]
- Smith, S.J.; Adams, J.S.; Bailey, C.N.; Bandler, S.R.; Chervenak, J.A.; Eckart, M.E.; Finkbeiner, F.M.; Kelley, R.L.; Kilbourne, C.A.; Porter, F.S.; et al. Small Pitch Transition-Edge Sensors with Broadband High Spectral Resolution for Solar Physics. J. Low Temp. Phys. 2012, 167, 168–175. [Google Scholar] [CrossRef]
- Gottardi, L.; Akamatsu, H.; Bruijn, M.; Gao, J.R.; den Hartog, R.; Hijmering, R.; Hoevers, H.; Khosropanah, P.; Kozorezov, A.; van der Kuur, J.; et al. Weak-Link Phenomena in AC-Biased Transition Edge Sensors. J. Low Temp. Phys. 2014, 176, 279–284. [Google Scholar] [CrossRef]
- Bennett, D.A.; Swetz, D.S.; Schmidt, D.R.; Ullom, J.N. Resistance in transition-edge sensors: A comparison of the resistively shunted junction and two-fluid models. Phys. Rev. B 2013, 87, 020508. [Google Scholar] [CrossRef]
- Bennett, D.A.; Schmidt, D.R.; Swetz, D.S.; Ullom, J.N. Phase-slip lines as a resistance mechanism in transition-edge sensors. Appl. Phys. Lett. 2014, 104, 042602. [Google Scholar] [CrossRef]
- Irwin, K.D.; Hilton, G.C.; Wollman, D.A.; Martinis, J.M. Thermal-response time of superconducting transition-edge microcalorimeters. J. Appl. Phys. 1998, 83, 3978–3985. [Google Scholar] [CrossRef]
- Bennett, D.A.; Swetz, D.S.; Horansky, R.D.; Schmidt, D.R.; Ullom, J.N. A Two-Fluid Model for the Transition Shape in Transition-Edge Sensors. J. Low Temp. Phys. 2012, 167, 102–107. [Google Scholar] [CrossRef]
- Morgan, K.M.; Pappas, C.G.; Bennett, D.A.; Gard, J.D.; Hays-Wehle, J.P.; Hilton, G.C.; Reintsema, C.D.; Schmidt, D.R.; Ullom, J.N.; Swetz, D.S. Dependence of transition width on current and critical current in transition-edge sensors. Appl. Phys. Lett. 2017, 110, 212602. [Google Scholar] [CrossRef]
- Morgan, K.M.; Becker, D.T.; Bennett, D.A.; Doriese, W.B.; Gard, J.D.; Irwin, K.D.; Lee, S.J.; Li, D.; Mates, J.A.B.; Pappas, C.G.; et al. Use of Transition Models to Design High Performance TESs for the LCLS-II Soft X-ray Spectrometer. IEEE Trans. Appl. Supercond. 2019, 29, 1–5. [Google Scholar] [CrossRef]
- Kupriyanov, M.Y.; Likharev, K.K.; Lukichev, V.F. The Js(ψ) Relationship, Abrikosov Vortices and Josephson Vortices in Variable Thickness Bridges; North-Holland: Amsterdam, The Netherlands, 1975. [Google Scholar]
- Smith, S. Studies of weak-link phenomena in Mo/Au TESs. In Poster Presentation. TES Workshop. Applied Superc. Conference 2014; ASC Inc.: Charlotte, NC, USA, 2014. [Google Scholar]
- Sadleir, J. Unexpected nonlinear effects in superconducting Transition-Edge Sensors. In TES workshop. Applied Superc. Conference 2016; ASC Inc.: Denver, CO, USA, 2016. [Google Scholar]
- Zhou, Y.; Ambarish, C.V.; Gruenke, R.; Jaeckel, F.T.; Kripps, K.L.; McCammon, D.; Morgan, K.M.; Wulf, D.; Zhang, S.; Adams, J.S.; et al. Mapping TES Temperature Sensitivity and Current Sensitivity as a Function of Temperature, Current, and Magnetic Field with IV Curve and Complex Admittance Measurements. J. Low Temp. Phys. 2018, 193, 321–327. [Google Scholar] [CrossRef]
- Fraser, G. On the nature of the superconducting-to-normal transition in transition edge sensors. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2004, 523, 234–245. [Google Scholar] [CrossRef]
- Fàbrega, L.; Camón, A.; Pobes, C.; Strichovanec, P.; González-Arrabal, R. Large current-induced broadening of the superconducting transition in Mo/Au transition edge sensors. Supercond. Sci. Technol. 2018, 32, 015006. [Google Scholar] [CrossRef]
- Lindeman, M.A.; Dirks, B.; van der Kuur, J.; de Korte, P.A.J.; den Hartog, R.H.; Gottardi, L.; Hijmering, R.A.; Hoevers, H.F.C.; Khosropanah, P. Relationships Between Complex Impedance, Thermal Response, and Noise in TES Calorimeters and Bolometers. IEEE Trans. Appl. Supercond. 2011, 21, 254–257. [Google Scholar] [CrossRef]
- Takei, Y.; Gottardi, L.; Hoevers, H.F.C.; de Korte, P.A.J.; van der Kuur, J.; Ridder, M.L.; Bruijn, M.P. Characterization of a High-Performance Ti/Au TES Microcalorimeter with a Central Cu Absorber. J. Low Temp. Phys. 2008, 151, 161–166. [Google Scholar] [CrossRef]
- Kinnunen, K.M.; Palosaari, M.R.J.; Maasilta, I.J. Normal metal-superconductor decoupling as a source of thermal fluctuation noise in transition-edge sensors. J. Appl. Phys. 2012, 112, 034515. [Google Scholar] [CrossRef]
- Maasilta, I.J. Complex impedance, responsivity and noise of transition-edge sensors: Analytical solutions for two- and three-block thermal models. AIP Adv. 2012, 2, 042110. [Google Scholar] [CrossRef]
- Goldie, D.J.; Audley, M.D.; Glowacka, D.M.; Tsaneva, V.N.; Withington, S. Thermal models and noise in transition edge sensors. J. Appl. Phys. 2009, 105, 074512. [Google Scholar] [CrossRef]
- Wakeham, N.A.; Adams, J.S.; Bandler, S.R.; Beaumont, S.; Chervenak, J.A.; Datesman, A.M.; Eckart, M.E.; Finkbeiner, F.M.; Hummatov, R.; Kelley, R.L.; et al. Thermal fluctuation noise in Mo/Au superconducting transition-edge sensor microcalorimeters. J. Appl. Phys. 2019, 125, 164503. [Google Scholar] [CrossRef]
- Bruijn, M.P.; van der Linden, A.J.; Ferrari, L.; Gottardi, L.; van der Kuur, J.; den Hartog, R.H.; Akamatsu, H.; Jackson, B.D. LC Filters for FDM Readout of the X-IFU TES Calorimeter Instrument on Athena. J. Low Temp. Phys. 2018, 193, 661–667. [Google Scholar] [CrossRef]
- Bruijn, M.P.; Gottardi, L.; den Hartog, R.H.; van der Kuur, J.; van der Linden, A.J.; Jackson, B.D. Tailoring the High-Q LC Filter Arrays for Readout of Kilo-Pixel TES Arrays in the SPICA-SAFARI Instrument. J. Low Temp. Phys. 2014, 176, 421–425. [Google Scholar] [CrossRef]
- Kiviranta, M.; Seppä, H.; van der Kuur, J.; de Korte, P. SQUID-based readout schemes for microcalorimeter arrays. AIP Conf. Proc. 2002, 605, 295–300. [Google Scholar] [CrossRef]
- Gottardi, L.; van der Kuur, J.; Bruijn, M.; van der Linden, A.; Kiviranta, M.; Akamatsu, H.; den Hartog, R.; Ravensberg, K. Intrinsic Losses and Noise of High- Q Lithographic MHz LC Resonators for Frequency Division Multiplexing. J. Low Temp. Phys. 2019, 194, 370–376. [Google Scholar] [CrossRef]
- van der Kuur, J.; Gottardi, L.; Borderias, M.P.; Dirks, B.; de Korte, P.; Lindeman, M.; Khosropanah, P.; den Hartog, R.; Hoevers, H. Small-Signal Behavior of a TES Under AC Bias. IEEE Trans. Appl. Supercond. 2011, 21, 281–284. [Google Scholar] [CrossRef]
- Taralli, E.; Khosropanah, P.; Gottardi, L.; Nagayoshi, K.; Ridder, M.L.; Bruijn, M.P.; Gao, J.R. Complex impedance of TESs under AC bias using FDM readout system. AIP Adv. 2019, 9, 045324. [Google Scholar] [CrossRef]
- Gottardi, L.; Kozorezov, A.; Akamatsu, H.; van der Kuur, J.; Bruijn, M.P.; den Hartog, R.H.; Hijmering, R.; Khosropanah, P.; Lambert, C.; van der Linden, A.J.; et al. Josephson effects in an alternating current biased transition edge sensor. Appl. Phys. Lett. 2014, 105, 162605. [Google Scholar] [CrossRef]
- Coffey, W.T.; Kalmykov, Y.P.; Titov, S.V.; Cleary, L. Nonlinear noninertial response of a quantum Brownian particle in a tilted periodic potential to a strong ac force as applied to a point Josephson junction. Phys. Rev. B 2009, 79, 054507. [Google Scholar] [CrossRef]
- Coffey, W.T.; Déjardin, J.L.; Kalmykov, Y.P. Nonlinear impedance of a microwave-driven Josephson junction with noise. Phys. Rev. B 2000, 62, 3480–3487. [Google Scholar] [CrossRef]
- Gottardi, L.; Akamatsu, H.; van der Kuur, J.; Smith, S.J.; Kozorezov, A.; Chervenak, J. Study of TES-Based Microcalorimeters of Different Size and Geometry Under AC Bias. IEEE Trans. Appl. Supercond. 2017, 27, 1–4. [Google Scholar] [CrossRef]
- McDonald, J.; Clem, J.R. Microwave response and surface impedance of weak links. Phys. Rev. B 1997, 56, 14723–14732. [Google Scholar] [CrossRef]
- Kirsch, C.; Gottardi, L.; Lorenz, M.; Dauser, T.; den Hartog, R.; Jackson, B.; Peille, P.; Smith, S.; Wilms, J. Time-Domain Modeling of TES Microcalorimeters Under AC Bias. J. Low Temp. Phys. 2020, 199, 569–576. [Google Scholar] [CrossRef]
- Wilms, J.; Smith, S.J.; Peille, P.; Ceballos, M.T.; Cobo, B.; Dauser, T.; Brand, T.; den Hartog, R.H.; Bandler, S.R.; de Plaa, J.; et al. TESSIM: A simulator for the Athena-X-IFU. In Space Telescopes and Instrumentation 2016: Ultraviolet to Gamma Ray; den Herder, J.W.A., Takahashi, T., Bautz, M., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2016; Volume 9905, pp. 1795–1801. [Google Scholar] [CrossRef]
- Lorenz, M.; Kirsch, C.; Merino-Alonso, P.E.; Peille, P.; Dauser, T.; Cucchetti, E.; Smith, S.J.; Wilms, J. GPU Supported Simulation of Transition-Edge Sensor Arrays. J. Low Temp. Phys. 2020, 200, 277–285. [Google Scholar] [CrossRef]
- Jaeckel, F.T.; Ambarish, C.V.; Christensen, N.; Gruenke, R.; Hu, L.; McCammon, D.; McPheron, M.; Meyer, M.; Nelms, K.L.; Roy, A.; et al. Energy Calibration of High-Resolution X-ray TES Microcalorimeters With 3 eV Optical Photons. IEEE Trans. Appl. Supercond. 2019, 29, 1–4. [Google Scholar] [CrossRef]
- Jaeckel, F.T.; Ambarish, C.V.; Dai, H.; Liu, S.; Mccammon, D.; Mcpheron, M.; Nelms, K.L.; Roy, A.; Stueber, H.R.; Bandler, S.R.; et al. Calibration and Testing of Small High-Resolution Transition Edge Sensor Microcalorimeters with Optical Photons. IEEE Trans. Appl. Supercond. 2021, 31, 1–5. [Google Scholar] [CrossRef]
- Hoevers, H.F.C.; Bento, A.C.; Bruijn, M.P.; Gottardi, L.; Korevaar, M.A.N.; Mels, W.A.; de Korte, P.A.J. Thermal fluctuation noise in a voltage biased superconducting transition edge thermometer. Appl. Phys. Lett. 2000, 77, 4422–4424. [Google Scholar] [CrossRef]
- Gildemeister, J.M.; Lee, A.T.; Richards, P.L. Model for excess noise in voltage-biased superconducting bolometers. Appl. Opt. 2001, 40, 6229–6235. [Google Scholar] [CrossRef]
- Khosropanah, P.; Hijmering, R.A.; Ridder, M.; Lindeman, M.A.; Gottardi, L.; Bruijn, M.; Kuur, J.; Korte, P.A.J.; Gao, J.R.; Hoevers, H. Distributed TES Model for Designing Low Noise Bolometers Approaching SAFARI Instrument Requirements. J. Low Temp. Phys. 2012, 167, 188–194. [Google Scholar] [CrossRef][Green Version]
- Ullom, J.; Doriese, W.; Hilton, G.; Beall, J.; Deiker, S.; Irwin, K.; Reintsema, C.; Vale, L.; Xu, Y. Suppression of excess noise in Transition-Edge Sensors using magnetic field and geometry. Nucl. Instrum. Methods A 2004, 520, 333–335. [Google Scholar] [CrossRef]
- Jethava, N.; Ullom, J.N.; Irwin, K.D.; Doriese, W.B.; Beall, J.A.; Hilton, G.C.; Vale, L.R.; Zink, B. Dependence of Excess Noise on the Partial Derivatives of Resistance in Superconducting Transition Edge Sensors. AIP Conf. Proc. 2009, 1185, 31–33. [Google Scholar] [CrossRef]
- Wakeham, N.A.; Adams, J.S.; Bandler, S.R.; Chervenak, J.A.; Datesman, A.M.; Eckart, M.E.; Finkbeiner, F.M.; Kelley, R.L.; Kilbourne, C.A.; Miniussi, A.R.; et al. Effects of Normal Metal Features on Superconducting Transition-Edge Sensors. J. Low Temp. Phys. 2018, 193, 231–240. [Google Scholar] [CrossRef]
- Kozorezov, A.; Golubov, A.; Martin, D.; de Korte, P.; Lindeman, M.; Hijmering, R.; van der Kuur, J.; Hoevers, H.; Gottardi, L.; Kupriyanov, M.; et al. Electrical Noise in a TES as a Resistively Shunted Conducting Junction. J. Low Temp. Phys. 2012, 167, 108–113. [Google Scholar] [CrossRef]
- Likharev, K.; Semenov, V. Fluctuation Spectrum in Superconducting Point Junctions. Sov. Phys. JEPT Lett. 1972, 15, 442. [Google Scholar]
- Koch, R.H.; Van Harlingen, D.J.; Clarke, J. Quantum-Noise Theory for the Resistively Shunted Josephson Junction. Phys. Rev. Lett. 1980, 45, 2132–2135. [Google Scholar] [CrossRef]
- Wessel, A.; Morgan, K.; Becker, D.; Gard, J.; Hilton, G.; Mates, J.; Reintsema, C.; Schmidt, D.R.; Swetz, D.; Ullom, J.; et al. A Model for Excess Johnson Noise in Superconducting Transition-edge Sensors. arXiv 2019, arXiv:1907.11343. [Google Scholar]
- Kogan, S.M.; Nagaev, K. Fluctuation kinetics in superconductors at frequencies low compared with the energy gap. Zh. Eksp. Teor. Fiz 1988, 94, 262. [Google Scholar]
- Gottardi, L.; de Wit, M.; Kozorezov, A.; Taralli, E.; Nagayashi, K. Voltage fluctuations in ac biased superconducting transition edge sensors. Phys. Rev. Lett. 2021. accepted paper. [Google Scholar]
- Andrews, D.H.; Brucksch, W.F.; Ziegler, W.T.; Blanchard, E.R. Superconducting Films as Radiometric Receivers. Phys. Rev. 1941, 59, 1045–1046. [Google Scholar] [CrossRef]
- Gaskin, J.A.; Swartz, D.A.; Vikhlinin, A.; Özel, F.; Gelmis, K.E.; Arenberg, J.W.; Bandler, S.R.; Bautz, M.W.; Civitani, M.M.; Dominguez, A.; et al. Lynx X-ray Observatory: An overview. J. Astron. Telesc. 2019, 5, 021001. [Google Scholar] [CrossRef]
- Simionescu, A.; Ettori, S.; Werner, N.; Nagai, D.; Vazza, F.; Akamatsu, H.; Pinto, C.; de Plaa, J.; Wijers, N.; Nelson, D.; et al. Voyage through the Hidden Physics of the Cosmic Web. arXiv 2019, arXiv:1908.01778. [Google Scholar]
- Rothe, J.; Angloher, G.; Bauer, P.; Bento, A.; Bucci, C.; Canonica, L.; D’Addabbo, A.; Defay, X.; Erb, A.; Feilitzsch, F.V.; et al. TES-Based Light Detectors for the CRESST Direct Dark Matter Search. J. Low Temp. Phys. 2018, 193, 1160–1166. [Google Scholar] [CrossRef]
- Lita, A.E.; Rosenberg, D.; Nam, S.; Miller, A.J.; Balzar, D.; Kaatz, L.M.; Schwall, R.E. Tuning of tungsten thin film superconducting transition temperature for fabrication of photon number resolving detectors. IEEE Trans. Appl. Supercond. 2005, 15, 3528–3531. [Google Scholar] [CrossRef]
- Hubmayr, J.; Austermann, J.E.; Beall, J.A.; Becker, D.; Bennett, D.A.; Benson, B.A.; Bleem, L.E.; Chang, C.L.; Carlstrom, J.E.; Cho, H.; et al. Stability of Al-Mn Transition Edge Sensors for Frequency Domain Multiplexing. IEEE Trans. Appl. Supercond. 2011, 21, 203–206. [Google Scholar] [CrossRef]
- Nagayoshi, K.; Ridder, M.L.; Bruijn, M.P.; Gottardi, L.; Taralli, E.; Khosropanah, P.; Akamatsu, H.; Visser, S.; Gao, J.R. Development of a Ti/Au TES Microcalorimeter Array as a Backup Sensor for the Athena/X-IFU Instrument. J. Low Temp. Phys. 2020, 199, 943–948. [Google Scholar] [CrossRef]
- Finkbeiner, F.M.; Adams, J.S.; Bandler, S.R.; Betancourt-Martinez, G.L.; Brown, A.D.; Chang, M.P.; Chervenak, J.A.; Chiao, M.P.; Datesman, A.M.; Eckart, M.E.; et al. Electron-Beam Deposition of Superconducting Molybdenum Thin Films for the Development of Mo/Au TES X-ray Microcalorimeter. IEEE Trans. Appl. Supercond. 2017, 27, 2633785. [Google Scholar] [CrossRef]
- Parra-Borderias, M.; Fernandez-Martinez, I.; Fabrega, L.; Camon, A.; Gil, O.; Costa-Kramer, J.L.; Gonzalez-Arrabal, R.; Sese, J.; Bueno, J.; Briones, F. Characterization of a Mo/Au Thermometer for ATHENA. IEEE Trans. Appl. Supercond. 2013, 23, 2300405. [Google Scholar] [CrossRef]
- Fabrega, L.; Fernandez-Martinez, I.; Gil, O.; Parra-Borderias, M.; Camon, A.; Costa-Kramer, J.; Gonzalez-Arrabal, R.; Sese, J.; Briones, F.; Santiso, J.; et al. Mo-Based Proximity Bilayers for TES: Microstructure and Properties. IEEE Trans. Appl. Supercond. 2009, 19, 460–464. [Google Scholar] [CrossRef]
- Chervenak, J.A.; Finkbeiner, F.M.; Bandler, S.R.; Brekosky, R.; Brown, A.D.; Iyomoto, N.; Kelley, R.L.; Kilbourne, C.A.; Porter, F.S.; Sadleir, J.; et al. Materials Development for Auxiliary Components for Large Compact Mo/Au TES Arrays. J. Low Temp. Phys. 2008, 151, 255–260. [Google Scholar] [CrossRef]
- Orlando, A.; Ceriale, V.; Ceruti, G.; De Gerone, M.; Faverzani, M.; Ferri, E.; Gallucci, G.; Giachero, A.; Nucciotti, A.; Puiu, A.; et al. Microfabrication of Transition-Edge Sensor Arrays of Microcalorimeters with 163Ho for Direct Neutrino Mass Measurements with HOLMES. J. Low Temp. Phys. 2018, 193, 771–776. [Google Scholar] [CrossRef]
- Kunieda, Y.; Takahashi, H.; Zen, N.; Damayanthi, R.; Mori, F.; Fujita, K.; Nakazawa, M.; Fukuda, D.; Ohkubo, M. Characterization of Ir/Au pixel TES. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2006, 559, 429–431. [Google Scholar] [CrossRef]
- Lolli, L.; Taralli, E.; Portesi, C.; Rajteri, M.; Monticone, E. Aluminum–Titanium Bilayer for Near-Infrared Transition Edge Sensors. Sensors 2016, 16, 953. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, K.; Liu, J.; Liu, Q.; Li, G.; Liu, J.; Chen, W. Fabrication and Characterization of Superconducting Bilayer (Al/Ti) Transition-Edge Sensor Bolometer Array. J. Electron. Mater. 2019, 48, 925–929. [Google Scholar] [CrossRef]
- Huang, R.; Zhong, X.F.; Zhang, B.; Koza, J.; Smith, S.; Simmons, S. Super planarizing material for trench and via arrays. In Advances in Patterning Materials and Processes XXXVII; Gronheid, R., Sanders, D.P., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2020; Volume 11326, pp. 317–323. [Google Scholar] [CrossRef]
- Devasia, A.M.; Balvin, M.A.; Bandler, S.R.; Bolkhovsky, V.; Nagler, P.C.; Ryu, K.; Smith, S.J.; Stevenson, T.R.; Yoon, W. Fabrication of Magnetic Calorimeter Arrays With Buried Wiring. IEEE Trans. Appl. Supercond. 2019, 29, 1–6. [Google Scholar] [CrossRef]
- Yohannes, D.T.; Hunt, R.T.; Vivalda, J.A.; Amparo, D.; Cohen, A.; Vernik, I.V.; Kirichenko, A.F. Planarized, Extendible, Multilayer Fabrication Process for Superconducting Electronics. IEEE Trans. Appl. Supercond. 2015, 25, 2365562. [Google Scholar] [CrossRef]
- Ridder, M.L.; Khosropanah, P.; Hijmering, R.A.; Suzuki, T.; Bruijn, M.P.; Hoevers, H.F.C.; Gao, J.R.; Zuiddam, M.R. Fabrication of Low-Noise TES Arrays for the SAFARI Instrument on SPICA. J. Low Temp. Phys. 2016, 184, 60–65. [Google Scholar] [CrossRef]
- Bandler, S.R.; Chervenak, J.A.; Datesman, A.M.; Devasia, A.M.; DiPirro, M.J.; Sakai, K.; Smith, S.J.; Stevenson, T.R.; Yoon, W.; Bennett, D.A.; et al. Lynx X-ray microcalorimeter. J. Astron. Telesc. Instrum. Syst. 2019, 5, 1–29. [Google Scholar] [CrossRef]
- Miniussi, A.R.; Adams, J.S.; Bandler, S.R.; Beaumont, S.; Chang, M.P.; Chervenak, J.A.; Finkbeiner, F.M.; Ha, J.Y.; Hummatov, R.; Kelley, R.L.; et al. Thermal Crosstalk Measurements and Simulations for an X-ray Microcalorimeter Array. J. Low Temp. Phys. 2020, 199, 663–671. [Google Scholar] [CrossRef]
- Brown, A.D.; Bandler, S.R.; Brekosky, R.; Chervenak, J.A.; Figueroa-Feliciano, E.; Finkbeiner, F.; Iyomoto, N.; Kelley, R.L.; Kilbourne, C.A.; Porter, F.S.; et al. Absorber Materials for Transition-Edge Sensor X-ray Microcalorimeters. J. Low Temp. Phys. 2008, 151, 413–417. [Google Scholar] [CrossRef]
- Yan, D.; Divan, R.; Gades, L.M.; Kenesei, P.; Madden, T.J.; Miceli, A.; Park, J.S.; Patel, U.M.; Quaranta, O.; Sharma, H.; et al. Eliminating the non-Gaussian spectral response of X-ray absorbers for transition-edge sensors. Appl. Phys. Lett. 2017, 111, 192602. [Google Scholar] [CrossRef]
- Hummatov, R.; Adams, J.S.; Bandler, S.R.; Barlis, A.; Beaumont, S.; Chang, M.P.; Chervenak, J.A.; Datesman, A.M.; Eckart, M.E.; Finkbeiner, F.M.; et al. Quantum Efficiency Study and Reflectivity Enhancement of Au/Bi Absorbers. J. Low Temp. Phys. 2020, 199, 393–400. [Google Scholar] [CrossRef]
- Gottardi, L.; Adams, J.; Bailey, C.; Bandler, S.; Bruijn, M.; Chervenak, J.; Eckart, M.; Finkbeiner, F.; den Hartog, R.; Hoevers, H.; et al. Study of the Dependency on Magnetic Field and Bias Voltage of an AC-Biased TES Microcalorimeter. J. Low Temp. Phys. 2012, 167, 214–219. [Google Scholar] [CrossRef]
- Taralli, E.; Pobes, C.; Khosropanah, P.; Fabrega, L.; Camón, A.; Gottardi, L.; Nagayoshi, K.; Ridder, M.L.; Bruijn, M.P.; Gao, J.R. AC/DC Characterization of a Ti/Au TES with Au/Bi Absorber for X-ray Detection. J. Low Temp. Phys. 2020, 199, 102–109. [Google Scholar] [CrossRef]
- Lindeman, M.A.; Bandler, S.; Brekosky, R.P.; Chervenak, J.A.; Figueroa-Feliciano, E.; Finkbeiner, F.M.; Saab, T.; Stahle, C.K. Characterization and reduction of noise in Mo/Au transition edge sensors. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2004, 520, 348–350. [Google Scholar] [CrossRef]
- Smith, S.J.; Adams, J.S.; Bandler, S.R.; Busch, S.E.; Chervenak, J.A.; Eckart, M.E.; Finkbeiner, F.M.; Kelley, R.L.; Kilbourne, C.A.; Lee, S.J.; et al. Characterization of Mo/Au Transition-Edge Sensors with Different Geometric Configurations. J. Low Temp. Phys. 2014, 176, 356–362. [Google Scholar] [CrossRef]
- Zhang, S.; Eckart, M.E.; Jaeckel, F.T.; Kripps, K.L.; McCammon, D.; Morgan, K.M.; Zhou, Y. Mapping of the resistance of a superconducting transition edge sensor as a function of temperature, current, and applied magnetic field. J. Appl. Phys. 2017, 121, 074503. [Google Scholar] [CrossRef]
- Swetz, D.; Bennett, D.; Irwin, K.; Schmidt, D.; Ullom, J. Current distribution and transition width in superconducting transition-edge sensors. Appl. Phys. Lett. 2012, 101, 242603. [Google Scholar] [CrossRef]
- Miniussi, A.R.; Adams, J.S.; Bandler, S.R.; Chervenak, J.A.; Datesman, A.M.; Eckart, M.E.; Ewin, A.J.; Finkbeiner, F.M.; Kelley, R.L.; Kilbourne, C.A.; et al. Performance of an X-ray Microcalorimeter with a 240 m Absorber and a 50 m TES Bilayer. J. Low Temp. Phys. 2018, 193, 337–343. [Google Scholar] [CrossRef]
- Yoon, W.; Adams, J.S.; Bandler, S.R.; Betancourt-Martinez, G.L.; Chiao, M.P.; Chang, M.; Chervenak, J.A.; Datesman, A.; Eckart, M.E.; Ewin, A.J.; et al. Design and Performance of Hybrid Arrays of Mo/Au Bilayer Transition-Edge Sensors. IEEE Trans. Appl. Supercond. 2017, 27, 1–5. [Google Scholar] [CrossRef]
- Smith, S.J.; Adams, J.S.; Bandler, S.R.; Beaumont, S.; Chervenak, J.A.; Datesman, A.M.; Finkbeiner, F.M.; Hummatov, R.; Kelly, R.L.; Kilbourne, C.A.; et al. Toward 100,000-Pixel Microcalorimeter Arrays Using Multi-absorber Transition-Edge Sensors. J. Low Temp. Phys. 2020, 199, 330–338. [Google Scholar] [CrossRef]
- Sakai, K.; Adams, J.S.; Bandler, S.R.; Beaumont, S.; Chervenak, J.A.; Datesman, A.M.; Finkbeiner, F.M.; Kelley, R.L.; Kilbourne, C.A.; Miniussi, A.R.; et al. Demonstration of Fine-Pitch High-Resolution X-ray Transition-Edge Sensor Microcalorimeters Optimized for Energies below 1 keV. J. Low Temp. Phys. 2020, 199, 949–954. [Google Scholar] [CrossRef]
- Sakai, K.; Adams, J.S.; Bandler, S.R.; Chervenak, J.A.; Datesman, A.M.; Eckart, M.E.; Finkbeiner, F.M.; Kelley, R.L.; Kilbourne, C.A.; Miniussi, A.R.; et al. Study of Dissipative Losses in AC-Biased Mo/Au Bilayer Transition-Edge Sensors. J. Low Temp. Phys. 2018, 193, 356–364. [Google Scholar] [CrossRef]
- Akamatsu, H.; Gottardi, L.; Adams, J.; Bandler, S.; Bruijn, M.; Chervenak, J.; Eckart, M.; Finkbeiner, F.; den Hartog, R.; Hoevers, H.; et al. Performance of TES X-ray Microcalorimeters with AC Bias Read-Out at MHz Frequencies. J. Low Temp. Phys. 2014, 176, 591–596. [Google Scholar] [CrossRef]
- Gottardi, L.; Smith, S.J.; Kozorezov, A.; Akamatsu, H.; van der Kuur, J.; Bandler, S.R.; Bruijn, M.P.; Chervenak, J.A.; Gao, J.R.; den Hartog, R.H.; et al. Josephson Effects in Frequency-Domain Multiplexed TES Microcalorimeters and Bolometers. J. Low Temp. Phys. 2018, 193, 209–216. [Google Scholar] [CrossRef]
- Taralli, E.; Gottardi, L.; Nagayoshi, K.; Ridder, M.; Visser, S.; Khosropanah, P.; Akamatsu, H.; van der Kuur, J.; Bruijn, M.; Gao, J.R. Characterization of High Aspect-Ratio TiAu TES X-ray Microcalorimeter Array Under AC Bias. J. Low Temp. Phys. 2020, 199, 80–87. [Google Scholar] [CrossRef]
- Taralli, E.; D’Andrea, M.; Gottardi, L.; Nagayoshi, K.; Ridder, M.L.; de Wit, M.; Vaccaro, D.; Akamatsu, H.; Bruijn, M.P.; Gao, J.R. Performance and uniformity of a kilo-pixel array of Ti/Au transition-edge sensor microcalorimeters. Rev. Sci. Instrum. 2021, 92, 023101. [Google Scholar] [CrossRef]
- D’Andrea, M.; Taralli, E.; Akamatsu, H.; Gottardi, L.; Nagayoshi, K.; Ravensberg, K.; Ridder, M.L.; Vaccaro, D.; de Vries, C.P.; de Wit, M.; et al. Single pixel performance of a 32×32 Ti/Au TES array with broadband X-ray spectra. arXiv 2021, arXiv:2102.08103. [Google Scholar]
- Hoevers, H.F.C.; Ridder, M.L.; Germeau, A.; Bruijn, M.P.; de Korte, P.A.J.; Wiegerink, R.J. Radiative ballistic phonon transport in silicon-nitride membranes at low temperatures. Appl. Phys. Lett. 2005, 86, 251903. [Google Scholar] [CrossRef]
- Hays-Wehle, J.P.; Schmidt, D.R.; Ullom, J.N.; Swetz, D.S. Thermal Conductance Engineering for High-Speed TES Microcalorimeters. J. Low Temp. Phys. 2016, 184, 492–497. [Google Scholar] [CrossRef]
- Doriese, W.B.; Bandler, S.R.; Chaudhuri, S.; Dawson, C.S.; Denison, E.V.; Duff, S.M.; Durkin, M.; FitzGerald, C.T.; Fowler, J.W.; Gard, J.D.; et al. Optimization of Time- and Code-Division-Multiplexed Readout for Athena X-IFU. IEEE Trans. Appl. Supercond. 2019, 29, 1–5. [Google Scholar] [CrossRef]
- Vaccaro, D.; Akamatsu, H.; van der Kuur, J.; van der Hulst, P.; Nieuwenhuizen, A.C.T.; van Winden, P.; Gottardi, L.; den Hartog, R.; Bruijn, M.P.; D’Andrea, M.; et al. Frequency Shift Algorithm: Application to a Frequency-Domain Multiplexing Readout of X-ray Transition-Edge Sensor Microcalorimeters. arXiv 2021, arXiv:2102.06092. [Google Scholar]
- Akamatsu, H.; Gottardi, L.; van der Kuur, J.; de Vries, C.P.; Bruijn, M.P.; Chervenak, J.A.; Kiviranta, M.; van den Linden, A.J.; Jackson, B.D.; Miniussi, A.; et al. Progress in the Development of Frequency-Domain Multiplexing for the X-ray Integral Field Unit on Board the Athena Mission. J. Low Temp. Phys. 2020, 199, 737–744. [Google Scholar] [CrossRef]
- Durkin, M.; Adams, J.S.; Bandler, S.R.; Chervenak, J.A.; Chaudhuri, S.; Dawson, C.S.; Denison, E.V.; Doriese, W.B.; Duff, S.M.; Finkbeiner, F.M.; et al. Demonstration of Athena X-IFU Compatible 40-Row Time-Division-Multiplexed Readout. IEEE Trans. Appl. Supercond. 2019, 29, 1–5. [Google Scholar] [CrossRef]
- Bennett, D.A.; Mates, J.A.B.; Bandler, S.R.; Becker, D.T.; Fowler, J.W.; Gard, J.D.; Hilton, G.C.; Irwin, K.D.; Morgan, K.M.; Reintsema, C.D.; et al. Microwave SQUID multiplexing for the Lynx X-ray microcalorimeter. J. Astron. Telesc. Instrum. Syst. 2019, 5, 1–10. [Google Scholar] [CrossRef]
- Kempf, S.; Wegner, M.; Fleischmann, A.; Gastaldo, L.; Herrmann, F.; Papst, M.; Richter, D.; Enss, C. Demonstration of a scalable frequency-domain readout of metallic magnetic calorimeters by means of a microwave SQUID multiplexer. AIP Adv. 2017, 7, 015007. [Google Scholar] [CrossRef]
- Irwin, K.D. Shannon Limits for Low-Temperature Detector Readout. AIP Conf. Proc. 2009, 1185, 229–236. [Google Scholar]
- Yu, C.; Ames, A.; Chaudhuri, S.; Dawson, C.; Irwin, K.D.; Kuenstner, S.E.; Li, D.; Titus, C.J. An impedance-modulated code-division microwave SQUID multiplexer. Eng. Res. Express 2020, 2, 015011. [Google Scholar] [CrossRef]
- Doriese, W.B.; Abbamonte, P.; Alpert, B.K.; Bennett, D.A.; Denison, E.V.; Fang, Y.; Fischer, D.A.; Fitzgerald, C.P.; Fowler, J.W.; Gard, J.D.; et al. A practical superconducting-microcalorimeter X-ray spectrometer for beamline and laboratory science. Rev. Sci. Instrum. 2017, 88, 053108. [Google Scholar] [CrossRef]
- Smith, S.J.; Adams, J.S.; Bandler, S.R.; Beaumont, S.; Chervenak, J.A.; Denison, E.V.; Doriese, W.B.; Durkin, M.; Finkbeiner, F.M.; Fowler, J.W.; et al. Performance of a Broad-Band, High-Resolution, Transition-Edge Sensor Spectrometer for X-ray Astrophysics. IEEE Trans. Appl. Supercond. 2021, 31, 1–6. [Google Scholar] [CrossRef]
- Stiehl, G.M.; Doriese, W.B.; Fowler, J.W.; Hilton, G.C.; Irwin, K.D.; Reintsema, C.D.; Schmidt, D.R.; Swetz, D.S.; Ullom, J.N.; Vale, L.R. Code-division multiplexing for X-ray microcalorimeters. Appl. Phys. Lett. 2012, 100, 072601. [Google Scholar] [CrossRef]
- Weber, J.C.; Fowler, J.W.; Durkin, M.; Morgan, K.M.; Mates, J.A.B.; Bennett, D.A.; Doriese, W.B.; Schmidt, D.R.; Hilton, G.C.; Swetz, D.S.; et al. Configurable error correction of code-division multiplexed TES detectors with a cryotron switch. Appl. Phys. Lett. 2019, 114, 232602. [Google Scholar] [CrossRef]
- van der Kuur, J.; de Korte, P.; Hoevers, H.; Kiviranta, M.; Seppä, H. Performance of an X-ray microcalorimeter under AC biasing. Appl. Phys. Lett. 2002, 81, 4467–4469. [Google Scholar] [CrossRef]
- Hattori, K.; Akiba, Y.; Arnold, K.; Barron, D.; Bender, A.N.; Cukierman, A.; de Haan, T.; Dobbs, M.; Elleflot, T.; Hasegawa, M.; et al. Development of Readout Electronics for POLARBEAR-2 Cosmic Microwave Background Experiment. J. Low Temp. Phys. 2016, 184, 512–518. [Google Scholar] [CrossRef]
- Bender, A.N.; Anderson, A.J.; Avva, J.S.; Ade, P.A.R.; Ahmed, Z.; Barry, P.S.; Thakur, R.B.; Benson, B.A.; Bryant, L.; Byrum, K.; et al. On-Sky Performance of the SPT-3G Frequency-Domain Multiplexed Readout. J. Low Temp. Phys. 2020, 199, 182–191. [Google Scholar] [CrossRef]
- Bruijn, M.P.; Gottardi, L.; den Hartog, R.H.; Hoevers, H.F.C.; Kiviranta, M.; de Korte, P.A.J.; van der Kuur, J. High-Q LC Filters for FDM Read out of Cryogenic Sensor Arrays. J. Low Temp. Phys. 2012, 167, 695–700. [Google Scholar] [CrossRef]
- Rotermund, K.; Barch, B.; Chapman, S.; Hattori, K.; Lee, A.; Palaio, N.; Shirley, I.; Suzuki, A.; Tran, C. Planar Lithographed Superconducting LC Resonators for Frequency-Domain Multiplexed Readout Systems. J. Low Temp. Phys. 2016, 184, 486–491. [Google Scholar] [CrossRef]
- den Hartog, R.; Audley, M.D.; Beyer, J.; Boersma, D.; Bruijn, M.; Gottardi, L.; Hoevers, H.; Hou, R.; Keizer, G.; Khosropanah, P.; et al. Low-Noise Readout of TES Detectors with Baseband Feedback Frequency Domain Multiplexing. J. Low Temp. Phys. 2012, 167, 652–657. [Google Scholar] [CrossRef][Green Version]
- den Hartog, R.; Boersma, D.; Bruijn, M.; Dirks, B.; Gottardi, L.; Hoevers, H.; Hou, R.; Kiviranta, M.; de Korte, P.; van der Kuur, J.; et al. Baseband Feedback for Frequency-Domain-Multiplexed Readout of TES X-ray Detectors. AIP Conf. Proc. 2009, 1185, 261–264. [Google Scholar] [CrossRef]
- de Haan, T.; Smecher, G.; Dobbs, M. Improved performance of TES bolometers using digital feedback. In Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VI; Holland, W.S., Ed.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2012; Volume 8452, pp. 113–122. [Google Scholar] [CrossRef]
- van der Kuur, J.; Gottardi, L.; Akamatsu, H.; van Leeuwen, B.J.; den Hartog, R.; Kiviranta, M.; Jackson, B. Thermal Load Minimization of the Frequency Domain Multiplexed Readout for the Athenar X-IFU Instrument. IEEE Trans. Appl. Supercond. 2017, 27, 1–4. [Google Scholar] [CrossRef]
- Kiviranta, M.; Grönberg, L.; Sipola, H. Two-stage locally linearized SQUID readout for frequency domain multiplexed calorimeter arrays. Supercond. Sci. Technol. 2011, 24, 045003. [Google Scholar] [CrossRef][Green Version]
- van der Kuur, J.; Gottardi, L.; Akamatsu, H.; Nieuwenhuizen, A.C.T.; den Hartog, R.; Jackson, B.D. Active Tuning of the Resonance Frequencies of LC Bandpass Filters for Frequency Domain Multiplexed Readout of TES Detector Arrays. J. Low Temp. Phys. 2018, 193, 626–632. [Google Scholar] [CrossRef]
- Akamatsu, H.; Vaccaro, D.; Gottardi, L.; van der Kuur, J.; de Vries, C.P.; Bandler, S.R.; Bruijn, M.P.; Chervenak, J.A.; D’Andrea, M.; Gao, J.R.; et al. Frequency domain multiplexing technology of transition-edge sensors for X-ray astronomy. In Space Telescopes and Instrumentation 2020: Ultraviolet to Gamma Ray; den Herder, J.W.A., Nikzad, S., Nakazawa, K., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2020; Volume 11444. [Google Scholar] [CrossRef]
- Akamatsu, H.; Vaccaro, D.; Gottardi, L.; van der Kuur, J.; de Vries, C.P.; Ravensberg, K.; Kiviranta, M.; D’Andrea, M.; Taralli, E.; de Wit, M.; et al. Demonstration of a simultaneous readout of 37 Transition Edge Sensors X-ray microcalorimeters with frequency domain multiplexing. 2021; unpublished work. [Google Scholar]
- Kiviranta, M. Class-B cable-driving SQUID amplifier. arXiv 2020, arXiv:2011.11741. [Google Scholar]
- Kiviranta, M.; Grönberg, L.; van der Kuur, J. Two SQUID amplifiers intended to alleviate the summing node inductance problem in multiplexed arrays of Transition Edge Sensors. arXiv 2018, arXiv:1810.09122. [Google Scholar]
- Irwin, K.D.; Lehnert, K.W. Microwave SQUID multiplexer. Appl. Phys. Lett. 2004, 85, 2107–2109. [Google Scholar] [CrossRef]
- Mates, J.A.B.; Hilton, G.C.; Irwin, K.D.; Vale, L.R.; Lehnert, K.W. Demonstration of a multiplexer of dissipationless superconducting quantum interference devices. Appl. Phys. Lett. 2008, 92, 023514. [Google Scholar] [CrossRef]
- Mates, J.A.B.; Becker, D.T.; Bennett, D.A.; Dober, B.J.; Gard, J.D.; Hilton, G.C.; Swetz, D.S.; Vale, L.R.; Ullom, J.N. Crosstalk in microwave SQUID multiplexers. Appl. Phys. Lett. 2019, 115, 202601. [Google Scholar] [CrossRef]
- Richter, D.; Hoibl, L.; Wolber, T.; Karcher, N.; Fleischmann, A.; Enss, C.; Weber, M.; Sander, O.; Kempf, S. Flux ramp modulation based MHz frequency-division dc-SQUID multiplexer. arXiv 2021, arXiv:2101.06424. [Google Scholar]
- Alpert, B.; Becker, D.; Bennet, D.; Biasotti, M.; Borghesi, M.; Gallucci, G.; De Gerone, M.; Faverzani, M.; Ferri, E.; Fowler, J.; et al. High-resolution high-speed microwave-multiplexed low temperature microcalorimeters for the HOLMES experiment. Eur. Phys. J. C 2019, 79, 304. [Google Scholar] [CrossRef]
- Nakashima, Y.; Hirayama, F.; Kohjiro, S.; Yamamori, H.; Nagasawa, S.; Sato, A.; Yamada, S.; Hayakawa, R.; Yamasaki, N.Y.; Mitsuda, K.; et al. Low-noise microwave SQUID multiplexed readout of 38 X-ray transition-edge sensor microcalorimeters. Appl. Phys. Lett. 2020, 117, 122601. [Google Scholar] [CrossRef]
- Irwin, K.D.; Chaudhuri, S.; Cho, H.M.; Dawson, C.; Kuenstner, S.; Li, D.; Titus, C.J.; Young, B.A. A Spread-Spectrum SQUID Multiplexer. J. Low Temp. Phys. 2018, 193, 476–484. [Google Scholar] [CrossRef]
- Smith, S.J.; Adams, J.S.; Bandler, S.R.; Chervenak, J.A.; Datesman, A.M.; Eckart, M.E.; Finkbeiner, F.M.; Hummatov, R.; Kelley, R.L.; Kilbourne, C.A.; et al. Multiabsorber transition-edge sensors for X-ray astronomy. J. Astron. Telesc. Instrum. Syst. 2019, 5, 1–11. [Google Scholar] [CrossRef]
- Jackson, B.D.; van Weers, H.; van der Kuur, J.; den Hartog, R.; Akamatsu, H.; Argan, A.; Bandler, S.R.; Barbera, M.; Barret, D.; Bruijn, M.P.; et al. The focal plane assembly for the Athena X-ray Integral Field Unit instrument. In Space Telescopes and Instrumentation 2016: Ultraviolet to Gamma Ray; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; den Herder, J.W.A., Takahashi, T., Bautz, M., Eds.; SPIE: Bellingham, WA, USA, 2016; Volume 9905, p. 99052I. [Google Scholar] [CrossRef]
- Geoffray, H.; Jackson, B.; Bandler, S.; Doriese, W.B.; Kirivanta, M.; Prêle, D.; Ravera, L.; Argan, A.; Barbera, M.; van der Kuur, J.; et al. Conceptual design of the detection chain for the X-IFU on Athena. In Space Telescopes and Instrumentation 2020: Ultraviolet to Gamma Ray; den Herder, J.W.A., Nikzad, S., Nakazawa, K., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2020; Volume 11444. [Google Scholar] [CrossRef]
- van Weers, H. The X-IFU focal plane assembly development model integration and first test results. In Space Telescopes and Instrumentation 2020: Ultraviolet to Gamma Ray; den Herder, J.W.A., Nikzad, S., Nakazawa, K., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2020; Volume 11444. [Google Scholar] [CrossRef]
- Barbera, M.; Cicero, U.L.; Sciortino, L.; D’Anca, F.; Cicero, G.L.; Parodi, G.; Sciortino, S.; Rauw, G.; Branduardi-Raymont, G.; Varisco, S.; et al. ATHENA X-IFU thermal filters development status toward the end of the instrument phase-A. In Space Telescopes and Instrumentation 2018: Ultraviolet to Gamma Ray; den Herder, J.W.A., Nikzad, S., Nakazawa, K., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2018; Volume 10699, pp. 406–420. [Google Scholar] [CrossRef]
- Peille, P.; den Hartog, R.; Miniussi, A.; Stever, S.; Bandler, S.; Kirsch, C.; Lorenz, M.; Dauser, T.; Wilms, J.; Lotti, S.; et al. Quantifying the Effect of Cosmic Ray Showers on the X-IFU Energy Resolution. J. Low Temp. Phys. 2020, 199, 240–249. [Google Scholar] [CrossRef]
- Lotti, S.; Macculi, C.; D’Andrea, M.; Fioretti, V.; Dondero, P.; Mantero, A.; Minervini, G.; Argan, A.; Piro, L. Estimates for the background of the ATHENA X-IFU instrument: The cosmic rays contribution. In Space Telescopes and Instrumentation 2018: Ultraviolet to Gamma Ray; den Herder, J.W.A., Nikzad, S., Nakazawa, K., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2018; Volume 10699, pp. 397–405. [Google Scholar] [CrossRef]
- Gottardi, L.; van Weers, H.; Dercksen, J.; Akamatsu, H.; Bruijn, M.P.; Gao, J.R.; Jackson, B.; Khosropanah, P.; van der Kuur, J.; Ravensberg, K.; et al. A six-degree-of-freedom micro-vibration acoustic isolator for low-temperature radiation detectors based on superconducting transition-edge sensors. Rev. Sci. Instrum. 2019, 90, 055107. [Google Scholar] [CrossRef]
- Miniussi, A.R.; Adams, J.S.; Bandler, S.R.; Beaumont, S.; Chang, M.P.; Chervenak, J.A.; Finkbeiner, F.M.; Ha, J.Y.; Hummatov, R.; Kelley, R.L.; et al. Thermal Impact of Cosmic Ray Interaction with an X-ray Microcalorimeter Array. J. Low Temp. Phys. 2020, 199, 45–55. [Google Scholar] [CrossRef]
- Lotti, S.; D’Andrea, M.; Molendi, S.; Macculi, C.; Minervini, G.; Fioretti, V.; Laurenza, M.; Jacquey, C.; Piro, L. Review of the Particle Background of the Athena X-IFU Instrument. Astrophys. J. 2021, 909, 111. [Google Scholar] [CrossRef]
- Macculi, C.; Argan, A.; Brienza, D.; D’Andrea, M.; Lotti, S.; Minervini, G.; Piro, L.; Biasotti, M.; Barusso, L.F.; Gatti, F.; et al. The cryogenic anticoincidence detector for ATHENA X-IFU: Advancement in the project. In Space Telescopes and Instrumentation 2020: Ultraviolet to Gamma Ray; den Herder, J.W.A., Nikzad, S., Nakazawa, K., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2020; Volume 11444, pp. 686–697. [Google Scholar] [CrossRef]
- Cui, W.; Bregman, J.N.; Bruijn, M.P.; Chen, L.B.; Chen, Y.; Cui, C.; Fang, T.T.; Gao, B.; Gao, H.; Gao, J.R.; et al. HUBS: A Dedicated Hot Circumgalactic Medium Explorer. In Space Telescopes and Instrumentation 2020: Ultraviolet to Gamma Ray; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; SPIE: Bellingham, WA, USA, 2020; Volume 11444, p. 114442S. [Google Scholar]
- Wang, G.; Bruijn, M.; Nagayoshi, K.; Ridder, M.; Taralli, E.; Gottardi, L.; Akamatsu, H.; den Herder, J.W.; Gao, J.R.; Cui, W. Developing X-ray Microcalorimeters Based on TiAu TES for HUBS. In Space Telescopes and Instrumentation 2020: Ultraviolet to Gamma Ray; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; SPIE: Bellingham, WA, USA, 2020; Volume 11444, p. 114449J. [Google Scholar] [CrossRef]
- Sato, K.; Ohashi, T.; Ishisaki, Y.; Ezoe, Y.; Yamada, S.; Yamasaki, N.Y.; Mitsuda, K.; Ishida, M.; Maeda, Y.; Nakashima, Y.; et al. Super DIOS mission for exploring "dark baryon". In Space Telescopes and Instrumentation 2020: Ultraviolet to Gamma Ray; den Herder, J.W.A., Nikzad, S., Nakazawa, K., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2020; Volume 11444, pp. 960–969. [Google Scholar] [CrossRef]
- Nakashima, Y.; Hirayama, F.; Kohjiro, S.; Yamamori, H.; Nagasawa, S.; Sato, A.; Yamada, S.; Hayakawa, R.; Yamasaki, N.N.; Mitsuda, K.; et al. Development of microwave multiplexer for the Super DIOS mission: 38 transition-edge sensor X-ray microcalorimeter readout with microwave multiplexing. In X-ray, Optical, and Infrared Detectors for Astronomy IX; Holland, A.D., Beletic, J., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2020; Volume 11454, pp. 186–194. [Google Scholar] [CrossRef]
- Particle Data Group; Zyla, P.A.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.-J.; Lugovsky, K.S.; Pianori, E.; et al. Review of Particle Physics. Prog. Theor. Exp. Phys. 2020, 2020, 083C01. [Google Scholar] [CrossRef]
- Aker, M.; Altenmüller, K.; Arenz, M.; Babutzka, M.; Barrett, J.; Bauer, S.; Beck, M.; Beglarian, A.; Behrens, J.; Bergmann, T.; et al. Improved Upper Limit on the Neutrino Mass from a Direct Kinematic Method by KATRIN. Phys. Rev. Lett. 2019, 123, 221802. [Google Scholar] [CrossRef]
- Camilleri, L.; Nucciotti, A. The Use of Low Temperature Detectors for Direct Measurements of the Mass of the Electron Neutrino. Adv. High Energy Phys. 2016, 2016, 9153024. [Google Scholar] [CrossRef]
- Gastaldo, L.; Blaum, K.; Chrysalidis, K.; Goodacre, T.D.; Domula, A.; Door, M.; Dorrer, H.; Düllmann, C.E.; Eberhardt, K.; Eliseev, S.; et al. The electron capture in 163Ho experiment –ECHo. Eur. Phys. J. Spec. Top. 2017, 226, 1623–1694. [Google Scholar] [CrossRef]
- Alpert, B.; Ferri, E.; Bennett, D.; Faverzani, M.; Fowler, J.; Giachero, A.; Hays-Wehle, J.; Maino, M.; Nucciotti, A.; Puiu, A.; et al. Algorithms for Identification of Nearly-Coincident Events in Calorimetric Sensors. J. Low Temp. Phys. 2016, 184, 263–273. [Google Scholar] [CrossRef]
- Ferri, E.; Alpert, B.; Bennett, D.; Faverzani, M.; Fowler, J.; Giachero, A.; Hays-Wehle, J.; Maino, M.; Nucciotti, A.; Puiu, A.; et al. Pile-Up Discrimination Algorithms for the HOLMES Experiment. J. Low Temp. Phys. 2016, 184, 405–411. [Google Scholar] [CrossRef]
- Giachero, A.; Alpert, B.; Becker, D.T.; Bennett, D.A.; Borghesi, M.; De Gerone, M.; Faverzani, M.; Fedkevych, M.; Ferri, E.; Gallucci, G.; et al. Progress in the Development of TES Microcalorimeter Detectors Suitable for Neutrino Mass Measurement. IEEE Trans. Appl. Supercond. 2021, 31, 3051104. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. CP Conservation in the Presence of Pseudoparticles. Phys. Rev. Lett. 1977, 38, 1440–1443. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. Constraints imposed by CP conservation in the presence of pseudoparticles. Phys. Rev. D 1977, 16, 1791–1797. [Google Scholar] [CrossRef]
- Jaeckel, J.; Ringwald, A. The Low-Energy Frontier of Particle Physics. Annu. Rev. Nucl. Part. Sci. 2010, 60, 405–437. [Google Scholar] [CrossRef]
- Jaeckel, J.; Thormaehlen, L.J. Distinguishing axion models with IAXO. J. Cosmol. Astropart. Phys. 2019, 2019, 039. [Google Scholar] [CrossRef]
- CAST Collaboration. New CAST limit on the axion–photon interaction. Nat. Phys. 2017, 13, 584–590. [Google Scholar] [CrossRef]
- Armengaud, E.; Avignone, F.T.; Betz, M.; Brax, P.; Brun, P.; Cantatore, G.; Carmona, J.M.; Carosi, G.P.; Caspers, F.; Caspi, S.; et al. Conceptual design of the International Axion Observatory (IAXO). J. Instrum. 2014, 9, T05002. [Google Scholar] [CrossRef]
- Abeln, A.; Altenmüller, K.; Cuendis, S.A.; Armengaud, E.; Attié, D.; Aune, S.; Basso, S.; Bergé, L.; Biasuzzi, B.; De Sousa, P.T.C.; et al. Conceptual Design of BabyIAXO, the intermediate stage towards the International Axion Observatory. arXiv 2020, arXiv:2010.12076. [Google Scholar]
- Unger, D.; Abeln, A.; Enss, C.; Fleischmann, A.; Hengstler, D.; Kempf, S.; Gastaldo, L. High-resolution for IAXO: MMC-based X-ray Detectors. arXiv 2020, arXiv:2010.15348. [Google Scholar]
- Matteo, R. Hunting Season for Primordial Gravitational Waves. APS Phys. 2020, 13, 164. [Google Scholar] [CrossRef]
- Schillaci, A.; Ade, P.A.R.; Ahmed, Z.; Amiri, M.; Barkats, D.; Thakur, R.B.; Bischoff, C.A.; Bock, J.J.; Boenish, H.; Bullock, E.; et al. Design and Performance of the First BICEP Array Receiver. J. Low Temp. Phys. 2020, 199, 976–984. [Google Scholar] [CrossRef]
- Suzuki, A.; Ade, P.; Akiba, Y.; Aleman, C.; Arnold, K.; Baccigalupi, C.; Barch, B.; Barron, D.; Bender, A.; Boettger, D.; et al. The Polarbear-2 and the Simons Array Experiments. J. Low Temp. Phys. 2016, 184, 805–810. [Google Scholar] [CrossRef]
- Hazumi, M.; Ade, P.A.; Akiba, Y.; Alonso, D.; Arnold, K.; Aumont, J.; Baccigalupi, C.; Barron, D.; Basak, S.; Beckman, S.; et al. LiteBIRD: A Satellite for the Studies of B-Mode Polarization and Inflation from Cosmic Background Radiation Detection. J. Low Temp. Phys. 2019, 194, 443–451. [Google Scholar] [CrossRef]
- Jaehnig, G.C.; Arnold, K.; Austermann, J.; Becker, D.; Duff, S.; Halverson, N.W.; Hazumi, M.; Hilton, G.; Hubmayr, J.; Lee, A.T.; et al. Development of Space-Optimized TES Bolometer Arrays for LiteBIRD. J. Low Temp. Phys. 2020, 199, 646–656. [Google Scholar] [CrossRef]
- de Haan, T.; Suzuki, A.; Boyd, S.T.P.; Cantor, R.H.; Coerver, A.; Dobbs, M.A.; Hennings-Yeomans, R.; Holzapfel, W.L.; Lee, A.T.; Noble, G.I.; et al. Recent Advances in Frequency-Multiplexed TES Readout: Vastly Reduced Parasitics and an Increase in Multiplexing Factor with Sub-Kelvin SQUIDs. J. Low Temp. Phys. 2020, 199, 754–761. [Google Scholar] [CrossRef]
- Kilbourne, C.A.; Doriese, W.B.; Bandler, S.R.; Brekosky, R.P.; Brown, A.D.; Chervenak, J.A.; Eckart, M.E.; Finkbeiner, F.M.; Hilton, G.C.; Irwin, K.D.; et al. Multiplexed readout of uniform arrays of TES X-ray microcalorimeters suitable for Constellation-X. In Space Telescopes and Instrumentation 2008: Ultraviolet to Gamma Ray; Turner, M.J.L., Flanagan, K.A., Eds.; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; SPIE: Bellingham, WA, USA, 2008; Volume 7011, p. 701104. [Google Scholar] [CrossRef]
- Smith, S.J.; Adams, J.S.; Bandler, S.R.; Betancourt-Martinez, G.; Chervenak, J.A.; Eckart, M.E.; Finkbeiner, F.M.; Kelley, R.L.; Kilbourne, C.A.; Lee, S.J.; et al. Uniformity of Kilo-Pixel Arrays of Transition-Edge Sensors for X-ray Astronomy. IEEE Trans. Appl. Supercond. 2015, 25, 2369352. [Google Scholar] [CrossRef]
- Ullom, J.N.; Adams, J.S.; Alpert, B.K.; Bandler, S.R.; Bennett, D.A.; Chaudhuri, S.; Chervenak, J.A.; Denison, E.V.; Dawson, C.; Doriese, W.B.; et al. Time- and code-division SQUID multiplexing options for ATHENA X-IFU (Conference Presentation). In Space Telescopes and Instrumentation 2018: Ultraviolet to Gamma Ray; den Herder, J.W.A., Nikzad, S., Nakazawa, K., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2018; Volume 10699. [Google Scholar] [CrossRef]
- Akamatsu, H.; Gottardi, L.; van der Kuur, J.; de Vries, C.P.; Ravensberg, K.; Adams, J.S.; Bandler, S.R.; Bruijn, M.P.; Chervenak, J.A.; Kilbourne, C.A.; et al. Development of frequency domain multiplexing for the X-ray Integral Field unit (X-IFU) on the Athena. In Space Telescopes and Instrumentation 2016: Ultraviolet to Gamma Ray; den Herder, J.W.A., Takahashi, T., Bautz, M., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2016; Volume 9905, pp. 1675–1682. [Google Scholar] [CrossRef]
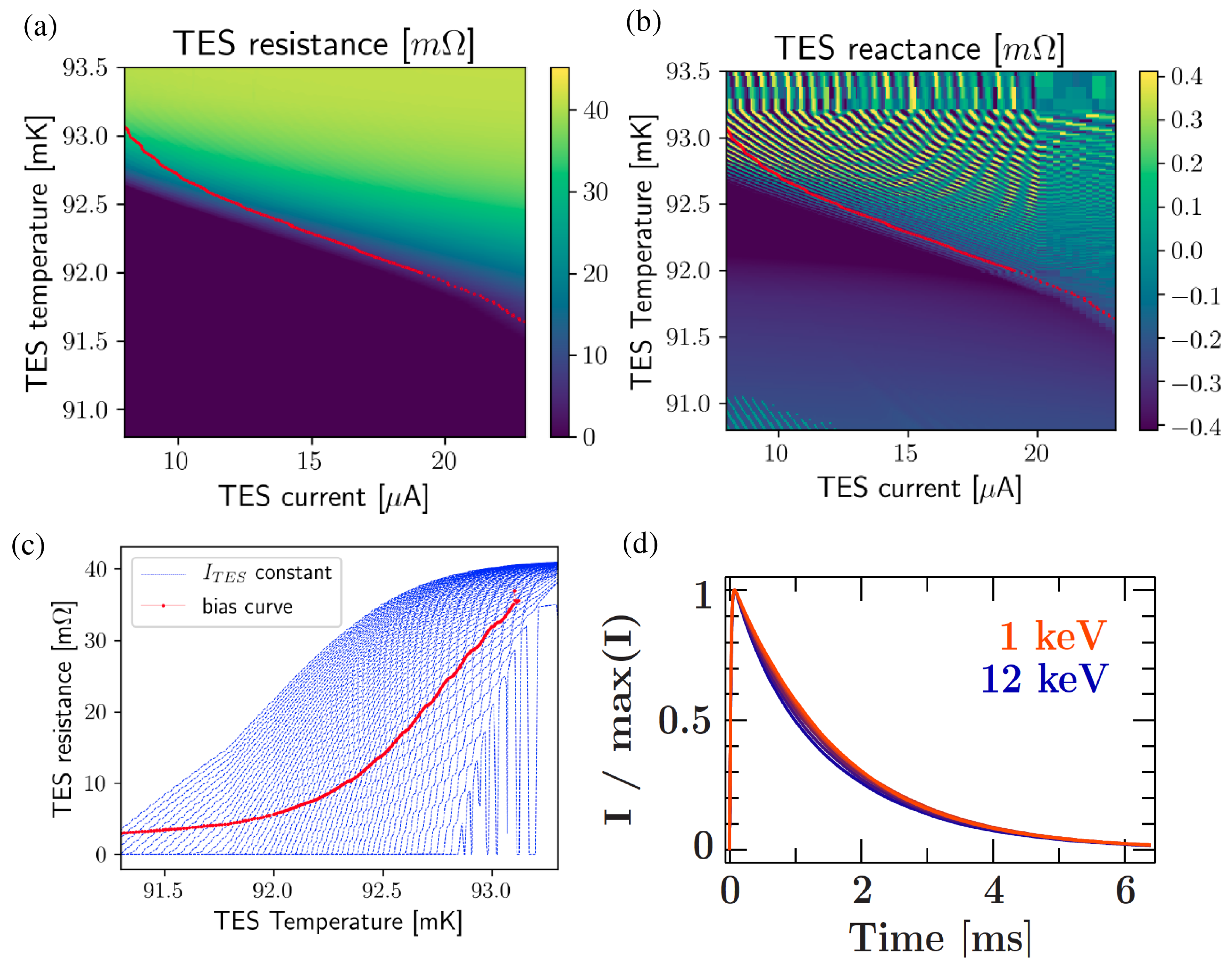
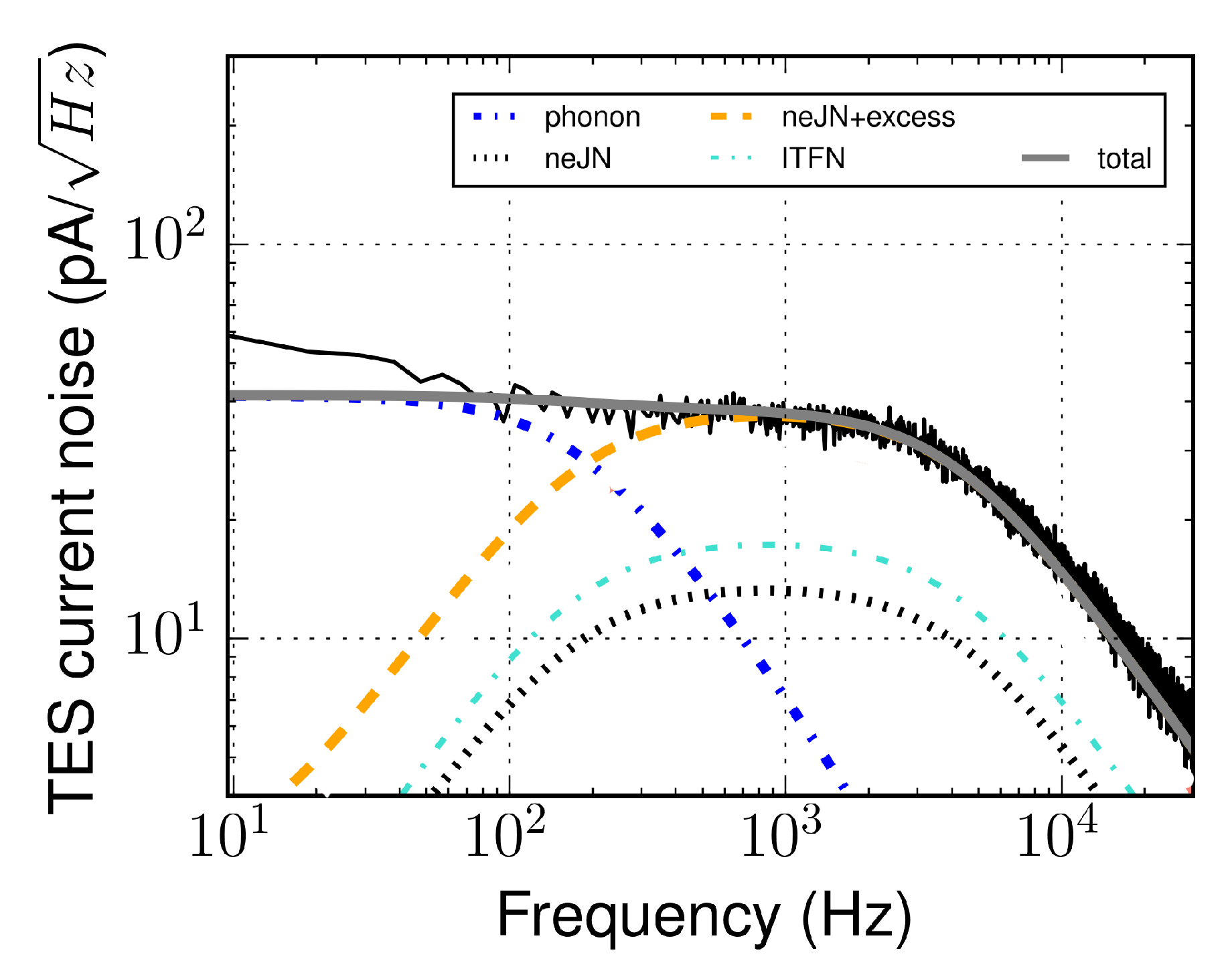
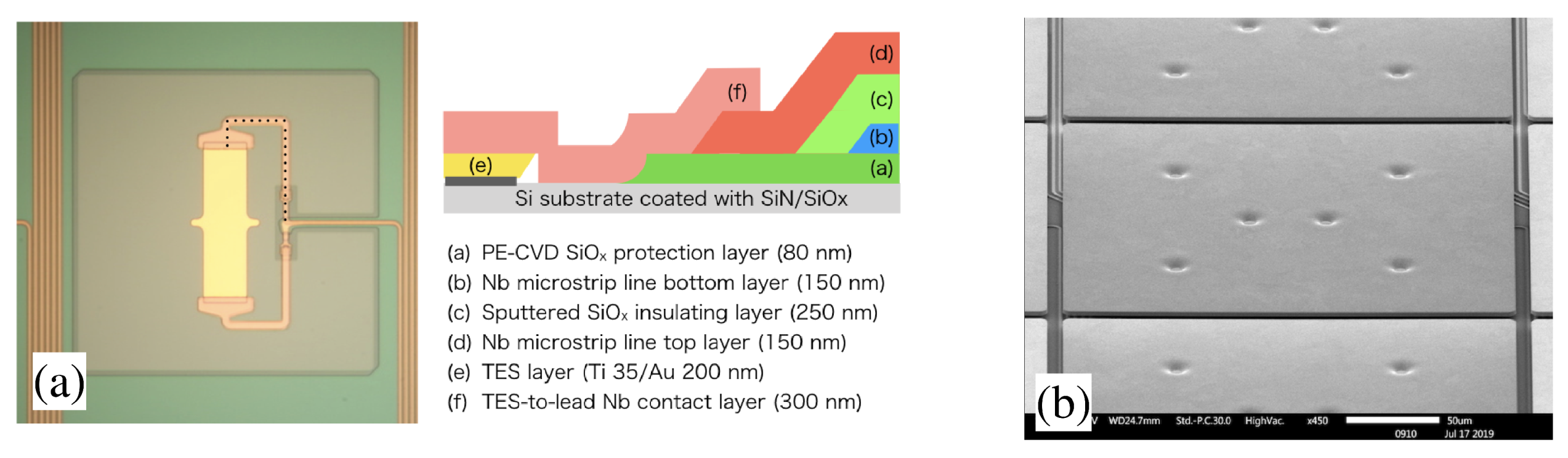

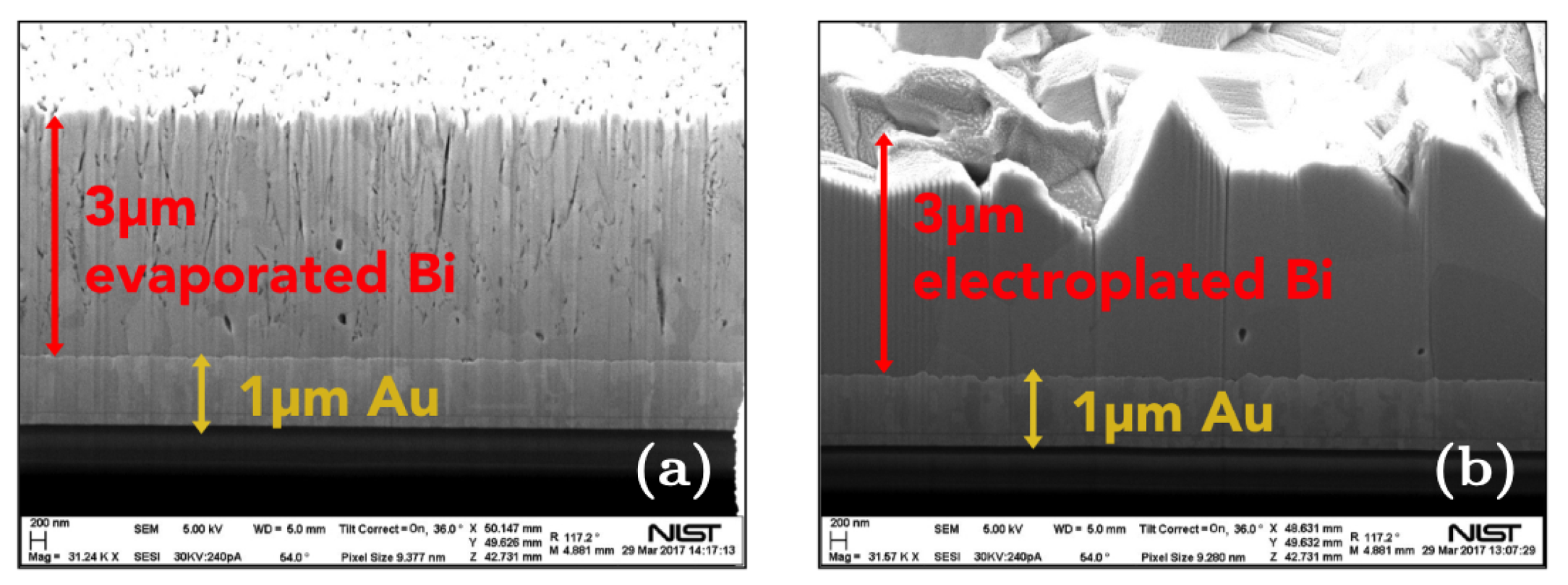
| Mission | F.o.V. | Angular Resolution | Number of Pixels | Energy | dE | Eff. Area |
|---|---|---|---|---|---|---|
| (Instrument) | arc min | arc sec | (eV) | (eV) | () @ 1 keV | |
| Athena (XIFU) | 5 | 5 | ∼3800 | 0.2–8 keV | 2–2.5 eV | 1.4 |
| HUBS | 60 | ∼60 | ∼3600 | 0.2–2 | 0.8–2 | ∼0.05 |
| Super DIOS | >30 | 0–15 | ∼30,000 | 0.2–2 | <2 eV | >0.1 |
| Lynx (LXM) | 1–5 | 0.5–1 | ∼100,000 | 0.2–7 | 0.3–3 | 0.2–2 |
| CWE | 60 | 5 | ∼1 M | 0.1–3 | 0.3 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gottardi, L.; Nagayashi, K. A Review of X-ray Microcalorimeters Based on Superconducting Transition Edge Sensors for Astrophysics and Particle Physics. Appl. Sci. 2021, 11, 3793. https://doi.org/10.3390/app11093793
Gottardi L, Nagayashi K. A Review of X-ray Microcalorimeters Based on Superconducting Transition Edge Sensors for Astrophysics and Particle Physics. Applied Sciences. 2021; 11(9):3793. https://doi.org/10.3390/app11093793
Chicago/Turabian StyleGottardi, Luciano, and Kenichiro Nagayashi. 2021. "A Review of X-ray Microcalorimeters Based on Superconducting Transition Edge Sensors for Astrophysics and Particle Physics" Applied Sciences 11, no. 9: 3793. https://doi.org/10.3390/app11093793
APA StyleGottardi, L., & Nagayashi, K. (2021). A Review of X-ray Microcalorimeters Based on Superconducting Transition Edge Sensors for Astrophysics and Particle Physics. Applied Sciences, 11(9), 3793. https://doi.org/10.3390/app11093793





