Application of a Novel Picard-Type Time-Integration Technique to the Linear and Non-Linear Dynamics of Mechanical Structures: An Exemplary Study
Abstract
1. Introduction
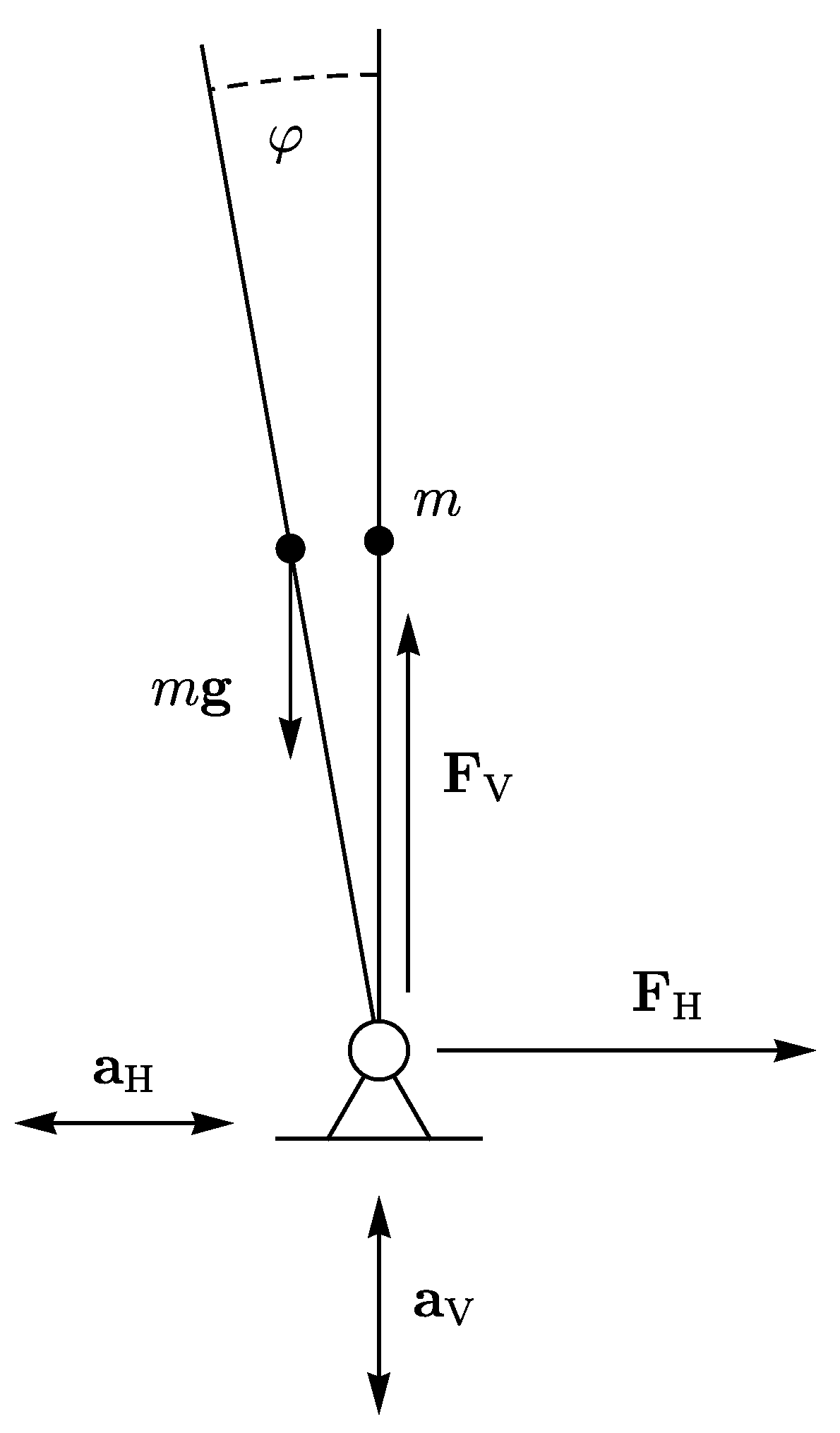
2. Rigid-Body Model of an Earthquake Excited Tower-Like Structure
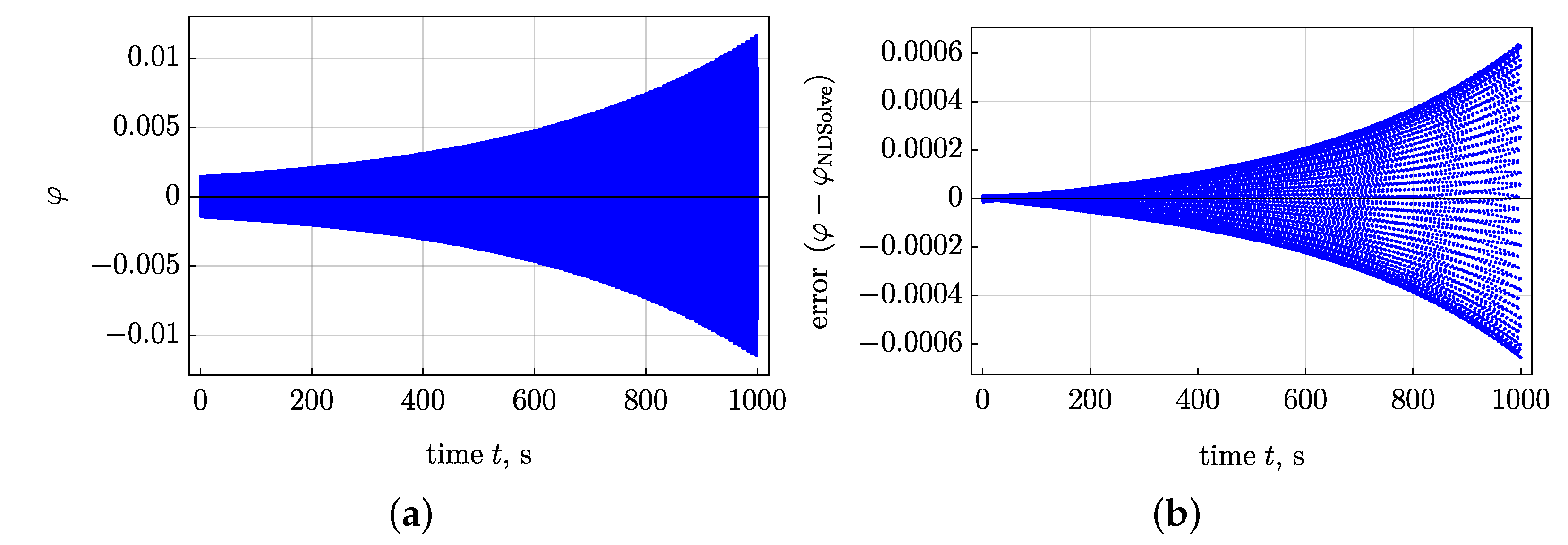
3. Oscillations under Harmonic Earthquake Excitation in Both Directions
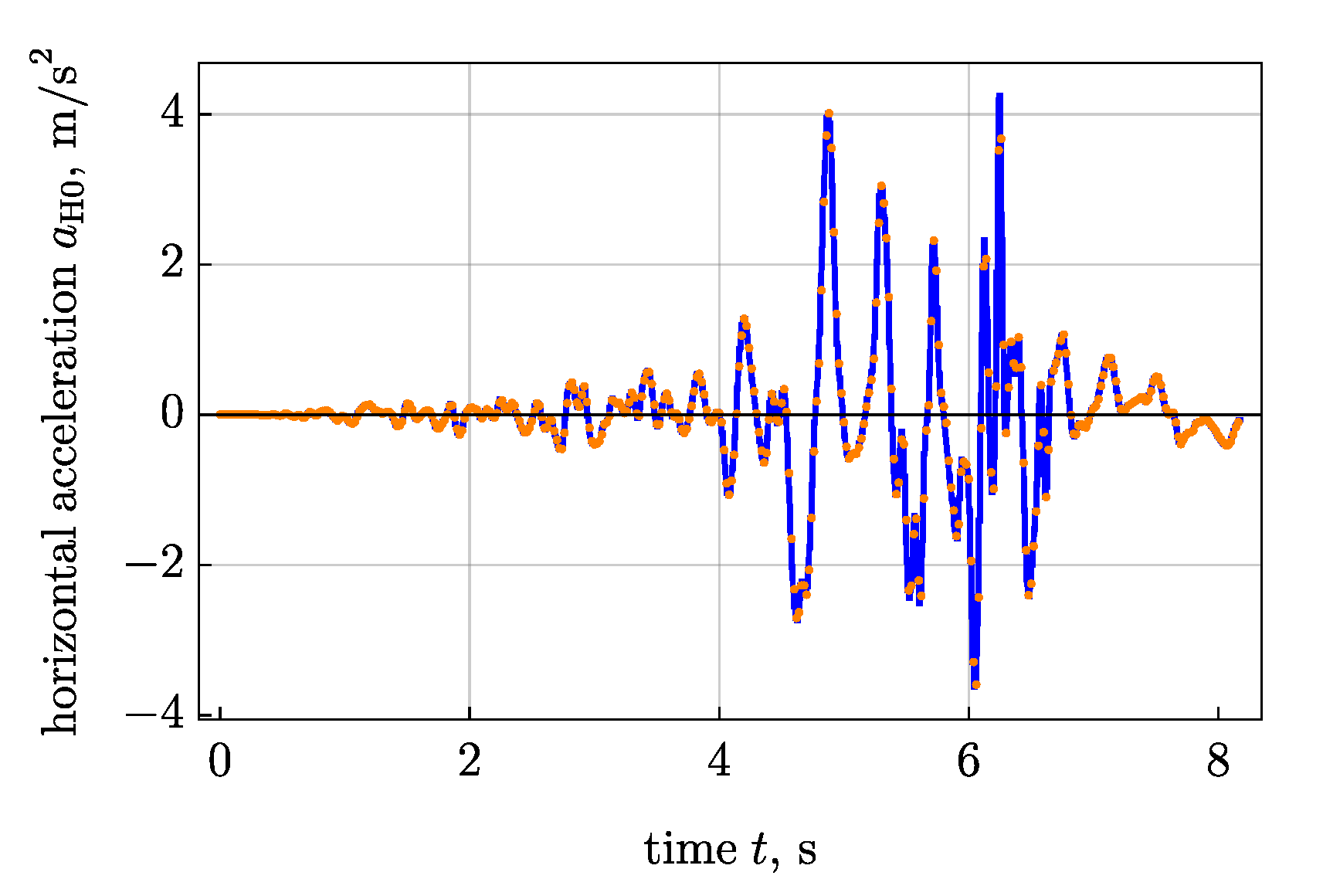
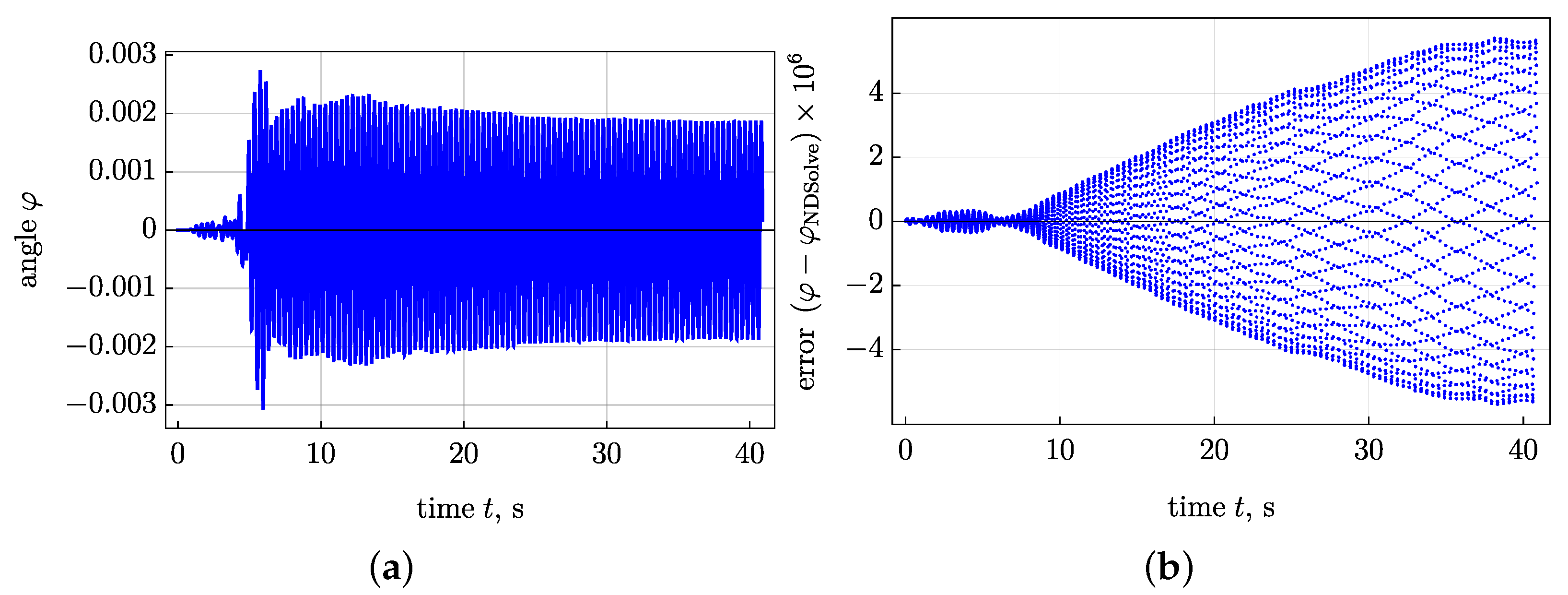
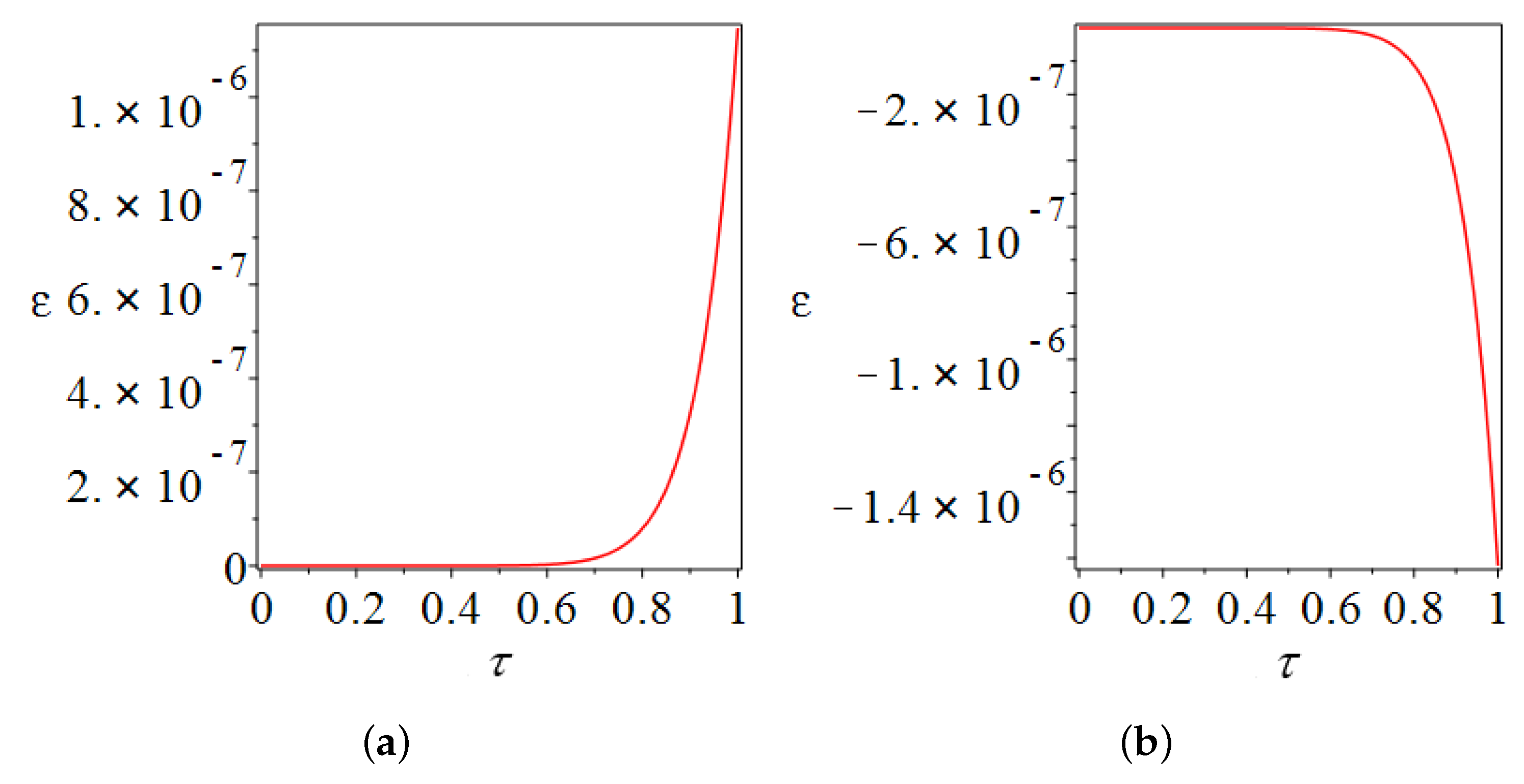
4. Numerical Results for Real Earthquakes
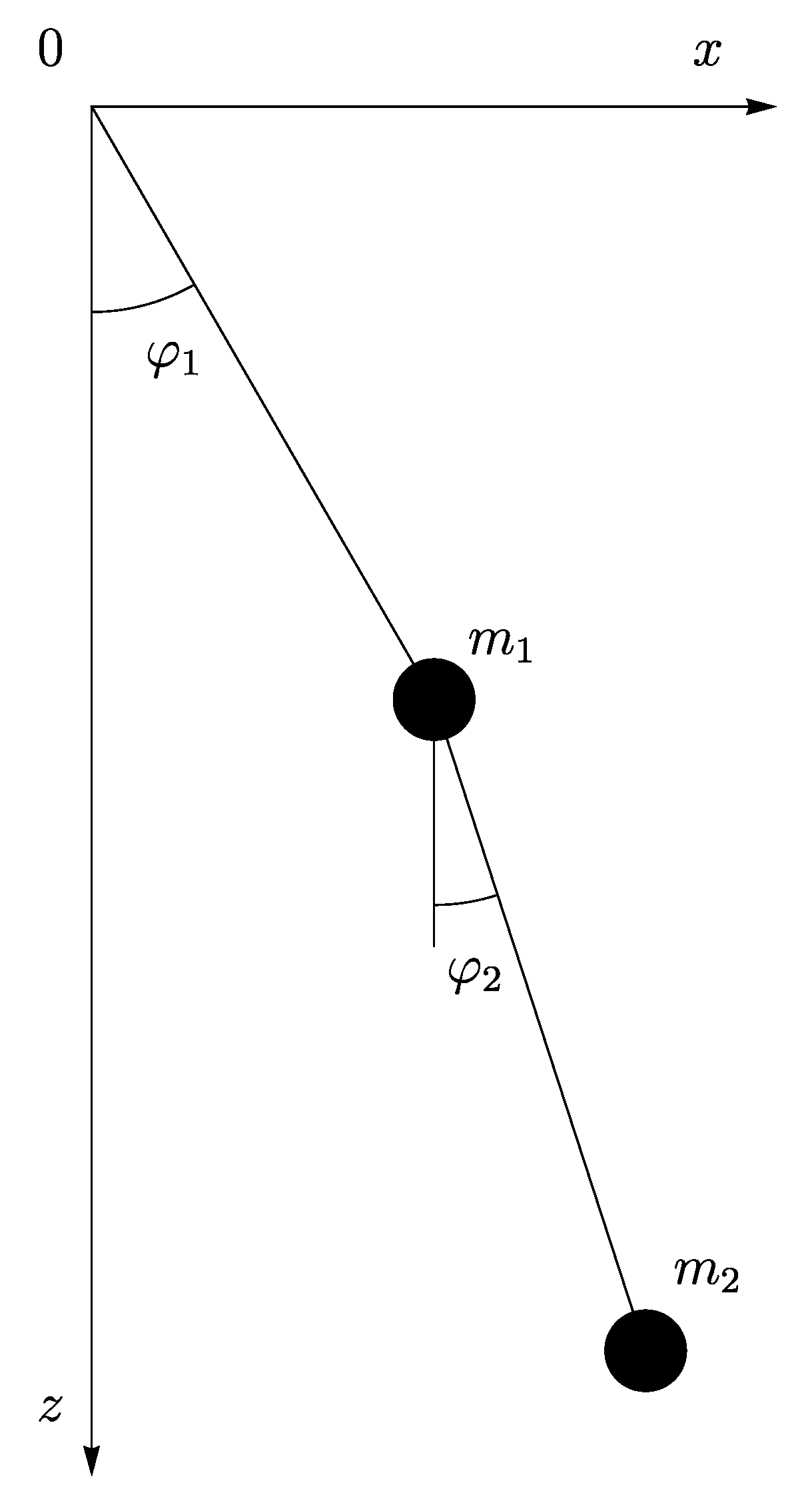
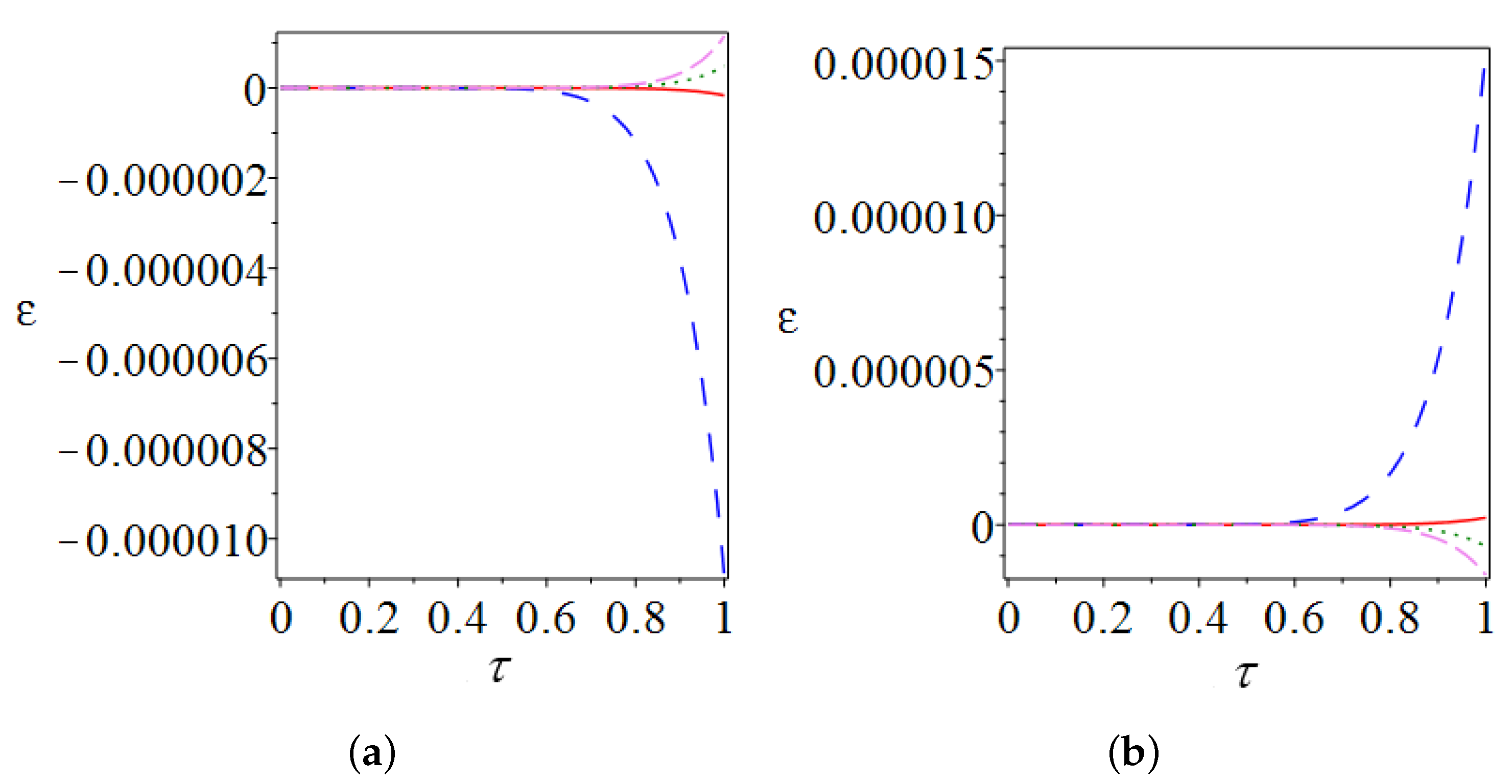
5. Double Pendulum
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Technical Details for Calculation with Harmonic Excitation
Appendix A.1. Algorithm
- Prescribe initial data.
- Define using Equation (9).
- Prescribe general initial conditions of the IVP.
- Prescribe the time step length and the number of time steps.
- Define and using Equation (11).
- Define the Runge–Kutta coefficients and formulas using Equation (15).
- Define the function that symbolically integrate polynomials.
- Symbolically integrate the truncated version of the Runge–Kutta formula.
- Add initial velocity to obtain the first iteration of .
- Symbolically integrate and add initial angle to obtain the first iteration of .
- Repeat integration to obtain a more accurate formula; in the present case, we use 3 iterations with (4, 6, 9) Taylor terms.
- Truncate the obtained formula by the third order of the Taylor series in initial conditions and of each time step.
- Compile the explicit formulas of time integration.
- Perform the iterative time-stepping method.
- Prepare graphs.
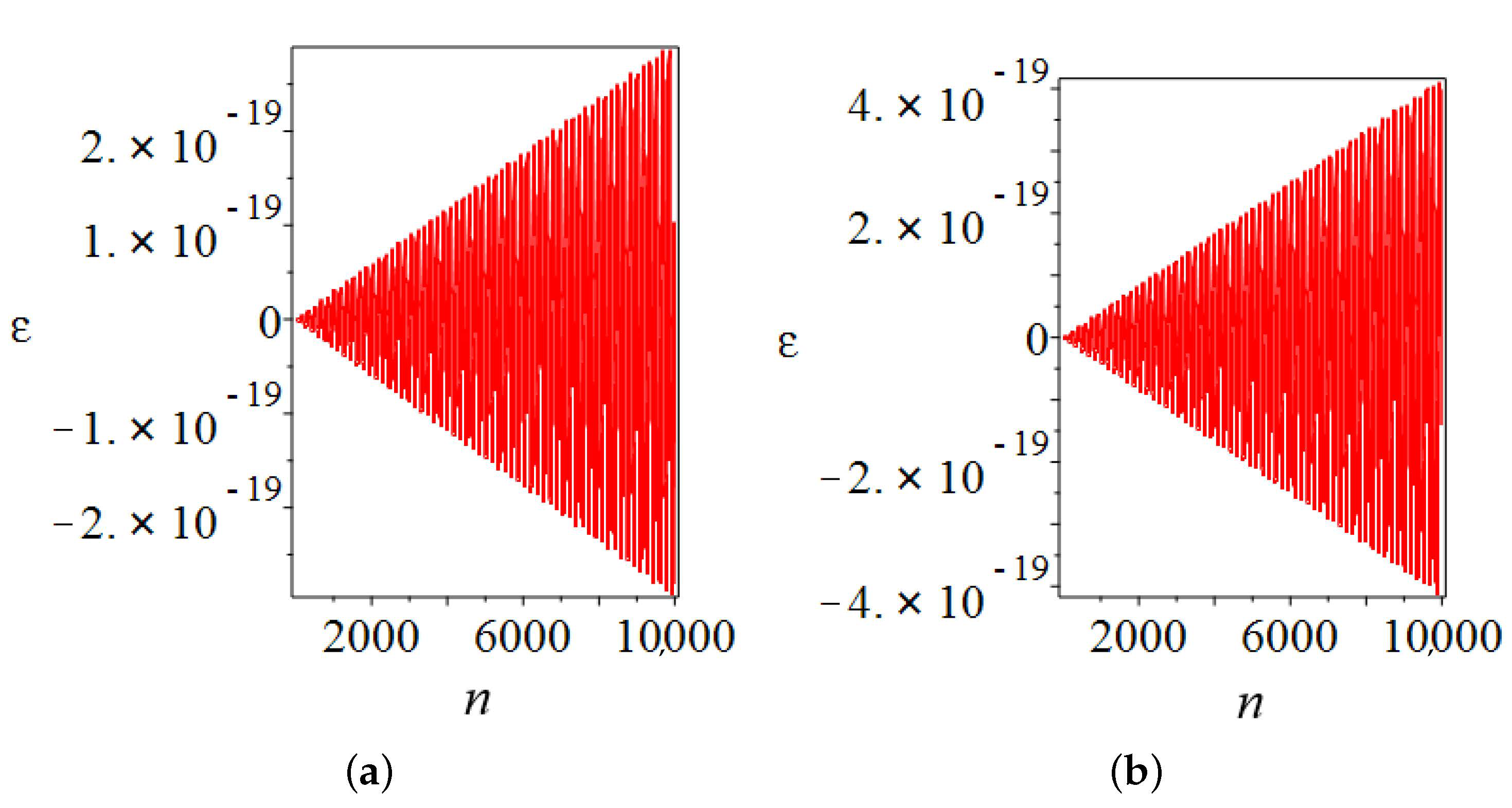
Appendix A.2. Effects of the Number of Terms of Taylor Expansion and of the Time Step
| Numbers of Taylor Terms | Computation Time | Maximum Deviation |
|---|---|---|
| 3, 5, 8 | 0.20 | |
| 4, 6, 9 | 0.20 | |
| 5, 7, 10 | 0.26 | |
| 6, 8, 11 | 0.28 | |
| 7, 9, 12 | 0.30 |
| Time Step Length | Number of Time Steps | Computation Time | Max. Deviation |
|---|---|---|---|
| 0.2 | 5000 | 0.096 | |
| 0.1 | 10,000 | 0.20 | |
| 0.05 | 20,000 | 0.45 | |
| 0.025 | 40,000 | 0.80 |
References
- Casciati, F.; Rodellar, J.; Yildirim, U. Active and semi-active control of structures—Theory and applications: A review of recent advances. J. Intell. Mat. Syst. Struct. 2012, 23, 1181–1195. [Google Scholar] [CrossRef]
- Basu, B.; Bursi, O.S.; Casciati, F.; Casciati, S.; Del Grosso, A.E.; Domaneschi, M.; Faravelli, L.; Holnicki-Szulc, J.; Irschik, H.; Krommer, M.; et al. European Association for the Control of Structures joint perspective. Recent studies in civil structural control across Europe. Struct. Control Health Monit. 2014, 21, 1414–1436. [Google Scholar] [CrossRef]
- Fei, Z.; Jinting, W.; Feng, J.; Liqiao, L. Control performance comparison between tuned liquid damper and tuned liquid column damper using real-time hybrid simulation. Earthq. Eng. Eng. Vib. 2019, 18, 695–701. [Google Scholar] [CrossRef]
- Huang, L.; Guo, T.; Chen, C.; Chen, M. Restoring force correction based on online discrete tangent stiffness estimation method for real-time hybrid simulation. Earth Eng. Eng. Vib. 2018, 17, 805–820. [Google Scholar] [CrossRef]
- Nagarajaiah, S.; Reinhom, A.M.; Constantinou, M.C. Nonlinear dynamic analysis of 3-D-base isolated structures. ASCE J. Struct. Eng. 1991, 117, 2035–2054. [Google Scholar] [CrossRef]
- Schlacher, K.; Kugi, A.; Irschik, H. Nonlinear control of earthquake excited high raised buildings by approximate disturbance decoupling. Acta Mech. 1997, 125, 49–62. [Google Scholar] [CrossRef]
- Irschik, H.; Schlacher, K.; Kugi, A. Control of earthquake excited nonlinear structures using Liapunov’s theory. Comput. Struct. 1998, 67, 83–90. [Google Scholar] [CrossRef]
- Liu, T.; Zhao, C.; Li, Q.; Zhang, L. An efficient backward Euler time-integration method for nonlinear dynamic analysis of structures. Comput. Struct. 2012, 106, 20–28. [Google Scholar] [CrossRef]
- Atmaca, B.; Yurdakul, M.; Ateş, S. Nonlinear dynamic analysis of base isolated cable-stayed bridge under earthquake excitations. Soil Dyn. Earthq. Eng. 2014, 156, 314–318. [Google Scholar] [CrossRef]
- Dastjerdi, S.; Akgöz, B. and Civalek, Ö.; Malikan, M.; Eremeyev, V.A. On the nonlinear dynamics of torus-shaped and cylindrical shell structures. J. Eng. Sci. 2020, 156, 103371. [Google Scholar] [CrossRef]
- Oborin, E.; Irschik, H. Improvement of discrete-mechanics-type time-integration schemes by utilizing balance relations in integral form together with Picard-type iterations. Int. J. Stab. Dyn. 2020, 20, 2050046. [Google Scholar] [CrossRef]
- Wolfram Research Inc. Mathematica, 12.1th ed.; Wolfram Research Inc.: Champaign, IL, USA, 2020. [Google Scholar]
- Picard, E. Sur l’application des méthodes d’approximations successives à l’étude de certaines équations différentielles ordinaires. Journal de Mathématiques Pures et Appliquées 1893, 9, 217–271. [Google Scholar]
- Irschik, H. A treatise on the equations of balance and on the jump relations in continuum mechanics. In Advanced Dynamics and Control of Structures and Machines; Irschik, H., Schlacher, K., Eds.; Springer: Vienna, Austria, 2004; Volume 444. [Google Scholar]
- Greenspan, D. A new explicit discrete mechanics with applications. J. Franklin Inst. 1972, 294, 231–240. [Google Scholar] [CrossRef]
- Hairer, E.; Norsett, S.P. Solving Ordinary Differential Equations I, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Petersen, C.; Werkle, H. Dynamik der Baukonstruktionen, 2nd ed.; Springer: Wiesbaden, Germany, 2017. [Google Scholar] [CrossRef]
- Adam, C.; Jaeger, C. Seismic collapse capacity of basic inelastic structures vulnerable to the P-delta effect. Earthq. Eng. Eng. Struct. Dyn. 2012, 41, 775–793. [Google Scholar] [CrossRef]
- Khan, N.A.; Khan, N.A.; Riaz, F. Dynamic analysis of rotating pendulum by Hamiltonian approach. Chin. J. Math. 2013, 2013, 237370. [Google Scholar] [CrossRef]
- Mazza, F.; Sisinno, S. Nonlinear dynamic behavior of base-isolated buildings with the friction pendulum system subjected to near-fault earthquakes. Mech. Based Des. Struct. Mach. 2017, 45, 331–344. [Google Scholar] [CrossRef]
- Yurchenko, D. Tuned mass and parametric pendulum dampers under seismic vibrations. In Encyclopedia of Earthquake Engineering; Beer, M., Kougioumtzoglou, I.A., Patelli, E., Au, S.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 3796–3814. [Google Scholar] [CrossRef]
- Bernardin, L.; Chin, P.; DeMarco, P.; Geddes, K.O.; Hare, D.E.G.; Heal, K.M.; Labahn, G.; May, J.P.; McCarron, J.; Monagan, M.B.; et al. Maple Programming Guide; Maplesoft: Waterloo, ON, Canada, 2020. [Google Scholar]
- Ziegler, F. Mechanics of Solids and Fluids, 2nd ed.; Springer: Vienna, Austria, 1995. [Google Scholar]
- Esper, P.; Tachibana, E. Lessons from the Kobe earthquake. Geol. Soc. Lond. Eng. Geol. Spec. Publ. 1998, 15, 105–116. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oborin, E.; Irschik, H. Application of a Novel Picard-Type Time-Integration Technique to the Linear and Non-Linear Dynamics of Mechanical Structures: An Exemplary Study. Appl. Sci. 2021, 11, 3742. https://doi.org/10.3390/app11093742
Oborin E, Irschik H. Application of a Novel Picard-Type Time-Integration Technique to the Linear and Non-Linear Dynamics of Mechanical Structures: An Exemplary Study. Applied Sciences. 2021; 11(9):3742. https://doi.org/10.3390/app11093742
Chicago/Turabian StyleOborin, Evgenii, and Hans Irschik. 2021. "Application of a Novel Picard-Type Time-Integration Technique to the Linear and Non-Linear Dynamics of Mechanical Structures: An Exemplary Study" Applied Sciences 11, no. 9: 3742. https://doi.org/10.3390/app11093742
APA StyleOborin, E., & Irschik, H. (2021). Application of a Novel Picard-Type Time-Integration Technique to the Linear and Non-Linear Dynamics of Mechanical Structures: An Exemplary Study. Applied Sciences, 11(9), 3742. https://doi.org/10.3390/app11093742






